Abstract
Brain function in “resting” state has been extensively studied with functional magnetic resonance imaging (FMRI). However, drawing valid inferences, particularly for group comparisons, is fraught with pitfalls. Differing levels of brain-wide correlations can confound group comparisons. Global signal regression (GSReg) attempts to reduce this confound and is commonly used, even though it differentially biases correlations over brain regions, potentially leading to false group differences. We propose to use average brain-wide correlations as a measure of global correlation (GCOR), and examine the circumstances under which it can be used to identify or correct for differences in global fluctuations. In the process, we show the bias induced by GSReg to be a function only of the data's covariance matrix, and use simulations to compare corrections with GCOR as covariate to GSReg under various scenarios. We find that unlike GSReg, GCOR is a conservative approach that can reduce global variations, while avoiding the introduction of false significant differences, as GSReg can. However, as with GSReg, one cannot escape the interaction effect between the grouping variable and GCOR covariate on effect size. While GCOR is a complementary measure for resting state-FMRI applicable to legacy data, it is a lesser substitute for proper level-I denoising. We also assess the applicability of GCOR to empirical data with motion-based subject grouping and compare group differences to those using GSReg. We find that, while GCOR reduced correlation differences between high and low movers, it is doubtful that motion was the sole driver behind the differences in the first place.
Key words: artifact removal, brain connectivity, functional magnetic resonance imaging, global signal regression, head motion effect, preprocessing, resting state
Introduction
Resting state functional magnetic resonance imaging (RS-FMRI) has become a very popular methodology for studying brain function with FMRI. It holds promise for understanding normal brain function and revealing brain regions involved in complex distributed disorders, such as autism (Fox and Greicius, 2010; Gotts et al., 2012). Part of the appeal of RS-FMRI is the relative ease with which the data can be acquired. However, drawing valid inferences, particularly for group comparisons, is fraught with pitfalls because of the sensitivity of the effect size to both unknown signals of interest, artifacts, and noise. A recent illustration of this difficulty was made in two publications (Power et al., 2012a; Van Dijk et al., 2012) that have caused considerable stir in the functional neuroimaging field and generated multiple responses (Carp, 2011; Power et al., 2012b; Satterthwaite et al., 2012, 2013; Yan et al., 2013). In essence, the studies showed that the presence of motion biases correlation measures and can thus, lead to false inferences when comparing groups with different levels of motion. In both of these studies and in more recent ones, the subject level preprocessing included a projection of the global brain signal average (GS) and related regressors derived by averaging the time series within tissue masks that included brain regions of interest (gray matter). The procedure is geared toward reducing overall subject-to-subject fluctuations in correlations that can be driven, in part, by different levels of physiological noise as well as motion. For example, changes in breathing depth during scanning can affect the degrees of correlation between voxels in the brain (Birn et al., 2006, 2008b; Chang and Glover, 2009; Gotts et al., 2012). However, the GSReg procedure has several drawbacks. On average, inter-voxel correlations are biased downwards, complicating the interpretation of negative correlations (Anderson et al., 2011; Fox et al., 2009; Jo et al., 2010; Murphy et al., 2009; Weissenbacher et al., 2009). More importantly, the bias introduced varies across regions in a way that depends on the covariance matrix of signals combined with noise across the brain (Saad et al., 2012b). As we show in the methods section, for an FMRI timeseries dataset of M voxels, the change in correlation between two regions is a sole function of the M×M covariance matrix of the entire dataset before GSReg was applied. When groups differ in this covariance structure (which is often part of the hypothesis being investigated), this bias will be different and can lead to group differences being propagated to regions where none actually existed. Such GSReg-induced biases might be behind the finding reported by Saad et al. (2012a) and Satterwaithe et al. (2013) that the distance-dependent motion bias on correlations between regions (Power et al., 2012a, b; Satterthwaite et al., 2012) is strongly exacerbated by the inclusion of the global brain signal average (GS) and related regressors derived by tissue-averaging in the time series preprocessing (Jo et al., 2013).
Ideally, one would estimate the noise parameters separately (perhaps from other data, such as from physiological monitoring), model their effects on the BOLD signal, and remove them from the RS-FMRI data. This is widely done for movement estimates, but unfortunately, less so for other important noise/artifact sources, such as respiration and heart rate (Bianciardi et al., 2009; Birn et al., 2008b; Chang and Glover, 2009; Glover et al., 2000; Gotts et al., 2012; Shmueli et al., 2007). For single-echo MR data, alternative methods exist to separate noise from signal sources with temporal independent or principal component decompositions (Beall, 2010; Beall and Lowe, 2007; Behzadi et al., 2007), regression of signals from soft tissue (Anderson et al., 2011), or through localized regression of eroded white matter signals (Jo et al., 2010). Newer approaches that aim to separate BOLD from non-BOLD signal components in multiecho data have also shown promise (Bright and Murphy, 2013; Kundu et al., 2012). Here we present a simple variant on the GSReg, readily applicable to existing single-echo data that can account for global correlation (GCOR) differences at the group level. To capture brain-wide correlation in a subject, we propose to compute the average pairwise Pearson correlation coefficient calculated over all possible combinations of voxels (Cole et al., 2010; Gotts et al., 2012), followed by averaging this estimate over the whole brain, resulting in one value for each subject's dataset. We show the importance of considering this subject-level measure for level-II (group) inferences, and revisit the applicability of GCOR corrections, such as GCOR and GSReg in resting-state FMRI. After an exposition of the approach, we use simulations to compare GCOR to GSReg and illustrate its advantages and limitations. Finally, we apply it to the data from two groups with differing levels of motion. In light of our empirical results, we end by discussing the relationship between motion and false inferences in resting-state FMRI and recently proposed motion-denoising approaches.
Methods
GCOR estimation and brain simulation
The GCOR measure is computed as the brain-wide average correlation over all possible combinations of voxel time series. In other terms, GCOR is the average of the entire brain correlation matrix. For a volume of M voxels, computing the entire correlation matrix requires computing a costly M(M−1)/2 correlation estimations. However, the calculation of GCOR can be markedly simplified, as shown below. (Variables are in italics or in Greek script, and matrices and vectors are in uppercase and lowercase boldface, respectively. All vectors are column-wise and all time series are de-meaned.)
Let N×1 column vectors yi(n) and yj(n) be the de-meaned observed time series at voxels i and j, respectively. The correlation between the zero-mean time series of the two voxels is given by:
rij=yiT yj/(Nσi σj)=uiTuj/N, with ui and uj being the unit-variance versions of yi and yj, respectively, and N the number of time samples. For brevity, the time index n is dropped and N is used instead of the (N-1) needed for an unbiased correlation estimate. The full M×M correlation matrix R can thus, be expressed as a function of the zero-mean and unit-variance N×M time series matrix U as:
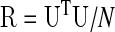 |
GCOR (γ) is the average of all correlations in R, therefore:
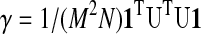 |
(1) |
=1/NguTgu, where 1 is an M×1 column of ones, and gu=1/M U 1 is the average of all unit variance time series in U.
As a result of Equation 1, the computation of the brain-wide average correlation is trivial; it is the average dot product of the average unit-variance time series. In practice, as part of AFNI's (Cox, 1996) processing stream, we estimate GCOR as follows:
(1) De-mean each voxel's time series and scale it by its Eucledian norm
(2) Average scaled time series over the whole brain mask
(3) GCOR is the length (L2 norm) of this averaged series
Correlations after GSReg are entirely predictable from data covariance
It is also instructive to reconsider the effect of applying GSReg on the correlation matrix in a more generalized manner than carried out by Saad et al. (2012b).* In the following, we will show that the correlation matrix after GSReg is a function only of the covariance matrix before GSReg. In keeping with the earlier notation, ym is an N×1 column vector of the de-meaned observed time series at voxel m in a volume of M voxels in total. The global signal regressor g is defined in terms of Y, the N×M data matrix of all de-meaned time series by: g=Yα, with α being an M×1 vector of 1/M. After GSReg, the signal at voxel m is given by:*
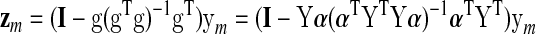 |
We simplify the notation by setting K=Y α (αT YTY α)−1 αT YT and write the data matrix after GSReg as: Z=(I–K)Y. (N.B.: K is an orthogonal symmetric projection matrix.)
The covariance matrix of the data P= 1/N YTY becomes Q=1/N ZTZ, after GSReg. Expanding, Q becomes:
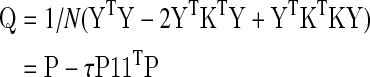 |
(2) |
where scalars τ=1/(M2 μP), μP=(1TP1)/M2 is the average of the covariance matrix and 1 is an M×1 vector of ones. The diagonals of P and Q contain the variance of each voxel's time series before and after GSReg, respectively. Letting σP and σQ be column vectors of the inverse square root of the diagonals of P and Q, respectively, we can express the correlation matrix after GSReg as:
S=Q * σQσQT, with * being the Hadamard (element wise) matrix product. The change in the correlation matrix after GSReg becomes:
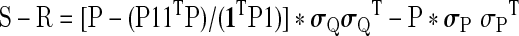 |
(3) |
In words, for any set of time series, the change in correlation after GSReg varies throughout the matrix and is entirely predictable from the initial covariance matrix of that data.
Simulated brain model
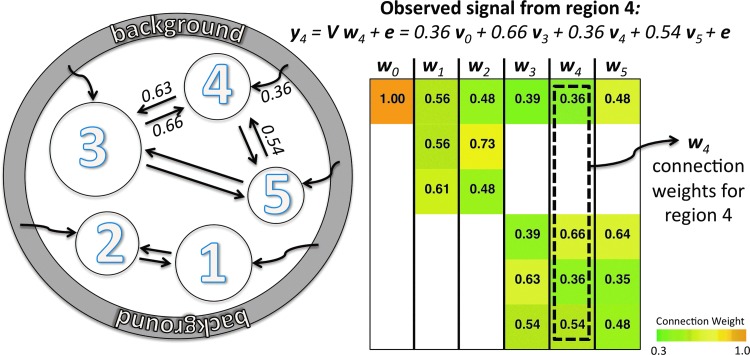
To describe impacts of GCOR and GSReg on level-II inference, we resort to simulations using a model where the brain is modeled as a set of K-1 interconnected regions with each region k, occupying a fraction αk of the whole brain, being Mαk voxels in size. Each region k produces its own representative (characteristic) latent signal vk, and the observed signal yk at voxels within region k is a weighted sum of the latent signals of all areas, plus a global signal source and random white noise. To simplify the notation, we include the background source (such as respiration fluctuations) in the model as the region at k=0 and which has no voxels (αo=0). More formally, yk=Vwk+e, with V being the N×K matrix of latent Gaussian N(0,1) white noise independent and identically distributed (i.i.d) signals, and wk a column vector containing the connection weights from each region to region k. e is Gaussian white noise N(0,0.5), i.i.d. across voxels. The collection of connection weight vectors forms the latent connectivity matrix W (not necessarily symmetric). We illustrate the generative model in Figure 1 with a background (outer ring, region 0) and only 5 regions (circular areas 1 to 5) for simplicity. Arrows between a pair of regions indicate a nonzero weight in the latent connectivity matrix W shown to the right. The connection weights are annotated for some of the connections in the model and on W's cells. For example, the observed signal from region 4 is given by the equation shown for y4. The model's purpose is to generate various groups of correlation matrices R. In the analyses discussed herein, models were varied from a default instance by changing: (1) the amount of global signal present, using a parameter controlling the top row of W, and/or (2) the connection weights between regions 1 and 2. Models also differed in the density of connections in W: in the reported results, we used either fully connected models, or a sparsely connected one (e.g., as illustrated in Fig. 1). In all the models considered, the background contributes signal to all the regions. We denote fully or sparsely connected control models with Ψ, additional suffixes indicate variations on Ψ with increased global background “B”, localized increased connection “L”, or both “BL”. For each model variation (groups), we generated 30 instances (the equivalent of subjects). The entire set of observed time series for each model and each subject is collected in the N×M “data” matrix Y, from which the covariance and correlation matrices, P and R, were computed per the equations above.
FIG. 1.
Generative model used to simulate time series with differing correlation structures. The model consists of 10 regions, only 6 of which are shown here for simplicity and region 0 is reserved for the background (outer ring). Arrows between a pair of regions indicate a nonzero weight in the latent connectivity matrix W shown to the right. The connection weights are annotated for some of the connections in the model and on W's cells. The observed signal from region 4 is given by the equation for y4.
Level-II models
In this work, we judge the outcome of corrections for GCORs by the effect on level-II analysis, and illustrate what happens to the mean correlations and mean correlation differences in one and two sample t-tests under different scenarios. The three linear models tested were as follows:
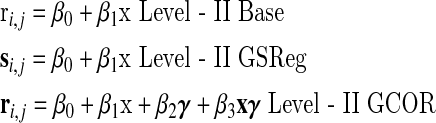 |
with x a binary vector encoding for subject grouping, γ a vector of GCOR values from all subjects. For equivalent one sample tests we drop all the terms involving x. The models are solved at each i,j cell of the correlation matrices using the “lm” function in the statistical computational environment R (R Development Core Team, 2008). We are performing tests on group changes in correlations between each voxel m (seed) and the rest of the model brain. Those results are displayed in an M×M matrix, where each column m contains the group mean (β0) or group mean differences (β1) in correlation with a seed at voxel m and the other voxels in the brain. β2 and β3 are covariate effects. Each column is one brain correlation group mean or mean difference map. Note that all of ri,j, and si,j are Fisher z-transformed correlations with unit correlations clamped at 0.999. Except where explicitly stated, GCOR covariates were centered on the global mean over the two groups. Note that, while both Level-II GSReg and GCOR models attempt to adjust for subject-to-subject GCOR differences, they do so at different stages of the analysis. With GSReg adjustment is carried out at the single-subject processing stage whereby the correlation estimate is obtained after projecting the GS from the time series, while with GCOR the adjustment is made at the group level test by adding GCOR as a covariate.
The tests on simulated data are constructed around the following scheme: we begin with a control group Ψ, then create a new group ΨL with local manipulations to the weighting matrix for regions 1 and 2, but no change in the background contributions. The level-II Base contrast in correlations between Ψ and ΨL is the gold standard: the true correlation differences between the two groups in the absence of differences in background contributions. We then fit models level-II GSReg and level-II GCOR and compare the contrasts to those of the gold standard. Ideally, for ΨL−Ψ those results would not differ, since there are no background correlation changes between the groups, and therefore, nothing to be corrected. We then create a new group ΨBL with the same local manipulations for regions 1 and 2, and increased background contribution. We perform the same three level-II tests and examine the extent to which the corrections, now that there are background changes between the groups, can recover the ideal contrast.
Empirical data and preprocessing pipeline
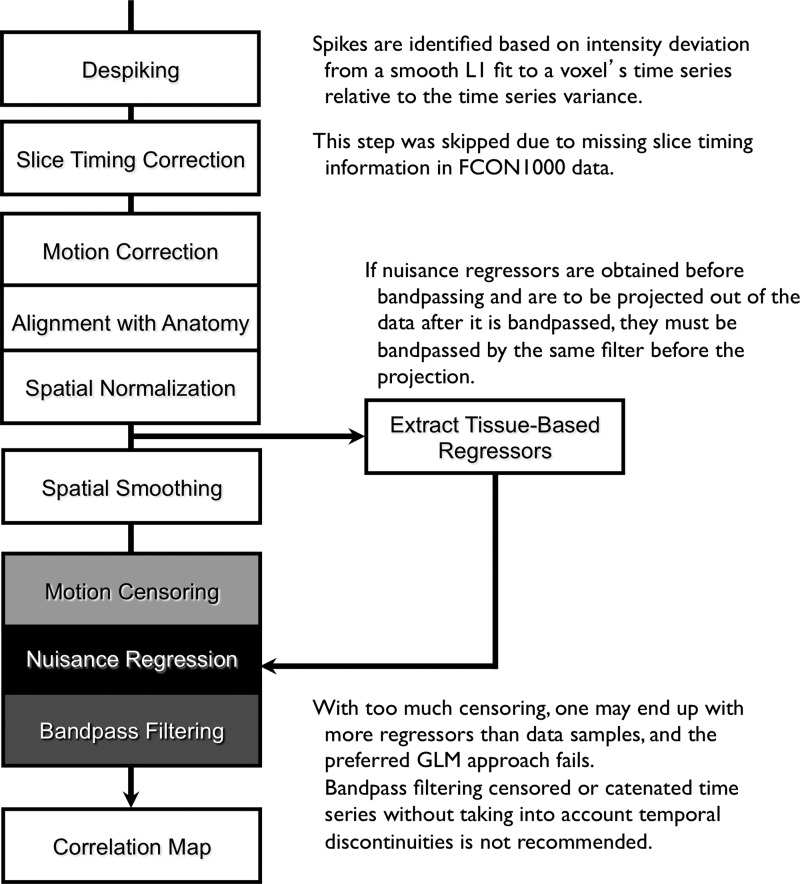
For an empirical consideration of GCORs, particularly as they relate to subject motion, we used two single-site collections of data from the FCON1000 dataset (Biswal et al., 2010) (http://fcon_1000.projects.nitrc.org/) that were comparable in size to the sub-groups used in the study by Van Dijk et al. (2012). The Cambridge_Buckner and Beijing_Zang sets were the largest with 184 and 156 subjects, respectively.† Similar to the methods of Van Dijk et al. (2012), we split the subjects from each site into two groups based on the average amount of inter-TR displacement during a run. The processing steps were similar to those outlined in Figure 2 and differed somewhat from those outlined in Van Dijk et al. (2012); however, for the purposes of this study, those differences did not qualitatively affect the results. A more expansive presentation of the processing steps can be found in Jo et al. (2013).
FIG. 2.
Annotated processing flowchart for resting state functional magnetic resonance imaging (RS-FMRI) analyses used in this study (and the currently implemented pipeline in AFNI).
Despiking and slice-timing correction
Despiking (AFNI's “3dDespike”) was the first step of the preprocessing pipeline to suppress local spikes in the signals due to hardware instability or to motion. Each voxel's time series is L1 fit to a Fourier series of order L, defaulting to L=N/30. The median absolute deviation (MAD) of the residuals is used to obtain a standard deviation estimate σ=1.4826 MAD that is robust to outliers. A spike is identifed where the residual at a particular time exceeds 2.5σ. Despiking consists of transforming spike values from the range of [2.5σ, ∞) to [2.5σ, 4σ)–the purpose of this gradual mapping is to make the despiking procedure be a continuous function of the data. In addition to reducing the contribution of sudden spikes to correlation estimates, we also found that despiking improved the convergence at the volume registration step (Jo et al., 2013). Slice-timing correction was not performed in these datasets since the NIfTI-1 formatted files contained no slice timing information.
Motion correction, spatial normalization, and spatial smoothing
Motion correction was done by rigid body registration of EPI images to a base EPI volume. Alignment of EPI data to the T1-weighted volume was accomplished via an affine transformation (Saad et al., 2009), as was the spatial nomalization of the T1-weighted volume to the MNI avg152 T1 template, in MNI stereotaxic coordinates. All three affine transformations were multiplied, and then applied at once to the original EPI data to prevent multiple resampling steps. Time points with excessive motion were flagged using ||d||2, the L2 norm of the first differences of motion estimates. This criterion is part of AFNI's standard processing stream, and while not identical to the frame-wise displacement in Power et al. (2012a) and similar variants (Jenkinson et al., 2002; Satterthwaite et al., 2013), it serves the same function. At a ||d||2 threshold of 0.2 mm (in a single TR), we censored on average 2.9% of the time series (0% and 32.8% at minimum and maximum, respectively). Data were subsequently spatially smoothed with an isotropic Gaussian smoothing kernel (full-width-at-half-maximum, FWHM=6 mm).
Simultaneous nuisance-removal, censoring, and bandpass filtering
The default regression model used here contains 6 motion estimates (angles and translations) and their first difference terms only. Variants include the addition of the global signal, the global signal's first difference, and second order versions of motion estimates and their first differences. Note that when tissue-based regressors, such as the global signal are to be used, they must be extracted before spatial smoothing and must be subject to the same bandpass filtering, if any, that was applied to the time series at the point of nuisance regression. Otherwise, frequency components in stop bands will be introduced back via the regressors of no interest. Here bandpass filtering, censoring, and nuisance-removal regression were done simultaneously. By combining these three subprocesses in one linear regression model, there is no conflict between bandpassing and censoring.
Individual correlation maps for DMN and Group Statistics
Subjects were separated into two subgroups (high- and low-motion groups) by 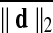 , the average of ||d||2 across time frames. There were 92 and 78 subjects in each group from the Cambridge-Buckner and Beijing_Zang cohorts, respectively. For each subject, Fisher z-transformed (Fisher, 1915) Pearson correlation volumes were computed using a seed time series extracted from a voxel in the Posterior Cingulate Cortex (PCC) located at (MNI 4L, 55P, 26S) mm in the MNI stereotaxic coordinate system (Greicius et al., 2003). After preprocessing and PCC seed correlations, we performed two-sample t-tests with or without GSReg and subject-level covariates, comparing correlations between the groups of largest and smallest movers. PCC locations from other studies [i.e., (Van Dijk et al., 2012)] yielded similar results. Other groupings, based on
, the average of ||d||2 across time frames. There were 92 and 78 subjects in each group from the Cambridge-Buckner and Beijing_Zang cohorts, respectively. For each subject, Fisher z-transformed (Fisher, 1915) Pearson correlation volumes were computed using a seed time series extracted from a voxel in the Posterior Cingulate Cortex (PCC) located at (MNI 4L, 55P, 26S) mm in the MNI stereotaxic coordinate system (Greicius et al., 2003). After preprocessing and PCC seed correlations, we performed two-sample t-tests with or without GSReg and subject-level covariates, comparing correlations between the groups of largest and smallest movers. PCC locations from other studies [i.e., (Van Dijk et al., 2012)] yielded similar results. Other groupings, based on 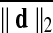 were also considered. In addition to the Big (top 50%) versus Small movers, we also split each population into quartiles with the first quartile comprising subjects with the top 25% of
were also considered. In addition to the Big (top 50%) versus Small movers, we also split each population into quartiles with the first quartile comprising subjects with the top 25% of 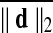 . Lastly to consider group contrasts under comparable amounts of movement, we rearranged subjects into two equally sized groups in a manner that minimized group averaged difference of
. Lastly to consider group contrasts under comparable amounts of movement, we rearranged subjects into two equally sized groups in a manner that minimized group averaged difference of 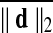 .
.
Results
GCOR in simulated brain
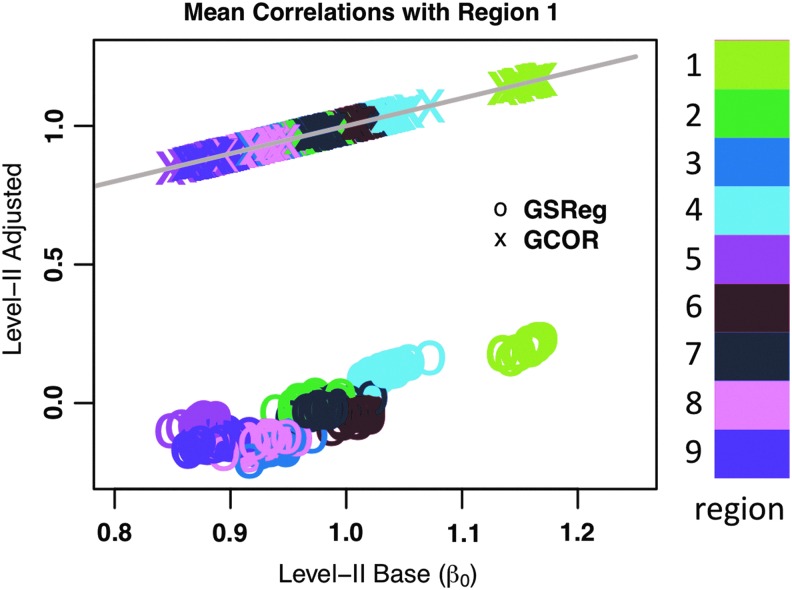
In what follows we compare group mean and mean difference in correlations between all region pairs in our simulated brain model. We begin by comparing mean correlations from the three level-II models with one sample t-tests on group Ψ created with a weighting matrix with fully interconnected regions. For the models simulated, correlation between any voxel pair is significantly different from zero. We focus first on how correlation values change under the three level-II models. Figure 3 is a scatterplot of group mean correlations (β0) under model Level-II Base (gold standard, x-axis), versus those from Level-II GSReg and Level-II GCOR. For clarity, only correlations with a seed from region 1 are shown. Correlations with voxels from a particular region are color-coded; “o”s are for group mean correlations after GSReg, and “×”s are for group mean correlations with GCOR (Level-II GCOR). The plot is a graphical depiction of what Equation 3 prescribes, that after GSReg the correlations are altered differently at different region pairs—that is, the GSReg correlations are not just a shifted-down version of the original values—in a manner entirely predetermined by the initial covariance of the data. With GCOR, the correlations are unchanged in the one sample t-test. A similar picture emerges for the seed placed in any other region of the simulated brain.
FIG. 3.
A scatterplot of group mean correlations (β0), under model Level-II Base (gold standard, x-axis), versus those from Level-II Global Signal Regression (GSReg) and Level-II Global Correlation (GCOR). Similar colors show correlations of the seed from region 1 with voxels from a particular region; “o”s are for correlations after GSReg (si,j), “×”s are for correlations with GCOR (ri,j, Level-II CGOR), and gray is for the x=y line.
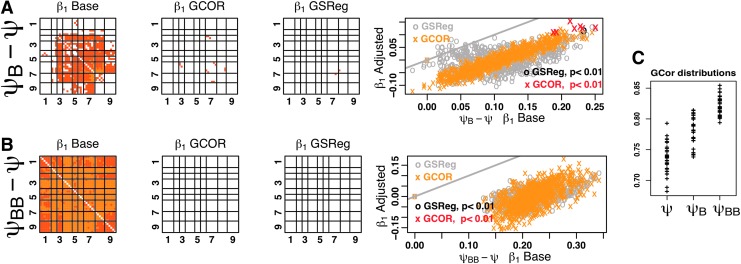
In all that follows, we consider what happens to means of correlation differences (β1) between two groups. For the first example, we consider two groups Ψ versus ΨB that differed only by the amount of background correlation. To generate ΨB, we uniformly increased the values in the first row of weights matrix W used for Ψ. This resulted in stronger fluctuations from the background source in group ΨB in all regions of the model. Naturally, when contrasting inter-regional correlations between the two groups, significant differences are ubiquitous as shown by the correlation contrast matrix (Fig. 4, ΨB–Ψ β1 Base). Axis labels and the black vertical and horizontal lines delineate the boundaries of the 9 regions forming the model. Each pixel in the matrix is colored to reflect the difference (β1) in Fisher z- transformed correlations between a voxel pair in the first group and the same pair in the second group. Contrasts that failed to reach significance at p<0.01, Bonferroni corrected for the number of region pairs, were not colored. To draw a parallel with brain imaging displays, each column m of the matrix represents the group contrast volume obtained with the seed time series taken from voxel m.
FIG. 4.
(A) Correlation contrast (β1) matrices from Level-II models Base, GCOR, and GSReg for the two groups Ψ and ΨB. Each pixel in the matrix is colored to reflect the difference in Fisher z-transformed correlations between a voxel pair in the first group and the same pair in the second group (β1). Contrasts that failed to reach significance at Bonferroni corrected p<0.01 were not colored. The scatter plot graph shows correlation difference obtained under Level-II GCOR (“×”s) and Level-II GSReg (“o”s) versus the difference from model Level-II Base. Here as in the remaining plots, differences from all voxel pairs are plotted and significant difference are highlighted with starker colors. Under Level-II GCOR significant differences are in red, while sub-threshold ones are in orange. Under Level-II GSReg significant differences are in black, while sub-threshold differences are in gray. The gray line marks x=y. (B) Distribution of GCOR values for groups Ψ, ΨB, and ΨBB. (C) Same as A, but for groups Ψ and ΨBB.
Since the only difference between the groups Ψ and ΨB was the background induced change in correlation, the ideal background adjusted contrast result should show no significant difference in inter-regional correlations. As the contrast matrices in the top row show, both of Level-II GCOR and Level-II GSReg show very few regions with significant differences. To consider the effects of the different approaches on the estimated correlation differences, we also graph the correlation difference obtained under Level-II GCOR (“×”s) and Level-II GSReg (“o”s) versus the difference from model Level-II Base. Compared to the default model, both GSReg and GCOR result in smaller correlation differences between Ψ and ΨB. However, the change with GSReg is considerably more variable than with GCOR and for some regions the correlation differences were higher than in the base model where background changes were ignored. In contrast, correlations differences with GCOR model were more linearly dependent on the initial correlation differences. It is important to note at this stage that the results from Level-II GCOR would change markedly if the covariate distribution in group ΨB is markedly offset from that of group Ψ. To illustrate, we generate another group ΨBB with background contribution weight increased by 0.6 relative to Ψ instead of 0.3 in group ΨB. Figure 4B shows the distributions of the GCOR values for the three groups Ψ, ΨB, and ΨBB. Row C in Figure 4 shows the results with ΨBB substituting for ΨB. Correlation matrices showed similar behavior as with the lower background increase (Fig. 4A); however, the correlation difference estimates became more variable under GCOR, reflecting the increasing correlation between the covariate and the grouping variable. The standard deviation of the residuals from a linear fit of β1 Adjusted to β1 Base increased five-fold in Figure 4C relative to Figure 4A. When background-induced correlations differ markedly between groups, the use of either GCOR as a covariate or GSReg can mask existing group differences.
Next, we examine level-II outcomes when focal changes in connection strengths exist between the two groups. To do so we increased the connection weights between regions 1 and 2 to generate group ΨL. We emphasize that this focal increase in connection weights does not necessarily result in correlation changes restricted to the regions with weight change. Changing the connection weight between regions 1 and 2 can also change the correlation of region 2 with other connected regions in the model in a manner that depends on the other weights in W. The partial derivative of the correlation between regions with respect to a change in one of the weights depends, in part, on other connection weights to this area. For example, the partial derivative of the expected correlation between voxels in regions 1 and 2 with respect to w1,2 is given by: w1,1/(σ1σ2)−(w1,2 w2Tw1)/(σ1σ23). Nonintuitively, the change in correlation between two regions can be positive or negative with an increase in a connection between them, depending on the initial connection weights. One can alter the weighting matrix W such that a focal weight change results in a focal correlation change between the affected region pair by disconnecting the two regions from everything but themselves and the background. We consider both scenarios in what follows, beginning with the widely connected W matrix that was also used for the data in Figure 5A.
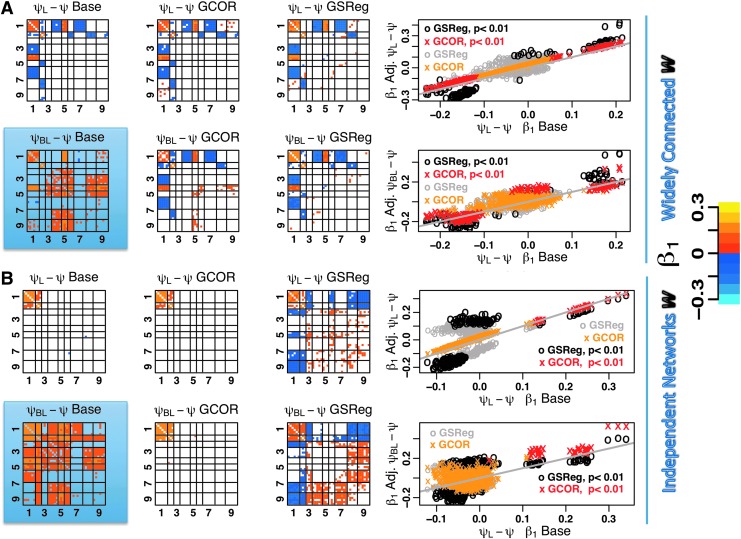
FIG. 5.
Group contrast matrices and corresponding scatter plots for widely connected models (A) and models with independent networks (B). The top row in each panel shows contrasts between groups Ψ and ΨL where only connections between regions 1 and 2 were increased. The second row shows contrasts between Ψ and ΨBL in which both local and background connections were increased. Shaded matrices show significant contrasts when background levels are different between groups but no corrections are applied. The x-axis in the scatter plots is the ideal contrast (from the top left matrix ΨL–Ψ Base) one wishes to recover after adjusting for global correlation differences with GSReg or GCOR. Coloring conventions follow those of Figure 4.
For group ΨL, we increased the two connection weights between regions 1 and 2, and carried out the computations up to and including the Level-II two-sample t-tests. The first matrix shows the correlation difference between two groups in the absence of background level differences. The results in this matrix constitute the “gold standard” correlation differences between ΨL and Ψ, and what one hopes to recover when differences in background signal levels are equalized. In this simulation, using the fully connected weighting matrix, we find that the increase in w1,2 and w2,1 resulted in significant increases in correlations of voxels in region 1 and region 2. There were also significant positive and negative changes in correlations between region 1 and regions 3, 4, and 6, and between region 2 and regions 5 and 7. A similar pattern emerges with level-II GCOR test (ΨL–Ψ GCOR) as shown in the second matrix in row 1. With level-II GSReg test (ΨL–Ψ GSReg), the pattern was also similar albeit with more accentuated differences in both directions. The change in effect size, the magnitude of the average correlation difference, with level-II models is more evident in the scatter plot of correlation difference under Level-II GSReg and GCOR versus the gold standard difference from ΨL–Ψ Base. As in the previous simulations, the differences with GCOR are more linearly dependent on those from the ideal base model, while those with GSReg were considerably less so. Nonetheless the regions showing significant differences were comparable to those of the gold standard. In the next simulation, shown in row 2, we created another group ΨBL where both background and local weights w1,2 and w2,1 were increased. As in the case with no difference in background levels, both GCOR and GSReg identify regions with significant correlation differences that are comparable with those from the ideal case. The correlation contrast matrix showing ΨBL–Ψ from the Base level II test is shaded as it now represents a contrast of no interest since no correction for background fluctuations was carried out.
A different picture emerges if we repeat the previous comparisons with a different generative model, where regions 1 and 2 are made independent from the remaining regions by severing their input from and output to all other regions, except for input from the background. The results, as shown in Figure 5B, are arrayed in the same manner as those for the widely connected models. For the ideal case, the average correlation matrices now show significant differences only between regions 1 and 2. This difference is recovered with level-II GCOR (row 3, ΨL–Ψ GCOR). However, the results from level-II GSReg (row 3, ΨL–Ψ GSReg) are markedly different with significant correlation differences appearing between region 1 and regions 3, 7, and 9, for example, where no correlation differences existed. The scatter plot still shows that overall; the difference estimates under GCOR are more linearly dependent on the ideal difference compared to GSReg. Comparing the estimates for ΨBL and Ψ, where the differences are from increases from both local connections and widespread background connections, GCOR does recover the regions with significant changes in correlation, while GSReg distorts the results considerably.
It is important to note from the scatter plots that both GCOR and GSReg bias correlation differences in a manner that depends on the initial covariance structure of the data. While this has been shown in closed form for the GSReg estimates in Equation 3, differential biasing also occurs when the covariate is derived from the same data in the regions of interest.
GCOR and head motion in empirical data
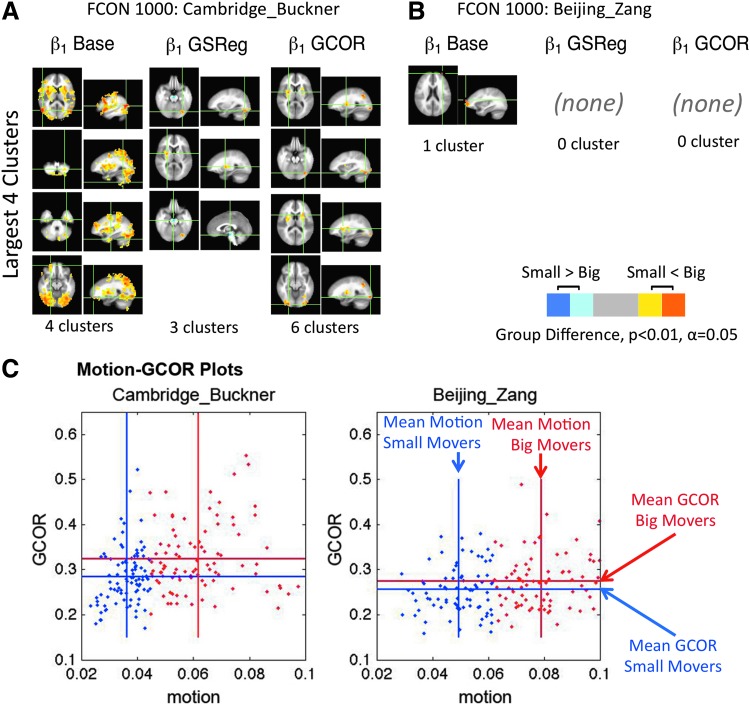
The above simulations showed that, while GSReg can help in attenuating GCOR differences between groups, it does so at the risk of introducing significant correlations and correlation differences where none may have existed before—and there is no obvious way to detect if this effect is present in any given dataset. In contrast, regressing GCOR in the Level-II analyses adjusted for differences in GCORs with fewer distortions. Turning to the empirical data, we now examine the three level-II models to alleviate GCOR differences induced, presumably or at least, in part, by head motion. Figure 6 shows the results of the high- versus low-movers group contrasts in real data from FCON-1000 projects (http://fcon_1000.projects.nitrc.org). Figure 6A shows group differences from the Cambridge set. The first column is from preprocessing that includes motion regressors only—without GSReg and without the GCOR covariate at the t-test level (Level-II Base). The contrast yielded false positives when no true positives would have been expected from this (presumably) uniform population of subjects. The t-test result from the data was quite dramatic: four clusters covering a volume of 412,209 mm3 (15,267 voxels) were observed (uncorrected p<0.01, FWE corrected α<0.05 (Saad et al., 2006), |t(182)|>2.575).‡ The results were markedly different when adding GSReg to the preprocessing (Fig. 6A, Column β1 GSReg), with a considerable reduction in the extent of regions showing significant differences. Using GCOR as a covariate at the group level, the reduction was also considerable as with the GSReg case compared to Level-II+GSReg (Fig. 6A, Column β1 GCOR). Figure 6B shows similar tests conducted with the Beijing_Zang set. The contrast in the first column, without GSReg and GCOR, resulted in just one significant cluster that barely met the relatively liberal statistical threshold; that cluster had 92 voxels when the cutoff for FWE correction was at 79 voxels (see Fig. 6B, Column β1 Base). Using GSReg or GCOR resulted in no significant differences between top and bottom movers.
FIG. 6.
(A) Two sample t-tests of group differences in correlations with a seed in the default mode network (Binder et al., 1999; Greicius et al., 2003). The two groups were formed from the Cambridge_Buckner portion of the FCON1000 dataset by splitting an otherwise homogenous group into the upper and lower 50% of movers. Time points of resting state EPI data with per-TR motion exceeding 0.2 mm were censored. Column β1 Base shows results from Level-II Base, where preprocessing included the six motion estimates and their derivatives. In column β1 GSReg, the global signal was added as a nuisance regressor in preprocessing. Column β1 GCOR is from data preprocessed the same way as for β1 Base, but the per-subject brain-wide average correlation (global correlation; GCOR) was used as a scalar covariate for the group analysis. Group differences were thresholded at an FWE-corrected significance level of 0.05. For each column only the largest 4 clusters are displayed. (B) Results from the Beijing_Zang set of FCON1000 data paralleling those of A. (C) Scatter plots of subject average motion versus GCOR. Blue and red dots show values from subjects in the bottom and top moving groups, respectively. For each group, vertical bars show the average amount of motion and horizontal bars show the average GCOR.
On average, GCOR is greater in subjects with more motion (Beijing_Zang; 29 μm average motion difference per TR, average ΔGCOR=0.02: t(154)=2.10, p=0.037; Cambridge_Buckner; 25 μm average motion difference per TR, average ΔGCOR=0.04: t(182)=3.91, p=0.00013); however, the correlation between GCOR and average motion is relatively weak (Beijing_Zang: R2=4.3%; Cambridge_Buckner: R2=11.0%) as shown in Figure 6C.
We also considered alternative random subject groupings, where the average motion difference was selected to be negligible (<0.1 μm), with group result tests summarized in Table 1 and Supplementary Figure S1 (Supplementary Data are available online at www.liebertpub.com/brain). Though not reliably present (practically none in the Cambridge_Buckner set if one corrects for the repeated testing, an average of 1 per grouping in the Beijing_Zang set), clusters generated from these groupings were comparable in size to those observed under the extreme motion difference grouping (see Table 2and Fig. 6A, B), once subject-to-subject fluctuations were accounted for with GSReg or GCOR.
Table 1.
Two-Sample t-Test Results Between Pseudo-Random Subgroups
| |
|
|
β1 Base |
β1 GSReg |
β1 GCOR |
|||
|---|---|---|---|---|---|---|---|---|
| Data set | Pseudo-random subgroups |
Group average difference in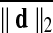 (mm) (mm)
|
Clusters | Voxels | Clusters | Voxels | Clusters | Voxels |
| FCON 1000: Cambridge_Buckner (N=184) | Set #01 | <0.0001 | 2 | 599 | 1 | 129 | 4 | 963 |
| Set #02 | <0.0001 | - | - | - | - | - | - | |
| Set #03 | <0.0001 | - | - | - | - | - | - | |
| Set #04 | <0.0001 | 1 | 112 | - | - | - | - | |
| Set #05 | <0.0001 | - | - | - | - | 3 | 268 | |
| FCON 1000: Beijing_Zang (N=156) | Set #01 | <0.0001 | - | - | 1 | 161 | - | - |
| Set #02 | <0.0001 | - | - | 1 | 100 | - | - | |
| Set #03 | <0.0001 | - | - | - | - | - | - | |
| Set #04 | <0.0001 | 1 | 116 | 1 | 227 | 1 | 160 | |
| Set #05 | <0.0001 | 1 | 97 | 1 | 122 | - | - | |
The seed location is in the left posterior cingulate cortex (PCC) at [4L, 55P, 26S] mm in MNI coordinates. The threshold level is FWE-corrected α<0.05. In column β1 Base, low order polynomials and motion estimates were the only nuisance regressors. In column β1 GSReg, the global signal regressor (GS) was added as a nuisance regressor. In column β1 GCOR, the global correlation averaged over the brain mask (GCOR) was added as a subject level covariate in the t-test.
Table 2.
Two Sample t-Test Results Between Motion-Based Groupings
| |
|
|
β1 Base |
β1 GSReg |
β1 GCOR |
|||
|---|---|---|---|---|---|---|---|---|
| Data set | Subgroups |
Group Average Difference in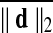 (mm) (mm)
|
Clusters | Voxels | Clusters | Voxels | Clusters | Voxels |
| FCON 1000: Cambridge_Buckner (N=184) | Big vs. small movers | 0.025 | 4 | 15,267 | 3 | 352 | 6 | 692 |
| Quartiles 1 vs. 2 | 0.0195 | 1 | 88 | 2 | 259 | 1 | 83 | |
| Quartiles 2 vs. 3 | 0.01 | 8 | 1,575 | 2 | 200 | 2 | 326 | |
| Quartiles 3 vs. 4 | 0.0091 | - | - | - | - | - | - | |
| FCON 1000: Beijing_Zang (N=156) | Big vs. Small Movers | 0.0292 | 1 | 92 | - | - | - | - |
| Quartiles 1 vs. 2 | 0.0174 | - | - | - | - | - | - | |
| Quartiles 2 vs. 3 | 0.0131 | - | - | - | - | - | - | |
| Quartiles 3 vs. 4 | 0.0147 | - | - | - | - | - | - | |
For comparisons named “Big versus Small Movers,” subjects are evenly divided into two subgroups by the levels of 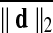 . For “Quartiles” comparisons, subjects are evenly divided into four subgroups by
. For “Quartiles” comparisons, subjects are evenly divided into four subgroups by 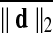 . Quartile 1 contains the subjects having the biggest head movements, and Quartile 4 includes the subjects having smallest head movements. The seed location is in the left posterior cingulate cortex (PCC) at [4L, 55P, 26S] mm in MNI coordinates. The threshold level is FWE-corrected α<0.05.
. Quartile 1 contains the subjects having the biggest head movements, and Quartile 4 includes the subjects having smallest head movements. The seed location is in the left posterior cingulate cortex (PCC) at [4L, 55P, 26S] mm in MNI coordinates. The threshold level is FWE-corrected α<0.05.
Discussion
Noise and brain-wide fluctuations
In this paper, we are considering that fluctuations in GCOR are dominated by nuisance sources, not emanating from the regions for which we seek to estimate correlation structure or more critically correlation structure changes, present to varying degrees throughout the brain, and therefore, warrant correction. (However, in some cases GCOR differences might largely be the result of differing functional connectivity between the regions of interest. Under such scenarios, correcting for GCOR difference would be ill advised.) One such proxy for a nuisance/noise source is end-tidal CO2 fluctuations known to strongly affect correlations, which as such would need to be eliminated (Birn et al., 2006; Chang and Glover, 2009; Gotts et al., 2012; Wise et al., 2004). Such a noise source is temporally coherent across the brain and can therefore, affect correlation levels between regions throughout the brain. Motion might also be considered such a noise source, to the extent that its effect on the signal is also coherent across wide regions of the brain. The most commonly used approaches for handling such noise sources involve linearly projecting models of their effect on the BOLD signal. Modeling physiological contributions, however, typically requires the acquisition of physiological parameters during the scan. Absent such recordings, one can rely on semi-ad hoc techniques to separate noise from signal (Beall, 2010; Kundu et al., 2012; Smith et al., 2012), or attempt to capture spatially coherent noise with the global signal (GS) and project it from the data as a nuisance regressor (GSReg). The GS can certainly reflect some noise fluctuations, and GSReg can render two groups with differing breathing depths (for example) more comparable, with correlations and correlation differences more consistent across scan runs and subjects (Fox et al., 2009; Satterthwaite et al., 2012; Yan et al., 2013). However, GSreg comes at a cost that cannot be ignored, and while the case against GSReg has been made in various forms, we are compelled to expand on it further because of its continued recommended use—in some cases, being requested by journal referees. Global nuisance fluctuations in correlation can also be measured with GCOR and in this work we explored whether or not it can be used to correct for brain-wide correlations in fluctuations.
Why not GSReg?
Given the common (and well-motivated) drive to use GSReg, we begin by addressing the following question that arises from the empirical results in Figure 6: If GSReg removed false positives between low and high moving groups, why do we recommend against its use? The principal reason we disparage its use has little to do with the increase in negative correlations (Fox et al., 2009; Murphy et al., 2009), the discarding of useful neuronal information potentially present in this average (Leopold and Maier, 2012; Scholvinck et al., 2010), or the uncertainty about the degree to which the GS captures noise induced features, such as motion, respiration, etc. Rather, the use of GSReg is particularly problematic when comparing groups with expected differences in the spatial structure of signal correlation Gotts et al., 2013. It is widely acknowledged that correlations are negatively biased on average with the use of GS regression; however, the crucial observation that this bias is variable between regions and fully dependent on the original covariance structure due to signal and noise is often ignored (Saad et al., 2012b)—and it is usually regional differences in correlations that are of interest in group studies. Adding unknown and potentially group-dependent biases to the correlations is a bad idea. In a single group, where it is reasonable to assume the same noise-free spatial correlation structure, this variable bias might be of less concern. However, single group tests are rarely the goal of resting state studies. Indeed, resting state studies that compare groups and whose principal hypotheses and results are predicated on there being differences in correlation structure between the groups, are precisely the case in which the inappropriate bias is most problematic. For the empirical data in this study, these distortions were not as much a cause for concern in the two-sample t-tests because the two groups are not expected to differ in their true inter-regional correlation patterns, since the groups were selected only based on their subjects' level of head motion. However, the GSReg-induced distortions could vary differently when groups have differing correlation structures (Saad et al., 2012b), not just a global change in common fluctuations [see Gotts et al. (2013), for a detailed example in the case of Autism Spectrum Disorders]. GSReg can then introduce differences between regions where none actually exists between the groups (or can mask differences that do exist). This can be seen from the closed form expression of correlation bias caused by GSReg (Eq. 3) and is best exemplified by the results in Figure 5, where the projection of the GS introduced correlation differences between the rest of the simulated brain and regions 1 and 2 where none existed before. Given the group contrast after GSReg, one is led to very different conclusions about brain connectivity changes than what was built into the model.
Naturally, the effect of applying GSReg depends on the underlying generative model. We have shown here that with a widely inter-connected model, GSReg level-II results recover the expected differences (Fig. 4); however, the results are markedly different when the changes are between relatively isolated (and here independent) sets of regions. We emphasize the obvious, that the generative models used here are very simple, but they are informative nonetheless. For example, in a highly connected model, changing the weight between only two regions can potentially result in correlation changes throughout the brain, particularly when one is not limited by SNR. The level-II changes one observes empirically are considerably more focal, and if the sparse nature of the differences is not due to high type-II errors, one would be inclined toward favoring more sparsely connected models where GSReg is particularly problematic.
Should GCOR always be used to correct for brain-wide correlation differences?
We have shown that GCOR, the average of the brain-wide correlation matrix, can be readily estimated from the time series data. This measure reflects brain-wide changes in correlation levels and as such it is tempting to consider it as a covariate at the group level to compensate for brain-wide correlation differences between groups of subjects that are mostly driven by nuisance sources. With GCOR used as a covariate centered on the overall (across both groups) mean, one can estimate group differences at the same level of GCOR. With GSReg, the average correlation across the brain is always zero in both groups; however, even though the average correlation is matched after GSReg, the process is mathematically different from covariate modeling at level-II. As with all applications of covariates, centering outside the range of observed values, is ill advised. Therefore, centering at GCOR of 0 is inappropriate, as a zero center would be distant from most GCOR values and the results would not be interpretable. For GCOR to be used as a covariate, it will be necessary for GCOR values to overlap considerably between the two groups. In cases with little overlap, the covariate becomes more correlated with the grouping variable and can easily mask true group differences. This makes GCOR conservative compared to GSReg, in the sense of reducing false positives. However, even under instances where GCOR distributions overlap between groups, there will always be an interaction between the GCOR variable and the grouping variable, if the two populations have different underlying correlation patterns. Thus, the magnitude of differences (effect size), including the sign, can be affected by the centering value. The same criticism carries to the use of GSReg; however, with GCOR, regions with significant group differences are more closely related to those expected under ideal cases compared with GSReg. Nonetheless, interpreting the magnitude of the correlation differences, whether using GSReg or using GCOR, can be misleading; with decreases appearing as increases and vice versa.
In the empirical case considered, here there was considerable overlap in GCOR distributions between the high and low moving groups in both cases, making the use of GCOR acceptable. However, if we consider a case where one population's breathing patterns differs markedly from the other, resulting in GCOR distributions with little overlap, GCOR's use as a covariate would mask any underlying group differences. Thus, one can say that the more one needs to equalize GCORs across groups, the less useable GCOR would be because it would eliminate true group differences. With GSReg, however, the comparison under these circumstances would yield significant differences that may be artifactual. At the very least, GCOR is useful in assessing the types of differences that exist between the two populations. Correcting for global changes in correlation is best carried out with time-series denoising procedures that do not entangle nuisance estimates with signals from the regions of interest. To draw parallels with the simulations, if one could sample the signal from the background source, it could much more safely be projected out of the data to correct for background signal differences. Though not carried out in this study for lack of data (physiological measures were not provided for the FCON1000 Cambridge and Beijing sets), physiological denoising is highly recommended, as physiological noise differences are certain to affect correlations over wide regions of cortex and can lead to false RS-FMRI inferences and/or Type II errors (Gotts et al., 2012). Adding the average inter-TR motion as another covariate is safe and should not eliminate true differences, as long as this covariate is also not highly correlated with the grouping variable.
Small motion differences are not a likely source of significant false positives
At first blush, the results in Figure 6 confirm the conclusions first presented by Van Dijk et al. (2012) that motion differences results in false positives, when comparing groups with systematically differing levels of motion. However, further probing invites more nuanced conclusions. With no GCOR or GSReg corrections, the same contrast between top and bottom movers using the Beijing_Zang set resulted in only one significant cluster that barely met the relatively liberal statistical threshold. This finding was quite surprising, since in the Beijing_Zang set the average difference in motion between top and bottom movers was larger (29 μm) than in the Cambridge_Buckner set (25 μm). Despite differences in image acquisition that might explain some of this discrepancy, it is difficult to reconcile these two findings if motion per se were the prominent driver of the spurious results under these groupings. As acknowledged in Satterthwaite et al. (2013), one does not know with certainty that resultant differences at the group level are driven by motion difference, despite motion being the grouping variable. In an effort to understand the factors behind this discrepancy between the two sets, we examined single-subject correlation results and found some to have markedly increased correlations compared to others. It is such differences that motivate the use of the GS as a nuisance regressor in the literature. Indeed, as shown earlier, either, including the GS as a regressor of no interest in the preprocessing stage or using GCOR as a covariate at the group level also greatly reduced the difference between top and bottom movers in the Cambridge_Buckner set and eliminated the one cluster in the Beijing_Zang set.§
These results show that the false positives are driven to a considerable extent by sources that can be captured with the GCOR measure as a covariate or by regressing out the GS. Such global measures (1 number or 1 time-series per subject) are unlikely to capture the spatially varying effects of motion considerably better than the 6, 12, or 24 regressors (Satterthwaite et al., 2013) used to model the motion, even if all these models fail to account for spin-history effects of motion. In fact, we find that in high motion datasets, correlation estimates with GSReg become more sensitive to the effect of motion (Jo et al., 2013). On average, GCOR is greater in subjects with more motion, although the correlation between GCOR and average motion is relatively weak. These global measures are likely also reflecting a combination of brain-wide fluctuations, both neuronal in origin (Leopold and Maier, 2012; Scholvinck et al., 2010), and signal changes related to breathing or heart rate changes (Beall, 2010; Bianciardi et al., 2009; Birn et al., 2008a; Birn et al., 2008b; Chang et al., 2009; Chang and Glover, 2009; Shmueli et al., 2007). To be clear, we are not suggesting that differences in motion cannot lead to false positives, as motion certainly biases correlation measures. However, the effect is not so pronounced that small differences in motion between groups, such as those considered here would necessarily result in significant group differences in correlation if appropriate preprocessing steps and/or group-level covariates have been applied. Further supporting this notion, is the appearance of above-threshold false positive clusters under alternative groupings where the average motion difference was negligible. Rather, we suspect the differences are more likely driven by differences in noise of physiological origins.
These results are a mixed blessing in that small differences in motion between groups are not necessarily cause for great concern. However, they also point to the importance of proper physiological denoising (Beall, 2010; Bianciardi et al., 2009; Birn et al., 2008a, 2008b; Chang et al., 2009; Chang and Glover, 2009; Shmueli et al., 2007; Wong et al., 2012) for group-level resting-state inferences, a practice that receives significantly less attention (to date) than GSreg. To ascertain properly whether or not minute motion differences can lead to false positives, we would require a dataset acquired with physiological recordings of respiration and heart rate, along with comparable data acquired with pulse sequences that lessen the effects of motion on the acquired volumes; thus, allowing for a more careful parcellation of noise sources. Denoising procedures that utilize external physiological measurements (Birn et al., 2008b; Chang et al., 2009; Glover et al. 2000; Shmueli et al., 2007) or that can decompose the data into noise and signal sources (Kundu et al., 2012) are important for reliable inferences from RS-FMRI data.
Degree-of-freedom loss
Despite our hesitation in ascribing unexpected false positives to the grouping by motion, it is important to model motion's contribution as best as practicable. It stands to reason therefore, that a better basis set for modeling motion would be more beneficial. Recent recommendations (Satterthwaite et al., 2013) suggest the use of 24 motion-derived regressors despite the diminished returns in terms of variance explained per regressor. However, there is a cost for pursuing such aggressive denoising that gets little attention in some papers: the number of nuisance regressors projected from resting state time series is quite large compared to, or in some cases larger than, the degrees of freedom in the data (see Counting Degrees of Freedom in Supplementary Material). To re-state the obvious, one should be more parsimonious when it comes to nuisance components. The residual's variance will invariably get reduced as we project out more and more components. There are approaches for selecting among a large number of explanatory variables (Miller, 2002); however, they may not be practical or appropriate for massively univariate FMRI data. Whether the goal is to reduce motion, respiration, or other noise sources, one must consider the cost and the benefit of the cleanup. In the context of motion, the benefit would be the elimination of significant artifactual differences attributable to motion. To that end, the processing approaches must result in a statistical group test with the usual multiple comparison corrections (Bullmore et al., 1996; Genovese et al., 2002; Nichols and Hayasaka, 2003; Smith and Nichols, 2009), not just maps of variance reduction, and a careful consideration of whether or not persistent differences may driven by factors other than motion.
Conclusion
GCOR is a readily computable parameter from any resting-state dataset that can be used to assess GCORs. In group comparisons, GCOR at the very least can be used to check whether or not considerable differences exist in GCORs between two groups. When GCOR differences exist and are considered to be driven by nuisance sources, the use of GCOR as a subject-level covariate can guard against false positives when external measurements of major contributors to these variations, such as respiration, are not available. As we show in simulations, this approach is an improvement over GSReg, which can introduce highly significant differences where none existed before. The approach is conservative, in that when GCOR is correlated with the grouping variable, true correlation differences fail to reach significance. However, the effect size (group differences in correlation) can be biased in either direction, confounding the interpretation of significant differences. Therefore, the use of GCOR as a covariate should only be a last resort because, as with GSReg, its interaction with the grouping variable is inevitable. The proper approaches for correcting nuisance-induced GCORs remain careful denoising procedures, including motion parameter estimates, physiological parameter measurements, and recent promising denoising decompositions or prospective methods in as far as these methods avoid contaminating nuisance estimates with signals aggregated over the regions of interest (gray matter).
We examined the relationship between GCORs measured with GCOR and the amount of motion in empirical resting state data and found it to be weak. While adding GCOR (or GSReg), considerably reduced the amount of false positives between high and low moving groups, we find reasons to doubt that the differences were caused primarily by motion. Rather, the differences may have been caused by differing physiological noise, which is reflected in GCOR.
Supplementary Material
Footnotes
In Saad et al. (2012b), the derivation of correlation difference assumed unit variance data time series and ignored variance change after GSReg.
Conditions for data exclusion: (i) Number of surviving time points after motion censoring are fewer than the minimum degrees of freedom needed for the denoising regression model, or (ii) the number of subjects was trimmed to be a multiple of 4, for ease of quartile selection.
We chose to report FWE corrected clusters instead of showing changes in z, because it is difficult to attach physiological meaning to magnitude changes in correlation measures, particularly since they are affected by changes in both signal and noise.
Adding a measure of average motion as a covariate in these tests completely wipes out the false positives; however, this constitutes no proof of its utility as it confounds with the subject-grouping variable in these synthetic tests. Nonetheless, in comparisons where there is considerable overlap in amounts of motion between groups, it would be recommended to include average motion magnitude as a covariate.
Acknowledgments
This work was greatly facilitated by the FCON-1000 initiative. We thank Chia-Yeh Carlton Chu for suggesting the speedup for GCOR computations. We also thank Kelly Barnes for her continued moderating feedback. This research was supported by the NIMH and NINDS Intramural Research Programs of the NIH.
Author Disclosure Statement
No competing financial interests exist.
References
- Anderson JS. Druzgal TJ. Lopez-Larson M. Jeong EK. Desai K. Yurgelun-Todd D. Network anticorrelations, global regression, and phase-shifted soft tissue correction. Hum Brain Mapp. 2011;32:919–934. doi: 10.1002/hbm.21079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beall EB. Adaptive cyclic physiologic noise modeling and correction in functional Mri. J Neurosci Methods. 2010;187:216–228. doi: 10.1016/j.jneumeth.2010.01.013. [DOI] [PubMed] [Google Scholar]
- Beall EB. Lowe MJ. Isolating physiologic noise sources with independently determined spatial measures. Neuroimage. 2007;37:1286–1300. doi: 10.1016/j.neuroimage.2007.07.004. [DOI] [PubMed] [Google Scholar]
- Behzadi YK. Restom J. Liau Liu TT. A component based noise correction method (COMPCOR) for BOLD and perfusion based FMRI. Neuroimage. 2007;37:90–101. doi: 10.1016/j.neuroimage.2007.04.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bianciardi M. Fukunaga M. van Gelderen P. Horovitz SG. de Zwart JA. Shmueli K. Duyn JH. Sources of functional magnetic resonance imaging signal fluctuations in the human brain at rest: a 7 T study. Magn Reson Imaging. 2009;27:1019–1029. doi: 10.1016/j.mri.2009.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Binder JR. Frost JA. Hammeke TA. Bellgowan PS. Rao SM. Cox RW. Conceptual processing during the conscious resting state. A functional MRI study. J Cogn Neurosci. 1999;11:80–95. doi: 10.1162/089892999563265. [DOI] [PubMed] [Google Scholar]
- Birn RM. Diamond JB. Smith MA. Bandettini PA. Separating respiratory-variation-related fluctuations from neuronal-activity-related fluctuations in FMRI. Neuroimage. 2006;31:1536–1548. doi: 10.1016/j.neuroimage.2006.02.048. [DOI] [PubMed] [Google Scholar]
- Birn RM. Murphy K. Bandettini PA. The Effect of respiration variations on independent component analysis results of resting state functional connectivity. Hum Brain Mapp. 2008a;29:740–750. doi: 10.1002/hbm.20577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birn RM. Smith MA. Jones TB. Bandettini PA. The respiration response function: the temporal dynamics of FMRI signal fluctuations related to changes in respiration. Neuroimage. 2008b;40:644–654. doi: 10.1016/j.neuroimage.2007.11.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal BB. Mennes M. Zuo XN. Gohel S. Kelly C. Smith SM. Beckmann CF. Adelstein JS. Buckner RL. Colcombe S, et al. Toward discovery science of human brain function. Proc Natl Acad Sci U S A. 2010;107:4734–4739. doi: 10.1073/pnas.0911855107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bright MG. Murphy K. Removing motion and physiological artifacts from intrinsic BOLD fluctuations using short echo data. Neuroimage. 2013;64:526–537. doi: 10.1016/j.neuroimage.2012.09.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullmore E. Brammer M. Williams SC. Rabe-Hesketh S. Janot N. David A. Mellers J. Howard R. Sham P. Statistical methods of estimation and inference for functional MR Image analysis. Magn Reson Med. 1996;35:261–277. doi: 10.1002/mrm.1910350219. [DOI] [PubMed] [Google Scholar]
- Carp J. Optimizing the order of operations for movement scrubbing: comment on Power et al. Neuroimage. 2011;76:436–438. doi: 10.1016/j.neuroimage.2011.12.061. [DOI] [PubMed] [Google Scholar]
- Chang C. Cunningham JP. Glover GH. Influence of heart rate on the BOLD signal: the cardiac response function. Neuroimage. 2009;44:857–869. doi: 10.1016/j.neuroimage.2008.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C. Glover GH. Relationship between respiration, End-Tidal Co2, and BOLD signals in resting-state FMRI. Neuroimage. 2009;47:1381–1393. doi: 10.1016/j.neuroimage.2009.04.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole MW. Pathak S. Schneider W. Identifying the brain's most globally connected regions. Neuroimage. 2010;49:3132–3148. doi: 10.1016/j.neuroimage.2009.11.001. [DOI] [PubMed] [Google Scholar]
- Cox RW. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comp Biomed Res. 1996;29:162–173. doi: 10.1006/cbmr.1996.0014. [DOI] [PubMed] [Google Scholar]
- Fisher RA. Frequency distribution of the values of the correlation coefficient in samples from an indefinitely large population. Biometrika. 1915;10:507–521. [Google Scholar]
- Fox MD. Greicius M. Clinical applications of resting state functional connectivity. Front Syst Neurosci. 2010;4:19. doi: 10.3389/fnsys.2010.00019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD. Zhang D. Snyder AZ. Raichle ME. The global signal and observed anticorrelated resting state brain networks. J Neurophysiol. 2009;101:3270–3283. doi: 10.1152/jn.90777.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genovese CR. Lazar NA. Nichols T. Thresholding of statistical maps in functional neuroimaging using the false discovery rate. Neuroimage. 2002;15:870–878. doi: 10.1006/nimg.2001.1037. [DOI] [PubMed] [Google Scholar]
- Glover GH. Li TQ. Ress D. Image-based method for retrospective correction of physiological motion effects in FMRI: retroicor. Magn Reson Med. 2000;44:162–167. doi: 10.1002/1522-2594(200007)44:1<162::aid-mrm23>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- Gotts SJ. Saad ZS. Jo HJ. Wallace GL. Cox RW. Martin A. The perils of global signal regression for group comparisons: a case study of autism spectrum disorders. Front Hum Neurosci. 2013 doi: 10.3389/fnhum.2013.00356. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gotts SJ. Simmons WK. Milbury LA. Wallace GL. Cox RW. Martin A. Fractionation of social brain circuits in autism spectrum disorders. Brain. 2012;135(Pt 9):2711–2725. doi: 10.1093/brain/aws160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius MD. Krasnow B. Reiss AL. Menon V. Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc Natl Acad Sci U S A. 2003;100:253–258. doi: 10.1073/pnas.0135058100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkinson M. Bannister P. Brady M. Smith S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage. 2002;17:825–841. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- Jo HJ. Gotts SJ. Reynolds RC. Bandettini PA. Martin A. Cox RW. Saad ZS. Effective Preprocessing Procedures Virtually Eliminate Distance-Dependent Motion Artifacts in Resting State Fmri. J Appl Math. 2013 doi: 10.1155/2013/935154. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jo HJ. Saad SZ. Simmons KW. Milbury LA. Cox RW. Mapping sources of correlation in resting state FMRI, with artifact detection and removal. Neuroimage. 2010;52:571–582. doi: 10.1016/j.neuroimage.2010.04.246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kundu P. Inati JS. Evans WJ. Luh WM. Bandettini PA. Differentiating BOLD and non-BOLD signals in FMRI time series using multi-echo EPI. Neuroimage. 2012;60:1759–1770. doi: 10.1016/j.neuroimage.2011.12.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leopold DA. Maier A. Ongoing physiological processes in the cerebral cortex. Neuroimage. 2012;62:2190–2200. doi: 10.1016/j.neuroimage.2011.10.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller AJ. Subset Selection in Regression. Boca Raton: Chapman & Hall/CRC; 2002. [Google Scholar]
- Murphy K. Birn MR. Handwerker AD. Jones TB. Bandettini PA. The impact of global signal regression on resting state correlations: are anti-correlated networks introduced? Neuroimage. 2009;44:893–905. doi: 10.1016/j.neuroimage.2008.09.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols T. Hayasaka S. Controlling the familywise error rate in functional neuroimaging: a comparative review. Stat Methods Med Res. 2003;12:419–446. doi: 10.1191/0962280203sm341ra. [DOI] [PubMed] [Google Scholar]
- Power JD. Barnes AK. Snyder ZA. Schlaggar BL. Petersen SE. Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuroimage. 2012a;59:2142–2154. doi: 10.1016/j.neuroimage.2011.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD. Barnes KA. Snyder AZ. Schlaggar BL. Petersen SE. Steps toward optimizing motion artifact removal in functional connectivity MRI; a reply to Carp. Neuroimage. 2012b;76:439–441. doi: 10.1016/j.neuroimage.2012.03.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2008. [Google Scholar]
- Saad ZS. Chen G. Reynolds CR. Christidis PP. Hammett RK. Bellgowan PS. Cox RW. Functional imaging analysis contest (FIAC) analysis according to AFNI and SUMA. Hum Brain Mapp. 2006;27:417–424. doi: 10.1002/hbm.20247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saad ZS. Glen RD. Chen G. Beauchamp SM. Desai R. Cox RW. A new method for improving functional-to-structural MRI alignment using local pearson correlation. Neuroimage. 2009;44:839–848. doi: 10.1016/j.neuroimage.2008.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saad ZS. Gotts JS. Murphy K. Chen G. Jo HJ. Martin A. Cox RW. Global Signal Regression Can Cause False Inferences in RS-FMRI, Not Just Negative-Correlations; 18th Annual Meeting of the Organization for Human Brain Mapping; Beijing, China. 2012a. [Google Scholar]
- Saad ZS. Gotts SJ. Murphy K. Chen G. Jo HJ. Martin A. Cox RW. Trouble at rest: how correlation patterns and group differences become distorted after global signal regression. Brain Connectivity. 2012b;2:25–32. doi: 10.1089/brain.2012.0080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD. Elliott AM. Gerraty TR. Ruparel K. Loughead J. Calkins EM. Eickhoff BS. Hakonarson H. Gur CR. Gur RE, et al. An improved framework for confound regression and filtering for control of motion artifact in the preprocessing of resting-state functional connectivity data. Neuroimage. 2013;64:240–256. doi: 10.1016/j.neuroimage.2012.08.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satterthwaite TD. Wolf HD. Loughead J. Ruparel K. Elliott AM. Hakonarson H. Gur RC. Gur RE. Impact of in-scanner head motion on multiple measures of functional connectivity: relevance for studies of neurodevelopment in youth. Neuroimage. 2012;60:623–632. doi: 10.1016/j.neuroimage.2011.12.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholvinck ML. Maier A. Ye QF. Duyn JH. Leopold DA. Neural basis of global resting-state FMRI activity. Proc Natl Acad Sci U S A. 2010;107:10238–10243. doi: 10.1073/pnas.0913110107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shmueli K. van Gelderen P. de Zwart JA. Horovitz SG. Fukunaga M. Jansma JM. Duyn JH. Low-frequency fluctuations in the cardiac rate as a source of variance in the resting-state FMRI BOLD signal. Neuroimage. 2007;38:306–320. doi: 10.1016/j.neuroimage.2007.07.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM. Miller LK. Moeller S. Xu J. Auerbach JE. Woolrich WM. Beckmann FC. Jenkinson M. Andersson J. Glasser MF, et al. Temporally-independent functional modes of spontaneous brain activity. Proc Natl Acad Sci U S A. 2012;109:3131–3136. doi: 10.1073/pnas.1121329109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM. Nichols TE. Threshold-free cluster enhancement: addressing problems of smoothing, threshold dependence and localisation in cluster inference. Neuroimage. 2009;44:83–98. doi: 10.1016/j.neuroimage.2008.03.061. [DOI] [PubMed] [Google Scholar]
- Van Dijk KR. Sabuncu MR. Buckner RL. The influence of head motion on intrinsic functional connectivity MRI. Neuroimage. 2012;59:431–438. doi: 10.1016/j.neuroimage.2011.07.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weissenbacher Kasess AC. Gerstl F. Lanzenberger R. Moser E. Windischberger C. Correlations and anticorrelations in resting-state functional connectivity MRI: a quantitative comparison of preprocessing strategies. Neuroimage. 2009;47:1408–1416. doi: 10.1016/j.neuroimage.2009.05.005. [DOI] [PubMed] [Google Scholar]
- Wise RG. Ide K. Poulin MJ. Tracey I. Resting fluctuations in arterial carbon dioxide induce significant low frequency variations in BOLD signal. Neuroimage. 2004;21:1652–1664. doi: 10.1016/j.neuroimage.2003.11.025. [DOI] [PubMed] [Google Scholar]
- Wong CW. Olafsson V. Tal O. Liu TT. Anti-correlated networks, global signal regression, and the effects of caffeine in resting-state functional MRI. Neuroimage. 2012;63:356–364. doi: 10.1016/j.neuroimage.2012.06.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan CG. Cheung B. Kelly C. Colcombe S. Craddock CR. Di Martino A. Li Q. Zuo XN. Castellanos FX. Milham MP. A comprehensive assessment of regional variation in the impact of head micromovements on functional connectomics. Neuroimage. 2013;76:183–201. doi: 10.1016/j.neuroimage.2013.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.