Breakdown of Brain Connectivity Between Normal Aging and Alzheimer's Disease: A Structural k-Core Network Analysis

Abstract

Brain connectivity analyses show considerable promise for understanding how our neural pathways gradually break down in aging and Alzheimer's disease (AD). Even so, we know very little about how the brain's networks change in AD, and which metrics are best to evaluate these changes. To better understand how AD affects brain connectivity, we analyzed anatomical connectivity based on 3-T diffusion-weighted images from 111 subjects (15 with AD, 68 with mild cognitive impairment, and 28 healthy elderly; mean age, 73.7±7.6 SD years). We performed whole brain tractography based on the orientation distribution functions, and compiled connectivity matrices showing the proportions of detected fibers interconnecting 68 cortical regions. We computed a variety of measures sensitive to anatomical network topology, including the structural backbone—the so-called “k-core”—of the anatomical network, and the nodal degree. We found widespread network disruptions, as connections were lost in AD. Among other connectivity measures showing disease effects, network nodal degree, normalized characteristic path length, and efficiency decreased with disease, while normalized small-worldness increased, in the whole brain and left and right hemispheres individually. The normalized clustering coefficient also increased in the whole brain; we discuss factors that may cause this effect. The proportions of fibers intersecting left and right cortical regions were asymmetrical in all diagnostic groups. This asymmetry may intensify as disease progressed. Connectivity metrics based on the k-core may help understand brain network breakdown as cognitive impairment increases, revealing how degenerative diseases affect the human connectome.

Introduction

Alzheimer's Disease (ad) is a progressive, degenerative brain disease affecting around one in eight people (13%) aged 65 or older (Alzheimer's Association Colorado, 2011). As AD progresses, many cognitive domains gradually decline, including memory (Filippi et al., 2012); beta-amyloid and tau proteins accumulate in the brain, leading to inflammation, neuronal atrophy, and cell death (Wang et al., 2012). The brain's gray matter shows widespread neuronal loss, and many studies have revealed widespread cortical and hippocampal atrophy in AD. As neurons are lost, white matter volume is also reduced, due to both myelin degeneration and axon loss in neural fiber tracts (Bartzokis, 2009; Braak and Braak, 1996; Braskie et al., 2012a, b; Hua et al., 2008). Fluid-attenuated inversion-recovery or T2-weighted scans are often used to evaluate white matter hyperintensities—a sign of cerebrovascular disease—and there is growing evidence that breakdown of the brain's fiber networks may explain some of the symptoms as the disease progresses.

As new methods emerge to assess brain connectivity, some research groups have begun to use diffusion-weighted imaging (DWI) and resting state functional magnetic resonance imaging (rs-fMRI) to study the global breakdown of network integration in degenerative disease (Buckner, 2005; Delbeuck et al., 2003; Gili et al., 2012; Wegrzyn et al., 2011). Neuropsychological deficits are often attributed to a disconnection between brain regions (Wernicke, 1874/1977; Lichtheim, 1885); the notion of a “disconnection syndrome” was introduced by Geschwind (1965).

Evidence supporting a disconnection process in AD has emerged from various techniques, including MRI, electroencephalography, and positron emission tomography (PET). On MRI, AD patients show a lower density of associative white matter fibers in the cingulum, the splenium of the corpus callosum and the superior longitudinal fasciculus (Rose et al., 2000). At the same time, interhemispheric functional synchronization also breaks down (Azari et al., 1992). Coherence studies by Wada and colleagues (1998) found disturbed interhemispheric functional connectivity in AD. Interhemispheric disturbances in AD have been linked to the disconnection syndrome observed clinically (Delbeuck et al., 2003). PET studies also show reduced metabolism in a network of regions, with greater amyloid deposition in the posterior cingulate, retrosplenial, and lateral parietal cortex (Buckner, 2005). fMRI also shows deactivated regions that overlap with medial parietal/posterior cingulate regions that show reduced resting metabolic activity in AD subjects, compared to normal elderly and young adults (Lustig et al., 2003).

Diffusion imaging has recently been added to several large-scale neuroimaging studies, including the Alzheimer's Disease Neuroimaging Initiative (ADNI), to monitor white matter deterioration using metrics not available with standard anatomical MRI. Diffusion MRI yields measures related to fiber integrity in AD, such as the mean diffusivity and fractional anisotropy of local water diffusion (Clerx et al., 2012); in addition, tractography methods can infer neural pathways and connectivity patterns, yielding additional, more complex mathematical metrics describing fiber networks.

Network analysis has only recently been applied to study AD. Many mathematically novel metrics have been proposed, such as a network's “structural backbone”—or k-core (Hagmann et al., 2008)—but have not yet been studied in AD. Here, we analyzed several network measures in normal elderly subjects, and people with early and late mild cognitive impairment (MCI), and AD. We mapped the whole brain, left, and right hemisphere “structural cores” of the brain in Alzheimer's patients and compared them to the cores in healthy controls. A network's structural core is based on using k-core decomposition (Hagmann et al., 2008) to find important sets of nodes that are highly and mutually interconnected.^* We hypothesized that the core graph of connections would highlight alterations and disconnections in regions that change structurally in AD versus controls, such as the temporal, parietal, and frontal association areas (Azari et al., 1992; Horwitz et al., 1987). We also expected network breakdown in the posterior cingulate, posterior medial cortex and lateral parietal cortex (Buckner, 2005; Lustig et al., 2003; Xie and He, 2012).

In addition to using k-core analysis for the first time to assess AD-associated anatomical network changes, we studied several global topological properties on the brain's binarized k-core. To avoid testing too many primary hypotheses, and thereby inflating the false positive rate or reducing power by applying a heavy correction for multiple comparisons, we chose for our primary analysis to strictly focus on the nodal degree, normalized characteristic path length, efficiency, normalized clustering coefficient, and normalized small-world effect, comparing AD patients and controls. All network properties were derived from the k-cores for each of the subjects. Also, we were interested in brain laterality in disease as some (but not all) prior studies report that the left hemisphere is more atrophied in AD with a greater reduction in gray matter (20–30% local loss), relative to the right hemisphere (Thompson et al., 2001). This lateralized brain dysfunction was also studied by Loewenstein and colleagues (1989) who reported left hemisphere hypometabolism in the frontal, temporal, parietal lobes, and basal ganglia-thalamus of AD patients. In their study, these apparent asymmetries were not correlated with the severity or duration of AD. Little is known about left-right hemisphere differences, and as interconnectivity may play a significant role in AD, we compared left and right hemisphere networks to see if first, network asymmetries were detectable in general, and second, if they were altered with the clinical progression of AD.

Methods

Subjects and diffusion imaging of the brain

Data collection for ADNI2 is still ongoing, at the time of writing (December 2012). The ADNI began in 2005 as a large multisite longitudinal study, which uses a variety of imaging methods (including MRI and PET) to study how AD progresses, and to define biomarkers to monitor and predict disease progression. The second phase of ADNI—known as ADNI2—added new imaging modalities—diffusion tensor imaging (DTI), rs-fMRI, and arterial spin labeling (Jack et al., 2010) to supplement the methods available to track disease progression.

Here we analyzed DWI from the 111 subjects with available data; Table 1 shows their demographics and diagnostic information. All 111 subjects underwent whole brain MRI scanning on 3 T GE Medical Systems scanners, at a variety of sites across North America. Table 2 shows a breakdown of the sites where the scans were acquired. Standard anatomical T1-weighted spoiled gradient echo sequences were collected (256×256 matrix; voxel size=1.2×1.0×1.0 mm³; inversion time [TI]=400 msec, repetition time [TR]=6.984 msec; echo time [TE]=2.848 msec; flip angle=11°) in the same session as the DWI (256×256 matrix; voxel size: 2.7×2.7×2.7 mm³; scan time=9 min). Forty-six separate images were acquired for each DTI scan: 5 T2-weighted images with no diffusion sensitization (b₀ images) and 41 DWI (b=1000 sec/mm²). This protocol was chosen after a comparison of several different protocols, to optimize the signal-to-noise ratio in a fixed scan time (Jahanshad et al., 2010; Zhan et al., 2012; Zhan et al., 2013b).

Table 1.

Demographic Information for Alzheimer's Disease Neuroimaging Initiative Subjects Scanned with Diffusion Magnetic Resonance Imaging

	Controls	eMCI	lMCI	AD	Total
N	28	57	11	15	111
Age	73.0	73.7	76.3	75.6	73.7
Sex	14M/14F	34M/23F	7M/4F	9M/6F	64M/47F

One hundred eleven subjects had been scanned at the time of writing (December 2012). Their minimum age was 55.3 and maximum age was 90.4. Based on a t-test, the control group did not differ in age from any of the cognitively impaired groups. p-Values from t-tests comparing the mean age of the controls to the ages of the eMCI, lMCI and AD groups were 0.67, 0.094, and 0.30.

AD, Alzheimer's disease; eMCI, early mild cognitive impairment; lMCI, late mild cognitive impairment.

Table 2.

Acquisition Sites

Site	1	2	3	4	5	6	7	8	9	10	11	12	13	14
# scans	12	3	9	7	10	4	8	0	13	12	10	7	9	7

Number of scans acquired at each of the 13 sites, note there are no images from Site 8.

Image analysis

Diffusion imaging may be used in conjunction with an automatically labeled set of regions from anatomical MRI to perform connectivity mapping and network analysis of the brain's fiber connections. Many analyses of brain connectivity have been conducted in this way (Dennis et al., 2012a, b; Dennis and Thompson, 2012; Jahanshad et al., 2011, 2012; Zalesky, 2009; Zhan et al., 2012). Connectivity matrices were compiled using a processing pipeline described previously (Braskie et al., 2012a, b; Dennis et al., 2012b; Jahanshad et al., 2011, 2012; Nir et al., 2012a, b).

Preprocessing and coregistration

Nonbrain regions were automatically removed from each T1-weighted MRI scan, and from a T2-weighted image from the DWI set using the FSL tool “BET” (http://fsl.fmrib.ox.ac.uk/fsl/). Anatomical scans subsequently underwent intensity inhomogeneity normalization using the MNI “nu_correct” tool (www.bic.mni.mcgill.ca/software/). All T1-weighted images were linearly aligned using FSL (with six degrees of freedom) to a common space with 1 mm isotropic voxels and a 220×220×220 voxel matrix. The DWIs were corrected for eddy current distortions using the FSL tools (http://fsl.fmrib.ox.ac.uk/fsl/). For each subject, the five images with no diffusion sensitization were averaged, linearly aligned, and resampled to a downsampled version of their T1-weighted image (110×110×110, 2×2×2 mm). b₀ maps were elastically registered to the T1-weighted scan to compensate for susceptibility artifacts. Images were visually inspected and there were no misalignments or cases where the field of view did not cover the full brain (i.e., cropping).

Tractography and cortical extraction

The transformation matrix from linearly aligning the mean b₀ image to the T1-weighted volume was applied to each of the 41 gradient directions to properly reorient the orientation distribution functions (ODF). We also performed whole brain tractography as described in (Aganj et al., 2011) on the sets of DWI volumes. Only linear registration was performed before tractography, as nonlinear registration before tractography could introduce possible processing artifacts. Gradient directions for each DWI volume were corrected for according to the transformation matrix obtained from the linear registration. The tractography method uses a fiber detection approach based on the Hough transform; the Hough transform algorithm is a probabilistic fiber tracking method that is based on a voting process. The algorithm tests candidate three-dimensional (3D) polynomial curves in a diffusion imaging volume by assigning a score to each curve that passes through a seed point in a d-dimensional space. The goal of the algorithm is to find all potential curves that pass through chosen seed points while computing their scores and finally, selecting the curve with the highest score. Curves with the highest scores are stored in a d-dimensional array, called the Hough transform, and can represent potential fiber tracts in the brain. The results are obtained through a voting process where real-valued local votes for curves that are derived from diffusion data help define the candidate tract score. If the curve passes through a voxel, the vote (which is the integrand of the score integral) outputs a value other than zero, and if it does not pass though a voxel, then the output is zero (Aganj et al., 2011); to better detect crossing fibers, the method uses a constant solid angle orientation density function (Aganj et al., 2010) rather than a diffusion tensor, to model the local diffusion propagator. The angular resolution of the ADNI data is limited to avoid long scan times that may tend to increase patient attrition. Even so, this ODF model makes best use of this limited angular resolution (even if the protocol is not ideal for resolving fiber crossing).

Elastic deformations obtained from the echo-planar imaging distortion correction, mapping the average b₀ image to the T1-weighted image, were then applied to each recovered fiber's 3D coordinates to more accurately align the anatomy (we assume that the anatomical scan serves as a relatively undistorted anatomical reference). Each subject's dataset contained ∼10,000 useable fibers (3D curves) in total.

Thirty-four cortical labels per hemisphere, listed in the Desikan-Killiany atlas (Desikan et al., 2006), were automatically extracted from all aligned T1-weighted structural MRI scans using FreeSurfer version 5.0 (http://surfer.nmr.mgh.harvard.edu/) (Fischl et al., 2004). The resulting T1-weighted images and cortical models were aligned to the original T1-weighted input image space and down-sampled using nearest neighbor interpolation (to avoid intermixing of labels) to the space of the DWIs. To ensure tracts would intersect labeled cortical regions, labels were dilated with an isotropic box kernel of width 5 voxels (Jahanshad et al., 2011).

N×N matrices representing structural connectivity

For each subject, a baseline 68×68 connectivity matrix was created (34 left and 34 right hemisphere regions of interest as listed in Table 3). Each matrix element represents the proportion of the total number of fibers, in that subject, connecting one cortical region to another. For the purposes of this paper, we use the word fiber to denote a single curve extracted via tractography; if all subjects had no detected fibers at all for a specific matrix element, then that connection was considered invalid, or insufficiently consistent in the population, and was not included in the analysis.

Table 3.

Index of the Cortical Labels Extracted from FreeSurfer

1	Banks of the superior temporal sulcus
2	Caudal anterior cingulate
3	Caudal middle frontal
4	—N/A—
5	Cuneus
6	Entorhinal
7	Fusiform
8	Inferior parietal
9	Inferior temporal
10	Isthmus of the cingulate
11	Lateral occipital
12	Lateral orbitofrontal
13	Lingual
14	Medial orbitofrontal
15	Middle temporal
16	Parahippocampal
17	Paracentral
18	Pars opercularis
19	Pars orbitalis
20	Pars triangularis
21	Peri-calcarine
22	Postcentral
23	Posterior cingulate
24	Precentral
25	Precuneus
26	Rostral anterior cingulate
27	Rostral middle frontal
28	Superior frontal
29	Superior parietal
30	Superior temporal
31	Supra-marginal
32	Frontal pole
33	Temporal pole
34	Transverse temporal
35	Insula

Index of the cortical labels extracted from the anatomical MRI scans using FreeSurfer (Fischl et al., 2004). In the latest version of FreeSurfer (version 5.0), cortical area #4 was not parcellated and is therefore, excluded; to ease comparison with prior papers using this numbering scheme, no region is assigned the number 4.

Brain network measures

Topological changes in the brain's networks may be analyzed using graph theory, a branch of mathematics increasingly applied to study structural and functional brain networks (Lee et al., 2012; Sporns, 2011).

These types of analyses on brain networks require that the brain's components be represented as a graph. The network's nodes are typically defined as regions of interest segmented automatically from coregistered anatomical MRI. In DTI studies, these network nodes are considered to be linked by “edges” with weights that denote some measure of the connectivity between the two regions, such as the density or integrity of fibers recovered using tractography (Bullmore and Sporns, 2009; Hagmann et al., 2008). Different measures of connectivity are used in different studies—connectivity matrices typically represent some descriptive parameter about the connection between all pairs of anatomical regions studied. The most common topological network measures used to describe the integrity of the healthy or diseased human brain network include the nodal degree, characteristic path length, efficiency, clustering coefficient and “small-worldness” (Sporns, 2011). The characteristic path length, a measure of integration, is the average shortest path length in a network:

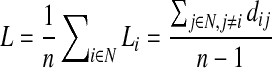(1)

where L_i is the average distance between node i and all other nodes in the networks, d_ij is the shortest path length, (i,j) is a link between nodes i and j, and n is the number of nodes (Sporns, 2011).

Efficiency is a global and generally robust measure, and is approximately the inverse of the characteristic path length:

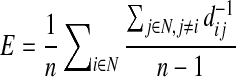(2)

The clustering coefficient, a measure of segregation, is the fraction of a node's neighbors that are neighbors of each other:

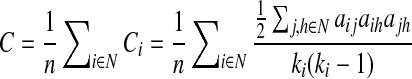(3)

where C_i is the clustering coefficient of node i (C_i=0, k_i<2), k_i is the degree of a node i, 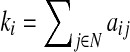where a_ij is the connection status between nodes i and j when a link between (i,j) exists (Sporns, 2011).

Furthermore, the small-world effect is the ratio of the mean clustering coefficient to the characteristic path length after both are normalized based on data from corresponding random networks:

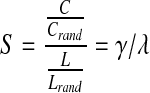(4)

where C and C_rand are the unrandomized and randomized mean clustering coefficients, while L is L_rand are the unrandomized and randomized characteristic path lengths (Sporns, 2011). The clustering coefficient was normalized by computing the ratio of the clustering coefficient in the brain network to the clustering coefficient computed in 100 simulated random networks and was denoted by gamma, γ. Similarly, the normalized path length was the ratio of the path length in the brain network to the path length computed in 100 simulated random networks, and was denoted by lambda, λ. These summary measures have been widely employed in studies using various imaging modalities and analytic methods (Dennis and Thompson, 2012), and their reproducibility has also been evaluated (Dennis et al., 2012c).

In graph theory, a connection matrix may be compiled that describes the topology of a network. A square matrix can represent any network of connections, but the network is normally displayed as a graph, that is, a discrete set of nodes and edges (Sporns, 2011). In our analysis, the matrix entries store the total number of fibers connecting each pair of regions (the nodes); these could also be considered as the “weights” of the edges that connect a pair of nodes. Some matrix entries are null (zero), as not all pairs of regions are connected. Based on these matrices for all 111 subjects, we went on to map the so-called “structural core” of each subject's anatomical network.

We analyzed the whole brain, left, and right hemispheres separately; in the single-hemisphere analyses, to focus our attention on the connections specific to the hemisphere we chose not to evaluate fibers that crossed between the hemispheres. In other words, we considered the subnetwork that only had nodes that were entirely within a specific hemisphere. Then, we compared the left and right hemispheres in healthy and AD subjects to analyze the topology and integrity of the fiber bundles.

To model the basic architecture of the neural networks, we used a k-core decomposition algorithm that disentangles hierarchical structure by focusing on what is called the “central cores” of the networks (Alvarez-Hamelin et al., 2006). The k-core decomposition outputs a network core that consists of highly and mutually interconnected nodes (Hagmann et al., 2008). This is done by identifying subsets of graphs (k-cores) by recursively removing nodes with degrees lower than k, such that k serves as a degree threshold for nodes (Alvarez-Hamelin et al., 2006). Then, each node is assigned a core number (Daianu et al., 2012b; Hagmann et al., 2008): larger values of k correspond to nodes that have larger degrees and are “more central” within a network (Alvarez-Hamelin et al., 2006).

For a graph G=(N,E) with |N|=n nodes and |E|=e edges, a k-core is computed by assigning a subgraph, H=(B,E|B) where set B⊆N is a k-core of order k if 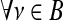: degree_H≥k, and H is the maximum subgraph satisfying this property (Alvarez-Hamelin et al., 2006). In other words, to compute the “18-core” (for example) of the connectivity matrix, all nodes that have a degree 18 or higher would be kept. These would be output in a 34×34 matrix (the same size as the connectivity matrix); nodes that do not satisfy this condition are replaced with zeroes. For this study, we selected a value of k=18; this value was selected empirically, as it represents the minimal value where the majority (>50%) of nodes within each hemisphere would still remain connected. In other words, most nodes would be connected to at least one remaining node. On the other hand, it is not required that the remaining nodes in a k-core must form one single totally connected graph, in which information could travel from any node to any other via a path of edges.

We also computed topological network measures including: (1) global nodal degree (average of all nodal degrees); (2) normalized characteristic path length (λ); (3) efficiency; (4) normalized clustering coefficient (γ); and (5) a parameter describing the normalized small-world effect for the whole brain, left, and right hemisphere binarized k-core matrices, in all subjects. These measures are detailed in (Sporns, 2011). We applied these measures to the whole brain 68×68 k-core matrices, left hemisphere 34×34 k-core matrices and the right hemisphere 34×34 k-core matrices. We compared the two brain hemispheres within each group (controls, early mild cognitive impairment [eMCI], late mild cognitive impairment [lMCI] and AD), to test for left/right asymmetries in connectivity. To assess diagnostic group differences, we analyzed the difference between the network measures in the whole brain in controls and whole brain in AD subjects, differences between the network measures in the left hemisphere in controls and the left hemisphere in AD subjects, and then we did the same for the right hemisphere.

We separately fitted a random effects regression model to the k-core matrices of controls and AD subjects to test for diagnostic group differences, in the left hemisphere, and then separately in the right hemisphere (with controls coded as 0 and AD subjects coded as 1). We covaried for age and sex and used acquisition site as a random regression variable. The fiber density strengths in the k-core structures were compared across every node that was in the k-core of at least one subject. The global network measures were compared across the whole brain, left, and right hemispheres, separately. To test how the clinical test scores were correlated with the fiber densities in the k-core matrices in the whole brain, left, and right hemispheres, we performed a random effects regression across all subjects and used the scanning site as a random regression variable while covarying for age and sex.

Furthermore, we also separately fitted a random effects regression to the connectivity matrix data from 28 controls, 57 eMCI, 11 lMCI, and 15 AD subjects to test for differences between the connectivity matrices of the left and right hemispheres (same setup as above). In this primary analysis, we did not covary for disease, to increase power. However, we tested if the asymmetry in the brain intensifies with disease progression using a random effects regression among subjects, while using site as a random regression variable and covarying for age and sex. To simplify the presentation, we show the regression results as a matrix, to indicate differences between the left, C_L(x,y), and right, C_R(x,y), hemisphere connectivity matrices across all 111 subjects (Fig. 3). Similarly, we applied a random effects regression to test for any differences in derived network topology measures for the left versus the right hemisphere subnetworks.

FIG. 3.

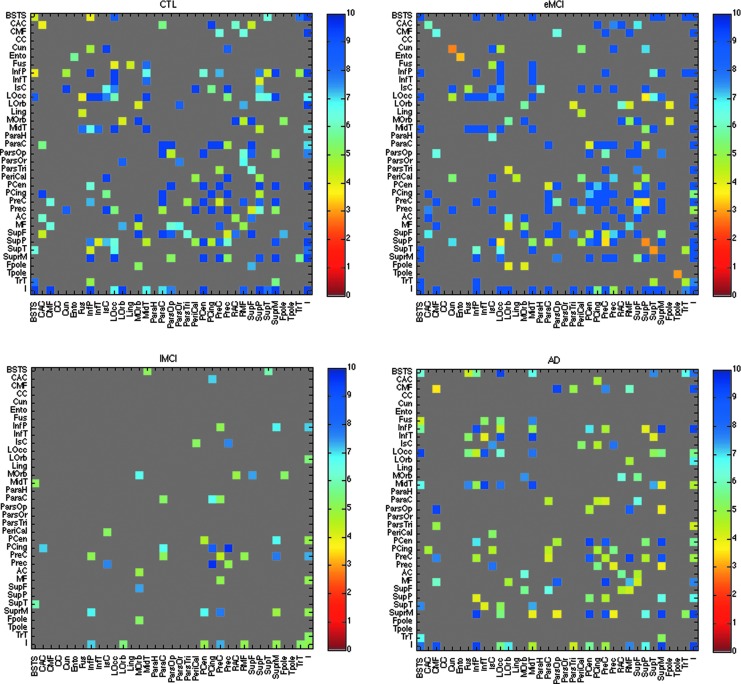
Asymmetries in anatomical connectivity in controls, early and late MCI, and AD. These maps show asymmetries in the density of connections between all pairs of cortical regions. We show, in color, the −log₁₀ of the p-values from the regression model comparing the left, C_L(x,y), and right, C_R(x,y), hemisphere connectivity matrices in 28 controls (top left, FDR critical p-value=0.020; higher critical values denote stronger effects) and 57 eMCI subjects (top right, FDR critical p-value=0.030), 11 lMCI subjects (bottom left, FDR critical p-value=0.007) and 15 AD subjects (bottom right, FDR critical p-value=0.021). We covaried for age and sex and used the scanning site as a random grouping variable in the regression. The same cortical regions were considered in all four groups. Dark gray regions indicate cortical areas where no significant hemispheric differences were detected. Based on a random effects regression, the asymmetry in the connection matrix intensified with disease progression. This could be due to the overall decrease in the number of fiber connections with increasing disease severity.

Results

First, we compared the connectivity matrices of the left and right hemispheres across all subjects (controls, eMCI, lMCI and AD) and found significant differences in a total of 115 connections, while covarying for age and sex and accounting for scanning site. A total of 208 “valid” connections were examined (i.e., connections that occurred in all subjects), so 115 is 55%, when analyzing connections that were present in >80% of the subjects (false discovery rate [FDR] p=0.037). By only examining edges that were present in nearly all subjects, we may still have somewhat underestimated the degree to which connectivity is asymmetric, but this is a reasonable estimate of the large degree of hemispheric difference in connections that are reliably extracted across an entire population. In other words, over half of the valid connections showed an asymmetry. We further “filtered” these connectivity matrices and thresholded the nodes by degree, to retain the majority (>50%) of the nodes that were connected within each hemisphere (k=18) in our 34×34 k-core matrices. After we defined the k-cores for the whole brain, left, and right hemispheres in healthy and diseased subjects, we tested for disease effects, and relationships to clinical scores.

Disease-related differences in networks

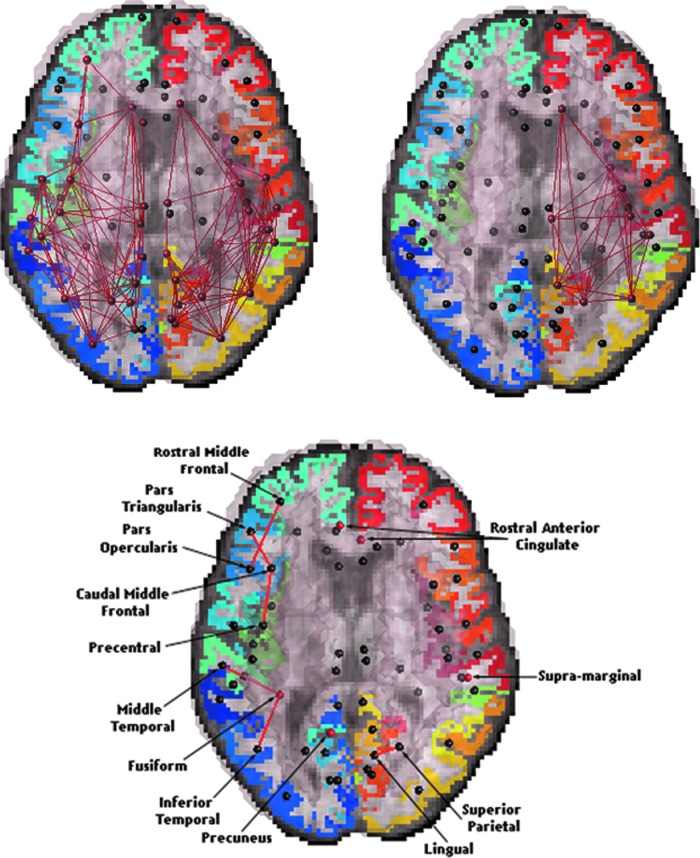
When the networks were pared down to the k-cores for all subjects (k=18)—the network “backbone”—we were able to detect disease effects on connectivity. In comparing AD and control groups, we found prominent group differences between the weighted k-core elements of different cortical regions across the entire brain. For this regression to be well-defined, we included only those nodes that are in the k-cores for at least one of the subjects. Considering the left hemisphere first, certain regions differed between AD and controls, and, as expected, showed lower fiber density in AD between the middle temporal and fusiform area, lower fiber density in AD between inferior temporal and fusiform area, lower fiber density in the pars triangularis and caudal middle frontal, lower fiber density between the precentral and caudal middle frontal, lower fiber density between the rostral middle frontal and pars opercularis, and a lower proportion of fibers in the fusiform, precuneus and rostral anterior cingulate (Fig. 1). The medial temporal lobe is among the first brain regions to show atrophy in MCI and AD (Thompson et al., 2003). Deterioration in its connectivity to other brain regions is in line with current thinking about disconnection in AD. Considering the right hemisphere, the AD group showed lower fiber density between the superior parietal and lingual areas relative to controls, a lower proportion of fibers in the rostral anterior cingulate and higher proportion of fibers in the supra-marginal region, relative to controls.

FIG. 1.

k-core networks of controls and Alzheimer's disease (AD) subjects. Set of nodes present in the weighted k-cores of all 28 controls, k=18, (top left panel) and all 15 AD subjects (top right panel). The k-value was preselected to include at least half (i.e., the majority) of the detectable connected nodes per hemisphere (34×34). Results are presented over the whole brain. With disease progression, the left hemisphere of AD subjects loses consistency in its k-core assignments (false discovery rate [FDR] critical p-value=0.0015). Bottom panel shows p-values from the whole brain from a random effects regression between the k-cores (k=18) of controls and AD subjects (where controls were coded as 0 and AD subjects coded as 1) using age and sex as covariates and site as a random grouping variable; the significant connections that survived FDR were between the following cortical regions: the middle temporal and fusiform, inferior temporal and fusiform, pars triangularis and caudal middle frontal, precentral and caudal middle frontal, rostral middle frontal and pars opercularis, and superior parietal and lingual; also, a significant difference in the proportion of total fibers was detected in the following regions: fusiform, precuneus, rostral cingulate, and supra-marginal. Small black spheres show cortical areas where group differences were not detected.

Relative to controls, the AD group lost all k-core connections in the left hemisphere (FDR critical p-value=0.0015). Note that this does not mean that all those fibers are gone from the brain; when defining the k-core, the thresholding operation on the nodal degree makes sure that only fibers with a very high number of connections are retained, and these no longer exist, at least in the left hemisphere. Figure 1 shows regions with the most drastic changes. Some, but not all, studies report a slightly greater effect of AD on the left hemisphere (i.e., group differences in some brain measures may show larger effect sizes on the left). Even so, any laterality may just reflect a recruitment bias where patients with language dysfunction, arising from left hemisphere atrophy, tend to enroll in greater proportions than those who do not have language problems (Thompson et al., 2003).

Brain network measures: global nodal degree, efficiency, normalized characteristic path length, normalized clustering coefficient and normalized small-world effect

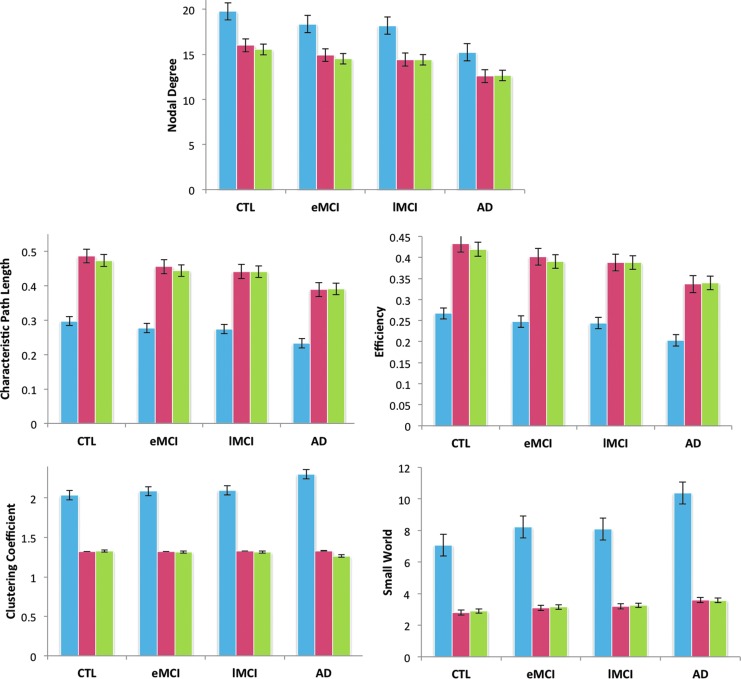
We computed the network nodal degree, efficiency, normalized characteristic path length, normalized clustering coefficient, and normalized small-world measures (these are global measures of the overall network properties) from the binarized k-cores of controls and AD subjects in the whole brain, left, and right hemispheres, separately. Based on a random effects regression between the brain network measures in healthy subjects and AD subjects, we determined that with increasing disease burden, the nodal degree, normalized characteristic path length and efficiency significantly declined in AD subjects, relative to controls in the whole brain, left, and right hemispheres (means are in Table 4 and p-values are in Table 5). Efficiency was expected to decline (according to prior studies, e.g., Lo et al. [2010]), while the small-world effect was expected to be altered, but not in a direction predictable a priori; here, the normalized small-world effect increased in AD in all analyses, relative to controls. The normalized clustering coefficient significantly increased in the whole brain of AD compared to controls and did not show detectable differences when the left and right hemispheres were considered independently.

Table 4.

Mean Network Measures in Controls (CTL) and Alzheimer's Disease Subjects

	CTL					AD
	NOD	λ	EFF	γ	SW	NOD	λ	EFF	γ	SW
WB	19.78	0.29	0.27	2.03	7.08	15.22	0.23	0.20	2.30	10.38
LH	16.00	0.49	0.43	NS	2.80	12.59	0.39	0.33	NS	3.60
RH	15.54	0.47	0.42	NS	2.90	12.66	0.39	0.34	NS	3.57

The mean nodal degree, normalized characteristic path length and efficiency decreased significantly between controls and AD subjects in all analyses. The normalized clustering coefficient increased in the whole brain of AD, while the normalized small-world effect increased in AD in all analyses, relative to controls. Mean values were rounded off to the nearest hundredth.

NOD, global nodal degree; λ, normalized characteristic path length; EFF, efficiency; γ, normalized clustering coefficient; SW, normalized small-world effect; WB, whole brain; LH, left hemisphere; RH, right hemisphere; NS, not significant.

Table 5.

Differences in Fiber Networks for the Whole Brain, Left, and Right Hemispheres Between Controls (CTL) and Alzheimer's Disease Subjects

	Network measures
CTL vs. AD(p-values)	NOD	λ	EFF	γ	SW
WB	3.86E-05	3.86E-05	4.02E-05	0.0038	9.06E-06
LH	2.91E-04	2.89E-04	3.08E-04	NS	2.99E-03
RH	1.51E-04	1.47E-04	1.85E-04	NS	9.03E-04

p-Values are shown, based on fitting a random effects model to the network measures (degree, normalized characteristic path length, efficiency, normalized clustering coefficient and normalized small-world) applied on the k-core (k=18) to test for diagnostic group differences between controls and AD subjects in the whole brain, left hemisphere, and then separately in the right hemisphere (with controls coded as 0 and AD subjects coded as 1). We covaried for age and sex and used acquisition site as a random regression variable.

The nodal degree, efficiency and normalized characteristic path length of the proportions of fibers (that passed FDR) were lower in AD in the whole brain, left, and right hemispheres, relative to controls. This decrease was consistent among the MCI groups: the eMCI and lMCI groups took intermediate values between those for controls and AD groups (Fig. 2). The normalized clustering coefficient of the proportion of fibers was higher in AD in the whole brain (no significant changes were detected in the left and right hemispheres between controls and AD). The slight increase in the clustering coefficient and decrease in the normalized characteristic path length led to an increase in the proportion of fibers in the small-world effect in AD in all analyses, relative to controls (Tables 4 and 5).

FIG. 2.

Mean values for network measures in the brain for all diagnostic groups. The bar graph shows mean values (and standard errors) for the fiber network nodal degree, normalized characteristic path length, efficiency, normalized clustering coefficient, and normalized small-world effect for controls (CTL), early mild cognitive impairment (eMCI), late mild cognitive impairment (lMCI) and AD groups in the whole brain (blue), left hemisphere (red) and right hemisphere (green). The nodal degree, normalized characteristic path length and efficiency declined in AD subjects, relative to controls in the whole brain, left, and right hemispheres (p-values in Table 4) based on a regression setting controls to 0 and AD subjects to 1; this can be seen by comparing each block of three bars to each succeeding block of three bars, which corresponds to increasing disease burden. The normalized small-world effect increased in AD, relative to controls, and the normalized clustering coefficient increased in the whole brain but did not show detectable differences in the left and right hemispheres individually between controls and AD subjects.

Relation to clinical scores

To assess whether the network breakdown related to differences in clinical test scores, we also ran a random effects regression to test for any associations with the most widely used clinical scores, namely the Mini Mental State Examination (MMSE), Clinical Dementia Rating Global Score (CDR-Glob), Clinical Dementia Rating Sum of Boxes (CDR-SOB), 11 item Alzheimer's Disease Assessment Scale-Cognitive Subscale (ADAS-11) and 13-item Alzheimer's Disease Assessment Scale-Cognitive Subscale (ADAS-13) scales. These regressions used clinical scores to predict any differences on the k-core across all subjects in the study.

Analyses were run on the whole brain, left, and right hemispheres separately (Table 6). Clinical test scores were all related to differences in some cortical regions. Consistent relationships with all clinical scores were found for the connections between the superior frontal cortex and caudal anterior cingulate (see in bold, Table 6). As MMSE scores decreased, the fiber density of the k-cores also decreased (as might be expected) between the superior frontal cortex and caudal anterior cingulate in the whole brain analysis. Also as expected, with increases in the disease burden scores ADAS-11, ADAS-13, CDR-Glob, and CDR-SOB, fiber density in the k-cores decreased between the superior frontal and caudal anterior cingulate, in the whole brain analyses.

Table 6.

Clinical Correlates of Network Breakdown

Scores	Whole brain	Left hemisphere	Right hemisphere
MMSE	1 connection: 63 and 37 (critical FDR p=8.50E-05)	15 connections: 3 and 3, 7 and 7, 8 and 7, 9 and 7, 9 and 9, 15 and 7, 15 and 9, 24 and 3, 27 and 3, 27 and 27, 29 and 7, 29 and 8, 30 and 7, 31 and 8, 35 and 7 (critical FDR p=0.004)	10 connections: 11 and 1, 24 and 22, 31 and 22, 31 and 24, 31 and 25, 31 and 31, 35 and 17, 35 and 31, 35 and 35 (critical FDR p=0.002)
ADAS-11	11 connections: 15 and 13, 25 and 15, 28 and 20, 45 and 42, 46 and 40, 51 and 48, 51 and 51, 60 and 23, 63 and 37, 64 and 25, 65 and 54 (critical FDR p=0.002)	13 connections: 7 and 7, 9 and 7, 9 and 9, 15 and 7, 23 and 8, 25 and 11, 25 and 23, 27 and 27, 29 and 18, 30 and 7, 30 and 9, 31 and 8, 35 and 7 (critical FDR p=0.004)	16 connections: 8 and 8, 9 and 1, 11 and 1, 22 and 18, 24 and 22, 31 and 17, 31 and 18, 31 and 22, 31 and 24, 31 and 25, 31 and 31, 35 and 3, 35 and 17, 35 and 24, 35 and 31, 35 and 35 (critical FDR p=0.004)
ADAS-13	10 connections: 15 and 13, 25 and 15, 28 and 20, 45 and 42, 46 and 40, 51 and 48, 51 and 51, 63 and 37, 64 and 25, 65 and 54 (critical FDR p=0.002)	13 connections: 7 and 7, 9 and 7, 9 and 9, 15 and 7, 23 and 8, 25 and 11, 25 and 23, 27 and 27, 28 and 18, 29 and 8, 30 and 7, 30 and 9, 31 and 8 (critical FDR p=0.004)	7 connections: 8 and 8, 11 and 1, 31 and 18, 31 and 22, 35 and 17, 35 and 24, 35 and 35 (critical FDR p=0.002)
CDR-Glob	28 connections: 14 and 12, 18 and 17, 20 and 12, 20 and 18, 20 and 20, 24 and 10, 25 and 15, 26 and 2, 27 and 14, 27 and 20, 27 and 24, 28 and 20, 30 and 11, 35 and 20, 43 and 10, 48 and 10, 48 and 25, 58 and 25, 60 and 13, 61 and 12, 61 and 26, 61 and 27, 61 and 28, 61 and 47, 61 and 61, 62 and 61, 63 and 37, 64 and 25 (critical FDR p=0.007)	23 connections: 7 and 7, 8 and 7, 8 and 8, 21 and 7, 23 and 8, 24 and 3, 24 and 10, 25 and 7, 25 and 8, 25 and 11, 25 and 13, 25 and 15, 25 and 17, 25 and 23, 25 and 24, 25 and 25, 28 and 3, 28 and 25, 28 and 28, 29 and 8, 29 and 25, 29 and 28, 30 and 7 (critical FDR p=0.007)	8 connections: 8 and 8, 29 and 8, 29 and 23, 29 and 29, 31 and 31, 35 and 24, 35 and 31, 35 and 35 (critical FDR p=0.002)
CDR-SOB	10 connections: 23 and 8, 24 and 10, 28 and 20, 30 and 11, 31 and 3, 37 and 37, 48 and 10, 48 and 25, 63 and 37, 64 and 25 (critical FDR p=0.002)	6 connections: 3 and 3, 7 and 7, 8 and 7, 15 and 7, 25 and 25, 28 and 3 (critical FDR p=0.001)	7 connections: 31 and 17, 31 and 25, 31 and 31, 35 and 17, 35 and 24, 35 and 31, 35 and 35 (critical FDR p=0.002)

Here we show various differences in brain networks that are associated with standard measures of clinical decline. Random effects regression tests were performed for clinical scores on the MMSE, CDR-Glob, CDR-sob, ADAS-11 and ADAS-13 in the whole brain, left, and right hemispheres separately for the k-cores of all subjects (controls, eMCI, MCI and AD) in connections present in 80% of subjects. We used site as a random regression variable, and controlled for age and sex. All the nodes that showed significant differences are listed. Significant connections that are common across all clinical scores are shown in bold and the critical FDR p-value for correcting over all valid connections is shown.

MMSE, Mini Mental State Examination; ADAS-11, 11 item Alzheimer's Disease Assessment Scale-Cognitive Subscale; ADAS-13, 13-item Alzheimer's Disease Assessment Scale-Cognitive Subscale; CDR-Glob, Clinical Dementia Rating Sum of Boxes; CDR-Glob, Clinical Dementia Rating Global Score; FDR, false discovery rate.

Effects on the fiber densities of the left and right hemispheres were found in cortical regions that mostly overlapped with the differences in the k-cores of AD subjects versus controls. Clinical test scores were all related to differences in some cortical regions—such as in the proportion of total fibers in the fusiform region for the left hemisphere, and in the proportion of total fibers in the supramarginal region for the right hemisphere in all subjects (except for the ADAS-13 score). All test scores increased as the fiber density of the k-cores decreased in the fusiform area of the left hemisphere, except for the MMSE score, which decreased as the fiber density also decreased. This result is expected, as higher MMSE scores denote better cognitive performance and higher scores on other tests represent greater cognitive impairment. For the right hemisphere, MMSE increased as the fiber density of the k-cores decreased in the supra-marginal region. In the meantime, ADAS-11, CDR-Glob, and CDR-SOB decreased as the fiber density also decreased in the supra-marginal region of the right hemisphere. Overall, there were no particular connections with significant correlations to all clinical scores; in fact, it was more that the aggregate number of connections linked with clinical scores was higher than would be expected by chance.

Left/right asymmetries in network

To further understand how these network alterations may differ by hemisphere with disease progression, we analyzed differences between left and right hemispheres in each group as well as the nodal degree measures applied to the structural k-core of each group. For these, we performed random effects regressions that returned significant differences between the left and right hemisphere connectivity matrices in each group: 28 controls, 57 eMCI, 11 lMCI, and 15 AD subjects (Fig. 3). We might expect the number of connections with significant asymmetries to increase, if the disease does not progress symmetrically, and if the variance does not also increase. For this, we computed the number of asymmetric connections for each subjects by taking the difference of the weighted connections (fiber densities) in the connectivity matrices between the left and right hemispheres and regressed it over the clinical scores while covarying for age and sex in all subjects and using site as a random regression variable. We found significant results for most scores with FDR critical p-values of 3.0E-03 for MMSE, 2.0E-04 for CDR-Glob, 4.0E-03 for ADAS-11, and 1.7E-03 for ADAS-13; no significant results were found for CDR-SOB. These results indicate that the asymmetry becomes more pronounced with disease progression. Similarly, as a post hoc exploratory test, we took the difference between the left and right hemisphere nodal degree measures in all subjects and regressed it against the clinical scores, while covarying for age and sex and using site as a random regression variable, but we did not detect significant effects.

Also, we performed random effects regression to test for differences between the left and right hemispheres in the weighted k-core and nodal degree. We found left-right hemisphere differences in the k-core matrices for all groups (Table 7). There were no significant differences in the network measures, nodal degree, efficiency, normalized characteristic path length, normalized clustering coefficient and normalized small-world between the left hemispheres in either diagnostic group. The number of k-core connections showed decreasing asymmetries between healthy and diseased for controls (151 connections), eMCI (145 connections), and AD (63 connections), except the lMCI group (nine connections) that might have been affected by the unevenly small number of subjects. We should also bear in mind that there are at least another two factors affecting the number of connections where asymmetries are picked up. First, the k-core loses nodes drastically as disease progresses, so the number of nodes present where asymmetry can be detected is falling rapidly. As such, there is a downward trend in the number of nodes showing an asymmetry. Second, one has to bear in mind that the sample size of the 4 diagnostic groups is uneven—28 for controls, 57 for eMCI, but only 11 for lMCI and 15 for AD. The power to detect asymmetry is higher when the sample size is higher, as a smaller effect size can be declared significant in a larger sample. Together, these processes seem to account for the changes in the number of connections declared asymmetric as the disease progresses.

Table 7.

Left-Right Asymmetries in Measures of Anatomical Brain Connectivity

	Left-right asymmetries
Network measures	Controls (28 subjects)	eMCI (57 subjects)	lMCI (11 subjects)	AD (15 subjects)
k-core elements	151 connections (p=0.020)	145 connections (p=0.027)	9 connections (p=0.0012)	63 connections (p=0.014)
NOD	NS	NS	NS	NS
EFF	NS	NS	NS	NS
λ	NS	NS	NS	NS
γ	NS	NS	NS	NS
SW	NS	NS	NS	NS

Connections that differed between left and right hemispheres, for the different diagnostic groups. Results are computed from a random effects regression model (using zeroes for the left hemisphere and ones for the right hemisphere) comparing the weighted k-core measures between the left and right hemispheres in 28 controls, 57 eMCI, 11 lMCI and 15 AD subjects (not all connections are named in this paper due to space limits), as well network measures applied on the binarized k-core matrices. The p-values reported here are the FDR critical p-values.

Analyzing the stability of the structural core: perturbation of k levels

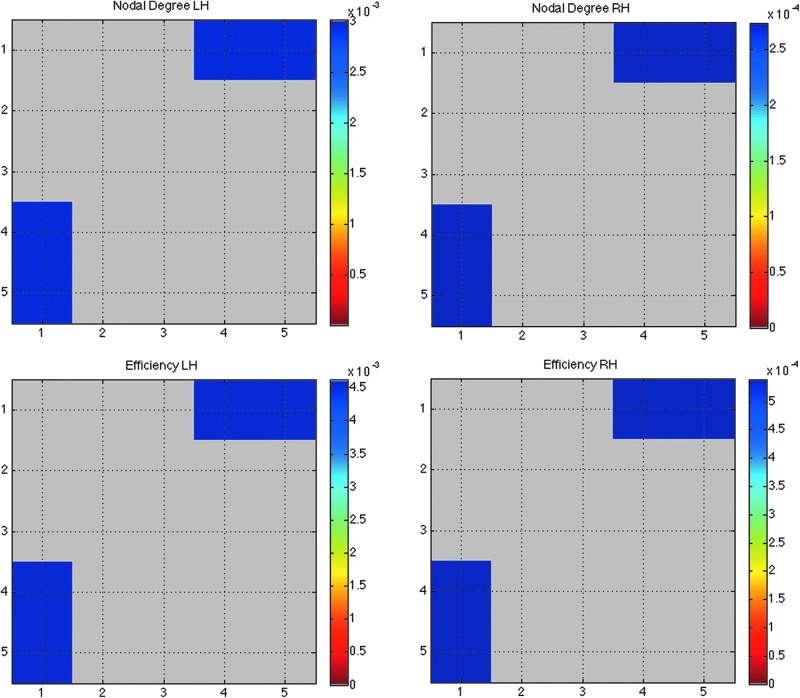
To understand how the different thresholds (different levels of k-core) affect graph theory measures, we computed the structural backbone using k=16, 17, 19 and 20, in addition to k=18 in all 111 subjects. We compared how the nodal degree, and the network efficiency—perhaps the most commonly computed measure in brain connectivity studies—changed as a function of k. We compared every k-level across all subjects in the whole brain, left, and right hemispheres separately with every other k-level in that group (i.e., nodal degree for all subjects at k1=16, 17, 18, and 19 was compared to nodal degree in all subjects at k2=(k1+1)=17, 18, 19 and 20 using a two-tailed paired t-test and performed FDR correction on all (5×5−5)/2 comparisons. Nodal degree FDR critical p-values in the left and right hemispheres are 3.0E-03 and 2.7E-03 and efficiency FDR critical p-values in the left and right hemispheres are 4.5E-03 and 5.4E-04 (Fig. 4).

FIG. 4.

Effects of perturbations in the k-core threshold on nodal degree and efficiency. Matrix (5×5) representing the p-values from a two-tailed t-test comparing nodal degree and efficiency measures across five k-levels (k=16,17,18,19 and 20) in all 111 subjects (nodal degree FDR critical p-values in the left and right hemispheres are 3.0E-03 and 2.7E-03 and efficiency FDR critical p-values in the left and right hemispheres are 4.5E-03 and 5.4E-04). In other words, we compared k-levels k1={16,17,18,19} to k2=(k1+1)={17,18,19,20} across all subjects. There were no significant differences across k-levels in the whole brain in all 111 subjects. The greatest differences in the network measures were found between lowest and highest k-values (blue p-values).

Discussion

Here we report how AD affects structural brain connectivity in a sample of 111 subjects (comprising patients, controls, and those at risk of AD). We studied fundamental anatomical brain subnetworks called the “k-cores”. AD affected a variety of network metrics describing the topological organization of the brain's white matter. From the k-cores, we determined the most highly interconnected networks in the left and right hemispheres and analyzed whether these regions remained intact or altered with disease progression. The k-core was found to be a useful distillation of the overall brain network, rather than using the full connectivity matrix, as it eliminated the least reliable connections; these less reliable connections can arise due to tract tracing errors. To the extent that they do contain errors, this may worsen the signal-to-noise ratio and make it more difficult to detect disease effects. As an empirical observation, the k-core did indeed enhance the disease effects, as the entire k-core was “lost” in the left hemisphere of AD subjects. These findings are important to locate brain regions that change with disease progression. Ultimately they may help in assessing effects of treatments, or other interventions, on the brain.

We found significant differences between the left and right hemisphere connectivity matrices in all subjects (FDR critical p=0.037), which led to further analyses of the core networks that survived with disease progression. In our k-core analyses comparing AD subjects to healthy controls, all the k-core elements in the left hemisphere were lost in AD subjects, suggesting that brain network topology changes drastically with disease progression (Fig. 1). We must emphasize that this does not mean that those fibers are completely absent in AD, but the thresholding implicit in creating the k-core homes in on the highly connected elements. So, according to this definition, none of these highly connected elements remained in the left hemisphere in AD. The main connections and regions that significantly differed in their k-core topology between controls and AD were found between the middle temporal and fusiform, inferior temporal and fusiform, pars triangularis and caudal middle frontal, precentral and caudal middle frontal, rostral middle frontal and pars opercularis, and superior parietal and lingual; also, a significant difference in the proportion of total fibers was detected in the following regions: fusiform, precuneus, and rostral anterior cingulate. Some of these nodes are part of the temporal and parietal lobes, which are known to be among the earliest regions consistently affected by AD pathology (Thompson et al., 2003). Yao and colleagues (2010) analyzed the “structural brain network” in patients with AD, and found that the regions that showed the most significant changes in the interregional correlations between 98 controls and 91 AD include the temporal lobe, fusiform, superior parietal region and orbital frontal gyrus (Xie and He, 2012; Yao et al., 2010). Most of these regions showed differences here, in groups with progressively advancing disease. We note, however, that the Yao and colleagues analyses assessed correlations among regional volumes using standard anatomical MRI. This is not the same definition of brain connectivity as that involved here with DTI, which assesses pathways between brain regions.

We computed five important network measures—global nodal degree, normalized characteristic path length, efficiency, normalized clustering coefficient and normalized small-worldness—that may be useful in the future as possible new biomarkers of AD. Nodal degree decreased with disease progression by 23% in the whole brain, 21% in the left hemisphere and 19% in the right hemisphere of AD subjects compared to controls. The normalized characteristic path length decreased by 22% in the whole brain, 20% in the left hemisphere, and 17% in the right hemisphere. Efficiency decreased by 24% in the whole brain, 22% in the left hemisphere of AD subjects compared to controls, and by 19% in their right hemisphere. This indicates that the disease effects can be quantified using network efficiency measures in the early stages of the disease such as in eMCI and lMCI patients. Here both efficiency and normalized path length measures were found to decrease. It is important to note that efficiency is expected to increase as characteristic path length decreases only when the path length is unnormalized. Path length should be normalized using appropriately constructed random networks, as the absolute (unnormalized) value of the path length provides limited information on the integration in the brain network (Sporns, 2011); the path length varies greatly with the size and density of individual graphs, whereas efficiency is a more robust measure—the average of the inverse of the distance matrix (Sporns, 2011), and was not normalized here. Also, the decrease in global efficiency is in general agreement with previous structural connectivity studies (Lo et al., 2010), bearing in mind the differences between the studies in acquisition and analysis. A lower efficiency may suggest a less optimal organization of the brain network structures in AD subjects (Xie and He, 2012) and perhaps even reduced signal propagation among brain regions (Lo et al., 2010).

Meanwhile, the normalized small-world effect increased by 47% in the whole brain, 28% in the left hemisphere and 23% in the right hemisphere of AD subjects, compared to controls. The increase in the normalized small-world effect was consistent among the eMCI and lMCI subject groups (Fig. 2). Small-worldness depends on several factors that are all changing in AD, and the results of all the changes may be nonintuitive or not predictable at the outset. Small-worldness may be a biologically or functionally advantageous property, as it is found in many biological networks and may be functionally advantageous relative to random networks. As such, one might not predict that the property would increase in AD, as there is clearly no functional advantage to having AD. Compared to random networks, which tend to have short average path lengths and relatively low clustering, the small world effect tends to be higher when a network has a high level of clustering, or when the average path lengths become shorter. This is because the small-worldness is based on the ratio of the clustering coefficient to the path length, after normalizing each of those to values in a random network. The loss of fibers in AD can remove some connections from a network that is thresholded based on the nodal degree. This led to a decrease in average normalized path length in the whole brain, left, and right hemispheres, while the normalized clustering coefficient increased in the whole brain by 13% (and did not change significantly in the left and right hemispheres), so the normalized small-world effect also increased in the whole brain, left, and right hemispheres. The increase in clustering coefficient does not always indicate a densely interconnected and coherent brain system; in fact, it can be disproportionately influenced by nodes with low nodal degree, which is a phenomenon observed in AD–the nodal degree decreases relative to controls (Fig. 2).

Furthermore, we found network asymmetries—between left and right hemispheres—in all diagnostic groups. This is not entirely surprising: as shown Figure 3, there is a clear asymmetry between the left and right hemisphere networks, regardless of the diagnostic group. This may even intensify as the disease progresses as the clinical scores between the left and right hemisphere connectivity matrices were significantly different. Regions with connectional asymmetry were scattered all over the brain. A related pattern of diffuse asymmetries was also observed in a recent developmental study of adolescents and young adults (Daianu et al., 2012a). These increasing asymmetries may be due to age or disease, or both, and it is not clear whether they are harmful or benign.

We further analyzed the differences in the k-core, nodal degree, normalized characteristic path length, efficiency, normalized clustering coefficient, and normalized small-world effect of the k-core in the left and right hemisphere in all groups (Table 7). We found differences in all diagnostic groups for the k-core measure; however, no differences were found for the rest of the network topology measures between the left and right hemispheres. We previously reviewed evidence for asymmetries in disease progression in AD (Thompson et al., 2003); evidence is mixed, and not all studies support an asymmetry, but the differences in connectivity measures and their variance by hemisphere make it plausible that some connections may show stronger differences in one hemisphere than the other. To corroborate this, longitudinal data will be helpful, when available, from a period long enough to show substantial decline.

Another important aspect to consider is that highly connected k-cores contain hubs that are thought to facilitate integrative processes due to their densely connected nodes. Hubs have high nodal degrees and tend to form a rich club—a set of high-degree nodes that are more densely interconnected among themselves than nodes of a lower degree (see, e.g., van den Heuvel and Sporns, 2011, which describes the rich-club organization of the human connectome). The “rich club of the hubs” is a related but separate concept from that of the k-core—used in the current study—as the rich club coefficient evaluates a range of k-core matrices (i.e., with k=1, 2, 3…, etc.); here, we analyzed the k-core at k=18 because this was the minimal value for which the majority (>50%) of nodes within each hemisphere would still remain connected. At k=18, we have a highly and mutually interconnected network of the brain. However, a smaller k value (<18) will apply a lower threshold to the network, including nodes with lower degrees, and leading to less interconnected networks. Recently (in Daianu et al., 2013), we found that the rich club coefficient increased in AD with increasing k and decreasing nodal degree in the residual k-core (i.e., when a smaller percentage of nodes are retained), relative to controls. The rich club is a slightly more elaborate concept than the k-core. The k-core is simply a network—part of the original network—found by thresholding the network to retain only those nodes with high nodal degree (i.e., with degree k or higher). The rich club coefficent, Φ(k), is a ratio of the number of connections among nodes of degree k or higher versus the total possible number of connections if those nodes were fully connected. The rich club is a more complex notion than the k-core: it is a function defined on all the k-cores, which can be tested statistically for signs of rich club organization.

To test the reliability of our measures, we analyzed the stability of the structural core at k=18 by comparing the k-core in all subjects over a variety of k-levels. Based on a two-tailed paired t-test, the perturbation in the k-levels was significant between the minimum and maximum k-level comparisons for the networks measures (nodal degree and efficiency) in the left and right hemispheres separately, while these perturbation did not affect the network measures significantly in the whole brain in all 111 subjects (Fig. 4). All significant changes were found between k-levels 16 and 19 and 16 and 20 for nodal degree and efficiency. There were no significant changes with small perturbations of k-levels (i.e., between k and k+1); as described above, all changes were detected between levels k and k+3 as well as k+4 (i.e., k=16 and k=19).

This study has several limitations. Our study was conducted at 3 T, so connectivity studies at higher fields, or with different protocols, may reveal group differences in additional regions (in Zhan et al., 2013a, we compare connectivity computed at 7 and 3 T in the same subjects). Even so, the use of higher fields may not necessarily become standard for academic or clinical studies in the near future. Another limitation of our work, is the small and uneven number of subjects in each diagnostic group (28 controls, 57 eMCI, 11 lMCI and 15 AD subjects). ADNI2 subjects are continuing to be scanned, so our future work will assess larger cohorts to verify how connectivity measures change over time as AD progresses. In future work, we will also aim to study the specific effects of amyloid pathology on brain network dysfunction using amyloid imaging. These changes may have a tighter relationship to amyloid than to clinical diagnosis, although that remains to be evaluated.

Another factor to consider is the tractography method used. In this paper, we generated around 10,000 fibers per subject, using the Hough transform method (Aganj et al., 2011), but some other tractography algorithms such as FACT (Mori et al., 1999) and TEND (Lazar et al., 2003) generate up to hundreds of thousands. As such, it is of interest whether this density of sampling is sufficient to compute network metrics that are stable, and have converged, and have sufficient power to pick up group differences. Our group previously studied the effect fiber density has on network measures and on the power to distinguish disease effects (Prasad et al., 2013). High-density fiber matrices were most helpful for picking up the more subtle clinical differences. However, based on the current study, the networks in AD are significantly different from controls so that the inference about differences between controls and diseased might not be influenced by fiber counts. One final limitation is our use of thresholding to define the k-core, even though the threshold was chosen in a principled way. Other mathematical work (Lee et al., 2012) has defined novel distance metrics on filtrations of networks, in an attempt to retain the full information on the set of all networks defined by thresholding the nodal degree at different thresholds. However, we tested the reliability of our structural core at k=18 by comparing it to k-cores computed at k=16, 17, 19 and 20 and found that immediate k-levels do not perturb the structural network significantly. Clearly, these and other more advanced metrics on graphs and graph filtrations may also show promise in defining how networks decay and change as disease progresses.

Conclusion

In this study, we tested for alterations in the core graph of connections in the brain caused by disconnections in AD and how the clinical progression of AD affects network measures and possibly, network asymmetries in the brain. We found that AD wipes out the core connections in the left hemisphere, relative to controls, and affects the topology of the brain network—therefore, altering the network measures. Lastly, we found that network asymmetries were present in all diagnostic groups and may intensify with disease progression.

Acknowledgments

Algorithm development and image analysis for this study was funded, in part, by grants to P.M.T. from the NIBIB (R01 EB008281, R01 EB008432). Data collection and sharing for this project was funded by the Alzheimer's Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: Abbott; Alzheimer's Association; Alzheimer's Drug Discovery Foundation; Amorfix Life Sciences Ltd.; AstraZeneca; Bayer HealthCare; BioClinica, Inc.; Biogen Idec, Inc.; Bristol-Myers Squibb Company; Eisai, Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; F. Hoffmann-La Roche Ltd. and its affiliated company Genentech, Inc.; GE Healthcare; Innogenetics, N.V.; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research and Development, LLC.; Johnson and Johnson Pharmaceutical Research and Development, LLC.; Medpace, Inc.; Merck and Co., Inc.; Meso Scale Diagnostics, LLC.; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Servier; Synarc, Inc.; and Takeda Pharmaceutical Company. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer's Disease Cooperative Study at the University of California, San Diego. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of California, Los Angeles. This research was also supported by NIH grants P30 AG010129 and K01 AG030514.

Author Disclosure Statement

No competing financial interests exist.