Set size, individuation, and attention to shape

Abstract

Much research has demonstrated a shape bias in categorizing and naming solid objects. This research has shown that when an entity is conceptualized as an individual object, adults and children attend to the object’s shape. Separate research in the domain of numerical cognition suggest that there are distinct processes for quantifying small and large sets of discrete items. This research shows that small set discrimination, comparison, and apprehension is often precise for 1–3 and sometimes 4 items; however, large numerosity representation is imprecise. Results from three experiments suggest a link between the processes for small and large number representation and the shape bias in a forced choice categorization task using naming and non-naming procedures. Experiment 1 showed that adults generalized a newly learned name for an object to new instances of the same shape only when those instances were presented in sets of less than 3 or 4. Experiment 2 showed that preschool children who were monolingual speakers of three different languages were also influenced by set size when categorizing objects in sets. Experiment 3 extended these results and showed the same effect in a non-naming task and when the novel noun was presented in a count-noun syntax frame. The results are discussed in terms of a relation between the precision of object representation and the precision of small and large number representation.

1. Introduction

The words we use to describe sets of items often vary with the number of items. We may talk about a person or some people when there are a few, but if the group is large enough, it becomes a crowd, a mass, or a mob. Our way of speaking suggests that group size influences our perception of individuality (see Middleton, Wisniewski, Trindel, & Imai, 2004 and Wierzbicka, 1988); it is as if individuals lose their identity in large sets. Here we examine the role of set size in how people categorize the individual objects in a set. The specific empirical question is studied in the context of two well-documented phenomena. The first concerns children’s bias to generalize names of objects by shape. The second concerns the effect of set size on the precise quantification of sets of discrete individuals.

1.1. Objects, shape, and quantification

When young children are shown a novel object, told its name, and then asked to generalize that name to new instances, they typically extend the name to objects of the same shape (Landau, Smith, & Jones, 1988; Soja, Carey, & Spelke, 1991). This bias to attend to shape when categorizing objects is consistent with the statistical regularities that characterize early-learned basic-level nouns; in English, basic-level nouns tend to name instances that share a common shape (Samuelson & Smith, 1999). Further, this categorization is related to syntax. In English, nouns are syntactically partitioned into categories of count and mass: count nouns take discrete quantifiers and the plural whereas mass nouns take continuous quantifiers and are not pluralized. The shape-based noun categories that dominate early-learned nouns are overwhelmingly count nouns, whereas nonsolid substances categorized by material are typically (the much less frequent) mass nouns within early vocabularies (Samuelson & Smith, 1999). Young children learning English are highly sensitive to the correlation between linguistic quantification and shape-based categories. When a novel object name is presented in a count-noun frame, categorization by object shape increases; when the name is presented in a mass noun frame, categorization by shape decreases (McPherson, 1991; Soja, 1992). Syntax, however, is not the only cue that increases categorization by shape; indeed, narrative frames or contexts that encourage conceptualization of an entity as a discrete object also increase generalizations to same shaped objects in novel noun learning tasks (Gelman & Bloom, 2000; Kobayashi, 1997; Lavin & Hall, 2001; Prasada, Ferenz, & Haskell, 2002). Other factors exist such as function and experienced instances that influence categorization (e.g., Blair & Somerville, 2009; Graham, Namy, Gentner, & Meagher, 2010; Hammer & Diesendruck, 2005; Hammer, Diesendruck, Weinshall, & Hochstein, 2009); however, within English, there is a strong relation between thinking and talking about an entity as an individual and attention to its shape.

Although languages of the world differ remarkably in how they individuate instances, much research suggests that the link between the conceptualization of a thing as a discrete object and categorization by shape holds across a variety of languages (Gathercole & Min, 1997; Imai & Gentner, 1997; Li, Dunham, & Carey, 2009). Japanese, for example, has no syntactic distinction similar to the count-mass distinction in English and no plural. This led to early hypotheses that speakers of the two languages might quantify or conceptualize objects differently (see Lucy, 1992); however, common object nouns in Japanese name categories of individual things that are similar in their shape just as do the comparable noun categories in English, and young children learning Japanese—like their counterparts learning English—also generalize names for novel objects by their shape (Colunga & Smith, 2000). Further, when asked to determine the quantity of sets, Japanese and English speakers do so in the same way. Specifically, when presented with sets of things that are instances of shape-based noun categories across the two languages (and that are labeled by count nouns in English), speakers of both languages judge quantity in terms of the discrete number of items. In contrast, when presented with sets containing nonsolid, continuous substances (that are labeled by mass nouns in English), speakers of both languages judge quantity in terms of total amount of stuff (Barner & Snedeker, 2005; Barner, Inagki, & Li, 2009). These findings are consistent with results from speakers of a variety of other languages, as well (Imai & Gentner, 1997; Li, Barner, & Huang, 2008; Roberts & Gathercole, 2006). Altogether, the results across languages and among early-learned noun categories suggest a relationship between conceptualizing entities as discrete things and categorization by shape. This leads to the following hypothesis: any task factor that decreases the likelihood that an entity is conceptualized as an individual thing should decrease the likelihood of categorization by shape.

1.2. Precise quantification for small sets and imprecise quantification for large sets

Without explicit counting, children and adults discriminate, compare, and quantify small sets of discrete items precisely but do not do so for large quantities (e.g., Feigenson, Carey, & Hauser, 2002; Kaufman, Lord, Reese, & Volkmann, 1949; Taves, 1941; Trick & Pylyshyn, 1994; Xu & Spelke, 2000; see also Cantlon, Platt, & Brannon, 2009 and Feigenson, Dehaene, & Spelke, 2004 for reviews). Precise quantification appears possible for sets of 1–3 and perhaps 4; direct apprehension of larger sets yields only an estimate of quantity and not an exact number. Although large set quantification is not exact, it is important to note that large numerositities are not represented as indistinguishable amounts in cognition. Results from many studies demonstrate that adults and children are quite good at discriminating large quantities of discrete items and do so in psychophysically lawful ways (Cantlon, Safford, & Brannon, 2010; Whalen, Gallistel, & Gelman, 1999; Xu & Spelke, 2000). The key point from studies of numerical quantification and for the present argument is this: discrimination and comparison of large sets is imprecise whereas small set quantification is exact. Moreover, some researchers have suggested that different systems underlie the representation of small and large sets (Carey, 2009; Feigenson et al., 2004, but see Cantlon et al., 2009 and Cordes, Gelman, Gallistel, & Whalen, 2001 for an alternative approach).

Carey (2009) and Feigenson et al. (2002) specifically proposed that the precision for small set sizes and the lack of precision for large set sizes is due to limitations on the number of discrete entities that can be individually represented in spatial working memory—a proposal that is consistent with theories of object tracking and subitizing (Kahneman, Treisman, & Gibbs, 1992; Trick & Pylyshyn, 1994). According to this view, the direct apprehension of number is limited to small set sizes because of the limit on the number of distinct entities that can be simultaneously represented in working memory (also known as parallel individuation, which is maximally 3 or 4 items). From this perspective, the precision of small set quantification is mediated by and therefore also potentially limited to the number of individual object file representations that can be maintained in working memory. In contrast, the imprecise quantification of large sets reflects a noisier analogue magnitude system that does not depend on working memory representations of the individual entities.

Are the differences in quantification of small and large numerosities related to the representation of individual items in small and large sets? In small sets, each individual may be apprehended and represented as such. By inference, the items in large sets may be less individualized; the perceiver may apprehend that there are many items without precisely representing each element with its respective properties. In this way, the distinction in precision of small and large set quantification may be related to representing the individual identity of items in sets and may in turn be related to how we conceptualize the items in small and large groups; that is, precision and imprecision for small and large sets may be related to how we think about a few people versus a crowd, and—as we test here—whether we attend to the individual shapes of the items. In sum, increasing set size should decrease the likelihood of representing each element as an individual and therefore also decrease the likelihood of categorizing those items by their shape.

1.3. Rationale for the experimental approach

We tested this prediction using variants of the novel-noun generalization task because this is a task in which both children and adults typically categorize individual objects by their shape and a task in which shape categorization has been shown to be sensitive to factors related to individuation. We used the kinds of stimuli (solid, well-defined forms) that result in robust categorization by shape when presented as single objects. In the experimental task, participants were shown a single exemplar object that was labeled with a novel name. The referent of the name is thus unambiguously about a single individuated thing; therefore, the expectation from past research is that participants will represent the named object as an individual, will attend to its shape, and will generalize the name to new items by shape. The experimental procedure tests adults’ and children’s ability to do this when the shape matching and alternative choices are presented in small and large sets. In Experiment 1, the participants were adults. In Experiment 2, the participants were 3–5-year-old children who were monolingual speakers of three different languages— English, Japanese, and Spanish. If the hypothesized effect of set size on shape categorization is due to fundamental properties of working memory and object representation, then the effect should be observed for speakers of different languages— despite their different systems for marking discrete and continuous entities. Experiment 3 replicated and extended the findings with English-speaking children comparing shape categorization in this task when objects were unnamed as well as when objects were presented in explicit count-noun syntax.

2. Experiment 1

2.1. Method

2.1.1. Participants

Forty undergraduates, (15 males) all monolingual speakers of English, received class-credit for participation.

2.1.2. Stimuli

As shown in Fig. 1, for each of 6 unique exemplars, there were six shape-matching collections with set sizes of 1, 2, 4, 6, 15, and 25 and 6 material (color and texture) matching items with a set size of 1. Three aspects of the stimulus sets were controlled: (1) the area covered by the sets was held constant across set sizes, (2) the distance between items in a set was held constant, and (3) the shapes and materials were selected such that when the material and shape matching choices were at a set size of 1, participants chose the shape match and did so when the exemplar and shape matching object differed by the maximum amount in size (e.g., when shape matching choice was 1/25 the size of the exemplar). These constraints on the stimulus sets are described below.

Fig. 1.

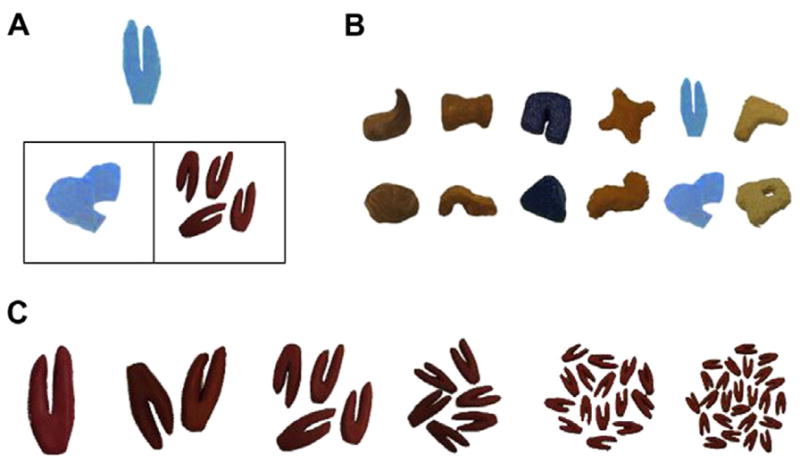
(A) Structure of the task, (B) exemplars and material matches and (C) example of shape matching set sizes.

The overall amount of material was controlled such that the exemplar, material match, and sets of shape matching objects covered approximately an 8 × 8 cm area when placed on the presentation tray. The proximity of the individual units in the collection sets was approximately the same within each collection such that the items were within 1/2 cm of one another but were not touching (that is, there was perceptible space between each element).

Because amount of material was controlled across sets, the size of elements in the shape matching sets decreased as set size increased. We chose to control for total amount of stuff rather than element size because past research has shown that object size (even 100 times differences in size) does not affect preschoolers’ attention to shape in novel noun generalization tasks (Landau et al., 1988). Because the goal is to examine the effect of set size in a task in which shape matches should dominate when choices are made between single individual objects, we also documented that this was the case for adults in a pilot study given the shapes, materials, and using the largest and smallest sized objects in the experiment. More specifically, in this stimulus-validity pilot study, adults were tested with each exemplar and a single shape-matching element from either the largest set collection (and thus the smallest instance of that shape) or a single shape match that was the same size as the exemplar (from the set size 1). The procedure of the pilot study was the same as in the main experiment. Adults in this pilot study chose the shape matching item greater than 80% time both when the shape match was the same size as the exemplar as well as when the shape match was very small; there was no difference between the shape matching choices in the two object size conditions, t(19) = −.038, p = .89. The experimental question is whether changes in the set size in which the shape matching object is presented affects the likelihood of these choices.

2.1.3. Procedure

Because English is a count-mass language, it is difficult to name entities or ask for categorization choices in a neutral way that does not suggest an object or substance construal. Accordingly, in a prior pilot study with trials structured identically to those in the experiments but using objects and substances with known names (cup and sand), we tested phrasings and chose those that were judged acceptable with both kinds of nouns and with both small and large set sizes (Look at this cup/Look at this sand. Find more). In the experimental task, adults were first shown the exemplar and then shown two choices: a shape matching collection set and the material match. The experimenter said, pointing to the exemplar, “Look at the tiso,” and then, while pushing the tray with the choices forward, said “Find more.” Choices of one, several, or all of the items from the shape-matching set were considered a shape matching response. Each exemplar was named with a unique novel name (tiso, siba, mali, doff, coopa, and temu).

To limit possible carry-over effects, a between-subjects design was used. Each adult was assigned to one of the following set size conditions: a 1–2 set size, 4–6 set size or 15–25 set size. In each of the conditions, adults made six judgments, three within each of the two set sizes to which they were assigned. No exemplar was repeated. Two different random orders of trials were used within each set size condition.

2.2. Results

Fig. 2 shows the main result: Adults categorized by shape when shape-matches were presented in sets of one or two but not when presented in sets of four or more. A one-way ANOVA comparing shape matching choices as a function of Set Size (Set 1–2, Set 4–6, and Set 15–25) revealed a main effect, F(2, 39) = 3.26, p = .05 and post hoc analyses (α = .05, Tukeys hsd) showed that the difference between adult responses in the Set 1–2 and Set 15–25 conditions approached significance (p = .058) whereas the two largest set size conditions did not differ reliably from one another. Paired t-test comparisons of the two different set sizes within a condition yielded no reliable differences. Shape matching choices differed reliably from chance in only the Set 1–2 condition, t(12) = 2.86, p = .01. There were individual differences within the set size conditions. Specifically, 25% of the adults in the Set 4–6 condition and another 25% in the Set 15–25 condition chose the shape-matching set on more than 80% of the trials; these adults thus did not show the decreased attention to shape at larger set sizes that characterizes the group results.

Fig. 2.

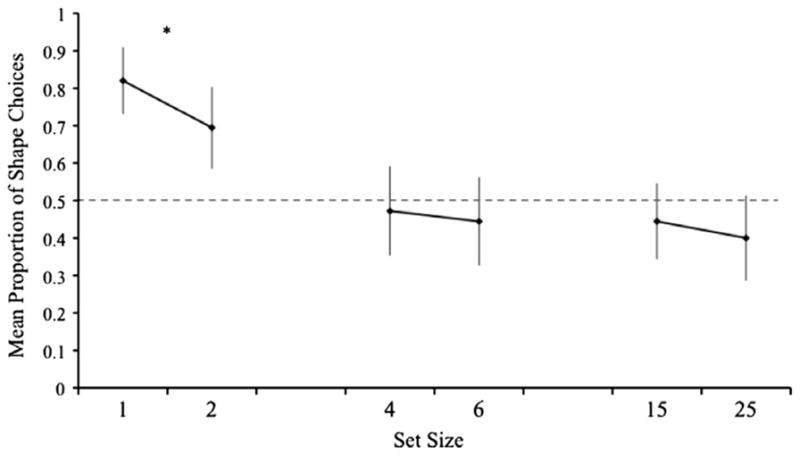
Adults’ shape match responses as a function of set size in Experiment 1.

Overall the results suggest that the number of items in a set influences attention to and categorization by shape; adults are more likely to attend to the shapes of objects in small sets than they are to the shapes of objects in large sets. It is as if, given a set of many same shaped items, perceivers do not focus on the individuating properties of the objects such as shape; rather, adults may focus on the material of the items or the numerosity of the set. The finding that this effect of set size characterizes the choices of many but not all adults may also be informative. Since there was no time limit on how long adults could inspect the objects, they could have expended time and effort to single out and perceptually individuate elements. Some adults—those who made shape matches at the larger set sizes—may have done so; but critically, for most adults, the shapes of the individual items is not the most salient property when making category decisions involving sets with four or more items.

3. Experiment 2

Experiment 2 used the same task as in Experiment 1, but tested 3–5 year old children. The participants were children who were monolingual speakers of three different languages: English, Spanish and Japanese. These languages differ in how they individuate nouns; past research has shown cross-language differences in some aspects of the shape bias for children learning these languages (Colunga, Smith, & Gassar, 2009; Gathercole & Min, 1997; Hahn & Cantrell, 2012; Imai & Gentner, 1997; Yoshida & Smith, 2003). Thus, the comparison of children speaking these different languages provides a strong test of the universality of the effect of set size on individuation and attention to shape; if the effect is supported by basic perceptual and cognitive processes then set size should affect speakers across languages with varying ways of marking individuation.

3.1. Method

3.1.1. Participants

Participants were 208 children, 3–5 years of age who were monolingual speakers of English (n = 88, 39 males, age range = 35.3–69.6, mean age = 52.3 months), Spanish (n = 77, 46 males, age range = 36.8–70.7 months, mean age = 54.3 months) or Japanese (n = 43, 23 males, age range = 36–59.8 months, mean age = 51.1 months). The English-speaking children were tested in daycares in Bloomington, Indiana. The Spanish-speaking children were tested in daycares in Mexico City, Mexico, and the Japanese-speaking children were tested in daycares in Fujiyoshida, Japan. To examine possible age-related changes in performance, the children in each language group were also partitioned into younger (36–53 months old) and older (54–71 months old) children.

3.1.2. Stimuli

The stimuli were the same as in Experiment 1. A pilot test with eight 3–5 year old English-speaking children and similar to that with adults was conducted to ensure that children could identify and match the exemplar and shape-matching test object by shape even when the exemplar was large and the test objects were very small. Children in the pilot study were tested in a novel noun generalization task using the exemplars and single shape match items from the largest set sizes. The distractor objects—in contrast to the analogous pilot study with adults—did not match the exemplar on any property. Children chose the shape-matching object—despite the maximum size difference in the stimuli sets—100% of the time.

3.1.3. Procedure

Children were tested in their native language by an experimenter fluent in that language. The phrasings used in each language were neutral to the conceptualization of the named entity as an object or a substance. The phrasings in each language were chosen to be acceptable translations (as judged by a native speaker of each language) of each other (in both directions). Because of this constraint, the phrasing in English differed slightly from that used with adults in Experiment 1. In English the experimenter said, “Look at the tiso. Find the tiso here.” In Japanese the experimenter said, “Kore wa tiso dayo. Jya, tiso sagashite,” and in Spanish the experimenter said, “Mira el tiso. Busca el tiso aquí.” If, in response to this request, a child selected by pointing, picking up, or giving one, several, or all of the items from the shape matching set, it was scored as a shape-matching response. All other aspects of procedure and design were the same as in Experiment 1.

3.2. Results

As shown in Fig. 3, children’s shape matching responses decreased as set size increased. An ANOVA for a 2 (Younger vs Older) by 3 (Language) by 3 (Set Size condition) design yielded only a main effect of Set Size, F(2, 190) = 11.33, p < .01. Post hoc analyses (Tukeys hsd, α < .05) revealed reliable contrasts between all three conditions, with children choosing shape matches more often in Set 1–2 than Set 4–6 (p = .03), and more often in Set 4–6 than in Set 15–25 (p < .01). Further, shape choices were reliably above chance in Set 1–2, t(64) = 4.29, p < .01, and reliably below chance in Set 15–25, t(62) = −3.81, p < .01. There were no reliable differences of set size within each of the three conditions. Unlike the adult data in Experiment 1, there was no evidence of individual differences at the smallest (1–2) or largest set sizes (15–25). However, at the 4–6 breaking point, some children (40%) chose the shape match more than 80% of the time, whereas some (41%) chose the material match more than 80% of the time. The evidence from the children, like that from the adults, indicates that the number of items in a set influences attention to the shapes of those items.

Fig. 3.

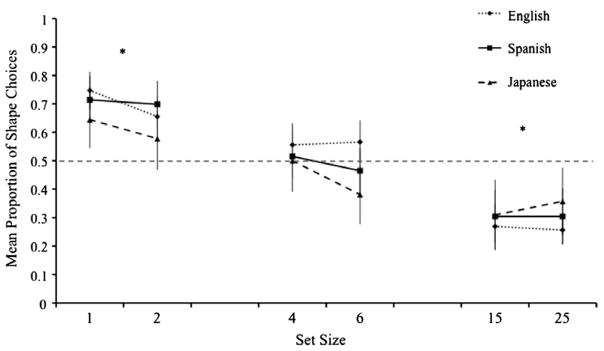
English-, Spanish-, and Japanese-speaking children’s shape match responses as a function of set size in Experiment 2.

The pattern in the child data is like that of the adults in that shape matches dominate choices in sets sizes of 1 or 2 but not in set sizes of 4 or greater. The finding that the upper limit (albeit in the present task with the present stimuli) is 4 may be interesting in that this is the proposed upper limit on the number of items that can represented by the object file system and that can by precisely quantified. The pattern from the child data differs from the adult pattern in that the material match dominates at large set sizes for children, whereas there are individual differences among adults in shape or material choices at these large set sizes. One explanation for this developmental difference is the lack of time constraints in this task, which, as we suggested earlier, may also be responsible for the individual differences observed in the adult data. Given unlimited time, some adults may have expended extra cognitive effort to visually isolate the individual objects in an array leading to less of a decrease in shape matching responses at the highest sets sizes. Children may be much less likely to do this without other visual or linguistic supports (see Cowan, 2001; Feigenson & Halberda, 2004).

4. Experiment 3

Nouns name individuals and cue attention to their shape. It is therefore possible that the observed effect of set size in this task is due to children’s (and adults’) expectations about how people talk about individuals and sets. Although the results of Experiment 2 show no cross-linguistic differences in the relation between set size and attention to shape, the task was a naming task for all children and thus might have activated expectations that characterize speakers of all these languages about how names map to kinds of categories. Accordingly, in Experiment 3, we compare English-speaking children’s judgments in two conditions: a noun generalization task in which the novel noun was presented in an explicit count noun frame (including plural marking) and a categorization task in which children were asked to find unnamed “matches.”

The embedding of novel object name in a count-noun frame is of particular interest because count-noun syntax has been shown to increase English-speaking children’s categorizations by shape when the stimuli are ambiguous with respect to their status as an object or substance (Soja, 1992). If children’s choices in Experiment 2 reflect the ambiguity of the elements of large sets as individual objects, then explicit count noun syntax might effectively compete with the set size effect. Alternatively, set size might pose an overwhelming influence on individuation such that objects are not individuated and shape is not attended to even when linguistic marking explicitly indicates that the items in the set are discrete individuals.

Experiment 3 also used a non-naming version of the task because some studies of the shape bias suggest decreased attention to shape when objects are not named (Jones, Smith, & Landau, 1991; Landau et al., 1988;). If children’s choices primarily reflect what they know about how people talk about objects and sets, then an effect of set size on shape choices might not be observed in this condition. If, in contrast, the number of entities in a set is a strong determiner of whether the elements are conceptualized as individuals, then an effect of set size on the likelihood of shape categorizations may be evident even in a non-naming categorization task.

Additionally, Experiment 3 altered the nature of the choices. In Experiments 1 and 2, a single standard was presented to the participants; the two test options were a choice between a shape match that differed from the exemplar in material (and often number) and a material match that differed in shape from the exemplar but always matched the exemplar in the number (it was always one item). Thus, in Experiment 2 children might have switched from choices that matched in shape for small set sizes to choices that matched in material or to choices that match in number for large set sizes (Cantlon, Fink, Safford, & Brannon, 2007; see also Cantlon & Brannon, 2007). To examine whether the decrease in shape matching choices at higher set sizes (and the preference for material matching choices) was the result of numerical matching between the material and exemplar object, in Experiment 3, the two test choices always differed from the exemplar in number by the same ratio. That is, the two test choices (shape match and material match) were the same number of items and the number of the elements comprising both choices varied together across the set size conditions.

4.1. Method

4.1.1. Participants

Participants were 135 children (52 males), 3–5 years of age (range = 37.8–69.6, mean = 54.1 months) who were monolingual speakers of English. The children were tested in daycares and in the laboratory in Bloomington, Indiana. The children were partitioned into younger (36–53 months old) and older (54–71 months old) groups to again test for any age related effects that might be related to the two linguistic conditions.

4.1.2. Stimuli

The stimuli were the same as in Experiments 1 and 2 with the following change: the material matching choices varied in number and size just as did the shape matching choices as illustrated in Fig. 4. Therefore, a child in the 4–6 set size condition was shown options that were matches to the named single standard in shape or material and were both numerically equivalent to each other (e.g., there were 4 shape matching items versus 4 material matching items). The material and shape matching response options were equivalent in overall amount of stuff and individual item size.

Fig. 4.

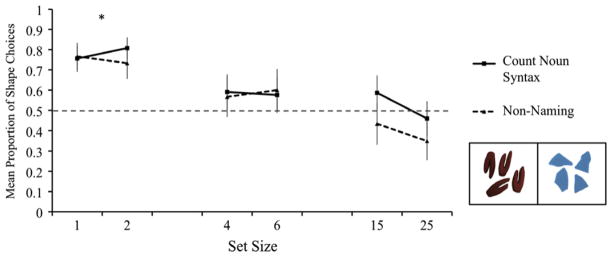
Children’s shape match responses as a function of set size and language condition in Experiment 3 and an example of shape and material test choice options.

4.1.3. Procedure

Children were randomly assigned to either a count noun syntax condition (n = 74) or a non-naming condition (n = 60). The general procedure was similar to Experiment 2 except for the phrasing used in each condition. In the count noun syntax condition, children were shown the exemplar and the experimenter named it saying “Look! It’s a tiso!” then prompted the child for his or her response using phrasing appropriate to the number in the sets by saying “Can you find some tisos here? Where are the tisos?” for sets of more than one and “Can you find another tiso?” for set size 1. Children in the non-naming condition were shown the exemplar and told “Look!” The experimenter then prompted the child to make a choice by saying “Find what we just saw!” In this condition no name was used to label any of the objects and no other quantifying words were used to bias children to attend to shape or material matches. As in the previous experiment, if the child pointed to, picked up, or handed the experimenter one or more of the shape matching items, the response was coded as a shape matching response; likewise if the child pointed to, picked up, or handed the experimenter one or more of the material matching items, the response was coded as a material matching response.

4.2. Results

The main results are in Fig. 4. An ANOVA for a 2 (Count Noun Syntax vs Non-Naming) by 2 (Older vs Younger) by 3 (Set Size Condition) design yielded only a main effect of Set Size, F(2, 129) = 9.538, p < .01. Children attended to and categorized by shape above chance only for the smallest size of 1–2, t(45) = 6.35, p < .01. Responses did not differ from chance for the Set Size conditions of 4–6 and 15– 25. Post hoc analyses (Tukeys hsd, α < .05) revealed a marginally significant difference between the smallest Set Size 1–2 and 4–6 (p = .07) and a significant difference between Set Sizes 1–2 and 15–25 (p < .01); however, there was not a reliable difference between Set Size 4–6 and the largest Set Size 15–25. There were no reliable within subject differences between sets of 1 and 2 for the smallest set condition or between 4 and 6 for the medium set size condition; however, a paired comparison t test revealed a reliable within subject difference between the 15 and 25 at the highest set size, t(44) = 2.35, p = .02.

Overall the pattern in Experiment 3 is similar to that of adults in Experiment 1; children’s shape choices decreased as set size increased but were not reliably biased to material choices for the largest set sizes. This may indicate that at least some children in Experiment 2 were switching to categorizations by number—not material—when the set size for the shape match was large. There is also a hint in the data that count-noun syntax pushed attention to shape for the largest set sizes: 44% of children chose the shape matching items on more than 66% of the trials in the count noun condition for sets 15–25, whereas only 28% of the children did so in the non-naming condition. Both of these aspects of the finding suggest that set size may not trump but rather interact with other factors such as language and stimulus properties that are known to be relevant to individuation. Nonetheless, the observed pattern of set size effects on shape categorization across ages, across children speaking different languages, and in different task contexts indicate a potentially fundamental relation between individuation, attention to shape, and the number of objects.

5. General discussion

Much research with both children and adults indicates that entities that are discrete and bounded are classified by their shape. In the present studies, the exemplar object was always introduced by itself—a discrete and bounded thing. In Experiment 3 that individual object was even explicitly named with a count noun (“a tiso”)—a frame that 3–5 year old children fully understand as indicating a category of things alike in their shape (Soja, 1992)—and in that experiment, the children were also asked to find the match using the plural (“find the tisos”)—a linguistic marker that children this age understand as a reference to multiple discrete instances of the same kind (Berko, 1958; Kouider, Halberda, Wood, & Carey, 2006). The tasks were untimed; adults and children could have singled out one element from a set of many to determine its shape. Yet when set size was increased beyond 4 items, neither children nor adults robustly chose the shape-matching set. The findings suggest that—given a set of many—children and adults were less likely to conceptualize the items as individuals, less likely to attend to individual object shape and/or less likely to take the experimenter’s request as being about individual items in these sets. It seems that when individual things are in a set of many things, the bounded shapes of the individuals are less relevant for categorization than the properties of the set as a whole; the properties that characterize the group such as color, texture, or number may become more salient. It is as if the presence of many things—a crowd of items—shifts attention to the mass and perception of the set as a whole dominates while saliency of the individual elements and their individualizing properties such as shape become less important.

Past research has shown both individuation and categorization by shape to be context dependent (e.g., Blair & Somerville, 2009; Diesendruck & Bloom, 2003; Diesendruck, Hammer, & Catz, 2003; Gelman & Bloom, 2000; Hammer et al., 2009; Kobayashi, 1997 Landau et al., 1988; Lavin & Hall, 2001; Prasada et al., 2002; Soja et al., 1991). There are task contexts and language that encourage the conceptualization of a thing as an individual bounded entity and these contexts also increase categorization by shape. These factors include the rigidity of the shape, its complexity, as well as narrative and linguistic frames that single out individuals. The present results may be understood as demonstrating an additional contextual factor that is relevant to individuation and attention to object shape: the set size of the collection in which the object is presented. Small set sizes encourage the conceptualization of the entities in the set as individual bounded things, but large set sizes, in some way, encourage an alternative conceptualization.

The specific findings across the three experiments—that set size influences categorization by shape and does so for both adults and children and in different linguistic contexts— may also indicate a deeper relation between object shape and number: attention to the shapes of things in small sets may depend on the same processes that underlie precise small set quantification. Decreased attention to the shape of entities in large sets, in turn, may be related to the processes that underlie large set quantification. We offer, next, a more specific hypothesis about how attention to object shape may be related to small and large set quantification. This hypothesis is suggested by the present findings but is under determined by them. The hypothesis, however, clarifies the contribution of the present findings and the value of systematic study of possible links between the processes underlying numerical judgments and the representation of object shape. We note several of the testable hypotheses generated by this approach.

5.1. Precise number and shape

The effect of set size on attention to shape may arise because the perceptual system is both limited in terms of the number of objects it can individually represent at one time and because it has options as to what counts as an object. As Kahneman et al. (1992) noted, a single object may consist of one element or of multiple elements bound together as a single unit. One shape in an array, or a clump of elements, or the whole array itself could be represented, tracked, or counted as one unified object; the selection of the object depends upon contextual factors that influence the perceiver’s interpretation of a scene or group of items. Given the limit on the number of objects that can be simultaneously represented in human visual working memory, the number of individual elements in a set may play a direct role in how units are selected for representation. If the number of items in a set exceeds the limits on simultaneous visual representation, the cognitive system may be biased to select the whole group or clusters of the whole group as the unit(s). Because attention to shape depends upon object selection, if the individual elements in an array are selected as the individual objects, then their shapes are represented; if the whole group of elements is taken as one object, then individual element shape may not be represented. Ultimately, then, an increase in number of items in a set decreases attention to the individual items’ shapes because these are not apprehended as the objects but, rather, the whole group may be selected as the unit of representation.

Research on the perceptual segregation of scenes into objects at different scales indicates that contrast, connectedness, density, symmetry as well as the familiarity of the potential forms matter (e.g., De Lillo, Spinozzi, Truppa, & Naylor, 2005; Dukette & Stiles, 2001; Hoffman, 1980; Navon, 1977; Quinn & Schyns, 2003). There is already some suggestive evidence that these factors matter to numerical judgments as well. Adults’ explicit numerical estimations of large quantities are affected by the density, gestalt, spacing of items, and item category (Sophian & Chu, 2008; Ginsburg, 1974; Allik & Tuulmets, 1991; Bevan & Turner, 1964; Taves, 1941; Kreuger, 1982; Ginsburg & Courtis, 1974). Recent work has also demonstrated that small set quantification is influenced by spatial and temporal presentation factors (Hyde & Wood, 2011). If attention to shape and numerical quantification are connected through processes of the same core systems, then the same factors should influence both. This means that those factors shown to matter for attention to shape such as language, syntax, or narratives that encourage conceptualization of entities as objects (and therefore attention to shape) should affect numerical judgments—given enough time for top-down conceptual factors to play a role in these judgments. Similarly, if spacing and temporal presentation influence numerical comparisons, these factors should also matter for attention to item shape. Further, if factors that allow for precise quantification also support individual object construal and attention to shape, then large imprecise quantification may support mass construal and attention to material (texture and color) of sets. Ongoing research being conducted in our laboratory is currently testing many of these predictions.

If attention to object shape is linked in these ways to the core cognitive systems involved in representing objects and quantifying sets, then there may be a mechanistic explanation for why we talk about groups in the ways that we do—why we talk about a group as a crowd, for example— and there may be specific perceptual factors that drive our speaking and thinking about these real world collections. Testing spontaneous speech and memory for sets of items while manipulating the properties that are shown to influence quantification would be a first step in understanding how and if the current results and proposed hypothesis indeed underlie some aspects of language evolution and our real-world thinking about groups.

6. Conclusion

In many—if not nearly all the world’s languages (see Lucy, 1992 for a possible exception)—being bounded, individuated, countable, and categorized by shape tend to go together. The present results suggest a link between attention to shape and numerical quantification, and offer a potential explanation for how we conceptualize and label sets of things. The effect of set size on attention to shape may occur because the definition of a psychological object derives from the architecture of the human cognitive system; more specifically, object selection and conceptualization derives from the characteristics of spatial working memory, which limits the number of items that may be simultaneously localized, counted or quantified, and perceptually unitized as bounded shapes. The present finding that attention shifts away from the shapes of individuals in an array at set sizes of three or four—the same as the limit reported for precise quantification and object tracking—implies that these are related perceptual phenomena.