Free energy changes and components implicit in the MWC allosteric model for the cooperative oxygen binding of hemoglobin.

Abstract

Hill’s plots of oxygen binding isotherms reveal the presence of a transition between two different oxygen affinities at the beginning and end of the isotherm. They correspond to the two conformations anticipated by the MWC model, namely the T and R conformations at the beginning and end of oxygen binding, when the lower affinity of the T form develops into the higher affinity of the R form. The difference between the binding Gibbs free energies changes of the two affinities (ΔG_L) is the free energy of binding cooperativity. Notably ΔG_L is positive in favor of the T form, that moves to a higher energy level upon oxygen release. Osmotic stress reveals a higher volume/surface ratio of deoxyHb, with a positive ΔG_W also in favor of the T form . Increasing protein concentration shifts the isotherms to the right indicating the formation of intermediate polymeric forms. Enthalpy of the intermediates show a strong absorption of heat at the third oxygenation step due to polymers formation with quinary, and above, structures. The disassembly of intermediate polymers releases energy with a negative ΔG that compensates and allow the positivity of ΔG_L. High energy polymers are the barrier preventing the relaxation of the T and R conformations into one another. The MWC allosteric model is the best justification of oxygen binding cooperativity .

Introduction

To explain the cooperativity of oxygen binding isotherms Monod et al. ^{[1 ]} proposed the presence of two Hb forms with low (T form) and high (R form) oxygen affinity. In the absence of oxygen the allosteric equilibrium constant Lo=To/Ro is in favor of To, while with increasing Hb saturation Ro becomes the favored species.

Consistent with the model, linear extrapolation of the very first and very last saturation data of Hill’s plots isotherms define the presence of two hyperbolic binding for the first and last oxygen bound to Hb ^[2]. They have a higher and lower P₅₀ reflecting a lower and higher oxygen affinity respectively. It is easy to reconcile the initial low affinity (K_T) with deoxyhemoglobin in the T form, and the final high affinity (K_R) with oxyhemoglobin in the R form. The overall binding affinity of the isotherm is defined by the value of PO₂ at 50% saturation of the isotherm (P₅₀), or the value of P_m when available.

Thermodynamic implications of the MCW allosteric model

As mentioned above, Hill’s plots of cooperative isotherms clearly indicate the presence of two different hyperbolic oxygen affinities of hemoglobin with lower (K_T) and higher (K_R) oxygen affinity, respectively.

The difference between the respective binding free energy changes, ΔG_T and ΔG_R, is

$$\Delta G_L=\Delta G_T-\Delta G_R$$ (1)

where ΔG_L defines the free energy change of cooperativity.

The lower affinity of the initial isotherm implies that ΔG_T > ΔG_R. Thus, in the difference, ΔG_L has a positive value, indicating that during deoxygenation the system in the T form gains a ΔG_L amount of free energy, so that the T form is at higher energy level than the R form. Implied in eq (1) is a scalar L_L defined as :

$$L_L=\exp \left(\frac{\Delta G_L}{\mathit{RT}}\right)$$ (2)

which is equivalent to the allosteric constant, Lo, of the Monod model ^[1]. Iimplied in eq (2), we have

$$K_R={L_L}^{\ast }{K}_T$$ (3)

as in the model ^[1,2].

It should be stressed that the evolving equilibrium between the T and R forms during the binding event implies a barrier of energy that prevents their mutual collapsing into a single conformation system.

Also in eq (1) ΔG_L is non zero and positive, while conformational equilibrium requires a zero balance of all free energy exchanges as in

$$\Delta G_{\mathit{eql}}=\Delta G_T-\Delta G_R+\Delta G_{\mathit{corr}}=\Delta G_L+\Delta G_{\mathit{corr}}=0$$ (4)

In the equation ΔG_corr is the free energy that allows the relaxation of the R form into the higher energy level of the T form.

For the origin of ΔG_corr, a possible hypothesis is the presence of a third intermediate component(s) that upon formation absorbs heat and energy from the environment (positive ΔG_on). Then, by degrading, would release the absorbed energy (negative ΔG_off) to the system and/or the environment. The ΔG_balance would be the net sum of positive and negative ΔG_i’s related to assembly/disassembly of the third component(s) as in

$$\Delta G_{\mathit{balance}}=\sum _i\Delta G_i$$ (5)

At equilibrium it should be ΔG_balance = 0. A negative non zero balance would be the amount (ΔG_corr) released to the system, not to the environment, to compensate for the positive ΔG_L in eq (4) . A positive balance would invalidate the hypotheses formulated above.

It should be stressed that the third intermediate component(s) must be at higher energy level than T and R forms, in order to degrade into the lower levels of the two forms. Thus, the third component(s) would also provide the barrier necessary to prevent the mutual relaxation of the T and R forms into a single conformation system.

The implication of intermediate third components has been proposed also by Ackers et al., Perrella et al. and Smith et al. from data of equilibrium, cryo-electrophoresis and kinetics ^[3-5]. Ackers concludes that the data (his words) “imply the existence (in the Hb system, authors note ) of at least three molecular structures; while a degeneracy of multiple structure into only a few dominant free energy levels (the T and R forms, authors note) is frequently to be expected, the reverse situation is extremely unlikely” ^[3].

This report

In order to explore the thermodynamics involved in the binding statistics of the MWC model we monitored the response of oxygen binding isotherms to challenges of temperature, osmotic stress, and protein concentration. In our laboratories temperature dependence has been already explored ^[6], and is used here as reference data.

Materials

Human Hb was prepared as described ^[6].

Sebacyl crosslinked Hb (DECA) was prepared as described ^[7].

All reagents used in the various manipulations were reagent grade and obtained from Sigma-Aldrich Chemical Co. (St. Louis, MO).

Protocols

Measurements of OD changes were performed using a Varian 14 DS recording spectrophotometer.

Oxygen-binding isotherms were measured following the technique developed by Dolman and Gill, using a thin-layer Hb solution exposed to successive dilution of the initial PO₂ with nitrogen. ^[8].

Osmotic dependence of the isotherms was measured at osmotic pressures varying from 1.0 to 80 Atm, using betaine concentrations up to 5 M. Buffer osmolality was measured using a Wescor osmometer (Logan, UT). Protein concentration was near 30 mg mL⁻¹ in 0.2 M borate buffer at pH 9.0, at 30°C.

Protein-concentration dependence of the isotherms was measured at Hb concentrations varying from 5 to 50 mg mL⁻¹ in 0.1 phosphate buffer at pH 7.4, at 37°C.

Numerical Analyses

Numerical analyses of the isotherms were based on the binding polynomial, P_w ^[2]

$$P_W=(1+{\beta }_{1}X+{\beta }_2{X}^2+{\beta }_3{X}^3+{\beta }_4{X}^4)=1+\sum _i{\beta }_i{X}^i$$ (6)

from which the Adair’s sequential binding equation is obtained

$$Y=\frac{{\beta }_{1}X+2{\beta }_2{X}^2+3{\beta }_3{X}^3+4{\beta }_4{X}^4}{4(1+{\beta }_{1}X+{\beta }_2{X}^2+{\beta }_3{X}^3+{\beta }_4{X}^4)}=\frac{\delta \ln P_W}{4\delta \ln X}$$ (7)

In these equations, X is the partial pressure of oxygen (PO₂) and β_i are the Adair’s binding parameters at subsequent binding steps, i, from 1 to 4. Y is the fractional saturation with oxygen. The intrinsic binding constant at each step was computed from

$$K_i=\frac{i{\beta }_i}{(5-i){\beta }_{(i-1)}}$$ (8)

while the relative proportion, α, of each intermediate as function of PO₂ was computed from

$${\alpha }_i=\frac{{\beta }_i{X}^i}{P_W}$$ (9)

The median ligand activity was computed from

$$P_m=\frac{1}{\sqrt[4]{{\beta }_4}}={\beta }_4^{(-0.25)}$$ (10)

Alternatively, the value of P₅₀ and extent of cooperativity was estimated from the midpoint of the isotherm, using the Hill equation

$$Y=\frac{{\mathit{PO}}_2^n}{P_{50}^n+{\mathit{PO}}_2^n}$$ (11)

and its logarithmic transformation for the Hill’s plots. In the equation, Y is the fractional saturation of hemoglobin with oxygen and “n” is the cooperativity index. Due to the quasi symmetric shape of the isotherm, P_m and P₅₀ are practically identical.

Fitting minimization

Isotherms were globally minimized, grouping together those exposed to various temperatures or osmotic stresses. This technique substantially reduced the correlation between the floating parameters, allowing estimations within a range close to 1% of the estimated value.

Results

Temperature dependence

These data were previously reported by Bucci et al. ^[6]. Isotherms were measured at 7 temperatures between 20°C and 37°C. Numerical analyses were based on the binding polynomial

$$P_H=1+\sum _i{\beta }_{1,25}\cdot X^i\cdot \exp [\frac{\Delta H_i}{R}\cdot (\frac{1}{T}-\frac{1}{298.2}\left)\right]\mathrm{i}=1-4$$ (12)

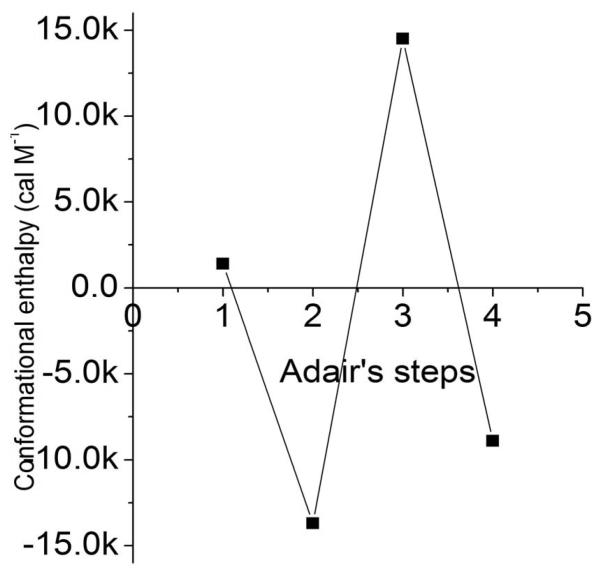
where the reference parameter β_i,25 at 25°C is corrected for the enthalpy at each binding step. The enthalpy of conformational changes per se was obtained by subtracting the enthalpy of the binding of oxygen to heme, estimated to be ΔH = −14 Kcal/heme. The corrected data are plotted in Fig. 1. Notably, the enthalpy of the third step of oxygenation shows a large heat absorption, ΔH = 14 Kcal M⁻¹ while the second and fourth oxygenation steps show large heat releases , ΔH = −13 and −8 Kcal M⁻¹ respectively.

Fig 1.

Conformational enthalpy of the intermediates of oxygenation of hemoglobin. In 0.1 M borate buffer at ph 9.0. Adapted from [6].

Osmotic stress

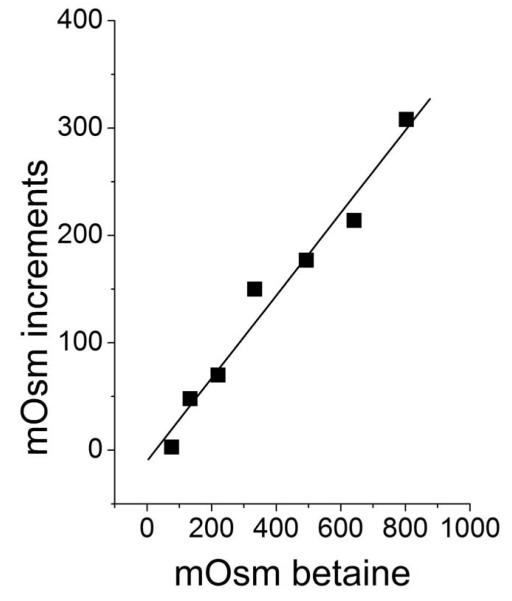
The osmolite of choice was betaine (trimethyl glycine MW 114.14 Da), which under the conditions of all experiments (0.2 M borate buffer at pH 9.0, at 30°C) did not bind to HbA, as is shown by the linearity of the increases of osmolality produced by increasing concentrations of betaine in the presence of Hb (Fig. 2).

Fig 2.

Increments of mOsm produced by increasing mOsm of betaine over a 240 mg ml⁻¹ hemoglobin. Note the linearity with a slope = 0.99. In 0.2 M borate buffer at ph 9.0, 30°C.

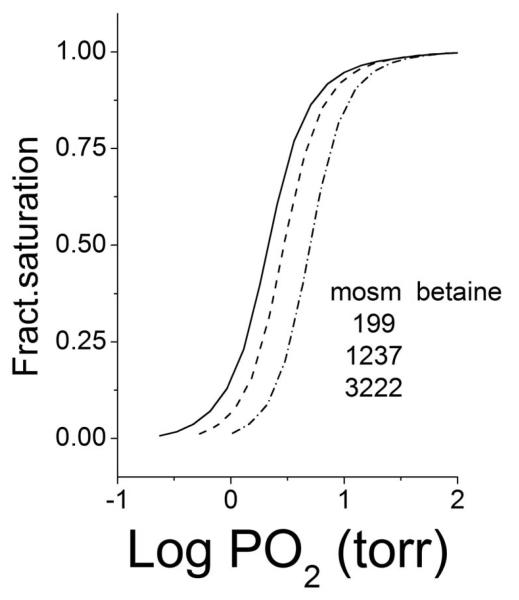
Isotherms at three different osmotic pressures are shown in Fig. 3. The presence of the osmolite right-shifts the isotherms, increasing their P₅₀ indicating that the free energy of oxygen binding to Hb is increased by osmotic stress, as in:

$$\Delta G_{\pi }=\Delta G_0+\pi \cdot \Delta V$$ (13)

where ΔV is a volume change produced by the osmolite, π = osm · RT is the osmotic pressure, and osm is the measured molality of the samples. The term πΔV is the free energy change, ΔG_W, of the osmotic stress that would increase ΔG₀ so reducing the oxygen affinity of Hb.

Fig 3.

Increasing right displacements of binding isotherms produced by the increasing osmolality of betaine listed in the graphic. In 0.2 M borate buffer at ph 9.0, 30°C.

Numerical analyses for estimating the ΔV_i’s produced by the osmotic stress at each step of oxygen binding were based on the binding polynomial

$$P=1+\sum _i{\beta }_{i,o}\cdot X^i\cdot e^{(\pi \cdot \Delta V_i)}$$ (14)

where ΔV_i’s are the volume change at each step.

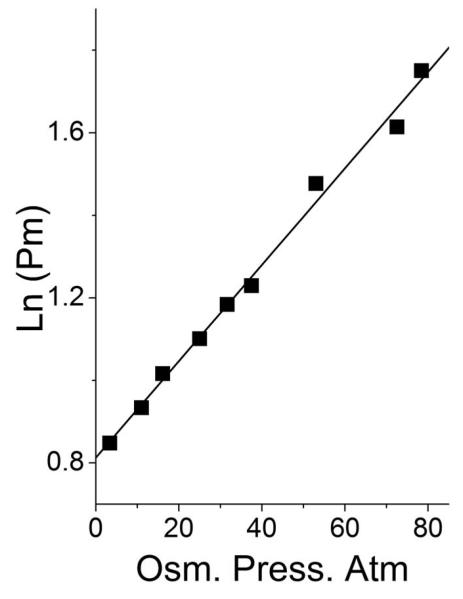
The overall volume change produced by the osmotic stress was also obtained from the slope of the plot of ln(P₅₀) against the measured osmolality of the buffer, using:

$$\ln \left(P_{50,\pi }\right)=\ln \left(P_{50,0}\right)+\mathit{osm}\cdot \Delta V_{o\nu r}$$ (15)

as shown in Fig. 4.

Fig 4.

Dependence on osmotic pressure of the oxygen affinity (ln (P_m)) of hemoglobin. In 0.2 M borate buffer at ph 9.0, 30°C.

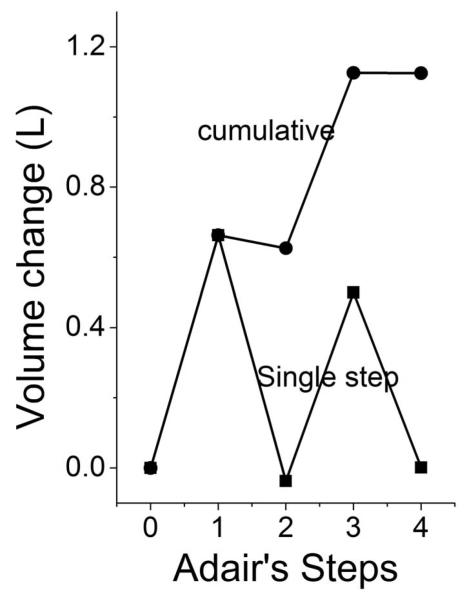
The numerical data obtained from these experiments show a very good correspondence between the cumulative and overall displaced volumes ΔV_ovr = Σ ΔV_i = 1.2 L M⁻¹ (Table 1). The step-by-step volume increases were not evenly distributed along the oxygen-binding steps (Fig. 5); they are evident only on the first and third steps.

Table 1.

)V_i values: overall and at individual Adair’s steps (1-4).

)Vi (L M−1) cumulative i=1 to 4	)Vi (L M−1) indiv.step i=1 to 4
0.663	0.663
0.626	−0.037
1.126	0.500
1.127	0.001
Overall )V (L M−1) 1.10

Fig 5.

ΔV increments and cumulus with oxygenation. In 0.2 M borate buffer at ph 9.0, 30°C.

Colombo et al.^[9] were first to notice that addition of sugars not binding to Hb lowered its oxygen affinity. They interpreted this phenomenon as a solvation change involving 66 moles of water per mole of hemoglobin. The volume of 66 moles of water is near 1.2 L M⁻¹, consistent with our ΔV values.

Concentration dependence

Experimental conditions were chosen for maximizing the effect of protein concentrations, similar to physiologic conditions: 0.1 M phosphate buffer at pH 7.4 and Hb concentrations between 5 and 50 mg mL⁻¹ at 37°C. Sebacyl crosslinked Hb (DECA) was chosen because the intramolecular crosslink eliminates dimers formation. DECA is characterized by a P₅₀ near 30 mmHg and a cooperativity with “n” above 2.0, very similar to the P₅₀ and cooperativity of normal blood ^[7].

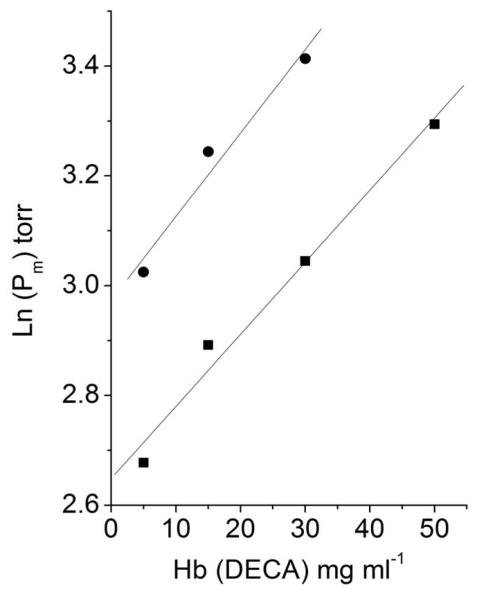
As shown in Fig. 6, the oxygen affinity of DECA decreases with increasing protein concentration, suggesting the association process of DECA tetramers into polymeric forms. The phenomenon can be described by:

$$\Delta G_p=\Delta G_0+K_{\mathit{pol}}{C}_{\mathit{Hb}}$$ (16)

where K_pol is a pseudo-association constant for polymer formation because it refers to the total Hb concentration C_Hb. The term K_pol C_Hb is the free energy changes, ΔG_C , of polymer formation that would increase ΔG₀ so reducing the oxygen affinity of Hb.

Fig 6.

Concentration dependence of oxygen affinity (ln (P₅₀)) of DECA (sebacyl crosslinked hemoglobin ^[7]). In the presence (● ) and absence of 3.0 M betaine (■). In 0.1 M phosphate buffer at pH 7.4, 37°C.

In numerical analyses, the Adair’s parameter β₃ was so low that it was difficult to estimate. Therefore, for the concentration-dependence data, we were unable to produce data for individual steps.

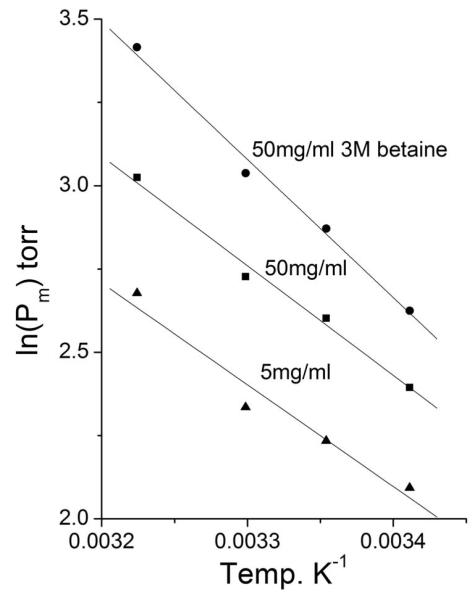
The negative slope (ΔH’s) of the van t’ Hoff plots at 5 mg mL⁻¹ and 50 mg mL⁻¹ hemoglobin concentration remained constant with ΔH = −6.1 kCal M⁻¹ and −6.5 kCal M⁻¹, respectively; only the intercept on the ordinates was higher at the higher Hb concentration. In the presence of 50 mg mL⁻¹ Hb concentration, addition of 3 M betaine further increased the ordinates intercept of the sloping line and the enthalpy slightly decreased to ΔH = −8.2 kCal M⁻¹. Fig. 7 shows the quasi-parallel upward displacement of the van t’Hoff lines under the three conditions.

Fig 7.

Van t’Hoff plots for DECA ^[7] at 5 mg ml⁻¹(▴), at 50 mg ml⁻¹(■) and at 50 mg ml⁻¹ + 3M betaine (●). In 0.1 M phosphate buffer at pH 7.4.

Discussion

Osmotic stress

Based on eq (13), as mentioned above, the right shift of the isotherm in response to increasing π reveals the presence of a term

$$\Delta G_W=\mathit{RT}\ln \left(\pi \Delta V\right)$$ (17)

that decreases the oxygen affinity of the system.

ΔG_W is the free energy change of the osmotic stress that, as proposed by Timasheff ^[10], is the expression of an increased solvent preferential exclusion from the protein surface that increases in size. In hemoglobin it is consistent with the increased hydrophobicity of the oxyHb surface, reported by Chothia ^[11].

The ΔV_i data shown in Table 1 are positive, in favor of the deoxy T structure . Therefore ΔG_W adds energy to the system in T form contributing to the free energy of cooperativity ΔG_L. Assuming that the free energy changes ΔG₁ and ΔG₄ listed in Table 2, correspond to ΔG_T and ΔG_R respectively, a comparison between ΔG_w, computed with eq (17), and ΔG_L computed with eq (1) is shown in Table 3.

Table 2.

Osmotic data for Hb in 0.2 M borate buffer at pH 9.0 at 30E C. The four rows at each π value correspond to the 4 Adair’s steps (1-4) from top to bottom.

π (Atm)	βi (torrBI)	Ki (mM−I)	ΔGi (cal M−1)
11	0.236	190	−7171
	0.094	855	−8059
	0.051	2620	−8720
	0.023	5810	−9189
16	0.207	166	−7094
	0.077	798	−8019
	0.045	2823	−8764
	0.017	4866	−9085
25	0.144	115	−6880
	0.056	834	−8045
	0.026	2242	−8628
	0.012	5945	−9203
31.5	0.122	98	−6782
	0.061	990	−8193
	0.019	1567	−8369
	0.009	725	−9181

Table 3.

Osmotic (ΔG_W) and analytical (ΔG_L) free energy changes for the conformational transition, with the corresponding scalars L_W and L_L, and the differences between analytical and osmotic values.

ATM	ΔGW Kcal M−1	ΔGL Kcal M−1	LW	LL	ΔGL-ΔGW cal M−1
11	1.56	2.01	13	30	450
16	1.79	1.99	19	29	200
25	2.06	2.32	29	46	260
31.5	2.20	2.40	37	52	200
37.5	2.30	2.37	44	50	70
					Average 236

In Table 3 ΔG_L is always higher than ΔG_W by a few hundred Kcal M⁻¹. The difference is better expressed by the respective values of the scalars L_W and L_L, eq (3). The differences are small and in the same direction. This may suggest that ΔG_W refers only to the solvation of Hb, while ΔG_L includes also the net sum of the positive and negative free energy changes resulting from the rearrangements of the T ↔ R conformation within the subunits and across their interfaces ^[12]. In other words ΔG_W only detects the different solvation resulting from the conformational change included in ΔG_L.

The third component(s) are polymeric

As shown in Fig. 6, the P₅₀ of DECA has a distinct dependence on protein concentration, implying the presence of a reversible associating system that modulates the oxygen binding isotherm, as shown by eq (16). It is a general phenomenon in hemoglobin systems, previously reported from our laboratory for human and bovine hemoglobins^[13].

In the experiments reported above, DECA is an intramolecularly crosslinked , non-dissociable tetrameric Hb^[7]. In the absence of dimers, the association process could be only a polymerization of tetrameric Hb molecules.

Detailed step analyses of the concentration dependent isotherms are not available because, as mentioned above, the Adair’s parameter of the third step, β_3, was so small to be undefined, suggesting that the tri-ligation fractional saturation of the isotherm results in the formation of components with very low oxygen affinity.

This phenomenon is concomitant with the strong heat absorption by the enthalpy of the third step of oxygenation, shown in Fig. 1 with ΔH₃ near 14 Kcal M^−1[6]. It can be proposed that the tri-ligation absorbs into the system the energy (ΔG_on) necessary for the formation of the stereochemistry of new polymeric forms with high energy levels and very low oxygen affinity.

The free energy release by the negative enthalpies detected at the 2^nd and 4^th steps (Fig. 1), with ΔH₂ near −13 Kcal M^−1[6] and ΔH₄ near −8 Kcal M^−1[6], would result from the disassembly (ΔG_off) of unstable polymers relaxing into lower energy, stable, tetrameric structures like the T and R forms.

Our data proposing the presence of unstable polymeric intermediates dovetail with Ackers’ hypothesis of at least a third intermediate component degenerating into more stable forms^[3].

Energetic relevance of the intermediates of oxygenation

Random-isodesmic aggregating polymers cannot be proposed because they would be at a lower energy level stabilizing intermediate forms, producing negative cooperativity, as described by Koshland et al. ^[14]. In fact, the equilibrium contribution of high energy components (the polymers) makes the average energy level of all of the intermediates higher than the levels of both the T and R forms. The high energy level of intermediates would be the barrier that prevents the T and R forms of Hb from relaxing into each other.

The high heat absorption at the third Adair’s step (ΔH₃^[6]) implies the formation of quinary, and above, polymeric forms. This hypothesis is supported by the fibers of HbS, which reveal the presence on the surface of tetrameric Hb of sites ready for the intermolecular contacts necessary to the self assembly and formation of perfectly designed quinary and higher order structures ^[15]. Similarly, also HbS fibers self assemble into a very low oxygen affinity. It is very tantalizing to propose that the HbS fibers are the mutation-stabilized form of an intermediate polymer. The history of measured isotherms in our laboratories and the data of Campbell et al ^[16] on fiber formation in vitro may support this proposition.

Osmotic stress offers a suggestion for the different shape of the R and T forms. A different solvation that involves 66 moles of water per mole of Hb, implies a larger surface/volume ratio of the molecule with a larger osmotic shell for oxyhemoglobin. Conversely the T form has a lower molecular surface/volume ratio. For the same mass, minimizing the surface gives to the T form a more compact and spherical shape, more spherical than that of the R structure with a larger surface/volume ratio.

The same reasoning can be applied to the hypothesis of Colombo et al.^[9] that 66 molecules of water bind directly on the surface of hemoglobin. ΔG_W would not distinguish between the equivalence of two hypotheses. The increased hydrophobicity of the system^[11] would support the hydration shell proposal.

Distribution of the intermediates

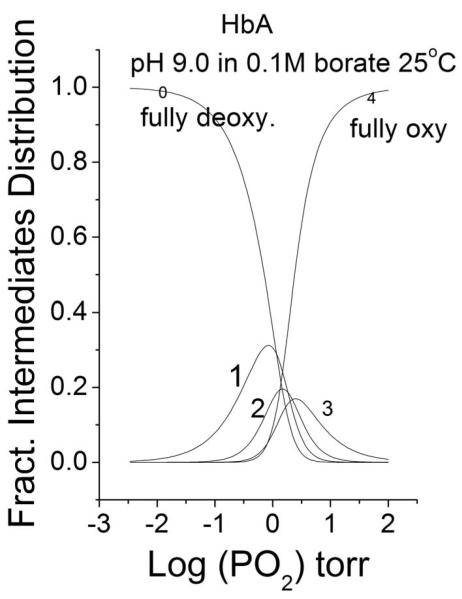
The Adair’s subsequent parameters β_i are statistical binding constants, referred to all intermediates of ligation present along the evolving oxygen saturation of the isotherm. They describe the changing distribution of species increasingly saturated with oxygen, as shown in Fig 8. This is why we prefer to define the subsequent oxygenation steps as “Adair’s steps”.

Fig 8.

Distribution of liganded species (eq (9)) as function of increasing PO_2. . In 0.1 M borate buffer at ph 9.0, 25°C . The numbers in the graphic reflect the Adair’s oxygenation steps.

Fig 5 shows the progress of ΔV_i’s along the four Adair’s steps. The progress is not linear with the steps. The maxima at the first and third step are probably due to local prevalence of the most asymmetric species.

Similarly, for the enthalpies, as shown in Fig 1,, the non linear progress would be due to local prevalence of certain ligated species. The maximum heat absorption at the third Adair’s step is reached when tri-ligation makes of the polymers the dominant species.

Comparisons of Fig 1,5 and 8 support the hypothesis that there are large equilibrium conformational fluctuations among the intermediates of oxygenation, resulting into a multiple forms single system.

The correction in eq(4)

The enthalpy values shown in Fig 1 are data taken from Bucci et al.^[6] obtained in the absence of betaine. They are the free energies either absorbed (ΔH₃) or liberated (ΔH₂,ΔH₄) from and to the environment upon the T↔R conformational changes. As discussed, they would correspond to formation and degradation of polymeric forms. The free energy balance between absorption and release can be estimated by

$$\Delta G_{\mathit{balance}}=\sum _{i=1}^{i=4}\Delta H_i^{\left[6\right]}=-7.5{\mathit{KcalM}}^{-1}$$ (18)

where the residual −7.5 Kcal M⁻¹ is the energy not released to the environment, because it is delivered to and absorbed by the intermediates of Hb oxygenation. The average, equally distributed over the four Adair’s steps, is near −1.9 Kcal M⁻¹ close to the ΔG_L’s in Table 3.

Apparently, it is formation and degradation of polymeric components that provides the ΔG_corr = −1.9 Kcal M⁻¹ corr necessary to have ΔG_eql = 0 in eq (4) that justifies the higher energy level of the T form.

The MCW model scenario

The energy necessary for the conformational change (ΔG_L=2.0 KcalM⁻¹) include the osmotic stress, ΔG_W= 1.6 Kcal M⁻¹ and the net free energy change near 300 Kcal M⁻¹ of structural conformational changes; which, within the MWC model^[1], can be considered allosteric effectors specific for the T form, that increase the energy level of the T form to a higher ΔG_T values with lower oxygen affinity.

Reversibility implies the release of a - ΔG_L free energy from the T form into the R structure. This decreases the energy level of the system and decreases the ΔG_R value to a higher oxygen affinity.

It appears that the MWC model implies an extra packet of about 2000 Kcal M⁻¹that is in turn either absorbed or released by the system modulating its oxygen affinity. The energy of the packet is provided by the release into the system of the energy absorbed from the environment by the enthalpies of the intermediates.

The data suggest that the T and R forms of Hb are separated at the two ends of a reversible thermal itinerary across the higher energy levels of the intermediates.

Besides providing the energy necessary for cooperativity, the high energy level of polymeric intermediates provide most of the barrier that prevents the T and R forms from relaxing into each other.

In this view the MWC allosteric model best describes a system where the evolving equilibrium between two conformations is regulated by intermediates all averaged by and included in the allosteric constant Lo.

Abbreviations

ΔH

enthalpy

ΔG_C

free energy change for polymer formation

ΔG_eql

equilibrium free energy change of cooperativity

ΔG_L

the free energy change of cooperativity

ΔG_off

free energy of polymers disassembly

ΔG_on

free energy of polymers formation

ΔG_R

free energy change of oxygen binding to R form

ΔG_T

free energy change of oxygen binding to T form

ΔG_W

free energy change of osmotic stress

DECA

sebacyl crosslinked hemoglobin

L_L

scalar of ΔG_L

L_W

scalar of ΔG_W

Appendix.

Initial and final parabolas

In eq (13,16) ΔG_w and ΔG_C are mass dependent extensive additive parameters that do not interfere with the intensive parameters of the system as shown in Fig. 7. Thus, referring to ΔG₁ and ΔG₄ (Table 2) as ΔG_T and ΔG_R, respectively, and from eq (13,16), for the hyperbolic binding of the T form we would have

$$\Lambda G_T=\Delta G_{\mathit{deoxy}}=\Delta H_0-T\Delta S_0+K_{\mathit{pol}}{C}_{\mathit{Hb}}+\Delta G_L.$$ (19)

where, according to eq(1), the positive ΔG_L parameter specifically adds energy to the system to form the T structure and decreasing its oxygen affinity.

Regarding the R form, reversibility implies an opposite negative ΔG_L in eq (1) , therefore for the R form we would have :

$$\Delta G_R=\Delta G_{\mathit{oxy}}=\Delta H_0-T\Delta S_0+K_{\mathit{pol}}{C}_{\mathit{Hb}}+(\Delta {G_L}^{\ast }-1)$$ (20)

where a negative ΔG_L specifically adds its negativity to ΔG_R decreasing the energy level of the system into the R form and further increasing its oxygen affinity.

It is as if there is a fundamental hyperbolic oxygen binding of Hb

$$\Delta G_0=\Delta H_0-T\Delta S_0$$ (21)

modulated by protein concentration, osmotic stress, and structural changes.

Governing equations

Fluctuations of the intermediates of oxygenation prevent their description with a universal equation. Only averages may be used. It is well known that the Hill’s equation (11) and its logarithmic transformation average in the scalar “n” all of the intermediates, and are very useful for estimating the overall oxygen affinity (P₅₀) and presence of cooperativity (n>1.0) in the isotherm. Most useful are the statistical Adair’s parameters, eq (6-10) for following the equilibrium distribution of the intermediates and computing P_m.

Simultaneous numerical analyses of groups of isotherms are useful for reducing the correlations among the floating parameters. Di Cera and Gill ^[17,18] have developed numerical procedures for obtaining the Adair’s parameters and oxygen saturation fractions from single isotherms.

The MWC binding model adequately describes the system and is useful for simulations. It cannot be used for numerical analyses because, as shown in eq (3), there is a correlation equal 1.0 between the floating parameters Lo and either K_R or K_T (depending on the equation spelling). This kind of correlation cannot be reduced by simultaneous group analyses and prevents minimizations.

Significance for Biochemistry

Cooperativity is physiologically relevant. In fact, at the periphery, the acquired lower affinity helps the mass action of oxygen release, which corrects for the asymmetry of slow oxygen supply from red cells and fast mitochondrial consumption ^[19,20]. At the lungs the acquired higher affinity assures a full saturation of Hb exposed to a modest PO₂.

It is tantalizing to present hemoglobin as a molecular machine that extracts oxygen from the lungs and expels it to the tissues under the pumping action of the assembly-disassembly of polymeric forms during the binding event. The MWC model best describe this mechanism with two switching conformations pumped by the allosteric constant Lo.

The thermodynamics of the T↔R conformational change finalize and justify the origin of the cooperativity of oxygen binding isotherms, after an almost century of search based on the binding statistics of non unique allosteric models.