Formulation and optimization of temozolomide nanoparticles by 3 factor 2 level factorial design

Abstract

The aim of this study was to investigate the combined influence of 3 independent variables in the preparation of temozolomide bearing Non-PEGylated and PEGylated nanoparticles by emulsification solvent evaporation method. A 3 factor 2 level design was used to derive a polynomial quadratic model and construct contour plots to predict responses. The independent variables selected were concentration of drug (A), concentration of PLGA/PEG-PLGA (B), PVA concentration in aqueous phase (C) and sonication time (D) and evaluated for percentage drug entrapment (PDE) and particle size (PS). A 3⁴ factorial design was used with 4 factors (A, B, C and D) at 3 levels and experimental trials were performed at all 82 possible combinations. In the present work, 28 runs are considered as the preliminary trials revealed that on increasing drug concentration from 2.5 to 5 mg the percent drug entrapment increases, but on further increasing the drug concentration (i.e., to 7.5 mg) no significant effect on the percent drug entrapment and particle size was observed. The 3⁴ factorial design was used to derive a polynomial quadratic model and construct contour plots to predict responses. Contour plots were constructed to show the effects of A, B, C and D on the PDE and PS.

Introduction

The design of experiments (DOE) technique was used to provide an efficient means to optimize the process variables of nanoparticles composition. DOE is an approach for effectively and efficiently exploring the cause and effect relationship between numerous process variables and the output. A sequence of experiments were performed that would yield the most information about the factors and their interactions in as few experiments as possible. A 4-factor 3-level factorial experimental design technique was employed to investigate the variables like particle size and percent drug entrapment using the statistical software package (Version 7). This technique was applied to quantify the influence of operating parameters on the production of nanoparticles.

The factorial design created various sets of the experiments in this study. The independant variables were drug concentration, polymer concentration, PVA concentration and sonication time. The software was also used to construct mathematical models for making response predictions for experiments. The goal of the experimental design was to find out, with the minimum number of experimental runs, the effect of various independent variables on the final product. The design is suitable for understanding the quadratic response surfaces.

Qualitative estimates of the influence of the individual variables could be made by inspection of the data. However, it would be difficult visually to make predictions as to whether the interactions actually existed between the variables, or which single variable had the most dominant effect. To achieve this, factorial statistical design methods were applied and these designs are good alternatives to a full factorial design, especially in the initial screening stage. In this study a 4-factorial design was used where main factor effects are confounded with two factor and higher order interactions. The main effects and interaction effects calculated for the responses of particle size and entrapment efficiency.^1,2

In the present study emulsification solvent evaporation method was used for preparation and optimization of temozolomide loaded Non-PEGylated and PEGylated nanoparticles, as this method is widely used for the encapsulation of hydrophobic drugs. The study reveals the effect of independent variables [drug concentration (A), PLGA/PEG-PLGA concentration (B), PVA concentration (C) and Sonication time (D)] on percent drug entrapment and particles size.

Traditional experiments require more effort, time and materials when a complex formulation needs to be developed. Various experimental designs are useful in developing a formulation requiring less experimentation and providing estimates of the relative significance of different variables.

Results and Discussion

Shape and surface morphology of the transferrin appended nanoparticles were evaluated by SEM. SEM study revealed that nanoparticles are smooth and spherical in shape. The synthesized conjugate, PEG-PLGA was used to prepare PEGylated nanoparticles bearing drug. For comparing the efficacy of the PEGylated nanoparticles, Non-PEGylated nanoparticles were also prepared.

The Non-PEGylated and PEGylated nanoparticles bearing TMZ was prepared using emulsification solvent evaporation method technique reported by Avgoustakis, (2004). The various process and formulation variable i.e., drug concentration, polymer concentration, PVA concentration and sonication time were optimized to get small sized nanoparticles with maximum percent drug entrapment. These variables were optimized by applying 3⁴ factorial design using Design Expert Software.

In this method of optimization, it is difficult to develop an optimized formulation as the method reveals nothing about the interaction among the variables. The independent variable selected were, concentration of drug (A), concentration of PLGA/PEG-PLGA (B), PVA concentration in aqueous phase (C) and sonication time (D). Hence, a 3⁴ factorial design was used with 4 factors (A, B, C and D) at 3 levels and experimental trials were performed at all 82 possible combinations which reveals that on increasing drug concentration 2.5 to 5 mg the percent drug entrapment increases, but on further increasing the drug concentration (i.e., 7.5 mg) no significant effect on the percent drug entrapment and particle size was observed. The 3⁴ factorial design was used to derive polynomial quadratic model and construct contour plots to predict responses of independent variables on percent drug entrapment and particle size (dependent variable).

Data analysis

Percent drug entrapment

All the batches of formulations of nanoparticles within the experimental design yielded nanoparticles which were evaluated for their size and percent drug entrapment. In this design, only fewer experiment (28 batches from one class of formulations) were studied where formulations are having 5 mg drug as optimum concentration of drug than full factorial design (82 batches). The transformed values of all the batches (28 each) for Non-PEGylated and PEGylated nanoparticles bearing separately TMZ along with the results are shown in Tables 1 and 2. The results show that formulations numbers 6, 8, 9 and 18 from both class of formulations are exhibiting maximum percent drug entrapment i.e., > 78% for Non-PEGylated nanoparticles of TMZ, while it is decreased about 3% in case of PEGylation of nanoparticles. The PDE (dependent variable) obtained at various levels of 4 independent variables (A, B, C and D). The response surface quadratic models were generated using Expert Design Software. These were subjected to multiple regression to yield a second order polynomial equations (full model). The correlation coefficient for the models were also calculated which are found to be > 0.94 indicating good fit. The PDE values measured for various batches showed wide variation i.e., ranges from a minimum of 52.89% to a maximum of 77.96% in case of temozolomide bearing Non-PEGylated nanoparticles, while a minimum of 49.62% to a maximum of 75.91% in case temozolomide bearing PEGylated nanoparticles. It is clearly indicated that the PDE is strongly affected by the variables selected for the study. It is observed that as on increasing the concentration of PLGA polymer in the matrix of nanoparticles the percent drug entrapment was found to increased up to the level of medium (i.e., 50 mg) at 5 mg of drug concentration then very little change in PDE was observed which could be due to completely entrapment of the drug into the polymer matrix.

Table 1. Factorial design of non-PEGylated nanoparticles bearing temozolomide.

Formulation code	Independent variable level				Percent drug entrapment (%)	Particle size (nm)
	Drug (mg)	PLGA (mg)	PVA (%)	ST (sec)
1	0	-1	-1	-1	54.23	115.67
2	0	0	-1	-1	74.34	116.56
3	0	1	-1	-1	76.09	117.49
4	0	-1	0	-1	56.21	116.63
5	0	0	0	-1	77.32	117.61
6	0	1	0	-1	77.96	118.76
7	0	-1	1	-1	56.54	118.49
8	0	0	1	-1	77.43	119.49
9	0	1	1	-1	77.74	120.88
10	0	-1	-1	0	53.67	113.98
11	0	0	-1	0	73.61	115.49
12	0	1	-1	0	75.23	115.92
13	0	-1	0	0	55.61	114.96
14	0	0	0	0	76.56	116.37
15	0	1	0	0	77.21	116.84
16	0	-1	1	0	55.97	116.82
17	0	0	1	0	76.89	117.47
18	0	1	1	0	77.19	119.35
19	0	-1	-1	1	52.89	111.91
20	0	0	-1	1	72.77	113.67
21	0	1	-1	1	74.41	113.62
22	0	-1	0	1	54.32	112.83
23	0	0	0	1	75.41	113.85
24	0	1	0	1	76.1	114.98
25	0	-1	1	1	54.32	114.89
26	0	0	1	1	75.67	115.58
27	0	1	1	1	76.02	117.37
28	0	0	0	0	76.02	112.93

Table 2. Factorial design for PEGylated nanoparticles bearing temozolomide.

Formulation code	Independent variable level				Percent drug entrapment (%) (PDE)	Particle size (PS) (nm)
	Drug (mg)	PLGA (mg)	PVA (%)	ST (sec)
1	0	-1	-1	-1	51.85	119.14
2	0	0	-1	-1	71.85	120.41
3	0	1	-1	-1	74.03	121.78
4	0	-1	0	-1	54.32	119.45
5	0	0	0	-1	75.01	121.2
6	0	1	0	-1	75.72	122.01
7	0	-1	1	-1	54.71	120.33
8	0	0	1	-1	75.91	122.31
9	0	1	1	-1	75.34	123.76
10	0	-1	-1	0	51.45	117.81
11	0	0	-1	0	71.25	119.32
12	0	1	-1	0	73.23	121.43
13	0	-1	0	0	53.43	118.79
14	0	0	0	0	73.83	120.32
15	0	1	0	0	75.12	121.02
16	0	-1	1	0	53.88	119.32
17	0	0	1	0	74.86	121.2
18	0	1	1	0	74.33	122.45
19	0	-1	-1	1	49.62	116.31
20	0	0	-1	1	70.37	118.32
21	0	1	-1	1	71.93	120.67
22	0	-1	0	1	52.85	113.84
23	0	0	0	1	73.12	119.21
24	0	1	0	1	73.71	119.82
25	0	-1	1	1	52.81	118.33
26	0	0	1	1	72.96	120.82
27	0	1	1	1	72.88	121.35
28	0	0	0	0	75.12	117.23

The main effect of A, B, C and D represents the average result of changing variable at a time from its low level to high level. The interaction terms (AB, AC, AD, BC, BD, CD, A², B², C² and D²) show how the PDE changes when 2 variables are simultaneously changed. The negative coefficient for all the independent variables (D, AC, BD, A², C² and D²) indicate unfavorable effect on the PDE while others are exhibiting positive interaction which indicate favorable effect on the PDE as its concentration in all selected formulation is kept unchanged. Among the four independent variables the lowest coefficient value is for D (-0.36 and p < 0.05) indicating that this variable is insignificant in the prediction of PDE. It is also observed that the PDE does not significantly change (p < 0.05) because as on changing sonication time from 30 sec to 90 sec there is very little decrease in the PDE which shows very less amount of drug loss due to size reduction of the nanoparticles. Similarly, the effect of PVA on the PDE of various nanoparticles was observed and as on increasing the PVA concentration from 0.5 to 1% in nanoparticles the PDE increases significantly while on further increasing PVA concentration no significant change in PDE was observed in all the cases of nanoparticles formulations (Eqns. 1 and 3). This shows an appropriate concentration of PVA (surfactant 1%) for the better formation of emulsion. The Variance Inflation Factor (VIF) measures how much the variance of that model coefficient is inflated by the lack of orthogonality in the design and calculated for Non-PEGylated and PEGylated formulations for temozolomide which is found to be near 1 indicating good estimation of the coefficient (Tables 3 and 4). Similarly Ri-squared is near to zero which is leading to good model. The model F value calculated in the range of 75.15 to 81.00 which implies the models are significant. The values of Prob > F less than 0.05 are indicating that model terms are significant. In all cases A, B, C, D, AB, A² and B² are significant model terms. The lack of fit values “F-value” for Non-PEGylated nanoparticles was found to be 61.86, which implies the lack of fit is not significant relative to the pure error and there are only 10–11% chances of large lack of fit “F-value” which could occur due to noise and non-significant lack of fit “F-value” is good fit of model. Similar results were obtained in PEGylated nanoparticles bearing temozolomide where lack of fit “F-value” was found to be 11.44% which is non-significant related to pure error. In both these cases 17–23% chances of large lack of fit “F-value” could occur due to noise. In both cases “Pred R-squared” values are in reasonable agreement with the “Adj R-squared” values. The Adeq-Precision is the measures of the signal to noise ratio. A ratio > 4 is desirable. In our case the Adeq-Precision value is in range of 26–28 which indicates an adequate signal (Tables 5 and 6).

Table 3. A. Design matrix evaluation for response surface quadratic model of non-PEGylated nanoparticles bearing temozolomide.

Table 3A
Degrees of freedom for evaluation
Model	14
Residuals	67
Lack of Fit	66
Pure Error	1
Corr Total	81

Table 3B
Term	Standard Error**		VIF	Ri-squared	Power at 5% α level for effect of
					0.5 Std. Dev.	1 Std. Dev.	2 Std. Dev.
A	0.136083		1	0	44.10%	95.20%	99.90%
B	0.136083		1	0	44.10%	95.20%	99.90%
C	0.136083		1	0	44.10%	95.20%	99.90%
D	0.136083		1	0	44.10%	95.20%	99.90%
AB	0.166667		1	0	31.50%	84.10%	99.90%
AC	0.166667		1	0	31.50%	84.10%	99.90%
AD	0.166667		1	0	31.50%	84.10%	99.90%
BC	0.166667		1	0	31.50%	84.10%	99.90%
BD	0.166667		1	0	31.50%	84.10%	99.90%
CD	0.166667		1	0	31.50%	84.10%	99.90%
A^2	0.233069		1.001626	0.0016234	56.10%	98.80%	99.90%
B^2	0.233069		1.001626	0.0016234	56.10%	98.80%	99.90%
C^2	0.233069		1.001626	0.0016234	56.10%	98.80%	99.90%
D^2	0.233069		1.001626	0.0016234	56.10%	98.80%	99.90%

^**Basis s.d = 1.0.

Table 4. Design matrix evaluation for response surface quadratic model of PEGylated nanoparticles bearing temozolomide.

Table 4A
Degrees of freedom for evaluation
Model	14
Residuals	67
Lack of Fit	66
Pure Error	1
Corr Total	81

Table 4B
Term	Standard error**	VIF	Ri-squared	Power at 5% α level for effect of
				0.5 Std. Dev.	1 Std. Dev.	2 Std. Dev.
A	0.136083	1	0	44.10%	95.20%	99.90%
B	0.136083	1	0	44.10%	95.20%	99.90%
C	0.136083	1	0	44.10%	95.20%	99.90%
D	0.136083	1	0	44.10%	95.20%	99.90%
AB	0.166667	1	0	31.50%	84.10%	99.90%
AC	0.166667	1	0	31.50%	84.10%	99.90%
AD	0.166667	1	0	31.50%	84.10%	99.90%
BC	0.166667	1	0	31.50%	84.10%	99.90%
BD	0.166667	1	0	31.50%	84.10%	99.90%
CD	0.166667	1	0	31.50%	84.10%	99.90%
A^2	0.233069	1.001626	0.0016234	56.10%	98.80%	99.90%
B^2	0.233069	1.001626	0.0016234	56.10%	98.80%	99.90%
C^2	0.233069	1.001626	0.0016234	56.10%	98.80%	99.90%
D^2	0.233069	1.001626	0.0016234	56.10%	98.80%	99.90%

Table 5. ANOVA sheet of non-PEGylated nanoparticles bearing temozolomide on percent drug entrapment.

Table 5A
Response―PDE ANOVA for Response Surface Quadratic Model Analysis of variance table [Partial sum of squares-Type III]
Source	Sum of squares	df	Mean square	F-Value	p-value Prob > F
Model	10077.61	14	719.8295	81.00017	< 0.0001	significant
A-Drug	3856.411	1	3856.411	433.9499	< 0.0001
B-PLGA	3202.892	1	3202.892	360.4115	< 0.0001
C-PVA	62.46827	1	62.46827	7.02936	0.01
D-ST	43.722	1	43.722	4.919901	0.0299
AB	797.5917	1	797.5917	89.75052	< 0.0001
AC	0.831136	1	0.831136	0.093525	0.7607
AD	0.0324	1	0.0324	0.003646	0.952
BC	0.315469	1	0.315469	0.035499	0.8511
BD	0.026678	1	0.026678	0.003002	0.9565
CD	0.225625	1	0.225625	0.025389	0.8739
A^2	1116.205	1	1116.205	125.603	< 0.0001
B^2	917.3058	1	917.3058	103.2216	< 0.0001
C^2	11.23415	1	11.23415	1.264144	0.2649
D^2	2.025956	1	2.025956	0.227974	0.6346
Residual	595.4132	67	8.886765
Lack of Fit	595.2674	66	9.019204	61.86011	0.1008	not significant
Pure Error	0.1458	1	0.1458
Cor Total	10673.03	81

Table 5B
Standard deviation	2.981068	R-Squared	0.944213
Mean	63.94866	Adj R-Squared	0.932556
C.V. %	4.661658	Pred R-Squared	0.917066
PRESS	885.1574	Adeq Precision	28.43542

Table 5C
Factor	Coefficient		Standard error	95% CI low	95% CI high	VIF
	estimate	Df
Intercept	74.458	1	0.942696	72.57637	76.33963
A-Drug	8.450741	1	0.405672	7.641016	9.260465	1
B-PLGA	7.701481	1	0.405672	6.891757	8.511206	1
C-PVA	1.075556	1	0.405672	0.265831	1.88528	1
D-ST	-0.89981	1	0.405672	-1.70954	-0.09009	1
AB	4.706944	1	0.496845	3.715238	5.69865	1
AC	0.151944	1	0.496845	-0.83976	1.14365	1
AD	-0.03	1	0.496845	-1.02171	0.961706	1
BC	-0.09361	1	0.496845	-1.08532	0.898095	1
BD	0.027222	1	0.496845	-0.96448	1.018928	1
CD	-0.07917	1	0.496845	-1.07087	0.912539	1
A^2	-7.78674	1	0.694793	-9.17355	-6.39993	1.001626
B^2	-7.05896	1	0.694793	-8.44578	-5.67215	1.001626
C^2	-0.78119	1	0.694793	-2.168	0.605628	1.001626
D^2	-0.33174	1	0.694793	-1.71855	1.055073	1.001626

Final equation in terms of coded factors: PDE = 74.45+ 8.45A + 7.70B + 1.07C – 0.89D + 4.70AB + 0.15AC - 0.03AD – 0.09BC + 0.02BD – 0.07CD – 7.78A² – 7.04B² – 0.78C² – 0.33D²… Eqn. 1.

Table 6. ANOVA sheet of PEGylated nanoparticles bearing temozolomide on percent drug entrapment.

Table 6A
Response―PDE | ANOVA for Response Surface Quadratic Model | Analysis of variance table [Partial sum of squares-Type III]
Source	Sum of Squares	df	Mean Square	F-Value	p-value Prob > F
							Model	9876.487	14	705.4634	75.1158	< 0.0001	Significant
A-Drug	3816.122	1	3816.122	406.3302	< 0.0001
B-PLGA	3168.176	1	3168.176	337.3387	< 0.0001
C-PVA	55.89636	1	55.89636	5.951691	0.0174
D-ST	59.09482	1	59.09482	6.292254	0.0146
AB	785.5875	1	785.5875	83.6472	< 0.0001
AC	1.1236	1	1.1236	0.119638	0.7305
AD	2.1025	1	2.1025	0.223868	0.6376
BC	8.400336	1	8.400336	0.894445	0.3477
BD	0.001736	1	0.001736	0.000185	0.9892
CD	0.298844	1	0.298844	0.03182	0.859
A^2	1082.655	1	1082.655	115.2782	< 0.0001
B^2	827.0542	1	827.0542	88.06246	< 0.0001
C^2	4.171924	1	4.171924	0.444215	0.5074
D^2	4.849833	1	4.849833	0.516397	0.4749
Residual	629.2424	67	9.391677
Lack of Fit	628.4103	66	9.521369	11.44326	0.2315	not significant
Pure Error	0.83205	1	0.83205
Cor Total	10505.73	81

Table 6B
Standard deviation	3.064584	R-Squared	0.940105
Mean	61.81098	Adj R-Squared	0.927589
C.V. %	4.957994	Pred R-Squared	0.912094
PRESS	923.5207	Adeq Precision	27.6636

Table 6C
Factor	Coefficient		Standard error	95% CI low	95% CI high	VIF
	Estimate	Df
Intercept	71.92667	1	0.969107	69.99232	73.86101
A-Drug	8.406481	1	0.417037	7.574072	9.238891	1
B-PLGA	7.65963	1	0.417037	6.82722	8.492039	1
C-PVA	1.017407	1	0.417037	0.184998	1.849817	1
D-ST	-1.04611	1	0.417037	-1.87852	-0.2137	1
AB	4.671389	1	0.510764	3.6519	5.690878	1
AC	0.176667	1	0.510764	-0.84282	1.196156	1
AD	-0.24167	1	0.510764	-1.26116	0.777823	1
BC	-0.48306	1	0.510764	-1.50254	0.536434	1
BD	0.006944	1	0.510764	-1.01254	1.026434	1
CD	-0.09111	1	0.510764	-1.1106	0.928378	1
A^2	-7.66883	1	0.714258	-9.09449	-6.24316	1.001626
B^2	-6.70272	1	0.714258	-8.12838	-5.27705	1.001626
C^2	-0.47605	1	0.714258	-1.90172	0.949617	1.001626
D^2	-0.51327	1	0.714258	-1.93894	0.912394	1.001626

Final Equation in terms of Coded factors: PDE = 71.92+ 8.40A + 7.65B + 1.01C – 1.04D + 4.67AB + 0.17AC - 0.24AD – 0.48BC + 0.01BD – 0.09CD – 7.66A² – 6.70B² – 0.47C² – 0.51D²…. Eqn. 3.

Particle size

Nanoparticles are formed when specific concentration of PLGA and PVA were mixed together. All the batches of Non-PEGylated and PEGylated nanoparticles within the experimental design were also evaluated for their particle size. The transformed values for particle size of all the batches (28 each) of Non-PEGylated and PEGylated nanoparticles bearing temozolomide TMZ along with the results are shown in Table 1 and 2. The results show that formulations no. 10, 19, 20 and 22 from each class of formulations are exhibiting minimum particle size, i.e., < 114 nm for Non-PEGylated nanoparticles, while it is increased about 6nm more in case of PEGylation of nanoparticles which might be due to the diffusion of the copolymer solubilized in the organic phase leads to an homogenous distribution of the PEG chain on the surface of the droplets and on the surface of the NPs after solvent evaporation. The PS (dependent variable) obtained at various levels of 4 independent variables (A, B, C and D). The response surface quadratic models were generated using Expert Design Software. These were subjected to multiple regression to yield a second order polynomial equations (full model). The correlation coefficient for the models were also calculated which are found to be > 0.96 indicating good fit. The particle size of various nanoparticles formulations showed wide variation i.e., ranges from a minimum of 111.91 nm to a maximum of 120.88 nm in case of Non-PEGylated nanoparticles and 116.31 nm to 123.76 nm in case of PEGylated nanoparticles bearing temozolomide. It is clearly indicated that the particle size of the nanoparticles is strongly affected by the variables selected for the study. It is observed that as on increasing the concentration of PLGA polymer in the matrix of nanoparticles the particle size was found to increase upto the level of medium (i.e., 50 mg) at 5mg of drug concentration then little change in particle size was observed which could be due to saturation of the polymer matrix.

It is also observed that the PS was significantly changed (p > 0.05) because as on changing sonication time from 30 sec to 90 sec there is decrease in the PS of the nanoparticles which could be due to the production of high energy and released with rapid dispersion to form small size nanoparticles. Similarly, the effect of PVA on the PS of various nanoparticles was observed and as on increasing the PVA concentration from 0.5 to 1% concentration in nanoparticles, the PS increases insignificantly while on further increasing PVA concentration to 1.5% significant change in PS was observed in all the cases of nanoparticles formulations. This shows the appropriate concentration of PVA (surfactant 1%) for the better formation of tight surface of PVA macromolecules at high concentration which increased diffusion resistance of drugs from aqueous phase and stabilized the emulsion. But too much of PVA was susceptible in the nanoparticles because it could not be totally biodegraded in vivo and could decrease cellular uptake of nanoparticles. On the other hand too much of PVA was difficult to remove.

The main effect of A, B, C and D represent the average result of changing variable at a time from its low level to high level. The interaction terms (AB, AC, AD, BC, BD, CD, A², B², C² and D²) show how the particle size changes when 2 variables are simultaneously changed. The negative coefficient for all the independent variables (D, AB, BC, BD, A², B², C² and D²) indicate unfavorable effect on the particle size while others are exhibiting positive interaction which indicate favorable effect on the nanoparticles size. Among the 4 independent variable the lowest coefficient value is for D² (-0.02 and p < 0.05) indicating that this variable is insignificant in the prediction of PS as the concentration of drug was kept unchanged. The Variance Inflation Factor (VIF) measures how much the variance of that model coefficient is inflated by the lack of orthogonality in the design and calculated for Non-PEGylated and PEGylated formulations which is found to be near 1 indicating good estimation of the coefficient.

The model F value calculated in the range of 287.94 to 128.02 which implies the models are significant. The values of Prob > F less than 0.05 are indicating that model terms are significant. In all cases A, B, C, D, AB, A² and C² are significant model terms.

The lack of fit values “F-value” for Non-PEGylated nanoparticles was found to be 0.03 which implies the lack of fit is not significant relative to the pure error and there is a 100% chances of large lack of fit “F-value” could occur due to noise and non-significant lack of fit “F-value” is good fit of model. Similar results were obtained in PEGylated nanoparticles where lack of fit “F-value” was obtained 0.07 for TMZ which are non-significant related to pure error. In these both cases 99.95% chance of large lack of fit “F-value” could occur due to noise.

In all cases “Pred R-squared” values are in reasonable agreement with the “Adj R-squared” values. The Adeq-Precision is the measures of the signal to noise ratio. A ratio of greater than 4 is desirable. In our case the Adeq-Precision value is in range of 48–72 which indicates an adequate signal (Tables 7 and 8).

Table 7. ANOVA sheet of non-PEGylated nanoparticles bearing temozolomide on particle size.

Table 7A
Response―PS ANOVA for Response Surface Quadratic Model Analysis of variance table [Partial sum of squares-Type III]
Source	Sum of squares	df	Mean square	F-value	p-value Prob > F
Model	1086.671	14	77.61934	287.9431	< 0.0001	Significant
A-Drug	715.4784	1	715.4784	2654.198	< 0.0001
B-PLGA	51.58756	1	51.58756	191.3735	< 0.0001
C-PVA	113.9414	1	113.9414	422.6863	< 0.0001
D-ST	171.842	1	171.842	637.4793	< 0.0001
AB	0.103469	1	0.103469	0.383839	0.5377
AC	0.297025	1	0.297025	1.101868	0.2976
AD	0.028336	1	0.028336	0.105118	0.7468
BC	0.238469	1	0.238469	0.884646	0.3503
BD	0.005625	1	0.005625	0.020867	0.8856
CD	0.092011	1	0.092011	0.341332	0.561
A^2	28.44803	1	28.44803	105.5332	< 0.0001
B^2	0.016815	1	0.016815	0.062377	0.8035
C^2	4.484401	1	4.484401	16.6357	0.0001
D^2	0.506602	1	0.506602	1.879333	0.175
Residual	18.06084	67	0.269565
Lack of Fit	12.14404	66	0.184001	0.031098	1	not significant
Pure Error	5.9168	1	5.9168
Cor Total	1104.732	81

Table 7B
Standard deviation	0.519196	R-Squared	0.983651
Mean	115.273	Adj R-Squared	0.980235
C.V. %	0.450406	Pred R-Squared	0.977501
PRESS	24.85564	Adeq Precision	70.73664

Table 7C
Factor	Coefficient		Standard error	95% CI low	95% CI high	VIF
	estimate	Df
Intercept	115.856	1	0.164184	115.5283	116.1837
A-Drug	3.64	1	0.070654	3.498975	3.781025	1
B-PLGA	0.977407	1	0.070654	0.836382	1.118433	1
C-PVA	1.452593	1	0.070654	1.311567	1.593618	1
D-ST	-1.78389	1	0.070654	-1.92491	-1.64286	1
AB	-0.05361	1	0.086533	-0.22633	0.119109	1
AC	0.090833	1	0.086533	-0.08189	0.263553	1
AD	0.028056	1	0.086533	-0.14466	0.200776	1
BC	0.081389	1	0.086533	-0.09133	0.254109	1
BD	-0.0125	1	0.086533	-0.18522	0.16022	1
CD	0.050556	1	0.086533	-0.12216	0.223276	1
A^2	-1.24311	1	0.121008	-1.48464	-1.00158	1.001626
B^2	0.030222	1	0.121008	-0.21131	0.271756	1.001626
C^2	0.493556	1	0.121008	0.252022	0.735089	1.001626
D^2	-0.16589	1	0.121008	-0.40742	0.075645	1.001626

Final Equation in terms of coded factors: PS = 115.85+ 3.64A + 0.97B + 1.45C – 1.78D – 0.05AB + 0.09AC + 0.03AD – 0.08BC – 0.01BD – 0.05CD – 1.24A² – 0.03B² – 0.49C² – 0.16D²…. Eqn. 2.

Table 8. ANOVA sheet for PEGylated nanoparticles bearing temozolomide on particle size.

Table 8A
Source	Sum of squares	df	Mean square	F-value	p-value Prob > F
Model	749.4104	14	53.52932	128.02	< 0.0001	Significant
A-Drug	471.6476	1	471.6476	1127.986	< 0.0001
B-PLGA	101.9563	1	101.9563	243.8373	< 0.0001
C-PVA	67.15645	1	67.15645	160.6104	< 0.0001
D-ST	57.57736	1	57.57736	137.7012	< 0.0001
AB	0.005625	1	0.005625	0.013453	0.908
AC	0.1444	1	0.1444	0.345345	0.5587
AD	0.001344	1	0.001344	0.003215	0.9549
BC	0.056803	1	0.056803	0.135849	0.7136
BD	0.595469	1	0.595469	1.424116	0.2369
CD	0.0441	1	0.0441	0.105469	0.7464
A^2	42.29364	1	42.29364	101.1489	< 0.0001
B^2	0.43066	1	0.43066	1.029961	0.3138
C^2	8.163949	1	8.163949	19.52479	< 0.0001
D^2	0.00791	1	0.00791	0.018917	0.891
Residual	28.01488	67	0.418133
Lack of Fit	23.24083	66	0.352134	0.07376	0.9995	not significant
Pure Error	4.77405	1	4.77405
Cor Total	777.4253	81

Table 8B
Standard deviation	0.646632	R-Squared	0.963965
Mean	118.9363	Adj R-Squared	0.956435
C.V. %	0.543679	Pred R-Squared	0.949605
PRESS	39.1785	Adeq Precision	46.84067

Table 8C
Factor	Coefficient		Standard error	95% CI low	95% CI high	VIF
	Estimate	Df
Intercept	119.6103	1	0.204483	119.2022	120.0185
A-Drug	2.95537	1	0.087995	2.779731	3.13101	1
B-PLGA	1.374074	1	0.087995	1.198434	1.549714	1
C-PVA	1.115185	1	0.087995	0.939546	1.290825	1
D-ST	-1.03259	1	0.087995	-1.20823	-0.85695	1
AB	0.0125	1	0.107772	-0.20261	0.227614	1
AC	-0.06333	1	0.107772	-0.27845	0.15178	1
AD	0.006111	1	0.107772	-0.209	0.221225	1
BC	0.039722	1	0.107772	-0.17539	0.254836	1
BD	0.128611	1	0.107772	-0.0865	0.343725	1
CD	-0.035	1	0.107772	-0.25011	0.180114	1
A^2	-1.51573	1	0.15071	-1.81655	-1.21491	1.001626
B^2	-0.15295	1	0.15071	-0.45377	0.147867	1.001626
C^2	0.665938	1	0.15071	0.365121	0.966756	1.001626
D^2	-0.02073	1	0.15071	-0.32155	0.280089	1.001626

Final equation in terms of coded factors: PS = 119.61+ 2.95A + 1.37B + 1.11C – 1.03D + 0.01AB - 0.06AC + 0.01AD + 0.03BC + 0.02BD – 0.03CD – 1.51A² – 0.01B² + 0.66C² – 0.02D²…. Eqn. 4.

Optimum formula

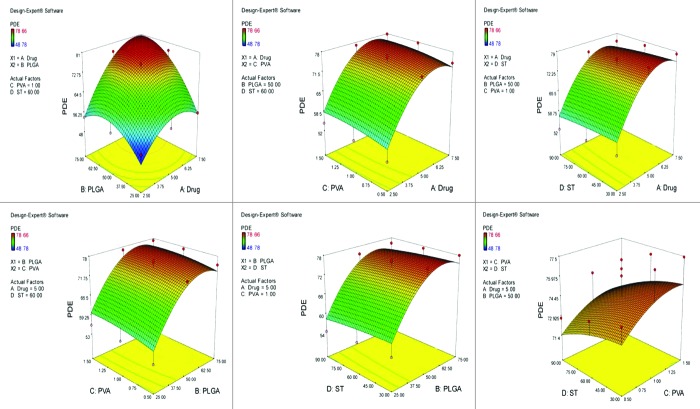
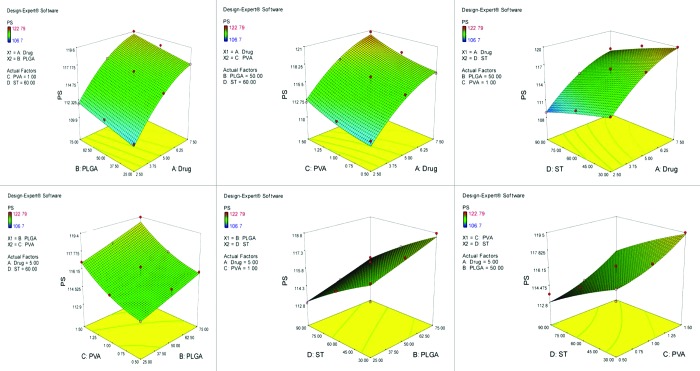
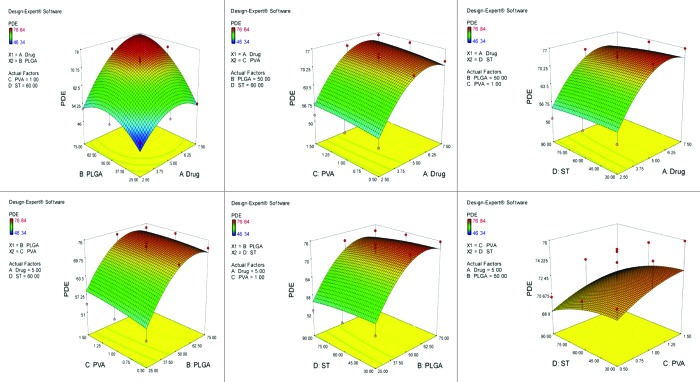
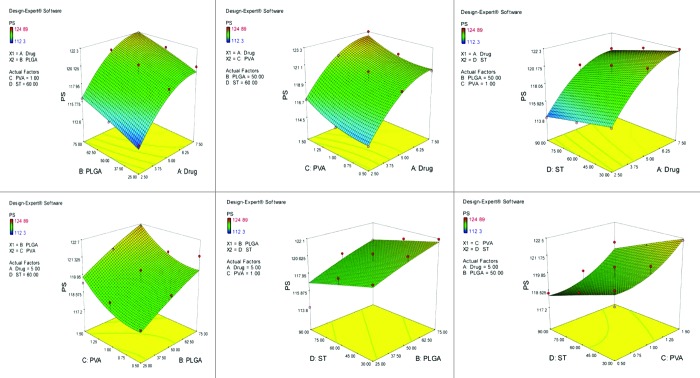
After studying the effect of the independent variables on the responses, the levels of these variables that give the optimum response were determined. It is evident from the polynomial quadratic model and construct contour plots (Figs. 1, 2, 3, 4 and 5) that there is no significant effect on the percent drug entrapment and particle size was observed when drug concentration was increased (i.e., 7.5 mg). Hence, the medium level was selected as optimum, which gives high value of PDE (76.02%) and a small PS (112.93 nm) for Non-PEGylated and high value of PDE (75.12%) and a small PS (117.23 nm) for PEGylated nanoparticles.

Figure 1.

Graph showing the effect of drug and PLGA, drug and PVA, drug and ST, PLGA and PVA, PLGA and ST and PVA and ST on percent drug entrapment of non-PEGylated nanoparticles bearing temozolomide.

Figure 2.

Graph showing effect of drug and PLGA, drug and PVA, drug and ST, PLGA and PVA, PLGA and ST and PVA and ST on particle size of non-PEGylated nanoparticles bearing temozolomide.

Figure 3.

Graph showing effect of drug and PLGA, drug and PVA, drug and ST, PLGA and PVA, PLGA and ST and PVA and ST on percent drug entrapment of PEGylated nanoparticles bearing temozolomide.

Figure 4.

Graph showing effect of drug and PLGA, drug and PVA, drug and ST, PLGA and PVA, PLGA and ST and PVA and ST on particle size of PEGylated nanoparticles bearing temozolomide.

Figure 5.

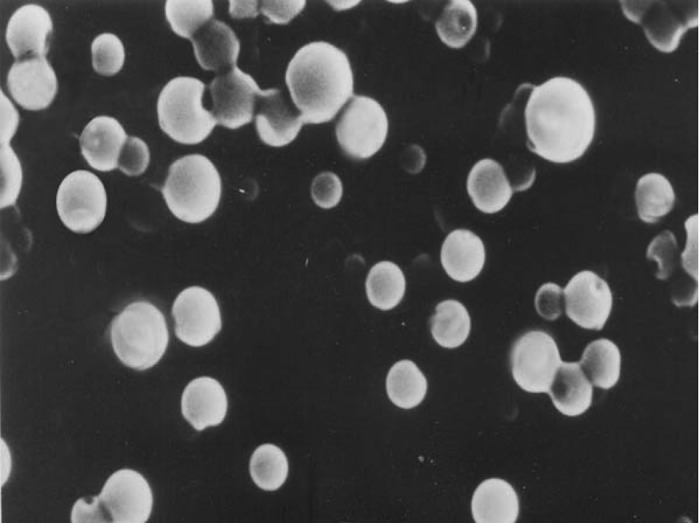
Scanning electron microscopy of PEGylated nanoparticles.

Materials and Methods

Temozolomide was obtained as a gift sample from the Kandelwal Lab, Mumbai, India. Poly (D-L-lactic-Co-glycolic acid) (PLGA) with L:G molar ratio of 50:50 and Mw of 20,000, Bis-amine-PEG, Polyvinyl alcohol (PVA), Stannous octoate, were procured from Sigma Chemicals. Cellophane membrane (molecular weight cut off, 12000–14000 dalton) was procured from Himedia Ltd., Mumbai, India. All other reagents used in this study were of HPLC grade. Water wherever used was unionized and sterile water for injection.

The traditional approach to developing a formulation is to change 1 variable at time. By this method it is difficult to develop an optimized formulation, as the method reveals nothing about the interactions among the variables. Hence, a 3⁴ factorial design was used with 4 factors (A, B, C and D) at 3 levels and experimental trials were performed at all 82 possible combinations. The dependent and independent variables are listed in Table 9.

Table 9. Variables and their levels in polynomial quadratic model.

	Low (-1)	Medium (0)	High (+1)
A- Drug Concentration	2.5 mg	5.0 mg	7.5 mg
B- PLGA Concentration	25 mg	50 mg	75 mg
C- PVA Concentration	0.50%	1.00%	1.50%
D- Sonication Time	30 Sec	60 Sec	90 Sec

Dependent variables
Y1- Percent Drug Entrapment (PDE)
Y2- Particle Size (PS)

Synthesis of PEG-PLGA copolymer conjugate

Copolymer of PEG-PLGA was synthesized using solution polymerization process under nitrogen, using stannous octoate as catalyst.³ Stannous octoate has been approved by the US FDA for surgical and pharmacological application. This compound is the most widely used initiator as it provides high reaction ratio, and high molar mass even under relatively mild conditions.⁴

Briefly, lactide and glycolide in a molar ratio of 4:1 and the specified amount of Bis-PEG were put in thick-walled glass tubes. The total weight of the feed was about 3 g. Stannous octoate was dissolved in hexane and added at a concentration of 0.03% by the weight of the feed. Then, the tubes were heated at 190°C for the 2 h. The resulting copolymer was purified by dissolving in chloroform and then precipitating in an excess methanol. The purified copolymer was dried under vaccum.⁵

Preparation of non-PEGylated nanoparticles

Drug loaded Non-PEGylated nanoparticles were prepared using emulsification solvent evaporation method (Avgoustakis, 2004) which is widely used for the encapsulation of hydrophobic drugs. Briefly, temozolomide (5 mg) and PLGA (50 mg) were dissolved in acetone (5 ml) (organic phase). The organic phase was added at a constant flow rate (0.3 ml/min) into 20 ml of aqueous phase containing 1% of PVA under intense shear using probe sonicator (Lark Innovative Fine Tecknowledge). The resultant mixture was further stirred for 2 h using magnetic stirrer. The organic solvent was then evaporated off under vacuum using a rotavapor (Steroglass). Then NPs were lyophilized (Heto Drywiner) at -46°C, 0.001 atm for 24 h with 5% w/w mannitol which was used as cryoprotectant (Yin et al., 2006).⁶

Preparation of PEGylated nanoparticles

PEGylated nanoparticles were also prepared by emulsification solvent evaporation method. All the parameters were kept same except the PLGA polymer was replaced with PEG PLGA Copolymer. These Non-PEGylated and PEGylated nanoparticles were stored in a tightly closed container until further evaluation.

Characterization of non-PEGylated and PEGylated nanoparticles

Shape morphology

The Non-PEGylated and PEGylated nanoparticles were characterized for the shape by Scanning Electron Microscopy (SEM, Philips XL 30 scanning microscope, Philips). The nanoparticles were coated with gold-palladium alloy (150–250 Å) using a sputter coater. The coater was operated at 2.2 kV, 20 mV, 0.1 torr (argon) for 90 sec at an accelerating voltage of 15 kv. The samples were viewed under a scanning electron microscope.

Particle size

The size of the nanoparticles was determined with the help of laser diffraction particle size analyzer (Cilas 1604L). Non-PEGylated and PEGylated nanoparticles were suspended in the chamber of particle size analyzer containing milli-Q water and the vesicles size were determined using the software provided with the instrument.

Percentage drug entrapment (PDE)

The amount of drug encapsulated in nanoparticles was determined using the method reported by Khuller and Pandey.⁵ The lyophilized non-PEGylated and PEGylated nanoparticles were digested in 5 ml of 0.1 M NaOH at 50°C for 10 min to release the drug content and resultant mixture was filtered. The volume was adjusted to 10 ml with 0.1M NaOH. The amount of drug was quantified by HPLC method.

Drug encapsulation efficiency (%) = Amount of drug released from the lysed NPs/amount of drug initially taken to prepare the NPs × 100.

Checkpoint analysis

A checkpoint analysis was performed to confirm the role of the derived polynomial equation and contour plots in predicting the responses. Values of independent variables were taken at 3 points.

Conclusion

Optimization of Non-PEGylated and PEGylated nanoparticles is a complex process that require one to consider a large number of variables and their interactions with each other. The present study demonstrates the use of quadratic model in optimization of nanoparticles formulations. The derived equation and contour plots aid in predicting the values of selected independent variables for preparation of optimum nanoparticles with desired properties.

Disclosure of Potential Conflicts of Interest

No potential conflicts of interest were disclosed.