Neural representations of events arise from temporal community structure

Abstract

Our experience of the world seems to divide naturally into discrete, temporally extended events, yet the mechanisms underlying the learning and identification of events are poorly understood. Research on event perception has focused on transient elevations in predictive uncertainty or surprise as the primary signal driving event segmentation. We present human behavioral and functional magnetic resonance imaging (fMRI) evidence in favor of a different account, in which event representations coalesce around clusters or ‘communities’ of mutually predicting stimuli. Through parsing behavior, fMRI adaptation and multivoxel pattern analysis, we demonstrate the emergence of event representations in a domain containing such community structure, but in which transition probabilities (the basis of uncertainty and surprise) are uniform. We present a computational account of how the relevant representations might arise, proposing a direct connection between event learning and the learning of semantic categories.

Introduction

As we observe and act in the world, perceptual information arrives in a more-or-less continuous manner over time, yet we do not experience the world as an unpunctuated stream. Instead, we apprehend coherent and bounded sub-sequences that have beginnings, middles and ends. In the cognitive literature, these segments have been termed events, and a core problem has been to understand how and why the continuous flow of experience is partitioned in this way. Operationally, segmentation is often measured by having participants observe some temporally extended episode and explicitly judge where the boundaries between sub-sequences lie. Such judgments are quite reliable^1,2 — but how do we come to know where events are bounded?

Prediction error or surprise have a central role in most accounts of event parsing^3-6, and sequence parsing⁷ more generally. In this class of explanations, event boundaries are identified on the basis of non-uniform transition probabilities. Within an event, a given observation is highly predictable from preceding observations, whereas the observation beginning a new event is less predictable. Thus, uncertainty about an upcoming observation, or surprise at the occurrence of an unpredicted observation, can provide a cue for segmentation.

We present an alternative account of event comprehension and segmentation that does not rely on predictive uncertainty and does not require the presence of non-uniform transition probabilities. Instead, we consider how representations of stimuli within an event are shaped by their temporal context. We propose that stimuli associated with similar temporal contexts are grouped together in representational space, forming clusters that provide the basis for event discrimination. This idea has a counterpart in theories of object semantics, which have aimed to explain why everyday objects seem to fall into natural categories. According to these theories, semantic category structure reflects a clustering of object representations in an internal representational space: Items belong to the same category when they are represented as similar to one another and as dissimilar to other familiar items^8-10. The degree to which items are represented as similar depends on the extent to which they are observed to share attributes.

We hypothesize that events are like semantic categories in this sense. Individual items ‘go together’ to form events because they are situated near each other in an internal representational space, and they lie near to one another because they share attributes. In object semantics, the attributes are the intrinsic properties of objects (for example, their parts, shapes, behaviors, functions and so on). In event representation, the relevant attributes are temporal associations. In particular, we hypothesize that items will fall close together in representational space when they are preceded and followed by similar distributions of items in familiar sequences. The resulting representational clustering grounds event perception and segmentation, just as the representational clustering involved in object semantics grounds category identification.

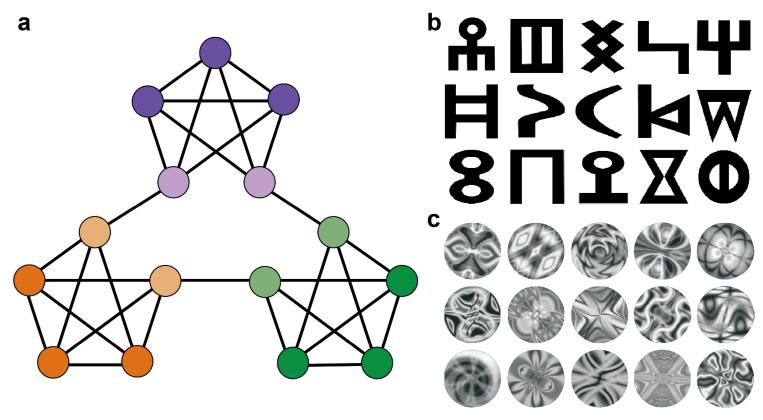
To make this idea concrete, consider the graph in Figure 1a. Imagine a scenario in which each node in the graph is associated with a particular visual stimulus and each edge indicates a possible transition between stimuli. Given that each node has exactly four neighbors, a random walk through the graph (used to generate a stream of stimuli) would produce uniform transition probabilities over all neighbors. Because the set of possible successor items on each step depends only on the current item, this uniformity in transition probabilities holds whether one takes into account only the most recent item or the n most recent items (Supplementary Fig. 1). As every transition that occurs is equally likely, the graph never gives rise to moments of relative uncertainty or surprise.

Figure 1.

Design and stimuli. (a) Graph with community structure, used to generate stimulus sequences. (b) Stimuli in experiment 1. (c) Stimuli in experiments 2 and 3.

Despite this uniformity, the graph remains highly structured, in that it contains three clusters of densely interconnected nodes. Although any individual node connects to four other nodes, nodes within a cluster tend to connect to one another and not to nodes in other clusters. In research on complex networks, this kind of clustering is referred to as community structure^11,12. Community structure is ubiquitous across a wide range of natural systems^13,14, and the construct has proven useful in analyzing networks describing sequential transition probabilities¹⁵, as in the case considered here. Note that in this sequential setting, nodes in the same cluster or community overlap in their temporal associations—they are likely to be preceded and followed by overlapping sets of nodes— whereas those lying in different clusters do not overlap as much in their temporal associations. Even in the presence of uniform transition probabilities, this pattern of temporal overlap provides a potential basis for dividing sequences of stimuli into events.

Using the graph in Figure 1a, we conducted three experiments testing two specific predictions of our theory. First, after exposure to sequences generated from the graph, human observers should parse sequences at points corresponding to transitions between communities. Whereas prior work on parsing has investigated transition probabilities as the main factor of interest, the graph in Figure 1a controls for this factor, leaving only community structure as a basis for parsing. Experiments 1 and 2 demonstrated reliable parsing at community boundaries, supporting the hypothesis that community structure can drive the formation of event representations. Second, stimuli belonging to the same community in the graph should come to have more similar neural representations following the sequence exposure. This prediction is supported by functional magnetic resonance imaging (fMRI) adaptation and multivoxel pattern analysis results in experiment 3.

Results

Experiment 1

Participants viewed a 35-min sequence of individual characters (Fig. 1b), each presented for 1.5 s, in an order generated by a random walk on the graph in Figure 1a. During this phase, participants performed a cover task requiring them to decide whether each stimulus was rotated away from a canonical orientation (Methods). Task instructions avoided any allusion to the structure or relevance of the order of stimuli. In the next phase of the experiment, participants were shown another 15-min sequence and were asked to segment the stream by pressing the spacebar at times that felt like natural breaking points. This sequence alternated between blocks of 15 images generated from a random walk on the graph and blocks of 15 images generated from a randomly selected Hamiltonian path through the graph (a path visiting every node exactly once). The purpose of interspersing Hamiltonian paths was to ensure that parsing behavior could not be explained by local statistics of the sequence (for example, after seeing items within a cluster repeat several times, participants might use the relative novelty of an item from a new cluster as a parsing cue).

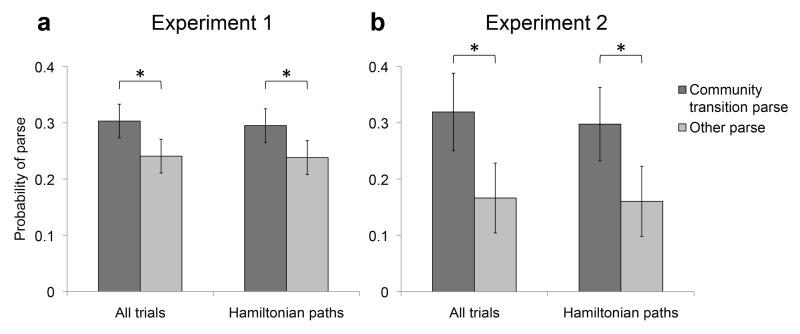
Accuracy on the rotation detection task indicated task compliance, with participants detecting rotated images with high A’ sensitivity (mean = 0.901, s.d. = 0.091; versus chance, t[29] = 24.19, P < 0.001; see Supplementary Table 1 for reaction times). In the parsing phase of the experiment, participants pressed the spacebar on passage into a new cluster significantly more often than at other times in the sequence (t[29] = 2.27, P < 0.05; Fig. 2a). Restricting the analysis to Hamiltonian paths did not change the result; new-cluster parses were significantly more likely even in these sequences (t[29] = 2.25, P < 0.05).

Figure 2.

Behavioral results. (a,b) For experiment 1 (a) and experiment 2 (b), the proportions of times participants parsed at a cluster transition and elsewhere in the sequence out of all opportunities to do so. Data were analyzed for all trials and restricted to Hamiltonian paths. *P < 0.05. Error bars denote 1 s.e.m. (30 participants for a, 10 for b).

Experiment 2

The purpose of this experiment was to replicate the results of experiment 1 while overcoming a subtle limitation of that experiment. The introduction of random Hamiltonian paths into the testing sequences of experiment 1 resulted in non-uniform transition probabilities within and between clusters. Specifically, within the set of Hamiltonian paths, the probability of transitioning from one cluster boundary node (one of the pale nodes in Fig. 1a) to the adjacent one, if not yet visited, is always exactly 1, whereas the probability of transitioning from the latter boundary node to each of the adjacent non-boundary nodes is one-third. To eliminate this difference, we employed one fixed Hamiltonian path for each subject, rendering uniform transition probabilities in both random walk and Hamiltonian paths. The Hamiltonian cycle was entered at different points, depending on where the preceding random walk terminated, and backward and forward traversals were included, chosen randomly for each Hamiltonian block. In addition to refining the procedure from experiment 1, we used a stimulus set with less obvious visual similarity relations and that did not invite verbal labeling (Fig. 1c).

Accuracy on the rotation detection task indicated task compliance, with participants detecting rotated images with high A’ sensitivity (mean = 0.818, s.d. = 0.130; versus chance, t[9] = 7.72, P < 0.001). As in experiment 1, participants pressed the spacebar on passing into a new cluster significantly more often than at other times in the sequence (t[9] = 2.30, P < 0.05; Fig. 2b). Restricting the analysis to Hamiltonian paths once again preserved this result (t[9] = 2.35, P < 0.05). Control analyses evaluated the possible contribution of associations formed between temporally nonadjacent items (Supplementary Fig. 1).

Experiment 3

In this fMRI experiment, we aimed to test our second prediction, namely that items lying in the same graph community should have more similar neural representations than items occupying different communities following exposure to the sequence. The experiment began with a pre-scan exposure phase, which was identical to the exposure phase of experiment 2. Participants then underwent fMRI as they continued to perform the orientation-detection cover task (note: not the parsing task) on sequences structured as in the parsing phase of experiment 2. To avoid potential issues raised by local item repetitions, we performed all analyses only on the data from Hamiltonian paths. Accuracy on the rotation detection task indicated task compliance, with participants detecting the rotated images with high A’ sensitivity in pre-scan (mean = 0.865, s.d. = 0.047; versus chance, t[19] = 34.73, P < 0.001) and scanning phases (mean = 0.893, s.d. = 0.081;versus chance, t[19] = 21.70, P < 0.001).

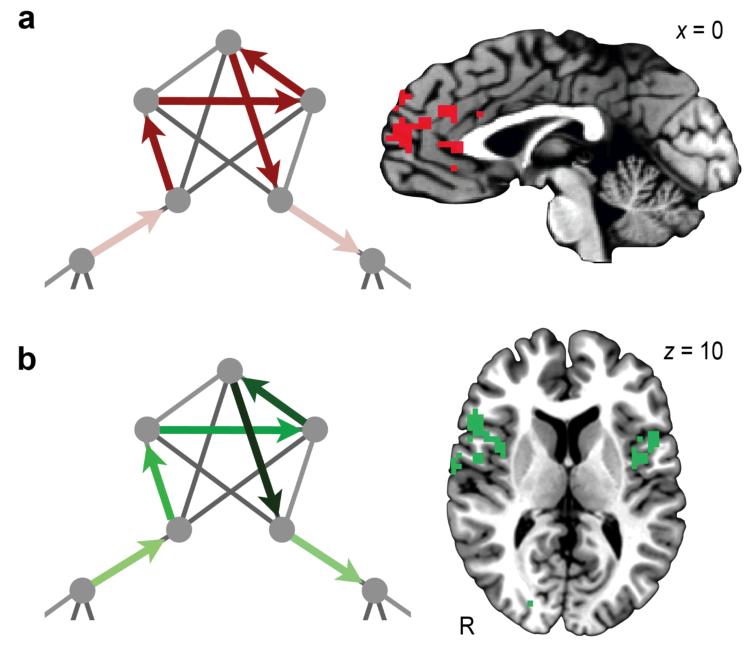
As an initial analysis, and to match the approach taken in previous fMRI studies of spontaneous event segmentation¹⁶, we ran a general linear model (GLM) with a regressor that indicated the transitions from one cluster to another. No areas were positively correlated with this event boundary regressor. A large cluster in medial prefrontal cortex (mPFC) was negatively correlated with the regressor (Fig. 3a), however, suggesting that this area is engaged during an event and transiently disengaged at event boundaries (P < 0.05 corrected; Table 1). To confirm that the effect was temporally specific and not an artifact arising from the design of the GLM, we ran two additional analyses: one with the event boundary shifted two steps back in the sequence and another with the event boundary shifted two steps forward. In both of these cases, there were no regions that reliably exhibited the same behavior.

Figure 3.

Results of GLM analyses. (a) mPFC was engaged throughout the duration of an event. This response reflects stronger activity within a community (dark red arrows) compared with at a community boundary (light red arrows). The arrows outline a possible Hamiltonian trajectory through the displayed portion of the graph. (b) Bilateral IFG and insula showed a repetition enhancement effect, reflecting progressively greater activity as more items from the same community were viewed, illustrated here with darker shades of green later in a community traversal (20 participants for a,b). R, right.

Table 1.

Reliable clusters in Experiment 3

Region	Brodmann areas	x	y	z	Extent (voxels)
Boundary regressor
mPFC	9/10/24	−1.4	43.6	16.5	205
Adaptation regressor
Left IFG/insula	13/44	−43.7	0.0	13.1	100
Right IFG/insula	13/44/45	49.6	8.5	7.7	109
Cuneus	18/19	11.7	−80.7	22.5	84
Pattern analysis
Left IFG/insula/ATL	13/38/47	−40.2	10.9	−5.9	150
Left STG	21/22	−52.7	−23.0	−0.8	107

Clusters reliable at p < 0.05 corrected. Coordinates are in Talairach space and correspond to the center of mass of the cluster.

To test our prediction that items in the same community would come to be represented similarly, we ran a GLM with a regressor that modeled an fMRI adaptation response. Previous research has shown that the a blood oxygen level-dependent (BOLD) response to an item can be affected by previous presentation of an item that engages an overlapping neural population, causing either a decreased response (repetition suppression) or, less commonly, an increased response (repetition enhancement)^17,18. Insofar as items within a community are represented by similar neural populations, we expected that responses to these items would become progressively suppressed or enhanced as more time is spent in the community. Consistent with this prediction, a repetition enhancement effect was observed in bilateral inferior frontal gyrus (IFG) and anterior insula (P < 0.05 corrected; Fig. 3b and Table 1), with progressively stronger responses as each of the five nodes in a community was traversed. We also found this profile in the cuneus (P < 0.05 corrected; Table 1).

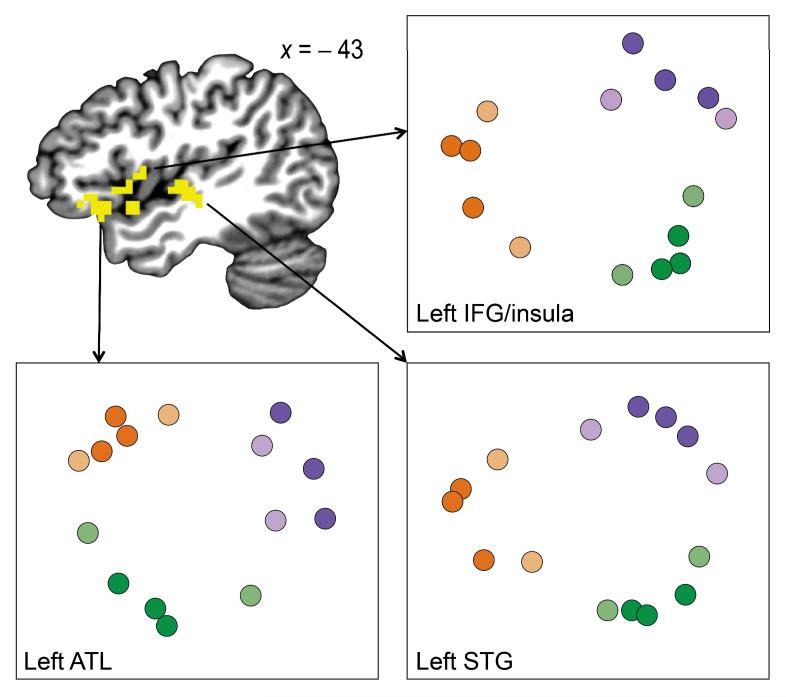
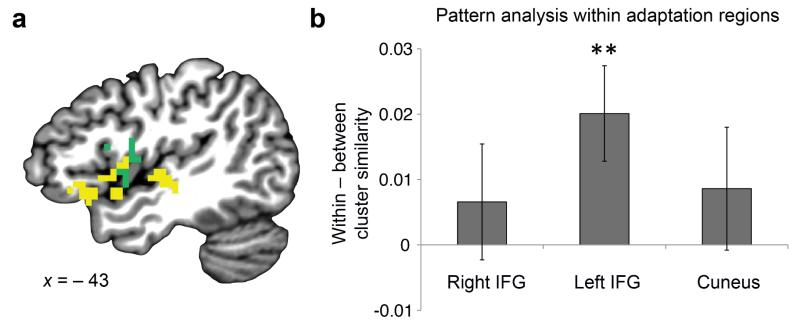
While these enhancement effects indicate overlapping representations within individual voxels¹⁸, the similarity structure predicted by our theory may also manifest in distributed patterns of responses across voxels. Thus, another way to test our prediction that items in the same community are represented more similarly is to examine whether the multivoxel response patterns evoked by each item come to be clustered by community. We examined these patterns over local searchlights throughout the entire brain, using Pearson correlation to determine whether activation patterns were more similar for pairs of items from the same community than for pairs from different communities. Two clusters of searchlights covering left IFG, anterior temporal lobe (ATL), insula and superior temporal gyrus (STG) showed this effect across participants (P < 0.05 corrected; Fig. 4 and Table 1). The adaptation and pattern analyses were performed independently over the whole brain and were sensitive to different components of the fMRI signal, yet they identified neighboring regions in left IFG and insula (Fig. 5). No areas showed higher similarity for between- than for within-community item pairs.

Figure 4.

Pattern similarity results. Clusters in left IFG and insula, left ATL, and left STG showed reliable community structure in the BOLD response in a whole-brain searchlight analysis. The similarity structure in each area was visualized by performing multi-dimensional scaling on the distances between the multivoxel pattern evoked by each item with each other item (averaged across searchlights within the area). Items are color-coded in accordance with the graph nodes in Figure 1a (20 participants).

Figure 5.

Neighboring regions found in adaptation and pattern analysis. (a) To visualize the proximity of the regions, the adaptation (green) and pattern analysis (yellow) results are displayed on the same brain. (b) To provide a sensitive measure of possible overlap between these results, we calculated the average multivoxel pattern analysis effect across searchlights within each of the three clusters identified by the adaptation analysis. In the left IFG cluster only, we found higher pattern similarity for within-versus between-community items. **P < 0.01. Error bars denote ± 1 s.e.m. (20 participants for a,b).

For each community, the three internal items (darker nodes in Fig. 1a) had more overlapping temporal associations than the two boundary items did with each other. Thus, if the evoked neural response in these regions expresses overlap in temporal associations, then the internal items should be more correlated with one another than with the boundary items. This highly specific prediction was supported by a marginally significant difference in the left STG cluster (t[19] = 1.71, P = 0.052 one tailed; other regions, P > 0.16).

Computational model

The fMRI adaptation and pattern analysis results from experiment 3 confirmed that temporal community structure shapes representational similarity, giving rise to clustered item representations, with transitions between clusters signaling event boundaries, as measured by parsing behavior in experiments 1 and 2. To articulate a specific hypothesis about the mechanisms underlying these results, we constructed a three-layer neural network model (Fig. 6a). The network took input representing the current stimulus and was trained to predict which stimulus would occur next. To simulate the stimulus sequences involved in our experiments, we included 15 localist units in both the input (current item) and output (next item) layers. Note that there was therefore no direct overlap between items in either the inputs or target outputs presented to the model.

Figure 6.

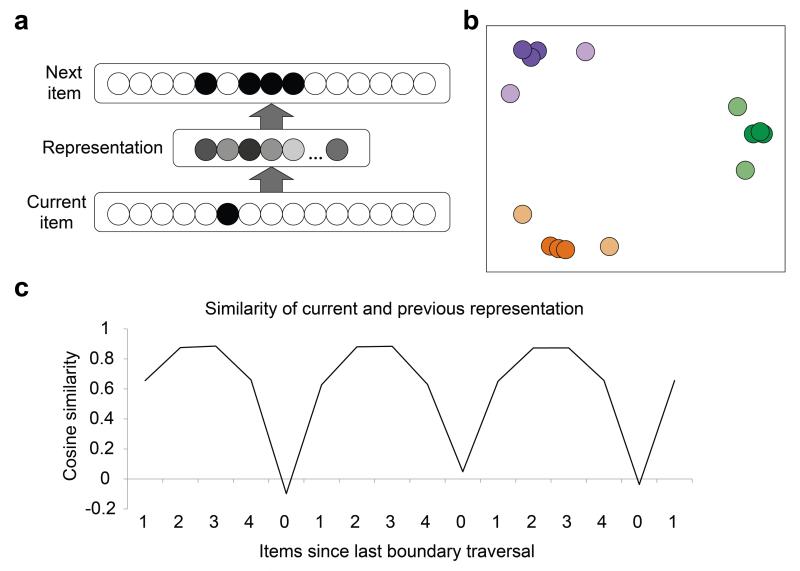
Model architecture and results. (a) Feed-forward neural network model that predicts subsequent observations given the current observation. (b) Multi-dimensional scaling of the hidden unit representations after sequence exposure. The dot colors correspond to positions on the graph shown in Figure 1a. (c) The average cosine similarity in the hidden layer representations between the current item and the last item in a traversal through a Hamiltonian path of the graph. Results represent an average over 20 networks initialized with different random seeds.

We exposed 20 randomly initialized networks to the same sequences viewed by participants. On each step of the sequence, the current item was shown as input and the model guessed which items might occur next. The model modified connection weights from the current-item layer to the internal (representation) layer and from the internal layer to the next-item layer to learn to activate only the four possible successor items for a given current item. Given that items in the same community generated similar predictions about which items would come next, the model naturally came to represent such items similarly in the internal layer.

The internal representations learned by the networks can be visualized by performing a multi-dimensional scaling of the activation patterns evoked by each of the 15 images, just as was done for visualization of evoked fMRI responses. The resulting plot (Fig. 6b) mirrors the community structure of the graph, as well as the similarity relations found in left IFG and insula, left ATL, and left STG (Fig. 4). Nodes within a community lie closer to one another (that is, are represented as more similar) than nodes from different communities (t[19] = 140.84, P < 0.0001). The nodes at the boundaries of communities do not share as many predictions as the other community members do with each other, and are therefore farther away from nodes that are more internal to the community (t[19] = 22.82, P < 0.0001). As a result of this structure, as the network traverses a Hamiltonian path, the similarity between the current and previous item representation is strongest for items most internal to a community, slightly weaker passing to a boundary item and weakest passing to a new community (Fig. 6c). The resulting temporal variation provides a sufficient basis for event parsing (even in the absence of explicit instructions to parse the sequence). Note that it also mirrors the pattern of activity that we observed in mPFC (Fig. 3). The latter observation prompts the speculation that mPFC may track changes in activity patterns in regions with community-based representational similarity, providing a signal that could underlie parsing decisions.

The neural network model demonstrates one simple way that neural representations might come to reflect environmental community structure. It is closely analogous to models of object semantics that describe how object representations cluster on the basis of their overlapping features¹⁰. The only difference is that the relevant overlap occurs in the distribution of items over time in the sequence, rather than in the intrinsic properties associated with each item. Specifically, the relevant features for the model are the items that a current observation predicts will occur in the future.

Discussion

Our behavioral and fMRI data support an account of event representation in which stimuli are grouped together into events because they share common temporal associations. In graphic representations of transition dynamics (for example, Fig. 1a), groups of items with shared contextual associations become clusters, or communities. In this sense, event representations arise from temporal community structure. When asked to mark event boundaries, participants segmented sequences at points corresponding to transitions between graph communities. Notably, this took place in the context of a generative process with uniform transition probabilities, excluding relative uncertainty or surprise as the only basis of parsing.

Our second theoretical proposal is that items with overlapping temporal associations coalesce into perceived events because such items give rise to similar internal representations. Our fMRI results provide direct evidence for this hypothesis. A pattern analysis revealed that areas of the left IFG, left insula, left ATL, and left STG represented items within a community as more similar than items from different communities. Notably, this effect emerged after only about an hour of exposure to the structured sequences, making this one of the first cases, to the best of our knowledge, in which multivoxel pattern analysis has been used to measure such acute learning-induced representational change¹⁹.

Also consistent with this proposal was a repetition enhancement effect in bilateral IFG and insula, where activity increased with dwell time in a single graph community. Although repetition suppression effects are more common¹⁸, repetition enhancement effects have been documented in numerous studies¹⁷ (including in IFG²⁰), especially when stimuli are degraded, novel or perceptually similar^21,22. One explanation for repetition enhancement in our study might be that evidence for the current community accumulated with each new item. Given the limited time for learning, each item may have carried partial or indefinite information about its own community membership, with confidence about the current community firming up over a succession of member items. Such a gradual accumulation of evidence would explain repetition enhancement in IFG and insula, in much the same terms that repeated presentation of a degraded visual stimulus leads to enhancement in visual cortex.

Both our adaptation and pattern analyses suggest that the left IFG is involved in representing events. This region has been associated with modality-independent semantic processing in diverse tasks, including verb generation, semantic classification and selection among competing semantic alternatives^23-26. The pattern analysis found that community structure was also captured by the left ATL and STG, regions that are strongly implicated in semantic processing²⁷. These findings are therefore consistent with our proposal that exposure to structured sequences generates representations similar to those that support object categorization. The IFG is also sensitive to sequential structure in a range of domains, including artificial grammar learning²⁸, language²⁹ and music^30,31 processing, and action perception and production^20,32. While such effects are clearly relevant to our work, they involve comparison of overall IFG activity between different experimental conditions. We compared the fine-grained pattern of activity within IFG across different individual stimuli, in a single task context. Understanding how the results obtained from this approach relate to those proceeding from earlier univariate studies of IFG will be an interesting target for investigation.

Whereas we found that representations in IFG captured the clustering of items within events, mPFC seems to support a different function. This region was engaged throughout the duration of an event, disengaging transiently at event boundaries. An extensive body of evidence links mPFC to event processing. For example, mPFC is more responsive to objects that are highly associated with a particular context³³; by definition, an item within a community is strongly associated with other members of the community, and thus with a particular context. Other work has implicated mPFC in integrating information when reading about events³⁴, processing structured compared to random sequences³⁵, thinking about highly familiar events³⁶, thinking about complex events³⁷, and elaborating on past and future events³⁸. Such findings are broadly consistent with our finding that mPFC was engaged during sub-sequences with tightly integrated temporal structure. Our modeling findings motivate the more specific hypothesis that mPFC may track changes in activity patterns in areas such as left IFG. One way of probing this possibility in the future (not afforded by the current design) would be to examine functional connectivity between mPFC and these other regions.

Both our theory and our fMRI findings suggest that stimuli with shared temporal associations come to be represented similarly. Our computational model illustrates how this similarity might emerge through learning. The idea that an item’s representation is shaped by the temporal structure of the episodes in which it participates has a long history in theories of language and conceptual knowledge. One influential model proposed that semantic and grammatical relationships among words are latent in the similarity structure of their linguistic contexts³⁹, an idea that has also been applied in the artificial grammar learning (AGL) literature⁴⁰. In research on natural language processing, the conceptual structure of words, phrases and even whole texts is often estimated by modeling the latent similarity structure of the contexts in which the text samples appear^41-43. Our proposal therefore builds on numerous precedents, establishing a new link between context-based representations in language and semantics and the phenomenon of event segmentation.

Our work also shares important links with statistical learning and AGL research^7,19,44,45, both of which are concerned with incidental learning of temporal regularities. In common with our study, statistical learning studies have often focused on segmentation of continuous stimulus streams and AGL studies have often considered how participants learn the sequential structure generated by a random walk on a graph. Our study, however, represents an important advance from these foundations. Both literatures have mainly emphasized variation in predictive uncertainty as the primary engine of segmentation and sequential knowledge generalization. In the case of segmentation, the central claim is that boundaries are detected when predictive uncertainty is high, a view that presupposes the existence of unequal transition probabilities. Even when previous studies have matched some transition probabilities, the underlying goal has been to isolate and test the behavioral effect of other, unequal transition probabilities⁴⁶. In AGL research, where judgments of grammaticality have been the main focus, the central claim has been that test sequences will be treated as grammatical if they have high conditional probability given the underlying graph, and as ungrammatical otherwise, again presupposing important differences in predictive strength across stimuli. To the best of our knowledge, our findings are the first to demonstrate identification of sequential structure in a context in which predictive strength is globally uniform and learning is instead driven by community structure.

Although we have focused on the implications for event representation, our results therefore have repercussions for theories of sequence representation more generally. For instance, a prominent idea in the AGL literature proposes that sequential structure, including segmental structure⁴⁷, is discovered by encoding commonly occurring sub-sequences (typically bigrams or trigrams) that are often referred to as fragments or chunks⁴⁵. An influential chunking model (PARSER⁴⁸), however, failed to identify the three communities in our graph when exposed to sequences structured as in our experiments (Supplementary Figs. 2 and 3). The reason is that all n-grams both within and between communities occur with equal probability in these sequences. As a result, any version of chunking that relies on differences in n-gram frequency will fail to explain the parsing behavior that we observed. One reason that this point is particularly noteworthy concerns the relationship between chunking and neural network models in AGL research. There has been considerable interest in understanding the relative strengths of these two formalisms, and this interest has naturally placed a premium on behavioral findings capable of adjudicating between them. Our results add to this set of findings by showing that the performance of chunking and neural network models can diverge when community structure is paired with uniform n-gram frequency.

One influential neural network AGL model proposed that items reflecting the same underlying state in a finite-state grammar come to be represented similarly because they occur in the same temporal context^40,49. Unlike the grammars examined in that work, and throughout the AGL literature, our graph never associates more than one stimulus with a single underlying state (node). Nevertheless, this proposal is clearly related to our assertion that items raising overlapping predictions will come to be represented similarly. Our work applies this general principle to the problem of event segmentation and provides neuroscientific evidence for its validity.

Our use of sequences with uniform transition probabilities served a critical methodological purpose, but invites the question of how our theory might apply to sequential domains (including naturalistic ones) that involve non-uniform and asymmetric transition probabilities. A useful context for addressing this is provided by the task most heavily used in statistical learning research. In the classical statistical learning experiment, items (for example, syllables or images) are grouped so that items within a group always appear in a fixed order, but the order of the groups is unpredictable. This sequential regime can be represented as a directed graph with communities that correspond to the item groupings (Supplementary Fig. 4). Thus, our account predicts that the representational changes observed in the current experiment should generalize to the statistical learning setting. This seems to be the case. After exposure to images that always occur in a fixed order in pairs, but in which the order of pairs is unpredictable, the neural representations of images in the same pair become more similar relative to images from distinct pairs¹⁹. This reorganization occurs throughout the hippocampus and medial temporal lobe cortex, as well as in the anterior temporal lobe, as we observed. Future work will be needed to understand how these areas interact and how different types of structure affect neural representations in different areas.

It is interesting to consider the extent to which our proposals concerning community structure, contextual overlap and representational clustering might provide alternative explanations for findings previously interpreted in terms of prediction error. The brain regions that we identified overlap partially with those observed in a statistical learning study¹⁹, but not with those reported in previous studies that emphasized the role of prediction error in event segmentation^5,16. The discrepancy may indicate that these other regions respond specifically to prediction error and do not provide a direct signal for event parsing, but could also reflect numerous differences in stimuli, methods, etc. Certainly our findings do not demonstrate that prediction error is never relevant to event segmentation, nor do they show that community structure is always involved. Working out the potential role for these two mechanisms, alongside others, such as goal-based processing⁵⁰, is a critical challenge for near-term research.

Methods

Participants

Members of the Princeton University community participated in exchange for monetary compensation ($12 per h for experiments 1 and 2, and $20 per h for experiment 3) or partial credit for a course requirement. Experiment 1 had 30 participants (17 females, mean age = 20.2 years, range = 18-30 years), experiment 2 had ten participants (four females, mean age = 22.0 years, range = 18-30 years) and experiment 3 had 20 participants (nine females, mean age = 20.9 years, range = 18-33 years). Data from one additional subject in experiment 3 was unusable because of procedural difficulties. Informed written consent was obtained from all participants, and the study protocol was approved by the Institutional Review Board for Human Subjects at Princeton University.

Stimuli and design

In experiment 1, the stimuli consisted of 15 glyphs from the Sabaean alphabet (Fig. 1b), an ancient Semitic language, which were generated from fonts downloaded at http://www.omniglot.com/. For each participant, the 15 glyphs were randomly assigned to the 15 nodes of the graph from Figure 1a. In experiments 2 and 3, the stimuli consisted of 15 abstract images (Fig. 1c) created in ArtMatic Pro (http://www.artmatic.com/). Again, these stimuli were assigned randomly to graph nodes for each participant.

In experiment 1, the sequence exposure phase consisted of viewing 1,400 stimuli generated from a random walk on the graph in Figure 1a. Stimuli were presented one at a time on a computer screen for 1.5 s each, with no interstimulus interval. In the parsing phase, participants viewed 600 stimuli, again presented one at a time for 1.5 s each. There were never any cues as to the structure of the graph; item presentation was continuous within and across clusters. In the parsing phase, sequence generation alternated between blocks of 15 items that were generated from a random walk on the graph and blocks of 15 items that were generated from a randomly drawn Hamiltonian path through the graph in which each node of the graph was visited exactly once. The purpose of interspersing Hamiltonian paths in the parsing phase was to ensure that parsing behavior could not be explained by local statistics of the sequence. If participants parse sequences at cluster boundaries in the Hamiltonian paths, then they must be relying on previously learned statistics. We did not use exclusively Hamiltonian paths in the parsing phase because we wanted to minimize unlearning of the temporal statistics.

Experiment 2 was identical to experiment 1 except that abstract, nonverbalizeable stimuli were used and the Hamiltonian paths were not randomly drawn in each block for each subject. Instead, one path was drawn for each subject, and the forward and backward versions of this path were chosen randomly for each block. This was done to remove the possibility that participants could be parsing on the basis of statistics learned during the parsing phase about the structure of randomly drawn Hamiltonian paths.

Experiment 3 was identical to experiment 2, except that there was a scanning session after the exposure phase. The scanning session had the same structure as the parsing phase, with alternating random walks and Hamiltonian paths, as concerns about the local statistics of the random walk also applied to our interpretation of the neural data. A rapid event-related design was used in the scanning session, with items presented for 1 s each with a jittered interstimulus interval (1, 3 or 5 s) such that the response to individual items could be modeled separately. There were five scanning runs lasting 616 s, with 160 items per run.

Procedure

In the exposure phase of all three experiments and the scanning session in experiment 3, participants were first shown the entire set of stimuli on the screen and told that they would be asked to detect when the stimuli appeared rotated from this initial orientation. Participants pressed one key on the keyboard when they thought the stimulus was rotated from its initial orientation and a second key otherwise, thus responding on every trial. Key assignment was counterbalanced across participants. Except in the scanner, a beep at one frequency was played when the response was incorrect and at another frequency when the response was not within the time frame that the stimulus was displayed. In the scanning session in experiment 3, participants responded with a button box, using the same fingers they had used on the keyboard in the exposure phase. Stimuli were rotated 90° from their initial orientation about 20% of the time in experiments 1 and 2, and 12.5% of the time in experiment 3. This rotation-detection task was used to keep participants engaged and attentive to the stimuli. Participants were given the opportunity to take a self-paced break about every 7 min in experiments 1 and 2, and between runs in experiment 3. The instructions did not mention anything about sequential aspects of the experiment, and we recruited participants who were naive to the purposes of the experiment.

In the parsing phase of all three experiments, participants were told that they would see sequences of items in the correct orientation and to “simply press the spacebar at times in the sequence that you feel are natural breaking points” (“spacebar” was replaced with “any button” in experiment 3). We viewed the parsing data in experiment 3, collected during an anatomical scan, as unreliable because of reports from multiple subjects that their strategy in the task was heavily influenced by the timing of acoustic scanner noise (Supplementary Fig. 5).

For parsing analyses, we operationalized passage into a new community as involving arrival into any community following at least four consecutive steps in another single community. The imposition of this four-step restriction was based on the a priori prediction, independent of our central theory, that participants might show a simple reluctance to press the parse button twice in close temporal succession. The specific choice of four steps was based on the fact that this criterion was met by two-thirds of all boundary-traversal events. However, the same qualitative pattern of results was obtained in additional analyses employing both less restrictive (1-3 steps) and more restrictive (5 steps) criteria (Supplementary Table 2).

fMRI acquisition and preprocessing

MRI data were acquired using a 3T Siemens Allegra scanner at Princeton University, and were preprocessed using AFNI (http://afni.nimh.nih.gov/afni/) and SPM (http://www.fil.ion.ucl.ac.uk/spm/). An echoplanar imaging sequence was used to acquire 34 3-mm oblique axial slices with 1-mm gap, repetition time (TR) = 2 s, echo time = 30 ms, flip angle = 90°, and field of view = 192 mm. An MPRAGE anatomical scan was acquired at the end of the session, consisting of 176 1-mm axial slices, repetition time = 2.5 s, echo time = 4.38 ms, flip angle = 8°, and field of view = 256 mm. We performed slice acquisition time correction using Fourier interpolation and motion correction using a six-parameter rigid body transformation to co-register functional scans. A despiking algorithm was used to attenuate outliers in each voxel’s time course. Data were spatially normalized by warping each subject’s anatomical image to match a template in Talairach space using a 12-parameter affine and nonlinear cosine transformation. This transformation was then applied to functional data.

fMRI GLM analysis

For GLM analyses, data were spatially blurred until total estimated spatial autocorrelation was approximated by a three-dimensional 6-mm full width at half maximum Gaussian kernel. Signal in each voxel was then intensity-normalized to reflect percent change. We ran two GLM analyses using AFNI. Both contained zero- through fifth-order polynomial trends and estimated movement in six directions for 13 participants who had some detectable movement. Both also included regressors that indicated whether any stimulus was present, whether the stimulus was rotated, error trials, trials with no response, and whether the stimulus was generated from a Hamiltonian path. These indicators were convolved with a standard hemodynamic response function. One of the GLMs was designed to look at transient responses at event boundaries or responses lasting throughout a community traversal. It contained a regressor indicating event boundaries (specifically, arrival at an item in a new cluster) within Hamiltonian paths. We ran two additional control GLMs to test the specificity of the boundary effects: One shifted the boundary regressor two items back and the other shifted it two items forward such that they were misaligned in both cases with the true boundaries. The other GLM was designed to detect adaptation effects during traversal through communities. It contained a regressor with the (hemodynamic response function convolved) values 2, 1, 0, −1 and −2 assigned to the first, second, third, fourth and fifth node, respectively, in a Hamiltonian path through a given community. To test the reliability of beta weights across participants, we used randomise (http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/randomise) in FSL to perform permutation tests and generate a null distribution of cluster masses for multiple comparisons correction (cluster-forming threshold, P < 0.05 two tailed).

fMRI pattern analysis

We ran a searchlight multivoxel pattern analysis⁵¹ to assess the similarity structure of individual item representations after sequence exposure. We z scored each voxel’s activation values across time in each run from the preprocessed data. We then took the average z scored activation for all presentations of a particular item two TRs (4 s) after stimulus onset (which was always time-locked to a TR). We only included item presentations that occurred four or more steps into a Hamiltonian path to minimize the possibility of picking up on any neural responses from items in the preceding random walk. The activity pattern for each of the 15 items was extracted from a cube of 3 × 3 × 3 voxels (a searchlight) centered on every voxel in the brain and stored as vectors with 27 elements. The Pearson correlation between the vector corresponding to each item and the vector corresponding to each other item was calculated, yielding a 15 by 15 similarity matrix for each searchlight.

We created a statistic on this matrix to evaluate the extent to which a particular searchlight matched our predictions. The statistic was the average Fisher-transformed correlation between items in the same cluster minus the average Fisher-transformed correlation between items not in the same cluster. To ensure that temporal overlap of the hemodynamic response between item presentations could not bias the results, we only compared between- and within-cluster item similarities for pairs of items that appeared the same distance away in the sequence. For example, we compared item pairs that occurred four steps away within a cluster only to item pairs that occurred four steps away across clusters. We did this for one, two, three and four steps (five or more steps would not allow any within-cluster pairs) and then averaged the results. Across these steps, each item participated in exactly four within-cluster pair correlations and exactly four across-cluster pair correlations. The difference statistic was assigned to the center voxel of each searchlight for visualization and hypothesis-testing purposes.

We performed the same permutation test as with the GLM analyses to assess the reliability of each searchlight across participants. The searchlight procedure creates additional smoothness in the data, but this smoothness appears in the null distribution of clusters, making it appropriately more difficult to find a cluster mass large enough to reach significance. The searchlight statistic can thus be treated the same way as beta weights (or any other statistic) in the permutation test. As in the GLM analyses, the permutation test shuffles voxel values across subjects and uses a cluster forming threshold of P < 0.05 (two tailed).

Computational model

The model was a fully connected three-layer feedforward neural network implemented in Emergent (http://grey.colorado.edu/emergent/), with 15 units in the input and output layers (one for each of the 15 items in the experiments), and 50 units in the hidden layer. The choice of number of units in the hidden layer was arbitrary, and results were the same for a wide range of values. The model was exposed to a sequence of stimuli generated from a random walk on the graph in Figure 1a, the same as for participants in all three experiments. On each step of the sequence, the input unit corresponding to the item on that trial was set to a value of 1, and all other inputs were set to 0. Similarly, the output unit corresponding to the item on the next trial was set to a value of 1, and all other outputs were set to 0. The network adjusted weights from the input to hidden layer and from the hidden to output layer to predict what would come next in the sequence using back-propagation with a learning rate of 0.2. We trained 20 models with weights randomly initialized from a uniform distribution between −0.5 and +0.5 for 200 epochs (each epoch contained all 60 input-output possibilities).