Propulsion and navigation within the advancing monolayer sheet

Abstract

As a wound heals, or a body plan forms, or a tumor invades, observed cellular motions within the advancing cell swarm are thought to stem from yet to be observed physical stresses that act in some direct and causal mechanical fashion. Here we show that such a relationship between motion and stress is far from direct. Using monolayer stress microscopy, we probed migration velocities, cellular tractions and intercellular stresses in an epithelial cell sheet advancing towards an island on which cells cannot adhere. We found that cells located near the island exert tractions that pull systematically towards this island regardless of whether the cells approach the island, migrate tangentially along its edge or, paradoxically, recede from it. This unanticipated cell-patterning motif, which we call kenotaxis, represents the robust and systematic mechanical drive of the cellular collective to fill unfilled space.

Perhaps the most basic fact of monolayer biology is that neither epithelium nor endothelium tolerates unfilled space. Confronted by a cell-free gap, the monolayer ordinarily advances its free edge until available space is covered¹. To explain such behavior, gradients of morphogen or chemokine can be important but are not sufficient², and resulting cellular motions must be mediated through the agency of some mechanical force acting over some defined area, the ratio of which is a mechanical stress. Patterning motifs and underlying physical principles that might explain this basic process more fully remain obscure. While innate complexity of biological systems may be partly to blame, perhaps the greater obstacle to understanding has been that mechanical stresses at work within the monolayer itself have remained almost invisible. Indeed, to explain collective cellular migration the notion of intercellular stresses have been postulated in mathematical models³, inferred from structure⁴, and approximated from tissue recoil following laser microsurgery^5,6, but until the last few years have not been precisely defined or experimentally measured^7–11. Random eddy-like swirling motions and associated stress fluctuations are now known to comprise 10–50 cells moving in cooperative packs that dominate a landscape of intercellular stress that is rather rugged ^9,12. From these dynamic heterogeneities¹³ here we have isolated the smaller but systematic components of this stress landscape in relationship to the systematic migration velocities that they might cause. To make hidden forces visible we used monolayer stress microscopy^9,11 and to perturb migration dynamics we placed in the path of an advancing epithelial cell sheet an island upon which cells could not adhere. The advancing monolayer encounters this island but is unable to fill available space and is therefore said to become frustrated. Using this approach, we ask if a causal mechanistic formulation linking motion and stress might be discerned, or, short of that, whether novel patterning motifs might be identified.

Perturbing the advancing cellular sheet

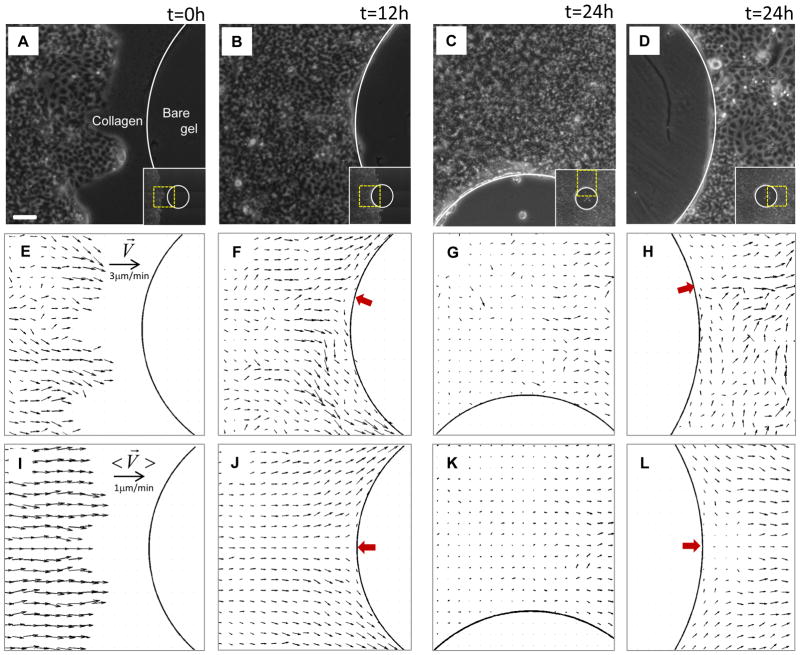
To perturb the advancing monolayer sheet we deposited a circular pillar of polydimethyl-siloxane (PDMS, diameter = 1mm) upon a polyacrylamide gel (Young’s modulus = 1.2kPa, thickness = 100μm). After coating the gel with collagen I, the pillar was carefully removed to leave a circular island of bare gel upon which cells could not adhere. We then seeded Madin-Darby Canine Kidney (MDCK) epithelial cells 3mm from the island and allowed them to adhere and grow to confluence; growth of a colony of MDCK cells on this substrate is insensitive to substrate stiffness¹⁰. After about 3 days, the advancing monolayer encounters (Fig. 1A) and ultimately surrounds this island (Fig. 1B,C,D; Supplementary Fig. S1). Local migration velocity was measured using particle imaging velocimetry (PIV)¹² (see Methods). For velocities as well as the other variables reported below, spontaneous fluctuations tend to be as large as or larger than corresponding local mean values. To probe the relationship among the mean values of these variables, we smoothed these fluctuations by averaging each field across an ensemble of six identical monolayer systems and denote such ensemble averages by brackets <…> (see Methods).

Fig. 1. Advancing monolayer of MDCK cells encounters and envelops a non-adherent island.

A–D: MDCK cells in phase contrast at a sequence of times. In each of these panels, the inset depicts the whole island at the corresponding time point. E–H: Corresponding vectors of instantaneous migration velocities (obtained from PIV) (see Methods). I–L: Migration velocities, <V̄>, averaged over an ensemble of 6 such islands. Three findings are of note. First, fluctuations of velocity are comparable to or exceed local mean values. Second, two points of zero velocity, called stagnation points (red arrows), are evident; the positions of these stagnation points fluctuate in time but reside on average at the equator. Third, as a result, the flow of cells divides into two streams at the upstream stagnation point and merge at the downstream stagnation point. Scale bar in panel (A): 100μm. Velocity scale bars in (E) and (I) applies to (F–H) and (J–L), respectively.

Systematic gradients of cellular velocity and substrate traction

Local velocity vectors point on average from west to east but also demonstrate velocity fluctuations associated with swirls that are a characteristic feature of collective cellular migration^9,12 (black arrows, Fig. 1E,I). When the free edge of the advancing front first encounters the island, and for all times thereafter, there is a point on the boundary at which the cellular velocity slows to zero and therefore defines a stagnation point (red arrow, Fig. 1F,J). The position of the stagnation point fluctuates with time but on average is located at the equator (Fig. 1J). After encountering this stagnation point, the cell stream divides into upper and lower half-planes, continues to migrate tangentially along the frustrated edge (Fig. 1F,G,J,K; Supplementary Movie SM1) and eventually envelops the island (Fig. S1). At the rear of the island another stagnation point develops, at which point the divided streams merge, stagnate and then turn sharply to rejoin the bulk migratory downstream flow (Fig. 1H,L).

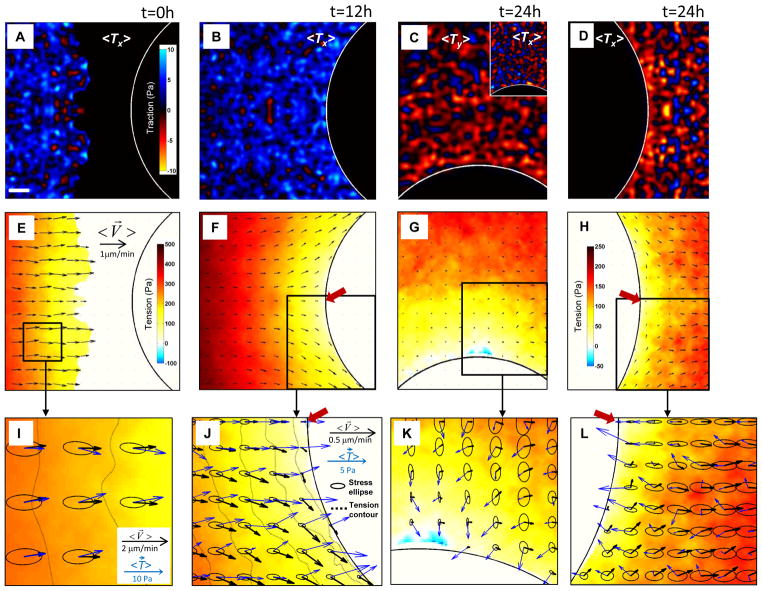
Local tractions exerted between the cell and its substrate was measured using Fourier-transform traction microscopy¹⁰ (see Methods). At each point the local traction exerted by the cell upon the substrate is necessarily equal and opposite to the traction exerted by the substrate upon the cell (Fig. S2); it is helpful to depict the latter of these here in order that maps of migratory motions versus those of associated tractions would be closely similar if the motions roughly follow substrate-to-cell tractions. Even after averaging across the ensemble, tractions demonstrate strong fluctuations in magnitude and even fluctuations in sign (Fig. 2A–D); such dynamic heterogeneity is also a characteristic feature of collective cellular migration^9,10,13. Upstream of the island the x-component of the traction vector,<T_x>, shows a preponderance of blue, indicating that average tractions upstream of the island tend to pull the monolayer eastward – toward the frustrated edge (Fig. 2B). But downstream of the island the x-component of the traction vector shows a preponderance of red, indicating that average tractions downstream of the island tend to pull westward, again toward the frustrated edge (Fig. 2D). Finally, near the north pole, the y-tractions, <T_y>, pull predominantly southward, yet again toward the frustrated edge (Fig. 2C). Importantly, regardless of cellular position along the frustrated edge, cells close to the frustrated edge exert tractions that tend to pull the monolayer toward that edge.

Fig. 2. Orientations of tractions, velocities, and principal stresses coincide, diverge, and recover.

A–D: Color maps of the ensemble averaged tractions exerted between the monolayer and its substrate (see text for sign convention). A,B,D: x-component of traction, <T_x>, west and east of the island. C: y-component, <T_y>, north of the island (the inset shows <T_x> on the north boundary). These components were selected to reflect the directions roughly normal to the island boundaries. Upstream versus downstream (A,D), <T_x>shows large fluctuations but systematic differences. Regardless of position near a frustrated edge, tractions pull toward that edge. E–H: Color maps showing the systematic buildup of tension and velocity fields (black arrows) at the same locations and times as in panels (A–D). (Due to large gradients of accumulated tensions, the color scale for panels (G) and (H) are expanded for clarity.) I–L: Expanded views of two regions from (F) and one each from (G) and (H). Together with tractions (blue arrows) and the velocity field (black arrows), monolayer stresses are depicted by ellipses, with axes and orientations corresponding to the principal stresses, and iso-tension contours by dashed lines in (I) and (J). Stagnation points are shown by red arrows in (J) and (L). Note the coincidence, divergence and recovery of orientations as the monolayer engulfs the island. Scale bar in panel (A): 100μm. Velocity scale bars in (E) and (J) applies to (F–H) and (I,J,J), respectively.

Buildup of intercellular stress and its gradients

Local stresses exerted between each cell and its immediate neighbors across cell-cell junctions were computed using monolayer stress microscopy^9,11,14 (Supplementary Fig. S2) (see Methods). This method rests on the assumption of a local balance of forces in which inertial effects are taken as being negligible; inertial effects scale roughly as tissue density times the square of tissue velocity, and are smaller than measured elastic stresses, frictional stresses, and traction stresses by roughly 14 orders of magnitude.

Local tension on average builds from zero at the advancing free edge to the highest tension at the center of the monolayer (color scale, Fig. 2E); this buildup of tension is known to occur as a result of a cellular tug-of-war that is characteristic of collective cellular systems, each cell pulling not only on the substrate but also on the one behind, thereby causing tension to build progressively with distance^10,15 (Supplementary Fig. S2). When the free edge of the advancing front encounters the island, small regions of compressive stress are occasionally observed, but the state of stress is overwhelmingly tensile; the stagnation point corresponds to the region of minimal tension, and systematic components of the tension gradient are readily apparent (Fig. 2F).

Tension alone is an incomplete description of the state of mechanical stress, however. Stress borne within the monolayer itself by the cytoskeleton and cell-cell junctions is a tensorial property possessing multiple tensor components, with the familiar tension as described above being the scalar corresponding to the trace of the stress tensor (Supplementary Fig. S2). Being a tensorial quantity, the intercellular stress need not be isotropic and, as shown below, is in fact strongly and systematically anisotropic. We display the local tensorial state of stress using an elliptical representation, wherein the major axis of each ellipse corresponds to the maximum principal stress, and the minor axis corresponds to the minimal principal stress. The sum of the two major radii of each ellipse is local tension, the departure of each ellipse from circularity is a measure of local stress anisotropy, and the orientation of each ellipse defines the local principal stress orientation.

Far from the frustrated edge, local traction vectors (blue arrows, Fig. 2I) act uniformly to pull the monolayer from west to east, and the direction of tractions corresponds closely to that of cellular motions (black arrows, Fig. 2I); velocity and traction directions are roughly coincident with average angular differences near 0°. Such an alignment between tractions and resulting motions might seem intuitive in so far as cells might move mainly along the direction of the tractions that they exert. And far from a frustrated edge these results would also be consistent with the notion of tension-induced cadherin-dependent cell polarization¹⁶, but has never before been demonstrated experimentally in monolayer sheets. Far from the frustrated edge, local orientations of maximal principal stress (major ellipse axes) versus local migration velocity (black arrows) coincide as well (Fig. 2I), and this coincidence is consistent with plithotaxis, defined as the tendency for each individual cell within a monolayer to migrate along the local orientation of the maximal principal stress, or equivalently, minimal intercellular shear stress^9,11,15,17. Approaching the frustrated edge, however, local velocity vectors veer systematically away from orientations of principal stress and away from orientations of local tractions by angles approaching 90° (Fig 2J). This extreme and systematic misalignment is neither intuitive nor consistent with tension-induced cell polarization. Regardless of cellular position or motion along the frustrated edge, tractions pull nearly perpendicular to that edge as if trying but failing to extend the monolayer into adjacent unfilled space (Fig. 2J,K). Moreover, local velocity vectors departing the frustrated edge, near the downstream stagnation point, veer away from local tractions by 180°, in anti-parallel fashion (Fig. 2L). In this neighborhood, the anti-parallel nature of tractions versus velocities is counterintuitive and paradoxical.

Contours of constant tension are denoted by dashed lines (Fig. 2I,J). One might have reasonably imagined that migrating cells progressively build the local tension gradient via a tug-of war mechanism^9,11,15,17, and therefore migrate down that local gradient, as demonstrated previously when no island is present ¹⁰. But near a frustrated edge this is not true (Fig. 2J). Velocity vectors do align with the tension gradient far from a frustrated edge (Fig 2I), but align nearly perpendicular to the tension gradient approaching a frustrated edge (Fig 2J).

Kenotaxis

Whether approaching a frustrated edge, migrating tangentially along it, or receding from it, the cell even several rows back from the edge is therefore seen to exert tractions tending to pull itself systematically toward that edge. This unanticipated but robust tendency of the cellular collective to generate local tractions pulling systematically and cooperatively toward unfilled space we call kenotaxis, from the Greek κενO meaning vacuum and τάξις meaning arrangement, and is not to be confused with the random manner in which cells migrating stochastically and independently might also fill an unfilled space¹⁸. Kenotactic tractions are fully revealed at a frustrated edge because motions into unfilled space that would have occurred otherwise have been stalled. Also revealed is the paradoxical uncoupling of these kenotactic tractions from local cellular velocities and from local intercellular stresses. Near an advancing free edge, of course, these multiple physical factors and their range of possible effects are not so readily discerned or separated. While it is perhaps not surprising that traction forces at a free edge should align with the direction of local cellular velocities¹⁹, it is not at all intuitive, at least to us, that traction forces at a frustrated edge should continue to pull towards that edge, and thus nearly perpendicular to local cellular velocities, or even contrariwise. Although these counterintuitive behaviors appear to prevail only when the monolayer encounters an obstacle, kenotaxis is seen to be at work along any edge separating filled from unfilled space.

At a migrating free edge²⁰ and throughout narrow strips with frustrated edges²¹ extracellular signal-regulated kinase (ERK) 1/2 is known to be activated. Using immunofluorescence staining, we observed that ERK 1/2 is activated but not preferentially at or near frustrated or free edges (Fig. S3); this discrepancy with previous reports may be attributable to different time scales; previous experiments spanned time scales of hours to one day^20,21 whereas ours spanned several days. When we inhibited ERK 1/2 using the inhibitor U0126 (10 μM), kenotactic tractions and migration velocities were little changed (data not shown). When we inhibited Src family tyrosine kinases using pyrazolopyrimidine (PP1, 10 μM)²⁰, kenotactic tractions decreased somewhat but cellular migration speed decreased dramatically (Fig. S4D, S4H). These findings represent another example of the surprising decoupling of migration velocities from tractions. This decoupling suggests redundant mechanisms by which edges are sensed.

One possible mechanism is mechanical. At the cell-cell junction, as well as within the cytoskeleton itself, the stress field back from the frustrated edge is predominantly tensile; our experiments show that tensile stress persists all the way to the cells encountering a frustrated edge. It follows that the traction exerted by the cell upon the substrate must polarize toward any adjacent unoccupied space in order to satisfy force balance locally. However, this is merely a description of the stress fields, and is not to be confused with a causal explanation of why cells cause tractions to polarize as they do. Do tractions polarize because the cell at the frustrated edge senses and responds to tension at its cell-cell junctions? Or instead do tractions polarize and tensions build because the cell senses and responds to unoccupied space? Either interpretation is consistent with local force balance. But which is the cause and which the effect remains unknown. Moreover, neither interpretation explains the relationship of the intercellular stress and the traction to the velocity vector. These represent important unanswered questions.

Kenotactic instabilities

Of some special interest in this regard is the motion of cells in the vicinity of the downstream stagnation point. In the wake of the island, such cells find themselves exerting traction antiparallel, not parallel, to their local migration velocities, and migrating up, not down, the local gradient in tissue tension. Compared with every other constituent cell anywhere else within the monolayer, such an alignment in both regards is topsy-turvy. Farther downstream, the orientation of local cellular tractions relative to that of local cellular velocities realign to the more usual parallel alignment. This realignment requires either clockwise or counterclockwise rotations of the traction vectors. The existence of both modes of reorientation with equal probability implies the possibility of unstable patterns, by analogy with a fair coin balanced on its edge, which may tip with equal probability either to the left or to the right. This leads us to the surprising prediction that mechanics of cellular migration within the wake must be not only complex but also mechanically unstable.

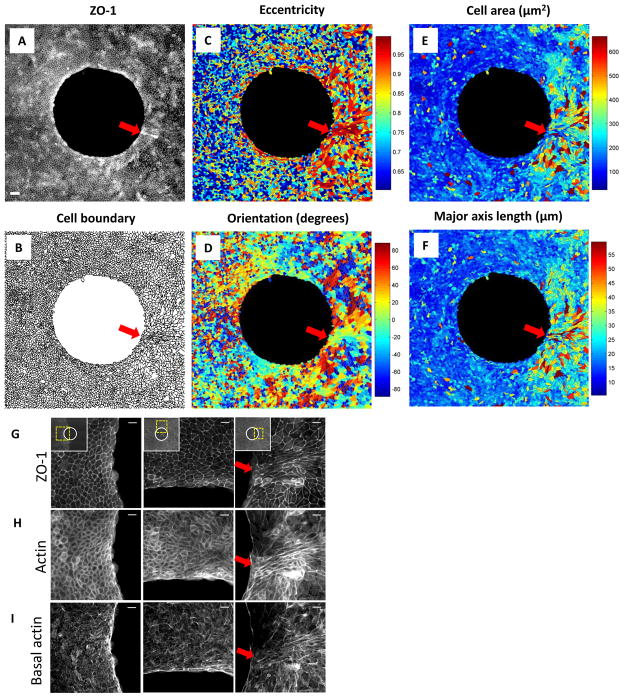
To test this prediction we looked for anomalies in downstream monolayer structure that are not evident elsewhere in the cellular migratory flow (Fig. 3). To demark cell boundaries, cell shape, and cell size we imaged the tight junction protein ZO-1, and to demark cytoskeletal structure we imaged f-actin. In the vicinity of the upstream stagnation point, the distribution of ZO-1 (Fig. 3A,G) and corresponding cell boundaries (Fig. 3B) were unremarkable. Cells approaching the frustrated edge showed some slight tendency toward modest eccentricity and alignment (Fig. 3C,D) but no tendency to become larger (Fig. 3E) or longer (Fig. 3F). Near the downstream stagnation point (arrow), by contrast, strong perturbation of nearly every structural metric was evident. Cells closest to the stagnation point were not any larger but were highly eccentric, aligned, and elongated (Fig. 3C–F), as if pulled from the frustrated edge like taffy candy. Indeed, for these cells local tractions exerted at the cell base pull westward whereas intercellular forces exerted at cell-cell junctions pull eastward, implying that shear forces in this special region go hand-in-hand with observed cellular axial extension (Supplementary Fig. S5). Just surrounding this region of cellular extension, cells were appreciably eccentric, lengthened, and enlarged (Fig. 3C–F) in a manner reminiscent of foreign-body epitheloid-cell granulomas as observed near sutures and micro-implants. Actin structure, similarly, was unremarkable except in the vicinity of the downstream stagnation point (Fig. 3H,I). Although it remains unclear from these experiments if the scale of these anomalous structural perturbations is set by the size of the island or rather by some feature of unstable inter-cellular dynamics, it is clear that these perturbations are strongest in the immediate vicinity of the downstream stagnation point, and that they ramify over a scale of distance much greater than cellular dimensions.

Fig. 3. Cellular morphology, tight junction structure and actin structure near the island.

A: ZO-1 immunofluorescence micrograph at t = 24h when a monolayer of MDCK cells fully enclosed the island. B: Cell boundaries retrieved from ZO-1 micrograph in panel (A). Segmentation was performed using a watershed algorithm. C–F: Eccentricity (C), orientation (D), cell area (E) and major axis length (F) determined from cell boundaries in panel (B). Red arrows depict downstream stagnation points. Scale bar in (A): 200μm. G: All projected actin immunofluorescence micrographs at t=24h when a monolayer of MDCK cells fully enclosed the island at west of the island, at northern pole and at east of the island. Basal actin (H) and ZO-1 (I) immunofluorescence micrographs at the same locations corresponding to locations in panel (G). Scale bars in (G,H,I): 20μm.

Just behind an advancing free edge, structures known as cryptic lamellipodia extend in the direction of sheet flow⁴, and tractions exerted by these cells are substantially larger than those generated in the rows far behind¹⁰. It has been argued that cryptic lamellipodia drive sheet flow⁴, although that interpretation has been disputed because leader cells contribute only insignificantly to the global buildup of tension gradients far behind the free edge¹⁰. Near a frustrated edge, by contrast, might cryptic lamellipodia exist, and, if so, in what direction might they extend? We found cryptic lamellipodia but found no consistent relationship between the direction of lamelipodium extension and that of the local velocity vector, the local traction vector, or the local principal stress orientation (Supplementary Movie SM2).

Patterning motifs of the cellular collective

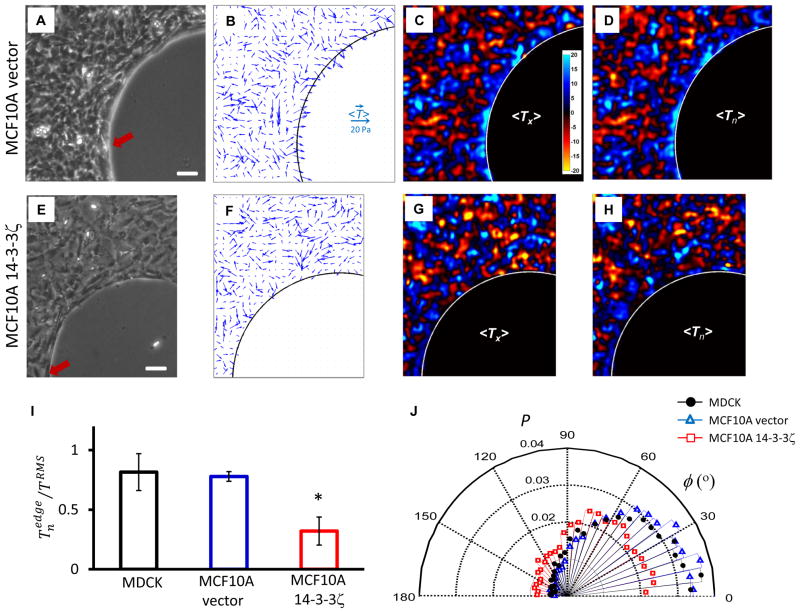
These findings seem not be restricted to our particular choice of experimental system. For example, when using rat pulmonary microvascular endothelial (RPME) cells²², which are spindle-shaped, the same kenotactic motif was evident (Supplementary Fig. S6). When using MCF10A mammary epithelial cells, and when overexpressing empty vector in those cells (Fig. 4A–D), the same motif was again evident, although overexpressing the oncogene 14–3–3ζ (Fig. 4E–H), which disrupts adherens junctions²³, caused tractions near the frustrated edge to become not only smaller (Fig. 4I) but also less well aligned toward the frustrated edge (Fig. 4J). When we inhibited myosin II using blebbistatin (25μM), tractions far from the island decreased dramatically and the bare island, which comprises elastic gel, recoiled centripetally, thus indicating of release of monolayer tension; tractions near the frustrated edge were attenuated but remained well aligned toward the frustrated edge (Supplementary Fig. S7). Finally, using a crescent-like island shape, tractions vectors were seen to align toward the frustrated edge in a manner that was indifferent to the sign of edge curvature (Supplementary Fig. S8). Accordingly, kenotaxis is not to be confused with any mechanism of wound closure that is driven by hoop tension acting through the law of Laplace over some positive (convex) local radius of curvature, as in the purse-string mechanism.

Fig. 4. Kenotactic tractions are evident in human mammary epithelial cells MCF10A vector, but are attenuated in MCF10A 14–3–3ζ, which disrupts adherens junctions.

A,E: Phase contrast images of nontransformed human mammary epithelial cell line, MCF10A, vector control (A) and cells overexpressing 14–3–3ζ which have decreased expression of cell-cell junctional markers (E)²³. B,F: Traction vectors, <T⃗>, averaged over an ensemble of 4 monolayers corresponding to cell types in panels (A,E) (see Methods). C,G: Color maps of x-component of tractions,<T_x>. D,H: Color maps of tractions normal to the frustrated edge, <T_n>. In case of nontransformed MCF10A vector cells, tractions near the frustrated edge are largest and oriented toward the edge (B,C,D). In case of MCF10A 14–3–3ζ cells, however, both the magnitude and alignment of tractions near the edge are attenuated (F,G,H). I: Normal component of tractions at the frustrated edge normalized by root-mean-square (RMS) traction across the entire maps, $T_n^{\mathit{edge}}/T^{\mathit{RMS}}$, for three cell types, MDCK (black), MCF10A vector (blue) and MCF10A 14–3–3ζ cells (red) (see Methods). *: $T_n^{\mathit{edge}}/T^{\mathit{RMS}}$ of 14–3–3ζ transfected MCF10a cells is smaller than that of vector-transfected MCF10A cells or that of MDCK cells (mean +/− standard error of the mean; p< 0.05 by Kruskal-Wallis test). J: The alignment angle, φ, between traction vectors at the frustrated edge and normal vectors to the edge for three cell types in panel (I). MDCK and MCF10A vector cells are seen to exert tractions highly oriented toward the frustrated edge, which are largest at that edge (I, J). In contrast, MCF10A 14–3–3ζ cells exert tractions in smaller extent toward the edge, the alignment angle of which are widely distributed, as if they are not frustrated by the edge (I, J). Scale bar in panels (A,E): 100μm. Each bar in (I) include observations from 6 monolayers of MDCK cells and 4 monolayers per each MCF10A cell type. Distributions in (J) have more than 7,000 observations.

Complete fields of cellular velocity, traction and intercellular stress are now laid bare. As such, discovery of a mechanistic equation of motion linking these factors based upon Newton’s laws together with constitutive cellular properties might now seem an attainable objective, but challenges remain formidable. For example, no theory presently in the literature has anticipated, or can explain, the cooperative patterning motifs implied either by plithotaxis or by kenotaxis. Nor does any theory presently predict or explain the downstream kenotactic instability reported here, although finger-like projections that arise at the free edge of the advancing monolayer are similarly suggestive of innate mechanical instability²⁴. Signaling via release of diffusible molecules and activation of non-diffusible structural molecules are almost certain to be involved. Similarly, tension-induced cadherin-dependent cell polarization¹⁶ might play a role but the important question of the surprising uncoupling of traction orientation from velocity orientation cannot be explained by that mechanism and remains open.

Compared with the physical picture of collective cellular migration previously imagined, these fields of velocity, traction and intercellular stress reveal dynamics that are mechanically richer, more intricate, and counter-intuitive. Compared with other mechanisms of patterning and guidance, including gradients of morphogens²⁵ and phase-gradient encoding of gene oscillations²⁶, kenotaxis is likely to be more primitive, but its ultimate physiologic effect seems clear. Simply put, kenotaxis drives non-random filling of unfilled space. Random motion of cells would eventually fill space in the plane¹⁸, of course, as can directed motion of cells guided by diffusible morphogens or physical cues including durotaxis or haptotaxis in special situations²⁷. Kenotaxis would be far more general, acting even in the absence of specific cues. In the practical matters of tissue engineering and regenerative medicine, central to any tissue engineering design are the polymers, nano-materials, or de-cellularized connective tissues that comprise the extra-cellular scaffold²⁸, and cells seeded within such a scaffold must migrate collectively while navigating particles, posts, and pores. To achieve desired attributes of cell colonization, the patterning motif expressed by cellular collectives, as reported here, is likely to provide an array of unanticipated considerations for rational engineering design²⁸.

Based upon evidence provided above, we conclude that kenotaxis comprises a systematic patterning motif, if not a dominant one, that provides the migrating cellular collective with redundant strategies to achieve robust and coordinated filling of space over distances as might occur during tissue engineering, wound healing, development, or invasion.

Methods

Cell culture

Madin-Darby canine kidney (MDCK) cells (strain II), rat pulmonary microvascular endothelial (RPME) cells, and human mammary epithelial cell lines MCF10A-vector, MCF10A overexpressing 14–3–3ξ were cultured following published protocols^10,22,29 and incubated at 37°C and 5% CO₂.

Monolayer preparation

Polyacrylamide gels (Young’s modulus = 1.2 kPa, thickness = 100μm) were prepared using the protocol described by Trepat et al¹⁰. PDMS (Sylgard 184 kit, Dow Corning) membranes were fabricated using the protocol described by Poujade et al³⁰. A circular pillar (diameter = 1mm) or a crescent-like pillar (diameter = 1.5mm, concave arc curvature = 1mm⁻¹) was punched from a membrane and deposited upon the gel. After coating the gel with collagen I (BD Biosciences), the pillar was carefully removed to leave a circular island of bare gel. Cells were gently seeded⁹ 3mm from the island and incubated at 37°C and 5% CO₂ for 48hours.

Measurement of local migration velocities and gel displacements

All experiments were conducted in culture environment on an inverted optical microscope (Leica, DMI 6000B). Fluorescence and phase contrast images were acquired at 5 minute intervals for 2 hours before an expanding edge of a monolayer encountered the island and for 10~22 hours after the encounter. Local migration velocities and gel displacements were obtained by particle image velocimetry (PIV) method^10,12. In this method, cross-correlation window size was 32×32 pixels, and window overlap was 28 pixels. Local migration velocities were quantified from phase contrast images with time interval of 5 minutes. Local gel displacements were quantified from an image of embedded fluorescent markers at any experimental time point and a reference image obtained after trypsinization.

Recovery of substrate tractions and monolayer stresses

To obtain substrate tractions, we used the numerical procedure from Fourier-transform traction microscopy (FTTM)^10,31. To obtain monolayer stresses, we used the numerical procedure from monolayer stress microscopy (MSM)^9,11,14. Briefly, we computed a map of the tractions, T, exerted by the substrate upon the cells using gel displacements. From these tractions, we obtained the distribution of intercellular stresses within the cellular sheet using straightforward and rigorous two-dimensional balance of forces as demanded by Newton’s laws (Fig. S2D). By rotating these stress components at each point in the cellular sheet, we computed the two principal stress components σ_max and σ_min and their corresponding, mutually perpendicular, principal orientations (Fig. S2E). We then computed the local tension within the cellular sheet defined as (σ_max + σ_min)/2 and the maximum shear stress defined as (σ_max − σ_min)/2.

Ensemble average

Maps of velocity, force and stress fields were obtained at three time points, at t=0h (2 hours before an expanding edge of a monolayer encountered the island), t=12h and t=24h, respectively, from six MDCK monolayers. For each monolayer, a circular island on a phase image was fitted to a circle to extrapolate a coordinate of the center. Using that coordinate, all the maps measured above from each monolayer were displaced with respect to the one from a chosen reference monolayer. The maps were then averaged over six monolayers at each time point. In panels of (Fig. 1I,J,L) and (Fig. 2A,B,D,E,F,H) each map was folded top to bottom in half and averaged. Note that all the local fields were forced to be zero at locations where all six maps do not overlap. For MCF10A cell lines, each map was averaged over 6 frames during 4 hours of measurements per each sample, and was averaged across an ensemble of 4 monolayers per each cell type.

Immunofluorescence microscopy and cell morphology measurements

Immunofluorescence experiments and cell morphology measurements were performed using the protocol described by Serra-Picamal et al¹⁴. Briefly, cells were fixed with 3% paraformaldehyde (Sigma-Aldrich) in PBS, permeabilized with 0.5% Triton X-100 (Sigma-Aldrich) in PBS, and blocking with 10% FBS (Sigma-Aldrich) in PBS. Primary antibody rabbit anti-ZO-1 (Zymed, Invitrogen) diluted at 1:100 in 10% FBS in PBS was incubated for 1 hour at room temperature, and detected using secondary antibody donkey anti-rabbit (Invitrogen). Actin was visualized using Alexa Fluor 564-conjugated phalloidin (Invitrogen) at 1:1000 in PBS. Primary antibodies rabbit anti-total-ERK 1/2 and mouse anti-phospho-ERK 1/2 (Cell Signaling Technology) diluted at 1:500 in 10% FBS in PBS were incubated for 1 hour at room temperature, and detected using secondary antibodies donkey anti-rabbit and goat anti-mouse (Invitrogen). Cell segmentation based on the ZO-1 immunostainings was implemented in MatLab using a watershed algorithm.

Calculation of tractions normal to the frustrated edge

To compute tractions normal to the frustrated edge, T_n, we defined vectors normal to that edge for each pixel within the monolayer using an approach described by Trepat et al¹⁰. In brief, we computed for each pixel its shortest distance to the edge. The spatial gradients of the shortest-distance map then defined the normal vectors everywhere in the monolayer. We also used this map to define cell strips with a defined range of distance to the edge; the strip width was chose to be 20μm, typically enclosing 1 to 2 cells. In the leading strip closest to the edge, we quantified the average $T_n^{\mathit{edge}}$ and normalized it with the root-mean-square traction magnitude (T^RMS); this allowed us to obtain the averaged $T_n^{\mathit{edge}}/T^{\mathit{RMS}}$ for each sample. To quantify the efficiency of kenotaxis, we measured at least 4 monolayers for MDCK and MCF10A cell lines. We then evaluated the statistical significance in the difference of $T_n^{\mathit{edge}}/T^{\mathit{RMS}}$ between two cell types using the Kruskal-Wallis test. The difference is regarded statistically significant if p-value is less than 0.05.