Why Is CA3 More Vulnerable Than CA1 in Experimental Models of Controlled Cortical Impact-Induced Brain Injury?

Abstract

One interesting finding of controlled cortical impact (CCI) experiments is that the CA3 region of the hippocampus, which is positioned further from the impact than the CA1 region, is reported as being more injured. The current literature has suggested a positive correlation between brain tissue stretch and neuronal cell loss. However, it is counterintuitive to assume that CA3 is stretched more during CCI injury. Recent mechanical studies of the brain have reported on a level of spatial heterogeneity not previously appreciated—the finding that CA1 was significantly stiffer than all other regions tested and that CA3 was one of the most compliant. We hypothesized that mechanical heterogeneity of anatomical structures could underlie the proposed heterogeneous mechanical response and hence the pattern of cell death. As such, we developed a three-dimensional finite element (FE) rat brain model representing detailed hippocampal structures and simulated various CCI experiments. Four groups of material properties based on recent experiments were tested. In group 1, hyperelastic material properties were assigned to various hippocampal structures, with CA3 more compliant than CA1. In group 2, linear viscoelastic material properties were assigned to hippocampal structures, with CA3 more compliant than CA1. In group 3, the hippocampus was represented by homogenous linear viscoelastic material properties. In group 4, a homogeneous nonlinear hippocampus was adopted. Simulation results demonstrated that for CCI with a 5-mm diameter, flat shape impactor, CA3 experienced increased tensile strains over a larger area and to a greater magnitude than did CA1 for group 1, which best explained why CA3 is more sensitive to CCI injury. However, for groups 2–4, the total volume with high strain (>30%) in CA3 was smaller than that in CA1. The FE rat brain model, with detailed hippocampal structures presented here, will help to engineer desired experimental neurotrauma models by virtually characterizing brain biomechanics before testing.

Introduction

In vivo animal traumatic brain injury (TBI) experiments have demonstrated heterogeneous injury patterns under various trauma conditions. In controlled cortical impact (CCI), despite the fact that the CA3 region of the hippocampus is positioned deeper beneath the impactor and is more resistant to hypoxia-ischemia, compared to CA1,¹ interestingly, the CA3 region was more injured compared to the CA1 region.^2–6 Through stereological analysis, Witgen and colleagues⁷ reported similar CA1 and CA3 injuries under lateral fluid impact, whereas with the similar fluid impact device and stereological estimation, Grady and colleagues⁸ observed a significant neuronal loss in CA3. Such regional susceptibility to trauma load may be the result of both regional mechanical responses and cellular or physiological processes. Understanding mechanisms for this heterogeneous pattern can help TBI researchers to better understand the experimental CCI model to facilitate the translation of knowledge from in vivo experiments to real-world TBI injuries more efficiently.

In vitro TBI models provide a unique method to directly investigate correlations between neural responses and mechanical loading, such as stretch and shear.^9–11 Morrison and colleagues started to test whether CA3 was more vulnerable to stretch loadings, compared to CA1, using a well-controlled uniform stretch in vitro experimental TBI model.^12–14 Results demonstrated that under the same stretch level, cell losses for CA1 and CA3 regions were similar.¹⁵ Elkin and colleagues have recently reported on mechanical property data for the rat brain at a spatial resolution not previously achieved.^16,17 In their studies, the CA1 region was the stiffest brain region measured, whereas the CA3 region was one of the softest. These studies lead to the question of whether CA3 does, in fact, experience higher tensile strains, compared to CA1, during CCI experiments, despite its deeper location away from impact. The ideal solution is to measure brain tissue tensile strain under CCI directly, which is currently nearly impossible for high-rate CCI loadings. Alternatively, the next best approach is to use a high-resolution three-dimensional (3D) finite element (FE) rat brain model to simulate CCI experiments and predict tissue stretch in CA1 and CA3 regions during CCI. For these simulations to successfully recreate in vivo brain response to CCI, the model requires accurate material definitions. The new material data^16–18 make it possible to develop a detailed 3D rat brain model with heterogeneous hippocampus substructures, which were not yet achieved based on the review of available anatomically detailed 3D rodent brain models.^19–26

The aim of this study was to first develop a high-resolution 3D FE rat brain model including detailed CA1, CA2, CA3, and dentate gyrus (DG) structures in the hippocampus. The next aim was to use the model to simulate three CCI experimental settings. Both homogeneous and heterogeneous material properties of hippocampal structures were numerically tested to study the effect of recently measured heterogeneity on regional brain tissue strain responses. This would explain the stereotypical pattern of cell death observed in CCI with more damage in CA3, compared to CA1.

Methods

Rat brain model with detailed hippocampus structures

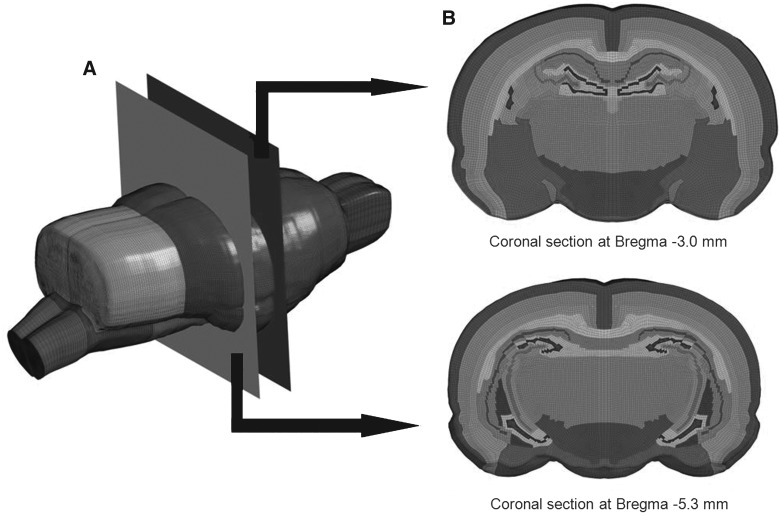
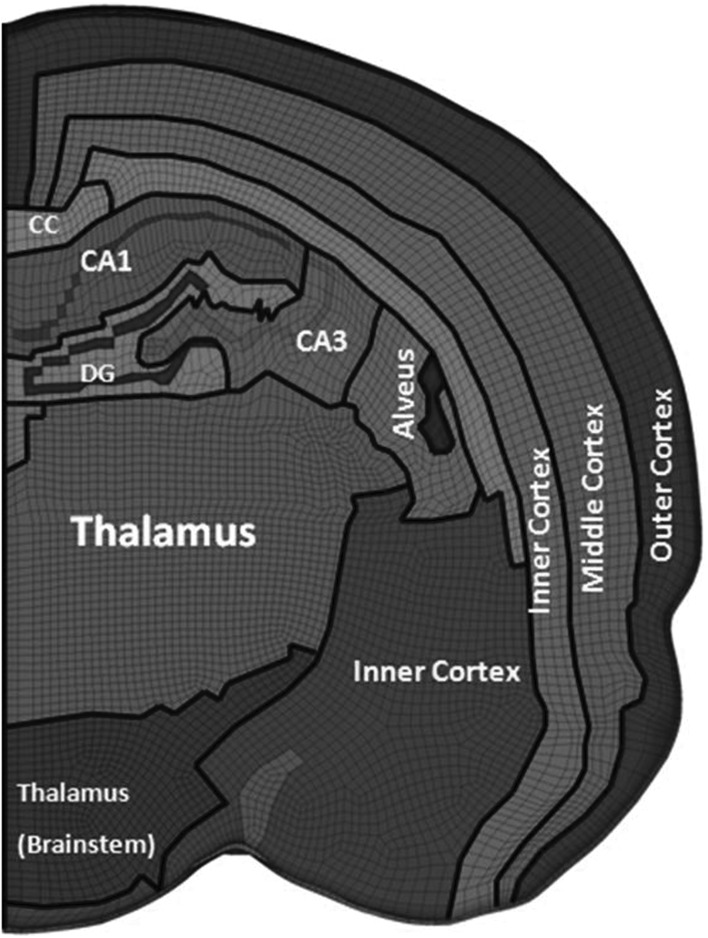
The previously developed and validated 3D FE rat brain model²² was improved to develop a higher resolution FE rat brain model incorporating heterogeneous hippocampus structures. Hypermesh 10.0 (Altair, Troy, MI) was used to divide each hexahedral element of the previous rat brain model²² into eight hexahedral elements, which increased the total number of hexahedral elements of rat brain from 255,700 to 2,045,600. Forty-one coronal images from bregma −1.72 mm to bregma −6.48 mm of the rat brain atlas²⁷ were digitalized using Scion image software (National Institutes of Health, Bethesda, MD) to get feature curves for inclusion of a detailed hippocampus, which were then imported into HyperMesh software. The fine 3D hippocampus hexahedral meshes were then carefully adjusted to match hippocampus substructure feature curves. The developed detailed FE rat brain model includes CA1, CA2, CA3, and DG for hippocampus (as shown in Fig. 1). In total, 2,222,216 elements, including 2,045,600 hexahedral and 176,616 quadrilateral shell elements, were developed. For 3D hexahedral elements, 99.1% of elements had a Jacobian matrix level above 0.4. Further, 0.03% of elements had a warpage of over 50, 0.01% of elements had an aspect ratio above 8.0, 0.05% of elements had a minimum angle of less than 25 degrees, 0.08% of elements had a maximum angle above 160 degrees, and 0.02% of elements had a skew angle above 65 degrees. For two-dimensional quadrilateral elements, 0.005% of elements had a Jacobian matrix level below 0.40, 0.001% of elements had a warpage above 45, 5% of elements had an aspect ratio over 4, and 0.01% of elements had a skew angle over 65 degrees. Figure 2 shows one coronal section through bregma −3.0 mm, indicating the specific region selections for material definition in more detail. The cerebellum white matter was not defined in the FE rat brain model; as such, the cerebellum gray matter was used for the entire cerebellum. Regarding mesh density, Mao and colleagues²⁸ reported that the rat brain model with a mesh size less than 0.2 mm could be deemed as convergent for CCI simulation. The current fine rat model with a typical 0.1-mm element length was considered acceptable.

FIG. 1.

Detailed rat brain model. (A) Global view of the rat brain model. (B) Coronal sections.

FIG. 2.

Region selections for material definitions. CC, corpus callosum; DG, dentate gyrus.

Material properties

Three sets of simulations were performed with different material properties specific for the hippocampus. Group 1 consisted of the most recent heterogeneous nonlinear material properties for the hippocampus.¹⁶ Group 2 consisted of heterogeneous linear viscoelastic material properties for the hippocampus.¹⁵ Group 3 consisted of homogeneous linear viscoelastic material properties for the hippocampus defined as the average of those in group 2. Group 4 consisted of homogeneous nonlinear material properties for the hippocampus based on data for group 1. Material properties for other regions of the brain were the same for each material group. Table 1 lists material constants for various brain regions for each material group.

Table 1.

Material Constants for Four Groups

	Group 1			Group 2			Group 3			Group 4
Region	μ1 (Pa)	α1		G0 (Pa)	G∞(Pa)	beta (s^−1)	G0 (Pa)	G∞(Pa)	beta (s^−1)	μ1 (Pa)	α1
CA1P	12.3	20.6		4060	1860	59.1	3568	1643	63.0	8.9	18.3
CA1SR	8.3	21.4		4060	1860	59.1
CA3P	9	15.9		3385	1587	58.6
CA3SR	8.1	15.7		3385	1587	58.6
Dentate Gyrus	8	14.3		2951	1320	81.1
Inner cortex	10.8	17.3		2701	1362	52.5	2701	1362	52.5	10.8	17.3
Middle cortex	9.9	16.4		2553	1261	51.5	2553	1261	51.5	9.9	16.4
Outer cortex	7.4	19.7		3234	1620	63	3234	1620	63.0	7.4	19.7

	G0 (Pa)	G∞(Pa)	beta (s^−1)							G0 (Pa)	G∞(Pa)	beta (s^−1)
Thalamus	3082	1303	58.1	3082	1303	58.1	3082	1303	58.1	3082	1303	58.1
Alveus	3603	1256	115.1	3603	1256	115.1	3603	1256	115.1	3603	1256	115.1
Corpus callosum	2399	950	68.5	2399	950	68.5	2399	950	68.5	2399	950	68.5
Brainstem	2549	940	84.9	2549	940	84.9	2549	940	84.9	2549	940	84.9
Cerebellum	2521	908	106.7	2521	908	106.7	2521	908	106.7	2521	908	106.7

P, pyramidal cells; SR, stratum radiatum.

Group 1

Heterogeneous nonlinear material properties were implemented with the LS-DYNA software (Livermore Software Technology Corporation, Livermore, CA) material definition, MAT_77_O (MAT_OGDEN_RUBBER). For this material, hyperelasticity is described by Equation 1, in which μ and α are parameters associated with strain energy and for which n was 1 in this study. Material parameters were derived from experimental results in adult rat brain tissue¹⁴ and are listed in Table 1.

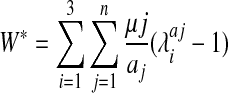(1)

Group 2

Heterogeneous linear viscoelastic material properties were implemented with Kelvin-Maxwell's model using the LS-DYNA software material definition, MAT_061: MAT_KELVIN-MAXWELL_VISCOELASTIC, shown in Equation 2. The short-term shear modulus (G₀), long-term shear modulus (G_∞), and decay constants (β) for different hippocampus structures as well as other brain regions for all simulation groups were defined according to recently reported experimental data.¹⁷ One decay term was sufficient to describe the mechanical behavior of the tissue over the short time scales relevant to the simulations.

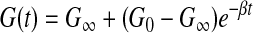(2)

Group 3

Homogeneous linear viscoelastic properties were implemented in LS-DYNA software, as for group 2, with material definition MAT_061. In this group, hippocampal material properties were homogeneous. The short-term shear modulus was defined as 3568 Pa, the long-term shear modulus as 1643 Pa, and the decay constant as 63 s⁻¹, representing the average of hippocampal substructure properties in group 2. In calculating average material properties, no weighting factor was used to account for differences in regional volumes.

Group 4

Homogeneous nonlinear material properties were implemented in LS-DYNA software, as for group 1, with material definition MAT_77_O (MAT_OGDEN_RUBBER). In this group, hippocampal material properties were homogeneous, where μ was defined as 8.9 Pa and α was defined as 18.3 in Equation 1 for all regions of the hippocampus. These material parameters represent a least-squares fit of Ogden's model to the measured strain-dependent modulus averaged across all adult hippocampal regions from Elkin and colleagues.¹⁶

Simulation of CCI experiment

CCI simulation

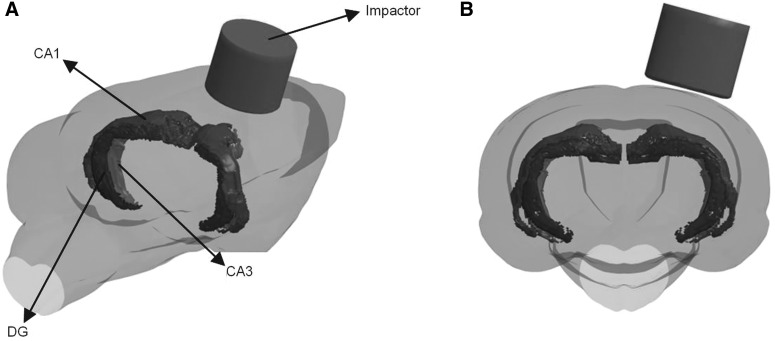
The CCI simulation was defined carefully to accurately represent experimental settings. A 6.0-mm-diameter craniectomy was simulated over the left frontoparietal cortex, with the center 3.0 mm posterior to bregma and 3.0 mm lateral to the midline. A flat impactor tip (5.0 mm in diameter) of the CCI device was positioned over the dura mater at a 15-degree angle and impacted the brain at a velocity of 6 m/s to a depth of 2.0 mm. Figure 3 shows the relative position between impactor and CA1/CA3 in the CCI simulation. Because of computational costs, the CCI simulation was solved for the first 5 msec, during which time the peak tissue strains were reached. Because strain magnitude was reported to be positively correlated with neuronal loss,^12,14,29 the rest of the strain history after 5 ms was not simulated. To investigate hippocampus responses under various CCI settings, including 4 mm diameter, flat impactor, and 5 mm diameter, sphere impactors were simulated.

FIG. 3.

Two views showing complete 3D rat brain and 3D impactor for CCI simulations. (A) Transparent view showing relative position between impactor and hippocampus structures. (B) Caudal (posterior) view showing how the impactor was offset from midline and perpendicular to the 3D brain surface. 3D, three-dimensional; CCI, controlled cortical impact.

Results

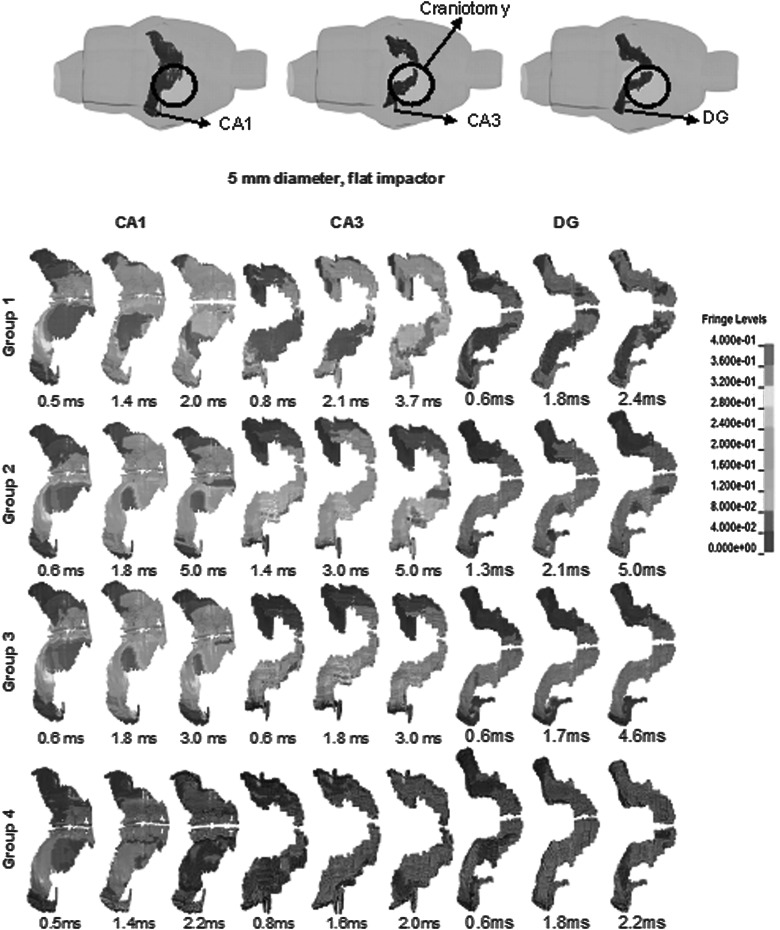
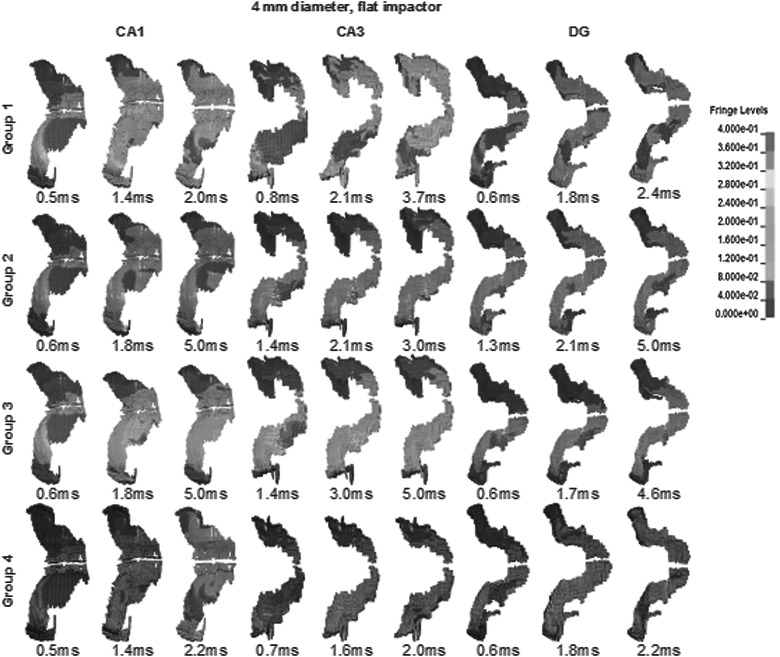
Approximately 142 h were required to finish up to 5 ms of a CCI simulation with linear viscoelastic material using four AMD Opteron™ 2380 Processors. Using Ogden's nonlinear materials, a slightly shorter length of time of 138 h was needed. Figures 4–6 show a typical strain distribution in CA1 and CA3 at various time points when the peak strains were experienced. Because simulations with different material groups demonstrated a heterogeneous strain pattern and local peak strains did not occur at the same time point across all groups, multiple time points were selected for Figures 4–6. With a homogeneous linear viscoelastic hippocampus (group 3), the volume of the CA1 region experiencing high strains (>30%) was 0.77 mm³, which was larger than 0.16 mm³ in CA3. Using heterogeneous linear viscoelastic material properties for the hippocampus (group 2), the volume of the CA3 region with high strains was 0.46 mm³, which was larger than that in CA3 of group 3, but still lower than 0.89 mm³ in CA1. For the simulation with a heterogeneous nonlinear hippocampus (group 1), the volume of the CA3 region with high strains was 1.77 mm³, which was larger than 1.65 mm³ in CA1. For the simulation with a homogeneous nonlinear hippocampus (group 4), the CA3 region with high strains was 0.97 mm³, which was smaller than 1.19 mm³ for CA1.

FIG. 4.

CA1, CA3, and DG strain contours for CCI case with 5-mm diameter, flat impactor. CA3 experienced largest areas of high strains when using group 1 heterogeneous nonlinear materials. Brain model was slightly rotated along the rostral-caudal axis to better demonstrate strain contours. These time points were selected when the maximum areas of large strain elements were observed, compared to nearby time points. DG, dentate gyrus; CCI, controlled cortical impact.

FIG. 6.

CA1, CA3, and DG strain contours for CCI case with 5-mm diameter, sphere diameter. CA3 experienced the largest areas of high strains when using group 1 heterogeneous nonlinear materials. Brain model was slightly rotated along the rostral-caudal axis to better demonstrate strain contours. These time points were selected when the maximum areas of large strain elements were observed, compared to nearby time points. DG, dentate gyrus; CCI, controlled cortical impact.

FIG. 5.

CA1, CA3, and DG strain contours for CCI case with 4-mm diameter, flat impactor. CA3 experienced largest areas of high strains when using group 1 heterogeneous nonlinear materials. Brain model was slightly rotated along the rostral-caudal axis to better demonstrate strain contours. These time points were selected when the maximum areas of large strain elements were observed, compared to nearby time points. DG, dentate gyrus; CCI, controlled cortical impact.

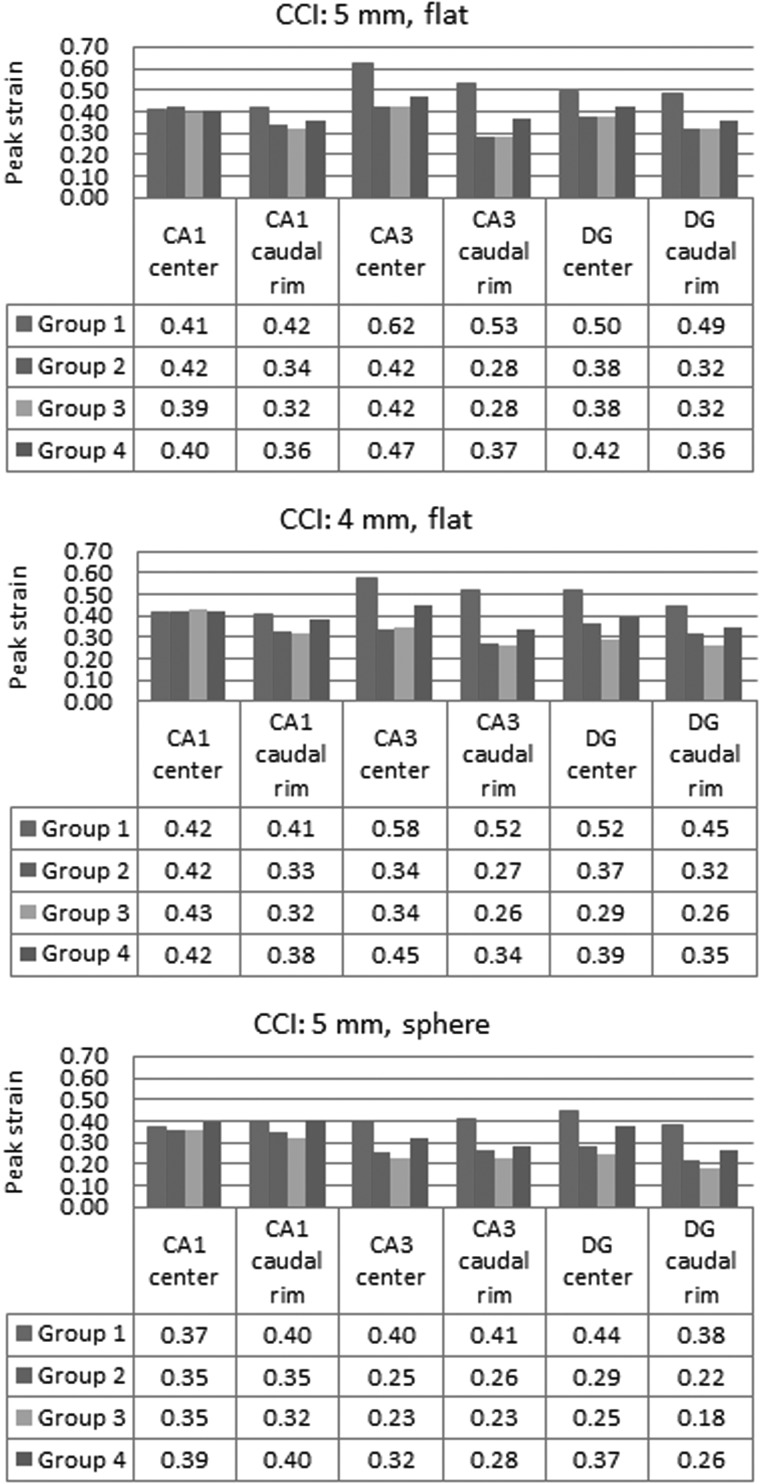
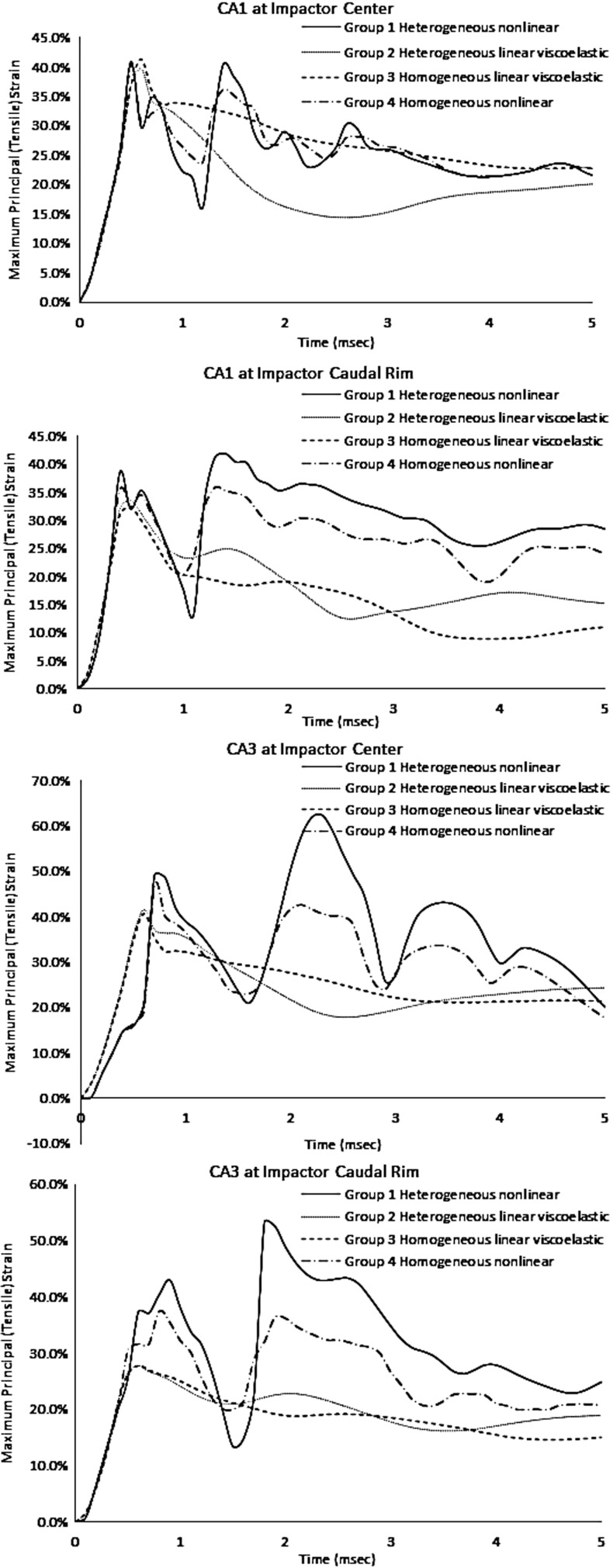
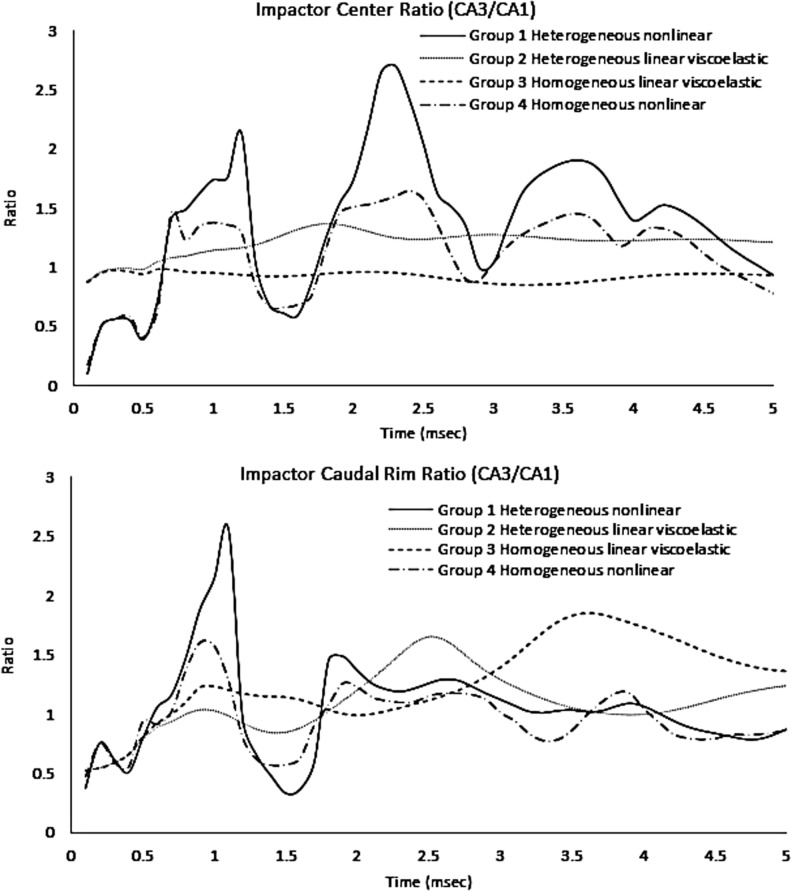
Figure 7 summarizes all the peak strains for 12 CCI cases. CA1 experienced the highest strains for group 1 with heterogeneous nonlinear hippocampus for all different CCI settings. The peak strains in this region were not affected much when using either homo- or heterogeneous linear viscoelastic materials (group 2 or 3). In contrast, when using the nonlinear material (group 1), the peak CA1 strain close to the caudal rim of the impactor was increased from 32 to 46%. The peak CA3 strain through the impactor center was increased from 42 to 62%, and the peak CA3 strain close to the posterior rim of the impactor was increased from 28 to 53%. Such increases were smaller when using homogeneous nonlinear materials of group 4. The time histories of tissue strains for the CA1 and CA3 regions beneath the impact center and close to the caudal (posterior) rim of the impactor are shown in Figure 8. Strains were calculated by averaging strains from four elements so as to avoid strains in one element from biasing the reported results. The elements at the caudal rim were selected at −5.3 mm to bregma for the 5-mm-diameter impactor and −4.8 mm to bregma for the 4-mm-diameter impactor. The ratio of CA3 to CA1 strain further demonstrated the effect of material heterogeneity and material laws, with the CA3 strain at the caudal rim of the impactor increasing to the greatest degree with the group 1 material properties (Fig. 9).

FIG. 7.

Summary of peak strains for 12 CCI cases. For all CCI cases with various impactor diameters and shapes, using group 1 nonlinear, heterogeneous materials, CA3 experienced the highest strains. Meanwhile, different material laws (groups 1 and 4 vs. groups 2 and 3) affected peak strain magnitudes, with nonlinear material property (MAT_77_O) induced high strains resulting from larger dynamic motion allowed for brain tissue. DG, dentate gyrus; CCI, controlled cortical impact.

FIG. 8.

Tissue strain histories in the hippocampus through the center of the impactor and in a coronal section near the posterior (caudal) rim of the impactor. These time histories were selected from four elements, which experienced the highest strains during CCI. Under different CCI loading conditions, peak strains occurred at different elements. CCI, controlled cortical impact.

FIG. 9.

Ratio of CA3 strain over CA1 strain at impactor center and impactor caudal rim.

Discussion

In this study, we developed a 3D FE rat brain model with detailed hippocampal structures to investigate the consequence of recently determined heterogeneous material properties on the pattern of tissue strain resulting from the CCI injury model within the hippocampus. The specification of nonlinear and time-dependent material behaviors critically altered the pattern of hippocampal strain when the impactor was held in position after striking the exposed cortex (Figs. 4–7). The inclusion of a nonlinear heterogeneous hippocampus (group 1) resulted in greater tensile strains in CA3 than in CA1, which may provide a biomechanical explanation for why CA3 is more vulnerable than CA1 during CCI. Using heterogeneous linear viscoelastic material properties for the hippocampus (group 2), strains in CA3 were elevated, compared to the homogenous case (group 3), but the volume of CA3 experiencing large strains (>30%) was still smaller than that for CA1. The major reason that strains in CA3 were much larger with nonlinear materials (group 1), compared to linear viscoelastic materials (group 2), is that the CA3 region was much softer than CA1 under larger tensile strain loading.¹⁶ Another reason could be because of the differences between Ogden's materials and linear viscoelastic materials in LS-DYNA software. These results suggest that the choice of material properties affects the predicted strain field in response to CCI and that accurate representation of both the heterogeneity and nonlinear viscoelasticity of the hippocampus can more accurately predict the experimentally observed pattern of brain damage.

FE predictions are inevitably model dependent. Hyperelastic or linear viscoelastic material laws with different material constants have been used for rodent brain models in the past.^{19,20–23,25,26} In this study, care was taken to minimize the bias of brain stiffness across the four groups of material properties simulated. Material parameters for group 1 were derived from experiments on adult rat brain tissue that probed the nonlinear elastic material behavior.¹⁶ For group 2, linear viscoelastic parameters were derived from experimental data.¹⁷ Once determined, these material properties were not altered to tune the FE model to produce a desired output, which is often done when attempting to fit simulations to experimental, histological data. For group 3 with a homogeneous hippocampus, the short-term shear modulus, long-term shear modulus, and decay constant were averaged from those used in group 2. Further, heterogeneity in other anatomical regions, such as cortex, corpus callosum, and thalamus, were identical for all three simulations.

Groups 1 and 4 with Ogden's nonlinear materials demonstrated biphasic strain peaks. A slight second peak was also observed for CA1 at the impactor posterior rim for group 2 with heterogeneous viscoelastic materials. The second peak strains in group 1 were much higher than those in group 4, indicating that material heterogeneity played an important role in regional strain responses. Meanwhile, differences between linear viscoelastic material and Ogden's nonlinear viscoelastic material indicated that the biphasic strain pattern was also related to the material model. Ideally, a material model that can represent both viscoelastic and nonlinear characteristics with damping control is desired. Nevertheless, this study demonstrated that a heterogeneous hippocampus model with nonlinear materials was critical to predict hippocampus mechanical responses, which explained the vulnerability of CA3 observed experimentally.

The ratios between CA3 and CA1 peak strain further demonstrated the effect of material heterogeneity in the hippocampus. For regions beneath the center of the impactor, strain in CA3 was slightly lower than that in CA1 when modeling a homogeneous hippocampus (Fig. 9, group 3). For regions beneath the caudal rim of the impactor, CA3 strains generally were larger than CA1 strains. The maximum ratio obtained in this region was 2.6 for group 1 simulations. It should be noted that strains in the cortex and thalamus were not affected appreciably by the hippocampal material heterogeneity in terms of peak values and regions of high strains when using the same material constitutive models. These findings highlighted the importance of adopting a high-resolution FE mesh of the rat brain with advanced hippocampual material heterogeneity to study tissue biomechanics in the hippocampus. In terms of the mechanical response of the cortex and thalamus, a lower resolution model can still provide accurate predictions.

In the rat brain model, brain elements were connected without any sliding. Future in vivo quantifications of structure tethering, such as bonding strength between hippocampus and surrounding tissues, can be combined with this model to examine how tethering strength affects brain regional strain responses. The effect of hippocampal cell layer orientations was not considered in this study. For future studies, a submodeling approach can be introduced to study how dorsal hippocampal cells (perpendicular to the impact direction) and ventral hippocampal cells (parallel to the impact direction) affect hippocampus regional strains.

Conclusion

A 3D rat brain model with 2 million hexahedral elements was developed to thoroughly investigate region- and time-dependent CA1 and CA3 strain patterns during CCI at a cost of long computational time. Material heterogeneity of the hippocampus was found to be critical for FE model predictions. Representation of a heterogeneous hippocampus with nonlinear material properties predicted a large region of high strains in CA3, which provides a biomechanical explanation to the long-standing question as to why CA3 is damaged to a greater extent, compared to CA1, despite its deeper position from impact in CCI.

Acknowledgments

The authors appreciate Dr. Michelle LaPlaca's help in describing CCI experiments. The authors thank Mr. Amandeep Gill, Mr. Gurdeep Jandir, Mr. Amrinder Singh, and Mr. Chintan Shelat for their help, in part, with meshing and simulation. The authors acknowledge Mr. Abrar Wazir for proofreading. This work was supported, in part, by the National Highway Traffic Safety Administration (DTNH22-08-C-00088).

Author Disclosure Statement

No competing financial interests exist.