Simulating movement of tRNA through the ribosome during hybrid-state formation

Abstract

Biomolecular simulations provide a means for exploring the relationship between flexibility, energetics, structure, and function. With the availability of atomic models from X-ray crystallography and cryoelectron microscopy (cryo-EM), and rapid increases in computing capacity, it is now possible to apply molecular dynamics (MD) simulations to large biomolecular machines, and systematically partition the factors that contribute to function. A large biomolecular complex for which atomic models are available is the ribosome. In the cell, the ribosome reads messenger RNA (mRNA) in order to synthesize proteins. During this essential process, the ribosome undergoes a wide range of conformational rearrangements. One of the most poorly understood transitions is translocation: the process by which transfer RNA (tRNA) molecules move between binding sites inside of the ribosome. The first step of translocation is the adoption of a “hybrid” configuration by the tRNAs, which is accompanied by large-scale rotations in the ribosomal subunits. To illuminate the relationship between these rearrangements, we apply MD simulations using a multi-basin structure-based (SMOG) model, together with targeted molecular dynamics protocols. From 120 simulated transitions, we demonstrate the viability of a particular route during P/E hybrid-state formation, where there is asynchronous movement along rotation and tRNA coordinates. These simulations not only suggest an ordering of events, but they highlight atomic interactions that may influence the kinetics of hybrid-state formation. From these simulations, we also identify steric features (H74 and surrounding residues) encountered during the hybrid transition, and observe that flexibility of the single-stranded 3′-CCA tail is essential for it to reach the endpoint. Together, these simulations provide a set of structural and energetic signatures that suggest strategies for modulating the physical-chemical properties of protein synthesis by the ribosome.

INTRODUCTION

The dynamics of molecular machines span multiple length and timescales, and can encompass large-scale collective rearrangements, energy-releasing chemical steps, and order-disorder transitions. In contrast to macroscopic machines, which operate deterministically, biomolecular dynamics are stochastic, where movement can be described as diffusion across an energy landscape.^{1, 2, 3, 4, 5} Molecular simulations have been an instrumental means for exploring the relationship between energy landscapes and dynamics.^{6, 7} In the context of protein folding, simulations have helped demonstrate that the energetic gap between the folded and unfolded ensembles is much greater than the short-scale roughness. That is, the energy landscape of folding can be described as possessing a single dominated basin of attraction, centered about the native configuration.⁸ Inspired by this, investigations of large-scale rearrangements in biomolecules have explored the feasibility of describing functionally-relevant energy landscapes as possessing a few dominant basins of attraction, each corresponding to an experimentally-obtained configuration.⁶ In addition to providing an intuitive description of the landscape, they have the added benefit of being computationally inexpensive for smaller system (less than ∼1000 residues). With the reduced cost of each simulation, the phase space of rearrangements can often be exhaustively sampled, enabling rigorous investigation of the interplay between biomolecular flexibility, energetics, and function.

What has emerged from the studies with simple models is that order-disorder transitions and molecular sterics frequently determine large-scale functional dynamics.^{7, 9, 10, 11} Since the propensity for disorder is related to the stability and flexibility, and the steric content is determined by the excluded volume of each atom, simple models that accurately account for these properties are reliable tools for characterizing a range of dynamics associated with function. These models provide a means to identify likely modes of function, and extended models can mimic the cellular environment, including changes in ion concentrations,^{12, 13} and the presence of crowding agents,¹⁴ allowing one to quantify their physical-chemical impacts on folding and function.

A large asymmetric biomolecular machine for which experimentally-obtained atomic models are available is the ribosome.^{15, 16, 17, 18} The ribosome is composed of multiple RNA molecules and over 50 protein chains, for a cumulative mass of over 2 MDa. The ribosome undergoes a range of complex conformational rearrangements during its functional cycle.^{19, 20, 21, 22} In order for the ribosome to read mRNA and synthesize new proteins, it recruits tRNA molecules. On the ribosome, there are three tRNA binding sites (A, P, and E) on the small (30S) and large (50S) subunits, where each tRNA molecule sequentially transits all three sites.²³ During each round of elongation, a tRNA molecule first partially associates with the A site (i.e., initial selection). Subsequently, the tRNA fully associates (accommodation), and the incoming amino acid is added to the growing protein chain. The A-site and P-site tRNAs are then displaced by one binding site: a process known as translocation, where the P-site tRNA moves to the E site and the A-site tRNA moves to the P site. The pre-translocation configuration is commonly referred to as the A/A-P/P configuration. After translocation, the A-site tRNA is in the P site and the P-site tRNA is in the E site, resulting in formation of a P/P-E/E conformation. Translocation results in a vacant A site, thus enabling the ribosome to read the next frame of the mRNA.

tRNA translocation involves movement between binding sites, which is correlated with multiple large-scale rotations in the small subunit, as well as intermediate tRNA conformations.²⁴ Translocation is generally described as encompassing several major conformational rearrangements.^{25, 26, 27, 28, 29} The P-site tRNA adopts a “hybrid” P/E conformation,^{24, 28} where it bridges the P site of the small subunit and the E site of the large subunit. This is accompanied by rotation of the 30S body. The A-site tRNA adopts an A/P configuration, which is accompanied by a partial displacement of the mRNA between sites, and rotation of the 30S head. At the completion of translocation, the tRNA molecules relax into a P/P-E/E conformation, where the 30S body and head also adopt unrotated configurations.

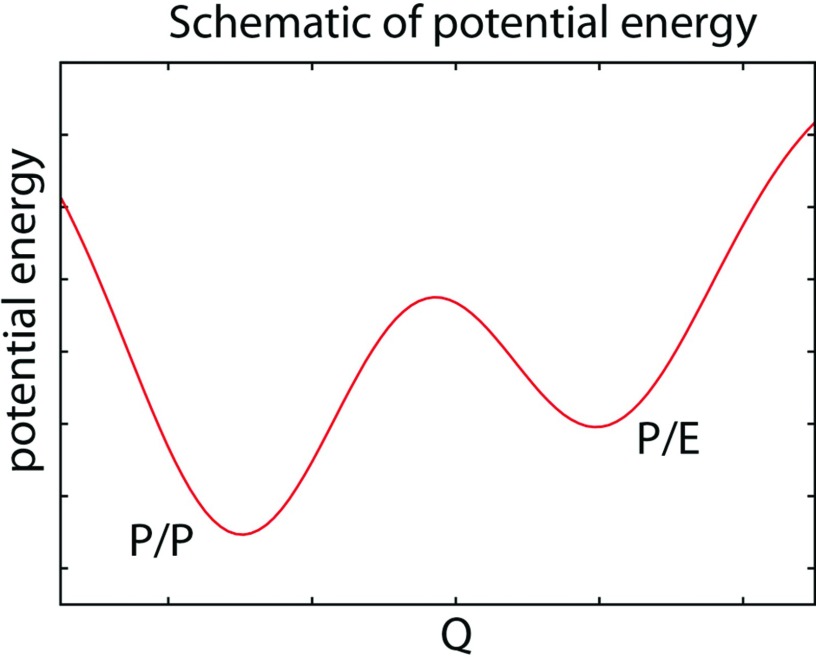
To elucidate physical-chemically-viable routes of tRNA translocation, we have constructed simplified energy functions for the landscape and have performed simulations of the first step of translocation: P/E formation. During the transition to the P/E conformation, the small subunit undergoes a ∼7° rotation, with respect to the large subunit, which is accompanied by a ∼20 Å displacement of the tRNA elbow and a ∼45 Å displacement of the 3′-CCA end (Figure 1). In the effective energy landscape used here, each tRNA can form stabilizing interactions with two binding sites on the ribosome. With respect to P/E formation, the relevant stabilizing interactions are between the tRNA with the P site and E site. This results in a multi-basin energy landscape, which describes tRNA energetics as being dominated by the well-established interactions with the P and E sites, where hybrid configurations can correspond to higher-energy intermediates (Figure 2). This is consistent with cryo-EM and crystallographic models that have implicated tRNA interactions with the P and E sites.^{22, 30} That is, experimental methods can provide atomic models if the configuration is a deep energetic minimum, resulting in it being significantly populated. To construct a multi-basin model, we explicitly represent all non-hydrogen atoms (i.e., an all-atom SMOG model,^{31, 32}) which ensures that the sterics of the process are properly accounted for. We previously showed that SMOG models provide a description of the global fluctuations that is consistent with explicit-solvent simulations and crystallographic B-factors.³³ In standard SMOG models, which are frequently used to study protein folding,^{31, 34} there is one basin of attraction. Here, we construct two SMOG models, one for the P/P configuration and one for the E/E configuration, and merge the stabilizing energetic terms to form a multi-basin SMOG model, similar to many studies on protein function.^{11, 35, 36, 37, 38, 39, 40, 41, 42} With this simple model, we focus our attention on investigating the relationship between tRNA and ribosome flexibility and sterics during hybrid-state formation.

Figure 1.

Overview of P/E hybrid formation. Before hybrid-state formation (a)–(d), the ribosome (grey and cyan) adopts an unrotated configuration, where the tRNAs are in classical P/P (red) and A/A (yellow) configurations (mRNA in green). In the P/E hybrid configuration (e)–(h), tRNA molecules are in the P/E and A/P*⁷⁶ configurations (f), and the small subunit of the ribosome is rotated by ∼7° (h). To measure movement of tRNA through the ribosome, we calculated the distance between the tRNA elbow (R_Elbow, defined previously³³, ⁵³), which changes from 36 Å to 58 Å during the transition. Movement of the 3′-CCA end of the P-site tRNA is measured by the center of mass distance between the side chain of A76 and A2411/A2412 of the 23S rRNA: R_CCA−E, which is 47 Å and 2 Å in the P/P and P/E configurations. Rotation of the 30S body is measured by a collective reaction coordinate θ_body (defined previously⁵⁴), which is 0° and 7° in the classical and P/E hybrid configurations. For visual clarity, proteins are not shown, though all simulations also included the ribosomal proteins.

Figure 2.

Schematic of the potential energy surface used to simulate hybrid-state formation. We constructed a multi-basin model, where each tRNA can be stably associated with multiple ribosomal binding sites. During P/E formation, the relevant interactions are with the P and E sites. When forming a hybrid configuration, the tRNA and ribosome are in an energetically strained configuration, where the P/P configuration is of lower energy than the P/E. Q denotes a structural reaction coordinate that can capture the endpoints and transition-state ensemble.

With the large size of the ribosome, sampling the dynamics in simulations can be extremely demanding, even when using simplified models. One strategy for obtaining an initial description of the process is to employ targeted molecular dynamics (TMD) protocols.^{43, 44, 45} In TMD simulations, an additional time-dependent restraint (or constraint) is introduced that induces the transition. The overall structural mechanism obtained with TMD can be consistent with unrestrained simulations when implemented appropriately. We previously showed that using a simple model with TMD yields the same order of events as observed in unrestrained simulations,³³ or TMD simulations with explicit-solvent.⁴⁶ In that comparison, we employed a form of TMD in which a time-dependent constraint is introduced on the dynamics. Here, to allow for flexibility of the biomolecule that is more consistent with unrestrained dynamics, we introduce a time-dependent harmonic restraint, rather than a constraint (see Methods section). While the restraint does perturb the landscape, this implementation allows for dynamics that are more susceptible to thermal fluctuations, and are therefore more consistent with unrestrained dynamics. As discussed in the results, this gentler form of TMD allows for more subtle signatures to be probed, such as steric barriers and the effects of disorder.

The presented simulations demonstrate how biomolecular sterics and flexibility contribute to the overall dynamics of tRNA during hybrid-state formation. While TMD simulations must be interpreted carefully, they clearly demonstrate the multi-dimensionality of tRNA movement during hybrid-state formation, which is consistent with numerous previous computational investigations of tRNA flexibility.^{33, 47, 48, 49, 50} This intrinsic flexibility of tRNA additionally provides structural insights into the likely routes of hybrid-state formation, which suggest additional degrees of freedom to be investigated experimentally. Finally, the interactions implicated by these simulations are likely to play a critical role in the ability of the ribosome to efficiently translocate tRNA molecules, and thus may be essential interactions that govern protein synthesis.

RESULTS

Hybrid-state formation is not monotonic

When simulating dynamics with TMD, it is possible for the restraining potential to overpower all other energetic/structural fluctuations, resulting in dynamics that are determined entirely by the targeting force. To avoid this scenario, it is important to consider the scale of the targeting potential, relative to the energy (kinetic and potential) of the system. In the employed SMOG model, the total stabilizing energy of the system is set such that there is, on average, one unit of stabilizing energy per atom.⁵¹ Additionally, according to the equipartition theorem, the average kinetic energy per atom is 1/2k_BT, and T = 0.46 (k_B = ɛ₀/T₀, where ɛ₀ and T₀ are the units of energy and temperature). In these simulations, the targeting potential is applied to all RNA and protein residues (145 273 atoms). Thus, the thermal energy of the targeted atoms is ∼33 000ɛ₀, which is comparable to the energetic constant of the targeting potential: 20 000ɛ₀/nm². Thus, this parameterization allows for structural fluctuations about the targeting minimum that are on the scale of angstroms to nanometers.

While ideally we could perform unrestrained simulations in which spontaneous transitions occur, as done for tRNA accommodation,³³ the current implementation of TMD does allow for smaller-scale fluctuations to spontaneously occur during the P/E transition. As the 3′-CCA end moves towards the E site, it frequently undergoes reversible fluctuations that are on the order of 10 Å (Figure 3b). The ability to sample these fluctuations in simulation is enabled by multiple factors. First, as discussed above, the energetic weight of the targeting potential is smaller than the scale of temperature-induced energetic fluctuations. Additionally, the timescale of the targeting potential is sufficiently slow that the reorganization time of the 3′-CCA end is significantly faster. The exact simulated timescale can only be estimated with these models,⁵² though the effective timescale is roughly on the order of microseconds.³³ From explicit-solvent simulations, it was shown that the local reorganization times of the tRNA elbow and 30S body are ∼20 ns⁵³ and ∼50 ns.⁵⁴ Since the 3′-CCA end is significantly smaller, it is anticipated that its reorganization time is smaller. Accordingly, the effective timescale (microseconds) of the TMD simulations is sufficiently long to allow for spontaneous rearrangements of the elbow and 3′-CCA end, though the average displacement of each is guided by the TMD restraint.

Figure 3.

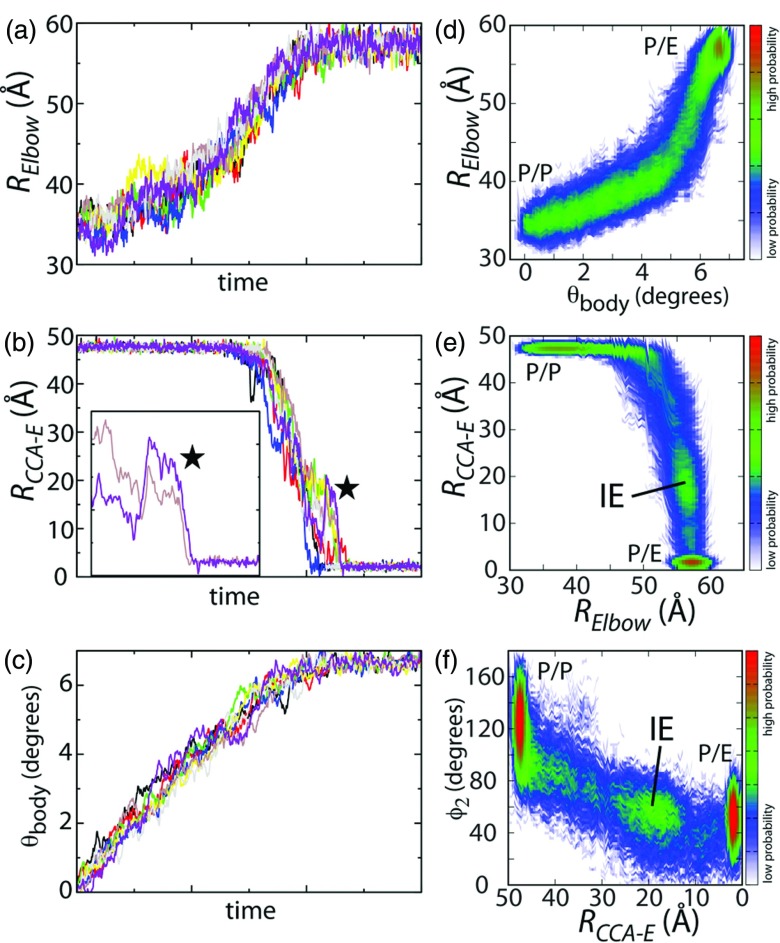
Movement along multiple coordinates is not simultaneous. During simulations of hybrid-state formation, large changes occur along the (a) elbow, (b) 3′-CCA and (c) 30S body rotation coordinates. Since the simulations employed a restraint-based form of TMD with a small energetic weight, spontaneous fluctuations are observed in each simulation (e.g., fluctuations of >10 Å are observed in the 3′-CCA end. See panel (b) and inset). Probability distributions along multiple coordinates highlight sequential rearrangements and suggest barriers. (d) Initially, the 30S body rotates, with minimal movement of the tRNA, which is followed by rapid movement of the elbow. (e) The tRNA elbow moves nearly 20 Å towards the E site before the 3′-CCA end releases from the P site. During this transition, there is a subtle peak that forms at R_{CCA − E} ∼ 20 Å. The presence of an intermediate ensemble (IE) is indicative of a steric (H74), or entropic barrier during hybrid formation. (f) The width of the distribution of 3′-CCA angles (measured by ∅₂³³, ⁴⁶) is roughly uniform as the 3′-CCA end moves towards the E site. This is in contrast to tRNA accommodation, where changes in the distribution of angles is significantly larger.⁷⁷

Sequential motion during P/E hybrid-state formation

To characterize the distribution of hybrid-formation routes, we performed 120 independent TMD simulations and measured the dynamics along multiple reaction coordinates (Figure 3). We found that the overall routes of hybrid-state formation are consistent between most runs, and that there is a preferred ordering of events. Specifically, after the 30S body undergoes partial rotation (several degrees), tRNA elbow displacement occurs concomitantly with rotation (Figure 3d). After significant displacement of the elbow, the 3′-CCA end moves from the P site to the E site (Figure 3e). A common feature between steps is that there is a large degree of independent movement along different coordinates. While there are uncorrelated fluctuations, overall, there is a propensity for a particular ordering of events, at longer timescales.

The first stage of hybrid formation involves rotation of the 30S body. This initial rotation of 5° occurs with minimal displacement of the tRNA (Figure 3d), as measured by R_Elbow, since it is experimentally accessible in single-molecule fluorescence resonance energy transfer (smFRET) experiments.^{55, 56} The ability of the 30S to rotate significantly before tRNA displacements (Figure 4b) demonstrates that it is possible for structural fluctuations in the 30S to be associated with partially-distorted and strained tRNA configurations. It is also feasible that external perturbations that impact the rotation of the 30S may lead to strained tRNA conformations. Structurally, strain may arise when the tRNA remains associated with the 30S P site, which is displaced as rotation occurs. This internal strain in the tRNA may then be partially relieved as the tRNA adopts a hybrid configuration. This mode of function of tRNA is consistent with the notion of tRNA acting as a nonlinear “molecular spring”⁵⁷ that can accumulate and release strain energy during elongation, which is analogous to how protein function is frequently described.⁷

Figure 4.

Structural characteristics of tRNA elbow movement during hybrid formation. (a) Initially, the tRNAs are in classical configurations, where the 30S subunit is in an unrotated orientation. (b) The majority of the subunit can rotate, with minimal movement (several Å) of the tRNA elbow. (c) Structural representation of residues that the tRNA elbow interacts with during hybrid formation. (d) Same as (c), with the P-site tRNA not shown. Residues that the tRNA contacts in more than 10% of the simulations are shown in stick representation. The coloring of the contacted residues ranges from red (contacted in 10% of the runs) to blue (contacted in 100% of the runs). As the tRNA elbow moves between the P and E sites of the large subunit, few interactions are formed between the elbow and ribosome. With the exception of interactions near the P site and with the L1 stalk, the tRNA only contacts protein L33. The minimal number of contacts is consistent with the absence of a pronounced peak in the probability distribution along R_Elbow and θ_body (Figure 3d).

These simulations suggest it is energetically viable for the 30S to rotate significantly prior to the displacement of tRNA, which suggests that movements are not related through strong energetic interactions,⁵⁸ consistent with observations of weakly-correlated fluctuations in single-molecule experiments.⁵⁹ As single-molecule methods continue to be applied to study each movement, the current findings highlight the need for multi-color FRET experiments,⁶⁰ with which it may be possible to simultaneously probe motion along the rotation and elbow coordinates.

Subsequent to 30S body rotation, we observe that the tRNA elbow moves towards the P/E configuration. During this initial movement, the 3′-CCA end remains associated with the P site of the 50S (Figures 3e, 5a). In the majority of the simulations, R_Elbow reaches 50 Å (i.e., 15 Å displacement) before the 3′-CCA end dissociates from the P site. This further highlights the large degree of flexibility in tRNA molecules. With regards to tRNA accommodation, we previously found that the tRNA elbow can enter a fully-accommodated configuration while the 3′-CCA end is over 50 Å from the PTC.³³ Here, we find that the tRNA elbow reaches a near-P/E configuration prior to 3′-CCA release from the P site. Similar to the observed sequential movement of the 30S body and tRNA elbow, these calculations suggest another degree of freedom to be considered when describing tRNA hybrid-state formation. Specifically, to fully describe hybrid formation, it will be necessary to, at a minimum, independently probe movement along 30S rotation, elbow and 3′-CCA coordinates.

Figure 5.

Structural characteristics of tRNA 3′-CCA end movement during hybrid-state formation. (a) As the hybrid configuration is adopted, the tRNA elbow reaches a near-P/E position before the 3′-CCA end dissociates from the P site. (b) P/E configuration, shown for comparison. Panels (c)–(e) depict which residues are contacted by the 3′-CCA end during hybrid formation. The representation is consistent with Figure 4. (c) All residues that are contacted are shown, as well as the P/P-configured tRNA. (d) Only the rRNA residues that are contacted are depicted. The 3′-CCA end is shown for reference. (e) Protein residues that are contacted are shown. The most dominant region of interaction is H74, which may serve as a guide, upon which the 3′-CCA end moves. In many simulations, the 3′-CCA end enters a pocket formed by residues near A2426 and H74, suggesting that H74 also gives rise to a significant steric barrier.

tRNA elbow movement and 30S body rotation do not exhibit pronounced steric barriers

When using a simplified model that employs an all-atom representation, along with a “soft” TMD method, it is possible that steric barriers will arise, which will lead to transient pauses along each coordinate. These pauses lead to the formation of peaks in probability distributions, as seen for other transitions in the ribosome.³³ For the presented simulations of hybrid formation, such features are not evident along the tRNA elbow and 30S rotation coordinates, suggesting that elbow movement is relatively unimpeded by the structure of the ribosomal machinery.

To clarify the atomic details of elbow movement, we identified which elbow-ribosome contacts are formed during hybrid formation, suggesting which atomic interactions are more likely to impact the kinetics. Here, a contact is considered formed if any two atoms are within 4 Å. From the simulated trajectories, we calculated the probability that each ribosomal residue interacts with the tRNA elbow region (Figures 4c, 4d). Residues that contact the tRNA elbow in each least 10% of the simulations are shown in stick representation (red = 10%, blue = 100%). Consistent with the lack of an intermediate population along the elbow and rotation coordinates, there are relatively few contacts formed between the elbow and the ribosome during hybrid-state formation. The most dominant regions that the tRNA elbow interacts with are the P site and the L1 stalk (formed in the E/E configuration).

The most pronounced feature that contacts the tRNA elbow at intermediate stages of movement is the protein L33. However, the interactions with L33 are also rather limited, where only 8 residues make contact in any runs, and only 3 residues make contact in more than 90% of the simulations. Since these interactions are between side chains at the surface of the proteins, which are typically mobile,^{31, 61} it is unlikely that L33 introduces a significant steric obstacle during hybrid formation. This does not preclude the possibility that interactions between L33 and the tRNA are attractive, which can thereby alter the energetic barriers of hybrid-state formation. In fact, in 100% of the simulations, contacts are formed with N29, T30, and N32, which are all polar residues. Thus, there is a possibility that these interactions may stabilize intermediate conformations of the tRNA molecule, consistent with numerous states identified in low-resolution cryo-EM reconstructions of tRNA during reverse translocation.⁶²

CCA movement is associated with an intermediate ensemble and “steric guide”

In contrast to tRNA elbow movement, which lacks significant steric barriers, there is a detectable intermediate population along the 3′-CCA coordinate (Figures 3e, 3f). When the 3′-CCA end is ∼20 Å from the 50S E site, it contacts many residues in H74 and residues near A2426. These residues form a pocket, which the 3′-CCA end appears to become transiently trapped in. At this point, it is important to emphasize that this feature is completely due to sterics and flexibility. In the presented simulations, the only stabilizing interactions are those between the tRNA and the P and E sites. At ∼20 Å from the E and P sites, the tRNA is beyond the length scale of the attractive interactions.

In addition to an intermediate ensemble developing from steric effects, the 3′-CCA end also makes many close interactions with residues in the 23S rRNA (Figures 5c, 5d). These residues span from the P site to the E site, and resemble a “track” upon which the 3′-CCA end moves between binding sites. The most dominant structural component of this track is H74. In H74, interactions with A2432 to U2437 are formed in 100% of the simulations. The prevalence of such close interactions between the tRNA and H74 suggests that a strategy for regulating hybrid-state dynamics may be to design antibiotics that bind H74, and therefore change the steric features that guide movement of the 3′-CCA end.

Sequence analysis⁶³ of the 23S rRNA residues that spatially separate the P and E sites identified 10 universally conserved nucleotides, including 7 nucleotides that do not interact with tRNA in crystallographic models of the endpoints. The identification of these nucleotides suggests features of the “hybrid corridor” will be consistent between organisms, and that aspects of the tRNA dynamics will be preserved. The universally conserved regions⁶⁴ of the corridor contain nucleotides from large subunit helices H74 (C2063, C2064, A2435), H80 (G2251), and H93 (A2602, G2603, G2595), as well as nucleotides A2450, A2451, and U2585 in the peptidyl transferase center. All but two of the universally conserved nucleotides (G2595 and G2603) interact with the tRNA molecule in every simulation. G2595 and G2603 display tRNA interactions in 93% and 98% of the simulations. The corridor also contains 25 nucleotides that are greater than 90% conserved. The hybrid corridor is analogous to the accommodation corridor that we previously identified,⁴⁶ for which the constituent molecular interactions have been experimental corroborated.^{65, 66, 67, 68, 69}

3′-CCA end is flexible during hybrid formation

In order for targeting of H74 to be an effective strategy for controlling hybrid dynamics, tRNA must move along a relatively well-defined route. That is, while the 3′-CCA end interacts with H74, the tRNA must not be sufficiently flexible to navigate around such obstacles. One measure of the mobility of the 3′-CCA end is the pseudo-dihedral angle ϕ₂.^{33, 46, 70} In the presented simulations, the values of ϕ₂ span ∼90° at each point during the transition to the P/E configuration. This degree of flexibility demonstrates that the tRNA pathways are not narrowly defined. Rather, there is a considerable amount of disorder as the tRNA moves between the P and E sites. This flexibility indicates that perturbations that effectively alter 3′-CCA dynamics will need to be structurally dispersed, in order to impose structural barriers on its full range of movement.

DISCUSSION

The role of sterics during ribosome function

The lack of barriers presented to the elbow during hybrid-state formation is in stark contrast to the dynamics of tRNA accommodation. Using similar models, we previously found that H89 gives rise to a steric barrier, such that it is transiently displaced to allow for movement of the tRNA.³³ One may then ask what functional role that steric barriers may fulfill, which may explain why specific barriers are present at specific transitions. In the case of accommodation, a step that is essential during tRNA selection, there must be barriers that enable for near- and non-cognate tRNAs to be efficiently rejected. While it has yet to be explicitly demonstrated, steric barriers may ensure that there are robust barriers associated with accommodation. By robust, we mean that the barrier will not be largely dependent on changes in the local environment, such as transient fluctuations in ion concentrations. Steric barriers fit this criterion, since the global fold of a molecule is typically robust to modest changes in cellular conditions. Therefore, so long as the molecule is in tact, the steric barrier will be present.

In the case of tRNA hybrid formation, there are no clear signatures of steric barriers during elbow movement. Since discrimination is primarily associated with accommodation, and not hybrid-state formation, this is reasonable to expect. tRNA hybrid formation is not related to selection, and it therefore does not necessarily have any long-lived intermediates, nor does it necessitate the presence of robust barriers. Rather, hybrid formation occurs after tRNA selection at the A-site. After accommodation, there is not an obvious reason why bacterial ribosomes would possess robust barriers that attenuate the forward kinetic. There are many interactions near the P-site that can serve to maintain a proper orientation during peptide bond formation. However, subsequent to peptide-bond formation, the tRNA must vacate the P site, and thereby allow the next step of elongation to take place. By reducing the steric obstacles present, the forward process may occur unimpeded.

Biological significance of 3′-CCA end flexibility

In our previous simulations of tRNA accommodation, we found that movement of the 3′-CCA end is associated with a large decrease in available phase space, as measured by ϕ₂.³³ Here, we find that the available angles remain roughly constant during the P/E transition, suggesting a roughly constant degree of configurational entropy. It is interesting to consider the potential biological relevance of these entropic signatures. In the case of accommodation, tRNA movement is associated with the fidelity of tRNA selection. Barriers during accommodation may then represent “turning points,” where discrimination may lead to the rejection of incorrect tRNA molecules by the ribosome. Accordingly, the final step during accommodation should be 3′-CCA entry into the PTC, since the 3′-CCA end carries the incoming amino acid. Once the amino acid is incorporated into the growing protein chain, any accommodation-related proofreading machinery becomes irrelevant. Considering this feature, we previously suggested that the large decrease in configurational entropy of the 3′-CCA end may serve to delay amino acid entry to the ribosome's catalytic core.⁷¹ In contrast to this, we find a nearly uniform flexibility of the 3′-CCA end during hybrid formation. This apparently constant configurational entropy suggests that changes in entropy will not impede hybrid dynamics. Since, during the P/E transition, the amino acid has already been added to the growing protein chain, the pressure to delay 3′-CCA is alleviated. Thus, this simple physical-chemical attribute of the 3′-CCA end may be used at particular steps of elongation to facilitate efficient and accurate translation.

Further computational modeling of ribosome dynamics

In the presented simulations, we employed simplified models that utilize an all-atom representation. At first glance, it may be tempting to apply coarse-grained models to study the dynamics of large systems, as one may expect that the larger the molecule, the less important the atomic details become. However, the presented simulations suggest the contrary. That is, we find that there are many ribosome-tRNA contacts formed transiently (i.e., atoms within 4 Å). If one were to apply a coarse-grained model, where, for example, each residue were represented by a single bead, then the steric contribution of the ribosome would be significantly altered, and it would be very likely that many artificial barriers would be introduced. This point is highlighted by the fact that the number of tRNA-ribosome contacts formed significantly increases as the contact definition is changed. That is, in the above analysis, we define a residue-residue contact as formed if any two atoms were within 4 Å during a simulation. If we increase this cutoff distance to 6 Å, we find that the number of contacts formed during hybrid-state formation increases by roughly a factor of two. Therefore, the effective size of each individual atom is an essential aspect when characterizing the relationship between structure and function in the ribosome. If the effective residue size in a coarse-grained model is too small, then steric barriers may be completely absent, such as the H89 barrier during accommodation, or the H74-A2426 barrier during hybrid-state formation. On the other hand, if the effective size is too large, then spurious steric barriers are likely to be introduced, thereby giving unreliable estimates of the scale of steric barriers, or even predicting barriers where there are none.

While there is a clear limitation when applying coarse-grained models to elongation, coarse-grained models have had tremendous success is elucidating the global relationships between protein folding and function.^{5, 6, 7, 72, 73, 74} This suggests a difference in the physics of folding and molecular machines. Specifically, in applications to the ribosome, molecular simulations are revealing strong signatures of sterics. That is, the shape of each molecule is complementary, such that minor perturbations in size have tremendous impacts on dynamics. In contrast, during protein folding, chain connectivity, and attractive interactions are extremely important. That is, the principle of minimal frustration states that native interactions are effectively stabilizing, which has given rise to the protein folding funnel paradigm.^{8, 75} When attractive interactions are dominant, the precise size of each atom is less important than the atom-atom distances corresponding to minima in the potential energy. Therefore, by coarse-graining in protein folding, the attractive aspects of the native interactions are not significantly perturbed by changes in the excluded volume. On the other hand, in the ribosome, there is such a large number of non-native interactions that transiently form, if each atom were smaller or larger, there could be very large effects on the energy of the system.

The precise relationship between flexibility, structure, energetics, and dynamics is essential to understand the basis for biomolecular machine-like function. To that end, the simulations presented here demonstrate how simple models may be applied to gain initial insights into these relationships, at a phenomenological level. Building on this foundation, it will be possible to quantitatively explore these relationships, at which point a precise theoretical understanding of machine dynamics may emerge.

METHODS

Potential energy surface

To approximate the energy landscape associated with translocation, we used a multi-basin all-atom structure-based model approach (i.e., multi-basin SMOG models). In a structure-based model, an experimentally-obtained configuration is defined as the lowest energy conformation.³¹ For example, in a single-basin SMOG model of the A/A-P/P configuration, all interactions formed in the A/A-P/P configuration are stabilizing, ensuring that it is the global energetic minimum. One advantage of SMOG models is the reduced computational cost, which allows for large-scale spontaneous fluctuations to occur, and in some cases, full-scale spontaneous transitions between competing functional configurations.³³

During translocation, each tRNA molecule is known to bind to two different binding sites. One tRNA is initially bound to the A site and finishes in the P site. Similarly, the other tRNA initially binds the P site and finishes in the E site. To account for these properties, we constructed two SMOG models using the smog-server webtool (http://smog-server.org³²), one for the A/A-P/P configuration and one for the P/P-E/E configuration. The structural model used for the A/A-P/P and P/P-E/E configurations are described elsewhere.⁷⁶ Each SMOG model defines the given configuration as the global energetic minimum. To account for the ability of each tRNA to bind to two different sites, we introduced attractive interactions between the tRNA and two ribosomal binding sites. That is, one tRNA can bind the P, or E site, while the other tRNA can bind the A, or P, site.

To describe the multi-basin SMOG model used here, it is useful to first consider the details of a single-basin SMOG model. A single-basin SMOG model has the following functional form:

$$\begin{array}{ccc}\hfill V& =& \sum _{\mathrm{bonds}}{K}_r{(r-r_0)}^2+\sum _{\mathrm{angles}}{K}_{\theta }{(\theta -{\theta }_0)}^2\hfill \\ & & +\sum _{\underset{\mathrm{dihedrals}}{\mathrm{planar}/\mathrm{improper}}}{K}_{\chi }{(\chi -{\chi }_0)}^2\hfill \\ & & +\sum _{\underset{\mathrm{dihedrals}}{\mathrm{backbone}}}{K}_{\varphi ,BB}{F}_D\left(\varphi \right)+\sum _{\underset{\mathrm{dihedrals}}{\mathrm{sidechain}}}{K}_{\varphi ,SC}{F}_D\left(\varphi \right)\hfill \\ & & +\sum _{\mathrm{contacts}}{\varepsilon }_C\left[{\left(\frac{{\sigma }_{ij}}{r}\right)}^{12}-2{\left(\frac{{\sigma }_{ij}}{r}\right)}^6\right]+\sum _{\mathrm{contacts}}{\varepsilon }_{NC}{\left(\frac{{\sigma }_r}{r}\right)}^{12},\hfill \end{array}$$

where,

$$F_D\left(\varphi \right)=(1-\cos (\varphi -{\varphi }_2))+\frac{1}{2}(1-\cos (3(\varphi -{\varphi }_2))),$$

where r₀, θ₀, χ₀, ϕ₀, σ_ij are the values corresponding to the input conformation and σ_r = 2.5 Å. K_r = 100ɛ₀/Ų, K_θ = 20ɛ₀/rad², K_χ = 40ɛ₀/rad², and ɛ_r = 0.1ɛ₀. Attractive atom-atom “contacts” are given a 12-6 potential energy function, where the minimum corresponds to the distance found in the experimental configuration σ_ij. A contact is defined as any atom pair that is not interacting via a dihedral angle, is separated by less than 4 Å and is at least 4 (proteins) or 1 (RNA) residues apart in sequence (i.e., a “cutoff” contact definition⁷⁸). Consistent with previous studies,^{31, 33, 79} contact and dihedral interactions were weighted, such that

$$\begin{array}{ccc}\hfill R_{BB/SC}& =& \frac{K_{\varphi ,BB}}{K_{\varphi ,SC}}=\frac{\mathrm{Strength}\mathrm{of}\mathrm{a}\mathrm{single}\mathrm{backbone}\mathrm{dihedral}}{\mathrm{Strength}\mathrm{of}\mathrm{a}\mathrm{single}\mathrm{sidechain}\mathrm{dihedral}}\hfill \\ & =& 2.0\left(\mathrm{protein}\right),1.0\left(\mathrm{RNA}\right),\hfill \\ \hfill R_{C/D}& =& \frac{\sum {\varepsilon }_C}{\sum K_{\varphi ,BB}+\sum K_{\varphi ,SC}}=2.0,\hfill \end{array}$$

and

$$\sum K_{\varphi ,BB}+\sum K_{\varphi ,SC}+\sum {\varepsilon }_C=N{\varepsilon }_0,$$

where N is the number of atoms and ɛ₀ = 1.0. Additionally, the energetic weights of RNA and protein backbone dihedrals were set to be equal. In this model, electrostatics are not explicitly included. That is, electrostatic effects at the endpoints are effectively described since electrostatic terms contribute to the overall stability of the endpoint configurations. Since electrostatic contributions between endpoint are not explicitly included, the primary utility of these models is to identify routes that are consistent with the flexibility and sterics of tRNA molecules. Further, these models are used to identify the role of ribosome sterics during large-scale rearrangements.

To construct a multi-basin model, single-basin models were first constructed for the A/A-P/P configuration and the P/P-E/E configuration. After the above normalizations were applied, the strength of contacts between the mRNA-tRNA and ribosome were rescaled by 0.4. This effectively destabilizes the tRNA-ribosome interface, which is consistent with tRNA molecules only transiently interacting with the ribosome. That is, stabilizing contacts that maintain structural integrity of the ribosome are stronger than tRNA-ribosome contacts, which accounts for the fact that tRNA-ribosome contacts are short-lived, relative to the interactions that maintain the overall structure of the ribosome. To mimic the multi-basin nature of the landscape that governs hybrid dynamics, all interactions in the A/A-P/P SMOG model were included, and contacts between the ribosome and mRNA-tRNA in the P/P-E/E model were additionally included. Since this form of basin-mixing is done contact-by-contacts (i.e., microscopic mixing⁷), it is possible for intermediate conformation to be stably formed, where some interactions from each basin are formed, such as during hybrid-state formation.

TMD description: Harmonic implementation

To induce transitions between the P/P and P/E configuration, we employed a targeted molecular dynamics approach.^{44, 45} That is, we employed the multi-basin SMOG model, which provides a description of the underlying energy landscape, and an additional time-dependent interaction that biases the system towards the end state configuration. The P/P model is nearly identical to a model from x-ray crystallography, and the P/E model was obtained from flexible-fitting of an atomic model to a cryo-EM reconstruction. The P/P and P/E models are described in Ref. 76.

Here, the biasing term is of the form

$$V_{\mathrm{TMD}}=E_{\mathrm{TMD}}{(RMSD-D_{\mathrm{TMD}}\left(t\right))}^2,$$

where RMSD is a weighted root mean-squared deviation,

$$RMS{D}^2=\frac{1}{N}{\sum }_{i=1}^N{W}^i{({\stackrel{\rightharpoonup }{x}}^i-{\stackrel{\rightharpoonup }{x}}_{\mathrm{target}}^i)}^2,$$

${\stackrel{\rightharpoonup }{x}}^i$ denotes the x, y, and z component of each atom, and $x_{\mathrm{target}}^i$ represented the coordinates of the target configuration. The values of Wⁱ were set such that Wⁱ = 1 if the distance between initial and target configurations (D_{f − i}) are below the threshold distance D = 20 Å, and $W^i=\frac{D}{D_{f-i}}$ if D_{f − i} > D. The rationale for introducing a threshold distance, above which the weights are reduced, is that the force on individual atoms is proportional to the distance from the target. Therefore, atoms that undergo larger rearrangements (such as the 3′-CCA end) would be subject to much larger forces from the TMD potential, if a threshold was not used. D_TMD(t) is a linear function in time that decreases from RMSD_initial to zero over a predescribed interval of time. Once D_TMD(t) reaches zero, it remains zero for the remainder of the simulation. All atoms were included in the calculation of RMSD. The RMSD between endpoints is 6.4 Å.

Simulation details

Each simulation was initiated in the A/A-P/P configuration, where the A/P*-P/E configuration was used as a target (described elsewhere⁷⁶). A time step of 0.0005 was used, and each simulation was performed for 1.5 × 10⁶ time steps, corresponding to an effective timescale of microseconds. See supplementary material of Ref. 33 for detailed discussion on timescale estimates in SMOG models. D_TMD(t) was linearly reduced in time for 1 × 10⁶ time steps. The energetic weight of the TMD potential was 20 000ɛ₀. A reduced temperature of 0.46 was used in all simulations. About 120 simulations were performed, where each one provided a single trajectory between the classical and hybrid configuration. Each simulation was performed using an in-house modified version of Gromacs v4.0.5.^{80, 81} Dynamic load balancing was employed, and each simulation was performed using 64 cores on the Lonestar Cluster at TACC.