Reconstructing the Demographic History of the Human Lineage Using Whole-Genome Sequences from Human and Three Great Apes

Abstract

The demographic history of human would provide helpful information for identifying the evolutionary events that shaped the humanity but remains controversial even in the genomic era. To settle the controversies, we inferred the speciation times (T) and ancestral population sizes (N) in the lineage leading to human and great apes based on whole-genome alignment. A coalescence simulation determined the sizes of alignment blocks and intervals between them required to obtain recombination-free blocks with a high frequency. This simulation revealed that the size of the block strongly affects the parameter inference, indicating that recombination is an important factor for achieving optimum parameter inference. From the whole genome alignments (1.9 giga-bases) of human (H), chimpanzee (C), gorilla (G), and orangutan, 100-bp alignment blocks separated by ≥5-kb intervals were sampled and subjected to estimate τ = μT and θ = 4μgN using the Markov chain Monte Carlo method, where μ is the mutation rate and g is the generation time. Although the estimated τ_HC differed across chromosomes, τ_HC and τ_HCG were strongly correlated across chromosomes, indicating that variation in τ is subject to variation in μ, rather than T, and thus, all chromosomes share a single speciation time. Subsequently, we estimated Ts of the human lineage from chimpanzee, gorilla, and orangutan to be 6.0–7.6, 7.6–9.7, and 15–19 Ma, respectively, assuming variable μ across lineages and chromosomes. These speciation times were consistent with the fossil records. We conclude that the speciation times in our recombination-free analysis would be conclusive and the speciation between human and chimpanzee was a single event.

Introduction

Reconstructing the history of human evolution is helpful for elucidating the phenotypic characteristics that may have generated the nature of modern humans. In addition to fossil records (Harrison 2010), molecular characteristics are highly informative for reconstructing the evolutionary history of humans. In the early age of molecular evolutionary studies, immunoprecipitation (antigen–antibody interactions) and electrophoresis of peptides and DNA–DNA hybridization were used for estimation of the phylogenetic relationships among human and their great ape relatives (Sarich and Wilson 1967; King and Wilson 1975; Sibley and Ahlquist 1984). These techniques have now been replaced by the in silico analysis based on nucleotide sequences. By comparing genome sequences between human and great apes, we can infer the phylogenetic relationships between these species and map their molecular and phenotypic signatures onto a phylogenetic tree. Characteristics associated with the lineage leading to modern humans are candidates for key factors in human phenotypic innovation.

The demographic history among closely related species is reconstructed using sets of orthologous nucleotide sequences in different genomic regions. If the divergence of sequences is determined by species divergence time alone, the extent of nucleotide sequence divergences between species can be the same for the entire genome. However, the nucleotide divergence varies among different regions. This variation partly reflects variation of segregation times due to different coalescence among regions caused by recombination as well as the stochastic variability of nucleotide substitutions. Takahata et al. (1995) pointed out that the parameters involved in a demographic history can be estimated using a single reference genome for each species. This is because during the course of evolution a large number of recombination events have divided genomes into large numbers of small blocks, each of which represents a single genealogy. Assuming that coalescence occurred at random in each of such blocks in an ancestral population, the coalescence times would be geometrically distributed (Kingman 1982), leading to the simultaneous estimation of the parameters involving the speciation time τ = μT and the ancestral population size θ = 4μgN, where μ, T, g, and N represent the mutation rate per site per year, speciation time between species, generation time in years, and the effective population size of common ancestors, respectively (Takahata et al. 1995). This estimation is usually conducted based on a maximum-likelihood approach (Takahata et al. 1995; Takahata and Satta 1997; Yang 2002, 2010), Bayesian (Yang 2002; Rannala and Yang 2003; Hey and Nielsen 2004; Burgess and Yang 2008; Hey 2010) or Hidden Markov Model (HMM) frameworks (Hobolth et al. 2007; Dutheil et al. 2009). Each method has advantages and disadvantages. The maximum-likelihood and Bayesian approaches are capable of addressing three or more species. However, alignment data in both approaches must be sampled so that each block represents a single genealogy for estimating τ and θ precisely. The HMM approach use an alignment of the entire genome and scan the alignments in small windows, while the approach can treat only three species. Some parts of the variation in nucleotide divergence may be subject to introgression after initial isolation (e.g., Wu and Ting 2004; Pinho and Hey 2010). The regions in which introgressions occurred may possess distinctly smaller nucleotide divergence than the genomic average.

Using the earlier-mentioned theoretical frameworks, the demographic history between human and chimpanzee has been inferred based on the limited numbers of randomly sampled genomic regions or protein-coding genes since the mid-1990s (Takahata et al. 1995; Takahata and Satta 1997; Yang 1997; Chen and Li 2001). Because of recent rapid progress in nucleotide sequencing, the whole-genome sequences of not only human but also great apes have become available (Chimpanzee Sequencing and Analysis Consortium 2005; Locke et al. 2011; Scally et al. 2012). Thus, it becomes possible to infer the demographic history of human and great apes using massive amounts of information.

Several attempts at estimating divergence times and ancestral population sizes have been conducted using relatively long sequences (>1 Mb), or even whole-genome sequences from human and great apes (Satta et al. 2004; Patterson et al. 2006; Hobolth et al. 2007, 2011; Burgess and Yang 2008; Yang 2010; Scally et al. 2012). However, the demographic history of human remains controversial. Most of these studies supported the occurrence of a simple speciation process between human and chimpanzee (allopatric speciation), which can be explained by a unique speciation time across the genomic regions. However, a few studies have indicated the existence of multiple speciation times across these genomes, implying that human and chimpanzee experienced a complex speciation history. A study performed by Patterson and colleagues resulted in the most debatable issue on the speciation between human and chimpanzee (Patterson et al. 2006). This study estimated a significantly more recent speciation time based on X chromosome than that on the autosomes, concluding that this observed heterogeneity would be due to recent introgression after initial isolation and subsequent strong selection favoring X chromosome hybrids (Patterson et al. 2006). Yang (2010) also showed multiple speciation times, even among the autosomes, using >5-Mb genomes of human, chimpanzee, and gorilla. Osada and Wu (2005) estimated different divergence times of human and chimpanzee between coding regions and intergenic regions, suggesting that genetic exchanges had occurred during the speciation history of human and chimpanzee. On the other hand, a few studies using Patterson’s data did not find the complex speciation (Innan and Watanabe 2006; Yamamichi et al. 2011). In addition, both gorilla and orangutan genome consortiums estimated speciation times using nearly whole genomes of human, chimpanzee, gorilla, and orangutan. However, they did not present a conclusion about the complex history of the human lineage (Locke et al. 2011; Scally et al. 2012).

To determine the evolutionary history of hominids comprehensively based on whole genomes, we inferred τ and θ using whole-genome alignments consisting of the most recent assemblies of the human, chimpanzee, gorilla, and orangutan genomes. This inference was conducted using Rannala’s Markov chain Monte Carlo (MCMC) framework (Rannala and Yang 2003). The MCMC approach requires optimal sampling of alignments, each of which ideally represents a single genealogy, to obtain precise estimations of τ and θ. Thus, we simulated the evolution of nucleotide sequences under certain demographic models to search for the optimal conditions about sizes of alignment blocks and the lengths of intervals between them. Inference of the demographic histories of hominids was conducted using the optimal conditions from this simulation. In addition, to estimate speciation times and ancestral population sizes correctly, an evolutionary model including variability of evolutionary rates across lineages was required. Variation in mutation rates has been observed between Old World monkeys and hominoid lineages, and even within the hominoids (Elango et al. 2006; Steiper and Young 2006; Steiper and Seiffert 2012). We assumed that the probability density function of the mutation rate on a branch was subject to that of the parental (adjacent older) branch. Through this analysis, we intend to settle the controversy about human–chimpanzee speciation described earlier.

Materials and Methods

Generation of Whole-Genome Alignments

The human (hg19), chimpanzee (panTro3), gorilla (gorGor3), and orangutan (ponAbe2) genome sequences were obtained from the UCSC genome browser (http://genome.ucsc.edu/, cited 2012 Sep 18). Orthologous alignments among the four species were constructed based on two procedures as described later. Orthologous pairwise alignments between the human and each great ape sequences were generated with the G-compass pipeline (Fujii et al. 2005; Kawahara et al. 2009) based on LASTZ local alignments (Harris 2007) and its unique and nonredundant reciprocal best hits. Subsequently, the human genomic regions that possessed the orthologous pairwise alignments to all the three great ape were extracted and multiply re-aligned with the corresponding sequences of the three apes with MAFFT (Katoh and Toh 2008).

Both ends (20 aligned sites) of each alignment were excluded due to the ambiguity of the alignments. The alignments were split into blocks of fixed lengths of 50 and 100 bp. To obtain the alignments showing unambiguous orthology, we extracted the alignment blocks satisfying d_HC < 0.05, d_HCO < 0.08, and the null hypothesis of d_H = d_C for a relative rate test (Tajima 1993), where d_HCO = (d_HO + d_CO)/2 and d_H and d_C represent the evolutionary distances from the branching point between human and chimpanzee to their leaves, respectively. In the relative rate test, we calculated the exact P values of binominal distributions because the observed values were >5 in most cases. A total of 97.4% alignments out of the total satisfied these conditions. The alignments that did not include ultramicro inversions (Hara and Imanishi 2011) were chosen. Gapped sites and CpG dinucleotide sites were excluded from the alignment blocks, and the alignments in which 80% or more of sites remained were subjected to the subsequent analyses. Finally, the alignments blocks were extracted with ≥5 kb of the intervals.

MCMC Inference of Demographic History

To infer the demographic history parameters τ and θ, we applied the Rannala's MCMC framework (Rannala and Yang 2003; Burgess and Yang 2008) with an extension of the evolutionary model that assumes heterogeneous evolutionary rates among lineages. Under this condition, we assumed that the mutation rate for a branch was subject to that of its parental branch; thus, the mutation rate for a branch was log-normally distributed given the mutation rate on its parent branch (Yang 2006). The mean and standard deviation of the proportion of the mutation rate of the branch to that of its ancestor were calculated from the phylogenetic trees based on the orthologous genome alignments (1.03 Gb in total) consisting of human, chimpanzee, gorilla, orangutan, and macaque sequences. The multiple alignments of the orthologous regions among the five species were generated using the same procedure as used for the four species described earlier. The phylogenetic trees were inferred by RAxML (Stamatakis 2006). We assumed a log-normal prior distribution of μ_k/μ_anc(k) with the sequence differences in the alignment, where μ_anc(k) is the mutation rate of the parent branch of k. In this analysis, μ_HGCO = μ_O, and the relative mutation rates were r = μ/μ_H. We could compute the relative ratios of the mutation rates between sister branches but not between a parent and a daughter. This is because we do not know the divergence times of the nodes separating the daughters in advance. Therefore, we assumed a prior distribution of μ_k/μ_anc(k) = r_k/r_k', where k' is a sister of k, instead.

In this analysis, we assumed the existence of three evolutionary conditions on the heterogeneity of the mutation rates among lineages and among genomic regions: 1) the model assuming uniform mutation rates across lineages and across genomic regions (uniform model); 2) the model assuming variations in mutation rates across lineages; and 3) the model assuming variations across lineages and across chromosome. In the method 3), we applied the proportion of an average of total branch length of a block on every chromosome to that of whole genome as the parameter representing the variability of mutation rates across the chromosomes (table 1).

Table 1.

Estimated Parameters for Each Chromosomal Alignment Set^a

Regionsb	Alignment Length (Mb)	τHC	τHCG	τHCGO	θHC	θHCG	θHCGO	Branch Lengthc	−ln L
Whole genomed	40.8	0.00330	0.00423	0.00819	0.00264	0.00229	0.00709	0.0352	−66,035,045
Autosomesd	38.7	0.00326	0.00423	0.00835	0.00286	0.00223	0.00659	0.0355	−62,585,914
Chr. 1	3.28	0.00313	0.00408	0.00778	0.00270	0.00216	0.00691	0.0335	−5,289,418
Chr. 2	3.49	0.00327	0.00426	0.00827	0.00284	0.00223	0.00671	0.0350	−5,650,076
Chr. 3	2.92	0.00324	0.00429	0.00837	0.00303	0.00225	0.00679	0.0352	−4,736,827
Chr. 4	2.79	0.00345	0.00434	0.00886	0.00288	0.00254	0.00676	0.0368	−4,545,603
Chr. 5	2.61	0.00327	0.00436	0.00855	0.00316	0.00221	0.00644	0.0354	−4,243,851
Chr. 6	2.43	0.00307	0.00423	0.00837	0.0036	0.00225	0.00629	0.0346	−3,934,109
Chr. 7	2.13	0.00345	0.00426	0.00826	0.00221	0.00227	0.00705	0.0352	−3,458,675
Chr. 8	2.09	0.00352	0.00453	0.00899	0.00311	0.00242	0.00650	0.0372	−3,419,007
Chr. 9	1.62	0.00332	0.00431	0.00786	0.00282	0.00215	0.00678	0.0340	−2,620,109
Chr. 10	1.86	0.00331	0.00422	0.00827	0.00263	0.00228	0.00723	0.0353	−3,027,929
Chr. 11	1.86	0.00324	0.00415	0.00827	0.00271	0.00233	0.00692	0.0348	−3,022,784
Chr. 12	1.93	0.00317	0.00408	0.00818	0.00264	0.00234	0.00671	0.0342	−3,127,323
Chr. 13	1.43	0.00321	0.00434	0.00878	0.00364	0.00239	0.00660	0.0361	−2,336,632
Chr. 14	1.29	0.00310	0.00413	0.00792	0.00296	0.00220	0.00721	0.0344	−2,093,555
Chr. 15	1.14	0.00317	0.00421	0.00786	0.00324	0.00216	0.00731	0.0343	−1,850,007
Chr. 16	1.07	0.00360	0.00459	0.00870	0.00277	0.00238	0.00730	0.0374	−1,755,416
Chr. 17	1.09	0.00294	0.00385	0.00726	0.00264	0.00195	0.00827	0.0330	−1,752,968
Chr. 18	1.11	0.00330	0.00433	0.00880	0.00342	0.00243	0.00616	0.0358	−1,801,757
Chr. 19	0.725	0.00315	0.00401	0.00751	0.00285	0.00237	0.00895	0.0350	−1,173,725
Chr. 20	0.878	0.00310	0.00415	0.00798	0.00325	0.00225	0.00706	0.0344	−1,418,404
Chr. 21	0.466	0.00337	0.00444	0.00910	0.00370	0.00278	0.00665	0.0376	−761,073
Chr. 22	0.454	0.00299	0.00401	0.00796	0.00328	0.00241	0.00744	0.0348	−733,646
Chr. Xe	2.07	0.00277	0.00371	0.00637	0.00153	0.00171	0.00627	0.0295	−3,286,104
Coding regionsd	2.37	0.00156	0.00249	0.00418	0.00367	0.00137	0.00552	0.0213	−3,632,995
FFD 3rd positionsd,f	0.351	0.00437	0.00548	0.0135	0.00401	0.00480	0.00708	0.05359	−598,524

^a95% CI of each estimated parameter and the estimates based on the sample 2 were shown in supplementary table S2, Supplementary Material online.

^bAnalyzed based on the method (2), assuming heterogeneity of mutation rates across the lineages (see Materials and Methods), except the regions with footnote d.

^cAverage of sum of the branch lengths in each locus.

^dAnalyzed based on the method (3), assuming heterogeneity of mutation rates across lineages and chromosomes (see Materials and Methods).

^eθ = 3μgN based on X chromosome.

^fFour-fold degenerate sites at third codon positions.

The MCMC computation was conducted by a PC cluster consisting of 128 CPUs parallelizing the calculation of the joint log-likelihood of each locus in each step using the OpenMPI library. The extension of the evolutionary model and parallelization were performed via modification of the source code of MCMCcoal1.2a developed by Yang (http://abacus.gene.ucl.ac.uk/software/MCMCcoal.html; cited 2012 Sep 18) (Rannala and Yang 2003; Burgess and Yang 2008). After 100,000 burn-in steps, τ, θ, and the relative ratio of μ were sampled every 10 steps until accumulating 50,000 samples. Median and 2.5 and 97.5% confidence interval (CI) was calculated for each parameter.

To calculate speciation times and ancestral population sizes, we applied the number of de novo mutations per generation to the mutation rate per site per year, which included 1.17 × 10⁻⁸ de novo mutations per site per generation from a family trio of Hap Map CEU populations, 0.97 from a trio from the Hap Map YRI populations (Conrad et al. 2011), 1.1 × 10⁻⁸ from a family quartet of Europeans (Roach et al. 2010), and 1.28 × 10⁻⁸ from the de novo mutation database of monogenic disorders (Lynch 2010). To exclude the effect of the mutations at CpG dinucleotide sites, these values were multiplied by the ratios of non-CpG mutations among the total, which were 0.86, 0.89, 0.82, and 0.86 for the respective studies. The first three were observed values, and the last was the average of the first three. We set the frequency of non-CpG dinucleotides in the whole human genome at 99% (Lander et al. 2001; Saxonov et al. 2006). In addition, we assumed the average generation time to be 20 years based on those from chimpanzee (Teleki et al. 1976), 19.1 years, and gorilla (Walsh et al. 2008), 22 years, though the generation time of modern humans is longer than those (Matsumura and Forster 2008). From these conditions, the mutation rates per site per year were calculated as 0.508 × 10⁻⁹, 0.436 × 10⁻⁹, 0.456 × 10⁻⁹, and 0.556 × 10⁻⁹, respectively. In this analysis, the maximum and minimum values among the four were used (table 3).

Table 3.

Estimated Speciation Times and Ancestral Population Sizes

μH (/Year·Site)	THC (Ma)	THCG (Ma)	THCGO (Ma)	NHC	NHCG	NHCGO	NHC(X)	NHCG(X)	NHCGO(X)
0.436 × 10−9	7.57	9.70	18.8	75,600	65,500	203,000	43,800	49,200	180,000
0.556 × 10−9	5.94	7.61	14.7	59,300	51,400	159,000	34,300	38,500	141,000
1.00 × 10−9a	3.30	4.23	8.19	33,000	28,600	88,600	19,100	21,400	78,400

^aThe value traditionally used. This value was not used for the conclusive estimation.

Simulation

We applied MaCS software (Chen et al. 2009) to simulate the demographic history among human and the three great apes at the megabase level. We generated the demographic history of 10 Mb regions of the four species, setting μ = 1 × 10⁻⁹ per site per year, the recombination rate at 10 cM/Mb for hotspots and 1cM/Mb for the other regions, the average generation time at 20 years, T_HC at 300,000 generations, T_HCG at 400,000 generations, T_HCGO at 700,000 generations, and the population sizes at N_H = 27,500, N_C = 50,000, N_G = 30,000, N_O = 33,000, and N_HC = N_HCG = N_HCGO = 60,000. Hotspots were distributed among 10%, 5%, and none of the regions at random, respectively. If adjacent regions were separated by recombinations but showed equal coalescence times, they are merged into a single genealogy. In the simulated region, blocks of a fixed length were set together with a fixed interval. The start site of the first block was randomly chosen within a length of the fixed interval from the end of the region. The blocks were subjected to examination of how many genealogies were included in a block and how blocks shared a genealogy with adjacent ones. Based on the demographic history estimated with MaCS software (Chen et al. 2009), random nucleotide sequences were evolved using Seq-Gen software (Rambaut and Grassly 1997). Alignments in blocks with fixed sizes (50 bp to 1 kb) and fixed intervals (500 bp to 5 kb) were extracted and subjected to estimation of τ and θ using Rannala's MCMC framework (Rannala and Yang 2003), assuming the uniform model [model (1) described earlier].

Results

Simulation of Coalescence

We simulated nucleotide sequences with MaCS software (Chen et al. 2009) to obtain the optimal condition about the size of the alignment blocks and the length of the intervals between them. This procedure is intended to obtain recombination-free alignments with a high frequency. MaCS is much faster than the other available demographic simulation software and, thus, suitable for studies using mega-base pair or longer sequences (Chen et al. 2009).

We assumed a 10-Mb region, in which recombination and coalescent events were generated according to a so far common feature of demographic history of human, chimpanzee, gorilla, and orangutan. The model included the following parameters: speciation times of humans from chimpanzee (T_HC), gorilla (T_HCG), and orangutan (T_HCGO) of 6, 8, and 14 million years ago (Ma), respectively; effective population sizes of the human (N_H), chimpanzee (N_C), gorilla (N_G), orangutan (N_O) lineages and the ancestral lineages (N_HC, N_HCG, and N_HCGO) of 27,500, 50,000, 30,000, 33,000, and 60,000, respectively. We considered a combination of two kinds of the recombination rates in a region. One represents an average recombination of 1 cM/Mb, equivalent to the average recombination rate across the human genome (Bouffard et al. 1997; Nagaraja et al. 1997; Pritchard and Przeworski 2001). The other represents a recombination rate of hotspots (Myers et al. 2005), 10 cM/Mb. Ninety of a given region exhibited the former rate, whereas the remaining regions possessed the latter rate. The hotspots were randomly allocated across the region.

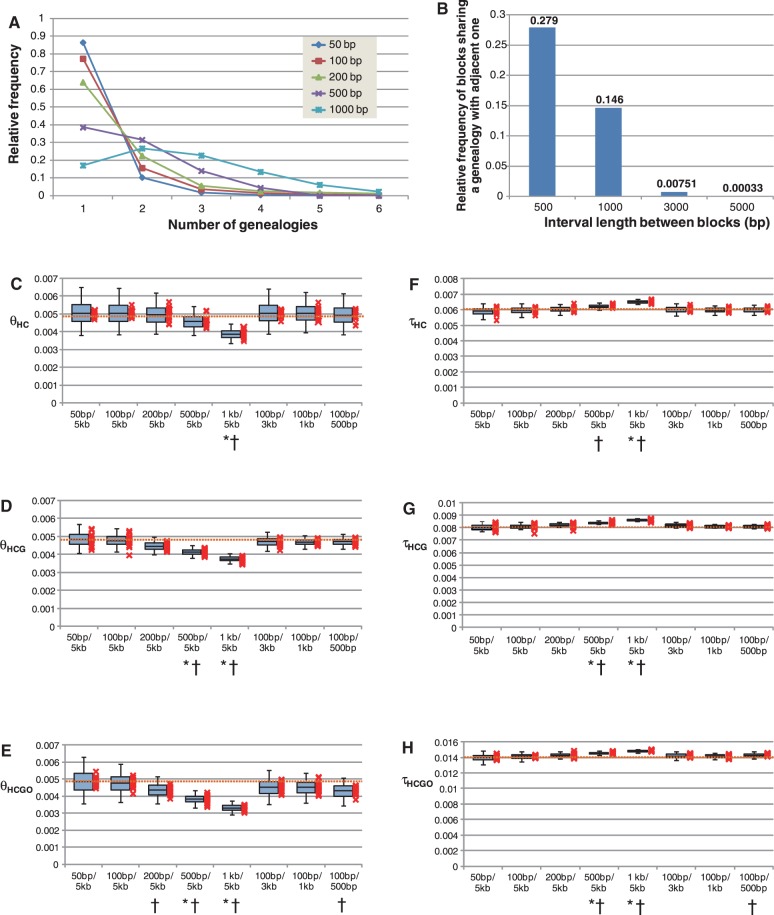
After constructing pieces of the genealogies in the 10-Mb region according to the procedure described earlier, we allocated blocks to the region with a fixed size ranging from 50 bp to 1 kb and intervals with a fixed length ranging 500 bp to 5 kb. Under each combination of a block size and an interval length, we examined the number of genealogies in every alignment block and the number of alignment blocks sharing a genealogy with an adjacent block. The result showed that blocks with small sizes frequently present a single genealogy (fig. 1A). Although 87% of the 50-bp blocks with 5-kb intervals showed a single genealogy, only 17% of the 1-kb blocks with 5-kb intervals did. Interestingly, these values are more or less the same in different proportion of the two recombination rates in a region (fig. 1A and supplementary fig. S1, Supplementary Material online). In addition, we found that the longer the intervals between the blocks, the less frequent the blocks share a genealogy (fig. 1B). 28% and 15% of blocks separated by 500-bp and 1-kb intervals shared a genealogy with the adjacent one, respectively. This was only true for 0.76 and 0.036% of blocks with 3- and 5-kb intervals, respectively.

Fig. 1.—

(A) Number of genealogies in a block under each of the block size conditions, setting the interval between the blocks at 5 kb. The frequency of hot spots was considered to cover 10% of the genomes (see text). The results in different proportion of two recombination rates were shown in supplementary figure S1, Supplementary Material online. (B) Number of blocks sharing a genealogy with an adjacent block under each of the interval length conditions, setting the block size at 100 bp. These values are the average of the 1,000 replications of the coalescence simulation. (C–H) The estimated θs and τs from simulated sequences. Each boxplot consists of the averages of the 2.5th percentile, lower quartile, median, upper quartile, and 97.5th percentile from 20 replications, from bottom to top. A mark of X represents the median of each of the 20 replications. Dotted lines represent the true values. Under each condition, asterisks indicate that the true value is outside of the 95th percentile, and daggers indicate that the true value is smaller than or larger than all of the medians in the 20 replications.

Once genealogies were determined, the sequences of four species were simulated. If alignment blocks are set to be short with longer intervals, the blocks would be frequently allocated to a single different genealogy, leading to the precise estimation of speciation times and population sizes. We examined the impact of block sizes and the interval lengths on the accuracy of the estimation of τ and θ using the 10-Mb sequence alignments of the four species. After 20 replications of this procedure, we found that if alignment blocks are set to be short with longer intervals, speciation times and population sizes were estimated precisely (fig. 1C–H). In most of the estimations of τ and θ with 50 and 100 bp blocks, the true values were included in the interquartile ranges, whereas in most of the τ and θ estimates based on 500 and 1 kb blocks, the true values were outside of the 95th percentiles. The variances in τ and θ were large in the simulation of the short alignment blocks due to the low numbers of alignment sites. However, the variances in a real genome dataset, which would be approximately 200 times the size of the simulation dataset, would be negligibly small even if we use such short alignment blocks. These results indicate that blocks of 100 bp or less are preferable for estimations. It is noteworthy that the variances of θs are larger than those of τs under all conditions. We also found that the interval length between blocks was moderately influential in the estimation compared with the size of the blocks (irrespective of the proportions of the two recombination rates). The estimated τ and θ with more than 1-kb intervals appeared to be equivalent to the true values, whereas the estimates with 500-bp intervals can be inconsistent with the true values: the τ_HCGO and θ_HCGO differed from the true values (fig. 1C–H).

Inference of τ and θ Using the Human and Great Apes Genomes

We inferred the τ and θ associated with the hominid demographic history using the human and three great apes genomes. We generated a total of 1.9 Gb of orthologous alignments using the human, chimpanzee, gorilla, and orangutan genomes. We inferred τ and θ using Rannala's MCMC framework (Rannala and Yang 2003), with modification of the heterogeneity of the mutation rates across the lineages (see Materials and Methods).

We used 50-bp alignment blocks together with 5-kb intervals to infer τ and θ but failed to compute realistic values: θ_HC was completely different from the values found in previous studies, and τ_HC was different between the four-species analysis and human–chimpanzee–orangutan analysis (supplementary table S1, Supplementary Material online). This may be because of failure of convergence in the Markov chain analysis (see Discussion). Therefore, we chose to use 100-bp blocks and 5-kb intervals instead.

To examine whether the estimated speciation times were unique between the autosomes and X chromosome, we inferred τ based on alignments of the autosomes and X chromosome separately (table 1 and supplementary table S2, Supplementary Material online). We estimated different τ_HC values between the autosomes and X chromosome: 0.00326 (95% CI: 0.00321–0.00331) for autosomes and 0.00277 (95% CI: 0.00263–0.00290) for the X chromosome. We also observed a similar difference in τ_HC between the autosomes and X chromosome when using the simplest model, which considers a uniform evolutionary rate across the lineage and across loci (supplementary table S1, Supplementary Material online). Furthermore, the estimated τ_HC for each chromosome varies, even across the autosomes (table 1). The observed variability of τ across the autosomes appears to be consistent with Yang's estimation that was based on 5.2 Mb of alignments among human, chimpanzee, and gorilla genomes (Yang 2010).

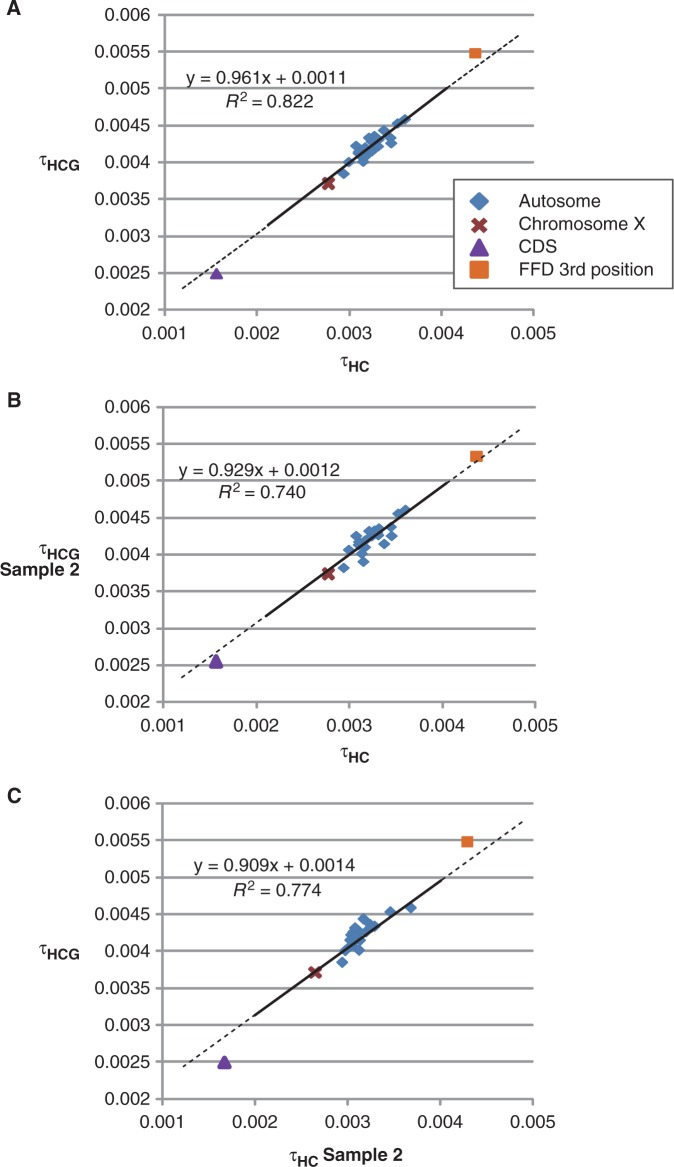
Because τ is the product of the mutation rate, μ, and speciation time, T (τ = μT), variation in τ across chromosomes can be explained by variability in T and/or μ. To determine which parameters affected the variation of τ, we plotted two τ values that reflect different species divergence time. The result showed that τ_HC and τ_HCG were strongly positively correlated across the chromosomes (R² = 0.822, P = 2.58 × 10⁻⁹) (fig. 2A). To examine whether this relationship was merely due to the fact that τ_HC and τ_HCG were simultaneously estimated from the same sequence data, we sampled alignment blocks that were not included in the original sample data and, using the new sample data (sample 2), estimated τ and θ (supplementary table S2, Supplementary Material online). Interestingly, it was found that τ_HC and τ_HCG even from different sample data were strongly positively correlated (R² = 0.740, P = 1.42 × 10⁻⁷ for fig. 2B and R² = 0.774, P = 3.24 × 10⁻⁸ for fig. 2C). These results strongly suggested that the relationship between τ_HC and τ_HCG could not be explained by the correlation of the data itself. This observation can be explained in two different ways. First, if τ_HC and τ_HCG are correlated, μ would vary across the chromosomes but T_HC and T_HCG would be constant. We further found that θ_HC and θ_HCG were significantly positively correlated across the chromosomes (R² ≥ 0.320, P ≤ 0.00494, supplementary fig. S2, Supplementary Material online) though the correlation coefficient between θ_HC and θ_HCG was lower than that between τ_HC and τ_HCG. This finding also supports the idea that μ varied across the chromosomes. The second explanation is as follows: even under the constant μ among chromosomes, the same bias of T_HC and T_HCG in each chromosome, if any, could explain the variation of τ values. The latter explanation is rather unlikely. Thus, it is plausible that μ varied across the chromosomes, and that the speciation times of T_HC and T_HCG were unique across the chromosomes.

Fig. 2.—

Plots and a regression line between τ_HC and τ_HCG for each chromosome: τ_HC and τ_HCG from the original sample (A), τ_HC from the original sample and τ_HCG from the sample 2 (B), and τ_HC from the sample 2 and τ_HCG from the original sample (C). Diamonds represent autosomes, and an a cross, a triangle, or a square represents an X chromosome, coding region, or 4-fold degenerate sites at the third codon positions, respectively. The regression line was calculated for autosomes and X chromosome and shown with its formula and the square of its correlation coefficient.

In addition to τ and θ, variation of mutation rates across lineages was simultaneously estimated by calculating the proportion of the mutation rate in a lineage to that in the human lineage (μ_H) through the MCMC procedure (table 2 and supplementary table S2, Supplementary Material online). Though both autosomes and X chromosome showed the slowdown during the course of the human evolution, the degree of the slowdown in X chromosome was higher than that in autosomes.

Table 2.

Estimated Relative Ratios of the Mutation Rates to μ_H

Relative Ratio to μH	μH	μC	μG	μO	μHC	μHCG	μHCGO
Whole genome	1	1.004	1.034	1.091	1.005	1.025	1.091
X chromosome	1	0.9965	1.073	1.159	1.001	1.070	1.159

Estimation of Speciation Times and Ancestral Population Sizes

Assuming that μ varies across lineages and across chromosomes based on the result described earlier, we estimated τ and θ based on the blocks sampled from the whole genome alignments of human and three great apes. We collected 100 bp alignment blocks separated by ≥5 kb intervals. Similar to studies using whole or nearly whole-genome sequences (Yang 2010; Hobolth et al. 2011; Scally et al. 2012), the τ values estimated in our analysis were smaller than those found in previous studies involving smaller samples (table 1) (Takahata et al. 1995; Yang 2002; Osada and Wu 2005).

We estimated speciation times using the mutation rate from a recent estimation based on the number of de novo mutations per generation (Lynch 2010; Roach et al. 2010; Conrad et al. 2011), which was approximately one-half of the mutation rate previously estimated (Nachman and Crowell 2000). According to Nachman and Crowell (2000), the rate was calculated based on the d = 2μT + 4μgN, where d represents the nucleotide difference between the species at a local region. For the estimation of μ, they assumed T = 5 Ma and N = 10,000, both of which were smaller than those widely thought recently (Roach et al. 2010). This would lead to the estimation of large value of μ (Roach et al. 2010). Based on de novo mutations, we set the mutation rate, excluding CpG sites, in the human lineage (μ_H) to be from 0.44 × 10⁻⁹ to 0.56 × 10⁻⁹ per site per year, assuming the average generation time at 20 years (see Materials and Methods). Taking into account the variability of the mutation rates across the lineages (table 2), the value of T_HC was calculated at 5.9–7.6 Ma, T_HCG at 7.6–9.7 Ma, and T_HCGO at 15–19 Ma (table 3). It should be noted that these estimated speciation times were consistent with those from the fossil records (Carroll 2003, see Discussion).

Based on the θ values, we also estimated the effective population sizes in the ancestral lineages. The population sizes of N_HC, N_HCG, and N_HCGO were estimated to be 59,300–75,600, 51,400–66,000, and 159,000–203,000, respectively. In addition, the ancestral population sizes of the X chromosome were estimated to be 34,300–43,800 for N_HC(X), 38,500–49,200 for N_HCG(X), and 141,000–179,800 for N_HCGO(X) (table 3). Considering the CI, all of the estimates of the ancestral population sizes for the X chromosome are roughly three-fourths of those for autosomes, as expected.

Discussion

To estimate accurate speciation times and ancestral population sizes using the MCMC framework, we conducted a systematic simulation about finding optimum method of sampling genomic regions that have single, independent genealogy. According to the simulation results, we inferred the demographic history of human and great apes based on whole-genome orthologous alignments of the human, chimpanzee, gorilla, and orangutan sequences. Finally, we obtained conclusive speciation times among human and great apes at the whole genome level and revealed that human–chimpanzee speciation was a single event.

In this study, we showed the importance of using recombination-free alignments to estimate precise τ and θ. Burgess and Yang (2008) stated that the length of loci has little influence on the estimation of τ and θ for alignments of hominids and Old World monkeys. However, our simulation targeting hominid alignments indicated that using alignment block of ≤100 bp was favorable for the estimation, but that block of ≥500 bp may result in poor estimations (fig. 1). This discrepancy is clearly caused by the fact that the alignment blocks with recombination events were frequently observed in the ≥500 bp dataset. The reason for Burgess and Yang’s observation is that they did not compare their estimated parameters to true values because the true values from real genome data are unknown (Burgess and Yang 2008). The greater the number of recombination events in alignment block is, the narrower the distribution of the evolutionary distance (d) of loci will centralize around the average. This leads to large τ and small θ estimates. Therefore, the appropriate size of loci should be used to infer τ and θ precisely. On the other hand, lengths of the intervals between blocks ranging from 500 bp to 5 kb had moderate impact on the estimation of τ and θ (fig. 1). Thus, it may be reasonable to choose a shorter interval between blocks and to collect a large number of blocks to reduce the variances of the parameters when the sequence information from genomes is limited. It is noteworthy that the appropriate size of alignment blocks and intervals does not rely on the proportion of the two different recombination rates. In summary, our simulation is useful for obtaining the optimal conditions for the sampling of genome alignments. It should be, however, noted that making inferences under preferable conditions in a simulation is not always practical for obtaining inferences using actual data. We failed to estimate τ and θ when using 50-bp alignment blocks and, instead, estimated them with 100 bp alignment blocks. One of the reasons of this inexpedience can be the broadness of the likelihood surface contour with small block size. The simple two-species maximum-likelihood analysis based on the simulation data indicated that if the alignment blocks are small, the likelihood surface contour plot becomes broad (supplementary fig. S3, Supplementary Material online). In such a case, furthermore, the innermost area of the plot can become separated into two or more parts (supplementary figs. S3A and B, Supplementary Material online), which can lead to the convergence in the suboptimal condition. It is noted that τ and θ with the 100 bp blocks were comparable with those with the 200 bp blocks (supplementary table S1, Supplementary Material online), suggesting that the inference with the 100 bp blocks were not in the convergence in the suboptimal condition which might occur with 100 bp in the simulation dataset (supplementary fig. S3B, Supplementary Material online).

We found that the variability of τ among the chromosomes can be explained solely by mutation rates, thus indicating a single speciation time between human and chimpanzee. This finding is inconsistent with Patterson’s conclusion (Patterson et al. 2006), but consistent with the results of follow-up analyses performed using Patterson et al.’s data (Innan and Watanabe 2006; Yamamichi et al. 2011). It is well known that the difference in mutation rates between autosomes and the X chromosome is due to the difference in the duration time in males, where most point mutations are generated in mammals. In contrast, the cause of the variation in mutation rates across autosomes remains unclear, though such variation is clearly observed between the human and chimpanzee genomes (Hodgkinson and Eyre-Walker 2011). We did not find statistically significant correlations between mutation rates and genomic characteristics such as GC contents, CpG proportions, chromosomal sizes, SNP densities, or recombination densities in the large genomic regions constituted by autosomes, implying that other mechanisms underlie the causes of chromosome specific mutation rates. On the other hand, the comparative genomics across the chromosomes in rodent genomes has revealed that large-scale genomic characteristics such as the degree of chromosomal rearrangements and replication time correlate to the variation in mutation rates across the chromosomes (Pink et al. 2009; Pink and Hurst 2010). Thus, to clarify the causes of chromosome-specific mutation rates in the human lineage, it would be required to examine the relationships between the mutation rates and the structural characteristics of chromosomes at large scale rather than the sequences themselves.

We then evaluated the possibility of complex speciation using a specific region such as coding sequences. Osada and Wu (2005) indicated that the coding regions in human-chimpanzee ancestors had experienced multiple genetic changes during the speciation history of these species. This result should be carefully interpreted, because these authors used a full-length cDNA as a single locus. A full-length cDNA can be mapped in segments by exons in the genome, and thus, a full-length cDNA can have more than one genealogy. Therefore, we attempted to perform speciation time estimations specifically using coding regions by selecting 100 bp blocks with intervals of ≥5 kb. In this analysis, we used the well-annotated coding regions that were characterized as H-InvDB category I (Imanishi et al. 2004). Using these alignments, we obtained τ_HCG and τ_HC values of 0.00249 and 0.00156, respectively (table 1). Although both of these values are lower than those from the whole-genome analyses, these values are quite close to the regression line between τ_HCG and τ_HC (fig. 2), suggesting that speciation time based on the coding regions is equivalent to that based on the whole genome analysis. From these 100-bp blocks of coding regions, we extracted 4-fold degenerate (FFD) sites at the third codon positions, which are likely under neutral evolution. The values of τ obtained from these data were also plotted very close to that regression line, consistent with the whole coding sequence analysis. Although the estimation is rough, N_HC(FFD) was only 1.1 times larger than the N_HC(WG), where N_HC(FFD) and N_HC(WG) were the N_HC of FFD sites at the third codon positions and the whole genomes, respectively. Thus, it is suggested that N_HC(CDS) was overestimated due to non-neutral evolution in coding regions, where N_HC(CDS) is N_HC of coding regions. It should be noted that our results did not completely reject the possibility of complex speciation processes between human and chimpanzee. It may be possible that introgressions occurred soon after the major speciation event, which may not be distinguishable from the stochastic variation of the distribution of coalescence times in the ancestral population.

The τ and θ values estimated in our analysis are slightly different from those reported by the gorilla genome consortium (Scally et al. 2012) based on the most recent whole-genome analysis under the HMM framework. The main reason for this difference is the alignments used in the two studies. We chose unambiguously aligned regions, removing the ends of the alignments, and excluded CpG sites from the alignments. In the human and chimpanzee genomes, a cytosine at a CpG dinucleotide site can mutate to thymine 15 times as frequently as that at other sites due to oxidative deamination of methylated cytosines at CpG sites (Elango et al. 2008). Therefore, the CpG site removal was to approximate the mode of nucleotide substitutions in the alignment to the simple Jukes-Cantor model (Jukes and Cantor 1969), which both we and Rannala and Yang applied. Exclusion of CpG sites from aligned sites also decreases the evolutionary distances (d), which correspond to θ + 2τ.

If the variation in τ and θ between us and Scally et al. (2012) are explained based on the difference in the mutation rates excluding or including CpG sites, the θs and τs ratios would be constant between these two analyses. However, the τ_HCG/τ_HC ratio was different between the two analyses: τ_HCG/τ_HC = 1.3 in our analysis and τ_HCG/τ_HC = 1.6 in Scally et al. (2012). Thus, the differences in τ can be explained by the other factors than CpG sites. One of such factors may be the correction of the heterogeneity of mutation rates across lineages. The analysis by Scally et al. (2012) corrected the variation in mutation rates after inference of τ and θ, simply by multiplying the proportion of μ to that of the human lineage (Scally et al. 2012). In contrast, we inferred the coalescence time of each locus using a model with variable mutation rates across the lineages. In summary, CpG-sites were excluded for fitting the sequence data to the evolutionary model that we used, heterogeneity of mutation rates among lineages was assumed in each locus for considering the variation in mutation rates in hominids, and four species were applied for increasing the inner-node speciation. Thus, we looked carefully at the condition for inferring the demographic history of human and the great apes precisely. However, these conditions do not seem to properly be dealt with in the analysis by Scally et al. (2012).

The speciation times observed in our analysis are also supported by fossil records of the Homininae (fig. 3). Nakalipithecus and Chororapithecus, which lived 9.8–9.9 and 10–10.5 Ma, respectively, are morphologically related to extant hominines and suggest that the origin of hominines was in Africa (Kunimatsu et al. 2007; Suwa et al. 2007). The estimated speciation time T_HCG (7.6–9.7 Ma) suggests that Nakalipithecus and Chororapithecus may be related to the stem of the Homininae. The speciation time between human and chimpanzee was estimated to be 5.9–7.6 Ma in our analysis, which is consistent with both the most recent findings obtained using a genomic approach (Scally et al. 2012) and the traditional view from fossil records (Carroll 2003). Orrorin (∼6 Ma) (Wood 2010) and Sahelanthropus (∼7 Ma) (Brunet et al. 2005) both lived around the time of human–chimpanzee speciation. In contrast, Ardipithecus was considered to emerge after this speciation, with Ar. kadabba found 5.2–5.8 Ma (Haile-Selassie 2001) and Ar. ramidus 4.4 Ma (White et al. 1994).

Fig. 3.—

Relationship between the estimated speciation times and the fossil records of ancestral great apes (Sawada et al. 1998; Ishida et al. 1999; Gabunia et al. 2001; Haile-Selassie 2001; Brunet et al. 2005; Kunimatsu et al. 2007; Suwa et al. 2007; Wood 2010), for details see Discussion. Dotted lines represent the upper and lower bounds of the 95th percentiles of estimated speciation times (orange for THC and purple for THCG) (table 3) .

Conclusion

Based on our analysis, we propose a new approach for data collection from whole-genome alignments to infer demographic parameters. Simulation of coalescence is helpful for determining the appropriate size of alignment blocks and the interval length between the blocks. This approach can be applied for closely related species in various lineages. Although the HMM framework can cover entire genomic regions by scanning alignments with small windows, the MCMC framework developed by Rannala and Yang uses a fraction of whole-genome alignments to avoid the effect of recombination. At this time, however, only the MCMC methods are capable of addressing three or more species simultaneously. When the genomic sequences of several closely related species are available, increasing the number of estimated points (speciation times and ancestral population sizes) would lead to more accurate estimations. Our method for inference of τ and θ, assuming heterogeneity of mutation rates across lineages, may also be preferable when addressing multiple species with different mutation rates. Although this approach assuming heterogeneity of mutation rates across both lineages and blocks is still under development for practical use, it could contribute to reconstructing more precise demographic histories of related species, including hominids.

Supplementary Material

Supplementary figures S1–S3 and tables S1 and S2 are available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).