A generalised model for individualising a treatment recommendation based on group-level evidence from randomised clinical trials

Abstract

Objectives

Randomised controlled trials report group-level treatment effects. However, an individual patient confronting a treatment decision needs to know whether that person's expected treatment benefit will exceed the expected treatment harm. We describe a flexible model for individualising a treatment decision. It individualises group-level results from randomised trials using clinical prediction guides.

Methods

We constructed models that estimate the size of individualised absolute risk reduction (ARR) for the target outcome that is required to offset individualised absolute risk increase (ARI) for the treatment harm. Inputs to the model include estimates for the individualised predicted absolute treatment benefit and harm, and the relative value assigned by the patient to harm/benefit. A decision rule recommends treatment when the predicted benefit exceeds the predicted harm, value-adjusted. We also derived expressions for the maximum treatment harm, or the maximum relative value for harm/benefit, above which treatment would not be recommended.

Results

For the simpler model, including one kind of benefit and one kind of harm, the individualised ARR required to justify treatment was expressed as required ARR_target(i)=ARI_harm(i) × RV_{harm/target(i)}. A complex model was also developed, applicable to treatments causing multiple kinds of benefits and/or harms. We demonstrated the applicability of the models to treatments tested in superiority trials (either placebo or active control, either fixed harm or variable harm) and non-inferiority trials.

Conclusions

Individualised treatment recommendations can be derived using a model that applies clinical prediction guides to the results of randomised trials in order to identify which individual patients are likely to derive a clinically important benefit from the treatment. The resulting individualised prediction-based recommendations require validation by comparison with strategies of treat all or treat none.

Article summary.

Article focus

• Randomised controlled trials provide relative group-level estimates of the beneficial and harmful effects of a treatment. However, the absolute size of those effects may vary across individuals according to their baseline risk.

• Models have been described previously to individualise results of superiority placebo-control trials in the case of a variable benefit/fixed harm scenario.

Key messages

• We provide a generalised model to individualise treatment recommendations. We start from the definition of the Clinically Important Difference: the size of treatment benefit that offsets the treatment harm, after adjusting for the patient's values.

• The model applies to a variable benefit and a fixed or variable harm, and to superiority (placebo and active control) and non-inferiority trials. It can accommodate more than one kind of benefit and/or harm.

• Clinical Prediction Guides are used to individualise the predicted risk of the target event and of the harm at trial entry.

Strengths and limitations of this study

• Strengths: the model adopts an individual perspective and is flexible and timely. It allows the calculation of an individual's maximum predicted absolute risk increase for the treatment harm, or the maximum relative value for harm/target, that would overturn the treatment decision.

• Limitations: economic costs are not modelled; uncertainty will exist for some quantities entering the model; the model awaits empirical validation.

Introduction

For questions of treatment and prevention, randomised controlled trials (RCTs) provide the most valid evidence concerning the benefits and, often, the harms of the intervention. However, RCTs typically report only group-level results, whereas treatment effects may depend importantly on characteristics of individual patients.

A clinical prediction guide (CPG)^1–3 uses patient-specific risk data to predict the level of risk for a clinical outcome of interest for an individual patient. CPGs applied to participants in clinical trials can predict the individual patient's level of risk at trial entry (baseline risk (BLR)) for the target outcome at which the treatment is directed, and also for harm caused by the treatment. If the relative risk reduction for the target outcome (or relative risk increase for the harm) is constant across the range of BLR, then the absolute treatment effects can be predicted in individual patients: absolute risk reduction (ARR) for the target outcome (the treatment benefit) and absolute risk increase (ARI) for the treatment harm.

But what size of ARR for the target benefit is sufficiently large to justify acceptance of a treatment that carries with it the potential for benefit and harm? That depends on the frequency of the harm caused by treatment, and the relative importance of the harm compared to the benefit. The size of treatment benefit that is large enough to offset the treatment harm is the patient's clinically important difference (CID).

The concept of CID has been incorporated in several prior formulations: the threshold ARR (inverted, the threshold number needed to treat⁴), the threshold for agreeing with treatment,⁵ the decision threshold (inverted, the number willing to treat (NWT)).⁶ Each of these constructs embodies the concept that for treatment to be justified, the predicted treatment benefit must exceed the predicted harm for that individual.

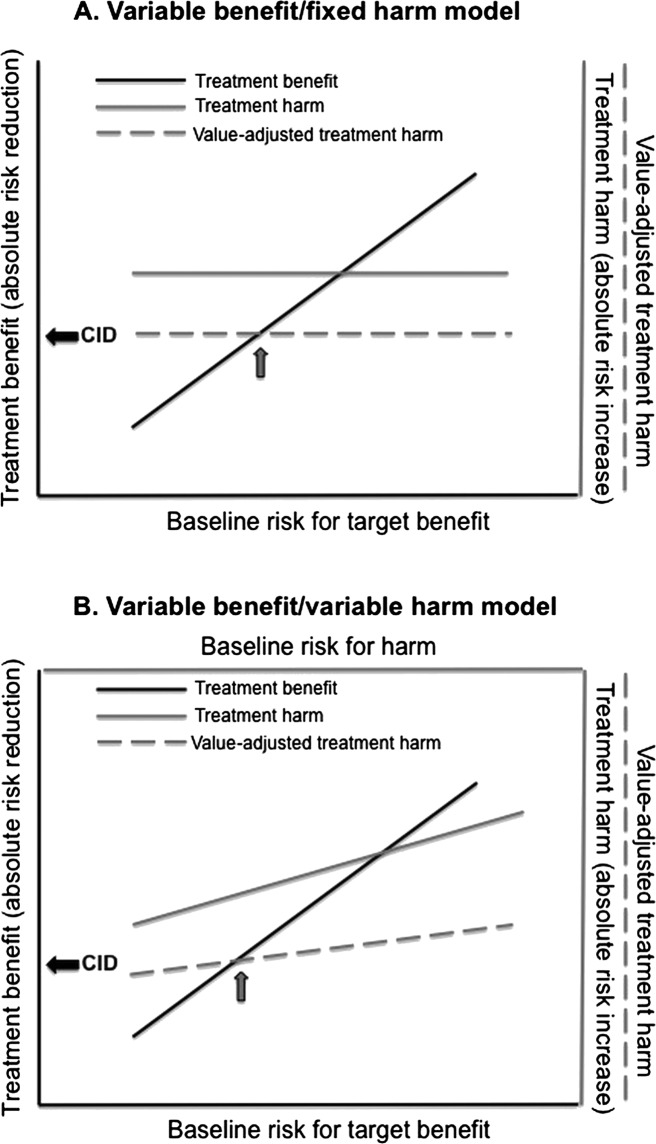
Absolute treatment benefits vary directly with BLR for the target benefit: for an effective treatment, the higher the BLR, the greater the predicted absolute benefit. When modelling absolute treatment effects across individuals, the assumed model usually has incorporated a variable benefit, but a fixed harm.^4–7 However, the absolute size of treatment harms may also vary across individuals, in which case a variable benefit/variable harm model would apply. The two models are illustrated in figure 1.

Figure 1.

Models for individualising treatment. Variable benefit/fixed harm (A) and variable benefit/variable harm (B) models are shown. In each model, treatment benefit, modelled as absolute risk reduction for the target event, varies directly with baseline risk for the target event. Treatment harm is modelled as the absolute risk increase for the harm of treatment. Harm is then value-adjusted based on a relative value (RV) assigned to the treatment harm as compared with the target event prevented. With a fixed harm (A), the absolute risk increase for the harm of treatment is constant. With a variable harm (B), the absolute risk increase for the harm of treatment varies with the baseline risk for the harm. As indicated by the arrow in each panel, the point at which the value-adjusted treatment harm intersects the treatment benefit defines the clinically important difference (CID) for the treatment benefit.

The objectives of this report were: (1) to derive an expression for CID that is flexible and applicable to either fixed or variable treatment harm and (2) to describe a generalised model for deriving a treatment recommendation based on CID, using group-level estimates of treatment effects provided by RCTs and CPGs for prediction of individualised absolute treatment benefit and harm.

Methods

We define CID as the size of benefit from the treatment that offsets the harm of the treatment. We define a benefit as the reduction of the occurrence of the target outcome, expressed as the negative outcome, for example, death, rather than the positive outcome, for example, survival. When the benefit is defined categorically, CID is the required ARR for the target outcome (ARR_target) obtained with the treatment compared with the control. The control can be no treatment (or placebo) or an active control. The model contains parameters for the predicted individualised treatment benefit, the predicted individualised treatment harm and the patient's values. The model accommodates more than one kind of benefit and more than one kind of harm. No economic cost, either direct or indirect, is included in the model.

When applied to individualise a treatment recommendation, the model provides an individualised required ARR_target. A decision rule recommends the treatment when the patient’s predicted ARR_target is greater than her required ARR_target.

Data requirements

Table 1 summarises the required quantities for entry into the model, distinguishing between group-level measures and individual-level predictions.

Table 1.

Quantities required for a generalised model for individualising treatment recommendations

Element	Group-level measures		Individualised predictions
	Quantity	Measured as	Quantity	Predicted as
Benefits	RRRtrial	1−RRtrial or 1−HRtrial	ARRi	RRRtrial×BLRi for benefit*
Harms fixed variable	ARItrial RRItrial	Risktreated−control RRtrial−1 or HRtrial−1	ARIi	ARItrial used as ARIi RRItrial×BLRi for harm†
Values	RV	Vharm/Vbenefit	RVi	Provide a range of RVs centred on typical group-level RV‡

*Estimate BLR_i for benefit using CPG for individualised prediction of outcome comprising the benefit.

†Estimate BLR_i for a variable harm using CPG for individualised prediction of outcome comprising the harm.

‡Estimate typical RV from formal utility-based analyses, patient groups or expert opinion.

ARI_trial, absolute risk increase for a fixed harm; ARR_i, ARI_i, BLR_i, RV_i, individualised predicted estimates; BLR, baseline risk (risk in control group); CPG, clinical prediction guide; HR, hazard ratio; RR, relative risk; RRI_trial, relative risk increase for a variable harm, from RCT(s) or best evidence; RRR_trial, relative risk reduction observed in RCT(s); RV, relative value.

Group-level quantities

Most of the shown group-level quantities are used to generate individualised estimates. For treatment benefits, the required group-level measure is the relative risk reduction. The data source can be a meta-analysis of large RCTs or a single large RCT. The required group-level quantities for the harms depend on the type of harm, fixed or variable. For fixed harms, we use a group-level absolute quantity, the ARI (ARI_harm). For variable harms, we use a group-level relative quantity, the relative risk increase (RRI_harm). Whether fixed or variable, the estimate of the treatment effect for harms comes from a meta-analysis of large RCTs, a single large RCT or best available observational evidence. Values are entered as the relative value (RV) of the harm compared with the target benefit. A group-level RV_harm/target can be derived from formal utility-based analyses, patient groups or expert opinion.

Individual-level quantities

The individualised treatment benefit is expressed as ARR (ARR_target(i)). The individualised treatment harm is expressed as ARI (ARI_harm(i)). For BLR, we mean the risk in the reference group (the control arm in the trial), whether it is represented by patients on no treatment or placebo or by patients on an existing treatment. Table 2 summarises the role of CPGs in individualising predicted treatment benefits and harms.

Table 2.

Clinical Prediction Guides (CPG) for individualising treatment effects

Type of trial	Type of control	CPG to predict control risk for target event: population	CPG to predict control risk for harm: population
Superiority trial	Placebo or no treatment	CPG developed on patients on placebo or no treatment	Fixed harm: CPG not needed
			Variable harm: CPG developed on patients on placebo or no treatment*
	Active control (EET)	CPG developed on patients on EET†	Fixed harm: CPG not needed
			Variable harm: CPG developed on patients on EET
Non-inferiority trial	Active control (EET)	CPG developed on patients on EET†	Fixed harm: CPG not needed
			Variable harm: CPG developed on patients on EET

*If a validated CPG developed on treated patients is used (see worked example on warfarin), the individualised risk for the harm off treatment can be obtained by dividing the risk on treatment by the group-level relative risk for the harm with the treatment compared with placebo or no treatment.

†If a validated CPG developed on patients on placebo or no treatment is used, the individualised risk for the target event while on EET can be obtained by multiplying the risk off treatment by the group-level relative risk for the target event on EET compared with placebo or no treatment.

EET, established effective therapy.

• Benefits modelling: The model allows the predicted ARR_target(i) to increase for increasing BLRs for the target outcome (BLR_target(i)), according to the equation: predicted ARR_target(i)=RRR_target×BLR_target(i). The group-level RRR_target is assumed to be constant across different BLRs. The BLR_target(i) for the target benefit is estimable using a validated CPG.

• Harms modelling. In the case of a fixed harm, the group-level estimate (ARI_harm(trial)) is used for the predicted ARI_harm(i). No CPG is needed to predict an individualised harm. When the receipt of the treatment per se is modelled as a fixed harm (as with risk/discomfort), that harm is experienced by every treated patient, so the ARI_harm(trial) for the harm is constantly equal to 1.0 (100%). In the case of a variable harm across patients, the predicted ARI_harm(i) is calculated by multiplying the group-level RRI_harm by the individualised BLR for that harm (BLR_harm(i)). The group-level RRI_harm is assumed to be constant across different BLRs. The BLR_harm(i) can be estimated using a validated CPG.

• Values modelling. An individual RV (RV_{harm/target(i)}) assigned by the patient enters the model. We recognise that an RV_{harm/target(i)} may not be ascertained reliably. Therefore, we modelled a range of RVs centred on a group-level RV.

When more than one benefit and/or more than one harm is included, for each benefit and harm the specific ARR_i/ARI_i/RV_i is separately calculated or assigned as above.

Construction of models for individualising a treatment recommendation

We constructed two models: a simple model where there is one kind of treatment benefit and one kind of treatment harm; and a complex model where there is more than one kind of benefit and/or more than one kind of harm. In both cases, the model equation is solved for the required ARR_target(i) to offset the treatment harm(s), given the predicted ARI_harm(i) and RV_{harm/target(i)}. The same basic equation can then be used to calculate:

1. The maximum ARI_harm(i) above which treatment would not be justified, given the predicted ARR_target(i) and RV_{harm/target(i)}.

2. The maximum RV_{harm/target(i)} above which treatment would not be justified, given the predicted ARR_target(i) and ARI_harm(i).

Results

Algebraic solution to the model

We derived the following equations to describe the model (see Appendix for algebraic details).

Simple model: one kind of treatment benefit, one kind of treatment harm

Required ARR_target(i)

The required size of the ARR_target that offsets the treatment harm, value-adjusted, for the patient i can be calculated as (Appendix section 1, equations (1) and (2))

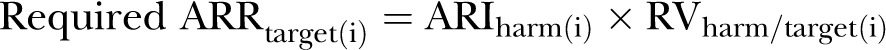(m1)

The equation includes the particular condition of a fixed harm when the ARI_trial can substitute for the ARI_i. When the treatment receipt is considered the harm, the ARI_trial is 1.0 and so the ARR_(target)i is directly predictable from the RV_{harm/target(i)} as

(m2)

Decision rule: In case of fixed harm and variable harm, the treatment would be justified for the patient i when

(d1)

Maximum ARI_harm(i) and maximum RV_{harm/target(i)}

The maximum ARI_harm(i) above which the treatment would not be justified for the patient i can be calculated as (Appendix equations (1) and (3))

(m3)

Decision rule: The treatment would not be justified for the patient i when

(d2)

where the predicted ARI_harm(i) can be fixed (=ARI_trial) or variable.

Similarly, the maximum RV_{harm/target(i)} above which the treatment would not be justified for the patient i can be calculated as (Appendix equations (1) and (4))

(m4)

Decision rule: The treatment would not be justified for the patient i when

(d3)

Complex model: multiple treatment benefits, multiple treatment harms

The model can be generalised to incorporate additional treatment benefits other than the reduction of the target outcome, and multiple harms, whether fixed or variable (Appendix section 2). A harm may have a fixed as well as a variable component. In that case, the fixed and variable components would be entered as separate harms, along with their separate RVs. The size of the ARR_target, which is required to offset the value-adjusted treatment harms and which accounts for other treatment benefits, is calculated for the patient i as (Appendix equations (5), (6) and (7))

(m5)

where k is the number of treatment harms, m is the total number of treatment benefits, and the benefit(2) to benefit(m) are the benefits other than the target benefit. Every RV_(i) is expressed as the value assigned to each outcome, prevented or caused by the treatment, compared with the value of the target benefit.

Decision rule: Similar to the case of only one benefit and one harm, the treatment would be justified for the patient i when

(d1)

The complex model can be used to predict the individualised maximum allowed ARI for a target harm and the maximum RV for the target benefit compared with a target harm, above which the treatment is not justified.

Applicability of the model

Theoretically, the model is applicable to every situation tackling the choice between two treatment strategies. Three examples are proposed to show the applicability of the model to individualised treatment recommendations: a superiority trial with a variable benefit/fixed harm scenario; a superiority trial with a variable benefit/variable harm scenario and the case of non-inferiority trials.

Superiority trial: variable benefit, fixed harm. Rosuvastatin for primary prevention of cardiovascular events

The Justification for the Use of Statins in Prevention (JUPITER) trial⁸ evaluated the effect of rosuvastatin versus placebo for reduction of cardiovascular events in apparently healthy men and women with low-density lipoprotein cholesterol levels <3.4 mmol/L and elevated high-sensitivity C reactive protein. The primary outcome was a composite of myocardial infarction, stroke, arterial revascularisation, hospitalisation for unstable angina or cardiovascular death. The group-level result showed a substantial relative benefit of rosuvastatin (HR 0.56, 95% CI 0.46 to 0.69). This is equivalent to an RRR_target of 0.44 (95% CI 0.31 to 0.54). Nevertheless, the individual's absolute benefit with rosuvastatin will vary according to her BLR (BLR_i.). Validated CPGs exist to predict the BLR for cardiovascular events. The Framingham risk score,⁹ for example, predicts the risk of cardiovascular events at 10 years combining risk factors such as age, gender, smoking, total and high-density lipoprotein cholesterol levels, systolic blood pressure and hypertension. Dorresteijn et al⁶ used the group-level quantities provided by the JUPITER study and CPGs, either existing^{9 10} or newly developed,⁶ to individualise the predicted BLR_i and absolute effect of rosuvastatin at 10 years (ARR_(target)i) among JUPITER's participants. They found an approximate 20-fold variation in the predicted BLR_(target)i. Thus, the predicted ARR_(target)i varied from about 1–20% at 10 years, with a slightly different patient stratification depending on the CPG used. Dorresteijn and colleagues then evaluated the application of these individualised predictions to recommend the treatment. They defined the ‘Number Willing to Treat (NWT)’ as the number of patients one is willing to treat in exchange for the prevention of one target outcome event. Its inverse ratio (1/NWT) was defined as the ‘decision threshold’ and is equivalent to the required ARR_(target)i defined for our model. They considered that the treatment receipt per se constituted the harm (fixed harm). Thus, the required ARR_(target)i (ie, 1/NWT) equalled the RV_{harm/target(i)} (m₂). They examined how the treatment recommendations varied across a range of hypothetical values for NWT.

Superiority trial: variable benefit, variable harm. Warfarin to prevent cardioembolic events in patients with atrial fibrillation

Six RCTs compared warfarin versus placebo/no treatment in patients with non-valvular atrial fibrillation to reduce the occurrence of stroke and systemic cardioembolism. Hart et al¹¹ meta-analysed those RCTs and found a pooled RRR for cardioembolic events (RRR_stroke) of 0.64—or 64%—(95% CI 0.49 to 0.74). On the other hand, warfarin was associated with a pooled RRI for major extracranial bleeding (RRI_bleed) of 1.3—or 130%—(95% CI 0.08 to 3.89; note: Hart et al¹¹ included the intracranial haemorrhages among the strokes in the efficacy analyses).

Several CPGs to predict the risk of stroke and bleeding have been developed and validated in patients with atrial fibrillation. Using the individual predictions for the BLR for stroke (BLR_stroke(i)) and for bleeding (BLR_bleed(i)), the absolute beneficial effect and also the absolute adverse effect with warfarin can be individualised as ARR_stroke(i)=RRR_stroke×BLR_stroke(i) and ARI_bleed(i)=RRI_bleed×BLR_bleed(i), respectively. As an example, for the prediction of the BLR_stroke(i), we adopted the CHADS₂ score developed on patients off anticoagulation.¹² For the prediction of the BLR_bleed(i), we adopted the HEMORR₂HAGES score.¹³ Since the HEMORR₂HAGES score was developed on patients on warfarin,¹³ the corresponding BLR_bleed(i) off warfarin was calculated by dividing the predicted risk on warfarin by 2.3, which is the reported relative risk for major bleeding for warfarin compared with placebo.¹¹ The results are shown in table 3. The predicted ARR_stroke(i) varied from 1.22% to 11.65%/year and the predicted ARI_bleed(i) varied from 1.07% to 6.95%/year. Comparing the individualised predictions for the benefit and the harm, value-adjusted, we then obtained individualised treatment recommendations for warfarin. A range of plausible values of the RV_bleed/stroke was examined.

Table 3.

Framework for application of prognostic risk scores for variable treatment benefit, variable treatment harm to particularise a treatment recommendation

				Risk for stroke (CHADS2)
				Score	0	1	2	3	4	5	6
				Predicted BLRstroke (%/year)	1.9	2.8	4.0	5.9	8.5	12.5	18.2
Risk for bleed (HEMORR2HAGES)				Predicted ARRstroke (95% CI) %/year*	1.22 (0.93 to 1.41)	1.79 (1.37 to 2.07)	2.56 (1.96 to 2.96)	3.78 (2.89 to 4.37)	5.44 (4.17 to 6.29)	8.00 (6.13 to 9.25)	11.65 (8.92 to 13.5)
Score	Predicted BLRbleed, %/year warfarin		Predicted ARIbleed (95% CI) %/year†	Required ARRstroke (95% CI) @ RVbleed/stroke 0.6 %/year	Tentative treatment recommendation‡
	Yes	No
0	1.9	0.83	1.07 (0.07 to 3.23)	0.64 (0.04 to 1.94)	T	T	T	T	T	T	T
1	2.5	1.09	1.41 (0.09 to 4.24)	0.85 (0.05 to 2.54)	T	T	T	T	T	T	T
2	5.3	2.30	3.00 (0.18 to 8.95)	1.80 (0.11 to 5.37)	DT	CC	T	T	T	T	T
3	8.4	3.65	4.75 (0.29 to 14.2)	2.85 (0.17 to 8.52)	DT	DT	DT	T	T	T	T
4	10.4	4.52	5.88 (0.36 to 17.6)	3.53 (0.22 to 10.6)	DT	DT	DT	T	T	T	T
≥ 5	12.3	5.35	6.95 (0.43 to 20.8)	4.17 (0.26 to 12.5)	DT	DT	DT	DT	T	T	T

Example: Warfarin versus placebo for stroke reduction in patients with atrial fibrillation.

*Predicted ARR_stroke and 95% CI if RRR_stroke is 0.64 (0.49 to 0.74) using warfarin.¹¹

†Predicted ARI_bleed and 95% CI if RRI_bleed is 1.30 (0.08 to 3.89) using warfarin.¹¹

‡Tentative treatment recommendations are based on predicted point estimates for ARR_stroke and ARI_bleed. Uncertainties in these estimates, indicated by 95% CIs above, must also be considered before actual treatment recommendations can be derived.

ARI, absolute risk increase; ARR, absolute risk reduction; BLR, baseline risk; CC, close all; DT, do not treat; RV, relative value; T, treat.

Required ARR_stroke(i) to justify warfarin

To justify warfarin, the predicted ARR_stroke(i) should be greater than the required ARR_stroke(i) (d₁), that is, greater than ARI_bleed(i)×RV_{bleed/stroke(i)} (m₁). Table 3 summarises the results of the application of the model to individualise warfarin recommendation in a hypothetical patient population, according to the coclassification of patients based on the CHADS₂ and HEMORR₂HAGES scores. We arbitrarily chose a group-level RV for a bleed/stroke of 0.6, an RV calculated from a lost-utility analysis over a 10-year time frame.⁴ Table 3 shows the resulting treatment decisions for each of the 42 cells formed according to the CHADS₂ and HEMORR₂HAGES scores.

As a base case, the table was obtained using for RRR_stroke the point estimate (0.64).¹¹ Since a treatment is accepted as superior compared with placebo/no treatment only when the upper bound of the 95% CI for the relative risk for the target outcome is below 1, we repeated the example using for RRR_stroke a value of 0.49 (corresponding to the upper bound for RR_stroke 0.51). In that case, the predicted ARR_stroke(i) is reduced and slightly fewer patients would be recommended for treatment. For example, a CHADS₂ 3 and HEMORR₂HAGES 4 patient would now not be recommended for warfarin treatment (results not shown). We also repeated the example, using for RRI_bleed a value of 3.89, corresponding to the upper bound of the 95% CI for RRI_bleed. Now, considerably fewer patients would be recommended for treatment (data not shown). The major differences in who would be recommended for treatment arise primarily from the great uncertainty in the estimate for ARI_bleed in this example. We caution that table 3 is presented only as a framework for presenting particularised treatment recommendations in a variable benefit/variable harm scenario. The recommendations shown there are based only on point estimates, and should not be accepted without taking into account the uncertainties in the estimates for ARR_stroke and ARI_bleed in deriving the treatment recommendations.

Maximum ARI_bleed(i) above which warfarin would not be justified

Figure 2 shows how the maximum ARI_bleed(i) (m₃) varies according to the different CHADS₂ scores and different values of RV_{bleed/stroke(i)} centred on a group-level RV_bleed/stroke of 0.6.

Figure 2.

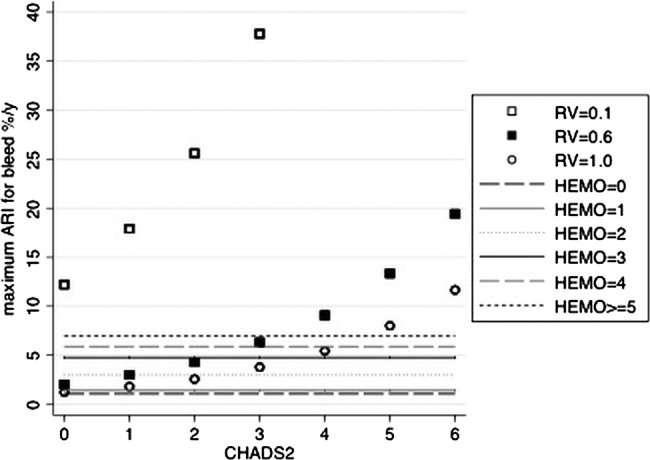
Maximum ARI_bleed for treatment to be justified, by CHADS₂ score and relative value_stroke/bleed. The scatter plot shows the maximum ARI_bleed (%/year) above which warfarin would not be justified, according to the CHADS₂ score and different RV_bleed/stroke. The horizontal lines depict the predicted ARI_bleed with warfarin for each HEMORR₂HAGES score. As examples: at RV_bleed/stroke 0.6, we would treat CHADS₂ score 0 patients only if their predicted ARI_bleed given warfarin were less than 2%/year. Accordingly, we would treat HEMORR₂HAGES score 0–1 patients because their predicted ARI_bleed (1.1, 1.4%/year (table 3)) is less than 2%/year. We would not treat HEMORR₂HAGES score ≥2 patients because their predicted ARI_bleed (3–7%/year (table 3)) is greater than 2%/year. Again at RV_bleed/stroke 0.6, we would treat CHADS₂ score 2 patients only if their predicted ARI_bleed were less than 4.3%/year. Thus, we would treat HEMORR₂HAGES score 0–2 patients because their predicted ARI_bleed (1.1–3%/year (table 3)) is less than 4.3%/year. We would not treat HEMORR₂HAGES ≥3 patients because their predicted ARI_bleed (4.8–7%/year (table 3)) is greater than 4.3%/year. At the RV_bleed/stroke set higher or lower than 0.6, fewer patients or more patients, respectively, would be recommended for treatment according to the model. ARI, absolute risk increase; RV, relative value.

Maximum RV_{bleed/stroke(i)} above which warfarin would not be justified

Similarly, given the CHADS₂ and the HEMORR₂HAGES scores of the patient, the model can calculate which is the maximum RV_{bleed/stroke(i)} (m₄) such that if the patient assigns an RV_bleed/stroke higher than this maximum, warfarin would not be justified. The variation of the maximum RV_{bleed/stroke(i)} according to the different CHADS₂ and HEMORR₂HAGES scores is depicted in figure 3.

Figure 3.

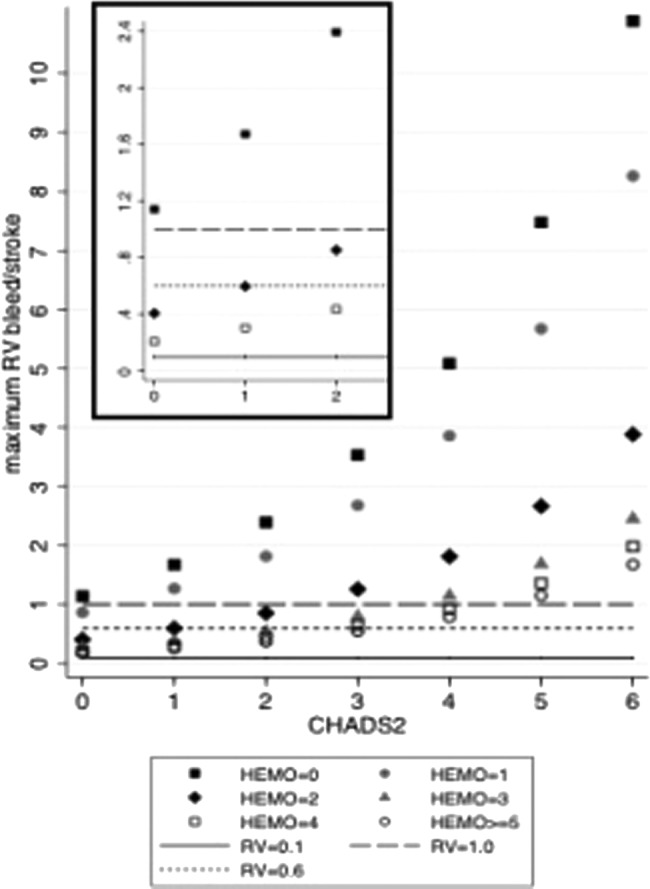
Maximum RV_bleed/stroke for treatment to be justified, by CHADS₂ score and HEMORR₂HAGES score. The scatter plot shows the variation of the maximum RV_bleed/stroke according to CHADS₂ and HEMORR₂HAGES (abbreviated as HEMO) scores. The horizontal lines depict three illustrative maximum relative values. The model predicts the maximum RV_bleed/stroke to vary over a range between 0.1 (ie, a value assigned to a stroke 10 times higher than that assigned to a major bleeding) and about 10 (ie, a value assigned to a major bleeding 10 times higher than that assigned to a stroke). As examples, the insert zooms in the results for patients with a CHADS₂ score of 0–2 and HEMO scores of 0, 2 and 4. Among patients with a CHADS₂ score of 0, warfarin would be recommended for HEMO 0 patients if their RV_bleed/stroke were <1.1; for HEMO 2 patients, if their RV_bleed/stroke were <0.4; for HEMO 4 patients if their RV_bleed/stroke were <0.2. For patients with a CHADS₂ score of 2, warfarin would be recommended for HEMO 0 patients if their RV_bleed/stroke were <2.3; for HEMO 2 patients if their RV_bleed/stroke were <0.8; for HEMO 4 patients if their RV_bleed/stroke were <0.4. RV, relative value.

Individualising recommendations for a non-inferior treatment

Application of model to non-inferiority trials

The objective of a non-inferiority trial is to show that the effect of a new treatment on a target outcome is not worse, compared with an established effective treatment (EET), by more than a prespecified margin. This ‘non-inferiority margin’ is the maximum loss of efficacy that is considered acceptable in exchange for a hypothesised reduction in harm, value-adjusted. At the design phase, the non-inferiority margin is expressed as either an absolute or relative increase in the target event rate. A group-level RV_harm/benefit is at least implicit when setting the specified margin. When interpreting the results of a non-inferiority trial at the group level, the CI for the observed treatment effect on the target outcome is compared with the non-inferiority margin. If the bound of the CI that reflects the maximal estimate for inferiority is less than the margin (does not ‘cover’ the margin), then it is concluded that the new treatment is non-inferior to EET.

In non-inferiority trials, the CID for a patient can be expressed as the required reduction of the harm which exactly compensates for the allowed increase of the target outcome, value-adjusted. Thus, for application to non-inferiority trials, the equation m₁ can be rewritten as:

Individualisation of the results of a trial demonstrating group-level non-inferiority

We individualise group-level results by using CPGs, as applicable (table 2), to predict BLR_(i) and thereby absolute treatment effects on the target outcome (ARI_target(i)) and the treatment harm (ARR_harm(i)). ARI_target(i) is derived as BLR_target(i) × RRI_trial. ARR_harm(i) is derived as BLR_harm(i) × RRR_trial. We value-adjust the treatment harm for the RV_{harm/target(i)}. We then compare the individualised predictions of treatment effects on the target outcome and on the harm to derive individualised treatment recommendations. A recommendation to treat with the non-inferior therapy would result when the predicted reduction in harm, value-adjusted, exceeds the predicted loss of efficacy, that is, when ARR_harm(i) × RV_{harm/target(i)} > ARI_target(i) (or, holding the same terminology as for superiority trials, when predicted ARR_harm(i) > required ARR_harm(i)).

To examine the worst case, we then repeat the comparison of reduction in harm and loss of efficacy by calculating ARI_target(i) using not the point estimate for RRI_trial but the bound of its CI that reflects the maximal inferiority of the new treatment.

Discussion

We presented an extension of the previously described models to individualise treatment recommendations, based on the use of CPGs to predict individual-level treatment effects, adjusted for the relative importance assigned by the patient to different outcomes.

Strengths

The adoption of an individual-level perspective represents the fundamental feature of the model. The individualising process requires the conversion of group-level into individual-level treatment effects and the use of the patient's values.¹⁴ The model presented here is more flexible than models for individualising treatment recommendations described previously.^{4 5} Either a fixed or a variable harm is accommodated in our model. LaHaye et al¹⁵ developed a decision aid specifically designed to individualise antithrombotic therapy in patients with atrial fibrillation that included a variable benefit/variable harm scenario and also the patient's RV_bleed/stroke. However, they did not explicitly conceptualise and generalise the underlying model. We showed the adaptability of our model to treatments causing multiple kinds of benefits and harms, as well as to non-inferiority trials. The concepts of the maximum ARI_harm and maximum RV_harm/benefit that would overturn the clinical decision had not been developed previously. The model is timely, given the increasing number of very large RCTs providing precise group-level estimates of treatment harms as well as treatment benefits, and the recent rapid rise in validated CPGs, catalogued and searchable in EvidenceUpdates,³ which makes the individualisation of those group-level quantities more feasible.

Limitations

In our model, we did not include economic costs, either direct or indirect. Like clinical benefits and harms, economic costs can be fixed or variable across patients. This raises the question of whether a group-level cost-effectiveness analysis of a treatment can be individualised.¹⁶ A step in that direction is to apply prognostic models to particularise group-level information on cost-effectiveness according to the predicted risk and patient subgroup.¹⁷ Our model provides a method for individualising the consequences of treatment. However, analyses of incremental cost-effectiveness or cost-utility at the individual level are constrained at present by the lack of reliable individualised data on the incremental direct and indirect costs of treatment.

Use and appropriateness of CPGs for individualising recommendations

We generically explained why, how and when model building requires the use of CPGs. CPGs are developed for different purposes. A particular application of a CPG is to individualise risk predictions in the control group of an RCT. There are some desirable features of a CPG for this specific application. In box 1, we provide an aid to guide the user in the search for and the evaluation of an appropriate CPG for individualising the group-level results of the RCT of interest.

Box 1. How to use a Clinical Prediction Guide (CPG) on risk prediction to individualise the results of an RCT.

Relevance

Will the CPG help me in making individualised risk predictions for patients in the control group of the randomized controlled trial (RCT) of interest?

• Were the patients on whom the CPG was developed or validated similar to the RCT's control group in regard to their clinical characteristics?

• Does the treatment status of the patients on whom the CPG was developed match that of the RCT's control group, that is, each on no treatment or placebo; each on established effective therapy?

• Does the CPG provide the absolute risk (or is it at least derivable) for the outcome of interest (target event or harm), in a specified period of time, according to risk factors/risk score?

Validity

Are the predictions made by the CPG valid?

• How was the CPG developed?

  Was the CPG developed on a well defined and representative sample of patients prospectively followed up?

• How well did the CPG perform in the population of derivation?

  Was the CPG's calibration tested? How accurate were the predictions of the absolute risk, that is, how good was the agreement between predictions and observed outcome?

  Were the CPG's discrimination (c-statistic) and reclassification tested? How good were they?

• Did the CPG undergo internal validation to quantify and eventually adjust for overfitting/optimism?

• Did the CPG undergo external validation?

  • Was the CPG's performance tested in patients different from those on whom it was developed? How good was it?

Precision

How precise were the predictions of the absolute risk, that is, how wide was the uncertainty around the provided estimates?

In the case of a variable benefit/variable harm, we look for two different CPGs to classify the patients according to the ‘baseline’ risks for the target event and for the harm. In this case, the predictions resulting from this coclassification might be constrained by a possible within-patient correlation between the two variable risks, since the target event and the harm may share some risk factors or may not be independent outcomes.

Uncertainty in group-level estimates and patient values

The results of an RCT are usually provided as point estimates accompanied by a measure of variability (CI). Often, as shown in the example in table 3, the within-trial estimates for the harm have been characterised by high imprecision. However, this situation may be improving with the increasing reports of very large active-control RCTs.¹⁸

Probably the major source of uncertainty is the patient's RV_harm/benefit and its elicitation. The scenario presented to the patient should uniformly include the major clinical outcomes of the treatment decision, including death if relevant, and the time frame of the consequences of the decision. Decision aids, which are tools specifically designed to prepare the patient to participate in the decision process, have been shown to improve patient knowledge and involvement, especially when they target explicit values clarification.¹⁹

One may embed in the calculation of the individual quantities a measure of the variance (eg, SE) of the group-level measures entering the model.²⁰ Additionally, one may estimate how much that uncertainty can affect the individual predictions in the most pessimistic direction, that is, using the CI bounds for the group-level estimate of the treatment effect on target corresponding to the worst scenario. We proposed an alternative approach to deal with the uncertainty around the quantities entering the model. We provided formulas for estimating the individualised maximum ARI_harm and RV_harm/benefit above which the decision to treat would be overturned.

Future research objectives

1. Resolution of uncertainty. In applying our model, methods are needed to resolve uncertainty arising from imprecision in the estimates of treatment benefit and treatment harm derived from group-level results from RCTs. In this paper, we addressed uncertainty by resorting to sensitivity analyses utilising bounds of CIs on treatment effects. However, in the field of cost-effectiveness analysis, investigators progressed to approaches dealing simultaneously with the stochastic uncertainty of all the quantities entering the model. These approaches include non-parametric bootstrapping, Fieller's theorem and Bayesian methods.²¹ We suggest as a future goal that such methods be explored for their applicability to resolution of uncertainty in clinical harm/clinical benefit analyses.

2. Net benefit and model validation. Vickers et al⁵ conceived a method to empirically test whether individualised recommendations based on CPG-based predictions of absolute treatment effects, value-adjusted, would actually result in a greater net benefit in real life compared with a policy of treating all patients or treating none. The method utilises the distribution of predicted individualised treatment effects in the randomly allocated treatment and control groups of a large RCT. One combines the patients whose predicted ARR_target(i) exceeded the required ARR_target(i) who were randomised to the treatment group, and the patients whose predicted ARR_target(i) did not exceed their required ARR_target(i) who were randomised to the control group. Those are the respective patients who would or would not be recommended for treatment and who used prediction-based treatment in real life. One then compares the observed outcomes in the trial of that combined group with the outcomes for the treatment arm of the RCT. The superiority of the prediction-based policy is validated if its net benefit is greater than the net benefit of treat all, or treat none. The empirical result, in the examples of Vickers et al⁵ and later Dorresteijn et al,⁶ was that a prediction-based policy was superior, but only within a limited range of the required ARR_target(i). If the required ARR_target(i) was extreme in either the low or high direction, a policy of treat all or treat none, respectively, was preferred.

Vickers et al⁵ and Dorresteijn et al⁶ used this approach to validate individualised recommendations in a fixed harm scenario, where the harm was receipt of the treatment per se. Nevertheless, the same approach can be used to validate individualised recommendations in variable harm scenarios, and for treatments tested in non-inferiority as well as superiority trials. As with Vickers’ method in general, individual-patient trial data must be available to identify the patients whose predicted ARR_target(i) did or did not exceed their required ARR_target(i).

Appendix: Algebraic derivation of the models

Legend:

Target = target outcome that the treatment can prevent

Harm = any increase of an adverse outcome due to the treatment

CID = clinically important difference

ARR = absolute risk reduction

ARI = absolute risk increase

V = value

RV = relative value

1. Derivation of the simple model (one benefit, one harm)

The CID corresponds to the ARR for the target benefit sufficiently large to exactly offset the treatment harm. Allowing for a different value assigned to the target outcome prevented by the treatment and to the harm caused by the treatment (V_target and V_harm, respectively), the condition at the CID can be expressed algebraically as:

(1)

1.1. Algebraic solution for the required ARR_benefit to offset the treatment harm

Dividing each side of the equation (1) by V_target

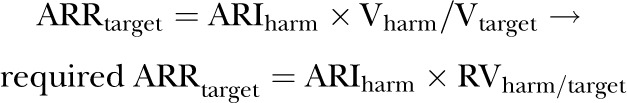(2)

1.2. Algebraic solution for the maximum ARI_harm above which treatment would not be justified

Dividing each side of the equation (1) by V_harm

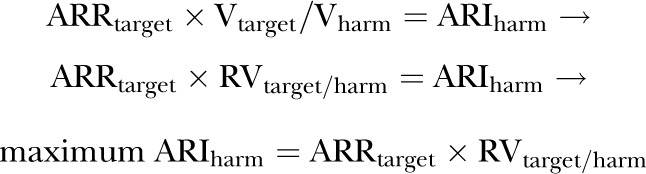(3)

or, expressed in terms of RV_harm/target

1.3. Algebraic solution for the maximum RV_harm/target above which treatment would not be justified

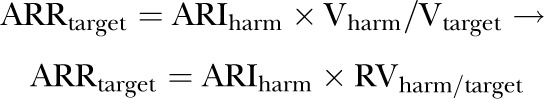dividing each side of equation by ARI_harm

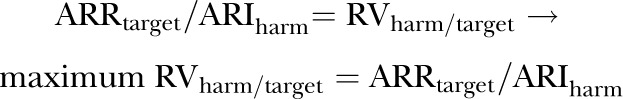(4)

2. Derivation of the complex model (multiple benefits, multiple harms)

Legend:

Benefit = any reduction of an adverse outcome additional to the target outcome.

At the CID, the sum of treatment benefits offsets the sum of treatment harms. Allowing for different values for every outcome prevented or caused by treatment, this can be expressed algebraically as:

(5)

where m is the total number of treatment benefits, the benefit(2) to benefit(m) are the benefits other than the target one, and k is the number of treatment harms. Or, likewise:

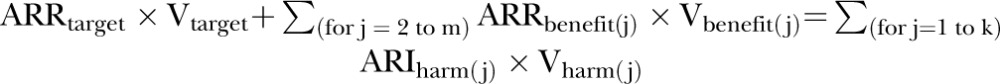(6)

Subtracting 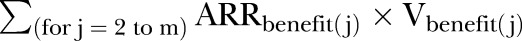from both sides and dividing both sides for V_target, we can obtain the required ARR_target such that the total treatment benefits offset the total treatment harms:

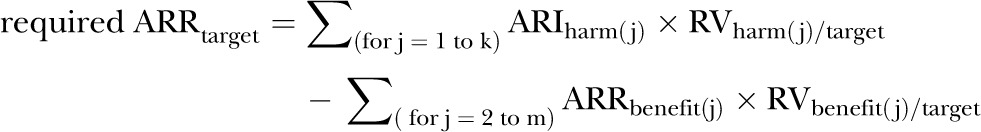(7)

where every RV is expressed as the value of that outcome, prevented or caused by the treatment, compared with the value assigned to the target outcome.