Ion Competition in Condensed DNA Arrays in the Attractive Regime

Abstract

Physical origin of DNA condensation by multivalent cations remains unsettled. Here, we report quantitative studies of how one DNA-condensing ion (Cobalt³⁺ Hexammine, or Co³⁺Hex) and one nonDNA-condensing ion (Mg²⁺) compete within the interstitial space in spontaneously condensed DNA arrays. As the ion concentrations in the bath solution are systematically varied, the ion contents and DNA-DNA spacings of the DNA arrays are determined by atomic emission spectroscopy and x-ray diffraction, respectively. To gain quantitative insights, we first compare the experimentally determined ion contents with predictions from exact numerical calculations based on nonlinear Poisson-Boltzmann equations. Such calculations are shown to significantly underestimate the number of Co³⁺Hex ions, consistent with the deficiencies of nonlinear Poisson-Boltzmann approaches in describing multivalent cations. Upon increasing the concentration of Mg²⁺, the Co³⁺Hex-condensed DNA array expands and eventually redissolves as a result of ion competition weakening DNA-DNA attraction. Although the DNA-DNA spacing depends on both Mg²⁺ and Co³⁺Hex concentrations in the bath solution, it is observed that the spacing is largely determined by a single parameter of the DNA array, the fraction of DNA charges neutralized by Co³⁺Hex. It is also observed that only ∼20% DNA charge neutralization by Co³⁺Hex is necessary for spontaneous DNA condensation. We then show that the bath ion conditions can be reduced to one variable with a simplistic ion binding model, which is able to describe the variations of both ion contents and DNA-DNA spacings reasonably well. Finally, we discuss the implications on the nature of interstitial ions and cation-mediated DNA-DNA interactions.

Introduction

Cation-modulated electrostatics of nucleic acids is fundamental to nucleic acids structure and function and has served as a model system of biomolecular electrostatics (1–6). Electrostatic interaction, being the strongest among noncovalent interatomic interactions, is of central importance in biology due to the prevalence of charges in all major types of biomolecules (7,8). Although the general principles of electrostatics (i.e., Coulomb forces) are well understood, biomolecular electrostatics is complicated by multiple inherent complexities including screening by ubiquitous ions, involvement of highly polar water molecules, and significant roles of entropy (i.e., thermal energy) (7–9). Despite extensive efforts in the past decades, quantitative knowledge of biomolecular electrostatics is still incomplete and many important questions remain unanswered (10).

In describing cation-modulated electrostatics of nucleic acids, quantitative agreement between experiment and theory has only been obtained for monovalent cations (11). For nucleic acids in monovalent salts (and divalent salts to some extent), mean-field theories based on the nonlinear Poisson-Boltzmann (NLPB) equations have provided reasonable explanations to measured quantities such as osmotic pressures of DNA solutions (12), cation competitions and spatial distributions around DNA (13–17), and interaction forces between freely floating DNA oligomers (18) and between parallel DNA strands beyond 1 nm surface separation (19). Recent literature has increased in theoretical sophistication by accounting for additional details such as different ion sizes (20) and DNA-DNA azimuthal angle dependence due to helical DNA-charge patterns (21). It is worth noting that linear Poisson-Boltzmann approaches also have been shown to be effective, once corrected for the nonlinear screening in the DNA vicinity by theorems such as counterion condensation (22) and charge renormalization (23). Given their underlying assumptions, the success of mean-field approaches for monovalent cations is likely attributed to the relatively weak electrostatic coupling between ions and charged surfaces and between themselves.

Meanwhile, quantitative understanding is yet to be attained for multivalent cations, especially cations with valence of three and higher. A notable example is the multivalent cation-mediated attraction between DNA helices, whereas mean-field based theories always predict repulsion (24). Physical origin of such like-charge attraction remains under debate. As the increase of ion valences results in qualitatively different electrostatic interactions, stronger electrostatic interactions between cations and DNA and/or between cations themselves are widely accepted to lead to DNA-DNA attraction. A number of theoretical models have been proposed, including cation density fluctuations between DNA helices (25–27), ion-ion correlations leading to Wigner-like lattices (28,29), strong counterion-DNA coupling (30–32), and counterion localization giving rise to ion bridging (33) or zipper-like cation-DNA charge correlation (34). Moreover, hydration force has been shown to dominate DNA-DNA interactions at DNA-DNA surface separations <1 nm, as a result of the perturbation of hydration shells (35). The role of cations is to restructure the hydration shells whose contraposition or complementarity leads to repulsive or attractive hydration force, respectively. On the other hand, computer simulations have provided detailed descriptions of DNA-ion interactions, but evaluating the underlying physical mechanisms is difficult due to varying levels of simplifications employed (36–42). The first all-atom molecular dynamics (MD) simulation of DNA-polyamine interactions was reported in 2008 by Dai et al (40). The proposed ion-bridging mechanism therein for chain-like polyamines is unlikely to be true for point-like multivalent cations. In a more recent all-atom MD study of 64 parallel DNA arrays (43), the commonly used force fields resulted in attraction between dsDNA with mono- and divalent ions. Tuning the force fields was necessary to avoid such inconsistency. It is worth noting that multivalent cation-mediated DNA condensation differs from DNA compaction by oppositely charged polyelectrolytes. Because the polyelectrolytes’ charged groups alone cannot condense DNA, the DNA compaction is understood in terms of polyelectrolyte-mediated bridging interactions (44). One example is DNA packaging by dendrimers for which the condensing force (45) and resultant structures have been characterized (46) and atomistic simulations have achieved remarkable success in describing the energetics of compaction and the roles of hydration forces (47,48). In sum, the true physical nature of multivalent DNA-condensing cations, especially compared with DNA-noncondensing cations, is the focal point of competing theories to explain the DNA-DNA attraction and consequently electrostatic interactions in the presence of multivalent cations.

On the other hand, quantitative measurements of cation behaviors in the DNA-DNA attraction regime are largely lacking, precluding stringent tests of theories of electrostatic interactions. Previous studies of DNA-condensing cations have determined their bulk threshold concentrations to condense DNA and the effects of monovalent cations and anions (49–52). Three commonly studied cations, Cobalt³⁺ Hexammine (Co³⁺Hex), Spermidine³⁺, and Spermine⁴⁺, were shown to have sub-mM threshold concentrations (49,53–55) and monovalent cations raise the threshold concentration as expected from ion competition. The spatial distribution around DNA of a DNA-condensing cation, Co³⁺Hex, has been measured below its threshold concentration (56). It has also been shown that DNA condensation is accompanied by an additional binding of multivalent cations and appears as an abrupt all or none process (54,57,58). More broadly, a wide array of experimental techniques, including isothermal titration calorimetry (53), light scattering (59,60), osmotic stress method (61), fluorescence microscopy (58), and nuclear magnetic resonance (62), have been applied to investigate the cation-induced DNA compaction process and DNA-cation interactions; however, much less is known about the ions within condensed DNA (in contrast to the ions in the bulk), although it is these ions that mediate the attraction between DNA helices. Such knowledge will be needed to identify the gaps in our understanding and elucidate the peculiarities of multivalent cations.

We have thus directly probed the interstitial ions in spontaneously condensed double-stranded DNA arrays by measuring the numbers of two competing ions (Co³⁺Hex and Mg²⁺) under a variety of ionic conditions in the bath solution. There are two previous studies on the ionic contents in cation-condensed DNA arrays to our knowledge. Teif (63) used isotope labeling to determine the number of Spermidine³⁺ ions needed to condense DNA arrays and Todd et al. (54) measured the competition between Co³⁺Hex and Spermidine³⁺ to determine their relative binding constant. Both previous studies are different from ours because either no ion competition was studied or the competition between two DNA-condensing ions was probed. Although Co³⁺Hex condenses DNA and Mg²⁺ does not, their behaviors likely differ qualitatively in the attractive regime and how they compete can provide insight into the physics of DNA-DNA attraction. Additionally, the previous studies measured only one type of ion in DNA arrays, whereas we have systematically quantified the numbers of both Co³⁺Hex and Mg²⁺ ions in DNA arrays. Furthermore, we measured the DNA-DNA spacings in the same samples, a parameter required for theoretical calculations. We found that the measured partitions of Co³⁺Hex are higher than predicted from mean-field approaches once the effect of ion pairing is corrected. Remarkably, the partition of the interstitial ions was observed to uniquely determine the DNA-DNA spacing, whereas there are two independent ion concentrations in the bath solution (Mg²⁺ and Co³⁺Hex). We further show that a phenomenological ion binding model is able to describe all experimental data reasonably well, resulting in a reduced solution parameter, [Mg²⁺]/[Co³⁺Hex]^2/3.

Materials and Methods

High-molecular-weight genomic DNA (>10 kilo basepairs) was purified from adult chicken erythrocytes as previously described (64). Salts of Co³⁺Hex Chloride and MgCl₂ were purchased from Sigma (St. Louis, MO) and used as received. Buffer of 2 mM pH 7.5 Tris·Cl was used in all solutions unless noted otherwise; the relatively low concentration was chosen to minimize the competition from the buffering ions. Each sample was first prepared by condensing ∼300 μg DNA into a liquid crystalline (LC) pellet by 2 mM Co³⁺Hex. The LC-DNA pellet was then equilibrated for 2 weeks in 1 ml of each studied salt condition with one interim buffer exchange. The pellet’s DNA-DNA spacing was then measured by x-ray diffraction (XRD) at 20°C with an in-house XRD setup (3 × 10⁷ photons/s, beam size of 0.8 × 0.8 mm) where radiation damage is negligible.

Each DNA pellet was recovered after XRD and reequilibrated in the original buffer for another week. The pellet was then picked up and care was taken to remove the equilibration buffer by pressing the pellet between weigh papers and wicking with a kimwipe. The pellet was then dissolved in 1 ml buffer of 1.5 M NaCl with gentle thermal agitation at 55°C and daily vortexing for 2 weeks. Once the LC-DNA pellet is fully dissolved, ultraviolet-visible (UV-vis) absorption measurements were first carried out to determine the concentrations of Co³⁺Hex (at 475 nm, an extinction coefficient of 0.056/mM/cm) and DNA (at 260 nm, 50 μg/ml for optical density of 1.0). Inductively coupled plasma atomic emission spectroscopy (ICP-AES) was then used to simultaneously measure the numbers of Co, Mg, and P (from the DNA) atoms in the same samples on an Optima 7300DV (Perkin Elmer, Waltham, MA). ICP-AES data were collected in the axial mode with five replicates per sample. Measurements were made in the linear range of the instrument at five different wavelengths for Co, four different wavelengths for Mg, and two different wavelengths for P, and then the concentrations from all respective wavelengths were averaged. Calibration was provided by 10 linearly spaced control samples of Co, Mg, and P that spanned the entire region of concentrations. Four independent measurements using two independent calibrations were averaged to obtain the final concentrations for each set of samples. For the samples with 0 mM MgCl₂ in the bath solution, the detected trace amount of Mg (<0.3% of P atoms) is treated as the baseline from the dissolvation buffer and subtracted from all data. Standard errors were determined statistically from these measurements.

To address the possible complication of incomplete buffer removal from the DNA pellet, test samples with only one type of cation were measured to verify that our experiment protocol leads to minimal excess buffer that is well below 20% of the LC-DNA pellet volume (∼1 μl). Importantly, the excess buffer, if carried by the DNA pellet, contributes little to the total numbers of ions measured, especially for Co³⁺Hex. This is because the effective Co³⁺Hex concentration in the pellet (∼140–700 mM) is at least 28–700 times that in the buffer (1–5 mM) under the studied conditions. The uncertainty introduced by the excess buffer is thus <1% for Co³⁺Hex. The relative uncertainty for Mg²⁺ could be significant when very few Mg²⁺ ions exist in the DNA pellet, however the Mg²⁺ concentration in the buffer is necessarily low and its absolute contribution should be small. This is also supported by the experimental data reported herein.

Results and Discussion

Experimental characterizations of spontaneously condensed DNA arrays

The multivalent-cation-condensed LC-DNA phase consists of locally hexagonally ordered DNA arrays (Fig. 1 a) made up of DNA, ions, and solvent. The system can be defined by a few variables, the interaxial DNA-DNA spacing (d), the number of Co³⁺Hex ions (n_Co), the number of Mg²⁺ ions (n_Mg), and the number of Cl⁻ ions (n_Cl). Here, we normalize the ion numbers by the number of DNA phosphates and do not explicitly consider the number of water molecules as no external osmotic pressure is applied on the DNA array. The interaxial spacing d is determined by XRD as shown in Fig. 1 b for LC-DNA samples under a constant [Co³⁺Hex] of 2 mM and varied [Mg²⁺]s from 0 to 30 mM. The DNA-DNA spacing is given by 2π/Q_peak × 2/√3, where 2/√3 accounts for the local hexagonal packing and Q_peak is obtained by peak fitting with a Lorentzian function. From Fig. 1 b, we observe that 2 mM Co³⁺Hex holds the DNA array in tight spacings ∼27.8 Å for [Mg²⁺]s up to 25 mM, and then an abrupt expansion occurs at 25–30 mM [Mg²⁺] consistent with a hexagonal to cholesteric phase transition (50). At [Mg²⁺] >30 mM the pellet dissolves and XRD cannot be applied.

Figure 1.

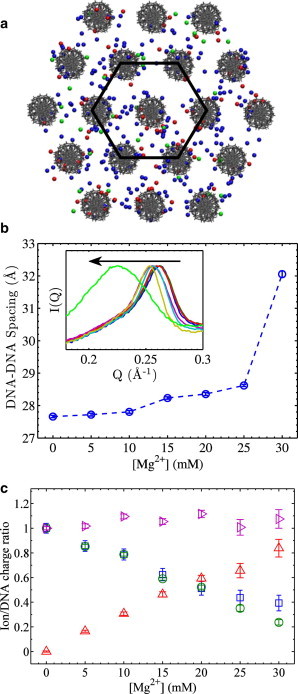
Illustrations of the studied system of DNA arrays and representative experimental data. (a) Cartoon of an ordered DNA array and its interstitial ions, Co³⁺Hex (red), Mg²⁺ (blue), and Cl⁻ (green). The hexagonal geometry is indicated by a hexagon drawn in black. Atomic radii are chosen to facilitate visualization only. Another view of the DNA array is shown in Fig. S1. (b) The DNA-DNA spacing as a function of Mg²⁺ concentration with constant 2 mM Co³⁺Hex in the bath solution. Inset shows the XRD peak profiles with the arrow pointing to increasing [Mg²⁺]s, indicating a hexagonal to cholesteric phase transition at the highest [Mg²⁺]. (c) The ion/DNA charge ratios as a function of [Mg²⁺] measured from the same samples shown in (b). The charge ratio of Co³⁺Hex/DNA (3 n_Co) was measured by both UV-vis (□) and ICP-AES (○), showing good agreement. The charge ratio of Mg²⁺/DNA (2 n_Mg) was measured by ICP-AES only (Δ). Their sum $(▹)$, 3 n_Co + 2 n_Mg, is very close to unity, indicating that Cl⁻ ions are essentially completely excluded by the DNA arrays under studied conditions. This also supports that minimal amounts of excess buffer were carried in the measured DNA pellets.

The measured numbers of the interstitial Co³⁺Hex and Mg²⁺ ions are shown in Fig. 1 c in the form of ion/DNA charge ratios (i.e., 3 n_Co, 2 n_Mg). As expected from ion competition, the fraction of Co³⁺Hex in the DNA array decreases upon increasing [Mg²⁺] in the bath solution. For the Co³⁺Hex/DNA charge ratios (3 n_Co) measured by both UV-vis and ICP-AES, good agreement was found. Slightly larger 3 n_Co values were obtained by UV-vis at high [Mg²⁺]s, which is attributed to the susceptibility of the UV-vis method to baseline variations when [Co³⁺Hex] is low. ICP-AES data are thus regarded more reliable and used in all subsequent analysis. ICP-AES also has the advantage of measuring Mg²⁺ in addition to Co³⁺Hex. Although our current instrumentation is not able to directly measure the co-ion Cl⁻, it is possible to derive its number n_Cl via the charge neutrality condition 3 n_Co + 2 n_Mg–n_cl = 1. However, we observe that the 3 n_Co + 2 n_Mg values are practically unity for all measured samples (Fig. 1 c and other data discussed later), indicating a negligible amount of Cl⁻ in DNA arrays (n_Cl ≈ 0) due to its electrostatic exclusion. The condition of 3 n_Co + 2 n_Mg = 1 thus holds for our studied conditions and simplifies our subsequent analysis. Taken all together, our XRD and ICP-AES measurements provide quantitative details of DNA arrays that can be directly compared with theoretical predictions.

Comparisons of the numbers of ions between experiments and mean-field theories

The well-defined states of DNA arrays allow direct comparisons with quantitative model predictions. Although it is preferred to compare with theories that predict DNA-DNA attraction, such theories often involve resource-demanding computations or their predictions are sometimes of qualitative nature. As a first step, here we choose to compare with two commonly used theoretical models based on the NLPB equations. The first is the primitive cylindrical cell model (CCM) (65) where DNA is treated as a 20-Å-diameter cylinder with a uniform charge density and ions are treated by density distributions. The NLPB equations are then solved within a cylindrical cell of diameter set by the measured DNA-DNA spacing, under the boundary condition of zero electric field at the outer boundary. As the actual DNA array is hexagonal, the cylindrical cell overestimates the DNA density by ∼10%. We verified that CCM calculations are insensitive to the DNA-DNA spacing and that a 10% change of the cell volume leads to negligible changes (see Fig. S2 in the Supporting Material). The second model takes into account the atomic structure of double-stranded DNA and solves the NLPB equations using the program Adaptive Poisson-Boltzmann Solver (APBS) (66). To represent the system of DNA arrays, hexagonal arrays of 19 DNA helices (24 basepairs of random sequences) are generated with the measured DNA-DNA spacings. Fig. 1 a shows the view down the axial direction and another view is shown in Fig. S1. The box for the ABPS calculation has dimensions of 225 × 225 × 150 Å, considerably larger than the size of the array (∼120 × 120 × 80 Å). The grid size is 0.45 Å and has been verified to be sufficient (Fig. S3). All ions are treated as spheres of 2-Å radius, which is used to determine the ion accessible volume during the APBS calculations (66). Uses of different ion radii lead to relatively small changes in the APBS results and do not affect the conclusions of our study (Fig. S4).

The CCM and APBS calculations make quantitative predictions of the ion/DNA charge ratios (3 n_Co, 2 n_Mg, and –n_Cl). Both models yield the electrostatic potential distributions, which in turn give the ion density profiles via the Boltzmann probability function and the total number of each ionic type via integration. For the APBS calculation where a finite atomic model of DNA arrays is used, to avoid the edge effects, only the core volume of the DNA array is analyzed by selecting the inner hexagonal region as indicated in Fig. 1 a (solid line) and the middle 12 basepairs along the axial direction. We verified that summing all ion/DNA charge ratios gives unity as expected from charge neutrality. We then directly compare the experimental values and theoretical predictions. Fig. 2, a and b, show the changes of 3 n_Co and 2 n_Mg (in the DNA array) at fixed Co³⁺Hex concentrations and varied Mg²⁺ concentrations (in the bath solution). The CCM and the APBS results overlap with each other nearly exactly. Their predictions of n_Cl < 0.01 for all studied conditions (except a few at highest [Mg²⁺]s) are consistent with experimental observations of n_Cl ≈ 0. At 1 and 2 mM Co³⁺Hex (Fig. 2, a and b), both model predictions appear to explain the 3 n_Co and 2 n_Mg curves fairly well. This may be somewhat surprising because both the CCM and APBS models do not predict DNA condensation, whereas the studied DNA arrays are spontaneously condensed. However, at 5 mM Co³⁺Hex (Fig. 2, a and b), both models considerably overestimate the 3 n_Co values and consequently underestimate the 2 n_Mg, as 3 n_Co + 2 n_Mg = 1 practically holds for both model calculations and experiments. These observations are qualitatively in contrast to the expectation that DNA-condensing cations (e.g., Co³⁺Hex) interact with DNA more strongly than mean-field theoretical predictions (e.g., the CCM and APBS models).

Figure 2.

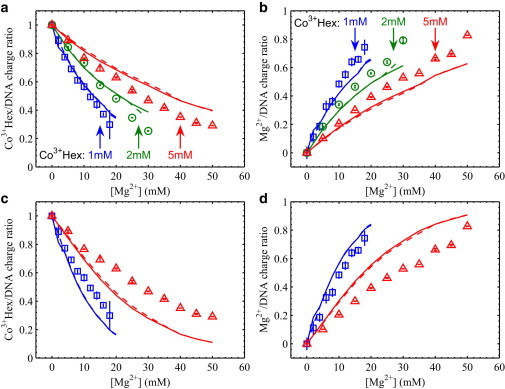
Measured ion/DNA charge ratios in the Co³⁺Hex-Mg²⁺ competition series compared with theoretical calculations. Symbols are experimental data at fixed [Co³⁺Hex]s of 1 mM (□), 2 mM (○), and 5 mM (Δ) and varied [Mg²⁺]s as the x axis. Lines in matched colors are the theoretical predictions under the same conditions from the CCM (solid) and APBS (dashed) models. (a and b) Show the Co³⁺Hex/DNA charge ratio (3 n_Co) and the Mg²⁺/DNA charge ratio (2 n_Mg), respectively, where all Co³⁺Hex ions are assumed to be completely dissociated in the trivalent state for the CCM and APBS calculations. (c and d) Show the same experimental data as in (a and b), respectively, where the effect of ion pairing between Co³⁺Hex and Cl⁻ pairing is considered for the CCM and APBS calculations. The dissociation constant K_d is 20 mM. The curves from the 2 mM Co³⁺Hex series are not shown to reduce data cluttering in the plots. Note that the large error bars (and slight deviation from charge neutrality) at the highest [Mg²⁺] for each series are due to the sample loss when handling these loosely packed DNA arrays.

To investigate the unexpected outcomes from the comparisons with mean-field theories, we next consider one effect that is known to be significant for multivalent cations at high concentrations, ion pairing (49). In this context, ion pairing refers to the association of trivalent Co³⁺Hex ions with Cl⁻ anions giving rise to effectively divalent Co³⁺HexCl⁻ ions, as a result of strong electrostatic attraction. The pairings of divalent cations and anions (i.e., Mg²⁺ and Cl⁻, Co³⁺HexCl⁻ and Cl⁻) are not considered as we have chosen to study relatively low ion concentrations (maximum [Mg²⁺] of 50 mM, maximum [Co³⁺Hex] of 5 mM). For the ion paring reaction Co³⁺Hex + Cl⁻ ↔ Co³⁺HexCl⁻, the dissociation constant K_d (from right to left) is defined as [Co³⁺Hex][Cl⁻]/[Co³⁺HexCl⁻] and was reported to be ∼20 mM (50). Although we have chosen to work with low Co³⁺Hex concentrations (1–5 mM), ion paring still has significant effects on the concentration of trivalent Co³⁺Hex ions in the bath solution. For example, in the presence of 20 mM MgCl₂, a nominal 1 mM Co³⁺HexCl₃ gives 0.32 mM (32%) trivalent species and a nominal 5 mM gives 1.4 mM (28%). Given such dramatic changes, it is somewhat surprising that the measured 3 n_Co + 2 n_Mg values are very close to unity, which suggests that the Co³⁺Hex ions within the DNA arrays are predominantly trivalent species. We speculate that the presumably bulky divalent Co³⁺HexCl⁻ ions compete poorly against Co³⁺Hex or Mg²⁺ ions and are thus largely excluded from the DNA array. If otherwise, we would expect the measured 3 n_Co + 2 n_Mg values to be significantly greater than unity.

As a result of ion pairing, the substantial decreases in the actual Co³⁺Hex ion concentrations lead to different predictions by the CCM and APBS models, noting that the divalent Co³⁺HexCl⁻ ions are not considered for reasons previously mentioned. As shown in Fig. 2, c and d, both models show to underestimate the numbers of Co³⁺Hex ions for all data series by as large as 40% and consequently overestimate the numbers of Mg²⁺ ions. This underestimation of the Co³⁺Hex competition is qualitatively different from the observations without the ion pairing correction (Fig. 2, a and b). We like to note that it is possible to match the experimental data with the CCM and APBS model predictions if an arbitrary K_d is used, e.g., a value of K_d = 120 mM was found to be able to give excellent agreements (Fig. S5), though the physical meaning of this is unclear. Overall, although we are not able to implement more sophisticated calculations, our measurement and analysis nonetheless quantify the deficiencies of mean-field approaches and can serve as quantitative tests of modern theories of DNA-DNA attraction.

Relations between the DNA-DNA spacings and the numbers of interstitial ions

Increasing the [Mg²⁺] in the bath solution not only changes the partition of Co³⁺Hex and Mg²⁺ ions in the DNA array, but also expands the DNA array before eventually dissolving it (Fig. 1 b). The smallest measurable Co³⁺Hex/DNA charge ratios (3 n_Co) correspond to the minimum charge fractions of Co³⁺Hex that incur net DNA-DNA attraction. Interestingly, for all nominal Co³⁺Hex concentrations studied (Fig. 2 a), essentially the same minimal 3 n_Co value of ∼0.2 (20% of DNA charges) is observed. This is not entirely expected as it is generally believed that ∼70–90% of the DNA charge needs to be neutralized by DNA-condensing ions for attraction to occur (24), e.g., 87% for Spermidine in 10 mM NaCl (53), 67% for Co³⁺Hex in 10 mM NaCl (53), and 80% for Spermine in 10 mM Tris buffer (55). Our measurement shows that this number is much smaller, i.e., as low as ∼20% of DNA charge neutralization by Co³⁺Hex is needed for condensation. This suggests against the need for significant cation-cation correlation to mediate DNA-DNA attraction. Rather, it may be explained because each Co³⁺Hex ion mediates a finite amount of attractive force independently and that ions mediate DNA-DNA forces additively, though concurrent measurements of DNA-DNA attractive forces would be needed for additional proof. Nonetheless, this observation does not contradict previous studies because the other 80% DNA charge is neutralized by Mg²⁺ in this study, whereas previous studies used low salts of monovalent ions. A different minimal 3 n_Co value is expected if Na⁺ is used instead.

As the DNA-DNA spacing is the equilibrium distance between DNA strands that balance the attractive and repulsive forces, it is of interest to examine its dependence on the interstitial ions modulating the forces. Fig. 3 a shows the DNA-DNA spacing as a function of [Mg²⁺] for each fixed nominal [Co³⁺Hex]. Qualitatively resembling trends are observed for all curves: the hexagonal to cholesteric phase transition at ∼29.5 Å and the complete dissolution at ∼33.8 Å. We then show the DNA-DNA spacing as a function of the measured Co³⁺Hex/DNA charge ratio in Fig. 3 b; remarkably, all series collapse onto one single curve. It also becomes clear that the hexagonal-cholesteric phase transition occurs at 3 n_Co ∼0.3 and the DNA array dissolves at 3 n_Co ∼0.2. The convergence indicates that the DNA-DNA spacing is practically solely determined by the partition of the interstitial ions, though this may not be surprising because it is the interstitial ions that mediate the forces. Given that n_Cl ≈ 0 and 3 n_Co + 2 n_Mg = 1, the state of the DNA array (d, n_Co, n_Mg, and n_Cl) is thus determined by only one independent variable.

Figure 3.

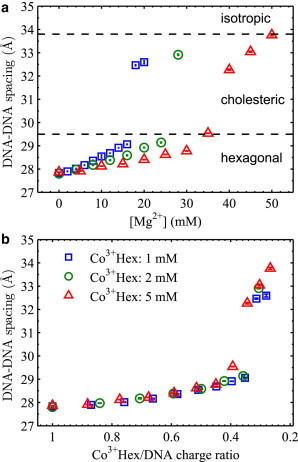
Measured DNA-DNA spacings in the Co³⁺Hex-Mg²⁺ competition series shown in Fig. 2. (a) The DNA-DNA spacings as a function of the nominal [Mg²⁺] in the bath solution. The nominal Co³⁺Hex concentrations in the bath solution for all data series are given in the legend in (b). The dashed lines delimit the regions for different structure phases as labeled. (b) The same DNA-DNA spacings as in (a) as a function of the corresponding measured Co³⁺Hex/DNA charge ratio, 3 n_Co. Note that the x axis is plotted in the reverse direction.

Relations between the numbers of interstitial ions and the bath ion concentrations: a phenomenological ion binding model

In our experiment, as there is free exchange of ions and solvent between the DNA array and the bath solution, the chemical potentials of all ions (μ_Co, μ_Mg, and μ_Cl) are equal between the two phases. It is the chemical potentials of ions that are directly varied via their concentrations in the bath solution and the changes of d, n_Co, n_Mg, and n_Cl in the DNA array are measured at constant temperature and pressure. For the ionic bath solution constrained by charge neutrality, two independent variables exist in the case of three ionic species with chemical potentials μ_Co, μ_Mg, and μ_Cl. However, previous discussions based on Fig. 3 suggest one independent variable for the state of the DNA array. Thus, it may be possible to reduce the variables of the bath solution in determining the state of the DNA array. For the benefit of simplicity, we consider a phenomenological ion binding model (IBM) treating the DNA array as composed of binding sites with a constant electrostatic potential φ. As the bath solution sets the ion chemical potentials by μ_Co = ln([Co³⁺Hex]) and μ_Mg = ln([Mg²⁺]), the ion binding equilibrium is established when the total free energy is unchanged by swapping δ number of Mg²⁺ with 2/3δ number of Co³⁺Hex between the two phases (due to charge neutrality). Because φ is assumed to be constant, no net change of electrostatic energies is incurred during the virtual swap of equal amounts of ion charges. Only the changes of the ion entropies need to be considered. Taking the entropy of bound (i.e., interstitial) ions in the form of ln(n_ion) (note that n_ion is defined as the ion/DNA-phosphate number ratio), we obtain,

$$\text{ln}\left({\text{n}}_{\text{Mg}}\right)-\frac{2}{3}\text{ln}\left({\text{n}}_{\text{Co}}\right)+\mathit{\xi }=\ln \left(\left[{\text{Mg}}^{2+}\right]\right)-\frac{2}{3}\ln \left(\left[{\text{Co}}^{3+}\text{Hex}\right]\right)=\ln \left(\frac{\left[{\text{Mg}}^{2+}\right]}{{\left[{\text{Co}}^{3+}\text{Hex}\right]}^{2/3}}\right).$$ (1)

Here, ξ is a constant to account for offsets due to the different choices of units for n_ion vs. [ion] and the likely different nature of reference states between in the bath solution and the DNA array. Given that 3 n_Co + 2 n_Mg = 1, this indicates that n_Co and n_Mg are uniquely determined by a single reduced variable of the bath solution, [Mg²⁺]/[Co³⁺Hex]^2/3. It should be noted that Rouzina and Bloomfield (67) have derived a more detailed model additionally considering the change of electrostatic potential due to ion exchange. The IBM model is used here for its simplicity and because the correction due to the varying electrostatic potentials is small (67).

With ξ as the fitting parameter for each series, the measured Co³⁺Hex/DNA charge ratios (3 n_Co) are fitted with the IBM as shown in Fig. 4 a. Note that the concentrations of trivalent Co³⁺Hex ions are corrected for the effect of ion pairing using K_d = 20 mM and that the divalent Co³⁺HexCl^- ions are considered to be excluded from the DNA array and do not compete. Fig. 4 a shows excellent fits to all curves, which is rather remarkable given the simplistic nature of the IBM and the use of only one fitting parameter for each series. Fig. 4 b shows the measured Mg²⁺/DNA charge ratios along the 1–3 n_Co values calculated from the IBM fits. Good agreements are observed as expected from charge neutrality for both the measurements and the IBM. The same data and IBM fits are shown as a function of [Mg²⁺]/[Co³⁺Hex]^2/3 in Fig. 4, c and d. Although we expect all curves to exactly collapse onto one single curve based on the IBM, the convergences of the Co³⁺Hex/DNA and Mg²⁺/DNA ratios are clear, but nonperfect. Likewise, similar levels of convergence of the DNA-DNA spacing are attained and shown in Fig. S6. The reason for these nonexact overlaps in Fig. 4, c and d is the slightly different ξ values obtained from the IBM fits, e.g., 2.68, 2.71, and 2.72 for the [Co³⁺Hex] series of 1, 2, and 5 mM, respectively. As the ξ values should be the same for all curves, this reflects deviations from ideal IBM behaviors, as well as the need for more sophisticated models. One possible consideration beyond the IBM is the change of the apparent ion binding energy with the increase of ionic strength. The logic is that the increase of n_Co, upon the increase of ionic strength at a fixed [Mg²⁺]/[Co³⁺Hex]^2/3, slightly contracts the DNA array (Fig. S6), which likely favors the binding of Co³⁺Hex more than Mg²⁺ (as indicated in Fig. S2 b). Nonetheless, the nearly universal dependence of the ion partitions on the single reduced variable of [Mg²⁺]/[Co³⁺Hex]^2/3 is evident. As the IBM only considers the entropy of mixing of ions, its validity again disfavors the presence of significant ion-ion correlations. The analogy of ion binding sites in the IBM may be explained by the confinement of cations by the local molecular fields on DNA surfaces. On the whole, given the need for the fitting parameter ξ, the IBM provides qualitative explanations of the trends of ion competition, but lacks quantitative power to predict absolute ion partitions.

Figure 4.

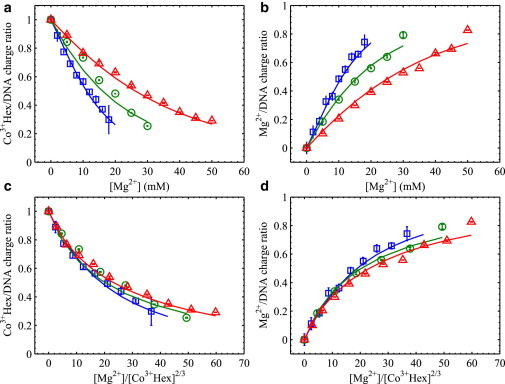
Measured ion/DNA charge ratios and fits using the IBM. Symbols show experimental data under fixed nominal [Co³⁺Hex]s of 1 mM (□), 2 mM (○), and 5 mM (Δ) in the bath solution (the same as in Fig. 2). Solid lines in matched colors are the IBM fits as described in the text. (a and b) Show the Co³⁺Hex/DNA charge ratio and Mg²⁺/DNA charge ratio as a function of [Mg²⁺] in the bath solution, respectively. (c and d) Show the same data in (a and b), respectively, but as a function of the [Mg²⁺]/[Co³⁺Hex]^2/3 in the bath solution.

Conclusion

In conclusion, we have carried out quantitative measurement and analysis of the partitions of DNA-condensing and non-DNA-condensing cations in spontaneously condensed DNA arrays. The availability of such data in the attractive regime has led to several interesting observations. First, mean-field calculations based on NLPB equations (considering DNA either as uniform cylinders or atomic structures) underestimate the fraction of Co³⁺Hex and overestimate that of Mg²⁺. Importantly, our study quantifies the discrepancies and provides valuable data sets to test advanced theories of electrostatics. Second, DNA-DNA attraction can be mediated when as low as ∼20% of the DNA charge is neutralized by Co³⁺Hex ions (the rest by Mg²⁺ ions), contrary to the generally accepted 70–90% neutralization of the DNA charge by DNA-condensing ions. Third, the competition between Co³⁺Hex and Mg²⁺ ions in the DNA array can be qualitatively explained by a minimalistic ion binding model whose predictions are derived from one reduced variable of the bath solution, which in turn determines the state of the DNA array (d, n_Co, n_Mg, and n_cl ≈ 0). These observations suggest interesting implications on the relationship between DNA-DNA forces and ion partitions, and the origin of such behaviors may be explained by the spatial placement of interstitial ions. Efforts in addressing these questions are underway.