A Cross-Bridge Cycle with Two Tension-Generating Steps Simulates Skeletal Muscle Mechanics

Abstract

We examined whether cross-bridge cycle models with one or two tension-generating steps can account for the force-velocity relation of and tension response to length steps of frog skeletal muscle. Transition-state theory defined the strain dependence of the rate constants. The filament stiffness was non-Hookean. Models were refined against experimental data by simulated annealing and downhill simplex runs. Models with one tension-generating step were rejected, as they had a low efficiency and fitted the experimental data relatively poorly. The best model with two tension-generating steps (stroke distances 5.6 and 4.6 nm) and a cross-bridge stiffness of 1.7 pN/nm gave a good account of the experimental data. The two tensing steps allow an efficiency of up to 38% during shortening. In an isometric contraction, 54.7% of the attached heads were in a pre-tension-generating state, 44.5% of the attached heads had undergone the first tension-generating step, and only 0.8% had undergone both tension-generating steps; they bore 34%, 64%, and 2%, respectively, of the isometric tension. During slow shortening, the second tensing step made a greater contribution. During lengthening, up to 93% of the attached heads were in a pre-tension-generating state yet bore elevated tension by being dragged to high strains before detaching.

Introduction

Modeling of the cross-bridge cycle provides powerful insights into how muscle produces force and movement (1–17). A model that accounted for the steady-state and transient mechanical properties of muscle would facilitate the prediction of quantities that are hard to determine experimentally, such as how the rates of the steps in the cycle, and the relative occupancies of the intermediates and their contribution to tension alter with velocity or in response to length or load steps. Such a model would aid the interpretation of a wide range of experiments and suggest new experiments to test current ideas.

A successful model should account for mechanical and energetic data (14) and be consistent with the kinetics of actomyosin ATPase in solution (18) and fibers (19), with structural studies on myosin head conformations (20,21), and with data on cross-bridge and filament compliance (22). The model should fit both shortening and lengthening limbs of the force-velocity relationship, the thermodynamic efficiency, and the time course of the tension transients after length or load steps. The dependence of the rate constants on strain should be no more complicated than necessary to fit the data (16), and preferably based on physicochemical principles. The Lymn-Taylor kinetic scheme for actomyosin ATPase implies that the minimum number of states in the cycle should be four, but there are indications that the number of attached states may be more than two (23,24). So it is important to determine whether four-state and five-state models can adequately model the kinetic and energetic properties of contracting muscle.

There is currently no consensus on the degree to which the myosin heads along a thick filament generate tension independently of one another (12–15), nor is there agreement on the number and stroke distances of the tension-generating steps. (It is important to distinguish conformational changes that generate tension from the working stroke that occurs only as the filaments slide (22). For brevity, we shall call a tension-generating step a tensing step and avoid the rather ambiguous term power stroke.) Classically, it was supposed that the conformational transition generating tension occurs in only one or two switchlike steps linked to product release, with attached heads undergoing the conformational change largely independently of one another (9,18,20,25). We term this a low-cooperativity mechanism (22). This view was challenged by reports that the cross-bridge stiffness was high and by studies of the time course of changes in the x-ray pattern in muscle subjected to rapid length or load steps (26–30). These reports were interpreted on the basis that tension generation occurs in four steps and that myosin heads may detach after any of them (28). It was also proposed that in an isometric contraction, all the attached heads were in similar states near the beginning of the working stroke, and that after a length step, the cross-bridges behaved synchronously. We call these high-cooperativity mechanisms (12,22). We discuss the difference between high- and low-cooperativity mechanisms more fully in Section 11a of the Supporting Material. Structural studies on myosin and actomyosin complexes have not given support for there being more than two tension-generating steps. X-ray crystallography has reported only two conformations that may be adopted by attached skeletal myosin heads: the closed conformation, equated to heads before their working stroke, and the closed-cleft conformation, equated to heads after their working stroke (31,32). The transition between these two conformations involves small relative movements of the subdomains of the head that are amplified into a large (70°) swing of the lever arm, causing the tip of the lever arm to move axially by ∼10 nm. However, electron micrographs of complexes of smooth muscle myosin heads with actin filaments in the presence and absence of ADP indicated that the lever arm swing for smooth myosin occurs in two stages, the second coupled to the release of the ADP (33). It is as yet unclear whether this could also be the case for skeletal myosin (34,35). Because models with four or more tensing steps are kinetically daunting, we think it important to test simpler models with fewer tensing steps to determine whether they are capable of explaining mechanical and energetic data.

The main question we address in this article is the extent to which a cross-bridge cycle with only one or two tensing steps can account for both shortening and lengthening limbs of the force-velocity relation, the dependence on velocity of ATP consumption, the thermodynamic efficiency with which ATP hydrolysis is used to produce mechanical work, and the time course of tension transients after length steps. We have chosen to model the anterior tibialis muscle of the frog Rana temporaria because the most detailed force-velocity data are from this source (36) and information on the time course of tension transients after length steps is available from this muscle (25,37).

Theory

The models

The model of the cross-bridge cycle with a single tensing step (scheme 1) is based on the Lymn-Taylor kinetic scheme for actomyosin ATPase (18). Although our modeling does not consider the structure or nucleotide composition of the intermediates of the cycle, the detached states can be pictured as being in the M.ATP state with an open conformation (38) or in the M.ADP.Pi state with a closed conformation (39). The transition between them is coupled to ATP hydrolysis and primes the head by changing the conformation to one resembling the start of the tensing step. M.ADP.Pi is taken to bind reversibly to a closely neighboring actin subunit (40) to give AM_pre.ADP.Pi. As there is strong evidence that the tensing step occurs before Pi release (23,24,41,42), the posttensing heads are grouped together regardless of their nucleotide composition.

Scheme 1.

For the model with two tensing steps, we introduce an additional attached state, the mid-tensing state (scheme 2). Attachment of the myosin head is taken to occur only for pretensing heads, whereas detachment does not occur after the first tensing step but only after the second. For both models we made the following simplifying assumptions, which are discussed in section 5 of the Supporting Material:

• 1.There is no competition between different myosin molecules for a given actin subunit.
• 2.The two heads of each myosin molecule behave independently of one another.
• 3.The compliant elements of the myosin head are Hookean, with constant stiffness regardless of the conformation of the attached head and whether the strain is positive or negative.
• 4.The stroke distance for a tensing step is constant and independent of load and velocity.
• 5.Tension during both shortening and lengthening is borne solely by cross-bridges.

Scheme 2.

Axial position (x) and strain (z) of an attached head

The variable x is used as a measure of the axial position of the actin subunit to which a myosin head is attached relative to a myosin crown (1,3). It is the axial strain in a pretensing head when attached to that subunit, and therefore the distance that the filaments would have to slide for the tension in that head to decrease to zero. Thus, for a pretensing head, x, the axial position of the actin subunit, and the strain, z, in the head attached to it, are equal. But if the head executed a tensing step, the axial position of the actin subunit would still be x, but the strain z in the head would increase to x + l. If there were two tensing steps with stroke distances l₁ and l₂, the strain z would be x + l₁ after the first step and x + l₁ + l₂ after the second.

The attachment and detachment of pretensing heads

Strain in the compliant element has a marked effect on the equilibrium of attachment of pretensing heads to actin. The work required to stretch the spring of the cross-bridge compliant element allowing the head to attach to an actin subunit at axial position x is κx²/2, where κ is the stiffness of the spring. This work term reduces the equilibrium constant for attachment by a factor of $\exp \left[-\kappa x^2/2k_{\text{B}}T\right]$ where k_B is the Boltzmann constant (0.013806 zJ K⁻¹) and T the absolute temperature (9,12). (Throughout this article, we express energies in zJ units. A zJ is the same as a pN.nm. For a temperature of 276 K, 1 k_BT is equivalent to 3.81 zJ.) The dependence on the axial position of the attached head (x) of the equilibrium constant for attachment of heads in the pretensing conformation is illustrated in Fig. 1 a. This equilibrium constant has a Gaussian distribution centered on x = 0. The high stiffness of the spring causes the distribution to be narrow, the equilibrium constant falling by a factor of 1/e when $x=\pm \sqrt{2k_{\text{B}}T/\kappa }$.

Figure 1.

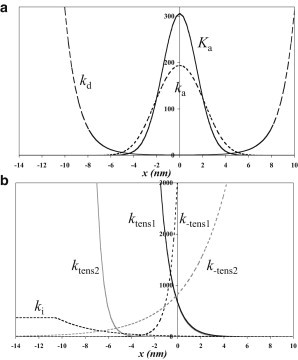
Effect of the axial position of an attached myosin head on the equilibrium and rate constants for steps in the cross-bridge cycle. (a) The attachment and detachment of heads to actin. $K_a^{\text{'}}$ (solid line) $k_a^{\text{'}}$ (dotted line) are the first-order equilibrium and rate constant for the attachment of pretensing heads at 1 mM actin, and k_d is the rate constant for the detachment of pretensing heads (dashed line). Attachment and detachment were calculated for the symmetric mode. (b) The tensing steps and the detachment of posttensing heads. k_tens1 and k_tens2 are the rate constants of the forward first and second tensing steps (black and gray lines, respectively), k_-tens1 and k_-tens2 are the rate constants of reverse first and second tensing steps (black and gray dotted lines, respectively), and k_i is the rate constant of detachment of posttensing heads from actin (black dotted line).

In previous studies (9,11,12), strain was assumed to affect attachment but not detachment. However, the rate of dissociation of a complex of two proteins, which occurs spontaneously in the absence of strain, can be enhanced by many orders of magnitude by force (43). This is because, when the two proteins move apart, their energy initially increases, reaching a peak at the transition state where they are separated by the interaction distance d before falling as the proteins become separated. In section 1 of the Supporting Material, we derive equations for the strain dependence of the rate constants for attachment and detachment of pretensing heads. We used principally the symmetric mode, where detachment of a head away from an actin filament can occur in any direction within a hemisphere (44). Fig. 1 a illustrates, for this mode, how the axial position of an actin subunit alters the rate constants of pretensing head attachment to and detachment from that subunit. The rate constant for attachment is a bell-shaped function with a peak at x = 0, and that for detachment is a U-shaped function with a minimum at x = 0.

Tensing step(s)

Strain has a large effect on the equilibrium constant of a tensing step (9,11,12). For a model with one tensing step, if a head is initially attached at axial position x, the energy stored in its compliant element is $\kappa x^2/2$. After this head undergoes a tensing step with stroke distance l, the head has strain (x + l) and the energy stored is now κ(x + l)²/2. Hence, the equilibrium constant for the tensing step is given by

$$K_{\text{tens}}^x=K_{\text{tens}}^{\text{AM}}\exp \left[\frac{-\kappa \left(l^2+2xl\right)}{2k_{\text{B}}T}\right]$$ (1)

where $K_{\text{tens}}^{\text{AM}}$ is the equilibrium constant for the tensing step for actomyosin in solution. For x = −l/2 the equilibrium constant for the tensing step is thus equal to that in solution. It equals unity when $x=[k_{\text{B}}T/\kappa l]\ln \left[K_{\text{tens}}^{\text{AM}}\right]-l/2$. At higher x values, the reversal of the tensing step is favored, and at lower x values, the forward tensing step is favored. The exponential factor increases by a factor of e for each reduction in the value of x by $k_{\text{B}}T/\kappa l$, so the equilibrium constant rises steeply as x becomes more negative (11). For a model with two tensing steps with stroke distances l₁ and l₂, the strain is x before the first tensing step and x + l₁ before the second tensing step. So the equilibrium constant for the first tensing step is obtained by replacing l in Eq. 1 by l₁, and that for the second tensing step by replacing x by x + l₁ and l by l₂. The equilibrium constant for the first tensing step reaches unity at a value of x, x₁, given by $x_1=[k_{\text{B}}T/\kappa l_1]\ln \left[K_{\text{tens}1}^{\text{AM}}\right]-l_1/2$, whereas the equilibrium constant for the second step reaches unity at a value of x, x₂, given by $x_2=[k_{\text{B}}T/\kappa l_2]\ln \left[K_{\text{tens}2}^{\text{AM}}\right]-l_2/2-l_1$. If the equilibrium constants for the first and second step are not too dissimilar, and l₁ and l₂ are similar, x₂ will be more negative than x₁ by ∼(l₁ + l₂)/2 or ∼5 nm for the models we shall be considering.

In section 2 of the Supporting Material, we derive equations for the exponential dependence on x of the rate constants for the forward and reverse tensing steps. The dependence on x of the rate constants for the two tensing steps and their reversal is illustrated in Fig. 1 b using the parameters for our best model with two tensing steps. Both the forward and reverse rate constants are strongly dependent on x. For the first tensing step, the reverse rate constant is slightly more dependent than the forward rate constant; for the second tensing step the forward rate constant is the more dependent.

Detachment of posttensing heads

To obtain an efficient muscle, k_i, the rate constant of the irreversible step that completes the cross-bridge cycle by detachment of the posttensing heads has to be dependent on strain. Specifically, following the suggestion of a transition state sensitive to strain (9), we assumed that for ADP release from posttensing heads, the heads have to suffer a thermal fluctuation to form a transition state with an increased strain of Δ_D. Hence, if the strain of posttensing heads, z > −Δ_D/2, then $k_i=k_i^{\text{AM}}\exp \left[-\kappa {\Delta }_{D}z/k_{\text{B}}T\right]$, where $k_i^{\text{AM}}$ is the rate constant in solution or at zero strain. So the rate constant decreases exponentially with z (and x). But for z ≤ −Δ_D/2, then $k_i=k_i^{\text{AM}}\exp \left[\kappa {\Delta }_D^2/2k_{\text{B}}T\right]$, i.e., it is invariant with x in this range. A plot of k_i versus x is included in Fig. 1 b.

Methods

Modeling of the actin filament

Initially, we modeled the actin filament as a linear array of subunits with an axial separation of 5.46 nm, ignoring the two-stranded helical character of the actin filament. Later, we assumed that the myosin heads of a crown could interact only with actin subunits in target areas of three subunits (45), alternating between the two long-pitched strands. We assumed an integral number (13) of actin subunits per turn of each of the long-pitched helical strands. Then, if actin subunits 1, 3 and 5 along a genetic helix form the first target area, the second target area is formed from genetic subunits 14, 16, and 18 and so on. The axial periodicity of these target areas is 13 × 2.73 = 35.5 nm.

Number of actin subunits considered

For an isometric contraction, we included an actin subunit in the calculations if its occupancy by myosin heads would be 0.0001 or greater. Where filament sliding occurs and the region of subunits that are labeled by a head moves along the actin filament, at every time interval, the pattern of labeling was revised and a subunit at the rear of the region was still included if its occupancy was 0.0001 or greater, but otherwise heads that were attached to that subunit were detached and that actin subunit was no longer included in the calculations. Conversely, at the growing end of the region we included a new actin subunit if its occupancy would reach 0.0001.

Non-Hookean filament stiffness

Initially, we assumed that the stiffnesses of both cross-bridges and filament were Hookean. However, there is good evidence that the stiffness of both thick and thin filaments increases with tension (46–50). Later, following Nocella et al. (50), we took the sarcomere stiffness to be proportional to tension. The resulting relation between filament stiffness and tension is given in section 3 of the Supporting Material.

Calculation of occupancies in an isometric contraction

We define the occupancy (state probability) of a molecular species as the fraction of all heads (detached as well as attached) that are present in that species. All calculations commenced with the calculation of the occupancies in an isometric contraction (see section 4 of the Supporting Material).

Relative stagger of myosin crowns and actin subunits

Because of the incommensurate nature of the actin and myosin periods, the axial position of the nearest actin subunit or target area relative to different myosin crowns varies over a distance equal to the actin repeat. The myosin crowns along a thick filament therefore need to be treated as different populations (40). We therefore calculated at each time interval the distribution of myosin heads and tension contributions for each of a set of staggers and then averaged the occupancies and tensions over the set. For models with a linear array of actin subunits, we used 11 equally spaced staggers covering the axial repeat distance of 5.46 nm. For models with actin target areas we used 39 staggers covering the axial repeat of target areas of 35.5 nm.

Calculation of occupancies during sliding

After calculating the distribution of heads for the isometric condition, we allowed the filaments to slide either at constant velocity or in response to a length step. The effect of filament compliance was modeled by taking the cross-bridges and filaments to contribute fractions c and (1 − c) of the isometric sarcomere compliance. The tension change in each time interval was first taken to be the same as in the previous time interval. Then, from the filament stiffness, the resulting elastic change in the length of the filament backbones could be calculated. Subtracting this from the change in half-sarcomere length gave an estimate of the filament sliding in that time interval. The change in occupancy of each species over the small interval of time was solved with bsimp, the stiff ordinary differential equation solver in the GNU Scientific Library. From this the resulting tension in each myosin head was calculated. Finally, a small adjustment to the tension change in the time interval could be made to equalize tension in cross-bridges and filaments. Rate constants were recalculated at every time interval that varied from 0.025 ms for the fastest sliding to 20 ms for the slowest.

Transient tension responses to length steps

To simulate the experimental data (37), releases of 6 nm/hs or smaller and a stretch of 1.5 nm/hs were made in 0.2 ms and releases of 9 or 12 nm/hs in 0.4 or 0.6 ms, respectively. The occupancies of the species were calculated at time intervals of 5 or 10 μs and the tension response was followed for 200 ms. The experimental tension-time traces (37) were digitized and tension values intrapolated at 0.1 ms intervals after normalization with respect to the isometric tension. The root mean-square (rms) deviation of the normalized tensions of the model from the experimental values was calculated in three time periods, 1), at 0.1 ms intervals from the end of the length step up to 4 ms; 2), at 0.1 ms intervals from 4 to 8 ms; and 3), at 0.2 ms intervals from 8 to 200 ms. The goodness-of-fit value for a model (the transient score) was taken as the sum of twice the rms deviation for time period 1 plus the deviations for time periods 2 and 3.

To obtain the T₁ and T₂ values of the model for each length step, the tension-time curves were analyzed as described (37). First, they were inspected to find the extreme tension (T₁) occurring during or at the end of the length step. The goodness-of-fit value for the normalized T₁ tension (the T₁ score) was taken to be the rms deviation between the model and the experimental normalized T₁ tensions for the five length steps from −6 nm/hs to +1.5 nm/hs. The subsequent tension recovery was then examined to determine if there was a maximum (for a release) or minimum (for a stretch) corresponding to the T₂ tension. If neither was found, a search for a point of inflection was made. If this was found, the tangent at this point was extrapolated back to the initial change during the length step to give the T₂ tension. If an inflection could not be found, the tension at the time for the end of phase 2 in the experimental data (37) for that length step was taken to be T₂.

Force-velocity relation

We compared the steady-state force-velocity relation of our models with the data of Edman (36). The goodness-of-fit value of a model (the pv score) was taken as the rms deviation of the normalized tensions of the model from those of experiment for 21 velocities, not counting the isometric contraction. The goodness of fit for the isometric tension (the P₀ score) was given by the modulus of the fractional deviation of the isometric tension from the experimental value of 1.6 pN/head (averaged over all heads) (51). The goodness of fit for the optimum thermodynamic efficiency (the efficiency score) was given by the modulus of the fractional deviation of the efficiency of the model from an experimental value of 40% (52,53).

Scoring of models

There is still considerable uncertainty about the value of the stiffness, κ, of cross-bridges, although we think the best estimate is 1.7 pN/nm (22). Later, any model with a cross-bridge stiffness <1.7 pN/nm, was penalized by calculating a goodness-of-fit value (the κ score) equal to the fractional difference between this and the model stiffness. Models with a cross-bridge stiffness >1.7 pN/nm were not penalized.

The total score for each model was obtained by summing the individual goodness-of-fit values for the characteristics described above, each multiplied by a weighting factor. The weighting factors were 100 for the force-velocity relation, 50 for the normalized T₁ tension, 10 for the transient tension responses, 1 for the isometric tension, 0.5 for the efficiency, and 2 for the cross-bridge stiffness.

Refinement of models

With the aim of achieving a global search of parameters, models were refined by minimizing the total score using simulated annealing with the program amebsa (54), followed by repeated downhill simplex runs. The starting simplex was created by incrementing or decrementing in turn each of the starting parameters by a fraction 0.2. The starting temperature was 1, and after every 20 iterations the temperature was reduced by a factor of 0.998. Programs written in C were converted for parallel programming with OpenMP protocols, and calculations were performed on the Bristol University high-performance computer BlueCrystal phase 2. Typically ∼100,000 models were examined and scored in each simulated annealing run.

Results

We started with 11 models with a single tensing step and 18 models with two tensing steps, requiring 13 and 17 parameters, respectively, to be defined. The parameters defining the starting models were chosen to fall at random within limits described in section 6 of the Supporting Material.

Refining models with one tensing step

Refinement produced a substantial improvement in the score of the models with one tensing step, and despite the starting models having very different combinations of the defining parameters, all but one of them converged to a single class with similar, but not identical, parameters. The stroke distance was ∼6.1 nm and the cross-bridge stiffness was ∼2.3 pN/nm. The parameters and properties of the best four of these models are summarized in Table 1 a. They gave a rather poor fit to both the steady-state and transient experimental data and had a relatively low thermodynamic efficiency (∼27%). Therefore, these models were rejected, consistent with previous arguments that models with a single tensing step are unsatisfactory (14,15).

Table 1.

Parameters, properties, and scores of best refined models

(a) Best models with one tensing step
Model	$k_a^{{\text{AM}}^{\prime }}$ (s−1)	$k_d^{\text{AM}}$ (s−1)	$k_{\text{hyd}}$ (s−1)	$k_{-\text{hyd}}$ (s−1)	$K_{\text{tens}}^{\text{AM}}$	$k_{\text{tens}}^{\text{AM}}$ (s−1)	$k_i^{\text{AM}}$ (s−1)	ΔD (nm)	κ (pN/nm)	l (nm)	d (nm)	f	c
276	627	1.15	33.5	4.60	91	621	19944	5.05	2.37	6.19	3.03	0.394	0.298
247	668	1.20	34.0	8.24	87	653	7980	4.74	2.27	6.21	2.99	0.400	0.307
249	740	1.22	33.2	7.51	78	706	7740	4.78	2.30	6.15	3.04	0.396	0.309
285	764	1.24	33.1	9.19	76	677	5879	4.55	2.37	6.11	2.98	0.390	0.299

Model	P0 (pN/head)	Isometric occupancy	Isometric ATPase (s−1)	Efficiency (%)	P0 score	Efficiency score	Pv score	κ score	T1 score	Transient score	Total score
276	1.60	0.511	0.828	27.0	0.000	0.162	1.904	0.000	0.118	1.945	4.129
247	1.60	0.515	0.786	27.2	0.000	0.160	1.950	0.000	0.115	1.924	4.149
249	1.61	0.516	0.838	27.3	0.005	0.158	1.959	0.000	0.116	1.919	4.157
285	1.60	0.514	0.771	27.4	0.002	0.158	1.981	0.000	0.118	1.903	4.161

(b) Best models with two tensing steps
Model	$k_a^{{\text{AM}}^{\prime }}$ (s−1)	$k_d^{\text{AM}}$ (s−1)	$k_{\text{hyd}}$ (s−1)	$k_{-\text{hyd}}$ (s−1)	$K_{\text{tens}1}^{\text{AM}}$	$K_{\text{tens}2}^{\text{AM}}$	$k_{\text{tens}1}^{\text{AM}}$ (s−1)	$k_{\text{tens}2}^{\text{AM}}$ (s−1)	$k_i^{\text{AM}}$ (s−1)	ΔD (nm)	κ (pN/nm)	l1 (nm)	l2 (nm)	d (nm)	f1	f2	c
340	266	0.857	100	4.18	234	173	2058	7672	332	0.698	1.70	5.60	4.55	2.16	0.402	0.851	0.546
345	277	0.850	100	4.18	195	127	2375	7844	313	0.950	1.70	5.41	4.66	2.18	0.388	0.830	0.548
347	276	0.799	100	4.66	210	127	2102	5111	324	0.808	1.70	5.59	4.63	2.21	0.408	0.783	0.537
304	352	0.722	99.9	12.7	185	59.6	1599	4657	289	1.16	1.70	5.53	4.52	2.28	0.401	0.672	0.509

Model	P0 (pN/head)	Isometric occupancy	Isometric ATPase s−1	Efficiency (%)	P0 score	Efficiency score	Pv score	κ score	T1 score	Transient score	Total score
340	2.21	0.545	0.253	38.3	0.379	0.021	1.052	0.000	0.142	1.667	3.260
345	2.22	0.554	0.186	39.6	0.389	0.006	0.984	0.000	0.148	1.742	3.269
347	2.20	0.554	0.195	38.9	0.378	0.014	1.012	0.000	0.137	1.734	3.274
304	2.24	0.571	0.132	40.0	0.398	0.000	0.966	0.000	0.113	1.860	3.337

Refining models with two tensing steps

The starting models with two tensing steps were similarly given parameters randomly assigned within upper and lower limits. While convergence occurred on refinement, it was now to four classes differing in the relative values of the first and second stroke distances. Table 1 b summarizes the final parameters, properties, and scores for the class of refined models with the lowest score. The models of this class had the first stroke distance (l₁) slightly greater than the second (l₂) and a cross-bridge stiffness close to the target value of 1.7 pN/nm. Compared with the models with a single tensing step, they had a much lower score and gave better fits to the force-velocity relation and the time course of the tension transients after length steps (Table 1). They also had the highest optimum thermodynamic efficiency (38–40%) similar to experimental estimates (36–40%) for frog muscle (52,53). They had an unloaded shortening velocity (v_max) of ∼1.75 nm/ms, similar to the experimental value (36), and an isometric occupancy of attached heads of ∼0.55. We chose model 340 as the best model. In the following sections, we describe the behavior of this best model during steady shortening or lengthening and in response to rapid length steps.

The force-velocity relation

The force-velocity relation of our best model with two tensing steps is compared in Fig. 2 a with data from the force-clamp studies of Edman (36) and the velocity-clamp studies of Ford et al. (55). The overall fit of the model with two tensing steps to both the shortening and lengthening limbs is reasonable, and superior to that with one tensing step. Close to the isometric point, the model with two tensing steps, like the experimental data, shows a steep rise in tension with increasing velocity. At higher lengthening velocities (>1 nm/ms) the give described by Katz (56) was also apparent, with the lengthening tension reaching a maximum ∼1.6 times the isometric tension. However, for small shortening velocities (∼0.3 nm/ms) the tension fell rather too steeply and the inflection in the plot at ∼78% of the isometric tension described by Edman resulting in a double hyperbolic plot was not obvious. Many models have not fitted this region of the force-velocity relation well (57), although others (11,16,57) are more successful. However, it should be noted that this feature is not consistently seen in mammalian muscle (58,59). At shortening velocities >1 nm/ms, the model tension closely resembled the experimental tension.

Figure 2.

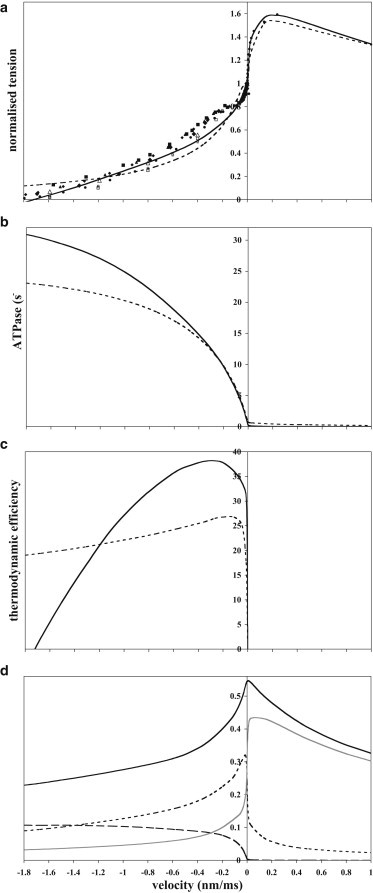
The effect of velocity on the mechanical and energetic properties. (a) Force-velocity relation for the models with two tensing steps (solid line) and one tensing step (dashed line). Solid symbols represent the experimental data of Edman (36) and open symbols those of Ford et al. (55). (b) The effect of velocity on the rate of turnover (ATPase) of the models with two tensing steps (solid line) and one tensing step (dashed line). (c) The effect of shortening velocity on the thermodynamic efficiency of the models with two tensing steps (solid line) and one tensing step (dashed line). (d) The effect of velocity on the occupancies of attached states for the model with two tensing steps. Shown are the occupancy of all attached heads (black line), pretensing heads (gray line), midtensing heads (dotted line), and posttensing heads (dashed line).

The experimental power output of frog skeletal muscle is maximal, 397 zJ/s/head (averaged over all heads and assuming an isometric tension of 1.6 pN/head), at a velocity of ∼0.63 nm/ms, i.e., about one-third the unloaded shortening velocity (36). The model gave a higher maximum power, 564 zJ/s/head, at a higher shortening velocity (0.81 nm/ms).

Turnover rate

The effect of velocity on the turnover rates (ATPase) of the cross-bridge cycle for the best models with one or two tensing steps is shown in Fig. 2 b. In isometric contraction the turnover rate for the model with two tensing steps was 0.25 s⁻¹. Although this was substantially below the reported value of 1.3 s⁻¹/head for intact muscle (60), the discrepancy may arise from the contribution of the sarcoplasmic calcium pump to the total ATPase. The models demonstrated a pronounced Fenn effect, an increase of the turnover rate with shortening velocity reaching 31 s⁻¹ for unloaded shortening, similar to the value calculated by Duke (11). The approximately hyperbolic dependence of the turnover rate on the shortening velocity resembles the biphasic dependence on velocity of total energy output in frog muscle (61,62). This Fenn effect arises because as the muscle shortens all attached heads become more negatively strained, causing the tensing steps and the detachment of posttensing heads to accelerate. Conversely, lengthening dramatically suppressed the turnover rate of the model; at a lengthening velocity of 1 nm/ms, the turnover rate fell to 0.005 s⁻¹. This sparing of ATP consumption during lengthening is consistent with experiment (63). This is due to the inhibition of the tensing steps when the pretensing heads become positively strained during lengthening.

Thermodynamic efficiency

Fig. 2 c shows the effect of velocity on the thermodynamic efficiency of the best model, assuming that the free energy of hydrolysis of ATP under cellular conditions is 83 zJ/molecule (52,53,64). The optimum efficiency (38.2%) was reached at a shortening velocity of 0.26 nm/ms, considerably lower than the velocity giving maximum power output as found experimentally. The efficiency of the model remained relatively high (>20%) over a wide range of shortening velocities from 1.2 to 0.004 nm/ms, consistent with experiment (65).

Fraction of heads in attached states

The velocity dependence of the fraction of attached heads for our model is shown in Fig. 2 d. In an isometric contraction, a relatively high fraction of the heads are attached (0.545). This fraction falls with an increase of shortening velocity, reaching 0.229 for unloaded shortening. This is broadly consistent with estimates from stiffness measurements on frog muscle (22,55,66). During lengthening, the occupancy of attached heads in the model also fell, but this was less pronounced than for shortening.

In an isometric contraction, 54.7% of the attached heads were in the pretensing conformation, 44.5% had executed only the first tensing step, and only 0.8% had executed both tensing steps. The fraction in the pretensing conformation steeply increased with lengthening velocity, and at lengthening velocities of 0.14 and 1 nm/ms it had risen to 86% and 93%, respectively. This fraction decreased initially steeply with shortening velocity but then more slowly with further increase of shortening velocity (Fig. 2 d). Reciprocally, the occupancy of the midtensing conformation decreased steeply with velocity around the isometric point and then more slowly with further increase in lengthening velocity. The occupancy of the posttensing state was very low in an isometric contraction or during lengthening but rose rapidly with shortening velocity, and at shortening velocities >1.5 nm/ms, it was the major attached state. The contributions to tension of each of the attached states are described in section 10 of the Supporting Material.

Transient tension response to length steps

Fig. 3 shows, for the best model with two tensing steps, the time course of the early tension recovery in response to a range of step releases and stretches. (Longer time courses are shown in Fig. S2 in the Supporting Material) These time courses show features similar to the experimental data from the anterior tibialis muscles of Rana temporaria (37) and R. esculenta (67). During phase 1 of a release, the tension fell from the isometric level (T₀) to a minimum (T₁) concurrent with the length change; for the larger releases, this minimum tension occurred before the end of the length step, because the early tension recovery was so fast. In phase 2, the time course of the early tension recovery to a value T₂ was biexponential, as we also found for the experimental data of Ford et al. (37). For releases up to 4 nm/hs T₂ was close to T₀, but for larger releases it decreased roughly parallel to the T₁ plot. In phase 3, the rate of tension rise decreased markedly or even reversed, and in phase 4, the tension slowly returned to the isometric level. For releases, the model gave a reasonable account of the time course of the early tension recovery, the rate increasing with the size of the release. For a stretch, the early part of the tension recovery was initially fast and similar to the experimental but it then slowed more than in the experimental trace. A similar result was found in the model of Piazzesi and Lombardi (6). We think it important that the initial rate of change of tension was similar for small stretches and releases.

Figure 3.

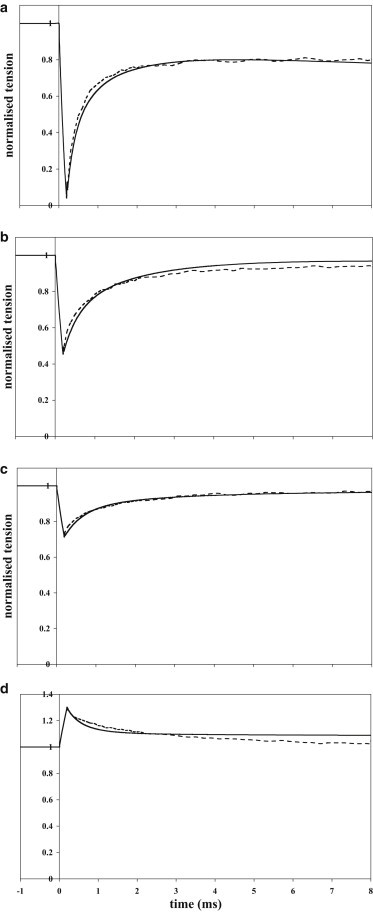
Early time course of tension transients after rapid length steps. Response of the model with two tensing steps (solid line) compared to the experimental data of Ford et al. (37) (dotted line). (a–c) Releases of 6 nm/hs (a) 3 nm/hs (b), and 1.5 nm/hs. (d) Stretch of 1.5 nm/hs.

Fig. 4 compares the dependence on the length step of the normalized T₁ and T₂ values for the best models with one or two tensing steps with the experimental values (37). The T₁ curves for the models closely resemble the experimental plot being linear for stretches and small releases but slightly curved for larger releases. The intercept on the length-step axis for these plots was −6.2 nm and that for the extrapolated linear part was −5.2 nm. The experimental T₂ plot for small releases and stretches is parallel to the length-step axis with normalized T₂ values close to 1 but curves downward for larger releases to give an intercept on the length-step axis of −13.9 nm. The T₂ plots for the models show similar features. The T₂ values for the model with two tensing steps are higher and those for the model with one tensing step lower than the experimental values. The intercepts on the length-step axis were −13.3 and −12.9 nm, respectively.

Figure 4.

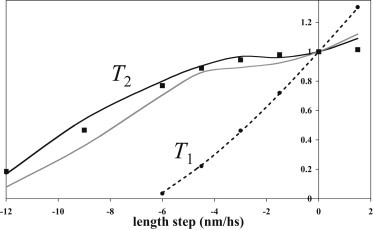
Dependence on length step of T₁ and T_2. Normalized T₂ data for models with two tensing steps (black line) and one tensing step (gray line) and experimental data from Ford et al. (37) (squares) are shown with normalized T₁ data for models with both two and one tensing steps (dotted line) and experimental T₁ data from Ford et al. (37) (circles).

Discussion

We have endeavored to produce a mechanokinetic model of the cross-bridge cycle that accounts not only for the lengthening as well as the shortening limb of the force-velocity relationship but for the full time course of the transient tension responses to a length step. The best model with a single tensing step gave a relatively poor fit to the experimental data and had a relatively low thermodynamic efficiency. It therefore could be rejected, although because of its simplicity it may prove useful in exploring some of the controversies concerning the cross-bridge cycle. The best model with two tensing steps gave a better fit to both shortening and lengthening limbs of the force-velocity relation and to the full time course of the tension transients after a length step and had a higher optimum thermodynamic efficiency. Its main features may be summarized as:

• 1.The model has two tensing steps with stroke distances of 5.6 nm and 4.6 nm independent of load. The sum of these stroke distances is 10.2 nm, close to the prediction from x-ray crystallographic studies of the myosin head of the total lever-arm swing.
• 2.The strain dependencies of the tensing steps indicate that both forward and reverse steps are strain-sensitive, unlike the model of Huxley and Simmons (25).
• 3.The first-order equilibrium constant for the attachment of heads is 272. This relatively strong attachment enables the pretensing heads to bear lengthening tension and thereby account for the lengthening limb of the force-velocity relation in a simple manner. However, we do not discount the possible existence of an initial weakly attached state (68) in rapid equilibrium with the detached state.
• 4.Detachment, as well as attachment, of pretensing heads is strain-sensitive.
• 5.The occupancy of attached heads in an isometric contraction is 55%. Although this is high compared with the estimates of 33% and 22% for muscles from rabbit and frog (R. esculenta) (69), there is considerable uncertainty about these values (22). From the intensity of actin layer lines in isometrically contracting rabbit muscle it was concluded that the occupancy of stereospecifically attached heads is 42% (70); the total occupancy of attached heads is likely to be even greater.
• 6.The model gave a high thermodynamic efficiency of 38%, resembling the experimental value of 36–40% (52,53).
• 7.Cross-bridges and filaments contribute about equally to the half-sarcomere compliance in isometrically contracting muscle.
• 8.The filament stiffness was non-Hookean.

Our model draws on previously published concepts concerning the cross-bridge cycle, including the kinetic pathway of actomyosin ATPase (18), the strain dependence of rate constants determined by transition state theory (9–11,14,15,25), the strain dependence of ADP release (5,9,10,14,15,71), and the concept that pretensing heads dragged to high strain bear lengthening tension (72). There have been several previous proposals that there are two, rather than one, tensing steps in the cross-bridge cycle (14,15,17,25,35,73). In Table S2, our model is compared with a selection of models of the complete cross-bridge cycle that have been used to fit the force-velocity relation and/or the tension transients after length steps. Despite its relative simplicity, our model most closely resembles the nine-state model of Smith and Mijailovich (15) in having two tensing steps, target areas of three subunits every 36 nm, filament compliance coupled with a relatively high cross-bridge stiffness, and a high thermodynamic efficiency. Their model differs from ours in considering the finite number of axial mismatches between actin sites and myosin heads along a half-thick filament rather than assuming a continuum, and by proposing that Pi release can occur after either tensing step. It also allows the binding of M.ADP and M.ATP to actin. A merit of our model is that it simulates the velocity dependence of lengthening tension by allowing the detachment, as well as the attachment, of pretensing heads to be strain-dependent. This obviates the need to have a special forced detachment step occurring only at high strains, allowing the pretensing heads to bear most of the tension when muscle is subject to ramp stretching. Further research is required to integrate our findings with the results of modeling of the kinetics of the attached pathway (5,13,23,24,42,74) obtained by changing the Pi and ADP concentrations. It is of particular importance to define the structural changes associated with the two tensing steps and the degree to which they are coupled to the release of Pi and ADP.

Number of tensing steps and magnitude of stroke distances

There is good evidence that for smooth muscle and nonmuscle myosin the working stroke occurs in two stages, the larger first step coupled to Pi release and the smaller second step coupled to ADP release (33). Skeletal myosin single-molecule studies have been interpreted to mean that here, too, there are two steps with stroke distances of ∼4 nm and 1 nm (35). The failure to observe any change in the angle of the lever arms when ADP is added to skeletal actoS1 has been explained (34) on the basis that the equilibrium constant for the second step coupled to ADP release may be large. Our modeling gives support for there being two tensing steps also in skeletal muscle. For our best model, the first stroke distance (5.6 nm) was only a little greater than the second (4.6 nm). Using Eq. S13a in the Supporting Material, these stroke distances combined with the occupancy of the pre- and mid-tensing heads in an isometric contraction account for the interval along the length axis between the T₁-T₂ intercepts. The existence of two tensing steps may help to reconcile the conflicting values of the stroke distance obtained from single-molecule studies (75–78) and the transient tension response to length steps (37). The first stroke distance, 5.6 nm, may correspond to that measured by single-molecule studies, with the sum of the two stroke distances accounting for the transient tension response.

It has been argued that because the average strain in an attached myosin head in an isometric contraction is only 1.5–2.3 nm, whereas the full sweep of the lever arm is ∼11 nm, there must be at least four tensing steps (28). This argument assumes that in an isometric contraction all attached heads are in similar states. However, our modeling shows that in an isometric contraction the same low average strain can be attained with less than half the attached heads having undertaken the first tensing step.

Detachment of pretensing heads

A feature of our model is a force-enhanced detachment rate of pretensing heads rising smoothly and continuously with force, rather than force detaching bridges only above a critical value of strain (8–10). Previously, forced detachment was treated as quite distinct from spontaneous detachment. Although it is unlikely that the force-enhanced detachment of heads is quite as simple as that in our symmetrical mode, the fitting of the lengthening limb of the force-velocity relation suggests that this type of approach is useful.

Value of cross-bridge stiffness

Our best model with two tensing steps had a cross-bridge stiffness of 1.7 pN/nm. Although it has been claimed based on x-ray data that the cross-bridge stiffness in the anterior tibialis muscle of R. temporaria is much higher (∼3.3 pN/nm) than that of rabbit muscle (1.7 pN/nm) (28,51), we have concluded that there is no compelling evidence that this is so (22). The rate constants of the tensing steps are exponentially related to κ, making it unlikely in our view that such a large difference could exist between species.

Our model offers insight into several aspects of the operation of the cross-bridge cycle.

Pretensing heads exert tension

A feature of our models is that in an isometric contraction a substantial fraction (54.7%) of the attached heads are in the pretensing conformation. This is reminiscent of the model of Huxley and Simmons (25), in which the pre- and posttensing heads were equally populated. But it contrasts with high-cooperativity models of the cross-bridge cycle, in which in an isometric contraction all the attached heads have similar conformations that are partway through the working stroke (28–30). In our model, pretensing heads make a significant contribution to isometric tension, as well as being the major contributor to lengthening tension.

Dependence of force and occupancy on velocity

The decrease of tension with shortening velocity is due partly to the decreasing number of attached heads and partly to their decreased strain, with an increasing number of heads having negative strain (64,79). We attribute the diminished occupancy of attached heads as the shortening velocity increases mainly to the increased rate of detachment of posttensing heads. In a similar way, the occupancy of attached heads falls with lengthening velocity due to the enhanced rate of detachment of pretensing heads as they become increasingly positively strained.

Events during sliding

The strain dependence of the two tensing steps shown in Fig. 1 b illuminates how the attached heads behave during a contraction. If in an isometric contraction one of the three actin subunits in a target area is aligned with a myosin crown, that subunit is nearly completely occupied, whereas the other two subunits have a very low occupancy. If the crown lies between two subunits within a target area, both subunits are partly occupied. If the crown lies outside the target area but within one actin subunit of it, only the nearest flanking subunit is partly occupied. If the head lies between two target areas, the nearest flanking subunits have a very low occupancy. When, during shortening or lengthening, filaments slide and a target area approaches a crown, the nearest flanking subunit becomes populated first, followed by the central subunit and then the far flanking subunit. With further sliding, only this last flanking subunit remains significantly populated, and when the crown is roughly midway between that target area and the following target area both are minimally populated. Due to the mismatch between the periodicities of the myosin and actin filaments, when one crown is aligned near the center of a target area, there will be other crowns along the half-thick filament aligned near the flanking subunits of other target areas, or between target areas. So at any instant of time, different target areas will be populated to greatly different extents and correspondingly will contribute very differently to tension. However, averaged over time, they contribute equally, the effect of filament mismatch being to smooth the tension during filament sliding.

The sum of the rate constants for the forward and reverse first tensing step in our best model is much higher than for the attachment/detachment steps, so the transition between attached states is much more rapid than the attachment and detachment of pretensing heads (Fig. 1, a and b) and the first tensing step is therefore nearly in equilibrium (11,12,25). The first tensing step is very unfavorable for heads with zero or positive strain. Only heads with x values more negative than −0.7 nm will undergo this step (11,12). This explains why in an isometric contraction a majority of the attached heads are pretensing and why the turnover of the cycle and ATP consumption is low. In slowly shortening muscle, a greater fraction of the pretensing heads reach this negative x value per unit time, after which they can execute the first tensing step and the resulting midtensing heads contribute more to tension. Yet unless these mid-tensing heads are dragged to x values more negative than −5.4 nm, they are more likely to revert to the pretensing state than to undertake the second tensing step, so ATP consumption is still relatively low. At higher shortening velocities, more heads reach x values more negative than −5.4 nm and go on to undertake the second tensing step, thereby increasing the occupancy of posttensing heads. However, only when the posttensing heads are dragged to x values more negative than −8 nm and hence have only a small strain are they more likely to detach (and therefore consume ATP) than revert to the midtensing state.

In section 11 of the Supporting Material, we discuss the wider implications of our model.