Detection of Cochlear Amplification and Its Activation

Abstract

The operation of the mammalian cochlea relies on a mechanical traveling wave that is actively boosted by electromechanical forces in sensory outer hair cells (OHCs). This active cochlear amplifier produces the impressive sensitivity and frequency resolution of mammalian hearing. The cochlear amplifier has inspired scientists since its discovery in the 1970s, and is still not well understood. To explore cochlear electromechanics at the sensory cell/tissue interface, sound-evoked intracochlear pressure and extracellular voltage were measured using a recently developed dual-sensor with a microelectrode attached to a micro-pressure sensor. The resulting coincident in vivo observations of OHC electrical activity, pressure at the basilar membrane and basilar membrane displacement gave direct evidence for power amplification in the cochlea. Moreover, the results showed a phase shift of voltage relative to mechanical responses at frequencies slightly below the peak, near the onset of amplification. Based on the voltage-force relationship of isolated OHCs, the shift would give rise to effective OHC pumping forces within the traveling wave peak. Thus, the shift activates the cochlear amplifier, serving to localize and thus sharpen the frequency region of amplification. These results are the most concrete evidence for cochlear power amplification to date and support OHC somatic forces as its source.

Introduction

Sound energy is carried by a sensory tissue and fluid wave that travels from the stapes in the base toward the apex of the cochlea. The cochlear traveling wave exhibits tonotopic tuning: at high frequencies the wave peaks in the cochlear base and at low frequencies in the apex. Hair cells (HCs) within the sensory tissue’s organ of Corti (OC) move with the wave. Mechanoelectric transduction of HCs depends on the relative motion between the reticular lamina (RL) and tectorial membrane (TM) that causes HC stereocilia to pivot (Fig. 1, C and D). When stereocilia pivot toward the tallest stereocilia (to the right in Fig. 1, C and D), transducer channels open, cations flow in, and the HC depolarizes (Fig. 1 D). Inner hair cell voltage modulation leads to neurotransmitter release, stimulating action potentials in the auditory neurons that contact the inner hair cells. In outer hair cells (OHCs), which are unique to mammals, voltage changes elicit mechanical forces via electromechanic transduction (Fig. 1 D). These forces act within the traveling wave to boost and sharpen the mildly frequency-resolved pattern of vibration of the passive cochlea (see Fig. 1 B). At its peak, the traveling wave motion is increased by a factor >100 for low sound pressure level (SPL) sounds and very little for high SPL sounds (1). Thus, active cochlear mechanics is compressively nonlinear. This compressive nonlinearity is the fundamental identifying feature of the cochlear amplifier.

Figure 1.

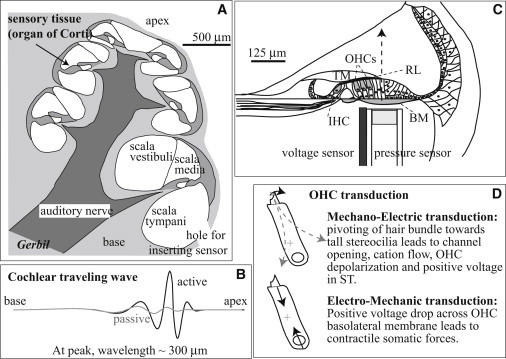
Experimental approach and cochlear electromechanics. The coiled structure of the mammalian cochlea (shown in cross section in A) is uncoiled in (B) to illustrate the sound-evoked cochlear traveling wave. The sensory hair cells are excited by the relative motion of the RL and TM, which pivots their stereocilia, leading to hair cell current and voltage via mechanoelectric transduction (C and D). BM motion is actively amplified by OHC-based forces via electromechanic transduction (B and D). To explore this synthesis of cell-level electromechanics and tissue-level mechanics, we introduced a dual pressure and voltage sensor into the cochlea’s scala tympani through a small hole in the bone, positioned it close to the BM, and recorded responses to sound stimulation in vivo, in gerbil (A and C). BM and TM = basilar and tectorial membrane, IHC and OHC = inner and outer hair cell, RL = reticular lamina, OC = organ of Corti, ST and SV = scala tympani and vestibuli. Positive displacement is defined as the direction from ST toward SV, along the z axis indicated by the arrow in (C). Voltage was measured relative to a reference electrode inserted into the tissue at the neck.

We probed the dynamics of cochlear amplification in vivo in gerbil, with spatially and temporally coincident voltage and pressure measurements at the sensory tissue’s basilar membrane (BM), a collagenous tissue supporting the OC (Fig. 1, A and C). To make coincident measurements we created a novel, to our knowledge, dual-sensor to measure pressure and voltage simultaneously at the same location (Fig. 1 C). At low-to-moderate stimulus levels the extracellular voltage could be interpreted as being predominantly from local OHCs (2) and the sound-evoked pressure at the BM is a measure of local cochlear mechanics. Beyond these primary measurements, BM displacement was estimated in the following way: Fluid displacement can be found by applying the linear and inviscid Navier-Stokes equation, $\nabla p=-\rho \partial v/\partial t$, which relates fluid pressure gradients and velocity. In that way the z component of fluid displacement at the BM was found. (Arrow in Fig. 1 C shows z axis.) The BM must move with the fluid, and so its displacement was assumed the same. Thus, $d_{BM}\approx 1/\rho {\omega }^2\Delta p/{\Delta z|}_{BM}$ (see section 1 in the Supporting Material and (3,4) for further explanation).

Pressure at the BM drives OC motion, leading to OHC voltage change (receptor potential). OHC voltage generates mechanical forces that enhance the local pressure and motion. Coincident pressure-voltage-displacement measurements expose the relationships between these intracochlear responses, so that the mechanics of cochlear amplification can be explored. Temporal coincidence is needed because cochlear activity is fragile and degrades in time when the cochlea is exposed for measurements. Spatial coincidence is needed to accurately determine the relative response phases because the wavelength of the cochlear traveling wave is only ∼300 μm where it peaks (5).

Materials and Methods

Animal Preparation

Experiments were performed in young adult gerbil. Animal preparation and single tone stimulation were as described in Dong and Olson (6) using procedures approved by the Columbia University Medical Center Institutional Animal Care and Use Committee (IACUC). After establishing the methodology, 17 experiments were performed, and data are shown from experiments in which the animal and cochlear condition remained good for the requisite several hours of experimentation. Ketamine was administered first to sedate the animal. Sodium pentobarbital was used throughout the experiment for anesthesia and the analgesic buprenorphine was administered every 6 h. At the end of the experiment the animal was euthanized with sodium pentobarbital. A tracheotomy was performed to maintain a patent airway. The animal core temperature was maintained at ∼37°C with a heating blanket. The dorsal surface of the skull was fixed to a head-holder with dental cement. The left pinna was removed and the bulla was exposed and widely opened with great care to access the cochlea. A small hole (diameter ∼200 μm) was hand-drilled through the bony wall of scala tympani (ST) at the turn one location with best frequency (BF) around 20 kHz. The cochlear condition was checked by compound action potential (CAP) threshold responses (threshold criterion ∼5 μV p-p) to tone pips, measured with an electrode on the bone surrounding the round window opening at several key time points during the experiments.

Sound stimulation and data acquisition

Pure tones were generated by a Tucker Davis Technology (TDT) (Alachua, FL) system III and delivered to the ear canal (EC) via a closed system by an electrically shielded Radioshack (Fort Worth, TX) tweeter. The sampling frequency of the TDT system was 200 kHz. Synchronization of the three data acquisition channels was checked and the third channel’s relative delay (<5 μs) was accounted for in the analysis. Stimulus and acquisition programs were written in MATLAB (The MathWorks, Natick, MA) and the TDT visual design studio. Responses were measured for ∼1 s and time-locked averaging was performed; the averaged data were stored in segments of 4096 points. The data were later analyzed by Fourier transform with MATLAB. Sound pressure levels are reported as dB SPL (decibels relative to 20 μPa peak). The SPL was calibrated within 3 mm of the eardrum using a 1/2 inch B&K probe tube microphone. The frequency-dependent transfer function of the probe tube microphone was accounted for when setting the SPL and analyzing the EC data.

Dual-sensor

Pressure sensor construction and calibration were introduced in Olson (3) and the pressure sensors of the present report had inner and outer diameters of 75 and 125 μm. The pressure sensor calibration is flat in frequency, with an example shown in Fig. S1. An isonel-insulated platinum wire electrode (AM Systems, Sequim WA) of outer diameter 28 μm was adhered to the pressure sensor’s side and cut to be approximately flush with the sensor tip. When measured at 1 kHz, the impedance of the electrode was ∼1 MΩ. The wire electrode’s frequency response was characterized as described in Baden-Kristensen and Weiss (7). At 40 kHz, the test electrode showed ∼2 dB amplitude attenuation and phase roll off of ∼30° (Fig. S1). This degree of low-pass filtering is consistent with the predicted electrode RC time constant of ∼1 μs, based on the isonel coating’s thickness (∼1.5 μm) and a 1 mm immersion depth (in experiments the immersion depth was 0.3 mm or less, which would result in a shorter time constant.) Both the pressure sensor and electrode (with their associated amplifiers) are broadband with mild low-pass filtering over the frequency range of interest. Their relative phase was for our purposes negligibly small and thus no phase correction was applied. The dual-sensor entered the cochlea through the ST hole, and was aimed at the sensory tissue (Fig. 1 C). A silver reference electrode was in the neck. Voltage was amplified with a differential amplifier with 100 MΩ input impedance (EG&G; PARC, Oakridge, TN). The sensor was advanced in micrometer steps with a motorized micromanipulator until contacting the BM, then retracted ∼10 μm. Responses were measured with pure tone stimulation over a wide range of frequencies and stimulus levels. The sensor was then retracted another 10 μm and another set of measurements was made. BM displacement was estimated from pressure and its spatial difference as described previously and in section 1 in the Supporting Material and (3,4,8).

Notes on pressure sensor perturbation and spatial resolution

The pressure sensor’s inner diameter is 75 μm, and it will respond to the pressure over that area. This is one-quarter of the 300 μm wavelength of the cochlear traveling wave in gerbil at the wave’s peak place at low-to-moderate SPL (see Fig. S3 and (5,9)). Thus, some local averaging occurs in the pressure measurement, especially at the peak. The voltage-pressure phase shift we describe in the Results section is at a frequency 0.5 octave lower than the peak, corresponding to a distance of 0.5 mm basal to the peak. There the wavelength is ∼1 mm, much larger than the sensor diameter, therefore averaging is less problematic. The spatial resolution of the voltage measurement is an issue that requires additional analysis, which is included in the Discussion section.

The sensor’s stiffness is ∼2 Pa/nm (3), which is similar to that of the BM in the base (reviewed in (9)). Its presence might perturb cochlear mechanics and this has been addressed in the past with measurements of CAP. CAP changes were on the order of 3 dB threshold elevation with the sensor close to the BM (4,6). In this report, the problem of perturbation is reduced by the simultaneity of the measurements; it would be a bigger problem if the pressure and voltage measurements were made sequentially, with different degrees of perturbation. The observation of negative resistance we describe in the Results section is based on small phase changes in pressure, and this result is therefore relatively susceptible to perturbation. The observation that negative resistance was most robust at low SPL, where cochlear amplification is largest, reassures the accuracy of the negative resistance observation. Nevertheless, the fact that wavelength varies with SPL could render the perturbation SPL-dependent and potentially lead to artifactual observations. However, wavelength changes are quite small; at the peak the change is ∼10% over 40 dB SPL (5), and see section 4 in the Supporting Material. In summary, the measurement technique has been examined for systematic problems and found to be reasonably reliable.

Results

Basic observations

The cochleae of this report possessed low-threshold auditory nerve CAP responses, indicating that surgery-induced damage was small. Figs. 2–4 show representative responses from animal wg165 that illustrate the main points, and repeatability is shown in Figs. 5 and 6. In points enumerated (i–iv) we describe the basic findings: i), at low SPL the voltage, pressure, and BM displacement were all tuned similarly to a BF of ∼24 kHz. With varying SPL, they were all compressively nonlinear (Fig. 2, B, E, and H). Normalized to the EC pressure, the voltage (Fig. 2 B), pressure (Fig. 2 E), and displacement (Fig. 2 H) responses at 30 dB SPL were respectively ∼250, ∼50, and 120 times greater than those at 90 dB SPL—this factor represents the degree of compression. Phases of voltage, pressure, and displacement all varied rapidly at frequencies around the BF with similar phase accumulation through several cycles, indicating that local traveling wave responses were dominant in the measured responses (Fig. 2, C, F, and I). The voltage phase underwent a phase shift at frequencies close to the onset of nonlinearity, which was not seen in the pressure or displacement. This phase region is identified in the gray dashed box in panels Fig. 2, C and F.

Figure 2.

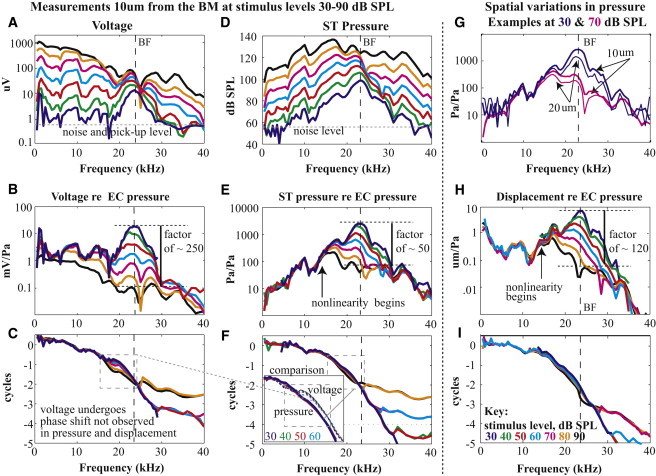
Characteristics of mechanical and electrical responses measured close to the BM, preparation wg165. The amplitude of voltage (A) and pressure (D) with pure tone stimuli varying from 30 to 90 dB SPL. (G) Pressure response amplitudes 10 and 20 μm from the BM. These and their corresponding phases were used to derive BM displacement. (B, E, and H) Voltage, pressure, and BM displacement amplitude normalized to EC pressure. (C, F, and I) Voltage, pressure, and displacement phase relative to EC pressure. Positive displacement corresponds to BM displacement toward SV (Fig. 1C). The inset in panel F contrasts the pressure and voltage phase in the gray dashed box region of C and F; for clarity high stimulus level results were excluded in the inset.

Figure 3.

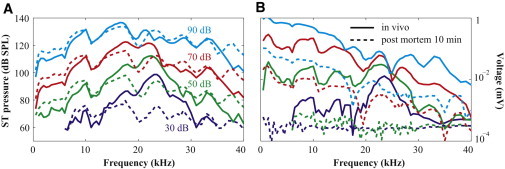
Physiological vulnerability of pressure and voltage measurements. (A) Amplitude of pressure. (B) Amplitude of voltage. Solid and dashed lines represent conditions in vivo (healthy) and postmortem, respectively. Sound stimulation was 30 to 90 dB in 20 dB steps (wg165).

Figure 4.

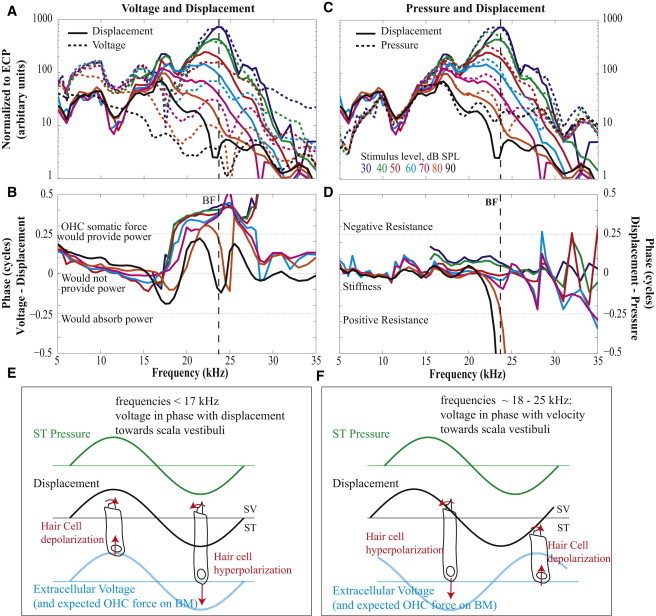
Comparison of pressure, displacement, and voltage. Pressure and displacement amplitude comparison (A) and relative phase (B). Displacement and voltage amplitude comparison (C) and relative phase (D). Schematic illustration of the phase relationship among pressure, displacement, and voltage at frequencies below the response peak (E) and within the peak (F).

Figure 5.

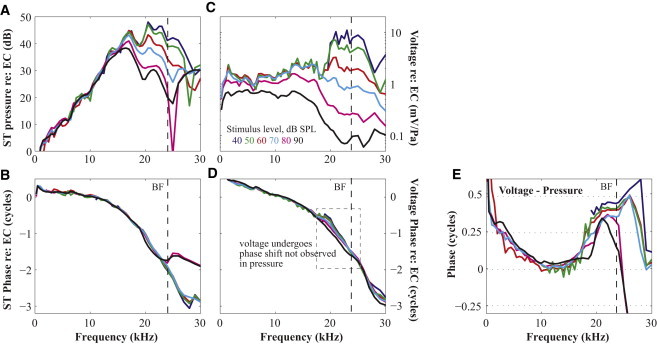
Characteristics of mechanical and electrical responses measured close to the BM in another preparation (wg154). The amplitude of pressure (A) and voltage (C) normalized to the EC pressure showed compressive nonlinearity with pure tone stimuli varying from 40 to 90 dB SPL. Phases of pressure (B) and voltage (D) show typical traveling wave phase accumulation. In D the phase-shift region is within the gray dashed box. Phase difference between voltage and pressure is shown in (E).

Figure 6.

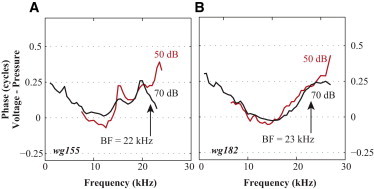
Further confirmation of voltage-pressure phase shift. Relative phase between voltage and pressure measured close to the BM in two additional active cochleae also show the phase shift slightly below the BF.

Just postmortem the pressure responses decreased substantially at low SPL, but not much at high SPL (Fig. 3); the postmortem pressure responses were linear (dashed lines in Fig. 3 A (4,6)). Postmortem the voltage responses fell into the noise level at 30–50 dB SPL and were greatly diminished at 70 and 90 dB SPL (dashed lines in Fig. 3 B). The residual voltage responses did not scale linearly, consistent with the site of nonlinearity residing in mechanoelectric transduction.

Beyond the first-order similarity, the differences between the pressure, voltage, and displacement responses are key to understanding the electromechanical interactions that produce cochlear activity. ii), Voltage had a greater degree of compression than pressure and displacement (Fig. 2, B, E, and H). iii), At low SPL where tuning was most pronounced, the low frequency side of the voltage peak was steeper than that of pressure and displacement (Fig. 4, A and C), and the voltage, which had been approximately in phase with displacement and pressure at lower frequencies, shifted to lead the displacement by slightly >1/4 cycle (Fig. 4 B). The steep slope on the low frequency side of the peak is reminiscent of tuning in auditory nerve fibers, which sometimes shows a notch separating the response peak and a lower frequency tail (10) that is not observed in BM motion.

Voltage-displacement phase indicates effective forcing by OHCs

At frequencies below that of the phase shift the voltage phase was as predicted by the transduction model proposed by Davis in the 1960s (11), in which upward displacement of the BM pivots the stereocilia to open ion channels, increasing the positive current flowing into the HCs and depolarizing them. The positive current continues through the cell and causes positive voltage in the ST. Thus, in the Davis model, upward displacement of the BM leads to positive ST voltage and this is what we observed at frequencies below ∼17–19 kHz, where the voltage and displacement were in phase (Fig. 4, B and E). Above that frequency the voltage underwent the phase shift, to lead displacement (Fig. 4, B and F). The frequency where the phase shift occurred approximately coincided with the onset of nonlinearity in the mechanical responses (Fig. 4 C, arrows in Fig. 2, E and H), and the shift produced advantageous OHC somatic forcing within the OC: Positive ST voltage corresponds to positive change in OHC voltage (depolarization), which is in phase with forces of contraction (Fig. 1 D, Fig. 4 F) (12). Thus, when ST voltage leads BM displacement by ∼1/4 cycle, OHC somatic force leads BM displacement by ∼1/4 cycle. Velocity always leads displacement by 1/4 cycle, thus OHC force is in phase with BM velocity. When velocity and force are in phase, power is delivered at frequencies above the phase shift, OHC somatic forces are timed to supply power to the cochlear traveling wave (Fig. 4 F and Fig. 1 B). For completeness, we must account for the fact that OHC transmembrane voltage will lag ST voltage, because the OHC membrane RC-filter frequency is lower than the RC-filter frequency of the cochlear scalae (13). Recent whole-cell measurements of OHC RC-filtering quantified this lag (14). Measurements were done on rat and gerbil OHCs from locations ranging in BF from 4 to 12 kHz, and their RC cutoff frequency increased with location BF. Extrapolation of the results predicts a cutoff frequency of ∼10 kHz for an OHC at the 20 kHz BF location, which would introduce an OHC phase lag relative to ST voltage at 20 kHz of ∼60° or less. Our ST voltage led displacement by ∼130° (Fig. 4 B), and so the OHC transmembrane voltage would lead displacement by 70°. Thus, after accounting for the OHC RC-filter, we still observed power delivery by OHCs.

Pressure-displacement phase shows power amplification

Observation (iii) showed that in the frequency region where responses were compressive, OHC forces were phased to supply power, and we would like to know whether these forces were sufficient to produce net power gain. Net power gain would appear as a negative resistance in the OC’s mechanical impedance, the quantitative relationship between the driving pressure and the resulting motion (15,16). In Fig. 4, C–F, we examine the ST pressure-BM displacement relationship of the data in Fig. 2. iv), Pressure and displacement were almost in phase, and their amplitudes showed similar tuning. Thus, the OC’s mechanical impedance was stiffness dominated through and above the BF. This is consistent with our recent report of mechanical impedance, made with simultaneous laser interferometer and pressure measurements through frequencies slightly lower than the BF (17). However, at the lowest SPLs, 30 and 40 dB SPL, the displacement phase led the pressure phase slightly but robustly at frequencies from 15 kHz (the low-frequency limit of displacement that was out of the noise) through 25 kHz (see Fig. 4 D). This phase indicates negative resistance: power being delivered to the traveling wave from the sensory tissue. (The large departures at 80 and 90 dB SPL and the phase swings above ∼27 kHz are not of particular interest to this study; they occurred when the pressure was fast-mode dominated (in fast-mode plateau) while the displacement was traveling-wave-mode dominated, as can be confirmed by referring to Fig. 2, F and I.)

Confirmation in other preparations

Fig. 5 shows ST pressure and extracellular voltage results from another preparation. Both pressure and voltage had compressive amplitude responses that peaked at ∼23 kHz at low SPL (Fig. 5, A and C), and showed traveling wave phase accumulation through several cycles (Fig. 5, B and D), evincing local responses. The low-frequency side slope of the voltage was relatively steep at low-to-moderate stimulus levels (40–60 dB SPL), and a clear phase shift of voltage relative to pressure was evident at ∼17 kHz (Fig. 5, D and E), close to the frequency for which nonlinearity appeared in the amplitude responses. Thus, the observations from preparation wg165—compressive nonlinearity in the peak region, traveling wave phase that evinced localized responses, and a phase shift that would activate cochlear amplification—are confirmed. Fig. 6 confirms the voltage-pressure phase shift in two additional preparations. Fig. S2 confirms the negative resistance finding.

Discussion

Voltage-displacement phase

The fact that the observed voltage-pressure phase shift (Figs. 2–6) indicates OHC power delivery was discussed in the Results section above, and provided motivation for the exploration for negative resistance in the pressure-displacement relationship. Here, we discuss the shift with respect to previous measurements. Past extracellular voltage measurements observed a similar shift in voltage (18). The results of one recent report of sequential measurements of BM displacement and extracellular voltage in guinea pig were similar to ours in many ways, but did not include the phase shift (19). This is likely due to the character of the phase shift and experimental methodology. The shift was subtle in some preparations, for example wg155, Fig. 6 A. In our highlighted preparation, wg165, after many hours of experimentation the shift was less abrupt and smaller. A subtle phase variation could be obscured in sequential measurements, in which small changes in measurement location and/or preparation condition are inevitable. The wire electrode used in our measurements did not low-pass filter the voltage signal significantly (see Fig. S1), thus no compensation was needed. In contrast, the glass electrode used by (19) low-pass filtered the signal above 2–8 kHz. Corrections for a given electrode were determined in situ and might render a subtle phase shift unremarkable. It is notable that a more recent report from the same laboratory (Fig. 5 of (20)) does show an increasing voltage-displacement phase as frequency increased through the BF. The frequency-dependent phase increase was mildly SPL-dependent from 45–80 dB SPL, similar to our results. The size of the increase through the frequencies reported was ∼25°, smaller than our >90° phase shift, but the lowest frequency shown was only 1/3 octave beneath the BF, which would correspond to ∼19 kHz in our preparation of wg165, a frequency midway through the phase shift. Thus, previous reports do suggest the presence of the phase shift we report and further measurements directed at probing the voltage-displacement phase with different techniques and species are warranted.

Explorations of voltage responses with a cable model

It was important to know whether key aspects of our voltage observations might simply be due to contributions to the voltage from distant OHCs. To this end, we made a linear cable model to predict extracellular voltage in the cochlea, similar to models that have been developed by others (19,21–24). The model was not meant to be very realistic—its purpose was to determine whether some of our more interesting voltage findings could be attributed to a simple summation of current from distant OHCs. In the cable model OHC transducer current was linearly proportional to BM displacement, and the extracellular voltage was proportional to a weighted sum of the transducer current decreasing exponentially with longitudinal distance along the cochlea. The model did not include saturation because our most interesting results were robust at a low stimulus level, 30 dB SPL, where saturation would be relatively small. It also did not include micromechanics within the OC. The model’s purpose was to test whether our interesting findings could be produced by a simple summation of responses, without the need for frequency-dependent micromechanics.

Fig. 7 illustrates the model implementation: Fig. 7, A and B, show BM displacement results from the sensor place in animal wg165, at 30 dB SPL; these are the representative data we used as input to the model for this explanatory figure. The blue line in Fig. 7 B is the phase data and the green line is the phase data after subtracting the known middle ear delay of gerbil, which is a first step. From these frequency response results, the spatial response at one frequency was calculated by applying the concept of scaling symmetry (9,25) and the known tonotopic map of gerbil (26) (Fig. 7, C and D). The spatial domain responses are shown for a stimulus tone of 15 kHz, but this frequency is not a critical parameter because the responses will be recast to the frequency domain. In Fig. 7 E, the displacement pattern is shown in blue and the exponential weighting function in red, the arrow gives the idea that this function is swept along to generate a weighted average of the blue curve at every location (process of convolution).

Figure 7.

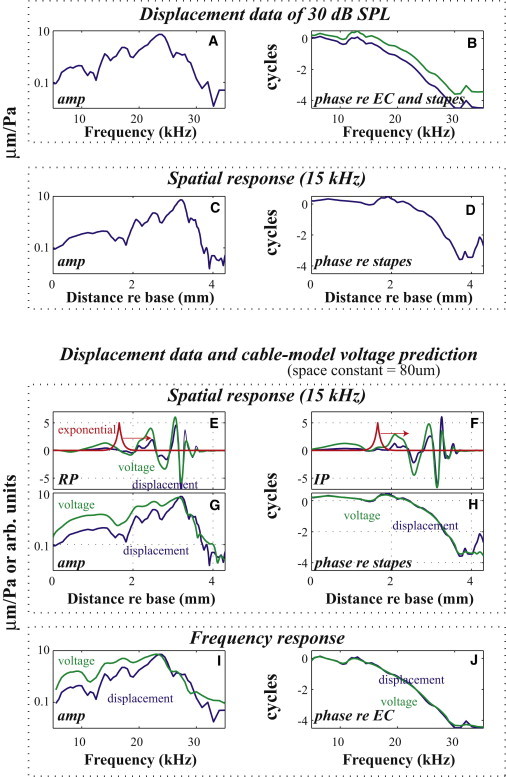
Cable model development. (A and B) Frequency response BM displacement observations. (C and D) Same data recast in the spatial domain. (E and F) Blue curves are the real and imaginary parts (RP and IP) of the spatial response pattern. Red curve shows an exponential function that represents the weighted average of current from OHCs along the cochlea. Green curve is the resulting voltage spatial pattern when the red curve is convolved with the blue. (G and H) Voltage predictions and BM displacement data in the spatial domain. (I and J) Same data recast in the frequency domain. Color on-line only.

The exponential space constant is a parameter that in a cable is based on longitudinal and transverse electrical impedances. Xue et al. (24) derived a frequency dependent space constant for the cochlea’s scala media, which in their derivation varied by a factor of 1.7 from 10 to 40 kHz (our frequency range of greatest interest). This variation is small enough that we regarded the space constant as a frequency-independent parameter. The cochlear literature includes a wide range of space constants, from 42 μm to 2 mm and longer. A space constant of ∼80 μm was necessary to produce extracellular voltages roughly in line with those we observed. This is close to the 42 μm space constant measured by Fridberger et al (19). Their study was similar to ours, with extracellular voltage measured close to the BM, and thus it was reasonable that the space constant they measured was applicable to our study.

The result of the weighted average, shown in the green curve in (Fig. 7 E), forms the simple cable model prediction of extracellular voltage. This step was carried out using both the real (Fig. 7 E) and the imaginary (Fig. 7 F) part of the displacement wave, to transfer the results back to amplitude and phase in Fig. 7, G and H. The voltage spatial pattern was recast as a frequency response, by reapplying the concept of scaling symmetry (Fig. 7, I and J). The green curve is the voltage prediction, the blue the original displacement data.

In Fig. 8 cable model results are shown at 30, 50, 70, and 90 dB SPL. The displacement curves are the data from Figs. 2 and 3, and the voltage curves are the cable model prediction, comparable to the voltage data in Figs. 2 and 3. Both the model voltage prediction and experimental voltage results show interference notches at 29 kHz that were not present in the displacement (green arrows in Fig. 8). Interference notches appeared in the model at frequencies for which the displacement phase varied rapidly, leading to phase cancellation between local and distant voltage sources. The prediction of interference notches was as expected, and we were interested in whether the cable model would predict other aspects of our observed voltage. We explored two specific questions: I), How does the predicted voltage compression compare with the displacement compression? The predicted voltage compression was smaller than the displacement compression (Fig. 8 A). This makes sense because the predicted voltage was a weighted average of the displacement data and in this averaging both linear and nonlinear regions contributed, diminishing the voltage compression relative to the displacement compression. However, this prediction was opposite to the observation in the data, in which there was a greater degree of compression in the voltage compared to displacement. The results pertaining to question (I) support the view that cochlear nonlinearity is based in HC mechanoelectric transduction, which was not included in the simple model. To appreciate this, hypothesize that the compression resides in mechanoelectric transduction. Compression will then be directly evident in the voltage response and in the active OHC electromechanical force. On the other hand, BM displacement and pressure at the BM are driven by both active OHC forces and passive (linear) forces, and thus would be less compressive than voltage. This is consistent with the experimental observations, and the hypothesis is supported. Thus, the greater compression in voltage than displacement in the experimental data supports the view that cochlear nonlinearity is closely related to mechanoelectric transduction (27,28). II), How does the predicted voltage phase compare to the displacement phase? The predicted voltage and displacement were generally in phase, with small erratic departures (Fig. 8 C). The extreme departures at 90 and 50 dB SPL are due to the predicted voltage plateau occurring at a lower frequency than the displacement (green arrows in Fig. 8, B and C). Most importantly, the experimental voltage’s smooth quarter-phase shift relative to displacement at a frequency slightly below the BF and phase elevation that extended through the peak (Fig. 4 B) is not predicted by the model, and thus is not due to contributions to voltage from more distant sources. A deeper look at the experimental data of Fig. 2 strengthens this conclusion. In the peak region both the voltage and mechanical responses will be relatively local and the locality of the responses is affirmed in the traveling wave phase accumulation observed in this region. Thus, the peak region at low-to-moderate SPL is robust against interference. (At the high levels of 80–90 dB SPL the pressure and voltage phases changed character, reasonably due to fast-mode contributions to pressure and distant OHC contributions to voltage, and those data can be excluded from consideration.) Exploring further, the voltage in the lower frequency region might have a substantial contribution from distant sources, and we will consider this next. The lower frequency region would have little phase accumulation at the measurement location; therefore, the best possibility for sources that produce phase cancellation would be further apical, from the BF regions of those tones. However, the linearity of the voltage responses at frequencies below 17 kHz up to 70 dB SPL argues against significant contributions from more apical regions, because these responses would be nonlinear at low and moderate SPL. In summary, the analysis of question II shows that the interesting voltage-displacement phase relationship can be considered to represent local activity, particularly at the low and moderate stimulus levels where it is most prominent. The phase relationship in the experimental data indicates that OHC excitation is governed not just by BM motion but also by micromechanical motions of the OC.

Figure 8.

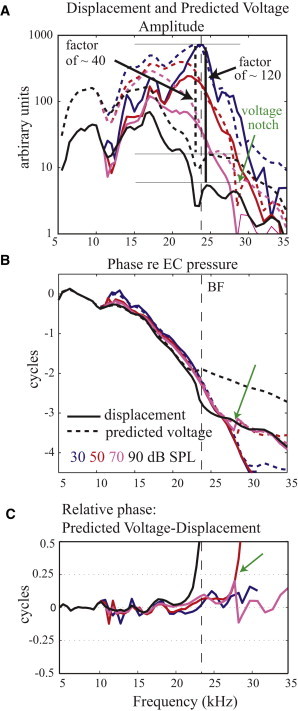
Cable model prediction of extracellular voltage. (A) Amplitude; (B) phase; (C) relative phase between voltage and displacement. Solid and dashed lines represent displacement and voltage, respectively. Voltage scale is arbitrary and was the same at all SPLs.

Negative resistance

Negative resistance is not an intuitive concept, but it can be illustrated with a simple picture: Imagine a child on a swing set. Gravity and mass allow the swing to oscillate. Resistance in the swing set will reduce the motion and to keep the swing oscillating an external force is required (mom, corresponding to the driving pressure). To be effective, mom pushes when the swing is heading back down. The relationship between the timing of mom’s force and the velocity of the swing indicates the presence of positive resistance in the swing set. To increase the swing amplitude the child starts to pump the swing and to limit the increase in amplitude mom begins to push during the upswing—the timing of her force and the swing’s velocity then indicates negative resistance in the swing set. The detection of negative resistance in the OC’s mechanical impedance means that an internal component, presumably OHCs, is pumping the motion.

The force exerted by isolated OHCs has been measured by others and provides a comparison to our data. We start by using our pressure data to estimate the local OHC active pressure. OHC action boosts the peak in the pressure and displacement responses, but because the enhanced responses at a given location are thought to reflect amplification that accumulates over some longitudinal distance, one cannot use the difference in enhanced and unenhanced responses directly to quantify local OHC force. However, in a region of negative resistance, the component of pressure that gives rise to the negative resistance is due to local OHC force and thus we can use this aspect of our data to estimate its size. For clarity, we will consider 20 kHz: close to the peak and a frequency where negative resistance was relatively prominent. At SPLs of 30 and 40 dB SPL the phase between pressure and displacement was ∼0.1 cycles (0.6 radians) (Fig. 4 D), signifying a component of negative resistance, presumably due to OHC-based pressure. This active pressure is P_amplitude × sin(0.6). From Fig. 2 D P_amplitude at stimulus levels of 30–40 dB SPL was ∼90 dB SPL, or ∼0.6Pa, so the local active pressure was ∼0.4Pa.

Based on isolated OHC data, can OHCs reasonably exert such a pressure on the BM? OHC somatic force is voltage dependent. In terms of force, isolated OHCs exert 30–100 pN/mV (transmembrane voltage) over a wide range of frequency (12,29). To estimate the OHC electromechanical force that is present in our measurements, we need to know the OHC transmembrane voltage, and our measurement is of the extracellular voltage in ST. We can use our voltage data to estimate the transmembrane voltage by combining them with other results in the literature. The extracellular voltage saturated at ∼50 μV and was ∼5 μV at 30–40 dB: the voltage at 30–40 dB was a factor of 1/10 of the value at saturation. Recent measurements of OHC intracellular voltage show that it saturated at ∼20 mV, even at high frequency (14). (As an aside, the measurement of OHC potentials at high frequency is an experimental challenge, and it would be very valuable to have these important results repeated and expanded upon.) By assuming that our observed ratio of the size of the extracellular voltage at 30–40 dB compared to its saturation value applies also to the transmembrane voltage, at 30–40 dB the transmembrane voltage would be ∼2 mV. Therefore, we will estimate the force/OHC at 20 kHz and 30–40 dB SPL as 100 pN/mV × 2 mV = 200 pN/ HC. If the OC were blanketed with OHCs we would just divide by the basal area (∼1 × 10⁻¹⁰ m²) to find the active pressure exerted by OHCs, but because OHCs occupy only ∼1/4 of the BM width, we will divide this calculated pressure by 4. This gives OHC active pressure of ∼0.5 Pa, similar to the active pressure calculation above, based on the measured negative resistance. This agreement is consistent with the hypothesis that OHC somatic forces are responsible for amplification. In a recent study cochlear compression disappeared in cochleae in which OHC somatic motility was photonically inactivated and the support for OHC somatic motility as the primary force behind amplification is growing (30).

Negative resistance means power gain, and studies and observations by others have also indicated power gain in the cochlea. The basic characteristic of active BM motion, in which tremendous amplitude nonlinearity is accompanied by only mild phase nonlinearity, argues for negative resistance (15,16,31) and otoacoustic emissions indicate the existence of a source of acoustic energy within the cochlea (32). Compared to these, our measurements are direct, and the detection of negative resistance only at low stimulus levels and terminating at ∼25 kHz (Fig. 4 D), which is close to the upper frequency defining the peak, is compelling direct evidence for power gain. (As a caveat, the driving pressure needed to find the OC mechanical impedance is the pressure difference across the OC, and we only measured the pressure on the ST side.) In most cochlear models the pressures on either side of the OC are equal in size with opposite polarity, in which case only the ST pressure measurement is needed. However, those models do not include the cochlear fast-modes, which are approximately in phase with stapes motion throughout the cochlea (33). When fast modes are significant, for example at high stimulus level and frequencies more than approximately half an octave above the BF, ST pressure is a poor approximation for pressure difference across the OC. (In Fig. 2 F, fast modes were dominant at frequencies above ∼30 kHz, with the pressure amplitude and phase plateau.) However, close to the peak at low and moderate SPL, ST pressure provides a reasonable approximation for driving pressure, because the traveling mode pressure is amplified and the fast modes are not. Thus, in the peak region the ST pressure at the BM and BM displacement can be used to explore OC mechanical impedance. (See (3,4) for an analysis that includes an SV pressure measurement and accounts for the fast pressure mode.) In a previous report from our lab (4) pressure measurements were used to look for negative resistance, which was detected, but not as robustly as in the present case. Recent in vivo measurements of BM and RL motion (34) showed OHC length changes that were not obviously indicative of OHC-based power gain, but the authors pointed out that the relationship between OHC force and length change will depend on the mechanical load on the OHCs; displacement measurements alone are not able to detect power gain.

It is notable that although we observed negative resistance only at low SPL (40 dB and below), the voltage phase shift that seems to activate the amplifier—providing the phasing needed for OHC electromechanical boosting—was apparent at least through 70 dB SPL. This is not a conundrum. The lack of negative resistance (net power amplification) at moderate and high SPL is likely due to the hair cell voltage saturating and thus not being able to provide enough OHC force to produce net power amplification at the higher SPL, even though it is of the proper phase for amplification.

Micromechanical basis for activating the cochlear amplifier

The observed voltage phase shift, which appears to initiate amplification, is likely due to a frequency-dependent variation in the forces driving the OHC stereocilia. In an excised preparation, Gummer et al (35) observed resonant TM radial motion, and illustrated how the resonance would introduce the forcing phase needed for power amplification. Such a resonance-induced change in OHC excitation could produce a voltage phase shift like that we observe, and cochlear models that include TM resonance predict phase shifts at the onset of amplification (36–39). However, these models generally do not treat the fluid realistically so cannot predict pressure accurately, and the present results encourage the development of a model with realistic fluid and TM resonance. In the anatomically realistic model of (40), power amplification occurs when the short traveling wave wavelength close to the best place and the longitudinal anatomy conspire to produce force of the proper phase. This model accurately predicts several experimental observations, including tuning and compressive nonlinearity in both pressure and motion and a large degree of compression with a relatively small amount of negative resistance. However, it is not obvious that this model would produce the phase shift we observe, and further exploration is needed. Another proposed mechanism for activating the cochlear amplifier is via the interaction of two coupled waves (41). The excised TM was found to support mechanical waves with wavelengths similar to those on the BM, providing a physical mechanism for this scheme (42). The interaction of two waves can give rise to abrupt phase shifts and models of this nature deserve further consideration.

Voltage-displacement-pressure measurements like those of this study, coupled to the recent RL and BM motion measurements (20,34), and previous studies of the OHC force-voltage relationship (12) provide rich experimental data for models of cochlear electro-micro-mechanics.

Conclusion

In this study, we explored the operation of the cochlear amplifier by measuring spatially and temporally coincident electrical and mechanical responses (extracellular OHC voltage and pressure close to the BM, displacement of the BM) in vivo with a novel, to our knowledge, intracochlear sensor. The observations allowed us to probe the electromechanical interactions within the sensory tissue that produce cochlear activity. Both the electrical and mechanical responses increased compressively with SPL, were tuned to the local BF, and showed traveling wave phase accumulation through several cycles, evincing the locality of the responses, particularly at low and moderate SPL. Beyond their basic similarity, the differences between the electrical and mechanical responses illuminated the active process of the cochlear amplification. i), The phase shift of voltage relative to mechanical responses at frequencies slightly below the peak (BF) was consistent with the onset of the cochlear amplifier. ii), At frequencies above the phase shift OHC force and BM velocity were approximately in phase, so that power was delivered by OHC forces. iii), The apparent size of OHC forces calculated with the data of the current report was consistent with the size known from isolated OHCs. iv), The relative pressure and displacement phase at low SPL demonstrated the existence of negative resistance: net power being delivered to the traveling wave from the sensory tissue, providing power amplification. To close, our trio of voltage-pressure-displacement measurements shows the activation of the cochlear amplifier and intracochlear power gain, and support OHC somatic forces as the source.