Introducing Titratable Water to All-Atom Molecular Dynamics at Constant pH

Abstract

Recent development of titratable coions has paved the way for realizing all-atom molecular dynamics at constant pH. To further improve physical realism, here we describe a technique in which proton titration of the solute is directly coupled to the interconversion between water and hydroxide or hydronium. We test the new method in replica-exchange continuous constant pH molecular dynamics simulations of three proteins, HP36, BBL, and HEWL. The calculated pK_a values based on 10-ns sampling per replica have the average absolute and root-mean-square errors of 0.7 and 0.9 pH units, respectively. Introducing titratable water in molecular dynamics offers a means to model proton exchange between solute and solvent, thus opening a door to gaining new insights into the intricate details of biological phenomena involving proton translocation.

Solution pH is an important factor in biology. Although neutral pH in extracellular medium accounts for balanced electrostatics and proper folding of protein structures, pH gradients across cell membranes induce large conformational changes that are necessary for biological functions, such as ATP synthesis and efflux of small molecules out of the cell. To gain detailed insights into pH-dependent conformational phenomena, several constant pH molecular dynamics (pHMD) methods, based on either discrete or continuous titration coordinates, have been developed in the last decade (1–4). In the continuous pHMD (CpHMD) framework (2,4), a set of titration coordinates {λ_i} are simultaneously propagated along with the conformational degrees of freedom. Although the original CpHMD method based on the generalized Born (GB) implicit-solvent models (2,4) offers quantitative prediction of pK_a values and pH dependence of folding and conformational dynamics of proteins (5), its accuracy and applicability to highly charged systems and those with dominantly hydrophobic regions are limited due to the approximate nature of the underlying implicit-solvent models.

Motivated by the above-mentioned need, three groups have made efforts to develop a CpHMD method using exclusively the explicit-solvent models (6–8). In our development, the titration of acidic and basic sites is coupled with that of coions to level the total charge of the system (8). To further improve physical realism, here we replace the coions by titratable water molecules, which not only absorb the excess charge but also enable direct modeling of solute-solvent proton exchange in classical molecular dynamics simulations.

To illustrate the utility of the new methodology, we applied it to the titration simulations of three proteins that were previously used to benchmark the GB-based CpHMD. Although this work does not explore specific interactions between titratable waters and proteins, the methodology can be further tested or improved to provide a rigorous way for modeling proton transfer in molecular dynamics, which is a computationally efficient alternative to the empirical valence-bond theory-based methodologies (9,10).

We define titration of water as:

• 1.Loss of a proton to give a negatively charged hydroxide,

$${\text{H}}_2\text{O}\rightleftharpoons {\text{OH}}^{-}+{\text{H}}^{+},$$ (1)

or

• 2.Gain of a proton to give a positively charged hydronium,

$${\text{H}}_2\text{O}+{\text{H}}^{+}\rightleftharpoons {\text{H}}_3{\text{O}}^{+}.$$ (2)

We now couple the titration of hydroxide (Eq. 1) with that of an acidic site of the solute in the CpHMD simulation,

$$\text{HA}+{\text{OH}}^{-}\stackrel{K_{\text{a}}}{\rightleftharpoons }{\text{A}}^{-}+{\text{H}}_2\text{O}\text{.}$$ (3)

The use of hydronium is avoided here to prevent a potential artifact due to prolonged attraction with A⁻. Analogously, we couple the titration of hydronium (Eq. 2) with that of a basic site,

$${\text{BH}}^{+}+{\text{H}}_2\text{O}\stackrel{K_{\text{b}}}{\rightleftharpoons }{\text{H}}_3{\text{O}}^{+}+\text{B}\text{.}$$ (4)

Thus, effectively, a proton is transferred between the solute and solvent. However, we should note that in CpHMD simulations, titratable protons are represented by covalently attached dummies (2,4). Through varying the atomic charges and van der Waals interactions, they are seen by other atoms in the protonated state but not in the unprotonated state (see Table S1 in the Supporting Material). Furthermore, the solution proton concentration is implicitly modeled through a free energy term (2,4).

In CpHMD, the reference potential of mean force (PMF) for titration is that of the model compound (blocked single amino acid in water) along λ (2,4). In the presence of cotitrating water molecules, it is necessary to add the PMF for the conversion of water to hydroxide or hydronium. One-nanosecond NPT simulations at ambient pressure and temperature were performed to calculate the average force, 〈dU/d,θ〉 at given θ-values, which are related to λ by λ = sin² θ (see Fig. S1 in the Supporting Material). Thermodynamic integration was then applied to calculate the PMF. We found that the average force can be accurately fit when assuming the PMF is quadratic in λ (Fig. 1). The same applies to the PMFs for titration of models Asp, Glu, and His. After testing on the titration of model compounds (see Table S2), we performed 10-ns all-atom CpHMD simulations with the pH replica-exchange protocol for three proteins: HP36, BBL and HEWL (see the Supporting Material for details). Most of the calculated pK_a values were converged in 10 ns per replica (see Fig. S3). Results are summarized in Table 1 and Fig. S4. Based on the 10-ns data, the root-mean-square (RMS) and average absolute errors are 0.9 and 0.7 pH units, respectively, while the largest absolute error is 2.5 (Glu³⁵ of HEWL). Linear regression of the calculation versus experiment gives R² of 0.8 and slope of 1.2.

Figure 1.

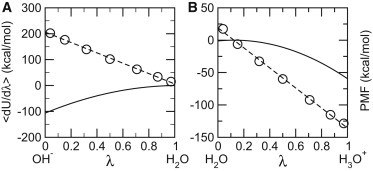
Average force and potential of mean force for converting a water molecule to hydroxide (A) and hydronium. (B) (Data points) Average forces. (Dashed curves) Best fits using a linear function, 2A(λ − B). (Solid curves) Corresponding potential of mean force.

Table 1.

Calculated and experimental pK_a values of three proteins

Residue	Experimenta	GBa	All-atom CpHMD
	Time (ns)b	0–1	0–5	5–10	0–10
HP36
Asp44	3.10 (0.01)	3.2 (0.1)	2.0	3.0	2.6 (0.5)
Glu45	3.95 (0.01)	3.5 (0.1)	4.3	4.5	4.4 (0.1)
Asp46	3.45 (0.12)	3.5 (0.1)	2.4	3.7	3.1 (0.6)
Glu72	4.37 (0.03)	3.5 (0.1)	4.4	4.4	4.4 (0.0)
BBL
Asp129	3.88 (0.02)	3.2 (0.0)	2.2	3.2	2.7 (0.5)
Glu141	4.46 (0.04)	4.3 (0.0)	4.0	4.4	4.2 (0.2)
His142	6.47 (0.04)	7.1 (0.0)	5.9	5.8	5.8 (0.0)
Asp145	3.65 (0.04)	2.8 (0.2)	3.0	3.1	3.1 (0.0)
Glu161	3.72 (0.05)	3.6 (0.3)	4.2	3.9	4.0 (0.2)
Asp162	3.18 (0.04)	3.4 (0.3)	2.9	3.5	3.2 (0.3)
Glu164	4.50 (0.03)	4.5 (0.1)	5.7	4.6	5.2 (0.6)
His166	5.39 (0.02)	5.4 (0.1)	4.4	4.4	4.4 (0.0)
HEWL
Glu7	2.6 (0.2)	2.6 (0.1)	3.6	3.4	3.5 (0.1)
His15	5.5 (0.2)	5.3 (0.5)	5.1	5.1	5.1 (0.0)
Asp18	2.8 (0.3)	2.9 (0.0)	2.5	3.3	2.9 (0.4)
Glu35	6.1 (0.4)	4.4 (0.2)	8.5	8.7	8.6 (0.1)
Asp48	1.4 (0.2)	2.8 (0.2)	−0.1	1.1	0.6 (0.6)
Asp52	3.6 (0.3)	4.6 (0.0)	5.4	5.6	5.5 (0.1)
Asp66	1.2 (0.2)	1.2 (0.4)	−0.6	0.8	0.3 (0.7)
Asp87	2.2 (0.1)	2.0 (0.1)	0.8	2.1	1.5 (0.7)
Asp101	4.5 (0.1)	3.3 (0.3)	6.1	5.7	5.9 (0.2)
Asp119	3.5 (0.3)	2.5 (0.1)	3.0	3.3	3.2 (0.1)
Maximum absolute deviation		1.8	2.4	2.6	2.5
Average absolute deviation (RMS deviation)		0.5 (0.7)	1.0 (1.2)	0.6 (0.9)	0.7 (0.9)
Linear fit R2 (slope)		0.7 (0.8)	0.8 (1.4)	0.7 (1.1)	0.8 (1.2)

^aTaken from Wallace and Shen (12). The pK_a's of BBL were recalculated.

^bSampling time per pH replica.

Breaking the simulations in two halves, we noticed that the second 5-ns sampling gave better agreement with experiment. The RMS deviation is reduced from 1.2 to 0.9 pH units, while the average absolute deviation is reduced from 1.0 to 0.6 pH units. The linear regression against experimental data is also improved, with the slope decreasing from 1.4 to 1.1 although R₂ remains the same. Comparing these second-half results with the GB-based simulations, we find that the RMS and average absolute deviations are about the same as the GB-CpHMD results; however, the all-atom simulations show a small systematic overestimation (regression slope >1), whereas GB simulations show a systematic underestimation (regression slope <1).

The improvement in the second halves of the simulations are seen mainly for residues involved in attractive electrostatic interactions, including Asp⁴⁴ and Asp⁴⁶ of HP36, Asp¹²⁹ of BBL, and Asp⁴⁸, Asp⁶⁶, and Asp⁸⁷ of HEWL. These residues are initially locked in salt-bridges or hydrogen bonds. However, in the second 5 ns, the attractive interactions weakened, leading to a decrease in the calculated pK_a shifts relative to the model values and better agreement with experiment. For instance, Asp⁴⁴ was initially in a salt-bridge distance from Arg⁵⁵. However, the salt-bridge positions were sampled less often in the second 5 ns (see Fig. S5), which explains the 1-unit reduction in the calculated pK_a shift. Significant fluctuation in ion-pair interactions was also observed in the work by Alexov (11). The carboxyl oxygen of Asp⁴⁶ was a hydrogen-bond acceptor with both the backbone amide and hydroxyl of Ser⁴³. These hydrogen bonds were less frequently sampled in the second 5 ns (see Fig. S6), leading to a decrease of the pK_a shift for Asp⁴⁶ by 1.3 units. These results indicate that extensive conformational sampling is necessary to give an accurate estimate of the ratio between the charged and neutral populations.

Limited conformational sampling is also a contributing factor to the overestimation of the pK_a shifts for buried residues (Table 1). In fact, we observed ionization-induced conformational changes for His¹⁶⁶ of BBL and Glu³⁵ of HEWL: they became more exposed to solvent when becoming charged as indicated by an increase in the solvent-accessible surface area (SASA) (see Fig. S7 and Fig. S8). The increase in SASA is correlated with the more frequent sampling of the states with λ close to 1, i.e., the deprotonated form (see Fig. S9). However, because Glu³⁵ was buried in the starting conformation and the transition between buried and exposed states is slow compared to the simulation length, the exposed state may not be sufficiently sampled, leading to overestimation of the pK_a shift.

In contrast to Glu³⁵, the SASA of Asp⁵² in HEWL is almost identical for both protonation states. The lack of conformational fluctuation is due to the strong hydrogen bonding with the side-chain amino group of Asn⁴⁶ and Asn⁵⁹ (data not shown). Overestimation of the pK_a shifts for buried residues can also be attributed to the limitation of the additive force field which underestimates dielectric response in protein environment (more discussion see Supporting Material) of the pK_a shifts for buried residues.

Finally, to ascertain if the presence of hydroxide/hydronium introduces artifacts, we studied the interaction between hydroxide/hydronium and the titratable sites/ions. Comparing the hydroxide/hydronium with respective chloride/sodium ions, we find that the spatial distributions are nearly identical (see plots of distance distributions and radial distribution functions in Figs. S10–S13). However, the relative occupancy of the hydroxide around the neutral Asp/Glu, positive histidine, or sodium ion is 2–3 times as that of a chloride. The water-bridged interaction between sodium and chloride ions becomes much weaker when chloride is replaced by hydroxide or sodium is replaced by hydronium. By contrast, the occupancy of the hydronium around the solute is similar to that of the sodium. Furthermore, similar pK_a results for these proteins were obtained when coions were used instead of titratable waters (data not shown). Thus, we believe that potential artifacts related to the ionized forms of water are negligible. Work is underway to further understand the limitations of the methodology and to explore applications to protein dynamics coupled to proton transfer.

In summary, we have developed and tested titratable water models for use in all-atom CpHMD simulations. Although the benchmark pK_a calculations indicate a comparable accuracy as the GB-CpHMD method, the all-atom method offers physical rigor and most importantly, it is applicable to systems that cannot be studied with GB-based simulations such as lipids and nucleic acids. We anticipate that the accuracy of this methodology can be further improved by incorporating the new-generation force fields that account for polarization. The coupling between proton titration of water and solute offers a computationally efficient way to model proton transfer in molecular mechanics simulations.