Bridging the gap between science and decision making

Abstract

All decisions, whether they are personal, public, or business-related, are based on the decision maker’s beliefs and values. Science can and should help decision makers by shaping their beliefs. Unfortunately, science is not easily accessible to decision makers, and scientists often do not understand decision makers’ information needs. This article presents a framework for bridging the gap between science and decision making and illustrates it with two examples. The first example is a personal health decision. It shows how a formal representation of the beliefs and values can reflect scientific inputs by a physician to combine with the values held by the decision maker to inform a medical choice. The second example is a public policy decision about managing a potential environmental hazard. It illustrates how controversial beliefs can be reflected as uncertainties and informed by science to make better decisions. Both examples use decision analysis to bridge science and decisions. The conclusions suggest that this can be a helpful process that requires skills in both science and decision making.

Most decisions are made quickly, based on feelings, past experiences, associations, habits, trivial consequences, or obvious preferences (1). For example, I made the decision to give a presentation at the National Academy of Sciences's Sackler Forum within a few minutes of receiving the invitation, based on my positive associations with the organizers and a feeling that this would be an interesting and novel experience. Some decisions deserve a slower and more deliberate approach, involving collection of information, obtaining advice from experts, formal evaluation, and analysis. For example, a few years ago, before deciding to accept a job offer as director of an international institute, I spent many days collecting and analyzing information and comparing the decision with staying at my home institution.

This article is about personal and policy decisions that require a significant amount of deliberation because the decision problem involves one or several of the features below:

• • important consequences

• • uncertainty

• • conflicting objectives

• • multiple stakeholders

• • complexity of the decision environment

• • need for accountability

For these types of decisions, science almost always does or should play a role. Unfortunately, scientific information is rarely accessible in a format useful for decision making. This paper shows how to provide a bridge between scientific knowledge and important personal and policy decisions.

Scientific knowledge is not easily accessible to lay people and policy makers. At its most arcane level, scientific knowledge is embodied in scientific journal articles and scholarly books that only a small group of scientific peers can understand. At the same time, decision makers have questions that are not easy to answer scientifically: for example, “Is genetically engineered food safe?” or “What are the risks of nuclear power plant accidents?” Answering these questions involves both challenging issues of the definition of safety and risk and significant uncertainty in scientific knowledge. As a result, there are no unqualified scientific answers, and many answers require responsible expressions of uncertainty.

The research literature relevant to bridging science and decision making includes risk communication (2, 3), science communication (4), and decision analysis (5–8). This paper emphasizes a prescriptive approach, based on decision analysis, to improve the use of science in decision making. Other papers in this issue of PNAS describe how science is in fact used (or ignored) and how scientific organizations and the information they provide are perceived by people.

The next section will provide a framework for bridging scientific knowledge and decision making through a formal analysis of beliefs and values. The subsequent two sections illustrate this framework with two examples, one personal and one from public policy. The last section will provide some conclusions and recommendations on how to improve the use of science in decision making.

Framework for Bridging Science and Decision Making

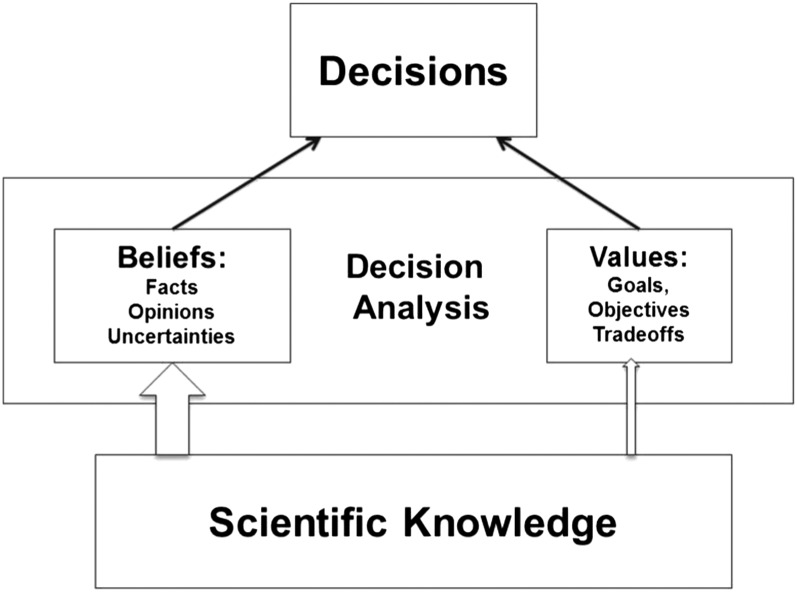
Most theories of decision making postulate that decisions are or should be based on two pillars: beliefs and values (Fig. 1). A decision maker’s beliefs are a reflection of his or her perceptions of reality, including facts, opinions, and uncertainties surrounding them. Beliefs can and should be informed by science. (This use is different from the notion of beliefs that cannot be confirmed and are instead a matter of faith or religion). A decision maker’s values reflect his or her sense of what to strive for or to achieve, including goals, objectives, and associated tradeoffs. This dual concept exists in all decision theories, including prescriptive ones like expected value theory, expected utility theory (9), and subjective expected utility theory (10), and descriptive ones like prospect theory and cumulative prospect theory (11, 12), as well as all other generalized expected utility theories (13). Decision analysis is applied decision theory (14). It includes models of beliefs and values and methods to quantify them. Beliefs are modeled as probabilities of events or probability distributions over uncertain quantities. Relationships between beliefs are modeled with influence diagrams or Bayesian networks, using Bayes’s theorem to link beliefs at different nodes. Values are modeled as multiattribute value functions or, when risk attitude matters, as multiattribute utility functions. Together, belief and value models are combined through the expected utility model—by multiplying probabilities of events with utilities of consequences and by summing these products over events.

Fig. 1.

Framework for linking decisions to scientific knowledge through models of beliefs and values.

These models can be exercised without any reference to science at all, merely by using a decision maker’s beliefs and values, whether they are informed by science or not. However, Bayesian statisticians and analysts take it for granted that beliefs are updated by information and that expert opinions matter when revising beliefs. Therefore, scientific knowledge—through established scientific facts or expert opinion—can and should influence the beliefs of decision makers (see the wide arrow in Fig. 1).

The relationship between scientific knowledge and values is more tenuous (as indicated in Fig. 1 by a narrow arrow). Many authors have noted the importance of values when making decisions (for examples, see refs. 15 and 16). Models incorporating values include cost–benefit analysis (17) and multiattribute utility analysis (6). Economists have explored the value of both publicly traded and nontraded goods and services in the context of cost–benefit analysis. In many economic studies, values are inferred from observable transactions in the market; for example, higher wages for riskier jobs reflect the value of taking on risks. In other studies, values are elicited through surveys in which members of the public are asked to express their willingness to pay for certain goods and services. These studies provide scientific guidance on how to place values on the consequences of decisions. An example is the value of avoiding the loss of a statistical life, which has been estimated to be around $6–7 million (18). Decision analysts have developed similar procedures to elicit values directly from decision makers and stakeholders (19).

In summary, scientific knowledge has a strong role to play in any theory of decision making that is built on beliefs and values. The question remains how to incorporate scientific knowledge into beliefs and values and thus to provide a bridge to decision making. Before answering this question, I will illustrate the framework with two real applications. The first one is a very personal decision that my wife and I faced 26 y ago. The second one is a public policy decision faced by the Public Utilities Commission of California in the mid-1990s. Both decisions involved the use of decision analysis to improve the communication of scientific information with the decision makers and stakeholders.

Personal Decision

When my wife was in the eighth month of her pregnancy with our first child, her gynecologist informed her that our baby was in a breech position (head turned up and feet pointing down). Given the advanced state of her pregnancy, it was unlikely that the baby would roll back into a normal birth position (head down) spontaneously. The gynecologist therefore recommended turning the baby manually in a controlled hospital environment. A couple of days before the planned procedure, my wife expressed some misgivings about the procedure, and I agreed to call the doctor and ask for more information.

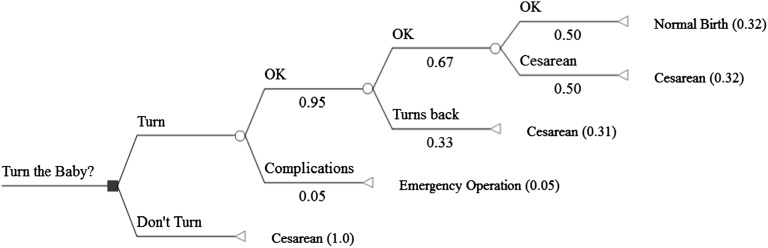
The next morning I called the doctor from my university office and asked her to discuss the pros and cons of the planned procedure. She interpreted this as the concerns of an over-anxious father and husband, and she assured me that the procedure was absolutely safe and painless and that she had done this many times in her professional career. Unbeknownst to her, I had loaded a decision tree program on my computer and a rudimentary tree was now on my screen showing the first two branches of Fig. 2. My plan was to record her answers in this decision tree as we went along in our discussion.

Fig. 2.

Decision tree for the decision on whether or not to turn the baby. Squares denote decision nodes, circles denote chance nodes, and triangles denote end nodes. At the end nodes, the outcomes are either a normal birth, a normal Cesarean delivery, or an emergency Cesarean operation.

The doctor first assured me that this procedure is harmless and involved few, if any, risks. She explained that the procedure involved a manual manipulation of the belly to move the baby into the normal birth position. I confirmed with her what my wife had already told me, namely, that in the case of not turning the baby, the birth would be scheduled as a Cesarean section, because a regular delivery would be too risky. I noted that at the end node of this branch as “Cesarean.” I did not ask whether the baby might roll spontaneously into a normal birth position, if she did not turn it. I later found out that this occurs sometimes, and, had I thought of it, I would have added this as another event node after “Don’t turn the baby.” However, in subsequent analyses, it turned out that including this event node would not change the conclusions.

My next question was whether there was any chance of complications during the attempt to turn the baby. She suggested that sometimes it was difficult to achieve the desired result, and, on very rare occasions, the baby could get strangulated on the umbilical cord. This seemed to me to be a very serious complication, but she explained that, even in this case, there would be no risk to the life of the baby, because under the controlled hospital conditions, they would immediately initiate an emergency Cesarean section and deliver the baby—although 1 mo prematurely.

I now was getting a bit skeptical and added the branches “OK” and “Complication” after the decision to turn the baby in Fig. 2 and asked for an order of magnitude probability of complications (1:10? 1:1,000?). The doctor again assured me that this was an extremely small risk. Complications like this had occurred to other colleagues in her hospital, but she clearly was not comfortable with giving me a numerical probability estimate. Given my experience with the overconfidence of experts (20), I assigned the branch complications a probability of 0.05, almost certainly too high, but with the satisfaction that I now had a placeholder for this important probability.

Next, I asked, more out of curiosity than expecting any interesting insights, what would happen after the baby was successfully turned. She very quickly said that, in a fair number of cases, the baby rolls back into its old breech position, either shortly after the procedure or sometimes within a day or two. The incidence rate that she gave me for this astounded me—about one in three cases—and I noted this by adding another event node with two new branches and the respective probabilities in my tree. I did not ask whether this roll back after turning the baby could lead to complications like strangulations and moved on. Later analyses concluded that including another roll back event in the decision tree would not have changed the decision either.

By now it seemed that the path to a normal birth position was shutting down quickly. So I asked, partly out of intellectual curiosity, partly to make the point that a normal birth was unlikely, what the chances were that my wife would have a Cesarean delivery even if the baby was in a normal birth position. After a brief look at my wife’s record, she indicated that this could be a fairly high chance, possibly close to 50–50, because my wife was already in her mid-thirties. In addition, I knew that doctors had a predilection for Cesareans to make life easier for themselves and their patients. So I added this branch and gave the Cesarean branch a probability of 0.50.

I now knew that the chances of having a normal birth when turning the baby—the main reason for doing this procedure—was only about one third (0.32) (the product of the probabilities of the branches leading to this event, noted at the end of the decision tree). In contrast, the chances of having a regular Cesarean were almost double that (0.63), along with the remaining chance of having a complication, possibly serious enough to warrant an emergency Cesarean delivery and a 1 mo premature baby. I thanked the doctor and decided to conduct some sensitivity analyses, which consisted of changing the three probabilities (probability of complications, probability of the baby rolling back, and probability of a Cesarean after a successful procedure and no roll back) through a reasonable range. These analyses suggested to me that it was probably not worthwhile to turn the baby even when using probabilities that favored the success of the procedure and no roll back.

This concluded the “belief” side of my decision analysis. It was informed by science, through the interview with the doctor. I later examined the decision tree and the probabilities by reading the scientific literature, which did not lead to substantial changes in the initial probability assessments. The two questions that I did not ask also did not change my assessment. Considering that the baby might roll spontaneously into a normal birth position without the procedure would only confirm the decision not to turn the baby. Complications during a spontaneous roll back could occur after both decisions, and there was no reason to assume that complications would be more likely or more severe without turning than with turning the baby.

The “value” side was almost entirely a matter of my wife’s judgment. (The word “almost” was added in a recent draft. The values of my wife could have been affected by a more scientific description of the nature of the three consequences. For example, considering the pain and late effects of a Cesarean delivery might have changed her judgment of the relative value of a normal birth vs. a Cesarean delivery.) When I returned home that evening, I told my wife that I had talked to the doctor and had gotten some useful insights, but I still needed her assessment of the relative value of a normal birth vs. a normal Cesarean vs. a situation in which turning the baby would lead to complications, including an emergency delivery by Cesarean section. It did not take me long to discover that she was close to indifferent between a normal birth and a regularly scheduled Cesarean delivery, and we even talked about when to schedule the delivery. This pretty much settled the case. I used several values scores for the three possible consequences, starting with a value score of 100 for a normal birth, 90 for a regular Cesarean, and −100 for an emergency Cesarean. With these scores or any numbers close to it, the expected value of turning the baby was less than the expected value of not turning her.

As a decision analyst, I now saw a clear reason why we should not turn the baby, and this reason was supported by many additional sensitivity analyses, varying the three probabilities and value scores simultaneously. Fortunately, the results of this analysis were completely consistent with my wife’s intuitive choice, and she told me that she had come to this conclusion herself by reading about the procedure. Her main concern was with the high probability of the baby rolling back after first turning it. She was (and still is today) a bit dismissive about the value of my “fancy analysis.” However, we jointly decided not to do the procedure, and my wife asked me to call the doctor to cancel the appointment to turn the baby.

The next morning, I called the doctor and explained to her that my wife and I had discussed the procedure, the possible complications, and the fact that she most likely would have a Cesarean delivery anyway and that, as a result, we decided against the procedure. The doctor, who seemed somewhat taken aback, stressed the value of a normal birth (her values) and her skill at avoiding complications, but in the end did not put up much of a fight. About a month later, she delivered our baby through a successful Cesarean section. Our daughter is now a healthy and beautiful 26-y-old.

This case illustrates that it is possible to capture relatively complex scientific information and to combine the factual and probability judgments of the scientific expert (my wife’s gynecologist) with the value judgments of the decision maker (my wife) to clarify an important personal decision. It showed that a simple analytical framework—in this case a decision tree—can be a useful aid for communication. Perhaps we were fortunate that both the analysis results and my wife’s personal conclusions were the same. However, even if they had diverged, the analysis would have provided a useful perspective for a further dialogue between my wife and her doctor. As a final note, the medical profession has made great strides in using decision analysis to inform medical decisions and to communicate with patients using decision trees and similar analytic devices. In fact, many articles in the journal Medical Decision Making are devoted to this topic.

Public Policy Decision

In 1979, Wertheimer and Leeper (21) published an article suggesting a statistical association between the proximity of living near electrical power lines and the incidence of childhood leukemia. Since that time, numerous studies have been conducted exploring the possible association between features of power lines and other electrical equipment and several health effects. Over 30 y later, the potential source of health effects has been narrowed down to the magnetic component of electromagnetic field (EMF) sources. However, no causal explanation has been found that explains how low frequency magnetic fields can cause or promote cancer, and some scientists believe that there exists no physically plausible explanation for this association. Nevertheless, many members of the public, especially those who live near power lines, remain concerned.

In the mid 1990s the California Public Utilities Commission (CPUC) initiated a major research program intended to examine policy options in light of the uncertain scientific evidence about EMF exposure and health effects. The CPUC asked the California Department of Health Services (CDHS) to oversee this program, which was funded by contributions from the electrical utilities. One project initiated by the CDHS was to examine policy options for changing the power grid and land use to reduce EMF exposure. An interesting feature of this study was that it was supervised by a “Stakeholder Advisory Committee,” consisting of representatives of the CPUC, major utilities in California, organizations representing residents who lived near power lines, health officials, unions, and others. I was the principal investigator of this study, which lasted for about 2 y (22); this section is based on von Winterfeldt et al. (22).

The major task in this project was to link science and engineering knowledge about EMF and its potential health effects to the CPUC’s policy options. It was important that this project be done in close collaboration with the stakeholders and the representatives of the CPUC. The major complications were that the association between EMF exposure and health effects was very uncertain and highly disputed by some stakeholders, that some of the options to reduce EMF exposure were extremely expensive, and that the values of properties located near power lines might be reduced due to publicity surrounding the EMF issue.

An important part of this project was to frame the decision problem in a way that reflected the stakeholders’ concerns and the CPUC’s capacity for making decisions. The belief side involved developing information about the costs and benefits of alternative policies, including consideration of uncertainty about health effects, costs, and other factors. The value side involved defining objectives for the alternative policies and tradeoffs between them. It turned out that, for most electrical powerline configurations, three types of policy alternatives existed:

• i) No change at this time.

• ii) Moderate mitigation measures to reduce fields, for example by compacting the power lines or reversing the flow of the electrical currents to obtain a partial field cancellation effect.

• iii) Undergrounding the power lines, which allowed a tight compaction of the lines, thus leading to a strong field cancellation effect and concentration of high fields only very near the underground line.

We interviewed the stakeholder groups separately to get a sense of their beliefs and values. It soon became clear that most utility representatives did not believe that EMF exposure had health effects and they were primarily concerned with the costs and unintended side effects of mitigation. The residents were concerned with health effects and property values and favored undergrounding. After interviewing all stakeholders, we identified 19 value-related concerns. After some preliminary analysis, we found that only four mattered, in the sense that they could make a difference in the policy choice:

• i) Health effects (measured as expected life-years lost)

• ii) Costs (measured as discounted lifecycle cost in dollars)

• iii) Property values (measured as total loss or gain of property values in dollars)

• iv) Outages (measured as number of person outage hours over a 35-y time period)

The reason for eliminating the remaining objectives was demonstrated to and accepted by the stakeholders involved in this project. This in itself was a major accomplishment because it focused the debate on the issues that mattered and simplified the subsequent analysis.

A major part of the project was to estimate the possible extent of health effects assuming that EMF is a health hazard. We defined “health hazard” as an elevated risk due to exposure of magnetic fields (expressed as a risk ratio of 2 or more) for several possible health end points, including childhood leukemia, adult leukemia, brain cancer, breast cancer, and Alzheimer’s disease. We convened an expert panel, which concluded that the highest probability of a hazard was for childhood leukemia. We considered several possible dose–response functions, including a linear time-weighted average (TWA) of exposure levels measured in milliGauss (mG) and several threshold functions. There is also some discussion in the literature that other characteristics of electromagnetic fields—such as transients and harmonic content—matter. We initially explored some of these metrics but did not pursue them further. Most reasonable dose–response functions correlated highly with the linear TWA exposure, which we used for the remainder of the analysis.

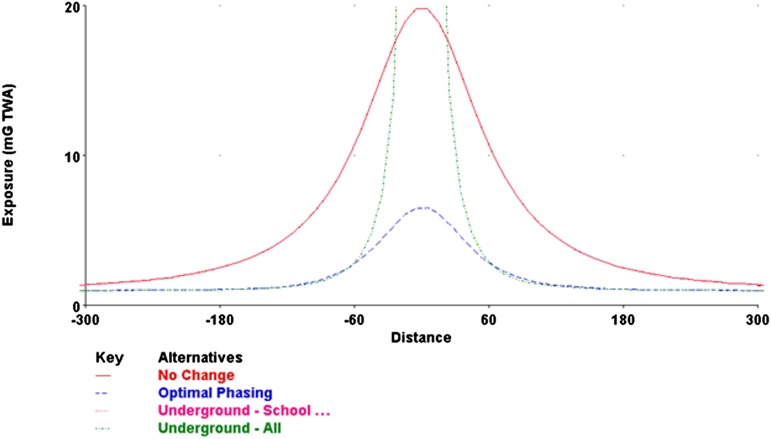
We developed detailed engineering models of EMF exposures surrounding power lines of various types and subsequently estimated health effects for given exposure levels, dose–response functions, and health end points. Fig. 3 shows the results of exposure calculations for a 115-kV powerline. The graphs plot the level of magnetic fields, measured in milliGauss, as a function of the distance from the center of the line for three options: no change, moderate mitigation (in this case through optimizing the current flow), and undergrounding. The right-of-way of this line was 100 feet from each side of the line. This figure shows that the reductions of the fields at the edge of the right-of-way by using both undergrounding and moderate mitigation were substantial.

Fig. 3.

EMF exposure profiles for different mitigation options. The figure shows exposures in milliGauss (TWA, time-weighted averages) as a function of the distance from the powerline. The red profile is for the no-change alternative, the blue profile is for the moderate mitigation alternative (optimal phasing), and the green profile is for undergrounding. Note that undergrounding has a high exposure near the centerline, but low exposures at a distance. Modified from (22).

We then estimated the typical number of people exposed at various distances from the powerline and used several dose–response functions with different shapes and slopes to estimate health effects over a 35-y period of operating the line. The results, on a per mile basis, were that the 35-y loss in life-years would be about 68 life-years for the no-change alternative, if EMF is a hazard. The moderate mitigation alternative would reduce this to about 12 life-years lost, and the undergrounding alternative would reduce this further to 1 life-year lost. These estimates were converted to expected life-years lost by multiplying the probability that EMF is a hazard with the life-years lost, if EMF is a health hazard (see “EMF health” row of Table 1, where we assumed that the probability of EMF being a health hazard was 0.10, a number confirmed by the expert panel).

Table 1.

Expected consequences of three mitigation alternatives for a 115-kV powerline for 1 mile and 35 y

Alternatives/expected consequences	No change	Rephasing	Underground
EMF health, life-years	6.8	1.2	0.1
Cost, $ (discounted)	574,016	577,436	3,773,049
Property values, $	$0	$0	−1,685,333
Outage, h	11,966	11,966	11,154

Producing cost estimates, although seemingly more straightforward, turned out to be complicated by the demands of some stakeholders to provide exceedingly detailed cost break-downs. We hired a technical cost estimation company for this purpose, which provided ranges of cost estimates for each alternative. We used the midpoint of these ranges for a base-case cost estimate and varied costs through a total range covering half the cost at the low end and twice the cost at the high end to reflect differences in engineering environments. In Table 1, these costs are represented in the “Cost” row. The costs for the no-change alternative include the costs of operating and maintaining the line for 35 y. The moderate mitigation alternative is only marginally more expensive, but undergrounding costs are substantial.

Property value impacts were also very hard to estimate. Credible estimates of property value losses due to the proximity of power lines range from 5% to 10%, mainly due to visual impacts and noise, even without considering the EMF issue (23). Residents claimed losses of 20% or more due to the EMF concern. Existing property value studies did not allow us to disentangle the effects of EMF exposure from other factors. We therefore used a base case of 10% depreciation and a high-end of 20% depreciation to estimate property value losses using typical housing densities and prices in California. The no-change alternative did not affect housing prices. The moderate mitigation alternative did not change the visual appearance of the power lines and thus was unlikely to reduce the EMF concern of potential home buyers. For undergrounding, the concern would disappear, leading to a corresponding appreciation of housing prices along the line. In our example, this would be about $1.7 million in appreciation for 50 houses per mile, including the appreciation due to improved aesthetics and reduction of noise.

The impact on outages was very controversial, and it took us some time to collect outage data for different types of power lines, both overhead and underground. We measured outages in terms of total person outage hours for 35 y, which combined incidence and duration of the outages. With these data, we established that undergrounding reduced outages for lower voltage classes (equal to or below 69 kV) but increased outages for higher voltage classes (115 kV and above). In our example, the total outage hours, however, did not differ very much among the alternatives.

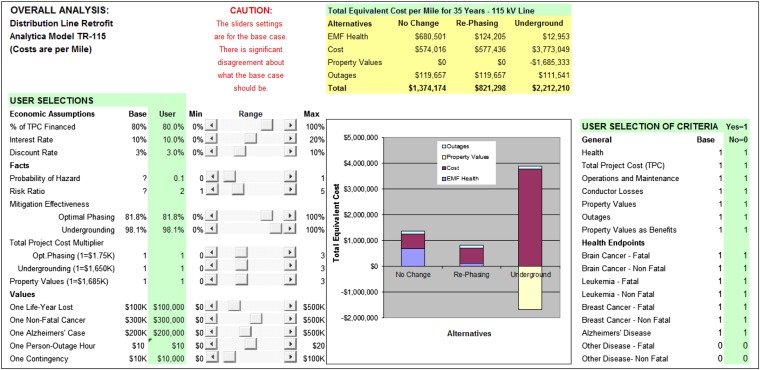
The above paragraphs and Table 1 describe how we translated science and engineering knowledge into the “facts” required to shape the beliefs of the stakeholders and the decision maker, the CPUC. To provide a sound basis for the decision, we also needed to take into account the stakeholders’ and decision maker’s values. In particular, we needed to reflect the tradeoffs between the four major value-related concerns: health, cost, property values, and outages. Cost and property values were already measured in dollars. We reviewed the literature on the value of life and health effects and found that a reasonable first cut valuation of saving or extending a life by one year is about $100,000, which is equivalent to about $8 million per life (18). We also found substantial evidence that the loss of electricity due to a 1-h outage is valued at about $10 per person. By using life-years as a unit for trading off the value of life into equivalent costs, we implicitly accounted for the higher value of a child (longer remaining life expectancy) vs. an adult (shorter remaining life expectancy). We also considered the value of nonfatal cancers, which we gave a base-case value of $300,000, considering both the medical costs and the lowered patient health status. We discussed these tradeoffs with the stakeholders, and they agreed with the base case, provided that we used appropriate ranges for them in our analysis (see Fig. 5 below for the ranges).

Fig. 5.

User interface to interact with the EMF mitigation model. Users can control all model inputs by moving sliders between a range of numbers. As a result, the total expected equivalent costs and the associated graph will change. Users can also select which criteria they want to use for the analysis (right side of the figure). Modified from (22).

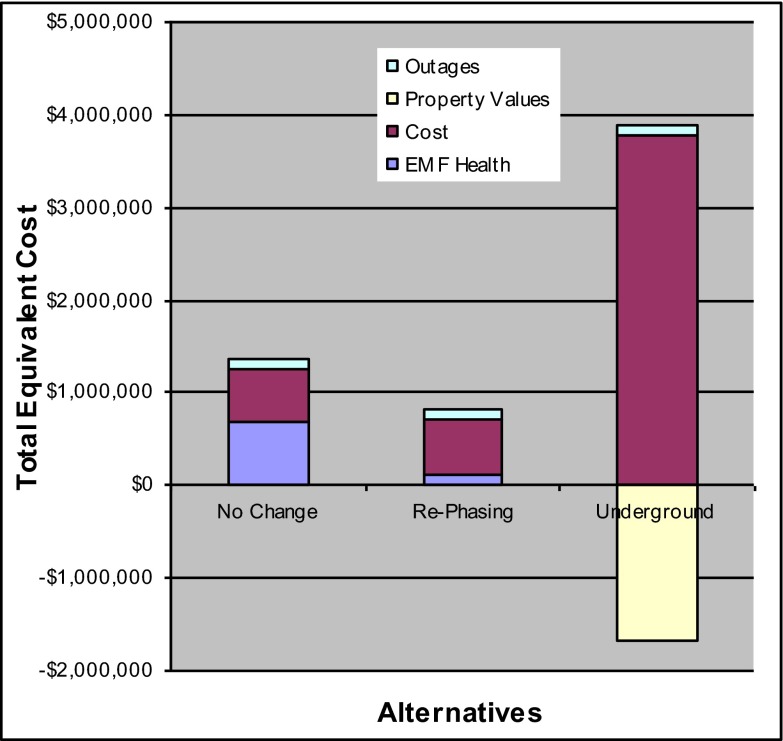
With the consequence estimates in Table 1 and the two value judgments about health effects and outages, we were able to convert all consequences into equivalent dollar costs and calculate the total equivalent expected costs for each alternative as displayed in Fig. 4. This figure shows that—at least for the base-case estimates and this example—the total equivalent cost of the rephasing alternative was substantially lower than that for both the no-change alternative and the undergrounding alternative.

Fig. 4.

Total expected equivalent costs for three alternatives to mitigate EMF exposure from a 115-kV powerline. Equivalent costs are the product of the consequences in each objective and the costs per unit of consequences. Expected equivalent costs are the product of the probability of obtaining consequences and their equivalent costs. The graph shows the expected equivalent costs broken down by the four mitigation objectives. Modified from (22).

The base-case analysis represented in Fig. 4 was only the starting point. All stakeholders took issue with one or more base-case estimates. We therefore needed a device to represent the ranges in our estimates. We chose to represent these ranges by providing sliding scales for all critical variables in the model, which allowed the stakeholders to set their estimates according to their own beliefs and values (Fig. 5). The ranges were deliberately wide, and none of the stakeholders argued that estimates should have been more extreme. We also allowed users of this model to down-select health endpoints—for example, to consider only childhood leukemia and ignore other health effects. The consistent finding was that the order of the equivalent expected costs in Figs. 4 and 5 stays the same for almost all reasonable settings of the sliders (i.e., moderate mitigation has the lowest expected equivalent cost, followed by no change, followed by undergrounding). The only way to make the no-change option win was by setting the probability of health effects to zero. The only way to make the undergrounding option win was by setting property value gains at or above 20%.

In short, many sensitivity analyses and interactions with the stakeholders suggested that inexpensive moderate mitigation options are superior to the no-change or undergrounding options. The CPUC had, in fact, chosen this option in a 1994 ruling for new powerline construction that required that up to 4% of new construction cost be used for EMF reduction. Our findings supported this regulation. Our findings also suggested, and the CDHS recommended, implementing a similar rule for retrofitting existing powerlines. However, the CPUC never acted on this recommendation, primarily because the energy crisis in California overshadowed all other issues soon after our study was completed.

The stakeholders expressed satisfaction with the analysis but remained divided about their preference for the best option—residents continued to prefer undergrounding, and utility representatives preferred no change or moderate mitigation at low cost. It is probably fair to say that they agreed to disagree. However, the analysis put their disagreements in sharp focus—they were primarily about property values and, to a lesser degree, about health effects.

In addition to this study, many other studies were conducted, both in California and elsewhere in the United States, to improve the understanding of the relationship between EMF exposure and health effects. In addition, significant efforts were made to better communicate the scientific findings to the lay public (24). No smoking gun has been found that would unequivocally prove that EMF exposure is a health hazard, and only occasional epidemiological studies remind us of this possibility. As a result, the EMF issue has all but disappeared from the public agenda.

This example used a decision analysis framework as a tool for communication of complex scientific issues with multiple stakeholders who were in strong disagreement. It illustrated how an analytic lens can provide a sharper focus on the areas where stakeholders disagree, while setting aside those areas where they agree (cost, for example) or where the disagreement does not matter (outages, for example). This analysis did not resolve the issue, but it provided a common language and framework to facilitate a stakeholder dialogue.

Conclusions

These two examples show that science can be effectively linked to decision making, both for personal choices and public policy decisions. They also illustrate that this is not a trivial task. In both cases, we used decision analysis tools to provide a logical interface between scientific knowledge and the information requirements of decision makers. In both cases, it was useful to separate beliefs and values when using science to inform decision making.

At a more general level, science can and should be important for all major decisions in life. However, linking science and decision making requires a special effort. In some cases, science panels can be used to provide advice to decision makers. The National Research Council was created for exactly this purpose and has done so with many boards, committees, and panels for over a century. Other efforts to facilitate science communication involve the creation of public participation processes and stakeholder panels or development of special communication materials (24, 25).

No matter what approach is chosen to link science and decision making, it is important to point out that this is not merely an exercise in improving the presentation of scientific knowledge to decision makers. Such efforts also require an understanding of the information needs of the decision makers. In short, bridging science and decision making requires a dialogue with many iterations (26).