Abstract
The nature of light interaction with matter can be dramatically altered in optical cavities, often inducing nonclassical behavior. In solid-state systems, excitons need to be spatially incorporated within nanostructured cavities to achieve such behavior. Although fascinating phenomena have been observed with inorganic nanostructures, the incorporation of organic molecules into the typically inorganic cavity is more challenging. Here, we present a unique optofluidic platform comprising organic molecules in solution suspended on a photonic crystal surface, which supports macroscopic Fano resonances and allows strong and tunable interactions with the molecules anywhere along the surface. We develop a theoretical framework of this system and present a rigorous comparison with experimental measurements, showing dramatic spectral and angular enhancement of emission. We then demonstrate that these enhancement mechanisms enable lasing of only a 100-nm thin layer of diluted solution of organic molecules with substantially reduced threshold intensity, which has important implications for organic light-emitting devices and molecular sensing.
Keywords: fluorescence enhancement, enhanced light–matter interaction
Organic molecules are pervasive in daily life: from natural proteins, to human synthesized fluorescing labels, to organic semiconductors. The interaction of light with such molecules is at the heart of important technological advances in biomolecular detection (1–4), fluorescent microscopy (5), and organic light-emitting devices (6–9), as well as more fundamental studies of cavity quantum electrodynamics (10–12) and various types of enhanced spectroscopy (13) and sensing (14). In all, it is frequently sought to alter (15–18) and often to enhance this interaction by allowing it to occur in a typically nanostructured cavity, where both the lifetime of the resonances and the optical density of states (DOS) (19) can be tailored. However, there are inherent challenges in incorporating organic molecules in such cavities: first, their dissimilar compositional structure makes it difficult to incorporate them within the high-dielectric regions of the cavity, where long-lifetime resonances concentrate their electromagnetic energy. Second, micro- and nanostructured cavities typically only have a small portion of their mode volumes extending outside their high-dielectric regions, making it challenging to bring external entities precisely to within that volume. Third, patterning of organic materials at the nanoscale is extremely challenging and incompatible with inorganic processes. As a result, experimental realizations of systems of excitons of organic molecules and optical resonances are limited compared with systems of inorganic quantum nanostructures.
Here, we present and study a unique dielectric surface that enables simple incorporation of organic molecules onto a macroscopic nanostructured resonant cavity. This system demonstrates strongly enhanced interaction of light with organic molecules that are brought to within 100 nm of its macroscopic surface. The surface, patterned with a subwavelength periodic structure, supports a special type of Fano resonances (20, 21), some of which are completely decoupled from free-space radiation due to symmetry arguments, and thus, in principle, maintain an infinitely long lifetime despite lying within the light cone. The novelty and simplicity of this system whereby delocalized resonances with an ultralong lifetime can exist above the surface, and consequently easily interact with added molecules anywhere along the surface, provide a unique optofluidic platform for molecular sensing and lasing purposes. The spectral and angular radiation pattern of the organic molecules placed close to the surface is dramatically modified compared with their free-space emission due to the strongly altered spectral density of states (SDOS) (19) presented by the photonic crystal (PhC). Sharp spectral features in their fluorescence spectra are observed, with enhancement of the differential radiated power (13) as high as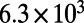 
-fold. We theoretically show that the origin of enhancement can be attributed to two mechanisms: enhancement of the local excitation field and enhancement of the extraction rate. We develop a theoretical model involving coupled mode theory (CMT) and expansion of the Green’s functions in the basis of Bloch modes to predict the contribution of each mechanism to the total enhancement. Furthermore, we show that the two enhancement mechanisms also contribute to reduce the lasing threshold by an order of magnitude compared with previously demonstrated laser cavities with the same gain medium [Rhodamine 6G (R6G), which was used here] (22–25). Demonstration of organic dye molecule lasing using this special type of Fano resonances is also provided.
Theoretical Framework of Emission Enhancement
We start by outlining the theoretical framework for the interaction of optical resonances and organic molecules in the weak-coupling regime. Without loss of generalities, we consider here a PhC covered with organic molecules in solution, shown schematically in Fig. 1. This PhC slab, made out of a periodic square array of holes, supports Fano resonances with delocalized wave functions and long lifetimes (20, 21). The electronic transitions of the fluorescence process in organic molecules are shown in Fig. 1A, involving the two lowest energy singlet states (13). The interaction of light with the organic molecules can be dramatically modified in the presence of optical resonances (26–28) through two mechanisms: (i) enhancement of the molecules’ absorption by coupling the pump into a resonance mode compared with bulk absorption,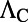 
, and (ii) enhancement of the extraction rate of generated photons into the far field in the presence of PhC compared with placed in the free space, 
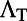. In this section, we derive a theoretical model for the two enhancement factors stressing effects involving the subwavelength structure of the resonator. Because the quantum yield of many dye molecules is close to unity (29), we assume it remains unchanged due to enhancement effects. However, it is important to note that, in general, the quantum efficiency changes in cavities via the Purcell effect (30).
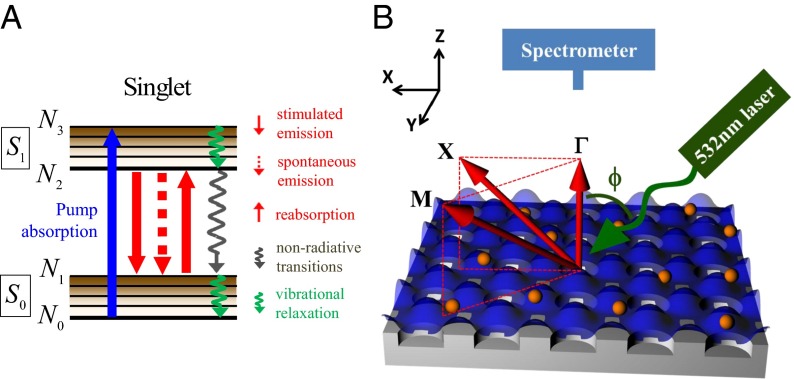
Fig. 1.
Optofluidic platform of organic molecules coupled to Fano resonances of the macroscopic photonic crystal. (A) Schematic drawing of the two lowest singlet energy levels of a dye molecule and the transitions it undergoes during fluorescence emission. (B) Schematic drawing of the experimental setup of the angle-resolved fluorescence measurements of R6G dissolved in methanol at the concentration of 1 mM placed on top of the PhC. The gray substrate is the macroscopic PhC slab. The orange spheres are schematic drawings of the R6G molecules in solution. The blue surface represents the equal energy density surface of the Fano resonance. Fluorescence spectra of the organic solution were recorded using a high-resolution spectrometer placed close to the normal of the PhC. By tuning the position of the spectrometer, fluorescence spectra of the molecules along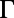 
to X and 
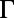to M were measured.
Excitation enhancement occurs in structures that support resonances for the excitation wavelength via the enhancement of the local electric field in the site of the molecules. Because the active volume of the organic material that interacts with the resonance is typically small (compared with the wavelength) in nanostructured resonances, only a small fraction of the excitation beam is absorbed in most cases. However, the local excitation field can be orders of magnitude higher than in free space when the pump is coupled to resonances with a long lifetime (the pump-resonance mode), and can therefore lead to enhanced absorption. The power absorbed by bulk molecules is given by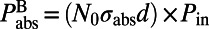 
, where 
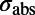is the absorption cross-section of molecules, 
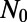is the number density of molecules, d is the thickness of the layer that the molecules occupy, and 
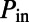is the pump power. Using CMT (31–33), the excitation enhancement can be shown to be:
 |
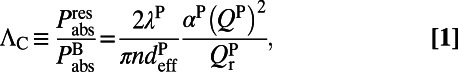where 
is the pump wavelength, n is the refractive index of the liquid where organic molecules are dissolved, 
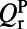is the radiative quality factor of the channel to couple the pump beam in, and 
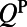is the total quality factor of the pump mode, 
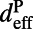is the effective length of the evanescent tail of the pump mode into the molecule layer, and 
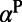is the energy confinement of the pump mode in the molecule layer. Note that all quantities in Eq. 1 can be found either by finite-difference time-domain (FDTD) simulation (34) or by fitting spectral reflection measurements to CMT (21). Details about how different Q’s are obtained are provided in Materials and Methods. Excitation enhancement, 
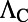, is maximized when the standard Q-matching condition between the total radiative and nonradiative Q of the pump mode, 
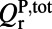and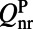 
, is satisfied (33).
The second mechanism is extraction enhancement due to strong modification of the SDOS in the presence of Fano resonances. The angular emission of molecules can be dramatically altered when coupled to a macroscopic nanostructure resonance compared with that in free space. When coupled to a resonance, the rate at which a uniform and isotropic collection of molecules generates photons with crystal momentum k at resonant frequency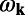 
can be written as:
 |
This result can be achieved by expanding the Green’s function in the basis of normalized Bloch modes with a finite lifetime (SI Materials and Methods). Here,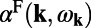 
is the energy confinement of the fluorescence resonance mode in the molecule layer, 
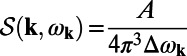is the SDOS of the system at k and 
, 
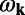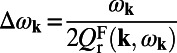is the line width of the resonance, A is the area of the macroscopic Fano resonance, and 
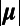is the electric dipole momentum of the molecules. From here on, all parameters of the fluorescence mode (
,
,
,
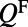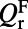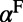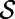, and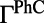 
) are for the specific mode of 
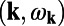, unless specified otherwise. The ratio between the extraction rate into the far field in the presence of the PhC (
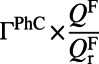; SI Materials and Methods) compared with the free space 
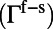, under the assumption that the radiation direction is close to normal, can be written as:
 |
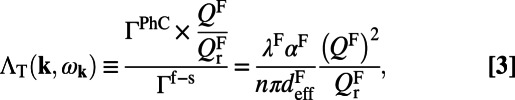where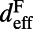 
is the effective length of the evanescent tail of the fluorescence mode in the molecule layer, 
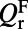is the radiative quality factor of the fluorescing channel, and 
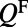is the total quality factor of the fluorescence mode. To maximize 
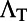, similar to the case of 
, one seeks to maximize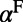 
, as well as to enforce the Q-matching condition of the fluorescence mode (
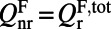; SI Materials and Methods), instead of to lower 
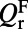in general as often suggested. Similar to Eq. 1, all quantities in Eq. 3 can be obtained from FDTD calculations and spectral reflection measurements. Note that there are three major differences between this formalism and local optical density of states (LDOS) (19) enhancement calculations in microcavity systems (35–40):
i) Here, we are considering the emission of a uniform and isotropic ensemble of molecules placed on a periodic macroscopic PhC into fixed crystal momentum k at frequency
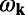, which is proportional to the SDOS of the system instead of the LDOS [proportional to the total emission of one dipole into all directions] (41–45).ii) To treat an infinitely large system, the basis adopted here to expand Green’s functions are Bloch modes under periodic boundary conditions instead of localized eigenmodes as often used in LDOS calculations.
iii) The portion
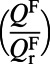of generated photons to be radiated coherently to the far field and to reach the detector is taken into account; therefore, the maximizing condition changes from adopting lower 
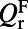in general to Q-matching consistent with the study of Seok et al. (46).
Given knowledge of the excitation and extraction enhancement, the total enhancement factor,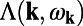 
, can be shown to be:
 |
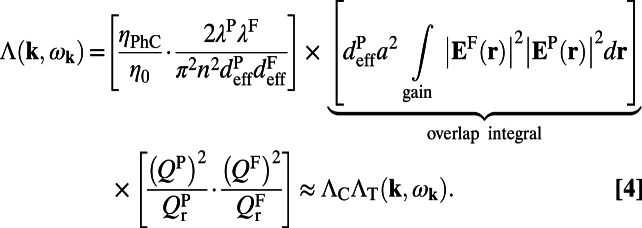Here,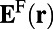 
is the normalized mode profile for the fluorescence mode and 
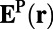is that for the pump mode. The approximation 
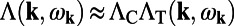in Eq. 4 is valid under two assumptions: (i) The quantum yield of the molecules remains constant as mentioned, and (ii) more importantly, the normalized pump and fluorescence mode profiles are roughly uniformly distributed in a similar region in space; therefore, the overlap integral in Eq. 4 can be simplified to be 
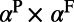. The latter approximation is commonly ignored in photonic systems; however, it can lead to further enhancement. Note that in many plasmonic systems, the origin of enhancement comes mostly from this mode overlap integral term and cannot be simplified.
Unlike plasmonic systems, the most significant contribution to the enhancement in photonic systems typically comes from the high Q’s of the resonances and is given by the last term of Eq. 4: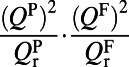 
. This term reaches its maximum of 
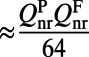under the Q-matching conditions stated previously. Accordingly, to achieve the highest enhancement, a photonic system is desired both to present resonances with high radiative and nonradiative Q’s and to possess a “tuning” mechanism such that the Q-matching condition can be achieved. The photonic crystal presented here satisfies all these requirements. This structure was demonstrated to achieve nonradiative Q as high as 
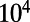(21), only limited by fabrication imperfections, and radiative Q approaching infinity due to the decoupling from free-space radiation based on symmetry arguments. Because the radiative Q of the resonances strongly depends on the wave vector k, 
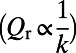, at small k, the Q-matching condition can always be satisfied at a certain angle.
One direct consequence of the enhancement mechanisms is the reduction in the lasing threshold of such systems. We experimentally observed a significantly reduced lasing threshold of the specific organic molecules, R6G, compared with previously reported results. The reduction of the lasing threshold in this unique type of dye laser that uses these special Fano resonances is due to two reasons. First, the excitation field is dramatically enhanced near the surface of the PhC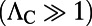 
, enabling substantial absorption of the pump within a thin layer of diluted molecules near the PhC surface. The second contribution originates from the enhanced emission rate of the molecules into the lasing mode compared with their free-space emission with similar mode volume. This enhancement can be introduced phenomenologically into the lasing rate equation through the spontaneous emission factor, β, which is classically defined as the ratio between the emission rate into the lasing mode and the total emission rate. The lasing threshold is typically inversely proportional to β; hence, it can be reduced in cases where the emission rate into the lasing mode is enhanced, whereas the total rate remains almost constant. A rigorous CMT model of the laser dynamics of the system of organic molecules in nanostructured cavities was developed by our group elsewhere, similar to the model described in ref. 47.
Experimental Results of Enhanced Fluorescence Emission and Comparison with Theory
We experimentally studied a system comprising a solution of R6G molecules in methanol suspended on top of a PhC slab supporting this special type of Fano resonances (21). A schematic drawing of the setup is shown in Fig. 1B, where the gray substrate is the PhC slab, consisting of a square lattice of air cylindrical holes (same as used in ref. 21). The PhC was placed in a liquid cell with a channel thickness of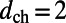 
μm and was filled with R6G solution dissolved in methanol at a concentration of 1 mM. The liquid cell was mounted on a precision motorized rotating stage, where the incident angle of the laser, ϕ, can be precisely controlled along the 
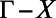direction (Materials and Methods). The molecules are excited by a 532-nm continuous wave (CW) laser at a power level of 20 mW, well below the lasing threshold of the system.
Fig. 2 shows a comparison of the fluorescence spectra of R6G molecules measured in the normal direction for three scenarios: on an unpatterned slab (dashed green line) and on the PhC (solid lines) pumped on-resonance (blue) and off-resonance (red). The spectrometer was fixed at the normal direction of the PhC sample, and switching between on- and off-resonance coupling was achieved by tuning the incident angle of the pump, ϕ. From FDTD calculations of the band structure (Fig. 2, Inset), the on-resonance coupling angle,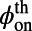 
, was determined to be 
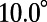, agreeing well with the measured 
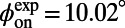. In the on-resonance case, the excitation field within 
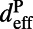from the surface is strongly enhanced compared with off-resonance, whereas the remainder of the bulk layer exhibits no enhancement. The excitation enhancement can be analyzed by comparing emission spectra for on-resonance (blue) and off-resonance (red) coupling. The difference between the two is solely due to excitation enhancement, because the extraction enhancement, 
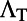, for the same wavelength at the same angle remains the same. Note that the channel thickness, 
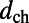, is generally different from 
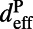. Because we are only interested in characterizing the enhancement due to the presence of the pump resonances, we restrict our analysis to only a thin layer within 
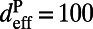nm (SI Materials and Methods). The excitation enhancement obtained from experimental results is given by: 
. 
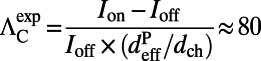and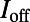 
are the measured fluorescence intensities for wavelengths far away from the three resonances at 
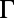. The theoretical prediction, 
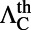, as calculated from Eq. 1, is 60, which agrees reasonably well with experiment (with the main source of difference stemming from the uncertainty in determining 
).
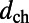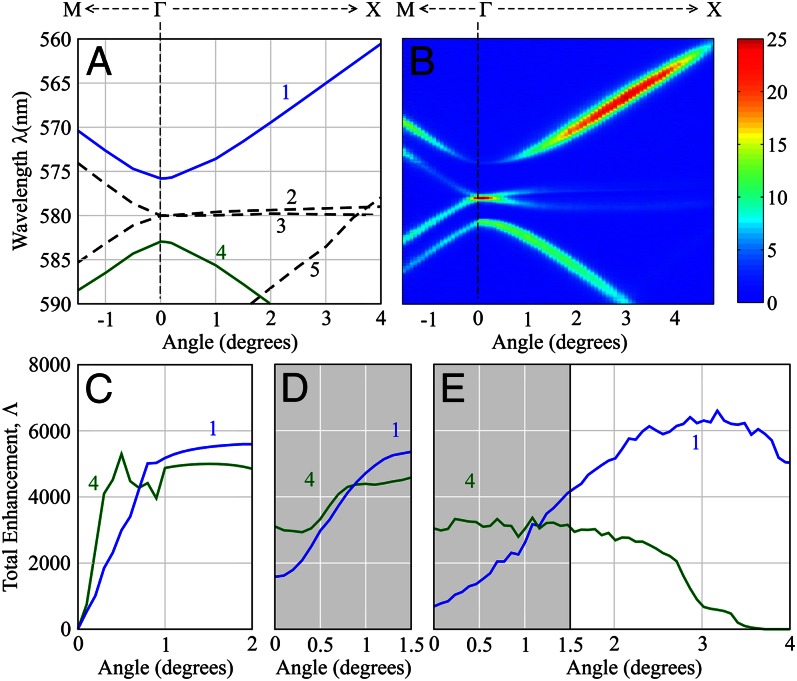
Fig. 2.
Significantly enhanced fluorescence emission from R6G molecules. Comparison of fluorescence spectra of R6G molecules measured in the normal direction on the PhC (solid lines) pumped on-resonance (blue) and off-resonance (red), as well as on a uniform unpatterned slab (dashed green line). *, blue line has been multiplied by a factor of 0.1 for the simplicity of comparison with others. By comparing the spectra, we obtain the excitation (
), extraction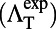 
, and total 
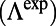enhancement factors, which are compared with the theoretical predictions, as described in the main text. (Inset) FDTD calculation results of the band structure from which the incident angle (ϕ) for on-resonance coupling is determined 
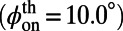, showing good agreement with experiments 
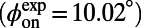. a.u., arbitrary unit.
The extraction enhancement,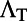 
, as in Eq. 3, depends on 
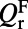, which is strongly angular-dependent near normal direction. Therefore, angle-resolved fluorescence measurements were carried out to study 
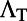experimentally. In total, the fluorescence signal was measured at 125 different angles up to 
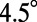along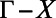 
and up to 
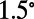along 
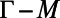, as shown in Fig. 3B. Each slice on the horizontal axis represents the emission spectrum at that angle. The incident angle of the pump was fixed at 
for on-resonance coupling in all measurements. For comparison, Fig. 3A shows the band structure of the PhC from FDTD calculations within the same range of angles. The bands are labeled as numbers 1 through 5 for the simplicity of further discussion. The first feature of Fig. 3B is that the fluorescence is always maximized around the Fano resonances of the PhC (figure 2 of ref. 21). This can be intuitively understood from Eq. S1 in SI Materials and Methods: The decay rate into frequency ω is proportional to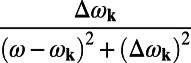 
, which is maximized at 
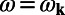. The second feature of Fig. 3B is the strong angular dependence similar to 
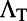. Although similar angular dependence has been previously reported (27, 28), we present here a rigorous quantitative model that faithfully predicts the experimental results.
Fig. 3.
Comparison between theoretical model and experimental results of the enhancement mechanisms. (A) Band structure of the PhC along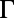 
-to-M and 
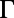-to-X directions. (B) Angle-resolved fluorescence measurements of R6G solution suspended on top of the PhC. The correspondence between the color and number of photons (arbitrary units) is given in the color bar on the side. (C) Total enhancement factors, 
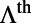, for mode 1 (blue line) and mode 4 (green line) calculated through the product of excitation enhancement, 
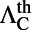, and extraction enhancement, 
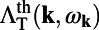, using the theoretical model. (D) Theoretical prediction of the averaged total enhancement factor, 
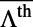, between 0° and 
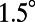, to be compared with experiments. (E) Total enhancement factor, 
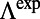, extracted from experimental results in B. A comparison between D and E for the same angle range (0–
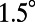) shows good agreement not only in trend but also in values.
Theoretical prediction of extraction enhancement,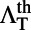 
, for bands 1 and 4 was calculated using Eq. 3 within 
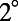along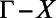 
. Based on this result, theoretical prediction of total enhancement, 
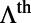, is plotted in Fig. 3C, with details provided in Materials and Methods. Note that 
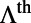goes to zero for both bands at 
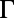because 
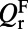of both modes approach infinity at 
(20, 21). Away from 
, 
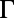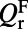of both modes drops 
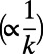, and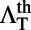 
is maximized when the Q-matching condition between 
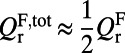and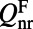 
is reached. From a study by Lee et al. (21), we see that 
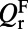of mode 1 drops much slower than that of mode 4, which explains why 
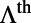of mode 1 increases much slower than that of mode 4 near 
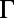. Finally, before we can directly compare theory with experiment, 
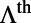needs to be averaged over the range of k corresponding to the acceptance angle of the spectrometer aperture, which is narrow in the x direction (the difference of resonance frequencies of allowed k within corresponding acceptance angle is small compared with the resonance line width) but wide 
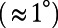in the y direction. Due to the limitation of the angles where 
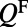was measured by Lee et al. (21), averaged total enhancement, 
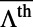, can be calculated only between 0° and 
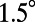along 
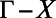, as shown in Fig. 3D. The behavior of bands 1 and 4 close to 
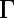are found to be very different: For mode 4, the Q-matching condition is satisfied close to 
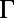(arou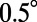nd 
) and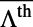 
is almost constant near 
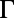; however, the Q-matching for mode 1 is reached far from 
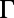, resulting in an almost linear increase in 
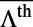at small angles. Fig. 3E presents the total enhancement factor, 
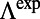, of both bands extracted from experimental results in Fig. 3B (Materials and Methods). Whereas 
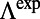of band 4 remains almost constant near 
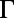and drops to 0 when the resonance falls out of the spectrometer range, 
of band 1 increases with angle before reaching its maximum of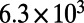 
around 
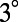. These experimental observations agree fairly well with the theoretical predictions in Fig. 3D, particularly if comparing the theoretical prediction of the maximum enhancement for band 1 (
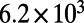; Materials and Methods) with experiments. For both bands, the comparison of 
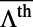in Fig. 3D and 
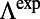in Fig. 3E within the angle range of 0–
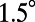shows good agreement not only in trends but in values (e.g., for band 4 at 
, 
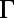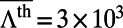compared with 
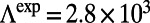, as shown in Table 1).
Table 1.
Comparison of the enhancement factors for band 4 at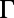 
| Approach |  |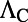
 |
 |
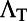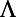| Theoretical prediction | 60 | 50 |  |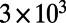
| Experimental results | 80 | 35 |  |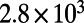
For mode 4 at 
, the results of excitation enhancement (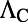
), extraction enhancement (
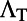), and total enhancement (
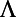) from theoretical prediction through the model presented in the main text are compared with the results extracted from experiments and show good agreement with each other.
Effects of Enhancement Mechanisms on Reducing Lasing Threshold
These two enhancement mechanisms also enable the lasing of a 100-nm thin layer of dilute R6G solution with reduced threshold intensity by an order of magnitude compared with previously demonstrated laser cavities with the same gain medium (22–25). We attribute the reduced threshold to three reasons: (i) high Q-factors of the special Fano resonances, (ii) substantially enhanced absorption of the pump by only a 100-nm thin layer of the diluted molecules enabled by the excitation enhancement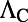 
, and (iii) enhanced spontaneous emission factor β for the lasing mode due to enhanced SDOS. These findings are consistent with previous conclusions that the threshold of such a lasing system of organic molecules is inversely proportional to Q and β.
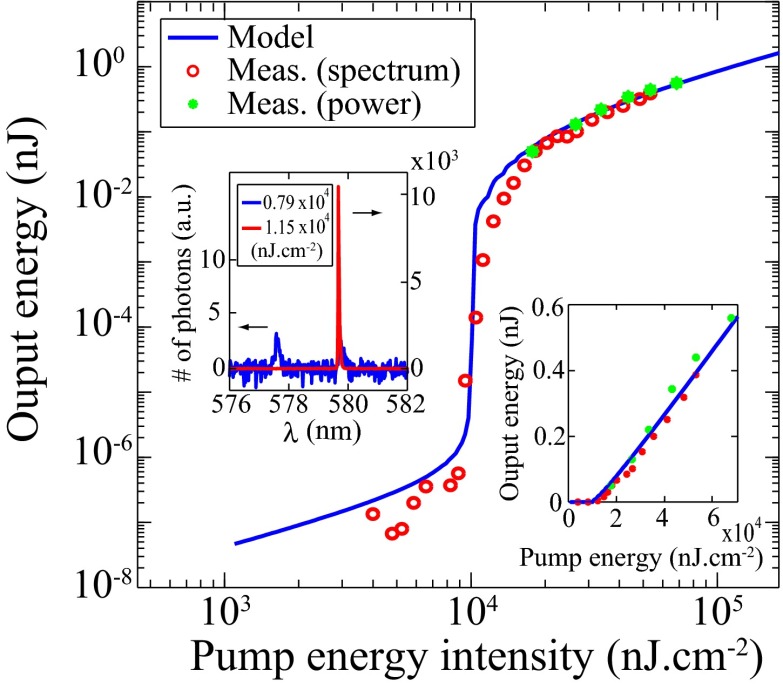
The lasing experiment was carried out using the same setup as the fluorescence measurements, other than replacing the CW pump with the 532-nm second harmonic of a 5-ns collimated neodymium/yttrium aluminum garnet (Nd:YAG)-pulsed laser at a repetition rate of 10 Hz. Narrow emission lines were observed at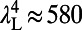 
nm first and then at 
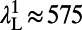nm, both well within the R6G’s emission spectrum. At 
, 
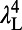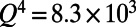was retrieved from results of Lee et al. (21). The emission spectra of the molecules when pumped below (blue) and above (red) threshold are shown in Fig. 4 (Upper Inset). Plugging the rates of electronic transitions in R6G and parameters of the PhC cavity into the CMT laser model (47), the pulse energy input–output curve is plotted against the measured data in Fig. 4. The jump in the log–log plot clearly indicates the onset of lasing. The same result in linear scale is shown in Fig. 4 (Lower Inset), where the output energy grows linearly with the pump energy beyond threshold. The theoretical predictions of both threshold and slope efficiency match reasonably well with the experimental results within experimental errors. In particular, the measured threshold energy is 
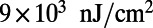(intensity of 
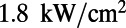), an order of magnitude lower than previously demonstrated laser cavities with the gain medium (22–25). We attribute this low lasing threshold of R6G to the two enhancement mechanisms: (i) the excitation enhancement, 
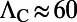, which enables 12.7% absorption of the pump energy within only a 100-nm thin layer of the dye solution, and (ii) the rate of spontaneous emission into the lasing mode in such a structure, which is proportional to 
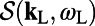and is enhanced over that in free space, yielding a higher value of β.
Fig. 4.
Low-threshold lasing of a 100-nm thin layer of R6G molecules in solution. Input–output energy characteristics of lasing through mode 4 (580 nm) under pulsed excitation are shown. The solid lines are analytical predictions from our lasing model, whereas the green circles are energies measured (Meas.) with a power meter. Red circles are measurement results using the spectrometer multiplied by an arbitrary constant for the simplicity of comparison. The jump in output power clearly indicates the onset of lasing. (Lower Inset) Same results in linear scale, where the output grows linearly with the pump energy beyond threshold. (Upper Inset) Measured spectrum of emission from the PhC slab at normal direction when pumped below (blue) and above (red) the lasing threshold. Single-mode lasing is attained at approximately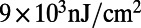 
(corresponding to an intensity of 
).
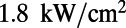This reduced threshold could be interesting with respect to using organic molecules toward a monolithic (no dye circulation) laser source covering the UV, visible, and near-IR spectrum range, much of which is inaccessible by inorganic-based lasers. Also, lasers with organic polymers have been shown to be sensitive analyte sensors when operated around their thresholds (48); the ability to reach the threshold with a very small amount of molecules, as in our case, could significantly improve the sensitivity.
Conclusion and Summary
In summary, we present and study a unique optofluidic platform that enables strongly enhanced light interaction with organic molecules due to the macroscopic Fano resonances in the nanostructured cavity. We experimentally demonstrated dramatic spectral and angular redistribution of fluorescence from molecules coupled to the special Fano resonances supported by the PhC. The theoretical framework of the system was developed to explain and calculate the enhancement mechanisms, showing good agreement with experiments. We found that to maximize the overall emission enhancements, Q-matching requirements need to be satisfied not only for the pump mode but for the fluorescence mode. Furthermore, we report lasing of a 100-nm thin layer of diluted organic dye molecule solution with a threshold that is an order of magnitude lower than any previously demonstrated laser systems using similar molecules. The reduction of the lasing threshold was further explained by these enhancement mechanisms. This lasing experiment highlights the novelty of this system whereby organic molecules or colloidal nanoparticles can be simply introduced and interact with resonances of a macroscopic nanostructured cavity anywhere along its surface. These results present exciting opportunities in optical molecular sensing and surface light-emitting devices due to the ability of simply introducing matter to the surface, the delocalized nature of the resonance modes, and the enhancement mechanisms presented in the system. Finally, we should point out that these results are proofs of concept only. In fact, lower lasing thresholds and higher fluorescence enhancements can be achieved by optimizing the structure using the theoretical model developed in this paper. Meanwhile, our results also suggest exciting new opportunities in optical molecular sensing due to the macroscopic nature of the active mode volume and the enhancement mechanisms.
Materials and Methods
Obtaining Different Q’s from CMT.
To make it simpler to keep track of the various Q’s that appear in this paper, we first summarize and label them with detailed explanations in Table 2. The processes to obtain different Q’s can be summarized as follows. First, we conducted angle-resolved reflectivity measurement of the PhC immersed in methanol without R6G molecules. Second, we modeled the whole system from the perspective of CMT. In this CMT model, we excited the system with an incident source propagating from the top and impinging onto the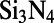 
layer resonant cavity. From the first-order perturbation to Maxwell’s equation, energy conservation considerations, and neglect of any higher order effects, we came up with a semianalytical model that predicts the reflectivity of the PhC with the parameters of the resonances as variables, including the central frequency positions and the values of all different Q’s. Finally, we fit the experimental results to the semianalytical model and obtained all the information about the resonances, including different Q’s, and used them as the input of the current study. Details are provided by Lee et al. (21).
Table 2.
Summary of all the Q’s
| Quality factors | Pump mode | Fluorescence mode |
| Total |  |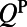
 |
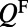| Nonradiative |  |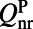
 |
| Radiative through the top |  |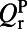
 |
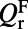| Total radiative |  |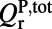
 |
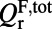For each resonance, total Q’s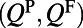 
represent the line width; nonradiative Q’s 
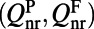are generated due to material absorption, scattering from imperfections in fabrication, and inhomogeneous broadening; radiative Q’s through the top 
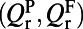account only for the leakage toward the top surface of the PhC that participates in the pumping and fluorescing processes; and total radiative Q’s 
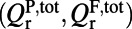account for all radiative channels and can be calculated from FDTD simulations.
Experimental Setup.
The fluorescence spectrum was collected using a spectrometer with resolution of 0.03 nm (HR4000; Ocean Optics) aligned close to the normal direction, because we were mainly interested in the special Fano resonance with k near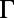 
. By tuning the position of the spectrometer with an xyz stage, we were able to detect fluorescence into different emission angles along 
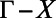and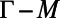 
directions.
Excitation Enhancement from Experimental Results,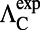 
.
For wavelengths away from the three resonances at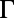 
, under off-resonance coupling, most of the emission comes from the absorption in the 
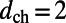-μm thick bulk layer. For on-resonance coupling, the majority (over 
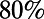) of the absorption happens within the evanescent tail of the pump resonance mode, although 
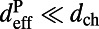. The absorption in 
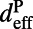for on-resonance coupling can be calculated from the difference of fluorescence signal between on- and off-resonance coupling, 
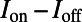, whereas that for off-resonance coupling can be calculated from the thickness ratio, 
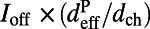. The effective length of the evanescent tail of the pump resonance mode in the molecule layer, 
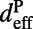, is defined similar to 
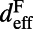. From FDTD calculation, we get 
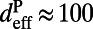nm, which is similar to 
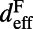. From Fig. 2, for frequencies away from the three resonances at 
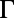, the typical number for 
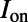(blue line) was chosen to be 200 and 
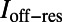(red line) was chosen to be 40; therefore, we get 
.
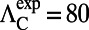Theoretical Prediction of Excitation Enhancement,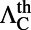 
.
The absorption in the evanescent tail for on-resonance coupling was calculated by plugging all quantities in Eq. 1. For the pump mode,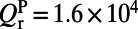 
, obtained from FDTD calculation; 
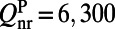, obtained from reflection measurements; 
nm, obtained from the previous section;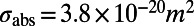 
, obtained from the literature (22); 
; 
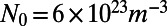, obtained from FDTD calculations;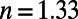 
for methanol; and 
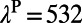nm. Therefore, 
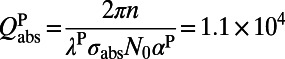. From Eq. 1, 
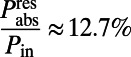, meaning the absorption in the 100-nm evanescent tail of the pump resonance is about 12.7% for on-resonance coupling. Also, from Eq. 1, 
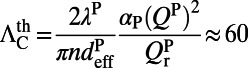. Note that the factor 
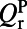is different from the total radiative Q of the pump mode 
: 
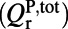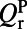only accounts for leakage of the resonance that can be coupled to the pump. Here, only leakage through the top surface is taken into account.
Total Enhancement Factors,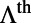 
and 
.
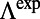The total enhancement for modes 1 and 4 was calculated using Eq. 4. Here,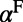 
for both mode 1 and mode 4 is ∼6%. 
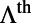is the product of 
, and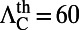 
. Nonaveraged results are shown in Fig. 3C for angles within 
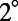from 
, consistent with the range where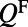 
can be fitted (21). For comparison with experiments, where the input aperture of the spectrometer corresponds to an acceptance angle of 
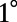, Fig. 3C is averaged over the same range, resulting in Fig. 3D. Accordingly, the range of angles with theoretical prediction is limited within 
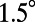from normal. 
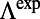was defined as the ratio between the fluorescence signal from the evanescent tail of the fluorescence mode 
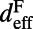for the case of on-resonance coupling and that for an unpatterned substrate, 
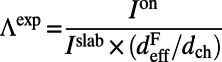. The maximum of total enhancement can be approximated under Q-matching between 
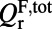and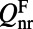 
. Taking 
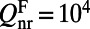(21), one can get 
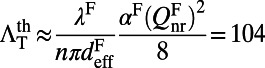. Combining with 
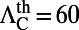, the maximum value of 
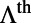of band 1 can be approximated to be 
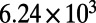, which agrees well with the maximum value of 
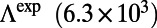in Fig. 3E. In Table 1, we also present a comparison of the enhancements for band 4 at 
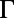between our theoretical prediction and experimental results.
Supplementary Material
Acknowledgments
We thank Chia Wei Hsu for help in the preparation of figures and Ognjen Ilic, Wenjun Qiu, and Prashanth S. Venkataram for useful discussions. B.Z., J.L., and M.S. were partially supported by the Solid-State Solar Thermal Conversion Center, an Energy Frontier Research Center funded by the US Department of Energy, Office of Science, and Office of Basic Energy Sciences, under Grant DE-SC0001299. B.Z. and M.S. were also partially supported by the US Army Research Office through the Institute for Soldier Nanotechnologies under Contract W911NF-07-D0004. S.-L.C. and J.L. were also partially supported by the Materials Research Science and Engineering Center Program of the National Science Foundation under Award DMR-0819762. A.W.R. was supported by the Defense Advanced Research Projects Agency under Contract N66001-09-1-2070-DOD. X.L was supported by the Air Force Office of Scientific Research Multidisciplinary Research Program of the University Research Initiative for Complex and Robust ON-Chip Nanophotonics under Grant FA9550-09-1-0704.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1311866110/-/DCSupplemental.
References
- 1.Donzella V, Crea F. Optical biosensors to analyze novel biomarkers in oncology. J Biophotonics. 2011;4(6):442–452. doi: 10.1002/jbio.201000123. [DOI] [PubMed] [Google Scholar]
- 2.Hoa XD, Kirk AG, Tabrizian M. Towards integrated and sensitive surface plasmon resonance biosensors: A review of recent progress. Biosens Bioelectron. 2007;23(2):151–160. doi: 10.1016/j.bios.2007.07.001. [DOI] [PubMed] [Google Scholar]
- 3.Hunt HK, Armani AM. Label-free biological and chemical sensors. Nanoscale. 2010;2(9):1544–1559. doi: 10.1039/c0nr00201a. [DOI] [PubMed] [Google Scholar]
- 4.Cooper MA. Optical biosensors in drug discovery. Nat Rev Drug Discov. 2002;1(7):515–528. doi: 10.1038/nrd838. [DOI] [PubMed] [Google Scholar]
- 5.Lakowicz JR. Principles of Fluorescence Spectroscopy. New York: Springer; 1999. [Google Scholar]
- 6.Reineke S, et al. White organic light-emitting diodes with fluorescent tube efficiency. Nature. 2009;459(7244):234–238. doi: 10.1038/nature08003. [DOI] [PubMed] [Google Scholar]
- 7.Adachi C, Baldo MA, Thompson ME, Forrest SR. Nearly 100% internal phosphorescence efficiency in an organic light-emitting device. J Appl Phys. 2001;90:5048–5051. [Google Scholar]
- 8.Meier M, et al. Emission characteristics of two-dimensional organic photonic crystal lasers fabricated by replica molding. J Appl Phys. 2001;86:3502–3507. [Google Scholar]
- 9.Notomi M, Suzuki H, Tamamura T. Directional lasing oscillation of two-dimensional organic photonic crystal lasers at several photonic band gaps. Appl Phys Lett. 2001;78:1325–1327. [Google Scholar]
- 10.Tischler JR, Bradley MS, Bulović V, Song JH, Nurmikko A. Strong coupling in a microcavity LED. Phys Rev Lett. 2005;95(3):036401. doi: 10.1103/PhysRevLett.95.036401. [DOI] [PubMed] [Google Scholar]
- 11.Kéna-Cohen S, Forrest SR. Room-temperature polariton lasing in an organic single-crystal microcavity. Nat Photonics. 2010;4(6):371–375. [Google Scholar]
- 12.Vucković J, Lončar M, Mabuchi H, Scherer A. Design of photonic crystal microcavities for cavity QED. Phys Rev E. 2002;65(1):016608. doi: 10.1103/PhysRevE.65.016608. [DOI] [PubMed] [Google Scholar]
- 13.Ru EL, Etchegion PG. Principles of Surface-Enhanced Raman Spectroscopy: and Related Plasmonic Effects. Amsterdam: Elsevier Science; 2008. [Google Scholar]
- 14.Lončar M, Scherer A, Qiu Y. Photonic crystal laser sources for chemical detection. Appl Phys Lett. 2003;82(26):4648–4650. [Google Scholar]
- 15.Yablonovitch E. Inhibited spontaneous emission in solid-state physics and electronics. Phys Rev Lett. 1987;58(20):2059–2062. doi: 10.1103/PhysRevLett.58.2059. [DOI] [PubMed] [Google Scholar]
- 16.Martorell J, Lawandy NM. Observation of inhibited spontaneous emission in a periodic dielectric structure. Phys Rev Lett. 1990;65(15):1877–1880. doi: 10.1103/PhysRevLett.65.1877. [DOI] [PubMed] [Google Scholar]
- 17.Petrov EP, Bogomolov VN, Kalosha II, Gaponenko SV. Spontaneous emission of organic molecules embedded in a photonic crystal. Phys Rev Lett. 1998;81(1):77–80. [Google Scholar]
- 18.Lodahl P, et al. Controlling the dynamics of spontaneous emission from quantum dots by photonic crystals. Nature. 2004;430(7000):654–657. doi: 10.1038/nature02772. [DOI] [PubMed] [Google Scholar]
- 19.McPhedran RC, et al. Density of states functions for photonic crystals. Phys Rev E. 2004;69(1):016609. doi: 10.1103/PhysRevE.69.016609. [DOI] [PubMed] [Google Scholar]
- 20.Fan S, Joannopoulos JD. Analysis of guided resonances in photonic crystal slabs. Phys Rev B. 2002;65(23):235112. [Google Scholar]
- 21.Lee J, et al. Observation and differentiation of unique high-Q optical resonances near zero wave vector in macroscopic photonic crystal slabs. Phys Rev Lett. 2012;109(6):067401. doi: 10.1103/PhysRevLett.109.067401. [DOI] [PubMed] [Google Scholar]
- 22.Li Z, Psaltis D. Optofluidic dye lasers. Microfluid Nanofluid. 2008;4(1-2):145–158. [Google Scholar]
- 23.Shopova SI, Zhou H, Fan X, Zhang P. Optofluidic ring resonator based dye laser. Appl Phys Lett. 2007;90(22):221101. [Google Scholar]
- 24.Gersborg-Hansen M, Kristensen A. Tunability of optofluidic distributed feedback dye lasers. Opt Express. 2007;15(1):137–142. doi: 10.1364/oe.15.000137. [DOI] [PubMed] [Google Scholar]
- 25.Shäfer FP. Dye Lasers. New York: Springer; 1990. pp. 91–120. [Google Scholar]
- 26.Ganesh N, et al. Enhanced fluorescence emission from quantum dots on a photonic crystal surface. Nat Nanotechnol. 2007;2(8):515–520. doi: 10.1038/nnano.2007.216. [DOI] [PubMed] [Google Scholar]
- 27.Ganesh N, et al. Leaky-mode assisted fluorescence extraction: Application to fluorescence enhancement biosensors. Opt Express. 2008;16(26):21626–21640. doi: 10.1364/oe.16.021626. [DOI] [PubMed] [Google Scholar]
- 28.Pokhriyal A, et al. Photonic crystal enhanced fluorescence using a quartz substrate to reduce limits of detection. Opt Express. 2010;18(24):24793–24808. doi: 10.1364/OE.18.024793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Penzkofer A, Leupacher W. Fluorescence behavior of highly concentrated Rhodamine 6G solutions. J Lumin. 1987;37(2):61–72. [Google Scholar]
- 30.Purcell EM. Spontaneous emission probabilities at radio frequencies. Phys Rev. 1946;69:681. [Google Scholar]
- 31.Joannopoulos JD, Johnson SG, Meade RD, Winn JN. Photonic Crystals: Molding the Flow of Light. Princeton: Princeton Univ Press; 2008. [Google Scholar]
- 32.Fan S, Suh W, Joannopoulos JD. Temporal coupled-mode theory for the Fano resonance in optical resonators. J Opt Soc Am A Opt Image Sci Vis. 2003;20(3):569–572. doi: 10.1364/josaa.20.000569. [DOI] [PubMed] [Google Scholar]
- 33.Chan DL, Celanovic I, Joannopoulos JD, Soljačić M. Emulating one-dimensional resonant Q-matching behavior in a two-dimensional system via Fano resonances. Phys Rev A. 2006;74(6):064901. [Google Scholar]
- 34.Oskooi AF, et al. MEEP: A flexible free-software package for electromagnetic simulations by the FDTD method. Comput Phys Commun. 2010;181(3):687–702. [Google Scholar]
- 35.Fan S, Villeneuve PR, Joannopoulos JD, Schubert EF. High extraction efficiency of spontaneous emission from slabs of photonic crystals. Phys Rev Lett. 1997;78(17):3294–3297. [Google Scholar]
- 36.Vučković J, Painter O, Xu Y, Yariv A, Scherer A. Finite-difference time-domain calculation of the spontaneous emission coupling factor in optical microcavities. IEEE J Quantum Electron. 1999;35(8):1168–1175. [Google Scholar]
- 37.Xu Y, Lee RK, Yariv A. Finite-difference time-domain analysis of spontaneous emission in a microdisk cavity. Phys Rev A. 2000;61(3):033808. [Google Scholar]
- 38.Shen C, Michielsen K, De Raedt H. Spontaneous-emission rate in microcavities: Application to two-dimensional photonic crystals. Phys Rev Lett. 2006;96(12):120401. doi: 10.1103/PhysRevLett.96.120401. [DOI] [PubMed] [Google Scholar]
- 39.Zhang Y, et al. High-Q/V air-mode photonic crystal cavities at microwave frequencies. Opt Express. 2011;19(10):9371–9377. doi: 10.1364/OE.19.009371. [DOI] [PubMed] [Google Scholar]
- 40.Englund D, et al. Controlling the spontaneous emission rate of single quantum dots in a two-dimensional photonic crystal. Phys Rev Lett. 2005;95(1):013904. doi: 10.1103/PhysRevLett.95.013904. [DOI] [PubMed] [Google Scholar]
- 41.Wijnands F, et al. Green’s functions for Maxwell’s equations: Application to spontaneous emission. Optical and Quantum Electronics. 1997;29(2):199–216. [Google Scholar]
- 42.Xu Y, Lee RK, Yariv A. Quantum analysis and the classical analysis of spontaneous emission in a microcavity. Phys Rev A. 2000;61(3):033807. [Google Scholar]
- 43.Sakoda K. Optical Properties of Photonic Crystals. Berlin: Springer; 2001. [Google Scholar]
- 44.Lagendijk A, Van Tiggelen BA. Resonant multiple scattering of light. Phys Rep. 1996;270(3):143–215. [Google Scholar]
- 45.Milonni PW. Semiclassical and quantum-electrodynamical approaches in nonrelativistic radiation theory. Phys Rep. 1976;25(1):1–81. [Google Scholar]
- 46.Seok TJ, et al. Radiation engineering of optical antennas for maximum field enhancement. Nano Lett. 2011;11(7):2606–2610. doi: 10.1021/nl2010862. [DOI] [PubMed] [Google Scholar]
- 47.Liang Y, Peng C, Sakai K, Iwahashi S, Noda S. Three-dimensional coupled-wave analysis for square-lattice photonic crystal surface emitting lasers with transverse-electric polarization: Finite-size effects. Opt Express. 2012;20(14):15945–15961. doi: 10.1364/OE.20.015945. [DOI] [PubMed] [Google Scholar]
- 48.Rose A, Zhu Z, Madigan CF, Swager TM, Bulović V. Sensitivity gains in chemosensing by lasing action in organic polymers. Nature. 2005;434(7035):876–879. doi: 10.1038/nature03438. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.