Snake model based lymphoma segmentation for sequential CT images

Abstract

The measurement of the size of lesions in follow-up CT examinations of cancer patients is important to evaluate the success of treatment. This paper presents an automatic algorithm for identifying and segmenting lymph nodes in CT images across longitudinal time points. Firstly, a two-step image registration method is proposed to locate the lymph nodes including coarse registration based on body region detection and fine registration based on a double-template matching algorithm. Then, to make the initial segmentation approximate the boundaries of lymph nodes, the initial image registration result is refined with intensity and edge information. Finally, a snake model is used to evolve the refined initial curve and obtain segmentation results. Our algorithm was tested on 26 lymph nodes at multiple time points from 14 patients. The image at the earlier time point was used as the baseline image to be used in evaluating the follow-up image, resulting in 76 total test cases. Of the 76 test cases, we made a 76 (100%) successful detection and 38/40 (95%) correct clinical assessment according to Response Evaluation Criteria in Solid Tumors (RECIST). The quantitative evaluation based on several metrics, such as average Hausdorff distance, indicates that our algorithm is produces good results. In addition, the proposed algorithm is fast with an average computing time 2.58s. The proposed segmentation algorithm for lymph nodes is fast and can achieve high segmentation accuracy, which may be useful to automate the tracking and evaluation of cancer therapy.

1. Introduction

Computed tomography (CT) is commonly used for detection, diagnosis, and staging of cancers. Lymph node detection and segmentation is particularly important for cancer staging and treatment monitoring, as lymph nodes are commonly affected in cancer. Lymph nodes nearby primary cancer regions are routinely assessed by clinicians to monitor disease progress and effectiveness of the cancer treatment. In longitudinal CT scans, the change in size of lymph nodes over time is critical to assess the status of the stability or progression of disease [1].

Quantitative assessment of cancer lesions is a core task for evaluating treatment response. Current criteria for response assessment such as RECIST (Response Evaluation Criteria in Solid Tumours) [1, 2] and IWC (International Workshop Criteria) [3] depend heavily on cancer lesion measurement. On the other hand, measuring cancer lesions is time-consuming and not coveted by radiologists, some of whom even contend should be the responsibility of oncologists [4, 5]. Though these measurements are crucial to clinical decision making, they are often not performed completely, and insufficient reporting of measurements is a common occurrence [6]. Approaches to improve quantitative imaging practices are needed, given their importance in cancer response assessment [4, 5].

A particularly challenging aspect of quantitative imaging assessment is locating the previously-reported lesions on follow-up imaging studies. An automated method to locate the corresponding lesions on follow-up studies and to segment them automatically could greatly improve not only the quality of quantitative imaging practice but also the efficiency of quantitative imaging assessment. In addition, automated methods could improve the ability of imaging to inform cancer care. Since lymph nodes are a frequent site of cancer lesions and account for many of the cases where multiple lesions need to be measured, our focus is automated assessment of cancer lesions in lymph nodes.

Automated segmentation of cancer lesions in lymph nodes is challenging. Lymph nodes are generally intermediate in signal intensity. Since parts of a lymph node boundary may be obscured due to partial volume effect, diffuse edges, sharing boundaries with surrounding tissues of similar intensities and potentially inhomogeneous density-values, it is difficult to reliably segment lymph nodes automatically. Rogowska et al. [7] evaluated five elementary segmentation techniques, such as watershed technique and thresholding, for lymph node segmentation and concluded that a high degree of model knowledge is needed for a reliable segmentation. One of the first attempts was a three-dimensional (3D) active surface approach by Honea and Snyder [8], based on image gradients and shape constraints. Unfortunately, the approach was only evaluated on synthetic images, not clinical data. Dornheim et al. [9, 10] presented a stable 3D mass-spring model for lymph node segmentation in CT datasets. This model allowed for the first time to incorporate the three characteristic features of lymph nodes (gray value range, contour information and shape knowledge) into one single 3D model. The stable mass-spring model was extended by Dornheim et al. [11] for enlarged and mostly well separated necrotic lymph nodes. Due to the size preserving property, the performance of the mass spring model is highly affected by the size of the target structures. Thus, a size invariant mass spring model [12] was introduced to address the prior limitation. The fast marching technique [13] needed heavy user interaction (barriers, etc.). Maleike et al. [14] proposed a semi-automatic shape model guided deformable surface model for segmenting enlarged lymph nodes in CT images, which was integrated into an application together with a tool for manual correction of the segmentation. Barbu et al. [15] presented a learning based method for the detection and segmentation of axillary lymph nodes. None of the aforementioned methods automatically segment lesions on longitudinal CT images, where the same lesions need to be consistently identified and segmented on each follow-up imaging study.

Several lymph node segmentation methods for longitudinal CT images have been previously described. Yu et al. [16] presented an automatic tracking of lymph nodes in follow-up thoracic CT images, where the tracking performance of using affine and non-rigid registration was compared. The free-form deformation (FFD) is superior to give a better precision. Moltz et al. [17] presented a general framework for automatic detection of matching lesions in follow-up CT, which is not specialized for a certain lesion type and does not need any organ-specific registration or segmentation. Yan et al. presented a marker-controlled watershed algorithm to semi-automatically segment lymph nodes in sequential CT images [18], where a lymph node was first identified by manually drawing a circle around it. Then, by incorporating information about the lymph node identified on the baseline scan with the matching result from the follow-up images, Yan et al. [19] developed a similar method to automatically determine the internal and external markers. Xu et al. [20] presented a method based on adaptive region-growing and clustering to automatically and reproducibly identify and segment abnormal lymph nodes in serial CT exams. Yu’s method [16] and Moltz’s framework [17] only provided the location of lesions, not the segmentation. The mark-controlled watershed algorithm [18] is semi-automatic, not automatic. The automatic method [19] and [20] is time-consuming due to the non-rigid image registration.

This paper presents an automatic and fast lymph node segmentation algorithm for serial CT images. The candidate slices from follow up imaging studies, which contain the same lymph node in the baseline images, are selected by using an affine registration, maximizing the normalized mutual information (NMI) implemented in the 3D rigid registration tool of the Image Registration Toolkit (IRTK)¹ [21]. Then the slice, with minimum mean square error (MSE) between each of the registered candidate slices and the baseline scan, is taken as the corresponding slice in the follow up scan. The details of this registration-based approach have been previously described [20]. Fig.1 shows the flowchart of the proposed algorithm, which we have initially developed in 2D. Based on the outline of lymph nodes created by radiologists in the baseline image, the automatic two-step registration in follow-up images is used to provide the initial evolving curve from the baseline image to locate and circumscribe the lesion in the follow-up images. Then, the initial evolving curve is refined with intensity and edge information to make the initial curve close to the boundaries of lymph nodes. Finally, the snake model is adopted to obtain the output result. Compared with our previous work [20], the proposed algorithm mainly has two differences: (1) FFD was replaced with the two-step registration to improve the segmentation speed; (2) snake model was adopted, instead of region-growing and clustering, to obtain smooth segmentation results.

Fig.1.

Flowchart of the proposed algorithm

2. Image registration

After obtaining the outlines of lymph nodes created by radiologists in the baseline image, a two-step registration in follow-up images is presented to speed the image registration, including the coarse registration and the fine template matching.

2.1 Coarse registration

In general, the position of each lymph node in longitudinal CT images is similar at each time point, and the intensity difference between body and background is usually moderately large. Fig.2 shows one example, namely serial CT images in a patient at four different imaging dates. Thus, in our algorithm we perform an initial coarse registration as follows: (1) Detect the body in the image with a pixel value threshold, (2) remove non-body regions connected with body region with a morphological operation, (3) fill hollow regions within body region, and (4) calculate the centroid, major orientation, and minor axis length of the body region, which are used to eliminate the influence of the translation, rotation and scale in subsequent steps. Fig.3 shows a demonstration of the calculation of the rigid registration parameters, which are used for the rigid registration between the baseline image and the follow-up images (Fig.5).

Fig.2.

Serial CT images in a patient at four different imaging dates (t0–t3), where the t0 scan is the baseline image. The lymph node to be tracked is circled with the red dash line.

Fig.3.

Rigid registration. The white region denotes the detected body region of Fig.2(a), and the red point, orange arrow, and blue line represent the centroid, major orientation, and the length of the minor axis, respectively.

Fig.5.

Image registration and initialization refinement results of Fig.2(b). Red circle: original position of the lesion in the baseline image. Blue circle: updated lesion position after the coarse registration. Green circle: fine registration result with the template matching. Yellow circle: boundary of the refined initialization.

Fig.5 indicates that the coarse registration (blue circle) makes the initial lymph node position (red circle) close to the real object region, but the precision of rigid registration is not high. To improve the registration precision, the template matching is adopted.

2.2 Template matching

Since the coarse registration brings the initial object contour close to the position of the lymph node in the follow-up images, the region to be searched using template matching can be restricted in a small neighborhood centered at the initial position of the lymph node to improve the matching precision and reduce the computing time. The key parameter for the template matching is the size of the template. The size should be small when the change of the surrounding background of the lymph node is large in the follow-up images, while the size should be large when the change of the surrounding background is small. For different cases, the change of the surrounding background is also different. Thus, it is not possible to use a template of fixed size.

Fig.4 shows the influence of the template size, where both of the small and large template contain the lymph node. The large template contained more background region, where the white background region in the lower left corner should not be contained because it greatly changed in the follow-up images, such as Fig.2(c). For Fig.8, a large template is more suitable than a small template because the change of the background near the lymph node is small.

Fig.4.

The size of template. The small and large templates are marked with the orange and red dash squares, respectively.

Fig.8.

Segmentation results without (Top) and with (Bottom) the snake model

In our experience for all of the test cases in section 5, object loss (no intersecting region between the estimated and real lymph nodes) happens when one template with a constant size is adopted. To make the template matching robust and precise, we present a template matching algorithm with two different sizes. Let an image patch $P_{(x,y)}^I$ located at (x, y) ε Ω on the image I be the set of all image values belonging to a spatially discretized local w × h neighborhood of I centered at (x, y), where Ω denotes the image domain. The width (w) and height (h) of the local neighborhood is defined as w = w₀ + r and h = h₀ + r (r εN), where w₀ and h₀ are the width and height of the smallest rectangle containing the initial lymph node in the baseline image, respectively. In this paper, r is set to 5 and 20 for small and large template, respectively (optimization of this and other parameters in the method are discussed in section 5.3). Then, the template matching formula is

$$d(x,y,p,q)={\Vert P_{(x,y)}^I-P_{(p,q)}^I\Vert }_{\mathit{1}}$$ (1)

(1) where ∥·∥₁ denotes 1-norm, namely the sum of the absolute values of the difference between two image patches.

In the small searching region (41 × 41 in this paper), two templates with different sizes are utilized to locate the lymph node in the follow-up images. Let d^k = {d^k (i)|i = 1, 2,…,m}be the kth (1 or 2) sorted template matching degree in ascending order, where m = 41 × 41 is the number of pixels in the searching region. The location corresponding to the minimum template matching degree is taken as the candidate lymph node location. Thus, we can obtain two candidate locations. To select among these two candidate locations and to evaluate the template matching results, the difference between the first and the ith matching degree is calculated:

$$\mathrm{\Delta }{d}_i^k=d^k(i)-d^k(\mathit{1})$$ (2)

(2) Since the searching neighborhood is the same for two templates, the small template has a higher probability to find similar regions than the large template. We assume that the 1st and 2nd templates are corresponding to the small and large templates, respectively. To make the evaluation more comparable, the value of i in (2) for small template should be larger. Based on empirical studies i in (2), it is set to 15 and 10 for small and large template, respectively.

An example of the template matching result is shown in Fig.5. After the template matching, the initial lymph node position is closer to the real object region than the coarse registration result (blue circle in Fig.5).

3. Initialization refinement

When the change of lymph nodes in longitudinal images is large, such as the size and shape, the rigid image registration cannot provide a very fine initialization. The snake model is likely to get trapped in a local optimal solution when the initial evolving curve is far away from object contour. To facilitate the following snake model, the fine registration results are further improved to make the initial lymph node contour closer to the real object boundaries. The initialization refinement is restricted in a narrow band generated with the fine registration contour. The narrow band generation method in [22] is used.

In addition, the local object region containing lymph node is smoothed to reduce the influence of noise on initialization refinement. The non-local means (NL-means) method [23] was adopted, because it can preserve edge information well. The NL-means method can be summarized as:

$$v(x,y)=\frac{{\int }_{\mathrm{\Omega }}u(p,q)w(x,y,p,q)dpdq}{{\int }_{\mathrm{\Omega }}w(x,y,p,q)dpdq}$$ (3)

(3) where u and v denote an original noisy image and the denoised image, respectively. The weight function w(x, y, p,q) depends on both the spatial similarity between points (x, y) and (p,q), as well as the range similarity between corresponding patches centered at (x, y) and (p,q). The detailed interpretation of the method can refer to [23].

Then, the intensity and edge information are utilized to refine the initialization, which is presented as follows:

1. Remove background based on intensity difference of image patches. The 3 × 3 central object region in the current image is taken as a template. For each pixel in the narrow band, if the distance of the image patch with the template is larger than a threshold, it will be removed. The definition of the image patch distance is similar with the Equation (1). The threshold is defined as thr = 8 · std, where std is the standard variation within the lymph node in the baseline image.

2. Partition object and background regions. Generate the edge image of the current image with the Canny edge detector, which is used to partition the object region generated after the background removal based on the intensity difference. The connected object region with a maximum area is taken as the refined initial lymph node region.

Fig.5 shows an example result after the initialization refinement. The initial object contour is very close to the real lymph node after the refinement, which will prevent the snake model running into the local optima.

4. Snake model

A traditional parametric active contour (or snake) is a curve X (s) = [x(s),y(s)],s ∈ [0,1], which moves through the spatial domain of an image to minimize the energy functional

$$E_{\mathit{\text{snake}}}={\int }_0^1\frac{1}{2}(\alpha |X\prime (s){|}^2+\beta |X″(s){|}^2)+E_{\mathit{\text{ext}}}(X(s))ds$$ (4)

(4) where α and β are weighting parameters that control the snake’s tension and rigidity, respectively, and X′(s) and X″(s) denote the first and second derivatives of X (s) with respect to s, which are the internal forces coming from within the curve itself. In this paper, the external energy function E_ext is designed to lead the active contour toward image edges

$$E_{\mathit{\text{ext}}}(x,y)=-{|\nabla I(x,y)|}^2$$ (5)

(5) where I (x, y) denotes the input image. Details about the numerical solution of the energy functional (4) were provided in [24]. In this paper, the parameters are fixed as α = 0.02 and β = 0.033.

An example of the finial segmentation result of the algorithm is shown in Fig.6. The finial object contour is smooth and precise after the evolution of the snake model.

Fig.6.

Final segmentation result (magenta circle) obtained with the snake model.

5. Experimental evaluation

The images were acquired on a LightSpeed CT scanner (GE Medical Systems, Milwaukee, Wis) with the slice thickness of 5 mm. We obtained 76 CT scans containing 26 distinct mediastinal and abdominal lymph nodes from 14 patients obtained at 3 or 4 different time points (i.e., each patient had 3 or 4 longitudinal CT imaging studies). The time interval between two consecutive CT studies averaged 12 weeks. The image resolution is about 0.8 mm/pixel (range = 0.6180 to 0.9766 mm/pixel). The image containing the lymph node in the earliest time point was taken as the baseline image, and the scans at the following time points were taken as follow-up images. For each case, a radiologist circumscribed the lymph node in the most representative cross-section in the baseline and follow-up CT images. The outlines the radiologist drew in the baseline image were used for the initial position and those drawn in the follow-up image served as the “gold standard” for evaluating our proposed algorithm. Lymph node sizes ranged from 0.6 to 4 cm with a mean of 1.8 cm on baseline scan; 0.5–3.9 cm with a mean of 1.9 cm on follow up scan. The change of size ranged from 0.3 to 7.8 mm with a mean of 2.2 mm over time. The algorithm was implemented in Matlab and run on a 2.83 GHz Pentium 4 PC with 3.37GB memory.

5.1 Quantitative evaluation

We evaluated the performance of our segmentation algorithm according to the RECIST criteria [1, 2] and several quantitative metrics. The RECIST criteria have been widely adopted in the assessment of treatment response. The length of the diameter (long axis) of enlarged lymph nodes in both baseline and follow-up images was calculated based on the circumscribed contour. A categorical value for disease response was given according to the change in the sum of the diameters (SLD) of target nodes from baseline image to follow-up images, i.e in RECIST 1.0. “Complete Response (CR)” for disappearance of all target lesions, “Partial Response (PR)” for at least a 30% decrease in SLD, “Progressive Disease (PD)” for at least a 20% increase, and “Stable Disease (SD)” for neither sufficient shrinkage to qualify for PR nor sufficient increase to qualify for PD. We compared the RECIST 1.0-based assessment of lymph node response computed from our segmentation to that computed from our gold standard. We also calculated quantitative metrics to evaluate our performance, including contour distance-based measurements: mean absolute distance (MAD) [25] and Hausdorff distance, and area matching-based measurements, e.g. the ratios of overlay, over-estimation and underestimation of our segmentation compared with the gold standard.

All 76 lymph nodes in the follow-up images were used to test our algorithm, and all of the test cases were successfully detected using the method described in Section 2, while 26/29 (89.7%) lymph nodes could be matched in the follow-up scans when registering with the fast FFD method in [19]. By “successful”, we mean that the deformed lymph node after registration overlaps with the target lymph node in the follow-up scan. A total of 38/40 (95%) of lymph nodes resulted with our method in the same RECIST 1.0 response category as the gold standard, where the numbers of CR, PR, PD and SD are 0, 3, 1 and 36, respectively.

Segmentation results for the 76 lymph nodes are provided in Table 1. By way of comparison, the average Hausdorff distance, overlap ratio and underestimated ratio of the related approach to automatic identification and tracking of lymph nodes by Yan [19] are 3.9mm, 73.0% and 16.3%, respectively. Compared with Yan’s method, our algorithm achieved good segmentation results, though different cases were used to evaluate Yan’s method and our method. The computing time of our algorithm is fast, as shown in Table 2. For the fast FFD method adopted by Yan, the computing complexity is high. Thus the time performance of our algorithm seems to be superior to the Yan’s method.

Table 1.

Summary statistics for the performance of the proposed algorithm based on comparison of computer results and “reference standard”

	MAD (pixel/mm)	Hausdorff Distance (pixel/mm)	Overlap Ratio	Over-estimated Ratio	Under-estimated Ratio
Mean	1.25/1.02	3.70/2.98	74.4%	16.2%	14.9%
Stddev.	0.56/0.49	1.56/1.25	12.6%	16.9%	11.2%
Min	0.33/0.31	1.00/0.94	43.9%	0.0%	0.0%
Max	3.40/3.19	9.22/8.64	93.5%	94.3%	54.5%

Table 2.

Computing time including the image registration and segmentation (unit: s)

	Total	Average
76 images	196.23	2.58

5.2 Qualitative analysis

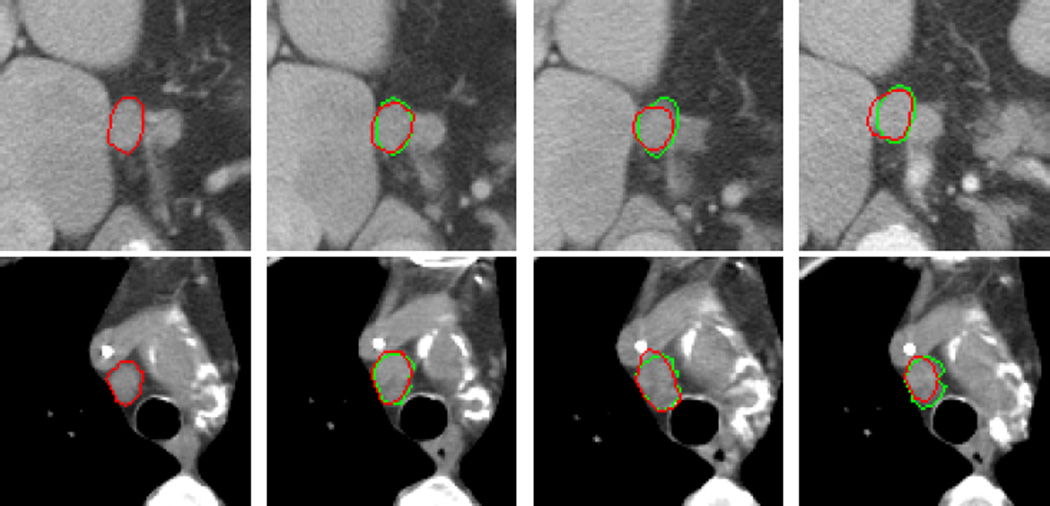
Fig.7 shows the automated segmentation results of Fig.2, where the red curve in Fig.7(a) is the hand-drawn circumscription of the lymph node in the baseline image, showing that the snake model can precisely segment the strong object edges and smoothly estimate the weak or lost object edges.

Fig.7.

Automatic segmentation results of Fig.2. The green and red curves in the follow-up images ((b)–(d)) are the gold standard and the automatic segmentation results with our algorithm, respectively.

Fig.8 shows the effect of the snake model. Depending on the internal forces of the snake model, the segmentation results with the snake model (the second row) are smoother than without the snake model (the first row). The smoothness is suitable with the lymph node characteristics. The image gradient based external force of the snake model can make the initial evolving curve closer to the object boundaries.

Fig.9 shows the segmentation results from four image series. The image density difference in some parts of the lymph node boundary is small, because the lymph nodes are connected with the tissues that have similar pixel values. The similarity distance based on image patch described in Section 3 can enlarge the difference between the lymph nodes and the surrounding tissues.

Fig.9.

Segmentation results in four image series

Fig.10 shows two inaccurate segmentation results where the second image of the first image series and the fourth image of the second image series are not accurately segmented. The reason is that the initial evolving curve is far away from the object boundaries after the image registration and initialization refinement, and the snake model ran into local optima. This illustrates that the position of the initial evolving curve is critical to obtain accurate segmentation results.

Fig.10.

Two inaccurate segmentation results

According to the evaluation above, it can be seen that the advantage of the proposed algorithm is that it is faster and generally more accurate than an existing algorithms to which we compared our results. However, the disadvantage is that the position of the initial evolving curve has a great influence for the segmentation accuracy. Since the external force of the snake model (4) depends on image gradient, the evolving curve cannot arrive at object boundaries when the initial evolving position is far away from the object boundaries, namely within inner object (top image of Fig.10(b)) or background (bottom image of Fig.10(d)). The reason is that the gradient within flat regions is too small to put the initial evolving curve move to the object boundaries. In order to extend the capture range, a new external force, gradient vector flow (GVF) [26], can be adopted.

5.3 Parameter evaluation

The values of all parameters in our algorithm were fixed for all 76 test cases. We assessed the sensitivity of the parameters based on overlap ratio in the following experiments.

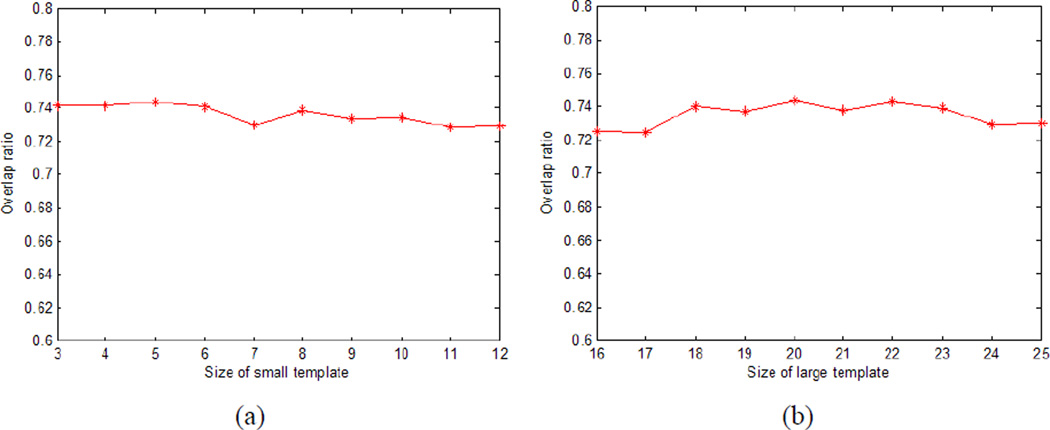
In the template matching (section 2.2), the size r is different for the small and large templates. Fig.11 shows the mean overlap ratio for different sizes of small (a) and large (b) templates. We varied the size of small template from 3 to 12, and the size of large template from 16 to 25. From Fig.11, we can see that the mean overlap is nearly constant with the different sizes of the templates, which means that our algorithm is relatively insensitive to the size of template.

Fig.11.

Mean overlap ratio for different sizes of small (a) and large (b) templates

The selection of the template matching degree (i in Equation (2)) is another free parameter in section 2.2. As discussed in section 2.2, the value of i for small template should be larger than that for large template. Fig.12 shows the overlap ratio for different i. We varied the difference Δi between the small and large templates from 0 to 7 with an interval of 1. The definition of difference Δi = i_small − i_large, where i_small and i_large denote the values of i for small and large templates, respectively. Fig.12 indicates that the difference Δi has a very limited influence on the average overlap ratio. In this paper, we set i_small = 15, i_large = 10, namely Δi = 5.

Fig.12.

Mean overlap ratio for the selection of template matching degree

In the snake model, there are two parameters, α and β, that can be tuned. Figs. 13(a) and (b) show the overlap ratio with different values of α and β, respectively. The change of the mean overlap ratio is small for different α, and the mean overlap ration is almost constant for different β. Thus the two parameters of the snake model have a small influence on the performance of our algorithm.

Fig.13.

Mean overlap ratio for the parameters of the snake model

6. Conclusions

This paper presents an automatic lymph node segmentation algorithm for longitudinal CT exams. Since the region of the human body in an image is very different from the background, a simple and robust coarse image registration is proposed based on the body detection. To deal with the change of the surrounding background, a template matching method with two different sizes is proposed to improve the coarse registration precision. The initial curve outlining the lymph node is refined based on image intensity and edge information to make the initial curve closely approximate the true lymph node boundaries. The final segmentation results are obtained by evolving the refined initial curve with the snake model. Experimental results demonstrate that our algorithm can successfully detect all of the 76 lymph nodes in the follow-up images and can achieve high segmentation accuracy; for example the average Hausdorff distance is 2.87mm. The speed of the proposed algorithm is fast; the average computing time, including the image registration and segmentation, is 2.58s. Comparing to the state-of-art works, the main novelties of our work include: (1) two-step image registration is performed to quickly and effectively detect lymph nodes; (2) a snake model was adopted to achieve smooth and accuracy segmentation results. In the future, we will try to improve the proposed algorithm in three aspects: (1) adopt better image registration method to improve the accuracy of the initial evolving position; (2) adopt more flexible active contour model to obtain more accurate segmentation results; (3) set the parameters of our algorithm adaptively to make the algorithm more robust for different sets of images; (4) extend our algorithm from 2D to 3D; (5) Test and improve the system by using more data, and adapt it to be usable by medical experts.