Abstract
White matter in the brain is structurally anisotropic, consisting largely of bundles of aligned, myelin-sheathed axonal fibers. White matter is believed to be mechanically anisotropic as well. Specifically, transverse isotropy is expected locally, with the plane of isotropy normal to the local mean fiber direction. Suitable material models involve strain energy density functions that depend on the I4 and I5 pseudo-invariants of the Cauchy–Green strain tensor to account for the effects of relatively stiff fibers. The pseudo-invariant I4 is the square of the stretch ratio in the fiber direction; I5 contains contributions of shear strain in planes parallel to the fiber axis. Most, if not all, published models of white matter depend on I4 but not on I5. Here, we explore the small strain limits of these models in the context of experimental measurements that probe these dependencies. Models in which strain energy depends on I4 but not I5 can capture differences in Young’s (tensile) moduli, but will not exhibit differences in shear moduli for loading parallel and normal to the mean direction of axons. We show experimentally, using a combination of shear and asymmetric indentation tests, that white matter does exhibit such differences in both tensile and shear moduli. Indentation tests were interpreted through inverse fitting of finite element models in the limit of small strains. Results highlight that: (1) hyperelastic models of transversely isotropic tissues such as white matter should include contributions of both the I4 and I5 strain pseudo-invariants; and (2) behavior in the small strain regime can usefully guide the choice and initial parameterization of more general material models of white matter.
Keywords: Constitutive modeling, Transverse isotropy, Brain tissue
1. Introduction
1.1. Background and motivation
Traumatic brain injury (TBI) is a common cause of death and disability in the United States (Coronado et al., 2011). In such injuries, linear and angular acceleration of the head leads to shearing and stretching of brain parenchyma (Bayly et al., 2005; Clayton et al., 2012; Gennarelli et al., 1982; Margulies and Thibault, 1992). Prediction of these injuries remains elusive, though it is a subject of intense research. Computer simulation methods, predominantly finite element (FE) simulations, have been proposed for prediction of injuries and development of preventive strategies (Ueno et al., 1995; Zhang et al., 2004). Predicted strains from simulations can be correlated with injury markers (McAllister et al., 2012) using strain-based thresholds for cellular and tissue injury determined in vitro (LaPlaca et al., 2005; Morrison et al., 2003; Wright and Ramesh, 2012).
A number of challenges remain before predictions of FE simulations can be applied with confidence. Brain–skull interactions play a central role in determining the brain’s response to head acceleration (Abney et al., 2011; Bayly et al., 2006, 2005; Brody et al., 2007; Clayton et al., 2012; Feng et al., 2010; Ji and Margulies, 2007; Ji et al., 2004; Sabet et al., 2008), but these boundary conditions have only recently been incorporated into FE models (Coats et al., 2007; Wright and Ramesh, 2012). The relationship between mechanical strain and cell death appears to be more complicated than can be predicted by a simple strain or strain rate criterion (Brody et al., 2007). Finally, a complete and accurate picture of the mechanical properties of brain tissue is needed.
The effort to characterize brain material properties has been sustained for over 50 years (Chatelin et al., 2010; Cheng et al., 2008; Elkin et al., 2011a; Fallenstein et al., 1969; Galford and McElhaney, 1970; Kaster et al., 2011; Shuck and Advani, 1972; van Dommelen et al., 2010). The current paper adds to this substantial body of literature by identifying necessary features of transversely isotropic hyperelastic models for modeling of white matter.
1.2. Characterization of mechanical properties of white matter
White matter tissue appears to be preferentially injured during brain trauma (Smith and Meaney, 2000), and the mechanics of white matter are important for predicting its deformation and associated injury. Since white matter consists predominantly of aligned axonal fibers and their myelin sheaths, it is hypothesized to be mechanically anisotropic, in contrast to gray matter, which is structurally isotropic (Prange et al., 2000). More specifically, where fibers are well-aligned, white matter is expected to be transversely isotropic with the fiber axis normal to the plane of isotropy.
The literature largely supports this hypothesis, though estimates of specific parameter vary. Brain mechanical properties have been studied both in vivo and in vitro. In one study, brainstem was found to demonstrate an anisotropic (transversely isotropic) response to oscillatory shear deformation in vitro (Arbogast and Margulies, 1998). Subsequent studies in vitro (Ning et al., 2006; Prange and Margulies, 2002) confirmed that gray matter appeared isotropic and that white matter from corona radiata, corpus callosum and brainstem appeared anisotropic when subjected to shear deformation at high strains and strain rates. Hrapko et al. (2008a) suggested that the anisotropy of corona radiata increases with the magnitude of shear deformation but decreases with increasing frequency during dynamic oscillatory shear tests. In contrast, Nicolle et al. (2005) observed that white matter from the corona radiata appeared isotropic in shear under small strain (0.0033%) and high strain rates (0.8 s−1). When uniaxial tensile tests were performed on strips of porcine corona radiata (Velardi et al., 2006), they appeared almost 3 times stiffer when the fiber axis was aligned with the direction of stretch than when stretched perpendicular to the fiber axis. In vivo studies of brain tissue using magnetic resonance elastography (MRE) are promising but still not conclusive on this topic, although recent MRE studies (Qin et al., 2012; Romano et al., 2012) have begun to address anisotropy. Most notably, Romano et al. (2012) estimated parameters of a transversely isotropic linear viscoelastic model of brain tissue using MRE, but the analysis has not been validated on materials with known properties.
Transversely isotropic materials may, in general, exhibit anisotropy in both shear and tension with respect to the fiber axis (Spencer, 1984). To our knowledge, prior experimental studies of white matter (Hrapko et al., 2008a; Prange and Margulies, 2002; Velardi et al., 2006) have focused on either shear or tensile anisotropy, but not both. Measurement of anisotropy in both shear and classical tensile tests requires separate samples, as gripping brain tissue for tensile tests damages the tissue. To overcome this measurement problem, dynamic shear tests can be combined with subsequent asymmetric indentation tests on the same sample, to measure the anisotropy of brain tissue. This protocol involves both fiber–matrix shear and fiber stretch (Namani et al., 2012). Each test requires only simple fixtures to hold the sample, and is non-destructive at small strains. Subject to certain assumptions described below, the combination can be used to estimate all the parameters of an incompressible, transversely isotropic, linear elastic model of brain tissue.
The current study focuses on clear characterization of the elastic component of the response during small deformations, rather than attempting to develop a complete nonlinear visco-hyperelastic model. Fully nonlinear, viscoelastic models require large amounts of data to parameterize, yet the correct choice of the basic form is often not clear. Although linear elasticity is not sufficient to describe the mechanical properties of soft tissue under large deformations, any hyperelastic model of white matter must match the predictions of linear elasticity in the limit of small strains. Linear elasticity is therefore valuable for guiding the selection of the form of a more general hyperelastic model. Similarly, the behavior of a viscoelastic solid is typically understood in terms of the underlying short-term and long-term elastic behavior. Thus a well-parameterized linear elastic model is fundamental to the development of hyper-viscoelastic material models.
The choice of the set of strain invariants upon which a hyperelastic model is based is critical. In general, the strain energy function of a transversely isotropic hyperelastic material depends on the invariants I1, I2, and I3 of the right Cauchy–Green strain tensor, and the pseudo-invariants I5 and I4 (which are invariant under rotation about the normal to the plane of isotropy). Structurally based models (Meaney, 2003), phenomenological, transversely isotropic, hyperelastic models (Cloots et al., 2012; Ning et al., 2006; Velardi et al., 2006) and a hyper-viscoelastic model (Chatelin et al., 2012) of white matter have been proposed previously. In published hyper-elastic models, a standard fiber reinforcement formulation (Merodio and Ogden, 2003; Qiu and Pence, 1997) has been used. In standard fiber reinforcement models, tissue anisotropy observed during tensile or shear tests is related to an additive term in the strain energy due to fiber reinforcement, captured by the pseudo-invariant I4 r. Holzapfel and Ogden (2009) have discussed the general requirements for full characterization of incompressible hyperelastic materials; they advocate use of a material model in which strain energy depends only on I1 and I4, unless evidence supports a more complicated constitutive law. Weiss et al. (1996) used a strain energy function dependent on I1, I2, and I4 to model the transversely isotropic behavior of ligaments and tendons. However, a material model that incorporates only I4 to model fiber reinforcement does not predict anisotropy in shear in the small strain regime (Merodio and Ogden, 2005; Spencer, 1984). In fact, anisotropy has been observed in shear tests of white matter (Prange and Margulies, 2002) and brain stem (Arbogast and Margulies, 1998). For a hyperelastic material to exhibit anisotropy in shear under small deformations, the strain energy function must depend on the pseudo-invariant I5 (Merodio and Ogden, 2005; Spencer, 1984). In this study we show experimentally that including both I4 and I5 in he strain energy function is essential to predicting the mechanics of white matter.
1.3. Study overview
The goal of our study is to clarify what features of constitutive models are needed to capture the mechanical anisotropy (transverse isotropy) of white matter. The predicted response of transversely isotropic material in the infinitesimal strain limit is compared to relatively simple experiments that identify the specific contributions of fiber stretch and fiber–matrix interaction. We tested samples of white matter (corpus callosum) and gray matter (cortex) from lamb brains, using a combination of dynamic shear testing (DST) (Okamoto et al., 2011) and asymmetric indentation tests (Namani et al., 2012). White matter was found to be anisotropic in both shear and indentation, while gray matter exhibited isotropic behavior. These results, while obtained in the small-strain regime, imply that in an accurate hyperelastic model of white matter, the strain energy function should depend on both I4 and I5.
2. Review of constitutive models of transversely isotropic materials
2.1. Transversely isotropic hyperelastic models
White matter is fibrous tissue in which a clearly defined, dominant fiber direction is typical. For example, fibers are predominantly oriented left-to-right in the corpus callosum, which connects the brain’s hemispheres. We define the fiber direction to be the x1 direction in Cartesian coordinates, so the plane of isotropy is perpendicular to x1 (Fig. 1). If F = ∂x/∂X is the deformation gradient, where X is a material vector in the reference configuration and x is the corresponding spatial vector in the deformed configuration, the right and left Cauchy–Green tensors are C=FTF and b=F FT. The volume ratio between the deformed and undeformed configurations is given by J=det F. The corresponding principal invariants of C and b are (Holzapfel, 2000; Spencer, 1984);
Fig. 1.
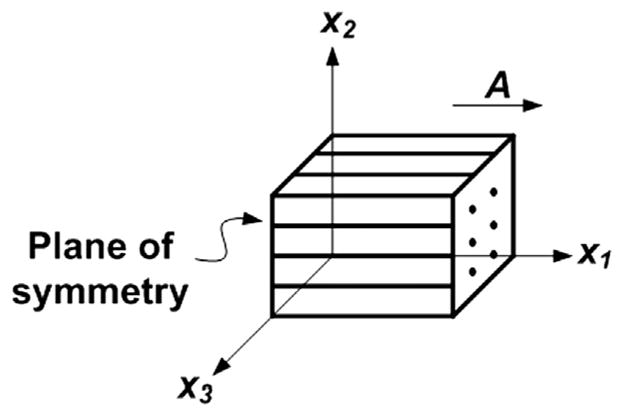
Basic model of a transversely isotropic (fibrous) material. Vector A indicates the fiber direction in the reference configuration. The plane of isotropy is perpendicular to x1.
| (1) |
| (2) |
and
| (3) |
In a transversely isotropic material, the strain energy may depend also on two additional “pseudo-invariants” I4 and I5 (Spencer, 1984); these quantities are invariant under rotation about the axis of symmetry. If A is the unit vector of the mean fiber direction in the reference configuration at a material point X, then
| (4) |
| (5) |
Fiber deformation is described by the vector a=FA, the direction of which is the local fiber axis in the deformed configuration and the magnitude of which represents the fiber stretch λ. We note that I4 = λ2 = |a|2.
The strain energy function ψ can be written generally in terms of the invariants listed above:
| (6) |
The general form of the Cauchy stress in terms of the invariants defined above, writing ψi = ∂ψ/∂Ii (i = 1,…, 5), is
| (7) |
Requiring both strain energy density and Cauchy stress to vanish in the undeformed (reference) state, leads to the following constraints on the strain energy function:
| (8) |
| (9) |
and
| (10) |
2.2. Transversely isotropic linear elastic models
The incremental behavior of hyperelastic materials can be described by linear elastic models (Holzapfel, 2000). In the limit of infinitesimal deformations, the Cauchy stress tensor is related to the small strain tensor by a fourth-order elasticity tensor. The components of the elasticity tensor can be derived in terms of the strain energy function (Merodio and Ogden, 2003, Eqs. (19)–(22)). These components may be arranged in a 6 × 06 matrix (Voigt notation) taking advantage of inherent symmetries. We can write the elements cij of this 6 × 6 elasticity matrix in terms of the partial derivatives of ψ with respect to the invariants (Eq. (11)). The constraints on the strain energy function in the undeformed state (Eqs. (8)–(10)) are used to derive the expressions for cij (Appendix A, Eqs. (A.1)–(A.8)). The elasticity matrix can thus be written:
| (11) |
where the 1-direction is aligned with A. The components cij are given in terms of ψ and its derivatives in Eqs. (A.2)–(A.7). Both I4 and I5 terms contribute to the difference between the elastic moduli in the principal directions:
| (12) |
where ψij = ∂2ψ/∂Ii∂Ij (i = 1, …, 5). We also observe that:
| (13) |
which shows that ψ must depend on I5 if the material exhibits different shear moduli in different orthogonal planes parallel and normal to the fiber axis for small strain. Since ψ5 is evaluated in the reference configuration, the form of ψ should be chosen so that (ψ5)(3,3,1,1,1) is not zero. Eqs. (12) and (13) are general results that illustrate the implications of small-strain behavior for general hyperelastic models.
Appendix B describes the application of these relationships to describe the small-strain response predicted by several hyperelastic material models of incompressible, or nearly incompressible, transversely isotropic materials. In Appendix B we show a minimal model that has a strain energy function of the necessary form required for consistency with our experimental data, although it may not be sufficient to describe larger deformations. Three general parameters describe the elastic response of each model during small deformations:
μ̃, the shear modulus in the plane of isotropy;
φ̃ = (μ1− μ2)/μ the (non-dimensional) difference in shear modulus μ1, relative to μ, for shear in planes perpendicular to the plane of isotropy; and
ζ̃ = (E1−E2)/E2, the non-dimensional difference in Young’s modulus for stretch along the fiber axis (E1) relative to Young’s modulus for stretch normal to the fiber axis.
3. Experimental materials and methods
We show in Appendix B that because white matter displays anisotropic behavior in both tension and shear, the simplest adequate transversely isotropic, incompressible material model of white matter involves three independent parameters (μ, ζand φ in our example model, Eq. (B.8)). These three parameters can be estimated from a combination of (1) simple shear with displacement either parallel or perpendicular to the fiber axis and (2) indentation with a tip of rectangular cross-section, in which the long axis of the tip is aligned either parallel or perpendicular to the fiber axis, with both tests performed on the same sample (Namani et al., 2012).
3.1. Sample preparation
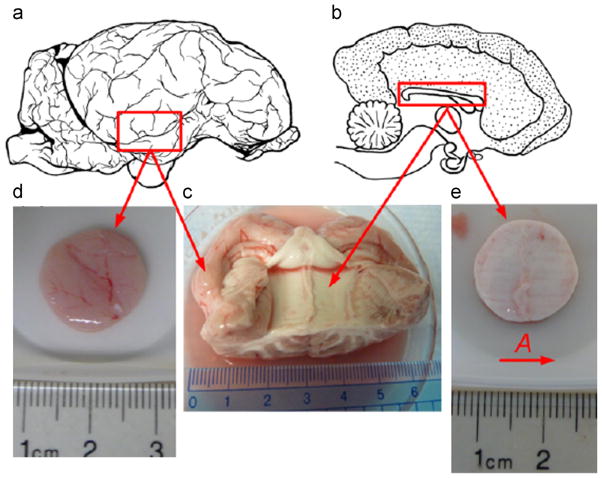
Lamb heads (8–10 months of age) were obtained from a local slaughterhouse one to 2 h post-mortem. The top of the skull was resected by cutting the bone on four sides. The dura mater, arachnoid and pia matter were resected with fine scissors, and the two hemispheres were separated. Gray matter tissue samples were harvested from the temporal lobe (Fig. 2(a,c)) close to the cerebellum. The cerebellum was separated from the two lobes by cutting the tentorium, and white matter tissue samples were harvested from the corpus callosum (Fig. 2(b,c)), where axonal fibers can be seen running across and connecting the left and the right brain hemispheres. Tissue samples were sliced using a vibrating microtome (Vibratome®, series 1000, St. Louis, MO), and test samples were punched from the cross-section to obtain predominantly gray matter (Fig. 2(d)) or white matter (Fig. 2(e)). Circular punched samples were ~2.8 mm thick and ~15.6 mm in diameter. All samples were submerged in ice-cold artificial cerebrospinal fluid (CSF) (Alexander and Godwin, 2005) before testing, which was conducted within 5 h post-mortem as recommended by Garo et al. (2007). Testing was performed at room temperature (21–23 °C).
Fig. 2.
(a) Lateral sagittal view of lamb brain. The red box indicates the temporal lobe region from which gray matter samples were harvested. (b) Medial sagittal view of the lamb brain; the red box indicates the corpus callosum region from which white matter samples were harvested. (c) Portion of lamb brain showing the corresponding region where (d) gray matter sample and (e) white matter sample were dissected and punched for experiment. The ruler below the sample has 1 mm scale increments. Vector A indicates the axonal fiber direction in the white matter sample. (For interpretation of the references to color in this figure caption, the reader is referred to the web version of this article.)
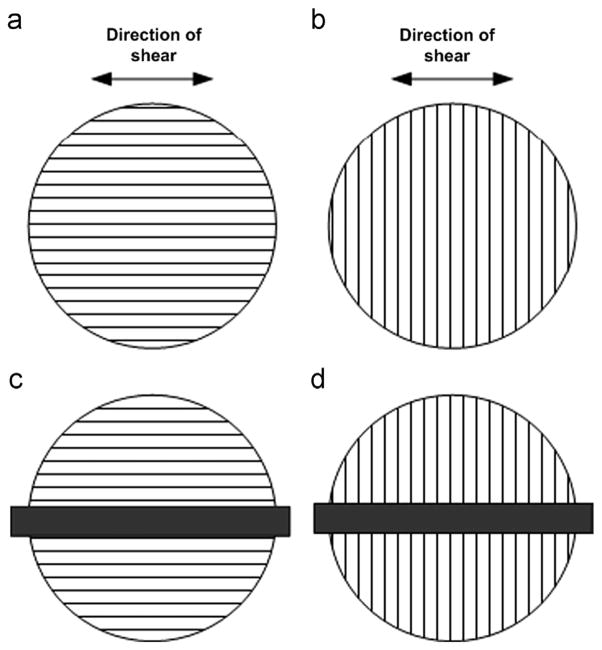
3.2. Dynamic shear testing (DST)
The complex shear modulus was measured using a dynamic shear testing (DST) device (Namani et al., 2012; Okamoto et al., 2011). Samples were held between two parallel plates with rough (sandpaper) surfaces and compressed 5% to ensure consistent contact and normal force. Vibratory shear displacement ux of the lower plate was produced by a voice coil, while shear force, Fs, was measured on the stationary upper plate. Data were acquired with a SigLab 20–22 data acquisition system (Spectral Dynamics, Inc., San Jose, CA) and stored on a PC. White matter samples were tested with the fiber direction either parallel (test 1, Fig. 3(a)) or perpendicular (test 2, Fig. 3(b)) to the direction of oscillation. Gray matter samples were also tested in two orientations, rotating the sample by 90° after the first test, with the first test marked as test A and second test as test B. The average shear stress on the sample’s stationary surface is given by τ = Fs/As, where As is the area of the sample’s circular face. The nominal shear strain was estimated as γ = ux/h = (Ux cos(ωt))/h, where Ux (~0.03 mm) is the amplitude of the horizontal shear oscillation, h is the sample thickness, and ω = 2πf, where f is the frequency (20–30 Hz, a frequency range in which inertial effects are minimal and signal-to-noise is high). Displacement amplitudes were limited to stay within the small strain regime, in which our analysis and models are approximately correct. The complex shear modulus, μ*, was calculated from τ and γ:
| (14) |
where μ′ is the storage modulus and μ″ is the loss modulus.
Fig. 3.
Sample configurations for mechanical testing of white matter (top view). In shear tests, each white matter sample was tested with axonal fibers (a) parallel and (b) perpendicular to the direction of imposed displacement. In indentation tests, each white matter sample was tested with axonal fibers (a) parallel and (b) perpendicular to the long side of the indenter head.
3.3. Asymmetric indentation
The indentation stiffness of each tissue sample was measured after the DST test. We used a custom-built asymmetric indentation device and adopted a 3-step indentation protocol used previously (Namani et al., 2012). The rectangular stainless steel indenter head was 19.1 mm long × 1.6 mm wide. As with DST, we tested each sample in two configurations, rotated by 90°. White matter samples were tested with axonal fiber tracts parallel (||, Fig. 3(c)) or perpendicular (⊥, Fig. 3(d)) to the longer side of the rectangular indenter head. Gray matter samples were placed on the device in an arbitrary orientation and then rotated by 90° after the first test, with the first and second test results noted as A and B respectively. Each sample was indented to a depth of 5% of its thickness and then held in that position for 1 min for tissue relaxation, which is sufficient for brain tissue to fully relax to a steady state isometric force (Elkin et al., 2011a; Gefen and Margulies, 2004; Prevost et al., 2011; van Dommelen et al., 2010). This process was repeated for a total of three indentation steps, reaching approximately 5%, 10%, and 15% of the sample thickness respectively. Each indentation step was completed within 0.5 s with an average strain rate during indentation of 0.1 s−1. The indenter was actuated by a piezo-electric actuator (Model M-227.5, Physik Instrumente, Auburn, MA) and the indentation force, Fi, was measured by a load cell (Honeywell Sensotec, Model 31, 150 g), where indices i=1, 2, 3 represent the three indentation steps. The vertical displacement of the indenter, di, was measured by a non-contact proximity probe (Model 10001-5MM, Metrix Instrument, Houston, TX). Custom written Matlab programs (The Mathworks, Natick, MA) were used for data acquisition and system control. The force–displacement curve during indentation was analyzed and the portion with approximately constant indentation velocity was fit to a line with a slope corresponding to the indentation stiffness k = Fi/di.
3.4. Interpretation of indentation results by finite element analysis
We interpreted indentation test results using 3-D finite element (FE) simulations in the Abaqus environment (Abaqus 6.10.1, Dassault Systems, Providence, RI), as described previously (Namani et al., 2012). Briefly, the tissue sample, modeled as a transversely isotropic, linear elastic disk, 3.0 mm in thickness and 15.0 mm in diameter was indented in the z-direction with a rigid, rectangular indenter of cross-sectional area 1.6 mm × 19.0 mm. The corners of the rectangular indenter were rounded so that the initial contact width was 1.0 mm and the initial contact area between indenter and gel was 15.0 mm2. To reduce the number of elements required, only one quarter of the sample was modeled and symmetry boundary conditions were applied to the straight edges of the model. The quarter model contained 103,925 eight node brick elements (C3D8) and the rigid rectangular indenter was discretized into 1686 rigid elements (R3D4). The displacements uz of all nodes on the lower surface of the sample were set to zero to approximate frictionless contact between the sample and rigid substrate. The remaining surfaces had traction-free boundary conditions. The nonlinear geometry option was used to account for large displacements. To explore the possible role of frictional forces on our results, we included friction in the indenter-sample and sample-substrate contact conditions. The contact friction was modeled as static Coulomb friction with a friction coefficient, cf, equal to 0, 0.1, 0.25, 0.5, 0.75, or 1 on both contacting surfaces.
The seven engineering constants required by the Abaqus FE software (two Young’s moduli, two shear moduli, and three Poisson’s ratios, of which only three are independent in the incompressible limit) were calculated from specified values of the nearly incompressible model parameters (κ, μ, ζ and φ). To generate the values for different combinations of the strain energy function parameters, the parameters φ and ζ were varied while the ratio κ/μ was fixed at 200. Indentation simulations were performed with the axis of transverse isotropy oriented perpendicular to the long axis of the indentation head (e1 = eX). To model indentation with the fibers aligned with the long axis of the indentation head, the local coordinate system of the material section was rotated by 90° without changing the orientation of the indenter (e1= eY). A quasi-static displacement boundary condition for uz was prescribed for the indentation head in increments of −0.01 mm and equations were solved with the Abaqus/Standard implicit solver. The maximum prescribed displacement of the indenter was uz= −0.15 mm, 5% of the simulated sample thickness, which corresponded to the displacement at the end of the first experimental indentation step.
Because the indentation caused primarily local deformation in the region of the indenter, we also developed a simplified model geometry consisting of a square sample (15 mm × 15 mm × 3 mm) with the same symmetry boundary conditions as the round sample geometry and a somewhat coarser mesh away from the indenter. This square model had fewer elements but yielded force–displacement estimates within 2% of the round model with a 10-fold reduction in solution time. The simplified model was used for all parametric studies.
4. Results
4.1. Experimental results
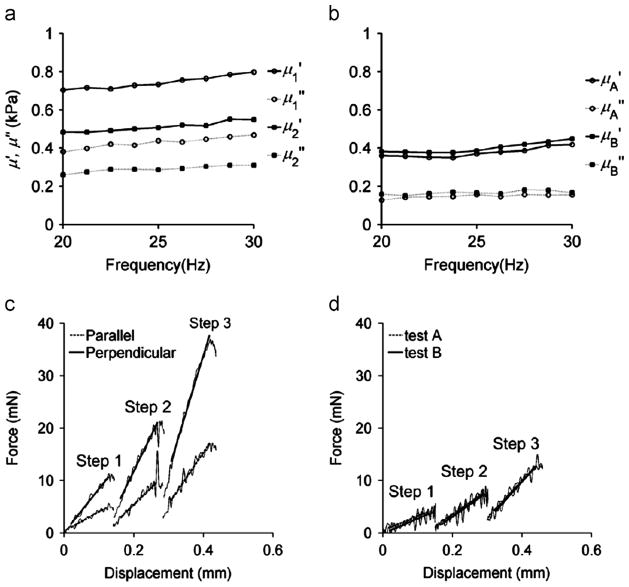
A total of 12 white matter samples and 9 gray matter samples were tested. For 6 of 12 white matter samples k⊥ was measured before k||, and for the remaining 6, k|| was measured before k⊥. Typical DST measurements for both white and gray matter samples are shown in Fig. 4(a,b). The peak horizontal displacement of the flexure, Ux, was 0.03 mm, corresponding to a nominal shear strain of ~1%. Typical indentation measurements for both white and gray matter samples are shown in Fig. 4(c,d). Consistent mechanical anisotropy was observed in both DST and indentation tests in corpus callosum white matter tissue.
Fig. 4.
Representative DST and indentation data from one sample. (a) DST of a white matter sample tested with the shear loading applied in a plane parallel to the axonal fiber direction (μ1), or in a plane perpendicular to the axonal fiber direction (μ2). (b) Gray matter sample tested in one orientation (μA) and then rotated by 90° (μB). Storage and loss modulus components of the complex modulus, μ′ + iμ″, were measured using DST over the frequency range 20–200 Hz (only 20–30 Hz is shown). Force–displacement curves in 3-step indentation were recorded for (c) white matter samples tested with the fiber direction either parallel (||) or perpendicular (⊥) to the long side of the indenter head, and (d) gray matter samples tested in one orientation (test A) and rotated by 90° (test B). The solid lines are linear fits to data obtained when the indentation head is at a constant velocity.
4.1.1. Results of shear tests
White matter samples were stiffer when tested with the fibers parallel to the direction of shear (Fig. 3(a)), while no orientation dependence was detected for the shear moduli of gray matter samples. To compare shear moduli between samples, we averaged the storage and loss moduli of each sample at frequencies between 20 and 30 Hz. We calculated the estimated shear wavelengths based on the average shear moduli values and found that the wavelengths were at least 6 times longer than the thickness of the sample, meaning that inertial effects could be neglected relative to elastic and viscoelastic effects.
The average storage and loss moduli for white and gray matter samples from the DST tests are shown in Fig. 5(a). The storage and loss moduli for white matter were significantly larger when the samples were tested with the primary axonal fiber direction parallel to the direction of shear regardless of the order in which the two orientations were tested. However, no significant differences were observed for gray matter between the two orientations tested (Fig. 5(b)). The storage and loss moduli ratios ( and ) of white matter samples were 1.41±0.26 and 1.43±0.29 respectively; for gray matter samples, the storage and loss modulus ratio ( and ) were 0.96±0.11 and 0.96±0.15 respectively.
Fig. 5.
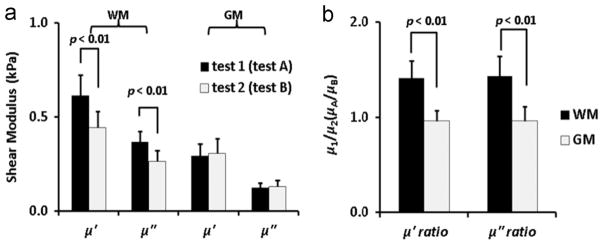
(a) Comparison of storage and loss components of the complex shear modulus of white matter (n=12 samples) and gray matter (n=9 samples). (b) Ratios of complex modulus components of white matter and gray matter, estimated by DST over frequency range of 20–30 Hz. Differences between storage moduli ( and ) and between loss moduli ( and ) for white matter samples were statistically significant (student’s t-test, p<0.01). Differences between storage moduli ratios ( and ) and between loss moduli ratios ( and ) for white and gray matter samples were statistically significant (student’s t-test, p<0.01).
4.1.2. Results of indentation tests
White matter samples appeared stiffer when indented with fibers perpendicular to the long side of the indenter head (Fig. 3(d)) compared to indentation when fibers were parallel to the long axis. In contrast, gray matter samples exhibited similar indentation stiffness in both the first and second tests. The indentation stiffness values for all samples are summarized in Fig. 6(a); indentation stiffness ratios (k⊥/k|| or kA/kB) are compared for gray and white matter in Fig. 6(b). Average values are also given in Table 1. For white matter samples, k⊥ was significantly greater than k||, regardless of the order in which the two tests were performed. This was true for each indentation step, although the stiffness ratio k⊥/k|| decreased for the second and third indentation step (2.3±0.7 and 2.1±0.6 respectively). For gray matter samples, there was no significant difference between kA and kB and the stiffness ratio kA/kB was not significantly different than one for any of the three steps. The relatively large standard deviations in the stiffness ratios was likely due to the uncertainty in establishing contact and local variations in thickness of individual samples. In addition, k|| of white matter samples for each indentation step was not significantly greater than kA or kB of gray matter samples for the corresponding step (Fig. 6).
Fig. 6.
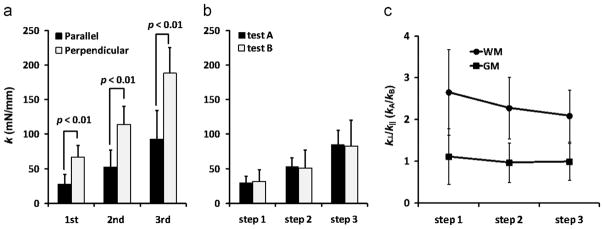
(a) Comparison of indentation stiffness of (a) white matter (n=12 samples) and (b) gray matter (n=9 samples) for each indentation step. Indentation stiffness measured for white matter is denoted (for axonal fiber direction parallel to the long axis of the rectangular indenter head) and k⊥ (fiber axis perpendicular to the long axis of indenter). Indentation stiffness measured for gray matter is denoted as kA and kB for two orientations of the sample 90° apart. At each indentation step, the difference between k|| and k⊥ was significant (student’s t-test, p<0.01), but the difference between kA and kB was not significant. (c) Indentation stiffness ratio of gray and white matter. Differences in the indentation ratio (k⊥/k|| or kA/kB) for each indentation step between white matter (WM) and gray matter (GM) samples were significantly different (student’s t-test p<0.01).
Table 1.
Summary of experimental DST and indentation test results and the associated material parameters of the strain energy function Ψ; (Eq. (B.8)) estimated from finite element (FE) models of indentation.
| Gray Matter | White Matter |
| Measured Elastic (Storage) Components of Shear Modulus | |||||
|---|---|---|---|---|---|
|
|
|
|
|||
| 0.29 ± 0.06 | 0.41 ± 0.42 | 1.41 ± 0.26 | |||
| Measured Indentation Stiffness | ||
|---|---|---|
| kA (mN/mm) | k|| (mN/mm) | k⊥/k|| |
| 31 ± 10 | 28 ± 15 | 2.7 ± 1.0 |
| Strain Energy Function Parameters Estimated from FE model of Indentation | |||
|---|---|---|---|
| cf | μ(kPa) | φ | ζ |
| 0.1 | 0.58 | 0.4 | 13 |
| 0.5 | 0.51 | 0.4 | 5.5 |
4.2. Finite element model results
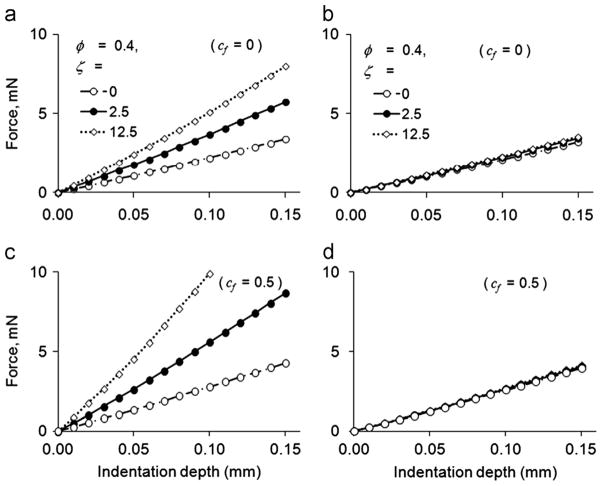
To demonstrate the implications of our experiments for modeling of white matter, we used FE simulations of the indentation experiments to relate indentation stiffness to the values of the three free parameters (μ; ζ; and φ) of the example constitutive model in Appendix B. Predicted force–displacement curves were obtained in both material orientations from FE simulations by setting the parameter φ equal to 0, 0.4 or 0.8 and ζ equal to 0, 2.5, 12.5, or 25 while μ was fixed at 500 Pa. The range for the parameter φ was chosen to span the ranges observed in DST experiments and the range of ζ was chosen to obtain maximum values of similar to our indentation experiments. This resulted in 12 combinations of φ and ζ. Representative FE force–displacement curves are shown in Fig. 7. The maximum magnitudes of shear strains (~0.2) and fiber strains (~0.1) occurred along the rounded edge of the indentation head; strains are typically much smaller (<0.05) in the rest of the domain.
Fig. 7.
Predicted force–displacement curves from finite element simulations of samples indented with fiber direction (a) perpendicular or (b) parallel to the long side of the indenter head (frictionless). (c) and (d) Force–displacement curves as in (a) and (b) but with coefficient of friction, cf, of contacting surfaces equal to 0.5. In all panels κ/μ = 200, μ = 500 Pa, and φ = 0.4, with ζ = 0, 2.5, or 12.5.
When the sample was indented with the fiber direction perpendicular to the long side of the indentation head, the resistance of the sample to indentation increased with ζ (Fig. 7(a)), indicating a stronger reinforcing effect by the fibers. The resistance to indentation was relatively insensitive to the parameter ζ when the sample was indented with the fiber direction parallel to the long side of the indentation head (Fig. 7(b)). These trends were observed in additional studies with cf = 0.5 (Fig. 7(c, d)) and with φ = 0.1, 0.25, 0.5 or 1.0 (results not shown). Additional FE simulations with isotropic model parameters (μ=500 Pa, φ =ζ=0 and cf = 0.1, 0.25, 0.5, or 1.0) were used to estimate the effect of friction on gray matter indentation stiffness (results not shown).
The model-predicted force–displacement curves for indentation depths of 0–0.15 mm were fit to a straight line and the slope was used to estimate the indentation stiffness. The stiffness values obtained with the long side of the indentation head perpendicular to and parallel to the fiber direction are denoted as k⊥ and k|| respectively. The predicted indentation stiffness ratio k⊥/k|| increased with ζ (Fig. 8(a)). The ratio k⊥/k|| also increased with φ, but the effect was minor over the range studied. Friction was important in determining, as shown in Fig. 8(b). When the long side of the indenter head was parallel to the fiber direction, contact friction with cf = 0.5 increased the predicted k|| by a factor of 1.2. However, when the long side of the indentation head was perpendicular to the fiber direction, this level of friction increased by up to a factor of 2.3. The net result was that friction increases the ratio k⊥/k||.
Fig. 8.
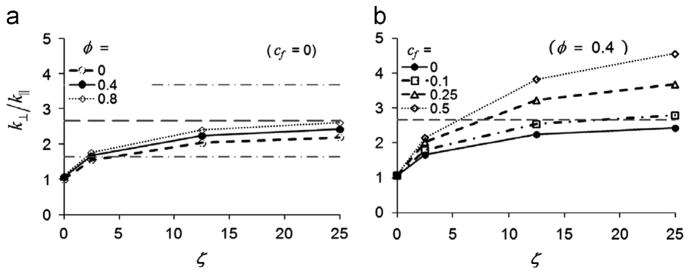
Predicted stiffness ratios (k⊥/k||) from the parametric finite element model study of asymmetric indentation.
(a) The increase in k⊥/k|| with ζ is shown for φ = 0, 0.4 or 0.8 with κ/μ = 200, μ = 500 Pa and frictionless contact (cf = 0). The dashed horizontal lines indicate the mean experimental value of k⊥/k|| for white matter samples, plus or minus one standard deviation. (b) The increase in k⊥/k|| with ζ is shown for cf = 0, 0.1, 0.25 and 0.5 with φ = 0.4 and μ = 500 Pa. The dashed horizontal line indicates the mean value of k⊥/k|| for white matter samples.
Since we do not know precise values of the friction coefficient cf for either contact surface, we estimated a range of possible ζ values for white matter by matching experimental values of and (Table 1) assuming that cf = 0.5 or 0.1. First, we identified the value of ζ that matched the experimental value of for φ =0.4 and cf = 0.5, resulting in a predicted value of ζ =5.5. We then estimated the value of μ by comparing the predicted value of |k| for the FE model (where μ=500 Pa with the experimentally measured value for white matter, shown in Table 1 and scaling, which yielded an estimated μ=0.51±0.27 kPa, slightly larger than the value of μ2 obtained from DST. For gray matter samples, we matched the experimental values of kA to the predicted value from FE simulations with ζ =φ=0 and cf = 0.5 to obtain an estimate for μ=0.58±0.17 kPa, which is larger than the value of μA obtained from DST (0.29±0.06 kPa). This process was repeated for cf = 0.1, resulting in estimates of ζ =13, and μ=0.58 kPa for white matter, and μ=0.70 kPa for gray matter (Table 1).
5. Discussion
In this study, we investigated the requirements for general hyperelastic, transversely isotropic models of white matter in the brain. Clear mechanical anisotropy of white matter was observed in both shear and indentation tests, while the properties of gray matter did not appear to depend on direction of loading (testing in arbitrary directions is not conclusive regarding isotropy in gray matter). We observe that, because white matter exhibits anisotropy in small deformations involving shear without fiber stretch, as well as during deformations involving fiber stretch, any strain energy function describing it must depend on both of the two pseudo-invariants I4 and I5.
5.1. Comparison of estimated tissue parameters to values from prior studies
The shear storage moduli measured in our study at 20–30 Hz ranged approximately from 0.40–0.62 kPa for white matter and 0.30 kPa for gray matter. These values are within the broad range of values reported in prior research on mammalian brain tissue (Chatelin et al., 2010) and consistent with previous tests of white matter tissue (corona radiata) under oscillatory shear tests at 23 °C (Hrapko et al., 2008a).
Our findings that white matter from the corpus callosum is mechanically anisotropic and gray matter is mechanically isotropic are consistent with the most prior studies. Our observation that the sample is stiffer when shear is applied in the plane parallel to the fibers, compared to shear in the plane perpendicular to the fibers, is consistent with the observations of Prange and Margulies (2002) for the corona radiata, though it differs from their findings in the corpus callosum. Hrapko et al. (2008a) also found that white matter tissue from the corona radiata region was mechanically anisotropic, with a stiffness ratio between maximum and minimum directions of about 1.3. We note also some conflicting evidence; early studies using human brain tissue (Shuck and Advani, 1972) suggest that white matter tissue from the corona radiata is isotropic in shear. A more recent study using DST and rotational rheometry (Nicolle et al., 2005) also concluded that porcine white matter tissue from the corona radiata does not exhibit significant anisotropy in shear.
Our measurements of shear modulus magnitude are generally consistent with those of other recent indentation studies. Indentation tests of porcine brain tissue (van Dommelen et al., 2010) using a spherical indenter (indentation depth 0.1–0.3 mm, indenter diameter 2 mm, sample thickness ranging from 1 to 2 mm) showed that gray matter has lower indentation stiffness and lower estimated average shear modulus (μ′=0.75 kPa) than white matter (μ′=1.0 kPa). Microindentation (indentation depth 40 μm) was recently used to investigate the regional mechanical properties of porcine brain tissue (Elkin et al., 2011a). These results suggest that the equilibrium (steady state) shear modulus is larger in the cortical gray matter than in white matter from the corpus callosum, but that at short time scales, corpus callosum white matter is stiffer than cortical gray matter, consistent with our results. However, in rodents (Christ et al., 2010; Elkin et al., 2011b), white matter was observed to be softer than gray matter tissue when indented. Using shear tests, Prange and co-authors (Prange and Margulies, 2002; Prange et al., 2000) investigated regional differences in porcine brain tissue, and concluded that the average equilibrium modulus of gray matter tissue was about 1.3 times stiffer than the modulus of white matter tissue from the corpus callosum. However, their shear strain amplitudes (2.5–50%) were much larger than in our tests (1%), and the equilibrium shear modulus was reported rather than the short-time shear moduli.
5.2. Relationship of model parameters to physical measurements and simulation
In the majority of hyperelastic, transversely isotropic models of fibrous tissue in the literature, the strain energy function is assumed to depend on the pseudo-invariant I4 but not on I5 (Ning et al., 2006; Qiu and Pence, 1997; Velardi et al., 2006). Such material models will predict the same shear modulus for simple shear in planes parallel to the fiber axis as for shear in planes perpendicular to the fiber axis (Qiu and Pence, 1997). This is inconsistent with the anisotropy that we observed in our experimental shear tests: the shear modulus is larger when displacement is applied along the fiber axis. We show that a simple hyperelastic model can explain the observed mechanical response of white matter, as long as it includes contributions from both I4 and I5 in the strain energy density function.
The example hyperelastic model we use to illustrate these points (Eq. (B.8), Appendix B) is based on a strain energy density function that depends in general on four parameters. The bulk modulus, κ was allowed to become arbitrarily large, to model the assumed near-incompressibility of white matter. Estimates of three remaining parameters could be extracted from the small strain data that we acquired. The three parameters were the shear modulus, μ, the non-dimensional relative shear anisotropy, φ, and the non-dimensional stretch anisotropy, ζ. Their appearances in the stress–strain relations (Eq. (B.9)) and the small strain limit of these constitutive laws (Eq. (B.10)) offer insight into their physical interpretations. Since a Neo-Hookean form was taken for the isotropic foundation of these models, the constants μ and κ could be fit to small strain data and retain their usual meanings in the limit of small strain. The shear anisotropy parameter φ appears in the small strain limit only to describe an additional shear resistance relative to the isotropic shear modulus μ. However, at larger strains, Eq. (B.9) reveals a potential coupling between this added shear resistance and the stress in the fiber direction. The tensile anisotropy parameter, ζ, appears only in terms associated with axial stretching for both small and large strains. This effect was measurable in indentation experiments, but only for tests in which specimens were indented with the long axis of the indenter perpendicular to the fibers.
The minimal constitutive law shown in Appendix B is a specialized example model that could be uniquely fit to data from the small-strain regime, and thus might not be accurate for injury-level deformation of white matter. However, the current observations should guide the development of more general, nonlinear hyperelastic models for larger deformations. Any such hyperelastic model should be consistent with the linear elastic model in the limiting case of small strain. Specifically, the compliance matrix in the small strain limit of all such models must reduce to the form of Eq. (B.10) with φ′ >0 μ1> μ2), which requires that the model must depend on both I4 and I5. Table B1 (Appendix B) lists the values for φ and ζ predicted by several well-known or recently published material models.
For the combination of shear and asymmetric indentation, experimental estimates of the values of parameters that govern shear (μ and φ in our example material model) could be determined with greater precision than the parameter (ζ in our example) that describes anisotropy due to fiber stretch. This is largely due to the effects of friction on indentation force. FE model results demonstrate that the indentation stiffness ratio k⊥/k|| depends on friction as well as on the parameter ζ, with both friction and anisotropy affecting the amount of energy stored in material directly beneath the indentor. Prior FE simulation studies of indentation on soft biological tissues treat the contact between sample and indenter head as frictionless (Bischoff, 2004; Cox et al., 2006). The current study shows that the effect of friction can be substantial in the indentation of anisotropic materials, because it affects the stiffness ratio for parallel and perpendicular indentations. Indentation stiffness perpendicular to fibers increased with friction, while stiffness during parallel indentation was relatively insensitive to friction.
In asymmetric indentation experiments the ratio k⊥/k|| may also be influenced by local variations in sample thickness, local fiber alignment, and initial contact force, making the standard deviation of the measured stiffness ratio relatively large. When combined with the uncertainty due to frictional effects, we conclude that precise determination of the parameter ζ is difficult if not impossible; however, the combination of the FE studies and our measurements show clearly that white matter has a substantial fiber reinforcement effect. Using Eq. (B.14) and assuming cf = 0.5, we can estimate the ratio E1/E2 = 6:5 for white matter from the lamb corpus callosum. This value is somewhat larger than corresponding estimates for white matter from porcine corona radiata found from uniaxial tests by Velardi et al. (2006); they obtained a fiber reinforcement parameter ζ =1.7, corresponding to E1/E2 = 2.7. It is possible that corona radiata white matter is in fact less anisotropic than corpus callosum, which is one of the most highly aligned white matter tracts.
6. Limitations and future work
In this study experimental data obtained at small strains were used to identify infinitesimal limits for suitable general functional forms of hyperelastic material models of white matter. Parameter values were estimated for a simple example material model. Identifying the functional forms of models that capture the large deformation constitutive response of white matter will require further experimentation. Any such model must meet the requirements described here, in the limit of small strains.
Nonlinear material properties may contribute to the observed increase of indentation stiffness with indentation depth (Fig. 6(a)). Also, although an elastic model was used to describe the mechanical response of brain tissue (focusing on the short-time response), brain tissue exhibits viscoelastic behavior. After rapid indentation the indentation force relaxed to about 40% of its peak value, similar to results reported by van Dommelen et al. (2010). However, the primary goal of this study was to describe the elastic component of the short-term response of white matter, which should guide the selection and parameterization of more general hyperelastic and viscoelastic models.
Our models of white matter assume a single, dominant fiber direction, and corresponding transversely isotropic behavior. Samples were taken from the corpus callosum, one of the most highly aligned white matter tracts, and our results are generally consistent with the transversely isotropic model. In white matter in general, and even in the corpus callosum, fiber crossing may invalidate the assumption of transverse isotropy, and a more general (orthotropic or other) model may be appropriate. Even if our model is accurate, mis-alignment between loading direction and fiber direction is possible, and would affect the accuracy of parameter estimates. Sensitivity analysis performed as part of a prior study (Namani et al., 2012) showed that mis-alignment of 15° between indenter and fiber axes led to approximately 10% reduction in the ratio k⊥/k||.
Experimental measurements were performed ex vivo in this study. Although all tests were conducted within 5 h of death, material properties may differ from those in the living, intact brain. Tissue was tested at room temperature (21–23°C), rather than body temperature (37° C), which likely affects its response, as do perfusion, residual stress, and metabolic state (Chatelin et al., 2010; Hrapko et al., 2008b). Magnetic resonance elastography (MRE) has been used to estimate the mechanical properties of soft tissues including brain, in vivo (Atay et al., 2008; Clayton et al., 2011; Green et al., 2008; Riek et al., 2011; Sack et al., 2008; Zhang et al., 2011). In MRE, shear waves are imaged by magnetic resonance techniques and the local wavelength is used to infer viscoelastic parameters. Recent studies of human brain tissue in vivo have suggested that the short-time shear modulus of white matter tissue is greater than gray matter (Kruse et al., 2008). In a study involving MRE of the feline brain, white matter also appeared stiffer than gray matter at 85 Hz (Pattison et al., 2010). MRE studies of anisotropic wave propagation are possible in the human brain (Romano et al., 2012), but the inversion problem is complicated by a number of factors and have not been completely validated. Importantly, for transversely isotropic materials that exhibit anisotropy in both shear and tension such as we observe, wave speed will depend strongly on the propagation and polarization directions of shear waves relative to fiber direction (Parker, 1984). Direct comparison between estimates of anisotropic parameters of white matter obtained in vivo by MRE and in vitro by mechanical testing is a future goal.
In this study we also demonstrate the utility and limitations of combining two types of tests to probe mechanical anisotropy of brain tissue. These tests were selected because they are both sensitive to the degree of mechanical anisotropy under distinct types of mechanical loading. A more direct measurement of the contribution of I4 might be obtained with tensile tests of brain tissue samples (Velardi et al., 2006); however, these tests are challenging, due to difficulty in gripping the samples and minimizing edge (or end) effects in small samples.
7. Conclusions
The combination of shear and indentation tests shows that white matter appears to be mechanically anisotropic (transversely isotropic) in both extension and shear with respect to the dominant axonal fiber direction. This anisotropy is likely due to both fiber stretch and fiber–matrix interactions. To account for this behavior, any hyperelastic material model of white matter should include contributions of both I4 and I5 in its strain energy density function.
Acknowledgments
Funding was provided by NIH grant NS055951.
Appendix A. Incremental behavior of hyperelastic materials
The incremental behavior of a hyperelastic material can be described using the equations of linear elasticity (Holzapfel, 2000). The elasticity matrix of a linearly elastic transversely isotropic material with X1 as its axis of symmetry has five independent parameters and can be written as (Bower, 2010)
| (A.1) |
The components of the elasticity matrix can be written in terms of the derivatives of the strain energy function with respect to the invariants, written as ψi = ∂ψ/∂Ii and ψij = ∂2ψ/∂Ii∂Ij (i,j = 1, …,5), are given by (Merodio and Ogden, 2003)
| (A.2) |
| (A.3) |
| (A.4) |
| (A.5) |
| (A.6) |
After applying the requirements for zero stress and zero strain energy in the reference configuration (Eqs. (8)–(10)), we obtain an alternative form for c23:
| (A.7) |
And substituting into the expression for c44, we obtain
| (A.8) |
Appendix B. Form of a candidate constitutive model
Prior studies, as well as our own experiments, suggest that white matter is nearly incompressible and anisotropic in both uniaxial stretch and simple shear deformations; i.e. in both cases the stress–strain relationships depend on whether displacements are imposed parallel or perpendicular to the fiber axis. To analyze this behavior, we find that models written in terms of an isochoric pseudo-invariant that contains no contribution from fiber stretch adopt particularly convenient forms. The deformation gradient may be decomposed into dilatational and distortional parts (Holzapfel, 2000): F = J1/3 F̄. The modified right and left Cauchy–Green strain tensors and fiber direction vector are
| (B.1) |
where C and b are the right and left Cauchy–Green tensors defined earlier. The corresponding modified principal invariants are
| (B.2) |
The strain energy Ψ can now be expressed in the form of the modified invariants. A convenient form of the strain energy function, which can be used successfully to model a variety of materials, is one written in the decoupled form (Holzapfel, 2000):
| (B.3) |
where Ψvolumetric and Ψisochoric are volumetric and isochoric components respectively.
We further separate the isotropic and anisotropic contributions to the isochoric component of strain energy (Merodio and Ogden, 2003; Ning et al., 2006):
| (B.4) |
In the example that follows, a neo-Hookean strain energy function is chosen for the isotropic part. Considering the anisotropic part, we note first that Ī5 contains contributions from Ī4 (Merodio and Ogden, 2003). We propose to use an alternative isochoric pseudo-invariant that contains no contribution from fiber stretch:
| (B.5) |
is a quadratic function of the shear strain in planes parallel to the fiber axis.
To describe the anisotropic component of the strain energy function in a simple material model, we combine a quadratic term of Ī4 that describes the additional strain energy due to fiber stretch, and a term proportional to that describes the effect of fiber–matrix interactions. The isochoric component of strain energy for this model is
| (B.6) |
Here μ is the isotropic shear modulus, and ζ and φ are parameters of the anisotropic model. Finally, we express the volumetric component of strain energy in terms of a bulk modulus κ and the change in volume (Bower, 2010; Ning et al., 2006):
| (B.7) |
To describe nearly incompressible materials like brain tissue, κ will have a large value relative to the quantities μ, μζμ and φμ. The complete candidate strain energy function is thus
| (B.8) |
and the corresponding Cauchy stress tensor is
| (B.9) |
As required, the values of Ψ and of all components of σ equal zero in the reference configuration (Eqs.(9)–(11)).
We now consider small deformations of an incompressible material of this type. The compliance tensor can be obtained, even for an incompressible material, since strains are unique for a given stress state. Accordingly, we use Eqs. ((11)–(13)) and ((A.2)–(A.7)) to obtain the elasticity matrix in terms of the parameters of the compressible strain energy function of Eq. (B.8): κ, μ, ζ and φ. We then invert the elasticity matrix to obtain the compliance matrix, and then take the limit as the bulk modulus κ→∞ and the dilatation J→1. Under these conditions the Voigt matrix form of the compliance tensor in the reference configuration is
| (B.10) |
In the left hand side of Eq. (B.10), the compliance matrix is expressed in terms of the three parameters of the isochoric part of the strain energy function: μ, ζ and φ. In the right hand side it is expressed in terms of classic engineering constants: two Young’s moduli (E1 and E2), two shear moduli (μ1 and μ2) and three Poisson’s ratios (ν12, ν21 and ν2). The two Young’s moduli describe the stresses that arise in uniaxial stretch parallel (E1) and perpendicular (E2) to the fiber axis. The shear moduli govern the shear stresses during shear in planes parallel to (μ1) or normal to (μ2) the fiber axis. The Poisson’s ratios νij describe the strain in the j-direction that arises as a result of stretch in the i-direction. Note that in general only five of the seven physical parameters are independent since the moduli and Poisson’s ratios are related by two additional equations; in the incompressible case the number of independent parameters is further reduced to three (Spencer, 1984). We see that for a transversely isotropic material, the shear moduli μ1 and μ2 differ by the value of the parameter φ, which is the parameter multiplying the term in the strain energy function. In the reference configuration:
| (B.11) |
| (B.12) |
| (B.13) |
Table B1.
Comparison of parameters μ̃, φ̃, ζ̃ in transversely isotropic material models in the limit of infinitesimal strain relative to the undeformed reference configuration.
| Reference | μ̃ | φ̃ | ζ̃ | ψ | |||
|---|---|---|---|---|---|---|---|
| Spencer (1984)a,b | μT |
|
|
|
|||
| Qiu and Pence (1997) | μ | 0 | γ |
|
|||
| Merodio and Ogden (2005) | μ | 0 | 4γ |
|
|||
| Velardi et al. (2006) | μ | 0 |
|
|
|||
| Ning et al. (2006) | 2C10 | 0 |
|
|
|||
| Gasser et al. (2006)c | μ | 0 |
|
|
|||
| Chatelin et al. (2012)d | 2(C10 + C01) | 0 |
|
|
|||
| Current example | μ | φ | ζ |
|
ε is the infinitesimal strain tensor; A is the fiber direction unit vector. This model is explicitly limited to small strains.
Spencer (1984) uses a stiffness matrix that relates the shear stress to the true strain vector, which introduces a factor of 2 in the elements of the stiffness matrix that govern shear in his Eq. (13).
For the case of a single fiber family with a mean orientation in the e1 direction, if the dispersion parameter κ equals zero, all fibers are aligned in the e1 direction. When κ = 1/3, the fibers are isotropically distributed. In the exponential term the quantity (1–3 κ)I4 is evaluated only if I4≥1.
where λ̃ is the stretch ratio in the fiber direction.
By comparing components of the compliance matrix and solving for the elastic modulus in the fiber direction (E1) and perpendicular to fiber direction (E2), we obtain
| (B.14) |
This equation shows that Young’s modulus is larger for stretch in the fiber direction due to the parameter ζ. Other engineering constants for the perfectly incompressible case can be found from μ, φ, and ζ using E2 = μ(4 ζ + 3)/ζ + 1, ν12 = 1/2, ν21 = ν12E2/E1, ν2 = 1− ν21 (Namani et al., 2012).
In the transversely isotropic linear elastic formulation of Spencer (Spencer, 1984), the fiber reinforcement effect is captured by the analogous parameter β (Namani et al., 2012; Spencer, 1984). It can be shown that for an incompressible material in the reference configuration:
| (B.15) |
Eqs. (B.9)–(B.14) indicate that to fully characterize anisotropy in white matter tissue, even for infinitesimal deformations, information is needed from tests that involve stretch and shear in planes both parallel and perpendicular to the fiber axis. We suggest that for transversely isotropic materials in general, and for white matter in particular, characterization in the small strain regime is a valuable step.
Motivated by these two example material models, we propose to characterize the elastic response of general, transversely isotropic, incompressible or nearly incompressible material models in the small-strain regime by these three parameters defined generally as
μ̃, the shear modulus in the plane of isotropy;
φ̃ = (μ1− μ)/μ, the (non-dimensional) difference in shear modulus μ1, relative to μ, for shear in planes perpendicular to the plane of isotropy; and
ζ̃ = (E1−E2)/E2, the non-dimensional difference in Young’s (tensile) modulus for stretch along the fiber axis (E1) relative to Young’s modulus for stretch normal to the fiber axis.
These three parameters can be estimated for any transversely isotropic, hyperelastic material model in the infinite-simal limit. Table B1 shows the values for several recent models.
References
- Abney TM, Feng Y, Pless R, Okamoto RJ, Genin GM, Bayly PV. Principal component analysis of dynamic relative displacement fields estimated from MR images. PLoS One. 2011;6:e22063. doi: 10.1371/journal.pone.0022063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alexander GM, Godwin DW. Presynaptic inhibition of corticothalamic feedback by metabotropic glutamate receptors. Journal of Neurophysiology. 2005;94:163–175. doi: 10.1152/jn.01198.2004. [DOI] [PubMed] [Google Scholar]
- Arbogast KB, Margulies SS. Material characterization of the brainstem from oscillatory shear tests. Journal of Biomechanics. 1998;31:801–807. doi: 10.1016/s0021-9290(98)00068-2. [DOI] [PubMed] [Google Scholar]
- Atay SM, Kroenke CD, Sabet A, Bayly PV. Measurement of the dynamic shear modulus of mouse brain tissue in vivo by magnetic resonance elastography. Journal of Biomechanical Engineering. 2008;130:21013. doi: 10.1115/1.2899575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bayly PV, Black EE, Pedersen RC, Leister EP, Genin GM. In vivo imaging of rapid deformation and strain in an animal model of traumatic brain injury. Journal of Biomechanics. 2006;39:1086–1095. doi: 10.1016/j.jbiomech.2005.02.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bayly PV, Cohen TS, Leister EP, Ajo D, Leuthardt EC, Genin GM. Deformation of the human brain induced by mild acceleration. Journal of Neurotrauma. 2005;22:845–856. doi: 10.1089/neu.2005.22.845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bischoff JE. Static indentation of anisotropic biomaterials using axially asymmetric indenters–a computational study. Journal of Biomechanical Engineering. 2004;126:498–505. doi: 10.1115/1.1785808. [DOI] [PubMed] [Google Scholar]
- Bower AF. Applied Mechanics of Solids. 1. CRC Press; Boca Raton, FL: 2010. [Google Scholar]
- Brody DL, Mac Donald C, Kessens CC, Yuede C, Parsadanian M, Spinner M, Kim E, Schwetye KE, Holtzman DM, Bayly PV. Electromagnetic controlled cortical impact device for precise, graded experimental traumatic brain injury. Journal of Neurotrauma. 2007;24:657–673. doi: 10.1089/neu.2006.0011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatelin S, Constantinesco A, Willinger R. Fifty years of brain tissue mechanical testing: from in vitro to in vivo investigations. Biorheology. 2010;47:255–276. doi: 10.3233/BIR-2010-0576. [DOI] [PubMed] [Google Scholar]
- Chatelin S, Deck C, Willinger R. An anisotropic viscous hyperelastic constitutive law for brain material finite-element modeling. Journal of Biorrheology 2012 [Google Scholar]
- Cheng S, Clarke EC, Bilston LE. Rheological properties of the tissues of the central nervous system: a review. Medical Engineering & Physics. 2008;30:1318–1337. doi: 10.1016/j.medengphy.2008.06.003. [DOI] [PubMed] [Google Scholar]
- Christ AF, Franze K, Gautier H, Moshayedi P, Fawcett J, Franklin RJ, Karadottir RT, Guck J. Mechanical difference between white and gray matter in the rat cerebellum measured by scanning force microscopy. Journal of Biomechanics. 2010;43:2986–2992. doi: 10.1016/j.jbiomech.2010.07.002. [DOI] [PubMed] [Google Scholar]
- Clayton EH, Garbow JR, Bayly PV. Frequency-dependent viscoelastic parameters of mouse brain tissue estimated by MR elastography. Physics in Medicine & Biology. 2011;56:2391–2406. doi: 10.1088/0031-9155/56/8/005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clayton EH, Genin GM, Bayly PV. Transmission, attenuation and reflection of shear waves in the human brain. Journal of the Royal Society Interface. 2012 doi: 10.1098/rsif.2012.0325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cloots RJ, van Dommelen JA, Geers MG. A tissue-level anisotropic criterion for brain injury based on microstructural axonal deformation. Journal of the Mechanical Behavior of Biomedical Materials. 2012;5:41–52. doi: 10.1016/j.jmbbm.2011.09.012. [DOI] [PubMed] [Google Scholar]
- Coats B, Margulies SS, Ji S. Parametric study of head impact in the infant. Stapp Car Crash Journal. 2007;51:1–15. doi: 10.4271/2007-22-0001. [DOI] [PubMed] [Google Scholar]
- Coronado VG, Xu L, Basavaraju SV, McGuire LC, Wald MM, Faul MD, Guzman BR, Hemphill JD. Surveillance for traumatic brain injury-related deaths—United States, 1997–2007. MMWR Surveillance Summaries. 2011;60:1–32. [PubMed] [Google Scholar]
- Cox MA, Driessen NJ, Bouten CV, Baaijens FP. Mechanical characterization of anisotropic planar biological soft tissues using large indentation: a computational feasibility study. Journal of Biomechanical Engineering. 2006;128:428–436. doi: 10.1115/1.2187040. [DOI] [PubMed] [Google Scholar]
- van Dommelen JA, van der Sande TP, Hrapko M, Peters GW. Mechanical properties of brain tissue by indentation: interregional variation. Journal of the Mechanical Behavior of Biomedical Materials. 2010;3:158–166. doi: 10.1016/j.jmbbm.2009.09.001. [DOI] [PubMed] [Google Scholar]
- Elkin BS, Ilankova A, Morrison B., 3rd Dynamic, regional mechanical properties of the porcine brain: indentation in the coronal plane. Journal of Biomechanical Engineering. 2011a;133:071009. doi: 10.1115/1.4004494. [DOI] [PubMed] [Google Scholar]
- Elkin BS, Ilankovan AI, Morrison B., 3rd A detailed viscoelastic characterization of the P17 and adult rat brain. Journal of Neurotrauma. 2011b;28:2235–2244. doi: 10.1089/neu.2010.1604. [DOI] [PubMed] [Google Scholar]
- Fallenstein GT, Hulce VD, Melvin JW. Dynamic mechanical properties of human brain tissue. Journal of Biomechanics. 1969;2:217–226. doi: 10.1016/0021-9290(69)90079-7. [DOI] [PubMed] [Google Scholar]
- Feng Y, Abney TM, Okamoto RJ, Pless RB, Genin GM, Bayly PV. Relative brain displacement and deformation during constrained mild frontal head impact. Journal of the Royal Society Interface. 2010;7:1677–1688. doi: 10.1098/rsif.2010.0210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galford JE, McElhaney JH. A viscoelastic study of scalp, brain, and dura. Journal of Biomechanics. 1970;3:211–221. doi: 10.1016/0021-9290(70)90007-2. [DOI] [PubMed] [Google Scholar]
- Garo A, Hrapko M, van Dommelen JA, Peters GW. Towards a reliable characterisation of the mechanical behaviour of brain tissue: the effects of post-mortem time and sample preparation. Biorheology. 2007;44:51–58. [PubMed] [Google Scholar]
- Gasser TC, Ogden RW, Holzapfel GA. Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. Journal of the Royal Society Interface. 2006;3:15–35. doi: 10.1098/rsif.2005.0073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gefen A, Margulies SS. Are in vivo and in situ brain tissues mechanically similar? Journal of Biomechanics. 2004;37:1339–1352. doi: 10.1016/j.jbiomech.2003.12.032. [DOI] [PubMed] [Google Scholar]
- Gennarelli TA, Thibault LE, Adams JH, Graham DI, Thompson CJ, Marcincin RP. Diffuse axonal injury and traumatic coma in the primate. Annals of Neurology. 1982;12:564–574. doi: 10.1002/ana.410120611. [DOI] [PubMed] [Google Scholar]
- Green MA, Bilston LE, Sinkus R. In vivo brain viscoelastic properties measured by magnetic resonance elastography. NMR in Biomedicine. 2008;21:755–764. doi: 10.1002/nbm.1254. [DOI] [PubMed] [Google Scholar]
- Holzapfel G. Nonlinear Solid Mechanics: A Continuum Approach for Engineering. John Wiley & Sons, Inc; 2000. [Google Scholar]
- Holzapfel GA, Ogden RW. On planar biaxial tests for anisotropic nonlinearly elastic solids. Mathematics and Mechanics of Solids. 2009;14:474–489. [Google Scholar]
- Hrapko M, van Dommelen JA, Peters GW, Wismans JS. Characterisation of the mechanical behaviour of brain tissue in compression and shear. Biorheology. 2008a;45:663–676. [PubMed] [Google Scholar]
- Hrapko M, van Dommelen JA, Peters GW, Wismans JS. The influence of test conditions on characterization of the mechanical properties of brain tissue. Journal of Biomechanical Engineering. 2008b;130:031003. doi: 10.1115/1.2907746. [DOI] [PubMed] [Google Scholar]
- Ji S, Margulies SS. In vivo pons motion within the skull. Journal of Biomechanics. 2007;40:92–99. doi: 10.1016/j.jbiomech.2005.11.009. [DOI] [PubMed] [Google Scholar]
- Ji S, Zhu Q, Dougherty L, Margulies SS. In vivo measurements of human brain displacement. Stapp Car Crash Journal. 2004;48:227–237. doi: 10.4271/2004-22-0010. [DOI] [PubMed] [Google Scholar]
- Kaster T, Sack I, Samani A. Measurement of the hyperelastic properties of ex vivo brain tissue slices. Journal of Biomechanics. 2011 doi: 10.1016/j.jbiomech.2011.01.019. [DOI] [PubMed] [Google Scholar]
- Kruse SA, Rose GH, Glaser KJ, Manduca A, Felmlee JP, Jack CR, Ehman RL. Magnetic resonance elastography of the brain. NeuroImage. 2008;39:231–237. doi: 10.1016/j.neuroimage.2007.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LaPlaca MC, Cullen DK, McLoughlin JJ, Cargill RS., 2nd High rate shear strain of three-dimensional neural cell cultures: a new in vitro traumatic brain injury model. Journal of Biomechanics. 2005;38:1093–1105. doi: 10.1016/j.jbiomech.2004.05.032. [DOI] [PubMed] [Google Scholar]
- Margulies SS, Thibault LE. A proposed tolerance criterion for diffuse axonal injury in man. Journal of Biomechanics. 1992;25:917–923. doi: 10.1016/0021-9290(92)90231-o. [DOI] [PubMed] [Google Scholar]
- McAllister TW, Ford JC, Ji S, Beckwith JG, Flashman LA, Paulsen K, Greenwald RM. Maximum principal strain and strain rate associated with concussion diagnosis correlates with changes in corpus callosum white matter indices. Annals of Biomedical Engineering. 2012;40:127–140. doi: 10.1007/s10439-011-0402-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meaney DF. Relationship between structural modeling and hyperelastic material behavior: application to CNS white matter. Biomechanics and Modeling in Mechanobiology. 2003;1:279–293. doi: 10.1007/s10237-002-0020-1. [DOI] [PubMed] [Google Scholar]
- Merodio J, Ogden RW. Instabilities and loss of ellipticity in fiber-reinforced compressible non-linearly elastic solids under plane deformation. International Journal of Solids and Structures. 2003;40:4707–4727. [Google Scholar]
- Merodio J, Ogden RW. Mechanical response of fiber-reinforced incompressible non-linearly elastic solids. International Journal of Nonlinear Mechanics. 2005;40:213–227. [Google Scholar]
- Morrison B, 3rd, Cater HL, Wang CC, Thomas FC, Hung CT, Ateshian GA, Sundstrom LE. A tissue level tolerance criterion for living brain developed with an in vitro model of traumatic mechanical loading. Stapp Car Crash Journal. 2003;47:93–105. doi: 10.4271/2003-22-0006. [DOI] [PubMed] [Google Scholar]
- Namani R, Feng Y, Okamoto RJ, Jesuraj N, Sakiyama-Elbert SE, Genin GM, Bayly PV. Elastic characterization of transversely isotropic soft materials by dynamic shear and asymmetric indentation. Journal of Biomechanical Engineering. 2012;134:061004. doi: 10.1115/1.4006848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicolle S, Lounis M, Willinger R, Palierne JF. Shear linear behavior of brain tissue over a large frequency range. Biorheology. 2005;42:209–223. [PubMed] [Google Scholar]
- Ning X, Zhu Q, Lanir Y, Margulies SS. A transversely isotropic viscoelastic constitutive equation for brainstem undergoing finite deformation. Journal of Biomechanical Engineering. 2006;128:925–933. doi: 10.1115/1.2354208. [DOI] [PubMed] [Google Scholar]
- Okamoto RJ, Clayton EH, Bayly PV. Viscoelastic properties of soft gels: comparison of magnetic resonance elastography and dynamic shear testing in the shear wave regime. Physics in Medicine & Biology. 2011;56:6379–6400. doi: 10.1088/0031-9155/56/19/014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parker DF. Elastic wave propagation in strongly anisotropic solids. In: Spencer AJM, editor. Continuum Theory of the Mechanics of Fibre-Reinforced Composites. Springer Verlag; New York: 1984. pp. 217–244. [Google Scholar]
- Pattison AJ, Lollis SS, Perrinez PR, Perreard IM, McGarry MD, Weaver JB, Paulsen KD. Time-harmonic magnetic resonance elastography of the normal feline brain. Journal of Biomechanics. 2010;43:2747–2752. doi: 10.1016/j.jbiomech.2010.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prange MT, Margulies SS. Regional, directional, and age-dependent properties of the brain undergoing large deformation. Journal of Biomechanical Engineering. 2002;124:244–252. doi: 10.1115/1.1449907. [DOI] [PubMed] [Google Scholar]
- Prange MT, Meaney DF, Margulies SS. Defining brain mechanical properties: effects of region, direction, and species. Stapp Car Crash Journal. 2000;44:205–213. doi: 10.4271/2000-01-SC15. [DOI] [PubMed] [Google Scholar]
- Prevost TP, Jin G, de Moya MA, Alam HB, Suresh S, Socrate S. Dynamic mechanical response of brain tissue in indentation in vivo, in situ and in vitro. Acta Biomater. 2011;7:4090–4101. doi: 10.1016/j.actbio.2011.06.032. [DOI] [PubMed] [Google Scholar]
- Qin EC, Sinkus R, Geng G, Cheng S, Green M, Rae CD, Bilston LE. Combining MR elastography and diffusion tensor imaging for the assessment of anisotropic mechanical properties: a phantom study. Journal of Magnetic Resonance Imaging. 2012 doi: 10.1002/jmri.23797. [DOI] [PubMed] [Google Scholar]
- Qiu GY, Pence TJ. Remarks on the behavior of simple directionally reinforced incompressible nonlinearly elastic solids. Journal of Elasticity. 1997;49:1–30. [Google Scholar]
- Riek K, Klatt D, Nuzha H, Mueller S, Neumann U, Sack I, Braun J. Wide-range dynamic magnetic resonance elastography. Journal of Biomechanics. 2011;44:1380–1386. doi: 10.1016/j.jbiomech.2010.12.031. [DOI] [PubMed] [Google Scholar]
- Romano A, Scheel M, Hirsch S, Braun J, Sack I. In vivo waveguide elastography of white matter tracts in the human brain. Magnetic Resonance in Medicine. 2012 doi: 10.1002/mrm.24141. [DOI] [PubMed] [Google Scholar]
- Sabet AA, Christoforou E, Zatlin B, Genin GM, Bayly PV. Deformation of the human brain induced by mild angular head acceleration. Journal of Biomechanics. 2008;41:307–315. doi: 10.1016/j.jbiomech.2007.09.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sack I, Beierbach B, Hamhaber U, Klatt D, Braun J. Non-invasive measurement of brain viscoelasticity using magnetic resonance elastography. NMR in Biomedicine. 2008;21:265–271. doi: 10.1002/nbm.1189. [DOI] [PubMed] [Google Scholar]
- Shuck LZ, Advani SH. Rheological response of human brain-tissue in shear. Journal of Basic Engineering. 1972;94:905–911. [Google Scholar]
- Smith DH, Meaney DF. Axonal damage in traumatic brain injury. Neuroscientist. 2000;6:483–495. [Google Scholar]
- Spencer AJM. Continuum Theory of the Mechanics of Fibre-Reinforced Composites. Springer-Verlag; New York: 1984. [Google Scholar]
- Ueno K, Melvin JW, Li L, Lighthall JW. Development of tissue level brain injury criteria by finite element analysis. Journal of Neurotrauma. 1995;12:695–706. doi: 10.1089/neu.1995.12.695. [DOI] [PubMed] [Google Scholar]
- Velardi F, Fraternali F, Angelillo M. Anisotropic constitutive equations and experimental tensile behavior of brain tissue. Biomechanics and Modeling in Mechanobiology. 2006;5:53–61. doi: 10.1007/s10237-005-0007-9. [DOI] [PubMed] [Google Scholar]
- Weiss JA, Maker BN, Govindjee S. Finite element implementation of incompressible, transversely isotropic hyperelasticity. Computer Methods in Applied Mechanics and Engineering. 1996;135:107–128. [Google Scholar]
- Wright RM, Ramesh KT. An axonal strain injury criterion for traumatic brain injury. Biomechanics and Modeling in Mechanobiology. 2012;11:245–260. doi: 10.1007/s10237-011-0307-1. [DOI] [PubMed] [Google Scholar]
- Zhang J, Green MA, Sinkus R, Bilston LE. Viscoelastic properties of human cerebellum using magnetic resonance elastography. Journal of Biomechanics. 2011;44:1909–1913. doi: 10.1016/j.jbiomech.2011.04.034. [DOI] [PubMed] [Google Scholar]
- Zhang L, Yang KH, King AI. A proposed injury threshold for mild traumatic brain injury. Journal of Biomechanical Engineering. 2004;126:226–236. doi: 10.1115/1.1691446. [DOI] [PubMed] [Google Scholar]