Increased apical Na⁺ permeability in cystic fibrosis is supported by a quantitative model of epithelial ion transport

Abstract

Cystic fibrosis (CF) is caused by mutations in the cystic fibrosis transmembrane conductance regulator (CFTR) gene, which encodes an anion channel. In the human lung CFTR loss causes abnormal ion transport across airway epithelial cells. As a result CF individuals produce thick mucus, suffer persistent bacterial infections and have a much reduced life expectancy. Trans-epithelial potential difference (V_t) measurements are routinely carried out on nasal epithelia of CF patients in the clinic. CF epithelia exhibit a hyperpolarised basal V_t and a larger V_t change in response to amiloride (a blocker of the epithelial Na⁺ channel, ENaC). Are these altered bioelectric properties solely a result of electrical coupling between the ENaC and CFTR currents, or are they due to an increased ENaC permeability associated with CFTR loss? To examine these issues we have developed a quantitative mathematical model of human nasal epithelial ion transport. We find that while the loss of CFTR permeability hyperpolarises V_t and also increases amiloride-sensitive V_t, these effects are too small to account for the magnitude of change observed in CF epithelia. Instead, a parallel increase in ENaC permeability is required to adequately fit observed experimental data. Our study provides quantitative predictions for the complex relationships between ionic permeabilities and nasal V_t, giving insights into the physiology of CF disease that have important implications for CF therapy.

Key points

• Cystic fibrosis (CF) is a common genetic disease caused by loss-of-function mutations in the cystic fibrosis transmembrane conductance regulator gene, which encodes a channel protein, selective for anions.

• In the lungs, the site of the most severe symptoms, CF causes abnormal electrolyte transport in epithelial cells which line the airways.

• Airway epithelial ion transport can be assessed by measuring the trans-epithelial potential difference (V_t) which shows characteristic changes in CF individuals. We developed a biophysical model of ion transport in human nasal epithelia, in order to investigate quantitatively which transport parameters underlie these observed bioelectric changes.

• We found that loss of apical Cl⁻ permeability alone is insufficient to explain the bioelectric properties of CF epithelia. An increase of apical Na⁺ permeability must also occur.

• This insight has important implications for our understanding of the physiology of CF disease, and hence for potential therapies aimed at correcting the CF ion transport defect.

Introduction

Cystic fibrosis (CF) is a mono-genetic disorder that impairs quality of life and greatly reduces life expectancy (Davies et al. 2007). It is the most common fatal inherited genetic disease found in people of European descent (Dodge et al. 2007). CF is a complex disease, affecting several organs; however, the most frequent cause of death amongst CF sufferers is lung failure resulting from persistent bacterial infections.

It is known that loss-of-function mutations in the CFTR gene product, an anion-selective channel, are the root cause of the disease. Thus, abnormal trans-epithelial electrolyte transport appears to be crucial to the pathogenesis of CF (Rowe et al. 2005). Measurements of the trans-epithelial potential difference (V_t) across nasal epithelia can be used to investigate airway epithelial ion transport and such measurements are often made in vivo to aid diagnosis of CF in the clinic. V_t measurements are also used as outcome measures in clinical trials of drug and gene therapies for the disease (Rowe et al. 2011). CF epithelia show hyperpolarised basal V_t (relative to non-CF epithelia), an increased depolarisation following block of the epithelial Na⁺ channel (ENaC) with its inhibitor amiloride, a reduced or missing response when the driving force for apical Cl⁻ efflux is increased, and no hyperpolarisation in response to raised intracellular cAMP levels (Knowles et al. 1995).

These bioelectric properties arise as a direct result of mutations in the CFTR gene, but whether or not they are simply a consequence of the loss of apical anion permeability is a matter of debate. It has been suggested that CFTR regulates the activity of other transport processes in epithelial cells, in particular ENaC, with the loss of CFTR resulting in higher basal levels of apical Na⁺ conductance (Stutts et al. 1995; Donaldson & Boucher, 2007). More recent studies, however, report that Na⁺ absorption in pig and human CF airway epithelial cultures is not increased (Chen et al. 2010; Itani et al. 2011). These studies suggest that the loss of anion conductance can account for hyperpolarised basal V_t, as well as the increased amiloride-sensitive V_t and altered short-circuit current, because of the way the CFTR currents are electrically coupled to other transport processes. Previous modelling work from a kidney epithelial cell line provides qualitative support for this idea (Horisberger, 2003).

To assess these conflicting views we developed a detailed mathematical model of ion transport in human nasal epithelial (HNE) cells, so as to quantitatively investigate the relationship between individual ionic permeabilities and commonly measured bioelectric properties of the integrated epithelial transport system, such as basal V_t and amiloride-sensitive V_t. Our model differs from most previous studies investigating airway epithelial physiology (Hartmann & Verkman, 1990; Duszyk & French, 1991; Warren et al. 2009; Falkenberg & Jakobsson, 2010) in that it focuses specifically on nasal epithelial cell components and parameter values. A modelling study focused on quantifying ionic permeabilities in non-CF HNE cells has recently been published, but this work did not consider ion transport in CF (Garcia et al. 2013). We use data from primary cultures of both CF and non-CF nasal epithelial cells for model validation, thus allowing us to investigate clinically relevant questions regarding how changes in the underlying transport components give rise to altered nasal V_t measurements in CF.

We found that while the electrical coupling between CFTR and ENaC currents can cause, qualitatively, the type of changes seen in CF, the magnitudes of these effects are not large enough to explain CF abnormalities. Instead, apical Na⁺ permeability must be increased in CF in order to quantitatively explain the differences observed in bioelectric properties between the non-CF and CF airway epithelium.

Methods

Model overview

Our mathematical model simulates a monolayer of HNE cells placed between two well-perfused compartments containing physiological saline solution (Fig. 1A), thus approximating the environment experienced by HNE cells in vivo during nasal V_t measurements when the airway surface is flooded (or in vitro during an Ussing chamber experiment). In this model Na⁺, Cl⁻, K⁺ and water move between interstitial fluid and airway lumen (paracellular route) and between the cell and external solutions via transport processes in the apical and basolateral plasma membranes (Fig. 1B). The magnitude of the ion flux due to each of these component processes in the model is proportional to a transport parameter that is related to the density of that component in the plasma membrane.

Figure 1. Schematic diagram of epithelial layer (A) and individual epithelial cell (B) separating the airway lumen from the interstitial fluid.

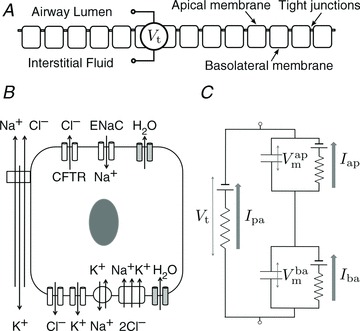
A and B, electrolyte transport occurs across the apical and basolateral membranes, and along the paracellular path through tight junctions. Transport parameters characterise flux through each pathway: CFTR and ENaC channels in the apical membrane are characterised by apical Cl⁻ permeability (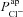) and apical Na⁺ permeability(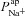), respectively; K⁺ and Cl⁻ channels in the basolateral membrane are characterised by the basolateral K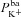⁺ () and Cl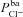⁻ () permeabilities; the transport parameters for the Na⁺–K⁺-ATPase pump proteins and NKCC cotransport proteins in the basolateral membrane are their densities per unit area of the membrane, ρ_NaK and ρ_NKCC, respectively. The state of the cell at any time is described by six variables, cell volume (W_i), moles of Na⁺, Cl⁻ and K⁺ in the cell (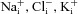, respectively), and apical (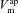) and basolateral (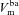) membrane potentials. C, equivalent electrical circuit representation of airway epithelium. 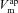and 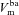are coupled electrically via the current along the paracellular pathway (I_pa). The trans-epithelial potential difference V_t is given by the difference between lumen and serosal potential (i.e. ).

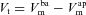We calculate the flux of ions from each individual transport pathway as a function of the driving force and associated transport parameter, and employ an equivalent electrical circuit description of the epithelium to determine membrane (apical, 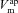and basal, 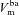) and trans-epithelial (V_t) potentials in the open circuit configuration (Fig. 1C). This framework allows us to vary transport parameters or extracellular solution composition, and calculate the resultant changes in membrane potentials and V_t in a quantitative manner. It also allows a quantitative investigation of how these responses to perturbations change when transport processes are varied.

Transport pathways included in model

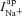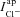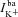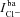There are four ion channel components included in the model. ENaC and CFTR channels will give rise to apical Na⁺ () and Cl⁻ () currents, respectively, and basolateral K⁺ and Cl⁻ channels facilitate the basolateral currents and . Apical K⁺ channels are not included since they do not contribute substantially to V_t (Knowles et al. 1983; Willumsen et al. 1989a). Channel currents were modelled using the Goldman–Hodgkin–Katz (GHK) flux equation (Hille, 2001), which relates the trans-membrane electrochemical driving force (determined by the membrane potential and concentration gradient) to the trans-membrane current, given the permeability of the membrane to a particular ion (see Supplemental material, section S1, available online only). For example, given apical membrane potential (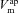), lumen and intracellular Na⁺ concentrations ([Na⁺]_l and [Na⁺]_i), and the permeability of the apical membrane to Na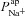⁺ (), we can compute the ENaC current (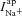). Paracellular ion currents (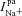, , , 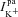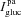) are also modelled using the GHK equation (with V_t as electrical driving force, and ion concentrations from the luminal and serosal compartments).

We include descriptions of the Na⁺-K⁺–2Cl⁻ co-transport protein NKCC1 and Na⁺–K⁺-ATPase pump protein in our model, which generate the basolateral ion fluxes J_NKCC and J_NaK, respectively. We use the model of Benjamin & Johnson to calculate flux from the Na⁺–K⁺–2Cl⁻ co-transporter (Benjamin & Johnson, 1997), and the model of Smith & Crampin to describe active transport by the Na⁺–K⁺-ATPase (Smith & Crampin, 2004; see Supplemental material, section S1, for full details). The total flux along these transport pathways is proportional to the density of the relevant protein in the basolateral membrane, ρ_NKCC and ρ_NaK.

In our model both apical and basolateral membranes are permeable to water. The trans-membrane water flux in both cases (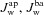) is assumed to be proportional to the trans-membrane osmolarity gradient ΔS, where the osmolarity here is given by the total Na⁺, Cl⁻ and K⁺ concentrations as well as the concentration of impermeable anions in that given compartment.

Transport kinetics

Cellular variables evolve in time based on the net influx or efflux of ions and water, and we described these kinetics with a system of coupled, non-linear ordinary differential equations.

Cell volume W_i changes if there is a net influx or efflux of water (water flux is positive in serosal to mucosal direction):

(1)

The ionic composition of the intracellular compartment changes due to the net trans-membrane ion fluxes (positive ion currents denote a flux of positive ions out of the cell, positive J_NKCC denotes ion flux into the cell, F is the Faraday constant and z_n is the valence of the ion n under consideration):

(2)

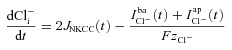(3)

(4)

The equivalent electrical circuit description of the epithelium (Fig. 1C) can be used to calculate how the membrane potentials change due to net apical, basolateral and paracellular currents (C_m is the capacitance per unit area of the plasma membrane):

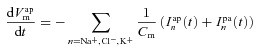(5)

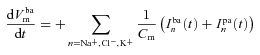(6)

The trans-epithelial potential difference, with the serosal compartment as the earth, is given by 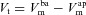(see Supplemental material, section S1).

Baseline transport parameter values

We initially found estimates of transport parameters (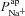, , 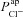, 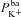ρ_NaK, ρ_NKCC, 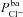) from the relevant scientific literature, and refer to these as baseline parameter values (Table 1; note that here we assume that the paracellular permeability, P_pa, is non-selective and does not change in CF; the rationale for this is discussed later; see also Supplemental material, section S4). These were used to give an order of magnitude estimate for each parameter and thus initially identify the region of parameter space on which our parameter estimation should focus.

Table 1.

Baseline values used (column 3) and numerical estimates found for parameter values in non-CF and CF cells (columns 5 and 6) for each free transport parameter (rows 1–6)

Parameter	Units	Baseline	Reference	Non-CF	CF
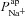	μm s−1	0.028	(Willumsen & Boucher, 1991b)	0.024	0.065
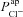	μm s−1	0.072	(Willumsen & Boucher, 1991b)	0.066	0.006
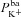	μm s−1	0.080	(Falkenberg & Jakobsson, 2010)	0.103	0.400
ρNaK	10−10 mol cm−2	0.400	*	0.127	0.489
ρNKCC	10−10 mol cm−2	0.400	*	0.188	2.000
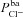	μm s−1	0.100	(Falkenberg & Jakobsson, 2010)	0.097	0.144

^*ρ_NaK and ρ_NKCC estimated by authors.

Results

CF epithelia have an increased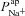

We set out to determine, then to compare, the value of 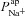in CF and non-CF nasal epithelial cells. To constrain the model we used extensive data sets obtained from cultured HNE cells, including time course data covering the addition of amiloride or reduction of [ Cl⁻]_l at the apical membrane (Willumsen et al. 1989a,b; Willumsen & Boucher, 1991a,b). We thus formulated an optimisation problem to minimise the residual errors between physiological properties predicted by the mathematical model, and those observed experimentally, by varying transport parameters of interest (see Supplemental material, section S2, for details).

Using simulations made with parameter values optimised for non-CF epithelia, our model accurately fits the observed initial and final steady-state values for membrane and trans-epithelial potentials (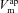, 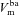and V_t) and concentrations ([ Na⁺]_i, [ Cl⁻]_i) both in amiloride addition and low Cl ⁻ experiments (Fig. 2). A similar analysis was carried out to identify parameter values best describing corresponding experimental data obtained on CF epithelia (Supplemental Fig. S3). The optimised parameter values for non-CF and CF epithelia are shown in Table 1.

Figure 2. Estimating transport parameters from electrophysiological recordings.

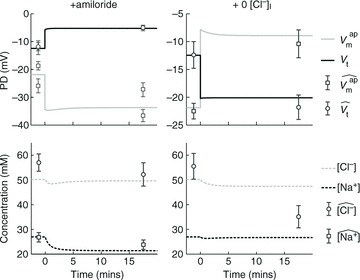
Model predictions for 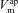, V_t, [ Na⁺]_i and [ Cl⁻]_i (continuous and dashed lines) are plotted for simulations of ‘+amiloride’ and ‘+ 0[ Cl⁻]_l’ experiments, and compared with their observed values (symbols). Data used are from non-CF HNE cells, and parameter values used for the simulation are those which were found to minimise the residual error between model output and these data (Table 1).

The optimal parameter values obtained for ENaC and CFTR permeability are similar to those estimated experimentally (Table 1). Examining the difference between optimal CF and non-CF parameter values, we found not only that in CF 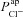must be reduced (as expected) but also that the value of 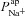must be significantly increased.

Very little experimental data are available on the magnitude and characteristics of paracellular permeability. In order to determine if increased 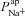in CF epithelia was dependent on assumptions we had made regarding paracellular ion transport, we repeated the parameter estimation analysis assuming a lower P_pa in CF (Willumsen & Boucher, 1989) and/or a cation-selective paracellular transport (Levin et al. 2006; Flynn et al. 2009). We found that while these differences in paracellular transport do have an influence over the exact value of 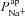or 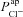estimated, they do not alter how each of these parameters changes in CF relative to non-CF epithelia (see Supplemental Tables S5 and S6).

Feasible ranges of 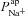differ between populations of non-CF and CF nasal epithelial cells

Although our optimisation results provide good evidence for a change in 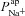, we were conscious that the data which we used for fitting in the optimisation problem were the mean of several experiments carried out on different primary cultures of HNE cells. Variations in the experimental results obtained from these cells show that a large range of values of, for example, intracellular [ Na⁺], are physiologically reasonable. We wanted to make sure that by optimising parameter fits to average data we did not exclude parameter sets that could account for both CF and non-CF data given the full range of possible variation (e.g. Willumsen & Boucher, 1991b).

To achieve this, we carried out a large number of simulations with the model, as illustrated schematically in Fig. 3. We first used Monte Carlo sampling to randomly generate 10⁶ parameter sets, sampling values for each transport parameter (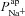, , 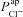, 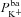ρ_NaK, ρ_NKCC, 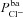) from a uniform distribution on a bounded region (from zero to five times) around the relevant baseline parameter value (Fig. 3A). This process provided a population of model parameter sets, each with a unique set of parameter values, steady-state variable values, kinetic properties and so on (Fig. 3B). We next separated the sample population (Fig. 3C) into 1975 parameter sets which predicted observed steady-state and kinetic properties of non-CF HNE cells and 2430 which reproduced the observed steady-state and kinetic behaviour of CF HNE cells (see Table 2 for both non-CF and CF filtering bounds). The other parameter sets which produced non-physiological values or unstable kinetics were discarded (see Supplemental material, section S3, for full details).

Figure 3. Monte Carlo filtering analysis approach to determine distributions of transport parameter values in CF and non-CF HNE cells.

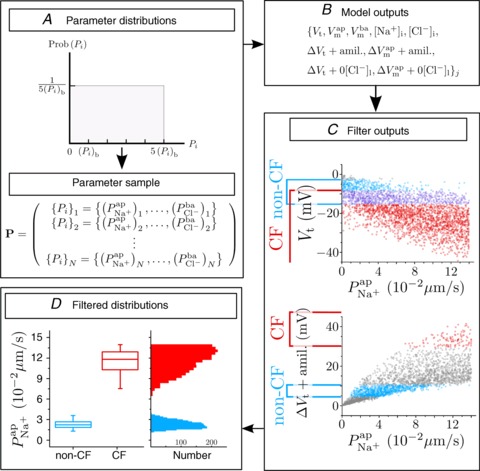
A, a large sample (N= 10⁶) of parameter sets was generated, each set is a vector 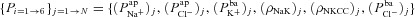. Each parameter i is sampled from a uniform distribution U(0, 5(P_i)_b) around its baseline value (see Table 1). B, for each parameter set {P_i}_j, the values of variables X_j at steady state and their value after ‘+amiloride’ and ‘+ 0[ Cl⁻]_l’ perturbations are calculated. C, bounds are placed on the allowed values of these model outputs, for both CF and non-CF states, and parameter sets are classified on this basis. D, filtered parameter distributions can be examined to assess how transport parameters vary between normal and disease states.

Table 2.

Constraints on allowed variable values in CF and non-CF cells, based on data from primary cultures of HNE cells

		Non-CF			CF
Property	Units	Lower	Upper	Source	Lower	Upper	Source
[Na+]i	mm	18.0	43.2	(Willumsen & Boucher, 1991b)	21.0	51.3	(Willumsen & Boucher, 1991a)
[Cl−]i	mm	32.5	84.4	(Willumsen et al. 1989a)	32.5	84.4	(Willumsen et al. 1989b)
	mV	−38.6	−14.9	(Willumsen & Boucher, 1991b)	−37.7	6.7	(Willumsen & Boucher, 1991a)
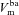	mV	−45.1	−24.2	(Willumsen & Boucher, 1991b)	−59.3	−33.6	(Willumsen & Boucher, 1991a)
Vt	mV	−15.5	−2.7	(Willumsen & Boucher, 1991b)	−59.2	−8.2	(Willumsen & Boucher, 1991a)
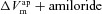	mV	−14.0	−5.5	(Willumsen et al. 1989a; Willumsen & Boucher, 1991b)	−47.4	−29.0	(Willumsen et al. 1989b; Willumsen & Boucher, 1991a)
ΔVt+ amiloride	mV	4.7	10.1	(Willumsen et al. 1989a; Willumsen & Boucher, 1991b)	30.1	47.1	(Willumsen et al. 1989b; Willumsen & Boucher, 1991a)
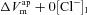	mV	9.2	15.0	(Willumsen et al. 1989a)	−5.3	11.1	(Willumsen et al. 1989b)
ΔVt+ 0[ Cl−]l	mV	−12.7	−6.1	(Willumsen et al. 1989a)	−16.5	9.9	(Willumsen et al. 1989b)

Figure 4 illustrates the distributions of transport parameter values which remain after applying the non-CF (blue) and CF (red) filters (see also Supplemental material Figs S4 and S5, and Tables S5 and S6, respectively). While the non-CF and CF distributions are similar for some parameters, the distributions of 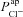and 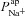differ markedly, CFTR permeability being decreased and ENaC permeability increased in the disease state. Thus, extending our analysis to take into account the full distribution of allowed cellular variable values, rather than focusing on mean behaviour, confirms that ENaC permeability must be increased in CF relative to non-CF cells, in order to explain the observed quantitative differences in electrophysiological properties.

Figure 4. Distributions of each transport parameter, found by constraining allowed model behaviour in non-CF (blue) and CF (red) states.

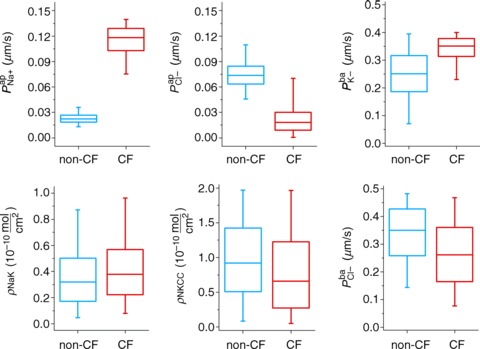
In sequence from low to high, features denoted in each boxplot are: 1st, 25th, 50th (median), 75th and 99th percentiles of the given parameter's distribution.

We repeated this Monte Carlo filtering analysis to determine whether or not decreased paracellular permeability in CF, and/or selectivity of the paracellular pathway, would significantly alter these conclusions. Again we found this was not the case: neither a higher shunt resistance in CF nor a cation-selective paracellular pathway affected our conclusions that permeability distributions were shifted in CF epithelia, with median CFTR permeability decreased and median ENaC permeability increased (see Supplemental material, section S4, Figs S6–S8).

Hyperpolarised V_t in CF can be explained by increased 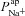, but not by reduced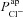

To further investigate the functional relationship between each individual transport parameter, P_i, and the epithelial bioelectric properties in question (i.e. model output variables basal V_t, ΔV_t+ amiloride, and ΔV_t+ 0[ Cl⁻]_l) we carried out a variance-based sensitivity analysis (Sobie, 2009; Taylor et al. 2009) using the 1975 parameter sets in the non-CF distribution along with their model outputs (see Figs 5 and 6, and Supplemental material, section S4). The coefficients we obtained (Figs 5C and 6C) gave us an objective means of quantifying the relative influence of each transport parameter on these bioelectric properties.

Figure 5. Sensitivity analysis investigating the influence of model parameters on V_t.

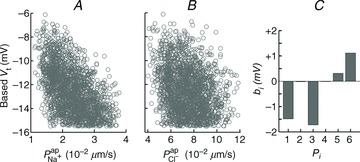
A multiple regression of the form 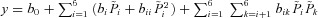was fitted using the set of normalised parameter values 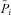in the non-CF parameter distribution as regressors, and the corresponding model output y={V_t} as the independent variable (see Supplemental material, section S4). Basal V_t is plotted as a function of 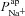(A) and 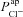(B), for the 1975 parameter sets belonging to the non-CF distribution. C, strength of linear interaction (b_i) between transport parameters 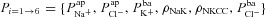and V_t, found via sensitivity analysis. 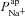hyperpolarises V_t (b₁=−1.49 mV), but changing 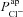has little influence (b₂=−0.02 mV).

Figure 6. Sensitivity analysis investigating the influence of model parameters on ΔV_t+ amiloride.

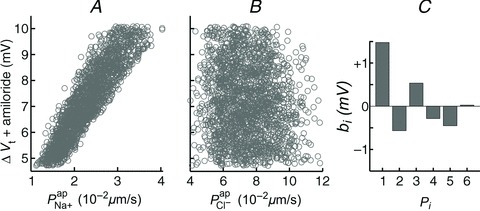
Amiloride-sensitive V_t is plotted against 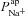(A) and 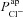(B), for their non-CF distributions. C, sensitivity analysis results plotting strength of interaction (b_i) between ΔV_t+ amiloride and transport parameters 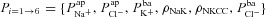. 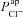tends to decrease this metric, despite its limited effect on basal V_t.

Figure 5A and B shows scatter plots of 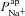and 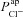, respectively (from the non-CF parameter value distributions), against basal (steady state) V_t predicted by each. Figure 5C summarises the results of the sensitivity analysis. There is a negative correlation between 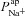and V_t apparent in panel A, and confirmed by the large negative regression coefficient b₁ (−1.49 mV) in panel C. A significant correlation between 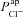and V_t is not clear in panel B. The sensitivity analysis confirms that while 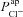does influence V_t to an extent, on average over this region of parameter space it has a much smaller effect than 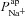, 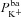or 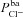(regression coefficient b₂=−0.02 mV, <2%b₁). Therefore an increase in 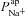is necessary to hyperpolarise basal V_t to the values seen in CF epithelia, while changes in 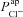do not influence V_t to the same extent.

Amiloride-sensitive V_t is inversely related to 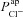, but is more strongly influenced by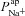

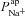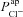Figure 6A and B illustrates the relationship between the and parameter values, respectively, from the non-CF distributions, and the corresponding predicted ΔV_t+ amiloride. Not surprisingly, there is a positive correlation between 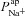and ΔV_t+ amiloride. However, the relationship between ΔV_t+ amiloride and 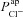is less obvious. The results of the sensitivity analysis in Fig. 6C show that 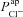has the second greatest influence on ΔV_t+ amiloride. While increasing 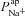tends to increase the magnitude of ΔV_t+ amiloride, increasing 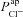tends to decrease its magnitude.

Loss of Cl⁻ conductance can hyperpolarise basal V_t, but not to the extent seen in CF

It is clear that 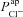can influence basal V_t, even if it does not do so to the same extent as 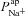. We wanted to determine, quantitatively, what magnitude of a change in basal V_t the model would predict upon loss of 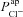alone, and compare this to the hyperpolarisation of V_t observed in CF. Therefore, for each parameter set producing plausible physiological values in the non-CF distribution, we set 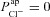and found the new steady state of the system. We define as the difference between this new V_t, and the initial basal V_t when .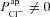

We can analyse the magnitude of 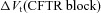and its relationship to ΔV_t+ 0[ Cl⁻]_l (change in V_t induced by reducing [ Cl⁻]_l) which is commonly used as a measure of the underlying Cl⁻ conductance (see Supplemental Fig. S9). For a given ΔV_t+ 0[ Cl⁻]_l, CFTR loss can depolarise or hyperpolarise V_t, depending on the magnitudes of the other transport parameter values. The average ΔV_t+ 0[ Cl⁻]_l observed experimentally in non-CF HNE cells was not greater than –15mV (Willumsen et al. 1989a), a value close to that reported in vivo, in nasal PD measurements. However, the maximum hyperpolarisation achieved by blocking 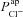was around −4 mV. This is much smaller in magnitude than the average hyperpolarisation seen in CF patients (and in primary cultures of CF HNE cells; Willumsen & Boucher, 1991b), which is around −20 mV (Knowles et al. 1995).

Discussion

We have developed a mathematical model of ion transport in human nasal epithelial cells. As the nasal epithelium is the site of in vivo measurements made on patients, it has been well characterised (Willumsen & Boucher, 1989, 1991b; Willumsen et al. 1989b) and is clinically important in the assessment of CF (Simmonds et al. 2011). The advantages of specifically modelling nasal epithelia are thus 2-fold. First, it offers the opportunity to exploit a very large body of existing measurements for validation and parameter estimation purposes. Second, by leading to a better quantitative analysis of nasal potential difference measurements, it improves our understanding of CF disease.

The agreement between our model predictions and the known physiology, in terms of capturing essential changes in membrane potentials and intracellular ion concentrations (Fig. 2), suggests that the model provides a realistic picture of the major epithelial ion transport processes which determine nasal trans-epithelial potential. Fitting the model to experimental data, we observed not only that 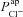must be reduced, but also that 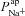had to increase (Table 1) to account for the bioelectric properties of CF epithelial cells. This prediction also held when we ran multiple simulations to take into account cell variability: parameter sets resulting in steady-state and kinetic characteristics typical of CF cells included not only reduced 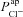but also increased 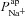(Fig. 4). The fact that our analysis did not make any initial judgements regarding how parameters should vary in the disease state, and hence did not bias us towards computing these results, gives us confidence in their validity and further demonstrates that the findings regarding ENaC and CFTR permeabilities are robust.

Impact of model assumptions

Inevitably, when describing a complex biological system with a mathematical model, one makes a number of assumptions in order to concentrate on the phenomena of interest, and to keep the analysis tractable. The main assumption we make is that Na⁺, Cl⁻ and K⁺ currents largely determine nasal V_t and that the membrane permeabilities of these ions can be estimated from trans-epithelial electrical recordings. In making this simplification we implicitly assume that bicarbonate transport does not substantially impact V_t. In our analysis we saw that 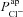has little effect on basal V_t (Fig. 5), and limited effect on ΔV_t+ amiloride (Fig. 6B and C). It is therefore likely that including bicarbonate transport would not alter this picture, as there is significantly less HCO₃⁻ transport through CFTR channels than Cl⁻ (Poulsen et al. 1994). Indeed a very recent paper carries out a similar analysis for non-CF nasal epithelia and essentially validates this approach (Garcia et al. 2013).

Initially, we also made the assumption that changes in paracellular permeability do not drive the bioelectric changes observed in CF. Later, by relaxing this condition, we found that while differences in paracellular permeability or selectivity do influence estimates of 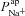and 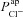, they do not alter how each of these parameters changes in CF relative to non-CF epithelia (see Supplemental material Tables S5 and S6, Figs S6–S8). The magnitude of the increase in 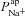will therefore be influenced by an increased shunt resistance (2-fold rather than 3-fold increase), but the increase of this transport parameter in the disease state is observed consistently.

Quantifying the influence of CFTR and ENaC currents on nasal V_t

Published modelling work investigating the electrical coupling of CFTR and ENaC fluxes (Horisberger, 2003) showed that increasing 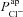could decrease amiloride-sensitive short-circuit current (I_sc) in a kidney epithelial cell model, and Falkenberg and Jakobsson note that I_sc is most sensitive to basal apical anion permeability, after the addition of amiloride (Falkenberg & Jakobsson, 2010). More recently, evidence from pig and human airway epithelial cell lines showed that experimentally decreasing apical Cl⁻ conductance can increase ΔV_t+ amiloride (Chen et al. 2010; Itani et al. 2011). Our analyis confirms that this relationship exists, qualitatively. However, our modelling approach allows us to quantitatively determine the influence each transport parameter has on the electrical properties of the epithelium (Figs 5 and 6). Thus, we can show that the magnitude of changes in going from non-CF to CF levels of anion permeability were not sufficient to explain the experimentally observed hyperpolarised basal V_t, the increased amiloride-sensitive V_t component, and the decreased ΔV_t+ 0[ Cl⁻]_l. In contrast, sensitivity analysis shows that 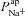significantly hyperpolarises basal V_t, and is the most important factor in determining the magnitude of ΔV_t+ amiloride. Without altering 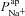from non-CF levels, the magnitude of the hyperpolarisation of basal V_t and of increased amiloride-sensitive V_t could not be explained.

One can intuitively understand how the relative influences of ENaC and CFTR permeability on basal and amiloride-sensitive V_t arise, by examining the driving force for movement of Na⁺ and Cl⁻ ions across the apical membrane. Basal V_t depends implicitly on apical Na⁺ and Cl⁻ currents, and the changes in these currents with respect to permeability are proportional to driving force. Hence the relative driving force for movement of different ions explains the relative sensitivity of V_t to different permeabilities.

In the representative example of best-fit non-CF parameter values (Table 1), the driving force for Na⁺ absorption across the apical membrane at steady state is −65.8 mV, as opposed to +1.1 mV for Cl⁻ transport. At these physiological potentials, the Cl⁻ driving force is thus < 2% of that for Na⁺, consistent with the results of our sensitivity analysis: 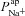has a much greater influence on V_t than 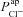. How then, can we explain the influence of 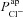on amiloride-sensitive V_t? After amiloride is added 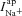is dramatically reduced and 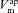changes, altering the apical Cl⁻ driving force and consquently 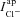. Again taking these best-fit parameters, this driving force goes from +1.1 mV to −9.5 mV for Cl⁻, while 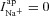. Therefore 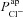now has a greater relative influence on 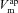and V_t, while 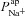can have no further effect.

The results of our sensitivity analysis are in agreement with a range of additional experimental data not used to constrain the model. For example, we observed basal V_t to be strongly dependent on 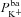(hyperpolarising). This was found experimentally by Mall et al. (2000) who blocked basolateral K⁺ channels in human bronchial epithelial (HBE) cells. Modelling studies have also shown that I_sc can be increased by stimulating basolateral K⁺ currents (Falkenberg & Jakobsson, 2010), supporting the hypothesis that increased basolateral K⁺ conductance is necessary to hyperpolarise the basolateral (and consequently, apical) membrane, providing an increased driving force for Cl⁻ secretion (Cotton, 2000). Further, V_t tends to be depolarised by 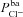in our model, which agrees with the observations of Fischer and colleagues in human and bovine tracheal primary cultures (Fischer et al. 2007) who also found V_t to be dependent on .

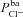Finally, it is interesting to note how our model predicts that the density of Na⁺–K⁺-ATPase pumps is higher in CF than non-CF cells. This may be necessary in order to deal with the increased rate of Na⁺ absorption, and higher pump expression has been reported in CF tracheal and nasal epithelia (Stutts et al. 1986).

Implications for clinical nasal potential difference measurements

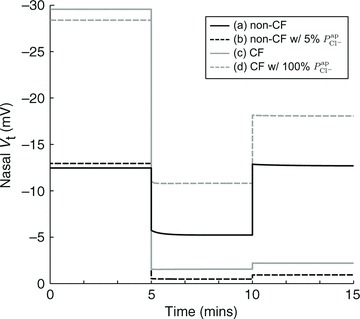
In Fig. 7 we show the output of simulations of the first three stages of a standard nasal potential difference (nasal V_t) clinical recording: measurement of a basal V_t value, relaxation to a new steady-state value following apical amiloride addition, and transition to a third V_t value upon transfer to Cl⁻-free conditions (while maintaining amiloride presence). Simulations were run with four different parameterisations: (a) optimal non-CF values (black), (b) optimal non-CF with reduced 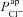(5% of optimal level, black, dashed), (c) optimal CF values (grey), and (d) optimal CF values with optimal non-CF 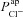levels (grey, dashed). These simulations illustrate the major findings of our study, and emphasise the potential utility of this mathematical modelling approach.

Figure 7. Simulations of first stages of a clinical nasal PD test.

Basal V_t is recorded initially for several minutes, then amiloride is added to the perfusing solution at t = 5 min to block ENaC channels (causing 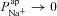), and the resultant change in V_t is recorded. At t = 10 min the solution perfusing the luminal surface is changed to a low Cl⁻ solution ([ Cl⁻]_l→ 3 mm) to introduce a diffusion potential for Cl⁻ efflux, and the resultant change in V_t is recorded. Restoring non-CF 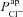levels in a CF cell does not correct hyperpolarised basal V_t (grey continuous line → grey dashed line). Also, reducing 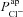alone to CF levels, in a non-CF cell, does not reproduce a typical CF trace (black continuous line → black dashed line).

Traces (a) and (b) illustrate how the loss of apical Cl⁻ permeability (in a non-CF HNE cell) alone cannot account for CF bioelectric properties. With a reduction to 5% of non-CF 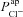levels, the level of ΔV_t+ amiloride increases and ΔV_t+ 0[ Cl⁻]_l decreases, but the change of tens of millivolts in basal V_t seen in patients is not observed as only a modest hyperpolarisation occurs.

Traces (c) and (d) illustrate how our model can be used to investigate strategies aimed at normalising ion transport in CF epithelia. Here we simulate the effect of theoretically increasing 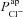from CF to non-CF levels, in a CF HNE cell. We see that this can ameliorate the ΔV_t+ amiloride and ΔV_t+ 0[ Cl⁻]_l responses towards non-CF magnitudes, but basal V_t remains hyperpolarised at a typical CF level. This simulation investigates the changes in V_t caused by a hypothetical therapy aimed at increasing Cl⁻ secretion alone. Although the exact pathophysiology of CF lung disease is controversial, the hyperpolarised V_t experienced by CF epithelia will undoubtedly alter driving forces for trans-epithelial ion (and water) movement, a factor which may contribute to the development of CF lung disease. Thus we can see that such a strategy (e.g. stimulating calcium-activated Cl⁻ channels in the apical membrane; Cuthbert, 2011) would not help with restoring basal V_t in native tissues to desired non-CF levels.

The measurement of nasal trans-epithelial potentials is widely used as an aid to CF diagnosis and clinical management. Hyperpolarised basal V_t and larger amiloride-sensitive V_t changes are hallmarks of CF disease and have, in recent years, also become central to the debate on the role of sodium hyper-absorption in CF pathology. These same altered bioelectric properties are the foundation of therapeutic approaches aimed at reducing ENaC activity (Hofmann et al. 1998; Coote et al. 2009). The correct interpretation of trans-epithelial potentials therefore carries important implications for both understanding CF and assessing potential therapies. The model presented here therefore can become a highly valuable tool for the interpretation of clinical nasal potential difference measurements and for the development of more effective treatment.

Glossary

CF

cystic fibrosis

CFTR

cystic fibrosis transmembrane conductance regulator

ENaC

epithelial Na⁺ channel

PD

potential difference

V_t

trans-epithelial PD

HNE cells

human nasal epithelial cells

Additional information

Competing interests

None.

Author contributions

All authors contributed to the conception and design of the mathematical model. D.L.O’D. performed the simulations, data analysis and interpretation of data. All authors contributed to the drafting and revision of the article, and have seen and approved the final version of the manuscript.

Funding

D.L.O’D. was supported by EPSRC grant EP/F500351/1.

Supplementary material

Supplemental material