The predictive value of childhood blood pressure values for adult elevated blood pressure

Abstract

Because of the paucity of serial blood pressure data on the same individuals, little is known about the accuracy of elevated blood pressure (BP) in childhood for predicting hypertension (HBP) later in life. The availability of long-term serial BP data from the Fels Longitudinal Study (FLS) presents the opportunity to link HBP in adulthood directly to BP measured decades earlier in the same individuals as children. We analyzed serial data from 965 men and 1114 women in the FLS. We used an autoregressive-moving average (1, 1) [ARMA (1, 1)] longitudinal model to predict adult HBP from childhood values. For 15-year-old boys with SBP 15 mmHg and 30 mmHg above the average SBP of 90 mmHg, the probabilities of having HBP at age 35 are 0.18 and 0.33, respectively. The corresponding probabilities for 15-year-old girls are only 0.04 and 0.08. This striking sex difference in risk of HBP at age 35 between 15-year-old boys and girls indicates that the risk of developing HBP in women is low regardless of their childhood blood pressure at any age from 2 to 17 years. Men are about 4.25 times more likely to have HBP at age 35 than women over a range of SBP of 90 – 140 mmHg at age 15. The ARMA (1, 1) model allows the identification of boys at risk for HBP as adult men.

1. INTRODUCTION

An increase in prevalence of HBP in children may lead to an increase in the prevalence of HBP in adults, assuming that BP in childhood and adolescence tracks with fidelity into adulthood. Rosen et al. reported a prevalence of HBP in 33% of men and 50% of women enrolled in a multi-ethnic study of the development of atherosclerosis in asymptomatic adults [1]. This high prevalence constitutes a public health threat because HBP engenders structural changes in the heart which frequently lead to congestive heart failure.

The variability of blood pressure makes it difficult to identify a hypertensive child at a single visit. Longitudinal modeling is an appealing way to build a predictive model for childhood blood pressure. Such an approach necessitates longitudinal blood pressure data that span the age range from childhood to adulthood so that the model's predictions are based on empirical longitudinal data. We have previously applied autoregressive models to longitudinal pulmonary function data [2,3]. These models were subsequently enhanced by the inclusion of random effects and were applied to longitudinal blood pressure data from the Fels Longitudinal Study (FLS) with follow-up from 1930 to 1989 [4]. Beckett et al. reported that damped autoregressive models and the autoregressive moving average model (ARMA) (1, 1) both provided a good fit the longitudinal data from 2 to 60 years of age [4]. We applied longitudinal models to analyze serial childhood BP data for their ability to predict HBP at age 35 years in the FLS and reported that a child's systolic blood pressure (SBP) measured on a single occasion and found to be above the 50th percentile of the CDC/NCHS 1999–2000 dataset predicts odds ratios of developing HBP as an adult ranging from 1.8 to 4.4 depending on sex and age [5].

The usual algorithm is to define children as hypertensive 1) if their systolic and/or diastolic BP is ≥95th percentile for age, gender and height on 3 consecutive visits [6]. Children are designated as pre-hypertensive if their systolic and/or diastolic BP is ≥90th percentile, or 2) if their SBP/DBP is above 120/80 and 3) they are not hypertensive. In this study we extend the analyses from birth to 80 years of age and the follow-up of the FLS cohorts through 2010, and we consider extensions of autoregressive models to account for measurement error and individual level time-to-time dependence. We include concurrent measures of BMI and height as time-varying covariates and include use of antihypertensive medication as an additional covariate in the models. The objectives are to:

• 1)Describe the patterns of change from childhood through late adulthood in SBP and DBP using longitudinal models;
• 2)Evaluate the effects of concurrent BMI, height, and antihypertensive medications on BP.
• 3)Employ fitted models to predict adult HBP or pre-HBP from childhood values in the same individuals;
• 4)Determine the risk of adult HBP for individual childhood values ≥ 0th percentile of the 4th Report relative to the risk of adult HBP for individual childhood values at the 50th percentile.

2. SUBJECTS AND METHODS

2.1. Study Sample

The FLS is the world's largest and oldest longitudinal observational study of human growth and body composition. [7,8] Initiated in 1929 in Yellow Springs OH, the FLS has been housed at Wright State University in Dayton, OH since 1977. Of the total enrollment of 2079 subjects eight percent have been lost to follow-up and 16 percent have died. Data of the lost and deceased participants are used where appropriate. Childhood measurements made from birth through age 7 years include anthropometrics and blood pressure. These data are recorded during scheduled examinations at birth, 1, 3, 6, 9, and 12 months, then semi-annually to 18 years, and biennially thereafter. Reliability in the FLS is excellent with reliability coefficients for most variables well above 90%.

2.2. Measurement Protocols

The body size measurements were taken following recommendations in the Anthropometric Standardization Reference Manual [9]. Weight was measured to 0.1 kg using a SECA scale. Height was measured to 0.1 cm using a Holtain stadiometer. Body Mass Index (BMI = weight/height²; kg/m²) was calculated. All the measurements were taken twice, with a third measurement taken if the difference between the first two exceeds established tolerance (0.3 kg for weight and 0.5 cm for height), and the average values are used for analysis.

SBP and DBP were measured with a mercury sphygmomanometer semiannually from ages two through 18 years and every two years thereafter. SBP and fourth and fifth phase DBP were measured by trained observers with the participant seated. After 1974 a rigorously standardized protocol similar to that used in the Multiple Risk Factors Intervention Trial (MRFIT, 1974) was followed [10]. Arm circumferences were measured, and cuffs were used that were long enough to completely encircle the arm and wide enough to cover two-thirds of the length of the upper arm. Three measurements were taken at a single examination, and the average of the second and third readings was used for data analysis.

The data from participants using medications were included in our model since antihypertensive medications are designed to attenuate HBP. Data generated by participants with HBP who are not taking medication were analyzed with the data for participants who do not have elevated BP. We established an index indicating which participants have HBP but take no medication; have HBP and take appropriate medication; and have no elevated BP. This index was incorporated as a covariate in our analyses.

2.3. Statistical Analysis

The longitudinal analyses used data from multiple examinations over time for each individual. The analyses included periods of time ranging from 2 to 80 years. Individual serial lifetime SBP measurements were modeled as a quadratic function of age and BMI and a linear function of height. We sought to determine how closely individual BP measurements taken at two different ages were correlated.

If BP measurements on different occasions follow a multivariate normal distribution, then the mean and covariance structure are sufficient to describe the process of change in BP over time. In particular, these parameters can be used to address whether elevated BP measurements in childhood presage HBP in adulthood.

The serial changes over time for SBP were modeled using a covariance pattern model, which allows for a relaxing of the independence assumption on the error terms. Independent variables in this model included a subject's age, BMI, height, and a dichotomous variable indicating whether a subject was on any blood pressure medications. The age (years) of the subject was each centered at age 40 (Age-40) and a quadratic function term was included to adjust for any non-linearity in the relationship between a subject's age and their SBP measure. A similar strategy was used for BMI (kg/m²), but with BMI centered at 20 (BMI-20). A subject's concurrent serial height (cm) was centered at 150 (Ht-150), and no quadratic term was included.

In a linear regression model, the error term is assumed to be independent across observations and normally distributed with a mean of zero and constant variance. In the covariance pattern model, the independence assumption is relaxed, and the error terms are allowed to be related within each individual. The vector of the error term still has zero expectation, but is allowed to have a variance-covariance matrix with a pre-specified structure. Three covariance structures were considered:

• 1)Compound Symmetry [CS]. In this model, all measurements at different times are assumed to have the same correlation. The covariance matrix has elements within each individual: σ² ρ · I (i ≠ j) + σ² · I (i = j), where 0 ≤ ρ ≤ 1.
• 2)Autoregressive (1) [AR (1)]. The correlation between measurements at examinations 1 year apart is ρ, 2 years apart is ρ² and so on. Within individual covariance has the form: σ²·ρ^|i−j|.
• 3)
  Autoregressive-moving average (1, 1) [ARMA (1, 1)]. The correlation between measurements taken one year apart and the correlation between examinations greater than one year apart are parameterized separately. In the covariance matrices fit in this analysis the elements have the following form:

  $${\sigma }^2\cdot [\rho \cdot \gamma {\cdot }^{\mid i-j-1\mid }\cdot I(i\ne j)+I(i=j\left)\right]$$

A similar but separate model was fit using DBP as the response. The means and covariances were estimated using the MIXED procedure from SAS. The analysis used measurements made at various ages as well as time-varying covariates, such as height and BMI and non-time-varying covariates, such as antihypertensive medication. It was assumed that missing values were missing at random and were estimated by a multiple imputation procedure. The maximum likelihood estimate (MLE) assumes that the mechanism that causes data to be incomplete is ignorable as defined by Rubin [11]. Comparisons between models were carried out by the Akaike Information Criterion (AIC) [12,13].

3. RESULTS

The demographic characteristics of the participants are shown in Table 1. Almost one-half of the study subjects were less than 17 years at initial measurement and 40% were ≥40 years old when final measurements were taken and were followed for ≥20 years. Ninety-eight percent were white, 965 were males, and 1114 were females. One hundred and eighty-eight men and 145 women of the 2079 FLS subjects have been prescribed antihypertensive medication.

Table 1.

Demographic characteristics of blood pressure measurements taken in participants in the Fels Longitudinal Study (N = 2079), southwestern Ohio, 1929–2010.

	Frequency	%
Age (years) at initial BP measurement
0–4	206	9.9
5–9	655	31.5
10–14	201	9.7
15–17	61	2.9
17+	956	46.0
Age (years) at final measurement to date
<11	111	5.3
11–19	283	13.6
20–29	379	18.2
30–39	335	16.1
40–49	274	13.2
50–59	261	12.6
60+	436	21.0
No. of years of follow-up
<6	890	47.1
6–9	145	7.7
10–19	312	16.5
20–29	185	9.8
30–39	244	12.9
40–49	113	6.0
50+	190	10.1
Sex
Males	965	46.4
Females	1114	53.6
Race
Caucasian	2023	97.7
Other	48	2.3

The mean values for SBP and DBP at each age were plotted from age 2 to 80 years as shown in Figure 1. The best fits were the first order autoregressive moving average criterion value based on the minimum AIC. The ARMA (1, 1) is an extension of autoregressive models that account for measurement error and thus perform better than the remaining two models: AR (1) and constant correlation (CS) (Table 2).

Figure 1.

Mean systolic blood pressure and diastolic blood pressure levels for 965 males and 1144 females in the FLS.

Table 2.

Model fit criterion. Most desirable/lowest value in bold.

	Male
	CS	AR (1)	ARMA (1, 1)
–2LL	67552.2	67612.5	66790.0
AIC	67556.2	67616.5	66796.0
AICC	67556.2	67616.5	66796.0
BIC	67556.0	67626.2	66810.6
	Female
	CS	AR (1)	ARMA (1, 1)
−2LL	70496.5	70264.1	69542.7
AIC	70500.5	70268.1	69548.7
AICC	70500.0	70268.1	69548.7
BIC	70510.5	70278.1	69563.7

This implies that the moving average variance structure, rather than the CS or the strict autoregressive (AR 1) model fits the data better. The ARMA (1, 1) covariance and the model parameters are shown in Table 3. In males and females SBP increases with age in a quadratic trend, and a significant quadratic trend exists for the relationship between BMI and SBP. Once an individual is taking antihypertensive medication, SBP decreases significantly. The results are shown for estimating the covariance parameters for the ARMA (1, 1) model, where ρ is the autoregressive parameter, and γ is the parameter associated with dependence of subsequent observations. All of the covariance parameters from the final model are shown in Table 3.

Table 3.

Parameter estimates for systolic and diastolic blood pressure from ARMA [1, 1] models in participants in the Fels Longitudinal Study, southwestern Ohio, 1929–2010. Information for the SBP and DBP are in separate sections.

Systolic Blood Pressure			Diastolic Blood Pressure
Males
Effect	Estimate	S.E.	p-value	Estimate	S.E.	p-value
Intercept	108.54	0.66	<0.0001	72.9	0.6	<0.0001
(Age-40) year	0.33	0.01	<0.0001	0.23	0.01	<0.0001
(Age-40)2	0.01	0	<0.0001	−0.01	0	<0.0001
(BMI-20) kg/m2	1.24	0.08	<0.0001	0.87	0.07	<0.0001
(BMI-20)2	−0.01	0	0.0109	−0.01	0	0.1123
(Height-150) (cm)	0.16	0.01	<0.0001	−0.04	0.01	0.0005
BPMeds	−3.35	1.29	0.0093	−3.23	1.28	0.0116
Covariance Parameter Estimates
Covariance Parameter	Estimate	S.E.	p-value	Estimate	S.E.	p-value
Rho (ρ)	0.95	0.01	<0.0001	0.87	0.01	<0.0001
Gamma (γ)	0.63	0.01	<0.0001	0.47	0.01	<0.0001
Residual (σ2)	150.77	5.23	<0.0001	108.9	2.42	<0.0001
Females
Effect	Estimate	S.E.	p-value	Estimate	S.E.	p-value
Intercept	104.44	0.53	<0.0001	67	0.47	<0.0001
(Age-40) year	0.49	0.01	<0.0001	0.19	0.01	<0.0001
(Age-40)2	0.01	0	<0.0001	−0.01	0	0.0461
(BMI-20) kg/m2	0.98	0.05	<0.0001	0.76	0.04	<0.0001
(BMI-20)2	−0.01	0	<0.0001	−0.01	0	<.0001
(Height-150) (cm)	0.13	0.01	<0.0001	−0.01	0.01	0.2472
BPMeds	−3.67	1.02	0.0003	−2.33	0.96	0.0151
Covariance Parameter Estimates
Covariance Parameters	Estimate	S.E.	p-value	Estimate	S.E.	p-value
Rho (ρ)	0.94	0.01	<0.0001	0.89	0.01	<0.0001
Gamma (γ)	0.62	0.01	<0.0001	0.52	0.01	<0.0001
Residual (σ2)	147.86	4.65	<0.0001	107.7	2.54	<0.0001

The ARMA (1, 1) model allows the identification of children at risk for elevated BP as adults. The probability of risk of a condition in adults, given certain values in the same individuals as children, can be estimated as shown in Beckett et al. [4]. The conditional probability of Y₂ being larger than a criterion value (e.g., SBP > 130 mmHg) given Y₁ of SBP of a certain value can be derived the fitted model, assuming that Y₁ and Y₂ follow a bivariate normal distribution. For example, Table 4 shows that if a 15-year-old male has a SBP of 115 mmHg, the likelihood of his SBP exceeding 130 mmHg at age 35 years is 0.28. The corresponding risk for a female is much lower at 0.06.

Table 4.

Predictive value of systolic and diastolic blood pressure at age 15 for risk of elevated BP (SBP > 130; DBP > 85 mmHg) at age 35 in participants in the Fels Longitudinal Study. Southwestern Ohio, 1929–2010.

DBP at age 15	Probability that DBP > 85 at 35		RR relative to BP = 60 at Age 15
	Males	Females	RR Male	RR Females
60	0.21	0.06	1.00	1.00
65	0.22	0.07	1.05	1.11
70	0.23	0.08	1.10	1.23
75	0.24	0.08	1.15	1.35
80	0.25	0.09	1.20	1.49
85	0.27	0.10	1.25	1.63
90	0.28	0.11	1.30	1.79
SBP at age 15	Probability that SBP > 130 at 35		RR relative to BP = 90 at Age 15
	Males	Females	RR Male	RR Female
90	0.08	0.01	1.00	1.00
95	0.10	0.02	1.35	1.39
100	0.14	0.03	1.78	1.89
105	0.18	0.04	2.30	2.55
110	0.22	0.05	2.90	3.38
115	0.28	0.06	3.58	4.40
120	0.33	0.08	4.33	5.66
125	0.40	0.10	5.14	7.17
130	0.46	0.13	5.99	8.96
135	0.53	0.16	6.84	11.03
140	0.59	0.19	7.69	13.38

In boys the probability of elevated BP at age 35 years is 0.46 with a SBP of 130 mmHg at age 15 years. The trends for the probabilities of elevated BP in adulthood for females were similar. For males, the probabilities increase from 0.18 to 0.33 with increased SBP at age 15 years from 105 mmHg to 120 mmHg, corresponding to a change in risk ratio from 2.3 to 4.3. Although the probabilities are much lower in girls, the corresponding increase in risk ratio for females ranges from 2.6 to 5.7.

Application of Findings

In practice, the conditional probability of the risk of adult values exceeding a cutpoint given a childhood value, p(Y₂ > y₂|Y₁ = y₁), is useful in screening programs. From the selected fitted models, the mean and the covariance of repeated measurements of blood pressure are ascertained, and the prediction of adult blood pressure, SBP ≥ 130 mmHg or DBP ≥ 85 mmHg can be made from childhood measurements, assuming that the measurements are normally distributed.

The probabilities of elevated BP at age 35 years with reference percentiles at the 50th, 90th, 95th, and 99th from the Fourth Report on the Diagnosis, Evaluation, and Treatment of High Blood Pressure in Children and Adolescents are shown in Table 5: e.g., if a 9-year-old boy has a SBP at the 90th percentile, the likelihood of his SBP at 35 years exceeding 130 mmHg is 30% [6]. In men, the probabilities of elevated BP at age 35 are highly dependent on their childhood blood pressure. In females, the probability of having elevated BP at age 35 is low regardless of childhood values.

Table 5.

Predictive value of childhood systolic blood pressure percentiles at 50th, 90th, 95th, and 99th for age at the median height for risk of elevated BP at 35 years of age in males and females [6].

SBP Male	Probability that Mean SBP >130 at 35 years				Risk ratio relative to mean SBP at 50th percentile
Age	50th	90th	95th	99th	50:90	50:95	50:99
2	0.20	0.27	0.29	0.33	1.35	1.45	1.65
3	0.20	0.27	0.29	0.34	1.37	1.48	1.69
4	0.20	0.27	0.30	0.34	1.39	1.51	1.74
5	0.20	0.27	0.30	0.35	1.38	1.51	1.79
6	0.20	0.28	0.31	0.36	1.44	1.58	1.84
7	0.20	0.29	0.32	0.37	1.47	1.62	1.89
8	0.19	0.28	0.31	0.37	1.46	1.62	1.91
9	0.19	0.30	0.33	0.39	1.53	1.70	2.02
10	0.19	0.29	0.33	0.40	1.52	1.70	2.09
11	0.19	0.30	0.33	0.41	1.56	1.75	2.17
12	0.19	0.31	0.34	0.43	1.65	1.81	2.25
13	0.19	0.32	0.36	0.44	1.69	1.92	2.35
14	0.19	0.33	0.36	0.46	1.74	1.93	2.45
15	0.18	0.33	0.38	0.47	1.80	2.07	2.56
16	0.18	0.34	0.39	0.49	1.86	2.15	2.69
17	0.18	0.35	0.40	0.51	1.93	2.25	2.83
Females
Age	50th	90th	95th	99th	50:90	50:95	50:99
2	0.033	0.05	0.05	0.059	1.52	1.52	1.79
3	0.033	0.05	0.05	0.063	1.52	1.52	1.91
4	0.033	0.05	0.05	0.063	1.52	1.52	1.91
5	0.033	0.05	0.05	0.065	1.52	1.52	1.97
6	0.032	0.05	0.06	0.070	1.56	1.88	2.19
7	0.032	0.05	0.06	0.070	1.56	1.88	2.19
8	0.032	0.05	0.06	0.073	1.56	1.88	2.28
9	0.031	0.05	0.06	0.076	1.61	1.94	2.45
10	0.031	0.05	0.06	0.079	1.61	1.94	2.55
11	0.030	0.06	0.07	0.086	2.00	2.33	2.87
12	0.030	0.06	0.07	0.091	2.00	2.33	3.03
13	0.029	0.06	0.07	0.095	2.07	2.41	3.28
14	0.029	0.06	0.07	0.096	2.07	2.41	3.31
15	0.028	0.06	0.07	0.102	2.14	2.50	3.64
16	0.027	0.06	0.07	0.108	2.22	2.59	4.00
17	0.026	0.07	0.08	0.120	2.69	3.08	4.62

Table 6 presents risks and risk ratios for developing elevated DBP in adulthood given childhood BP measurements at the 50th, 90th, 95th and 99th percentiles. In general the risks of developing elevated DBP are less at all ages and percentiles than for SBP.

Table 6.

Predictive value of childhood diastolic blood pressure percentiles at 50th, 90th, 95th, and 99th for age at the median height for risk of elevated BP at 35 years of age in males and females [6].

SBP Male	Probability that Mean DBP <130 at 35 years				Risk ratio relative to mean DBP at 50th percentile
Age	50th	90th	95th	99th	50:90	50:95	50:99
2	0.22	0.22	0.23	0.23	1.01	1.01	1.02
3	0.22	0.22	0.23	0.23	1.01	1.02	1.02
4	0.22	0.23	0.23	0.23	1.02	1.02	1.03
5	0.22	0.23	0.23	0.23	1.02	1.02	1.03
6	0.22	0.23	0.23	0.23	1.02	1.03	1.04
7	0.22	0.23	0.23	0.23	1.02	1.03	1.04
8	0.22	0.23	0.23	0.23	1.03	1.03	1.05
9	0.22	0.23	0.23	0.23	1.03	1.04	1.06
10	0.22	0.23	0.23	0.24	1.03	1.05	1.06
11	0.22	0.23	0.23	0.24	1.04	1.05	1.07
12	0.22	0.23	0.24	0.24	1.04	1.06	1.09
13	0.22	0.23	0.24	0.24	1.05	1.07	1.10
14	0.22	0.24	0.24	0.25	1.06	1.08	1.11
15	0.22	0.24	0.24	0.25	1.07	1.09	1.13
16	0.22	0.24	0.25	0.26	1.08	1.11	1.15
17	0.22	0.24	0.25	0.26	1.10	1.13	1.18
Female
Age	50th	90th	95th	99th	50:90	50:95	50:99
2	0.065	0.067	0.067	0.068	1.03	1.03	1.05
3	0.065	0.067	0.067	0.069	1.03	1.03	1.06
4	0.065	0.067	0.068	0.069	1.03	1.05	1.06
5	0.065	0.067	0.068	0.070	1.03	1.05	1.08
6	0.065	0.068	0.069	0.070	1.05	1.06	1.08
7	0.065	0.068	0.069	0.071	1.05	1.06	1.09
8	0.065	0.069	0.070	0.072	1.06	1.08	1.11
9	0.065	0.069	0.070	0.073	1.06	1.08	1.12
10	0.065	0.070	0.071	0.074	1.08	1.09	1.14
11	0.065	0.070	0.072	0.075	1.08	1.11	1.15
12	0.065	0.071	0.073	0.077	1.09	1.12	1.18
13	0.065	0.072	0.074	0.078	1.11	1.14	1.20
14	0.064	0.073	0.075	0.080	1.14	1.17	1.25
15	0.064	0.074	0.076	0.082	1.16	1.19	1.28
16	0.064	0.075	0.078	0.084	1.17	1.22	1.31
17	0.064	0.076	0.080	0.086	1.19	1.25	1.34

Figure 2 is shaded differentially to indicate age ranges during which the probability of elevated BP (SBP > 130 mmHg) at 35 y was either <10%, 10% – 19.9%, 20% – 29.9%, 30% – 39.9%, 40% – 49.9%, and ≥50%. For example, it can be seen in Figure 2 that a male aged 12 y with a SBP of 123 mmHg is at the 95th percentile for Fourth Report data [6]. The corresponding SBP value is toward the upper end of the distribution for the general US male population. Figure 3 also show the likelihood of HBP at 35 y depending on the DBP percentile during childhood.

Figure 2.

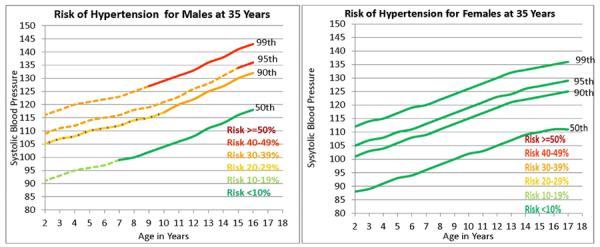
Selected percentiles for systolic blood pressure in males and females from the Fourth report on the Diagnosis, Evaluating, Treatment of High Blood Pressure in Children and Adolescents [6]. Segments of 50th, 90th, 95th, and 99th percentile lines are differentially shaded to indicate differences in the probability that systolic blood pressure at 35 y will be >130 mmHg [6].

Figure 3.

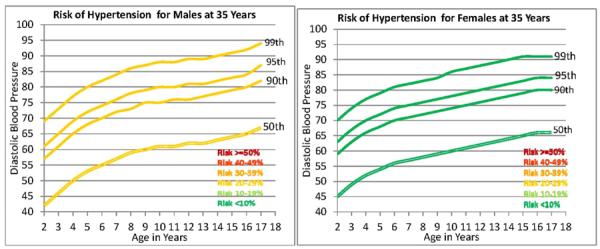
Selected percentiles for diastolic blood pressure in males and females from the Fourth Report on the Diagnosis, Evaluating, Treatment of High Blood Pressure in Children and Adolescents [6]. Segments of 50th, 90th, 95th, and 99th percentile lines are differentially shaded to indicate differences in the probability that systolic blood pressure at 35 y will be >130 mmHg [6].

4. DISCUSSION

The increasing prevalence of HBP is a public health threat because HBP engenders structural changes in the heart which may lead to congestive heart failure (CHF). The extent of the problem was documented by Coca et al. who reported that 73% of a population-based sample of 946 adults with essential HBP met the echocardiographic criteria of de Simone et al for LVH [14,15].

An increase in prevalence of elevated BP in children may lead to an increase in the prevalence of HBP in adults, assuming that BP in childhood and adolescence tracks with fidelity into adulthood. To address this tracking question definitively, Chen & Wang performed a meta-analysis of 50 cohort studies of measurements of BP over time and reported the average BP tracking correlation coefficients were 0.38 for SBP and 0.28 for DBP [16]. A more recent meta-analysis of BP tracking was performed in 29 cohort studies by Toschke et al who reported that the overall adjusted average SBP tracking coefficient was 0.37 between ages 10 and 20 years in males and females [17]. Rosner and coworkers reported that elevated BP in childhood is the strongest predictor of HBP in adulthood, outweighing the influence of childhood height and weight [18,19].

Little is known about the ability of childhood blood pressure to predict adult elevated BP because of the paucity of serial data collected on the same individuals over several decades. The FLS data enabled us to link HBP in adults to BP in the same individuals as children. The ability to predict HBP in adults by measuring BP in children is of clinical and public health importance, especially in view of the increasing prevalence of HBP in children in this country [20].

One approach to analyzing long-term serial blood pressure data is to build a longitudinal model for blood pressure which spans the range from childhood to adulthood and to make predictions based on the model. We have previously considered autoregressive models for longitudinal data which were applied to longitudinal pulmonary function data [2,3]. These models were subsequently enhanced with the inclusion of random effects and applied to longitudinal BP data from the FLS with follow-up from 1930 to 1989 [4]. In the current study we extend follow-up of this cohort through 2010; consider extensions of autoregressive models to account for measurement error; and incorporate BMI, height and antihypertensive medications to improve the accuracy of prediction. The ARMA (1, 1) model that takes into account measurement error was selected to predict adult elevated BP from childhood blood pressure values in the same individuals.

The present study shows that elevated BP during childhood is an important risk factor for HBP at 35 y in males and in females. The predictability of adulthood elevated BP from childhood blood pressure values in the present study has limitations. The present study analyzed data from a large longitudinal study of non-Hispanic Caucasians in SW Ohio that were collected between 1929 and 2010. However, analysis of this extensive longitudinal data set may elucidate biologic relationships that apply to all races and ethnicities.

There is a potential cohort effect or secular trend that needs to be taken into account when using these results in clinical or public health assessments. A secular trend toward higher blood pressure in children has been reported by Muntner et al. [21].

It is recommended that the findings reported here be applied to non-Hispanic Caucasian children with blood pressures greater than the 90th percentile for age, sex and height. The present findings may also be applied to children of other US ethnic groups, but the probabilities may differ from those for non-Hispanic Caucasian children. It is probable that the accuracy of the prediction in the present study could be improved by incorporating parental data, dietary patterns, smoking behavior, and physical activity.

4.1. Perspectives

The present study takes advantage of the unique FLS data set with a rich 80-year history of serial collection of data on BP and direct measurements of body composition. The data sets are characterized by high reliability. The ability to predict adult elevated BP by measuring levels of blood pressure in childhood as early as two years of age is of clinical and public health importance, especially in males whose average risk at age 15 years for elevated BP at age 35 years is more than four time that of females with comparable childhood blood pressures. Such prediction may signal the need for corrective interventions that could be made during childhood. This approach is preferable to waiting until adulthood when the deleterious clustering of risk factors has been established, and when lifestyle changes are difficult to implement.

4.2. Innovation and Significance

In most longitudinal studies of BP the period of observation usually does not extend from childhood to adulthood. In the present study, the period of serial observations of BP, BMI and height extends from infancy to old age. The longitudinal model that best fits the empirical data includes error functions, covariates, and imputation. As a result, the AR (1,1) model provides the most accurate predictions extant of HBP in adulthood from given values in childhood. This work is significant because the prevalence of childhood obesity has tripled in the general population over the past three decades, and has quadrupled among several ethnic and racial minority groups [22]. The increased prevalence of childhood obesity has been accompanied by an increase in the prevalence of high blood pressure (HBP) in children and adolescents [21,23]. We have found that childhood values of SBP between the 50th and the 95th percentiles predict HBP in adulthood, Heretofore little attention has been paid to children with BP levels in this range, currently considered to be normal.