Matching of additive and polarizable force fields for multiscale condensed phase simulations

Abstract

Inclusion of electronic polarization effects is one of the key aspects in which the accuracy of current biomolecular force fields may be improved. The principal drawback of such approaches is the computational cost, which typically ranges from 3 – 10 times that of the equivalent additive model, and may be greater for more sophisticated treatments of polarization or other many-body effects. Here, we present a multiscale approach which may be used to enhance the sampling in simulations with polarizable models, by using the additive model as a tool to explore configuration space. We use a method based on information theory to determine the charges for an additive model that has optimal overlap with the polarizable one, and we demonstrate the feasibility of enhancing sampling via a hybrid replica exchange scheme for several model systems. An additional advantage is that, in the process, we obtain a systematic method for deriving charges for an additive model that will be the natural complement to its polarizable parent. The additive charges are found by an effective coarse-graining of the polarizable force field, rather than by ad hoc procedures.

Introduction

Additive force fields have been very successful in reproducing condensed phase properties of macromolecules.¹ Nonetheless, it is generally recognized that the form of the energy function used in such simulations is inadequate to reproduce the molecular potential energy surface to within k_BT accuracy under standard conditions.^2,3 A major deficiency is the used of fixed point charges to represent intermolecular electrostatic interactions, neglecting atomic polarizability. The approximation of using fixed charges also leads to ambiguities in which charges should be chosen. For example, if charges are obtained by fitting to a molecular electrostatic potential,⁴ the results will invariably depend on the internal degrees of freedom of the molecule.^5–7 This is generally solved in an ad hoc way by fitting the charges simultaneously to a number of configurations,^8,9 but it is not clear what relative weights should be used in the fit. A second problem is that a condensed phase aqueous environment will tend to increase the overall polarization of a molecule.² This effect has been approximately included in various ways, including the use of an implicit solvent model in the calculation of the electrostatic potential,¹⁰ explicit consideration of interactions with water molecules,^11–13 or by using Hartee-Fock theory to determine a gas phase electrostatic potential (RESP fitting),^8,14 on the grounds that this tends to result in overpolarization due to the neglect of electron correlation. In summary, charges for additive force fields are usually determined by reasonable, but rather ad hoc, procedures. Choosing the best possible charges for additive models is very important, however, as such models are the only computationally practical approach to many problems. These issues are driving a renewed interest in methods for determining charges in additive force fields. For example, a recent study has proposed an iterative scheme using two alternating components: (i) simulations with the current additive charges in the condensed phase and (ii) derivation of new additive charges using a RESP scheme, but with selected solvent molecules from the simulation explicitly included.¹⁵ Our work presents an alternative approach to this problem.

The shortcomings of additive force fields have motivated the development of more sophisticated functional forms including many-body interactions,^16,17 in particular polarizable force fields.^18,19 The most sophisticated polarizable models aim to reproduce the energy surface to within 0.5 kcal/mol (~k_BT at 300 K), but come at a significant computational cost. Simulations with polarizable force fields typically run from ~ 2–3 (CHARMM Drude model in NAMD,²⁰ Amber ff02²¹) to ~10 (AMOEBA^3,22) times slower than simulations with additive force fields (and can be much slower for still more sophisticated models). For simulations of biomolecular dynamics, which are already challenging with additive force fields due to the rugged energy landscape,^23,24 this additional cost can be prohibitive. It would therefore be desirable to combine the advantages of polarizable and additive models, using additive models to improve sampling, and polarizable models for greater accuracy.

Iuchi et al. have previously shown that, for water, coarse-graining based on force-matching²⁵ can be used to produce a non-polarizable model that accurately reproduces bulk properties obtained from a fully polarizable water model.²⁶ In this paper, we propose to adopt a similar approach, viewing the derivation of charges for an additive force field as a coarse-graining problem. We start from the assumption that we have a polarizable force field of the desired accuracy available, noting that, in principle at least, determining electrostatic parameters for polarizable models from gas phase quantum chemical calculations should be less ambiguous than for additive models.³ We then choose the set of fixed charges which gives maximum overlap between the configurational distributions obtained with additive and polarizable models, for simulations in an aqueous environment. This approach has two important outcomes: firstly, it provides a well-posed definition of the optimal set of fixed charges. Secondly, it should also be the best choice for running “resolution exchange” simulations²⁷ in which polarizable and additive force fields are employed in a replica exchange scheme, allowing the goal of enhanced sampling with the additive force field to be realized. We present the application of the method to pure water, solutions of acetamide in water, and cyclohexane, and demonstrate its application in resolution exchange simulations of water and cyclohexane. We also discuss the issue of degeneracy of the solutions, how it can be overcome in practice and its relation to the variation in charge parameters within and across existing force fields.

Methods

Theory

Our starting point is the relative entropy formalism for comparing distributions, which has been proposed as the basis for a coarse-graining procedure by Shell.^28–32 In this approach, a “relative entropy” S_rel (or Kullback-Leibler divergence³³), measures the similarity between a “target” simulation T and a “model” simulation M with configuration distribution functions p_T(x) and p_M(x) respectively, where x represents a point in configuration space.

$$S_{\text{rel}}=\int p_{\text{T}}(x)ln\frac{p_{\text{T}}(x)}{p_{\text{M}}(x)}dx$$ (1)

Shell has proposed a gradient-based approach for variationally optimizing the parameters λ = λ₁, λ₂, … of the model energy function by means of a gradient minimization of the relative entropy^30,31 Using a Newton-Raphson approach for the minimization, the parameter update step is given by:

$${\lambda }^{k+1}={\lambda }^k-\chi {\mathbf{H}}^{-1}{\nabla }_{\lambda }{S}_{\text{rel}}$$ (2)

where χ is a parameter chosen to ensure stability of the algorithm, and the gradient ∇_λS_rel and the Hessian H of the relative entropy with respect of the parameters can be evaluated by averages over the target and model ensembles as follows:

$${\nabla }_{\lambda }{S}_{\text{rel}}=\beta {\langle \frac{\partial U_{\text{M}}}{\partial \lambda }\rangle }_{\text{T}}-\beta {\langle \frac{\partial U_{\text{M}}}{\partial \lambda }\rangle }_{\text{M}}$$ (3)

$${\mathbf{H}}_{ij}=\beta {\langle \frac{{\partial }^2{U}_{\text{M}}}{\partial {\lambda }_i\partial {\lambda }_j}\rangle }_T-\beta {\langle \frac{{\partial }^2{U}_{\text{M}}}{\partial {\lambda }_i\partial {\lambda }_j}\rangle }_{\text{M}}+{\beta }^2{\langle \frac{\partial U_{\text{M}}}{\partial {\lambda }_i}\frac{\partial U_{\text{M}}}{\partial {\lambda }_j}\rangle }_{\text{M}}-{\beta }^2{\langle \frac{\partial U_{\text{M}}}{\partial {\lambda }_i}\rangle }_{\text{M}}{\langle \frac{\partial U_{\text{M}}}{\partial {\lambda }_j}\rangle }_{\text{M}}$$ (4)

The drawback of using equations 3 and 4 is that they require the calculation of properties averaged over both the target and model ensembles. Since the model is a function of the parameters λ, this means that a simulation using the latest version of the parameters must be performed at every step in the minimization. Chaimovich and Shell³¹ have, however, noted that S_rel can be calculated via Equation 5:

$$S_{\text{rel}}=ln{\langle e^{\mathrm{\Delta }-{(\mathrm{\Delta })}_T}\rangle }_T$$ (5)

Where Δ = β(U_T − U_M) and U_T and U_M are the energies of configurations from the target ensemble evaluated using the target and model potentials, respectively. This expression allows us to calculate S_rel exactly without the averaging over the model ensemble, but the average over the exponential makes it prone to statistical error. If, however, we make the assumption that the distribution of Δ is Gaussian, as would be expected from a linear response approximation, we can calculate S_rel via Equation 6,³¹ reducing the statistical error.

$$S_{\text{rel}}\approx \frac{1}{2}{\text{Var}}_T[\beta (U_T-U_M)]$$ (6)

Using Equation 6 to calculate S_rel, we then evaluate ∇_λS_rel and H directly using finite differences, and use these quantities to iterate Equation 2 until λ converges to the value at which the relative entropy is a minimum. As an alternative, we have also used a Monte-Carlo-based method to optimize S_rel calculated via Equation 6: this is discussed further below.

While this is the method that we used in practice, we also note that the derivatives in Equations 3 and 4 can be obtained using a combination of energy evaluations in which the atomic partial charges in the atom-centered model are set to either unity or zero. This approach is outlined in detail in the Supporting Information. We note that in this case the problem of having to resample the model distribution can be potentially alleviated by reweighting for a certain number of steps until the overlap between model and target distribution becomes low enough that resampling is needed.³⁴ In principle, a weighted histogram method could even be used to combine information from multiple parameter sets, to suppress oscillations in parameter values.³⁵ However, as we found the finite difference method to be adequate, we did not pursue these methods here.

Simulation Methods

Sets of “target” configurations to be used in the relative entropy optimization were generated by running molecular dynamics (MD) simulations using the CHARMM Drude polarizable force field² in the program CHARMM.³⁶ Three such simulations were performed: one of liquid water (a cubic box of 250 molecules); one of a single ACEM molecule in a box of 250 water molecules, and one of a single CHEX molecule in a box of 250 water molecules. All simulations used the SWM4-NDP water model,³⁷ with ACEM and CHEX parameters from refs ^{38 and 39}, respectively. The simulations were performed using periodic boundary conditions, with the equations of motion integrated using a velocity Verlet integrator⁴⁰ and Drude particles treated via an extended Lagrangian double thermostat formalism.⁴¹ A mass of 0.4 amu was transferred from each heavy atom to its Drude particle and the second thermostat was applied to maintain the temperature of the Drude oscillators at 1K. A Nosé-Hoover thermostat^42,43 (relaxation time 1 ps) was applied to all atoms and a modified Anderson-Hoover barostat⁴⁴ (relaxation time 0.1 ps) was used to maintain a constant pressure of 1 atm. Covalent bonds to hydrogen were constrained using the SHAKE algorithm⁴⁵ and Lennard-Jones interactions were treated explicitly to 12 Å, with atom-based switch-smoothing applied over the range of 10–12 Å; a long-range correction⁴⁶ to the Lennard-Jones interactions was also included. Electrostatic interactions were treated using particle mesh Ewald⁴⁷ (PME) summation with a 32 point grid in each dimension, a coupling parameter of 0.34 and a sixth-order spline for mesh interpolation. Each simulation was run for 1.5 ns, starting from a pre-equilibrated box, with a 1 fs timestep and coordinates saved every 100 steps. For water, 1,500 of the saved configurations were used in the optimization of the relative entropy; for ACEM and CHEX, 10,000 and 5,000 of the saved configurations were used in the relative entropy optimization, respectively. These values were chosen to ensure the accurate computation of the relative entropy in all cases (Figure S1).

Radial distribution functions for each of the molecules, with the polarizable force field, were calculated from the simulations described above. Molecular volumes and enthalpies of vaporization for water were calculated using a simulation protocol identical to that described above, but with ten simulations, each of 150 ps duration, each starting from the same configuration but with velocities initiated using different random seeds. Final properties were then averaged over all ten simulations, with uncertainties calculated as the standard error of the mean. Diffusion coefficients, D, and dielectric constants, e, were obtained from four independent simulations, each of 5 ns with the final 4.5 ns used for analysis. Diffusion coefficients were calculated using the Einstein relation,⁴⁸ while dielectric constants were calculated as described in Ref. ⁴⁹, with final values averaged over all four simulations and uncertainties estimated as the standard error of the mean. High-frequency optical dielectric constants, ε_inf, were estimated using the Clausius-Mossotti equation. Hydration free energies for all molecules were calculated using free energy perturbation⁵⁰ (FEP) via the staged protocol of Deng and Roux,⁵¹ in a matter identical to that described previously.⁵² Final values are obtained as averages over five independent calculations, with uncertainties calculated as the standard error of the mean.

Following optimization of charge parameters using the relative entropy formalism, additional simulations were performed to calculate physical properties with the new, non-polarizable models. The simulation protocol used was the same as that described above, but without the inclusion of any Drude particles, which in turn permits the use of a 2 fs timestep. For the sake of comparison, analogous simulations were also performed using well-established, non-polarizable models: the TIP3P⁵³ water model; the TIP4P-Ew⁵⁴ water model; ACEM from CGenFF¹³ (the CHARMM General Force Field), and CHEX from the CHARMM sugar force field.³⁹

As a further test of the optimized parameters, a number of homo- and hetero-dimeric interactions with water were considered. In these calculations, the water geometry was fixed to the SWM4-NDP/TIP3P geometry while the solute was optimized within the force field of interest. With the geometries of both molecules fixed, the water molecule was then placed in a specific orientation relative to the solute molecule, and the separation of the molecules increased in increments of 0.1 Å with the total energy of the complex evaluated at every increment. The interaction energy was then defined as the difference between the energy of the complex and the sum of the energies of the two individual molecules.

Modifications to the CHARMM source code allowed us to run replica exchange molecular dynamics (REMD) simulations⁵⁵ involving the Drude polarizable force field, and to exchange configurations between polarizable and non-polarizable force fields. The principal challenge in implementing such a scheme is that the polarizable and non-polarizable force fields each contain different numbers of particles: there are no Drude particles present in the non-polarizable simulations. In practice, we dealt with this by including additional zero-mass, non-interacting dummy atoms in the non-polarizable simulations. We added these dummy particles to the additive CHARMM topology so that their positions in the final PSF were equivalent to the positions of the Drude particles in the polarizable PSF, ensuring that replica exchange would swap additive dummy atoms with polarizable Drude particles. Then, when an exchange was attempted, the following procedure was adopted: (i) before the attempted swap, the Drude particles were optimized in the polarizable model, and the energy re-evaluated; (ii) atomic coordinates were swapped between the systems, (iii) the positions of the Drude particles were again optimized via a full self-consistent field calculation in the polarizable force field, before the energies were re-evaluated for both polarizable and additive models, (iv) the move was decided according to the exchange criterion below. Thus, the energies for both sets of coordinates were for adiabatic Drude particles. The exchange criteria are given in Equation 7, where E_a(X_a) represents the energy of the coordinates from replica b evaluated using the potential function from replica a; Δ_i = E_i(X_i) − E_j(X_i); Δ_j = E_i(X_j) − E_j(X_j), and β_i = 1/k_BT_i.

$$P_{\text{i}\leftrightarrow \text{j}}=\{\begin{array}{ll}1\hfill & ({\beta }_{\text{i}}{\mathrm{\Delta }}_{\text{i}}-{\beta }_{\text{j}}{\mathrm{\Delta }}_{\text{j}})\le 0\hfill \\ e^{({\beta }_{\text{i}}{\mathrm{\Delta }}_{\text{i}}-{\beta }_{\text{j}}{\mathrm{\Delta }}_{\text{j}})}\hfill & ({\beta }_{\text{i}}{\mathrm{\Delta }}_{\text{i}}-{\beta }_{\text{j}}{\mathrm{\Delta }}_{\text{j}})>0\hfill \end{array}$$ (7)

The modified CHARMM code was used to perform replica exchange simulations that coupled polarizable and non-polarizable simulations for liquid water and liquid cyclohexane. The simulation protocols were the same as those described above, with replica exchange typically attempted every 100 steps. Velocities were exchanged together with coordinates and scaled by the factor (T_new/T_old)^1/2, where T_new and T_old are respectively the temperatures after and before exchange.⁵⁵

Results and Discussion

1. Additive Force Field Optimization

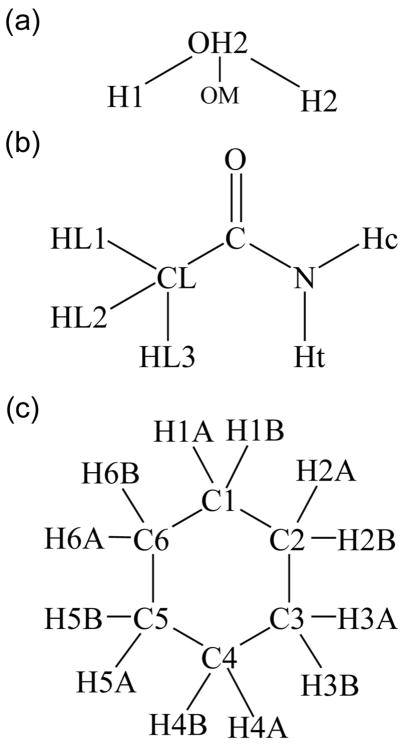
As our reference polarizable potential, we have used the CHARMM Drude force field.^{37–39,52,56–68} The development of this force field ultimately targets its application to biomolecular simulation,² and it has been implemented within the programs CHARMM³⁶ and NAMD.²⁰ Our work is implemented in CHARMM, where benchmark simulations show that the polarizable force field is ~5 times more costly than a comparable additive model. During development of this force field, a number of small molecules have been explicitly parameterized, and we have used the CHARMM Drude models of water;³⁷ acetamide⁶¹ (ACEM), and cyclohexane³⁹ (CHEX) (Figure 1).

Figure 1.

Atom naming used in this work for (a) water (b) acetamide and (c) cyclohexane.

1.1 Water

Water represents a natural starting point in any force field development project due to its ubiquity in nature, role in influencing biomolecular conformation and interactions^69–75 and the large body of existing work on the development/evaluation of water models.^76–80 Furthermore, in this work, optimization of a water model must be the first step because calculations employing the optimized water model are required to optimize parameters for ACEM and CHEX. Our reference model, the SWM4-NDP water model,³⁷ is a four-site water model with three sites located at the nuclear positions and the fourth located on the line bisecting the H-O-H angle (Figure 1). The geometry of the three atomic sites (i.e. hydrogen and oxygen nuclei) is the same as that of the TIP3P water model.⁵³ In addition to these sites, there is also a “Drude” particle. In the CHARMM Drude polarizable force field, these additional particles are added to each heavy atom, with their charge determined by a polarizability parameter assigned to that atom. For water, this means that a single Drude particle is included, attached to the O atom. Our objective was to identify, using the relative entropy framework described above, an additive water model giving the best possible reproduction of the configuration distribution obtained using the SWM4-NDP model. We have therefore adopted a 4-site model in which charges are located on both the O atom and the virtual site. To generate the initial non-polarizable water model, all parameters from the SWM4-NDP model were transferred directly to a non-polarizable analogue, termed SWM4A-INI (initial 4-site additive water model) in which the polarizability was removed from the O atom, with all charges maintained. In producing our final additive model, only the point charges were optimized: all internal and van der Waals parameters were maintained at the values obtained from the SWM4-NDP model (shown in Tables S1–S5). In principle, variation of any force field parameter could play a role in improving the fit of the additive model, but the results are expected to be weakly dependent on parameters other than charges. Optimizing additional parameters from noisy data is also likely to be challenging. Due to symmetry and overall charge neutrality, the task of fitting the 4-site water is reduced to optimization of only two parameters, thus lowering potential degeneracy in the fit. The final additive model obtained from relative entropy minimization was termed SWM4A-OPT (optimized 4-site additive water model). The final charges obtained from the relative entropy optimization are shown in Table 1.

Table 1.

Atomic charges used in the force fields described in the text. Atom naming is as shown in Figure 1.

	CHARMM Drude Model	Reference CHARMM Additive Model	Optimized Additive Model
Water
	SWM4-NDP	TIP3P	SWM4A-OPT
OH2	0.00000	−0.83400	−0.58430
OM	−1.11466	N/A	−0.48830
H1/H2	0.55733	0.41700	0.53630
Acetamide
	CHARMM Drude	CGenFF	ADD-OPT
CL	−0.21000	−0.27000	−0.20840
C	0.74900	0.55000	0.72210
N	−0.68700	−0.62000	−0.66910
Hc	0.34600	0.32000	0.33890
Ht	0.28900	0.30000	0.28870
O	−0.00100	−0.55000	−0.69450
HL1/HL2/HL3	0.04000	0.09000	0.07410
LPA	−0.37600	N/A	N/A
LPB	−0.23000	N/A	N/A
Cyclohexane
	CHARMM Drude	CHARMM aliphatic	ADD-OPT
C	−0.08000	−0.18000	−0.06954
H	0.04000	0.09000	0.03477

In Figure 2, we show the progress of the charge optimization. Using the gradient-based optimization discussed in Methods, the charges converge within five steps, accompanied by a significant decrease in the relative entropy. The relative entropies shown, along with the gradients used in the optimization, were calculated using Equation 6. As noted, this expression gives only an approximation of the true S_rel values obtained from Equation 5. To test whether the approximation was valid in this case, we also performed a 2-dimensional scan in q_O and q_LP, evaluating the relative entropy via both Equations 5 and 6 at every point. The numerical values of S_rel obtained with the two methods differed, but followed the same trends: both predicted the same minimum, and the overall correlation coefficient across 100 data points was 0.992. As a further test of the minimization approach based on Equation 6, we used Equation 3 to calculate the gradients at the final point of our optimization, confirming that it does represent a minimum. At this point, we also tested how much improvement might be expected from an optimization of the Lennard-Jones parameters on oxygen. However, while the initial charge optimization results in the relative entropy dropping from ~6000 to ~80, further optimization of the Lennard-Jones parameters results in a decrease to only ~66. Therefore, the improvement accessible by optimizing parameters other than charges was relatively small, and optimization of these parameters was subsequently neglected.

Figure 2.

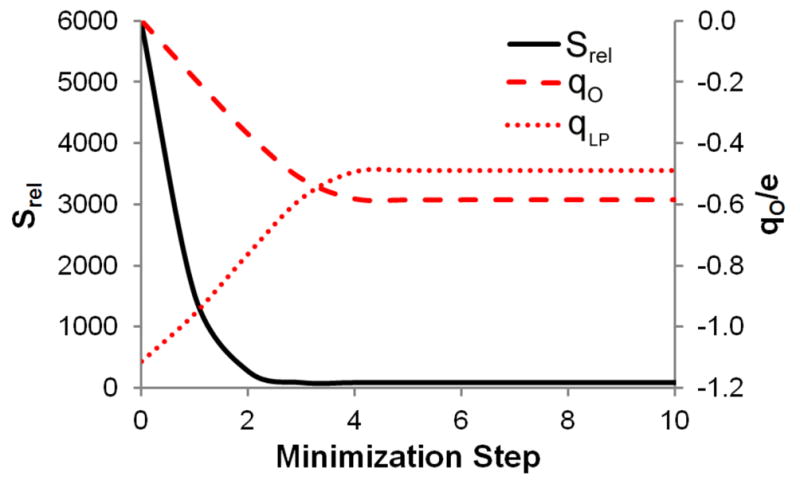
Water model optimization. Variation of the charge on the oxygen and dummy atoms, q_O and q_LP, respectively, during Newton-Raphson optimization of the relative entropy, S_rel. The starting point for the minimization is the SWM4A-INI model, and the end point is the SWM4A-OPT model.

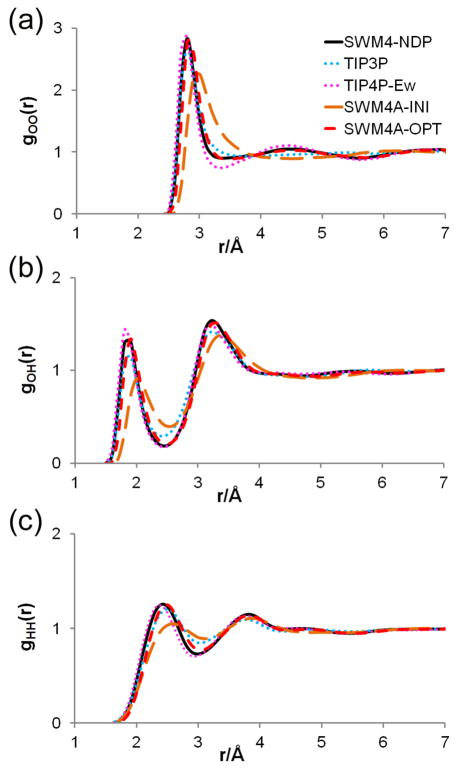
The final model, SWM4A-OPT, produced from this charge optimization yields physical properties in good agreement with those calculated using the reference polarizable force field. Figure 3 shows radial distribution functions calculated with various force field models. The SWM4A-INI model clearly provides a poor approximation to the SWM4-NDP model, while the SWM4A-OPT model is in very good agreement with its polarizable counterpart. It is also worth noting that the SWM4A-OPT model yields results closer to the polarizable model than does the widely-used TIP3P model, showing that optimizing charges via the relative entropy methods produces a model giving better agreement with the polarizable model than can be expected from an arbitrarily-chosen optimized water model. As a water model, SWM4A-OPT represents an improvement over TIP3P, which is known to be too weakly structured; the structural properties of the polarizable SWM4-NDP model are much closer to those inferred from experimental neutron scattering data.⁸¹ Comparing to a well-optimized 4-site additive model, TIP4P-Ew⁵⁴, also shows the SWM4A-OPT model to give results closer to those obtained with the polarizable force field. TIP4P-Ew is, in fact, more structured than the SWM4A-OPT model, and the pair distribution agrees better with the experimental data. The weaker structure of SWM4A-OPT is simply a consequence of the original polarizable SWM4-NDP model being too weakly structured.

Figure 3.

Radial distribution functions for simulations of liquid water with various force fields (see text for details).

Additional physical properties calculated with the various force fields are shown in Table 2. The SWM4A-OPT model performs poorly in reproducing gas-phase properties, but this is not unexpected. The gas phase is a very different dielectric environment from the aqueous liquid phase, and non-polarizable models simply cannot be expected to reproduce properties in both environments; this, of course, is the motivation for the development of explicitly polarizable models. Similarly the properties of the water dimers, which can be considered to be closer to the gas phase than the liquid phase, are not particularly well reproduced. In the liquid phase, however, the SWM4A-OPT model performs very well. Molecular volume and enthalpy of vaporization are explicitly considered as targets in the optimization of the CHARMM Drude polarizable force field, with the target being to reproduce the experimental values to within 2%,² and an error of magnitude up to 5% considered acceptable. Before comparing the values calculated for the heat of vaporization, however, we need to apply a correction due to the fact that the additive model of water, optimized for the condensed phase, effectively remains polarized even in the gas phase. That is, the energy associated with a condensed phase charge distribution is higher than the energy of the true gas phase charge distribution (an alternative viewpoint is that in the reverse process of condensation, the additive model incurs no energetic penalty for adopting the condensed phase charge distribution). Therefore, the heat of vaporization for an additive model is in general overestimated. An approximate correction for this effect, applicable to polarizable dipolar molecules, was derived by Berendsen et al.,⁸² in which the polarization energy E_pol is given by:

$$E_{\text{pol}}=\frac{1}{8\pi {\epsilon }_0\alpha }{N}_A{({\mu }_l-{\mu }_g)}^2$$ (8)

Table 2.

Water properties calculated using the polarizable and initial and optimized non-polarizable models. Experimental results and results obtained using the TIP3P water model are included for comparison.

	Experiment	SWM4-NDPg	TIP3Pg	TIP4P-Ewl	SWM4A-INI	SWM4A-OPT
Monomer
Dipole (D)	1.85c	1.85	2.35	2.32	1.85	2.46
Polarizability α(Å3)	1.44d	0.98	N/A	N/A	N/A	N/A
Dimer
Udimer (kcal/mol)	−5.40e	−5.15	−6.50	−7.42	−4.57	−7.43
dOO (Å)	2.98e	2.83	2.74	2.72	2.88	2.80
θA (deg)	58e	71	20	51	67	23
μdimer (D)	2.64e	2.06	3.87	3.00	1.82	4.14
Bulk Liquid
ΔHvap (kcal/mol)a	10.51f	10.50	10.44	11.72	7.38 ± 0.01	12.13 ± 0.01
ΔHvap (kcal/mol)b	n/a	n/a	9.19	10.58	7.38 ± 0.01	10.27 ± 0.01
Vm (Å3)	29.94g	29.91	29.90	30.0	33.90 ± 0.01	30.77 ± 0.02
<μ>(D)	2.95h	2.46	2.35	2.32	1.85	2.46
D (10−5 cm2/s)	2.3i	2.33 ± 0.02	5.1	2.4 ± 0.06	9.58 ± 0.02	2.81 ± 0.03
E	78j	79 ± 3	92	63.9 ± 0.9	25.8 ± 0.2	76.1 ± 1.4
ΔGhyd (kcal/mol)a	−4.4 – −6.3k	−5.9 ± 0.1	−6.1	−7.09 ± 0.05	−4.08 ± 0.06	−7.56 ± 0.07
ΔGhyd (kcal/mol)b	n/a	n/a	−4.85	−5.95 ± 0.05	−4.08 ± 0.06	−5.70 ± 0.07

^aExcluding polarization correction;

^bincluding polarization correction (Equation 8) with the experimental isotropic gas phase polarizability³⁷ of 1.44 ų.

^cFrom Ref. ⁹¹.

^dFrom Ref ³⁷.

^eFrom Ref. ⁹².

^fFrom Ref. ⁹³

^gFrom Ref. ³⁷.

^hFrom Ref. ⁶⁸.

ⁱFrom Ref. ⁹⁴.

^jFrom Ref. ⁹⁵.

^kFrom Refs. ^96–99.

^lFrom Ref. ⁵⁴.

In this expression, N_A is the Avogadro constant, α is the polarizability, ε₀ the permittivity of free space and μ_l and μ_g the molecular dipole moments in the liquid and gas respectively. The same correction with opposite sign is applied to the solvation free energies, ΔG_hyd (there is no difference in the gas phase entropy of the polarized and non-polarized molecules). To compute E_pol for the SWM4A-OPT model, we used μ_g = 2.46 D, the average dipole moment of SWM4A-OPT in the condensed phase, μ_l and = 1.85 D, the experimental gas phase dipole moment, and the experimental gas phase polarizability α = 1.44 ų. After including this correction, the SWM4A-OPT enthalpy of vaporization differs from the SWM4-NDP value by −2.1%, with the molecular volume differing by 2.8%. Since neither of these properties were explicitly considered in the parameter optimization, this agreement is remarkable. Perhaps even more remarkable is the agreement in the dielectric constant and the diffusion coefficient. Both properties are well reproduced by the SWM4A-OPT model – at a level comparable to the TIP4P-Ew model, and much better than by the TIP3P model, whose large diffusion coefficient is a well-known shortcoming. After including the gas phase polarization correction, the hydration free energy obtained using the SWM4A-OPT model is also in reasonable agreement with that obtained from the SWM4-NDP model.

Note that while both the enthalpy of vaporization and the hydration free energy of SWM4A-OPT are in reasonable agreement with the original polarizable model once polarization corrections have been applied, the inability of the model to capture both gas phase and solution environments is an inherent problem of additive force fields; polarizable force fields should be the most generally applicable to capturing different environments, particularly where interfacial effects are relevant. In choosing to focus on the liquid phase, we are making the necessary compromise entailed by coarse-graining, but with the aim of doing so in an optimal way.

1.2 Acetamide

As an analogue of the protein backbone, the acetamide functionality is an important component of any biomolecular force field targeting the simulation of proteins. It also represents a more demanding test for any parameter optimization scheme. A 4-site model of water contains only two independent charge parameters. Acetamide, however, possesses seven distinct atom types, resulting in six charge parameters for optimization (the seventh is determined by the requirement that the total charge on the molecule must be zero). An additional complication arises because the reference polarizable force field includes charge sites not located at the nuclear positions. In several force fields, additional point charges are included to better represent the anisotropy in the electron density around certain atoms,^83–86 and the CHARMM Drude polarizable force field includes additional point charges on H bond accepting atoms to represent “lone pairs”. In acetamide, this results in two additional point charges attached to the amide O atom, located at the points where one would intuitively expect to find lone pairs. To generate the initial non-polarizable water model, all parameters from the Drude model were transferred directly to a non-polarizable analogue, termed ADD-INI (initial additive model); the polarizabilities were removed from the heavy atoms, and the lone-pairs were also removed, with their charges transferred to their parent O atom. All other charges were maintained at the values used in the polarizable force field. Charge parameters for the additive model were optimized to give a model termed ADD-OPT (optimized additive model); as in the case of water, all internal and van der Waals parameters were maintained at the values obtained from the Drude model⁶¹ (Tables S1–S5). The reference simulations in this case were of a single acetamide molecule in a box of water; the acetamide parameters were optimized with the water molecules represented by the SWM4A-OPT model.

The charge optimization for acetamide proved to be less straightforward than that for water. Initial parameter optimization via the gradient-based method gave results in good agreement with the experimental properties, but we observed that initiating the optimization from different starting points gave different sets of charges with different relative entropies (Figure 4A). These are classic symptoms of a multiple minimum optimization problem, which we sought to address by a Monte Carlo simulated annealing (MCSA)^87,88 approach in which the Gaussian approximation to the relative entropy was used as the energy. With this method we were indeed able to obtain solutions with similar relative entropies starting from different initial charges, but the final charges were still rather different, indicating that there are multiple degenerate solutions, or multiple sets of charges that all perform equally well when measured by relative entropy. From an algorithmic point of view this is unsatisfactory: we would like to obtain a well-defined set of charges in an unambiguous and reproducible fashion. We discuss the degeneracy further below, but in order to obtain a well-defined solution to this problem we have imposed restraints on the charges by optimizing the target function S′_rel, defined by:

$$S_{\text{rel}}^{\prime }=S_{\text{rel}}+\frac{1}{2}{k}_q{\sum }_i{(q_i-q_i^{\text{ref}})}^2$$ (9)

Figure 4.

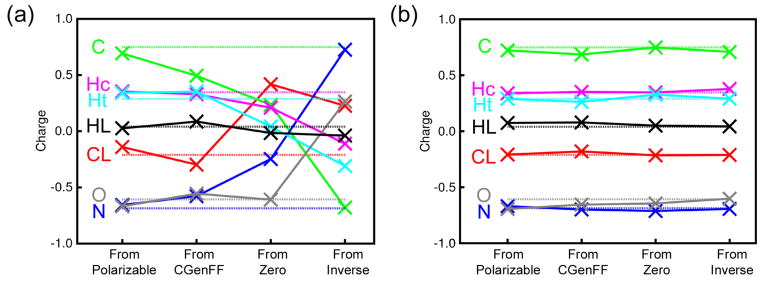
Graphs showing the final acetamide charges obtained from relative entropy optimizations starting from four different sets of initial acetamide charges. (a) shows charges resulting from calculations in which the relative entropy is optimized using minimization without restraints, and (b) shows charges resulting from calculations in which the relative entropy is optimized using a Monte Carlo simulated annealing algorithm including a restraint potential as shown in Equation 9 with a force constant k_q = 200. In both panels, the charges used in the polarizable model are indicated by the dotted lines.

Here, we use a harmonic restraint with force constant k_q to keep each charge q_i close to some reference value q_i^ref. The natural choice for the reference charges is the set of initial charges derived from the polarizable model. With both the MCSA and charge restraints implemented, we were able to remove the dependency of the final charges on the initial starting configurations, as well as the degeneracy of the solution, without increasing the final, minimized value of the relative entropy (Figure 4B). Since the relative entropy is proportional to the negative log-likelihood of the target distribution given the model,²⁸ this is equivalent to a Gaussian prior for the charges. Clearly, one parameter which remains to be defined is the value of the restraint constant k_q: we chose the value of k_q to be the largest that could be used in the Monte Carlo simulated annealing optimization without increasing the final value of the relative entropy. For acetamide, this value was found to be ~200 entropy units (Figure S2). The final charges obtained for ACEM using this approach are shown in Table 1, with properties calculated using the ADD-OPT model shown in Figure 5 and Table 3.

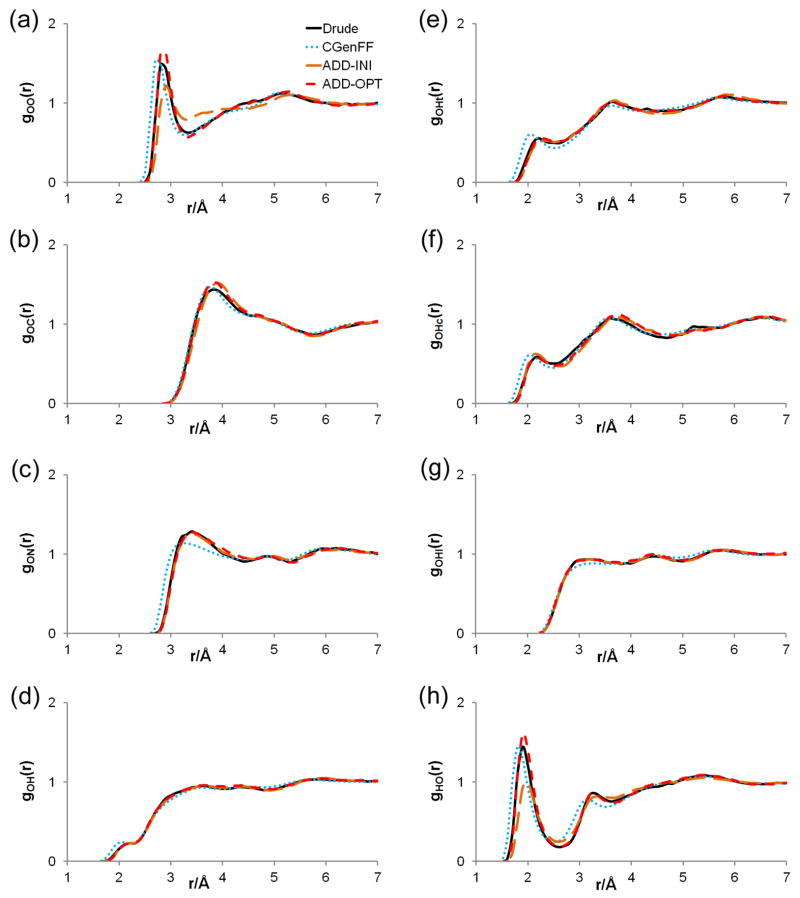
Figure 5.

Radial distribution functions obtained from simulations of acetamide in water, calculated using various force fields. Radial distribution functions are described as g_ab(r), where a represents the water atom type, and b represents the acetamide atom type.

Table 3.

Acetamide properties calculated using polarizable and initial and optimized additive models. Results obtained with the additive CGenFF model are included for comparison. Properties in aqueous solution are calculated using the SWM4-NDP water model with polarizable acetamide; the TIP3P water model with CGenFF acetamide, and the SWM4A-OPT water model with ADD-INI and ADD-OPT acetamide.

	Experiment	Drude	CGenFF	ADD-INI	ADD-OPT
Monomer
Dipole (D)	4.0c	3.7	4.2	4.1	4.9
Dimer
Udimer (kcal/mol)	−14.35d	−13.26	−10.98	−11.25	−13.17
dOHc (Å)	1.83d	1.95	1.83	2.03	1.99
Aqueous Solution
<μ> (D)		4.6	4.2	4.1	4.9
ΔGhyd (kcal/mol)a	−9.71e	−9.18	−8.79	−7.45 ± 0.12	−11.34 ± 0.11
ΔGhyd (kcal/mol)b	n/a	n/a	−8.49	−7.26 ± 0.12	−9.58 ± 0.11

^aExcluding polarization correction;

^bincluding polarization correction (in the absence of an experimental gas phase polarizability, we use the quantum mechanically calculated⁶¹ trace of the molecular polarizability tensor, 5.9 ų).

^cFrom Ref. ⁶¹.

^dFrom Ref. ¹⁰⁰.

^eFrom Ref. ¹⁰¹.

Acetamide-water RDFs are shown in Figure 5, and reveal good agreement between the polarizable and ADD-OPT models. Results from the ADD-INI model are noticeably worse than those with the ADD-OPT model, indicating that optimization of S_rel results in a significant improvement in the structural properties of the model, in spite of the relatively small changes in the magnitudes of the charges seen in Table 1. For reference, the RDFs obtained with the generic CGenFF force field are also shown in Figure 5, showing that the match with the polarizable force field is non-trivial. Other properties calculated with the ADD-OPT model (Table 3) also show acceptable agreement with those from the polarizable force field.

As alluded to above, in the absence of restraints on the charges, there is a certain amount of degeneracy in the optimal additive force fields for molecules with a large number of atom types such as acetamide. We characterize this degeneracy by noting that the negative log-likelihood of the target distribution T given the model charges {q} is²⁸ −lnL(T |{q}) = nS_rel where n is the number of configurations used to compute S_rel. Adopting a Bayesian approach and assuming a uniform prior distribution of charges, we can determine the posterior distribution of charges given the target ensemble, since then L({q}|T) ∝ L(T |{q}). We sample the posterior distribution by running Metropolis Monte Carlo simulations in which nS_rel plays the role of the energy. We have characterized this distribution by computing the standard deviation of the charges from unrestrained Monte Carlo runs, obtaining values of 0.04–0.09e, depending on the atom type, although the variations will clearly be correlated (Table S6). For comparison, we have also computed the standard deviation of the amide charges in non-prolyl amino acids in the Amber ff03 force field,¹⁰ in which each residue is permitted to have a different set of charges on the backbone atoms, and also the standard deviation of the amide charges on the Alanine residue in a range of current force fields. Interestingly, we find that the standard deviation of charges across the different residues in the ff03 force field, as well as the standard deviation across force fields, is very similar to the variation in different solutions of our acetamide model. These results suggest that such variations could be at least partly explained by the degeneracy of solutions when fitting point charge force fields, which may support the use of a uniform charge scheme for all backbone atoms.^8,89,90

In the development of the additive CHARMM force fields, charges are typically determined by considering heterodimeric interactions between the solute of interest and water molecules. The logic behind this is that it is a computationally cheap method that, to a first approximation, explicitly incorporates the effect of the environment into the parameterization,⁶⁶ ensuring that a correct balance between solute-water and water-water interactions is achieved.¹¹ This approach was originally adopted in the development of the CHARMM22 protein force field,¹¹ where the target energies and geometries were calculated ab initio at the HF/6–31G(d) level of theory, with interaction energies for neutral compounds multiplied by a factor of 1.16 and interaction distances offset by −0.2 Å. These latter corrections are introduced to account for deficiencies in the relatively low level of theory used (such as the omission of the dispersion interaction) and to yield target data “appropriate for the condensed phase”.¹³ Effectively, this method results in an overestimation of the gas phase interaction energies. This is turn facilitates development of useful non-polarizable force fields by ensuring that resulting gas phase dipole moments are overestimated,¹¹ implicitly accounting for the polarization induced by the aqueous environment.

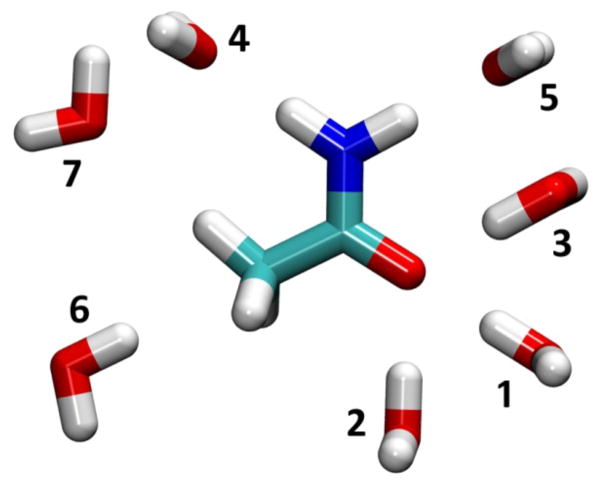
Since interactions with water molecules form such an important part of the charge parameter optimization scheme within the CHARMM force fields, it is interesting to check how well the models obtained from the relative entropy optimization can reproduce heterodimeric interactions with water. For ACEM we have considered the seven water interaction geometries shown in Figure 6. The corresponding minimum interaction energies and distances are shown in Table 4. Given that the ADD-OPT model has been optimized based on liquid phase data, one might expect it to provide a poor representation of gas phase dimers. This indeed seems to be the case, with interaction energies too favorable by more than 1 kcal/mol on average. Interestingly, however, in terms of the interaction energies, both the average difference and RMSD obtained with the ADD-OPT model are within 0.05 kcal/mol of the equivalent values obtained with the CGenFF force field, which was explicitly optimized based on the reproduction of interactions with water molecules.¹³ This very good agreement suggests that the use of target quantum mechanical data which overestimates the interaction energies approximately accounts for the difference between the gas phase and aqueous environments by requiring the individual molecules to be overpolarized in the gas phase.

Figure 6.

Orientations of interactions between acetamide and water. Analysis was performed on monohydrates; for the purpose of visualization all water interaction orientations are displayed simultaneously in this figure.

Table 4.

Acetamide-water heterodimer interaction energies and distances. E_int is the energy at the minimum interaction distance for a given water orientation in kcal/mol; R_min is the minimum interaction distance for a given water orientation in Å. Water orientations are as shown in Figure 6. Calculations use the SWM4-NDP water model with polarizable acetamide; the TIP3P water model with CGenFF acetamide, and the SWM4A-OPT water model with ADD-INI and ADD-OPT acetamide.

	Drude		CGenFF		ADD-INI		ADD-OPT
	Eint	Rmin	Eint	Rmin	Eint	Rmin	Eint	Rmin
Conf1	−5.33	1.93	−6.99	1.75	−6.45	1.91	−8.13	1.87
Conf2	−6.06	1.88	−6.68	1.77	−5.78	1.94	−7.39	1.89
Conf3	−7.14	1.82	−7.19	1.74	−6.27	1.90	−7.98	1.86
Conf4	−4.08	2.09	−6.55	1.89	−5.52	2.05	−5.76	2.05
Conf5	−3.95	2.04	−5.22	1.88	−5.10	2.01	−4.68	2.02
Conf6	−0.22	2.65	−0.68	2.60	−0.75	2.50	0.06	2.87
Conf7	−1.26	2.79	−2.74	2.66	−1.68	2.76	−1.96	2.67
Ave Diff			−1.14	−0.13	−0.50	−0.02	−1.11	0.00
RMSD			1.38	0.14	0.92	0.07	1.43	0.10

1.3 Cyclohexane

Water and acetamide are both important in the simulation of biomolecules, but neither molecule possesses any significant conformational flexibility. One of the objectives of this work is to use the newly-optimized additive force fields to enhance sampling in the polarizable simulations by connecting the different models via a replica exchange (“resolution exchange”) scheme. In order to test this approach, it is useful to study a system with high barriers, in which there is an equilibrium that is reached only relatively slowly. A natural example of such an equilibrium is the conformational exchange within the cyclohexane molecule (Figure 1). Cyclohexane can occupy several distinct conformations, most notably the “chair”, “boat” and “twist-boat” conformations. The chair conformation is the lowest in energy, separated from the twist-boat minimum, which is 6 kcal/mol higher in energy, by a barrier of around 12 kcal/mol. As such, a typical simulation at room temperature would be expected to interconvert between chair and non-chair conformations only infrequently. Replica exchange simulations could be a route to enhancing sampling of this conformational interconversion. An alternative example could be a polypeptide conformational equilibrium; however at the time of writing, the protein parameters for the CHARMM Drude model were not yet available.

With only two distinct atom types, cyclohexane has only one free charge parameter that can be optimized and is well within the capabilities of the gradient-based optimization scheme described in Methods. The optimized charge parameters are shown in Table 1, and with these in place, a good reproduction of thermodynamic (Table S7) and structural (Figure S3) properties is obtained. Since we are interested in assessing the ability of the new force field to accelerate sampling of conformational interconversions we have also calculated the gas phase potential energy surface connecting the chair, boat and twist-boat conformations (Figure S4). We find that the ADD-OPT model provides a very good reproduction of the potential energy surface calculated with the polarizable model.

2. Replica Exchange Simulations

One of the principal motivations for optimizing non-polarizable analogues of polarizable models is that, by achieving the best possible overlap between the configurational distributions obtained with the two models, we maximize the probability of being able to perform replica exchange between the two models. Because the non-polarizable model is more computationally efficient, performing this replica exchange should allow us to enhance sampling in the polarizable force field. As a first test of this approach, we considered liquid water. The criterion for determining whether exchange will occur comes from considering the energy difference distributions shown in Equation 7. Initial tests showed that there was little overlap in these distributions obtained from simulations performed with the polarizable and nonpolarizable force fields, so that it was not possible to exchange directly between them (Figure S5). However, we also note that there was much better overlap between SWM4-NDP and SWM4A-OPT model than between SWM4-NDP and either of the TIP3P of TIP4P-Ew models (Figure S5), demonstrating that a specifically matched force field will facilitate resolution exchange.

By employing intermediate systems in which the polarizability was gradually reduced, we were able to couple the SWM4-NDP and SWM4A-OPT force fields. Specifically, results from a scheme having five distinct replicas are shown in Figure 7. In this simulation, replica 1 used the full SWM4-NDP water model, and replica 5 used the SWM4A-OPT model. The remaining replicas were then constructed as linear weighted averages of these two models: the polarizabilities of replicas 2, 3 and 4 were respectively 75%, 50% and 25% of that of SWM4-NDP. For each set of polarizabilities, the fixed charges were re-optimized against the fully polarizable target model, using the relative entropy optimization described above By using such a scheme, we were able to obtain overlap between the energy difference distributions (Equation 7) obtained from adjacent replicas (Figure 7a), and hence exchange between them. Figure 7b shows that this scheme allows the simulations to move through all of the available replicas.

Figure 7.

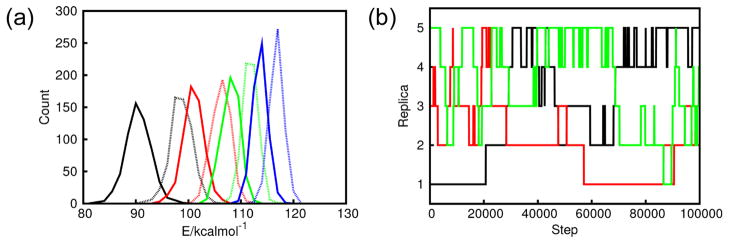
Hamiltonian REMD simulations of liquid water performed using five distinct replicas. Replica 1 corresponds to the SWM4-NDP model and replica 5 to the SWM4A-OPT model. Intermediate replicas employ weighted averages of these two models: replica 2 is 75% SWM4-NDP; replica 3 is 50% SWM4-NDP, and replica 4 is 25% SWM4-NDP. (a) Overlap of energy difference distributions from adjacent replicas, calculated as described for Equation 7. Matching colors are used to compare overlap between distributions from adjacent replicas; for each pair of replicas, solid lines represent Δ_i, with dashed lines representing Δ_i+1. (b) Tracking the progress of three of the replicas over the course of a 100 ps MD simulation.

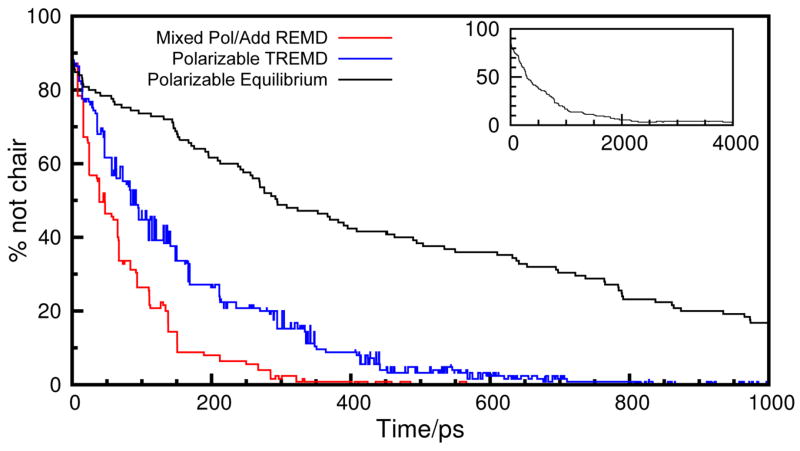
The results from the replica exchange simulations of water are important in their own right: they show that replica exchange between polarizable and non-polarizable force fields is possible, and since water is the largest component of any biomolecular simulation, this is a key requirement. However, since this water model is a simple molecule with no internal degrees of freedom, it is not possible to assess the impact of resolution exchange on sampling efficiency. To test this more thoroughly, we therefore also considered liquid cyclohexane. Cyclohexane can adopt a number of distinct conformations. As noted above, the global energy minimum is the chair conformation, with the distorted boat, or “twist-boat” minimum approximately 6 kcal/mol higher in energy and these two conformations separated by an energetic barrier of around 12 kcal/mol. Individual twist-boat conformations are separated by boat transition states at an energy of around 7.5 kcal/mol. Taking these energy differences into account, one would expect that, at equilibrium, more than 99% of all cyclohexane molecules would be in the chair conformation. To test the sampling efficiency of various simulation protocols we constructed a box of 125 cyclohexane molecules in which every molecule was in the boat conformation. After an initial 100 ps equilibration, during which 15 molecules converted to the chair conformation, we adopted three different protocols for sampling the cyclohexane system. The first was a standard equilibrium simulation using the polarizable force field at 300 K; the second was a temperature REMD simulation that included eight replicas, all simulated using the CHARMM Drude polarizable force field, at temperatures of 300, 310, 325, 340, 355, 370, 385 and 400 K; and the third was a combined resolution and temperature replica exchange simulation. This also had 8 replicas: the first used the polarizable force field at 300 K; the second used the ADD-OPT model at 310 K, and the remainder all used the ADD-OPT model at temperatures increasing in 15 K increments up to 400 K. Unlike the water simulations, no intermediate states were required to couple between the polarizable and non-polarizable force fields – direct exchanges occurred between the two; however, inclusion of more intermediates to bridge the polarizable and non-polarizable simulations should pose no problem, as we have demonstrated for water. To test the sampling achieved with the different schemes, we then measured how long it took for the cyclohexane box to reach a near-equilibrium point where fewer than 1% of molecules were not in a chair conformation. The results of these simulations are shown in Figure 8, and clearly indicate a modest enhancement of sampling by the use of the resolution exchange scheme. With the resolution exchange, equilibrium is achieved with around 400 ps of simulation in the low temperature, polarizable replica. With the polarizable temperature replica exchange scheme, it takes more than 800 ps of simulation with the low temperature replica before equilibrium is reached. We are achieving an approximately 2-fold speed-up by using the resolution exchange scheme. One of the main reasons for this is that the simulation timestep we can use is determined by the fastest motions present in the system. In the Drude polarizable force field, the fastest motions are those of the Drude particles, which dictate that a timestep of 1 fs is required. In the non-polarizable force field, a timestep of 2 fs can be used. This means that, in the combined resolution/temperature exchange scheme, in the time that the polarizable replica takes to complete 100 ps of simulation, each other replica has completed 200 ps of simulation. In comparison, in the polarizable temperature replica exchange simulations, each replica will have completed only 100 ps. The degree of acceleration is expected to be larger for polarizable models with a higher computational cost.

Figure 8.

Convergence toward equilibrium for a box of 125 cyclohexane molecules using several simulation protocols. Simulations were started from a configuration in which 88% of molecules were in the twist-boat conformation, which is ~6 kcal/mol higher in energy than the global energy minimum chair conformation. At each simulation step, we record the percentage of molecules that are not in the chair conformation: at equilibrium, one would expect <1% of molecules to be in anything other than a chair conformation. The inset panel shows the progress of the equilibrium simulation with the polarizable force field.

Concluding Remarks

We have developed a well-defined protocol for determining point charges in additive force fields, which has two advantages over standard methods for deriving such charges: (i) it provides an algorithmic method for including average polarization effects by explicitly matching the distribution in the condensed phase obtained with a polarizable force field, rather than by ad hoc procedures, and (ii) it permits the additive force field to be used to enhance sampling in the polarizable force field via multiscale simulations. The procedure is of course not limited to the CHARMM polarizable force field and could be generalized to target either more computationally demanding force fields, or even Born-Oppenheimer molecular dynamics simulations.²⁵

Abbreviations

RESP

Restrained Electrostatic Potential fitting