Bayesian Modeling for Large Spatial Datasets

1 Spatial process models for point-referenced data

With the emergence of highly efficient Geographical Information Systems (GIS) databases and associated software, the modeling and analysis of spatially referenced data sets have received much attention over the last decade. Spatially-referenced data sets and their analysis using GIS arise in diverse areas of scientific and engineering investigations including geological and environmental sciences (Webster and Oliver, 2001), ecological systems (Scheiner and Gurevich, 2001), digital terrain cartography (Jones, 1997), computer experiments (Santner et al., 2003), public health (Cromley and McLafferty, 2002) and so on. A wonderful compilation of current research trends in spatial statistics is presented by Diggle et al. (2010).

Two base units of measure and mapping are commonly encountered: locations that are areas or regions with well-defined neighbors (such as pixels in a lattice, counties in a map, etc.), whence they are called areally referenced data; or locations that are points with coordinates (latitude-longitude, Easting-Northing etc.), in which case they are called point referenced or geostatistical. Statistical theory and methods play a crucial role in the modeling and analysis of such data by developing spatial process models, also known as stochastic process or random function models, that help in predicting and estimating physical phenomena. This proposal deals with the latter: modeling of point-referenced data. The last two decades has seen significant developments in such modeling; see, for example, the books by Cressie (1993), Chilés and Delfiner (1999), Møller (2003), Schabenberger and Gotway (2004), and Banerjee, Carlin and Gelfand (2004) for a variety of methods and applications.

Spatial process modeling envisions a random surface y(s) representing some variable (e.g., temperature, precipitation) that conceptually exists in continuum over the domain s ∈ D but has been observed only at a finite set of locations and must be interpolated (or predicted) for other arbitrary locations. By interpolating at arbitrarily fine resolutions, these models estimate the random surface accounting for correlation between temperature and precipitation levels at locations closer to each other and produce a response surface for the dependent variable. Such interpolation from statistical models is often referred to as “kriging” and the response surfaces are called kriged surfaces.

2 Model-based kriging

The most common geostatistical setting assumes a response or dependent variable y(s) observed at a generic location s along with a p × 1 vector of spatially referenced predictors x(s). Model-based geostatistical data analysis often proceeds from spatial regression models such as,

$$y(\mathit{s})=\mathit{x}(\mathit{s})\prime \mathit{\beta }+w(\mathit{s})+ϵ(\mathit{s}).$$ (1)

The residual from the regression is partitioned into a spatial process, w(s), capturing spatial association, and an independent process, $ϵ(\mathit{s})\stackrel{\text{iid}}{~}N(0,{\tau }^2),$, also known as the nugget effect, modeling measurement error or micro-scale variation. Micro-scale variation is often modeled as a stationary spatial disturbance at a scale lesser than the minimum inter-site distance. Often modelers separate the micro-scale variation by inserting an η(s) into (1), whence η(s) captures micro-scale variation and ϵ(s) captures pure measurement error (see, e.g. Cressie, 1993, p.112).

With observations y = (y(s₁),…, y(s_n))′ from n locations, the data are treated as a partial realization of a spatial process modeled through w(s). The most popular specification w(s) ~ GP(0, C(·,·)) is a zero-centered Gaussian Process determined by a valid covariance function C(s_i, s_j) defined for pairs of sites s_i and s_j Typically the modeler specifies C(s₁, s₂) = σ²ρ(s₁, s₂; θ) where ρ(·;θ) is a correlation function and θ includes parameters quantifying the rate of correlation decay and the smoothness of realizations. The data likelihood is given by y ~ N(Xβ, Σ _y), where X is an n × p matrix of regressors whose i-th row is x(s_i)′, Σ_y = σ²R(θ) + τ²I_N and R(θ) is an n × n spatial correlation matrix with ρ (s_i, s_j; θ) as its (i, j)-th element. Likelihood-based inference proceeds by computing estimates from maximum likelihood (ML), restricted maximum likelihood (REML), or Generalized Estimating Equation (GEE) approaches and investigating their consistency and asymptotic properties. The books by Cressie (1993) and Schabenberger and Gotway (2004) provide excellent expositions of such methods.

We conclude with a few comments on stationarity of spatial processes. Stationarity is a common assumption when modeling spatial processes. A random field w(s) is called weakly stationary (or stationary) if it has finite second moments, its mean function is constant and its covariance function C(s₁, s₂) = C(h), where h = s₁ – s₂. This implies that the relationship between the values of the process at two locations only depends on the vector distance between these two locations. An isotropic process results when C(s₁, s₂) = C(‖h‖), where ‖h‖ is the distance between s₁ and s₂. Stationarity is a desirable property for spatial processes, but is usually a rather unrealistic assumptions for large spatial domains. There is an extensive literature on nonstationary models, e.g., Sampson and Guttorp, (1992), Nychka et al., (2002), Higdon et al., (1999), and Fuentes, (2002). Fuentes, (2005) introduces a nonparametric test for stationary.

3 Hierarchical models for spatial data

A different approach that has recently gaining popularity among spatial modelers follows the Bayesian inferential paradigm (Robert, 2001; Gelman et al., 2004; Carlin and Louis, 2008; Banerjee et al., 2004). Here one constructs hierarchical (or multi-level) schemes by assigning probability distributions to parameters a priori and inference is based upon the distribution of the parameters conditional upon the data a posteriori. By modeling both the observed data and any unknown regressor or covariate effects as random variables, the hierarchical Bayesian approach to statistical analysis provides a cohesive framework for combining complex data models and external knowledge or expert opinion.

Bayesian hierarchical models (e.g. Gelman et al. 2004; Banerjee et al., 2004) are widely recognized as versatile inferential tools for capturing the rich dependence structures underlying spatial data and offering full inference on spatial processes. For an n × 1 vector of observed outcomes, y = (y(s₁),y(s₂),…,y(s_n))′ with a first stage conditionally independent Gaussian specification and associated priors, we construct a Bayesian hierarchical model

$$p(\mathit{\theta },\mathit{\beta },\mathit{w}|\mathit{y})\propto p(\mathit{\theta })\times N(\mathit{\beta }|{\mathit{\mu }}_{\beta },{\mathrm{\Sigma }}_{\beta })\times N(\mathit{w}|\mathbf{0},\mathit{C}({\mathit{\theta }}_1))\times \underset{i=1}{\overset{n}{\mathbf{\Pi }}}N(y({\mathit{s}}_i)|\mathit{x}({\mathit{s}}_i)\prime \mathit{\beta }+w({\mathit{s}}_i),{\tau }^2),$$ (2)

where θ = {θ₁, τ²};. The parameter τ² is called the nugget and captures unstructured noise that may arise in the form of measurement error or micro-scale variability. Customarily, either a flat or a multivariate Gaussian prior is assigned to β. Zhang (2004) demonstrated, rather remarkably, that the process parameters θ₁ were not consistently (in the classical sense) estimable for a rather general class of covariance functions. This implies that the priors’ inferential impact is not obliterated with increasing sample size; hence, weakly informative priors will be needed to identify the process parameters.

Spatial data analysis seeks to estimate the regression coefficients β, the unknown process parameters θ = {θ₁, τ²}, which convey the nature of spatial associations and micro-scale variability, and the spatial effects w which elicit lurking spatial patterns in the residual. Estimating (2) customarily proceeds using Markov chain Monte Carlo (MCMC) methods (e.g. Robert and Casella, 2004). With Gaussian likelihoods, often we integrate out the spatial effects w. This replaces the likelihood and the prior for w by N (y | Xβ, C(θ₁) + τ²I_n). In any case, estimation involves n × n matrix decompositions of cubic order in the number of locations, which become exorbitant for large n. Evidently, multivariate and spatial-temporal settings aggravate the situation.

As modern data technologies acquire and exploit massive amounts of data, statisticians analyzing spatially referenced datasets confront settings where the number of geo-referenced locations is very large. This makes hierarchical modeling infeasible or impractical. The situation is further exacerbated in multivariate settings with several spatially dependent response variables, where the matrix dimensions increase by a factor of the number of spatially dependent variables being modeled. It is also aggravated when data is collected at frequent time points and spatiotemporal process models are used.

4 Hierarchical models for large spatial datasets

Modelling large spatial datasets have received much attention in the recent past. Vecchia (1988) proposed approximating the likelihood with a product of appropriate conditional distributions to obtain maximum-likelihood estimates. Stein et al. (2004) adapt this effectively for restricted maximum likelihood estimation. Another possibility is to approximate the likelihood using spectral representations of the spatial process (Fuentes, 2007). These likelihood approximations yield a joint distribution, but not a process that facilitate spatial interpolation. Another concern is the adequacy of the resultant likelihood approximation. Expertise in tailoring and tuning of a suitable spectral density estimate or a sequence of conditional distributions is required and does not easily adapt to multivariate processes.

Also, the spectral density approaches seem best suited to stationary covariance functions. Yet another approach considers compactly supported correlation functions (Furrer et al., 2006; Kaufman et al., 2008; Du et al., 2009) that yeild sparse correlation structures. More efficient sparse solvers can then be employed for kriging and variance estimation, but the tapered structures may limit modeling flexibility. Also, full likelihood-based inference still requires determinant computations that may be problematic. Another approach either replaces the process (random field) model by a Markov random field (Cressie, 1993) or else approximates the random field model by a Markov random field (Rue and Tjelmeland, 2002; Rue and Held 2006). This approach is best suited for points on a regular grid. With irregular locations, realignment to a grid or a torus is required, done by an algorithm, possibly introducing unquantifiable errors in precision.

In recent work Rue, Martino and Chopin (2009) propose a promising INLA (Integrated Nested Laplace Approximation) algorithm as an alternative to MCMC that utilizes the sparser matrix structures to deliver fast and accurate posterior approximations. This uses conditional independence to achieve sparse spatial precision matrices that considerably accelerate computations, but relaxing this assumption would significantly detract from the computational benefits of the INLA and the process needs to be approximated by a Gaussian Markov Random Field (GMRF) (Rue and Held, 2006). Furthermore, the method involves a mode-finding exercise for hyper-parameters that may be problematic when the number of hyperparameters is more than 10. Briefly, its effectiveness is unclear for our multivariate genetic models with different structured random effects and unknown covariance matrices as hyperparameters.

Adapting the above approaches to more complex hierarchical spatial models involving multivariate processes (e.g. Wackernagel, 2006; Gelfand et al, 2004), spatiotemporal processes and spatially varying regressions (Gelfand et al., 2003) and nonstationary covariance structures (Paciorek and Schervish, 2006) is potentially problematic.

A versatile approach pursues models especially geared towards the handling of large spatial datasets. Typically, these emerge from representations of the spatial process in lower-dimensional subspaces and easily generalize to multivariate and/or spatiotemporal processes. These are often referred to as low-rank or reduced-rank spatial models and have been explored in different contexts (Wikle and Cressie, 1999; Lin et al., 2000; Higdon 2002; Kamman and Wand, 2003; Ver Hoef et al. 2004; Paciorek, 2007; Stein, 2007, 2008; Cressie and Johannesson, 2008; Banerjee et al., 2008, 2010; Crainiceaniu et al., 2008; Latmer et al. 2009). Many of these methods are variants of the so-called “subset of regressors” methods used in Gaussian process regressions for large data sets in machine learning (e.g. Rasmussen and Williams, 2006). The idea here is to assume that the spatial information available from the entire set of observed locations can be summarized in terms of a smaller, but representative, sets of locations, or “knots”. When retaining richness and flexibility of hierarchical models is of primary interest, knot-based low rank models seem to be the preferred option.

Sun et al. (2011) offer a very detailed review of statistical methods for massive spatial datasets. Here, we consider one low-rank approach, referred to as Gaussian predictive process models, in some detail. Detailed descriptions of hierarchical Gaussian predictive process models are given in Banerjee et al. (2008), (2010) and Finley et al. (2009). Here, we offer a brief review.

Predictive process models use a fixed set of “knots” ${𝒮}^{*}=({\mathit{s}}_1^{*},\dots ,{\mathit{s}}_{n^{*}}^{*})$ with n* << n, which may, but need not, be a subset of 𝒮. An optimal projection of the process w(s) at a generic location s, based upon its realization over 𝒮*, is given by the “kriging equation” w˜(s) = E{w(s) |w*}, where ${\mathit{w}}^{*}=(w({\mathit{s}}_1^{*}),w({\mathit{s}}_2^{*}),\dots ,w({\mathit{s}}_n^{*}))\prime .$. We refer to w˜(s) as the predictive process derived from the parent process w(s). Banerjee et al. (2008) discuss several theoretical properties of the predictive process, including multivariate and spatiotemporal extensions.

For a zero-centered parent Gaussian process, say w(s), with covariance function C (s₁, s₂; θ₁), the predictive process is w˜(s) = E{w(s) | w*} = c(s, θ₁)′C*(θ₁)⁻¹w*, where c(s; θ₁)′ is the 1 × n vector whose j-th element is $C(\mathit{s},{\mathit{s}}_j^{*};{\mathit{\theta }}_1)$ and C*(θ₁) is the n* × n* covariance matrix with elements $C({\mathit{s}}_i^{*},{\mathit{s}}_j^{*};{\mathit{\theta }}_1).$. Since w* is multivariate normal with zero mean and n* × n* dispersion matrix C*(θ₁), w˜(s) is itself a nonstationary Gaussian process arising from a spatially adaptive linear transformation of the parent process over the set of knots. Replacing w(s) with w˜(s) in (2), yields its predictive process counterpart

$$p(\mathit{\theta },\mathit{\beta },{\mathit{w}}^{*}|\mathit{y})\propto p(\mathit{\theta })\times N(\mathit{\beta }|{\mathit{\mu }}_{\beta },{\mathrm{\Sigma }}_{\beta })\times N({\mathit{w}}^{*}|\mathbf{0},{\mathit{C}}^{*}({\mathit{\theta }}_1))\times \underset{i=1}{\overset{n}{\mathbf{\Pi }}}N(y({\mathit{s}}_i)|\mathit{x}({\mathit{s}}_i)\prime \mathit{\beta }+\tilde{w}({\mathit{s}}_i),{\tau }^2).$$ (3)

Computational gains are achieved since matrix computations now involve the n* × n* matrix C*(θ₁), where n* is chosen to be much smaller than n. Unlike several other knot-based approaches, the predictive process does not introduce additional parameters nor does it involve projecting data onto a grid. Thus, it avoids identifiability issues or spurious loss of uncertainty (see, e.g., Banerjee et al. 2008). Indeed, predictive process models are attractive since they are directly induced by the parent process without requiring choices of basis functions or kernels or alignment algorithms for the locations.

Being a low-rank process, the partial realizations of the predictive process produce a low-rank (degenerate) likelihood. Being smoother than the parent process, it tends to have lower variance which, in turn, inflates the residual variability often manifested as an overestimation of τ². In fact, the following inequality holds for any fixed 𝒮* and for any spatial process w(s):

$$\text{var}\{w(\mathit{s})\}=\text{var}\{\mathrm{E}[w(\mathit{s})|{\mathit{w}}^{*}]\}+\mathrm{E}\{\text{var}[w(\mathit{s})|{\mathit{w}}^{*}]\}\ge \text{var}\{\mathrm{E}[w(\mathit{s})|{\mathit{w}}^{*}]\}=\text{var}\{\tilde{w}(\mathit{s})\}.$$ (4)

If the process is Gaussian then standard multivariate normal calculations yields the following closed form for this difference for site s,

$${\delta }^2(\mathit{s})=\mathrm{E}\{\text{var}[w(\mathit{s})|{\mathit{w}}^{*}]\}=C(\mathit{s},\mathit{s};{\mathit{\theta }}_1)-\mathit{c}(\mathit{s},{\mathit{\theta }}_1)\prime {\mathit{C}}^{*}{({\mathit{\theta }}_1)}^{-1}\mathit{c}(\mathit{s},{\mathit{\theta }}_1).$$ (5)

One simple remedy for the bias in the predictive process model (Finley et al., 2009; Banerjee et al. 2010) is to use the process ${\tilde{w}}_{ϵ}(\mathit{s})=\tilde{w}(\mathit{s})+\widetilde{ϵ}(\mathit{s}),$, where $\widetilde{ϵ}(\mathit{s})\stackrel{\mathit{\text{iid}}}{~}N(0,{\delta }^2(\mathit{s}))$ and ϵ˜(s) is independent of w˜(s). We call this the modified predictive process. Now, the variance of w˜_ϵ(s) equals that of the parent process w(s) and the remedy is computationally effective – adding an independent space-varying nugget does not incur substantial computational expenses. However, the remedy is less effective in capturing small-scale spatial variation as it does not account for the spatial dependence in the residual process.

Hierarchical spatial models, including the predictive process models, are customarily estimated using Markov chain Monte Carlo (MCMC) methods (e.g. Robert and Casella, 2004). Further technical details on MCMC algorithms for hierarchical spatial models can be found in Banerjee et al. (2004) and particularly for predictive process models in Banerjee et al. (2008) and Finley et al. (2009).

5 Illustration

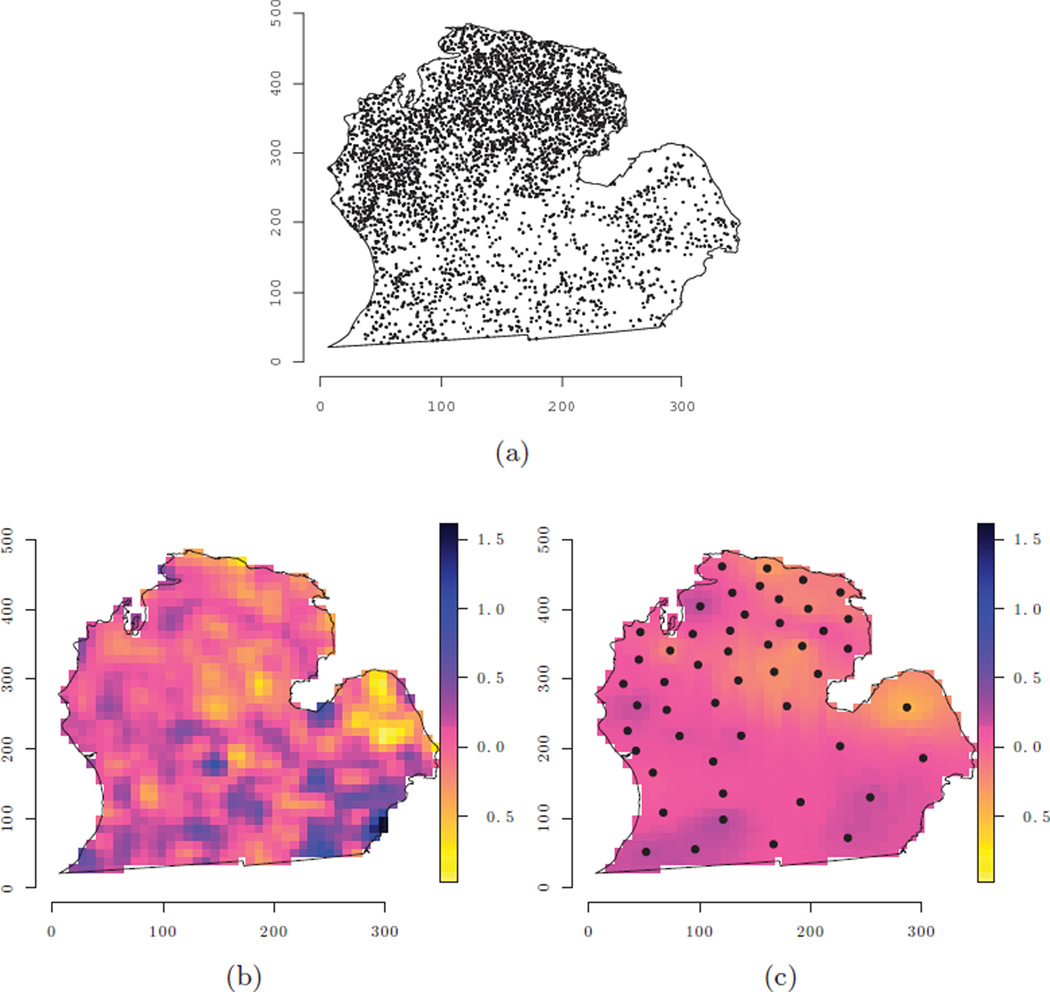
We present a brief illustration of hierarchical predictive process model using a forest biomass dataset recently analyzed by Guhaniyogi et al. (2011). Spatial modeling of forest biomass and other variables related to measurements of current carbon stocks and flux have recently attracted much attention for quantifying the current and future ecological and economic viability of forest landscapes. Interest often lies in detecting how biomass changes across the landscape (as a continuous surface) and how homogeneous it is across the region. In the United States, the Forest Inventory and Analysis (FIA) program of the USDA Forest Service collects the data needed to support these assessments. Here, we present a subset of the analysis in Guhaniyogi et al. (2011). Our outcome variable is log metric tons of forest biomass per hectare. A July, 2003 mosaic of Landsat TM imagery, was used to calculate tasseled cap components of brightness (TC1), greenness (TC2), and wetness (TC3) to serve as explanatory variables. Figure 1(a) illustrates the georeferenced forest inventory data consisting of 6,538 forested FIA plots measured between 1999 and 2006 across the lower peninsula of Michigan.

Figure 1.

Forest biomass dataset and associated estimates for the 50 knot predictive process models: (a) location of forest invetory plots; (b) interpolated surface of the non-spatial model residuals; and (c) predictive process model estimated spatial random effects with knot locations.

Candidate models included a simple non-spatial regression and a predictive process model. Knot locations were chosen by applying the k-means clustering algorithm to the observed locations. We assumed that the parent covariance function is exponential: C(s₁, s₂; θ₁) = σ² exp(−ϕ‖s₁ – s₂‖); therefore, θ₁ = {σ², ϕ}. Based on results from an initial variogram analysis of the non-spatial model’s residuals, the priors for τ² and σ² for the predictive process models followed IG(2 0.5) distributions (mean equaling 0.5), while the prior for the spatial decay parameter ϕ followed a U(0.006 3), which corresponds to support from 1–500 km. This is a broad range of support, given the maximum distance between any two plots is 460 km. For all models the regression coefficients each received a flat prior, i.e. ${\mathrm{\Sigma }}_{\beta }^{-1}=\mathit{O}$ a matrix of zeroes.

Posterior inference was based on three chains of 25, 000 iterations (the first 5,000 iterations were discarded as burn-in). The samplers were coded in C++ and Fortran and leveraged Intel’s Math Kernel Library threaded BLAS and LAPACK routines for matrix computations. All analyses were conducted on a Linux workstation using two Intel Nehalem quad-Xeon processors. Table 1 offers parameter estimates for the predictive process candidate models. Over the range of knot intensities, both the non-spatial and predictive process models produce comparable estimates of the regression coefficients – several of which explain a significant amount of variability in log biomass. The predictive process model seems to estimate a larger nugget, τ², and a smaller partial sill, σ². Figure 1(b) is an interpolated surface of the non-spatial model residuals. We would expect the fitted spatial random effects of the candidate models to look somewhat similar to this residual surface, which is evident from Figure 1(c).

Table 1.

Nonspaial and predictive process candidate models’ parameter posterior credible intervals (50 (2.5 97.5)) and model fit criterion for the forest biomass dataset. Run time is in hours for a single chain of 25,000 interations on a single non-hyperthreaded processor.

	Non-spatial		Predictive process
		50	100	200
β0	10.98 (10.95, 11.01)	10.99 (10.71, 11.26)	11.00 (10.68, 11.30)	11.01 (10.97, 11.06)
βTC1	0.07 (0.02, 0.12)	0.03 (−0.02, 0.09)	0.03 (−0.02, 0.09)	0.05 (0.00, 0.11)
βTC2	−0.03 (−0.09, 0.02)	−0.00 (−0.07, 0.06)	−0.01 (−0.07, 0.06)	−0.02 (−0.08, 0.04)
βTC3	0.45 (0.41, 0.49)	0.43 (0.39, 0.48)	0.43 (0.39, 0.48)	0.44 (0.39, 0.48)
σ2	–	0.17 (0.09, 0.33)	0.14 (0.08, 0.24)	0.28 (0.16, 0.48)
τ2	1.01 (0.97, 1.04)	0.93 (0.84, 0.98)	0.96 (0.87, 1.00)	0.74 (0.53, 0.86)
ϕ		0.016 (0.009, 0.051)	0.011 (0.007, 0.062)	0.016 (0.011, 0.023)
G	5935	5804	5759	5640
P	5939	5842	5830	5810
D	11874	11646	11590	11450
Run time (hours)	–	9.44	19.31	37.08

6 Summary and discussion

We have offered a brief overview of certain recent developments in the problem of fitting desired Bayesian hierarchical spatial modeling specifications to large datasets. To do so, we propose simply replacing the parent spatial process specification by its induced predictive process specification. One need not digress from the modelling objectives to think about choices of basis functions or kernels or alignment algorithms for the locations. The resulting class of models essentially falls under the setup of hierarchical generalized linear mixed models.

As in existing low-rank kriging approaches, knot selection is required and some sensitivity to the number of knots is expected (see Finley, Sang, Banerjee and Gelfand, 2009, for details). With a fairly even distribution of data locations, one possibility is to select knots on a uniform grid overlaid on the domain. Alternatively, selection can be achieved through a formal design-based approach based upon minimization of a spatially averaged predictive variance criterion (e.g., Diggle and Lophaven, 2006). However, in general the locations are highly irregular, generating substantial areas of sparse observations where we wish to avoid placing knots, since they would be “wasted” and possibly lead to inflated predictive process variances and slower convergence. Here, more practical space-covering designs (e.g., Royle and Nychka, 1998) can yield a representative collection of knots that better cover the domain. Another alternative is to apply popular clustering algorithms such as k-means or more robust median-based partitioning around medoids algorithms (e.g., Kaufman and Rousseeuw, 1990). User-friendly implementations of these algorithms are available in R packages such as fields and cluster and have been used in spline-based low-rank kriging models (Ruppert et al. 2003). While for most applications a reasonable grid of knots should lead to robust inference, with fewer knots the separation between them increases and estimating random fields with fine-scale spatial dependence become difficult. Indeed, learning about fine scale spatial dependence is always a challenge (see, e.g., Cressie, 1993, p.114).

It is also not uncommon to find space-time datasets with a very large number of distinct time points, possibly with different time points observed at different locations (e.g., real estate transactions). Predictive processes can be used to improve the applicability of a class of dynamic space-time models proposed by Gelfand et al. (2005) by alleviating a computational bottleneck without sacrificing model flexibility and with minimal loss of information. Recently, Finley et al. (2011) focused on the common setting where space is considered continuous but time is taken to be discrete. Here, data is viewed as arising from a time series of spatial processes. Some examples of data that fit this description include: US Environmental Protection Agency’s Air Quality System which reports pollutants’ mean, minimum, and maximum at 8 and 24 hour intervals; climate model outputs of weather variables generated on hourly or daily intervals, and; remotely sensed landuse/landcover change recorded at annual or decadal time steps.

Finally, we conclude with some remarks on computing. With multiple processors, substantial gains in computing efficiency can be realized through parallel processing of matrix operations. We intend continued migration of our lower-level C++ code to the existing spBayes (http://cran.r-project.org; Finley et. al. 2007) package in the R environment to facilitate accessibility to predictive process models.