Electrostatic Effects on Proton-Coupled Electron Transfer in Oxomanganese Complexes Inspired by the Oxygen-Evolving Complex of Photosystem II

Abstract

The influence of electrostatic interactions on the free energy of proton-coupled-electron-transfer (PCET) in biomimetic oxomanganese complexes inspired by the oxygen-evolving complex (OEC) of photosystem II (PSII), are investigated. The reported study introduces an enhanced Multi-Conformer Continuum Electrostatics (MCCE) model, parameterized at the density functional theory (DFT) level with a classical valence model for the oxomanganese core. The calculated pK_as and oxidation midpoint potentials (E_ms) match experimental values for eight complexes indicating that purely electrostatic contributions account for most of the observed couplings between deprotonation and oxidation state transitions. We focus on pK_as of terminal water ligands in [Mn(II/III)(H₂O)₆]^2+/3+ (1), [Mn(III)(P)(H₂O)₂]^3- (2, P = 5,10,15,20- tetrakis (2,6-dichloro-3-sulfonatophenyl) porphyrinato), [Mn(IV,IV)₂(μ-O)₂(terpy)₂(H₂O)₂]⁴⁺ (3, terpy = 2,2’:6’,2”-terpyridine) and [Mn₃(IV,IV,IV)(μ-O)₄(phen)₄(H₂O)₂]⁴⁺ (4, phen = 1,10-phenanthroline) and the pK_as of μ-oxo bridges and Mn E_ms in [Mn₂(μ-O)₂(bpy)₄]²⁺ (5, bpy = 2,2’-bipyridyl), [Mn₂(μ-O)₂(salpn)₂] (6, salpn= N,N′-bis(salicylidene)-1,3-propanediamine), [Mn₂(μ-O)₂(3,5-di(Cl)-salpn)₂] (7) and [Mn₂(μ-O)₂(3,5-di(NO₂)-salpn)₂] (8) which are most relevant to PCET mechanisms. The analysis of complexes 6-8 highlights the strong coupling between electron and proton transfers, with any Mn oxidation lowering the pK_a of an oxo bridge by 10.5±0.9 pH units. The model also accounts for changes in the E_ms due to ligand substituents, such as those in complexes 6-8, due to the electron withdrawing Cl (7) and NO₂ (8). The reported study provides the foundation for analysis of electrostatic effects in other oxomanganese complexes and metalloenzymes, where PCET plays a fundamental role in redox-leveling mechanisms.

INTRODUCTION

Multi-nuclear metal ion clusters play important catalytic roles in a wide range of chemical and biological systems.^1-3 These clusters usually contain both protonatable and redox-active sites. They can carry out electroneutral oxidation state transitions by coupling electron and proton transfer reactions. The underlying redox leveling mechanism can greatly diminish the free energy needed to make reactive high valence redox states that are essential for multi-electron reactions.^4-14 In general, understanding the electrochemistry of these metal centers and the coupling mechanism that tunes the cluster chemistry is challenging. The thermodynamics of oxidation and deprotonation steps can be regulated by the core geometry and protonation states as well as by the charge distribution and protonation states of the ligands. Here, we focus on the analysis of the E_ms and pK_as of a group of oxomanganese complexes inspired by the Mn₄O₅Ca cluster of the oxygen-evolving complex (OEC) of photosystem II (PSII).¹⁵

Many open questions about the OEC are common to both isolated and protein-embedded redoxactive metal ion clusters.^16-18 These include: what is the nature of oxidation state transitions, and how does it change as a function of pH; which acid-base/redox transitions are due to the inorganic core, and which ones are due to the influence of the ligands or the surroundings; what are the pK_as of oxo-bridges and terminal waters relative to each other, and how do they contribute to the deprotonation mechanism as a cluster is oxidized? A full, rigorous description of these processes is challenging and requires high level quantum mechanical treatments due to the importance of spin transitions, charge delocalization, Jahn-Teller distortion effects, and charge transfer interactions between Mn and the μ-O bridges. While several density functional theory (DFT) studies of oxomanganese clusters have been reported,^19-38 higher-level analyses including more accurate descriptions of the multi-reference character of the electronic structures have yet to be reported.^39,40 Such treatments, however, remain rather difficult and time-consuming, even for single clusters with welldefined redox and protonation states. Multi-metal center clusters, like the OEC, also present the challenge of evaluating a large number of possible states. For example, the OEC has four high-valent Mn centers in oxidation states III or IV, and five oxide bridges that can be either μ-hydroxo or μ-oxo, defining a total of 512 possible microstates. Furthermore, thousands of possible states need to be considered when including the possibility that some of the four terminal waters can also deprotonate. While the complexes analyzed in this paper are simpler than the OEC of PSII, they also involve a fairly large number of microstates. As an example, the di-oxo-manganese complex 5 (Fig. 1) has sixteen possible formal charge configurations, including two states for each Mn (+3 or +4 charge), two for each oxide bridge (O^-2 or OH⁻) and one for the ligands. In addition, for clusters with terminal waters (1-4), each possible deprotonation of a terminal water into hydroxo doubles the number of configurations. Therefore, the analysis of these complex clusters requires methods that can efficiently account for all oxidation and protonation states, to understand how different configurations contribute to the redox properties that regulate the thermodynamics of the reaction.

Figure 1.

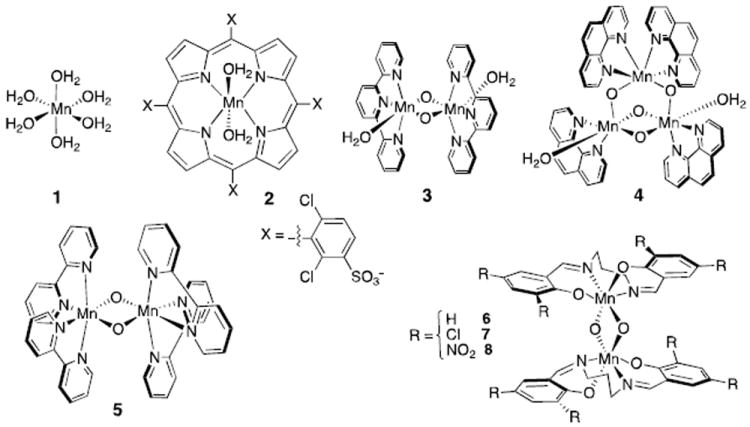
Model Mn complexes. (1) hexa-aqua Mn(II and III); (2) Mn(III) [5,10,15,20- tetrakis (2,6-dichloro-3-sulfonatophenyl) porphyrinato]^3-; (3) [Mn(IV,IV)₂(μ-O)₂(terpy)₂(H₂O)₂]⁴⁺ (terpy = 2,2’:6’,2”-terpyridine); (4) [Mn(IV,IV,IV)₃(μ-O)₄(phen)₄(H₂O)₂]⁴⁺ (phen = 1,10-phenanthroline); (5) [Mn(III,III, III,IV, and IV,IV)₂(μ-O)₂(bpy)₄]²⁺ (bpy = 2,2’-bipyridyl); (6-8) [Mn(III,IV and IV,IV)₂(μ-O)₂(3,5-di(R)-salpn)₂], R=H (6), Cl (7) or NO₂ (8) (salpn = N,N′-bis(salicylidene)-1,3-propanediamine). Each porphyrinato and salpn unit has a charge of -2. The other ligands are neutral.

Continuum electrostatic (CE) analysis, coupled to Monte Carlo methods as in the program Multi-Conformer Continuum Electrostatics (MCCE),⁴¹ makes it possible to sample a large number of microstates, to determine how redox midpoint potentials (E_ms) and pK_as are modified by the surrounding environment.^41-43 However, these methods have been generally used to analyze nonbonded interactions. Here, we apply an enhanced MCCE method, parameterized at the DFT level, with a novel classical valence model for the oxomanganse core to study the electrostatic influence of ligands on proton-coupled oxidation reactions in oxomanganese complexes. The goal is to model the changes in interactions on redox and protonation changes between metals and the atoms in their first coordination sphere with a properly parameterized continuum electrostatic analysis. We focus on the pK_as of terminal waters in four complexes (hexa-aqua Mn, Mn porphyrin, di-Mn terpy complex, and tri-Mn phen complex) in oxidation states II–IV (Figure 1: 1-4). In addition, we study the pK_as of the bridging oxygens in four di-oxo–manganese model complexes (Figure 1: 5-8) and how the Mn redox state and ligand substitutions affect them. The reported analysis provides fundamental insight into how changes in electrostatic interactions due to oxidation and protonation of the metal core or surrounding ligands affect the redox and protonation thermodynamics of oxomanganese cores inspired by the OEC of PSII.

METHODS

Enhanced MCCE electrostatic model

Complexes 1-8 are modeled by treating each Mn ion, oxide bridge, terminal water, and each asymmetric unit of the organic ligand in a cluster as an individual, gedanken fragment with integer charges. These fragments interact with each other only via electrostatic and Lennard-Jones potentials. Microstates of the complexes are defined according to the oxidation states of the Mn fragments and the protonation states of the oxide bridges and/or terminal water ligands. The Boltzmann distribution of microstates is obtained by Monte Carlo (MC) sampling, as a function of the solution electron and proton chemical potential (i.e., E_h and pH), using the MCCE program.⁴¹ These systems are small enough that all microstates could be enumerated to carry out full statistical mechanical calculations. However, the MC sampling is used in preparation for incorporating this valence analysis of metal clusters into proteins. The free energy of a microstate x, ΔG^x, is computed relative to the free energy of the separated fragments in a reference dielectric medium (e.g., water or acetonitrile (ACN)). ΔG^x is:^41,44

$$\mathrm{\Delta }{G}^x=\sum _{i=1}^M{\delta }_{x,i}\{[2.3m_i{k}_{b}T(\mathit{pH}-p{K}_{a,\mathit{sol},i})+n_{i}F(E_h-E_{m,\mathit{sol},i})]+\mathrm{\Delta \Delta }{G}_{\mathit{solv},i}+\sum _{j=i+1}^M{\delta }_{x,j}[\mathrm{\Delta }{G}_{\mathit{ij}}]\}$$ (1)

where M is the total number of states of all fragments; δ_x,i is 1 if fragment-state i is present in the microstate and 0 otherwise; m_i is 1 (0) for the protonated (deprotonated) form of a bridging or terminal oxygen i; k_bT is 25.37 meV at 298 K, the default temperature; n_i is the number of electrons gained, using the most oxidized state as the reference state (1 for Mn(III) and 0 for Mn(IV) here); and F is the Faraday constant. The pK_a,sol,i and E_m,sol,i is the reference pK_a and E_m for the primitive fragment, i, in the reference solvent dielectric medium. Thus, the first and second terms in Eq. 1 establish the reference free energy changes of the isolated fragment due to protonation at the solution pH and/or reduction at the solution E_h (relative to the normal hydrogen electrode (NHE)).⁴⁵ The last two terms establish the changes in energy as the fragments are assembled into the cluster. Continuum electrostatic (CE) interactions are computed with the Poisson-Boltzmann solver Delphi⁴⁶ given input atomic positions, radii and charges (see Supplemental Information S1). ΔΔG_solv is the loss of the CE solvation (reaction field) energy experienced by a fragment as it is moved from water or ACN into the cluster in that solvent. ΔG_ij is the pairwise electrostatic and Lennard-Jones interactions between fragments i and j present in the cluster microstate x. (Additional information about parameters required for the DelPhi CE analysis can be found in Supplemental Information S1 and S6.)

Structural Models

Where possible, initial coordinates of complexes 1-8 are defined according to available crystal structures from the Cambridge Crystallographic Data Center (CCDC). Crystallographic solvent molecules and counter ions are removed. Reference codes SAWYEU,⁴⁷ FIQFIU⁴⁸ and SOZMUP⁴⁹ are used for 3, 5, and 6, respectively. Structures are optimized at the DFT/B3LYP level of theory, using the LANL2DZ pseudopotential⁵⁰ for Mn and the 6-31G* basis set⁵¹ for all other atoms, as implemented in GAMESS⁵², JAGUAR⁵³ or Gaussian09.⁵⁴ In these initial structures, all terminal waters are neutral, bridging oxides deprotonated, and Mn ions are set to the oxidation states Mn(III) or Mn(IV), using broken symmetry wavefunctions⁵⁵ for di-Mn complexes, as reported in previous work.²² (See Supplemental Information S2 for further details.) The E_ms and pK_as derived using the Mn(III,IV) optimized geometries are used as the basis for the primary analysis. Values obtained with Mn(IV,IV) optimized structures are used to show how the outcome depends on the structure.

Atomic partial charges

In this model, formal, integer charges are used for each fragment and atomic positions are fixed. Mn atoms have a charge of +2, +3 or +4.

Each bridging oxygen has a formal charge of -2 in the deprotonated state. However, when protonated, a μ-hydroxo does not have the same charge distribution as a free OH⁻ due to interactions with the adjacent metal atoms. To account for this effect, atomic charges are adjusted to empirically reproduce the experimental pK_a shift of 8.7 pH units in the [Mn₂(bpy)₄(μ-O)(μ-OH)]^3+/4+ complex between the Mn(III,III) and Mn(III,IV) states.⁵⁶ Using the DFT optimized Mn(IV,IV) structure, this ΔpK_a is recovered with a charge of -1.7 on oxygen and +0.7 on hydrogen (See Supplemental Information S3). This charge distribution is used for all μ-hydroxo ligands regardless of solvent or microstate and is found to perform satisfactorily in all complexes.

Terminal waters have standard TIPS⁵⁷ partial charges, with a charge of -0.8 on the oxygen and +0.4 on each hydrogen. The terminal hydroxo has a net charge of -1 with charges of -1.2 on oxygen and +0.2 on hydrogen obtained by fitting the electrostatic potential of isolated OH⁻ in water in a DFT calculation (B3LYP/6-31G*) with the PCM solvation model for bulk water in Gaussian09.⁵⁴

A crucial element of the method is the use of quantum chemistry calculations to parameterize the atomic charge distribution of the organic ligands for subsequent classical electrostatic calculations. The atomic charges for all ligands except the terminal waters are fit to DFT-derived ElectroStatic Potentials (ESP), subject to the constraint that the constituent fragments have integer total charges, as defined by their formal oxidation/protonation numbers. Ligand partial charges and atomic positions are held fixed in the MC sampling of cluster redox or protonation state. The charges are reported in Table S6 for each cluster.

To assign ligand charges, two rounds of DFT calculations are performed with B3LYP/LANL2DZ, 6- 31G*.^51,58-61 First, ESP charges are obtained for the entire geometry-optimized cluster with all Mn in the Mn(IV) state. Then, ESP charges for an isolated ligand molecule with the appropriate net charge are determined with atom positions held fixed. The coordinated Mn is represented by a frozen fractional ESP charge, as determined in the entire complex, at the position found in the geometry- optimized full complex. The ligands parameterized are the porphyrin (2), terpy (3), phen (4), bpy (5), or salpn units (6-8). Each asymmetric ligand is given the same charge distribution; however, incorporating more than one ligand molecule in the fragment unit for charge determination does not change the outcome. The effect of charge transfer from the Mn into the ligand is included only implicitly through the distribution of ESP atomic charges within each fragment.

Reference values of E_m,sol and pK_a,sol

The reference values of midpoint potentials (E_ms) and pK_as for the gedanken constituent fragments in solution, E_m,sol and pK_a,sol, are obtained according to the thermodynamic cycles for Mn and OH-bridges shown in Figure 2 (panels A and C, respectively). E_m,sol and pK_a,sol are constants that allow the calculated values to be compared to the reference NHE and solution pH. They do not affect the slope of a line comparing the experimental and calculated values in a given solvent, only the intercept. The experimental values E_m^expt and pK_a^expt for one complex are used to derive the reference for all clusters. The E_m,sol and pK_a,sol are then used to calculate E_ms and pK_as in other clusters by computing the free energy of a microstate, according to Eq. (1).

Figure 2.

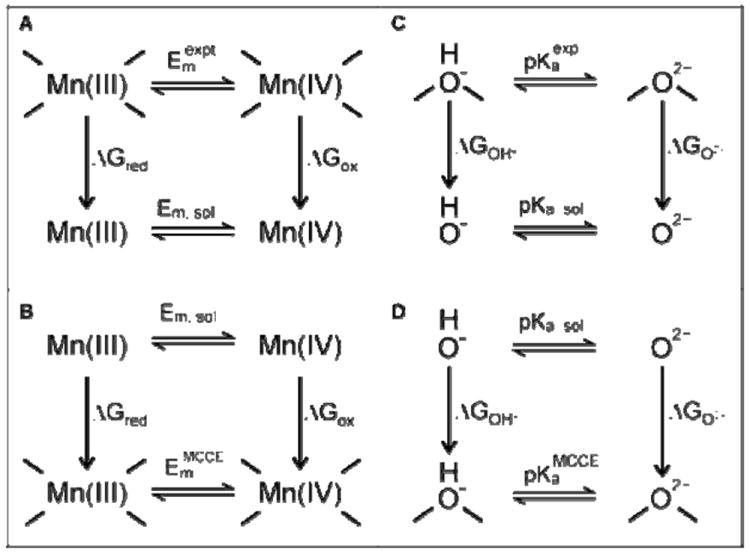
Thermodynamic cycles used to calculate the reference values of E_m,sol (A) and p_Ka,sol (C) for the constituent fragments Mn and hydroxo bridge, using the experimental values E_m^expt and pK_a^expt for one cluster. The free energy differences in the cluster and isolated in solution, ΔG_red, ΔG_ox, ΔG_OH- and ΔG_O2- for the gedanken fragments Mn(III), Mn(IV), OH⁻, and O^-2 are obtained by removing the interactions between the fragments as they are moved into solution. The derived E_m,sol and pK_a,sol are then used to calculate Mn E_ms (B) and bridging OH pK_as (D) in other clusters.

The well-studied mixed-valence bpy complex 5 is used as the reference for the E_m,sol in ACN. The measured reduction potential for [Mn(IV,IV)(μ-O)₂(bpy)₄]⁴⁺ of 1.51 V vs. NHE in ACN⁶² is used as E_m,expt (See Figure 2A), giving a derived E_m,ACN of 1.35 V for reduction of the isolated gedanken Mn. This E_m,ACN is used to calculate the midpoint potential of all the di-Mn complexes, independent of the initial redox state or μ-oxo protonation pattern.

The reference pK_a,H2O of a terminal water is taken to be 15.7 (see Supplemental Information S4). However, the pK_as of terminal water ligands in the Mn complexes are shifted due to electrostatic interactions within the cluster. The pK_a,sol for the loss of the proton from a hydroxo that represents the μ-oxo bridge is coupled to the calculation of the μ-OH^- charges. (see Supplemental Information S3).

While water is the preferred solvent for benchmark values of clusters in proteins,⁴⁵ most reported values for μ-OH deprotonation in di-Mn clusters are measured in ACN. Here, one experimental value in each solvent is used to set the reference pK_a,sol. For water, the second deprotonation in the Mn(III,IV) state of complex 5³⁷ is used to determine a pK_a,H2O of 29.8 using the Mn(III,IV) optimized structure. The pK_a,ACN is calculated to be 45.0 using a measured value for the first deprotonation of 6 in the Mn(IV,IV) state as a reference.⁶³ The derived pK_a,sol for deprotonation of OH⁻ in water and ACN differs by 15.2 units.

RESULTS AND DISCUSSION

Benchmark calculations of the pK_as of terminal water ligands

Table 1 reports the pK_a for deprotonation of terminal waters in complexes 1-4 (Table 1), as obtained with the enhanced MCCE methodology described in the previous section. The comparison of calculated and experimental values shows a root mean square deviation (RMSD) of 1.06 pH units (Supplemental Information S4) showing pK_a shifts of up to 15 pH units when a water moves from bulk solvent to become a Mn ligand. These calculations provide a stringent test of the MCCE methodology, as they are implemented with standard TIPS water atomic partial charges and the well established pK_a,sol value for bulk water of 15.7.

Table 1.

Calculated and experimental pK_as of terminal waters

		pKaM	pKaC	Error
[MnII(H2O)6]2+	1	10.6 64	10.3	-0.3
[MnIII(H2O)6]3+	1	0.7 64	2.7	+2.0
[MnIIIporphyrin(H2O)2]3-	2	4.4 65	4.9	+0.5
[Mn2IV(μ-O)2(terpy)2(H2O)2]4+	3	1.8 66	0.9	-0.9
[Mn3IV(μ-O)4(phen)4(H2O)2]4+	4	4.0 67	4.7	+0.7

Numbers 1-4 refer to Fig. 1. pK_a for first deprotonation in the cluster. pK_a^M: measured value; pK_a^C: calculated value. The geometry for each complex is optimized in the specified Mn redox state. The best-fit line has a slope of 0.88, y-intercept of 0.91 and R² of 0.92 (Supplemental Information Fig. S4).

The pK_a shifts arising when a terminal water is bound to the Mn complex result from a balance of changes in electrostatic interactions between the Mn in the appropriate valence state, OH⁻ and the ligands. The free energy changes can be decomposed into pairwise additive terms according to Equation 1.⁶⁸ The interactions with each Mn center lower the pK_a of the titrating water, while interactions with the other waters (complex 1), oxide bridges and ligands (2-4) raise it. Interaction with the surrounding solvent is lost (desolvation penalty) when the ligand, Mn or bridge is assembled into the cluster, which increases the pK_a. The effects of these changes are observed even for simple complexes, such as complex 1, [Mn^II(H₂O)₆]²⁺, for which the calculated pK_a of 10.3 is in good agreement with the experimental value of 10.6 (Table 1).⁶⁴ Here the shift of -5.4 pH units relative to bulk water represents a -7.4 kcal/mol net stabilization of the OH^- relative to bound water (1 pH unit is 1.367 kcal/mol). There is a +2.45 pH unit desolvation penalty reflecting the greater loss of the interaction with the solvent for the charged OH⁻ than the bound water. The pairwise electrostatic interactions with Mn^II stabilizes OH⁻ relative to the bound water by -9.4 pH units. Interactions of the OH^- with the other 5 waters arranged in octahedral coordination destabilize it by 1.54 pH units.

The enhanced MCCE method provides the pK_a or E_m shift when the gedanken fragments are moved from solution to the cluster. To go from a shift to a measurable pK_a or E_m a reference pK_a,sol or E_m,sol for each titrating fragment must be determined in each solvent using the thermodynamic cycle shown in Figure 2c. The experimental pK_as and E_m used to back calculate E_m,sol and pK_a,sol using the cycles described in figure 2c and 2a are shown as boxed numbers in Fig. 4 and 5.

Figure 4.

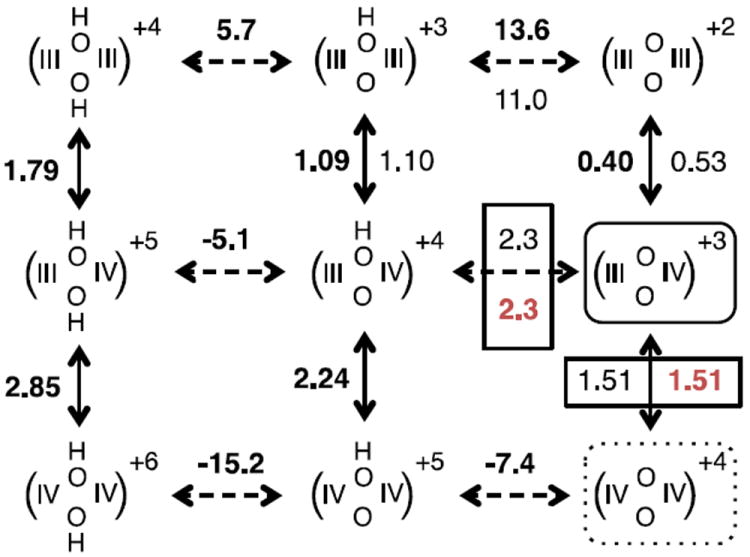
Calculated and experimental E_ms and pK_as of bpy complex 5. Each group in parenthesis shows the redox state of the two Mn (III or IV) and the protonation state of the two bridging oxygens (OH^- as OH or O^-2 as O). Calculated values of E_ms (V, bold, left of vertical arrows) compared to experimental data (light text, right of vertical arrows), and calculated (bold, above horizontal arrows) and experimental (below horizontal arrows) pK_as for redox/deprotonation state transitions. The experimental values used to determine the reference E_m,sol (pK_a,sol) are boxed. E_ms are given in ACN (solid arrows); pK_as in water (dashed arrows). Calculations are based on the fixed geometry optimized in the di-μ-oxo-Mn(III,IV) state (shown enclosed by a solid line). The fixed ligand charges are obtained in the symmetric di-μ-oxo-Mn(IV,IV) state (enclosed by a dotted line). Data taken from Supplementary Information Tables S1-S2.

Figure 5.

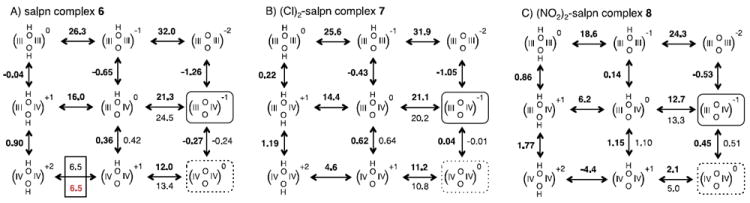
Calculated and experimental E_ms and pK_as of salpn complexes 6-8. See Figure 4 for full description.

A pK_a,sol of 29.8 for the μ-oxo bridge in water is obtained using the measured μ-oxo pK_a in complex 5. The experimental pK_a in complex 6 provides a pK_a,sol in ACN of 45.0. As water stabilizes the more highly charged O^-2 state better than ACN, the pK_a,sol (and resultant cluster pK_as) are lower in the more polar solvent. The same procedures is used to calculate the E_m,sol of the Mn of 1.35 V in ACN using data from complex 5. As all Mn E_ms were measured in ACN only this E_m,sol for this solvent can be determined.

Benchmark calculations of E_ms and pK_as of di-Mn complexes

Figures 3, 4 and 5 (and Supplementary Information Table S1) show the comparison of calculated and experimental values of 8 E_ms and 7 pK_as for Mn centers and oxide bridges, respectively, in di-Mn complexes. The bpy (5) and salpn (6-8) complexes share a common oxygen bridged dimanganese core that has been designed to explore the thermodynamic coupling between protonation and redox changes in high-valent Mn complexes. The pK_as of these oxide bridges, spread over a 24 pH unit range, include measured data for the bpy complex (5) in water⁵⁶ and salpn (6, three values), Cl-salpn (7, two values) and NO_2- salpn (8, two values) in ACN.⁶³ Calculations using the DFT minimum energy configuration in the Mn(III,IV) state give an R² ~ 0.95 and a slope of 0.96. This uses a pK_a,ACN = 45.0 (complex 6-8) for deprotonation of the fragment OH⁻ and pK_a,H2O = 29.8 (complex 5). For data taken in a single solvent pK_a,sol does not affect the slope of a line comparing the experimental and calculated values. Rather, the reference pK_a,sol determines the y intercept, which is -0.07. With structures optimized in the Mn(IV,IV) state, the slope is 1.2.

Figure 3.

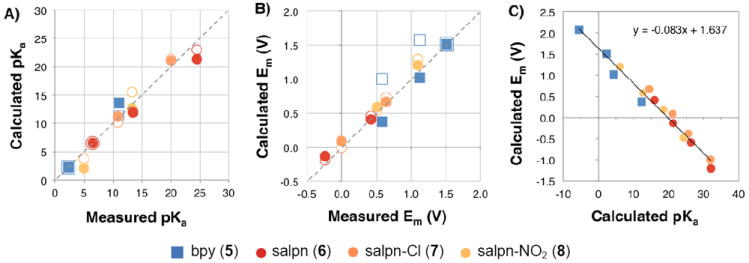
Calculated vs. experimental (A) pK_as and (B) E_ms for bpy (5), salpn (6), and dichloro- (7) and dinitro- (8) substituted salpns. Calculations use structures optimized in the Mn(III,IV) (filled symbols) and the Mn(IV,IV) (open symbols) states. Data from Figs. 4, 5, and Supplementary Information Table S1. Dashed lines show an ideal correlation through the origin with a slope of 1. (A) pK_as: The best-fit line with the Mn(III,IV) optimized structures has a slope of 0.96, y-intercept of - 0.07 and R² of 0.9. Using structures optimized in the Mn(IV,IV) state, the line has a slope of 1.20, y-intercept of 26 mV and R² of 0.92. (B) E_ms: The best-fit line with the Mn(III,IV) optimized structures has a slope of 0.99, y-intercept of -8 mV and R² of 0.96. Using structures optimized in the Mn(IV,IV) state it has a slope of 0.77, y-intercept of 22 mV and R² of 0.92. C) Correlation between E_ms and pK_as calculated with the Mn(III,IV) optimized structure for complexes 5-8 for oxidation or protonation reactions that increase the cluster charge by +1. Data is from Figs. 4 and 5. The best-fit line has a slope of -83 mV/pK_a, y-intercept of 1.64 V and R² of 0.97. All E_ms in all panels are calculated in ACN. All pK_as are in ACN except for complex 5, which is in water.

The experimental E_ms (Figs. 3, 4 and 5 and Supplementary Information Table 1) span 1.75 V and include data for bpy (5, two measured values^56,62,69), salpn (6, two values), Cl-salpn (7, two values) and NO₂-salpn (8, two values).⁶³ There is a very good agreement between calculated and experimental data using the Mn(III,IV) structures. The linear fit gives a slope of 0.99, RMSD of 70 mV and R² of 0.99.⁷⁰ With an E_m,ACN = 1.35 V the y intercept is -8 mV. As for the analysis of pK_as, calculations of E_ms based on the Mn(IV,IV) structures (open symbols in Figure 3B) gives a less satisfactory slope of 0.77.

The enhanced MCCE model greatly simplifies the analysis of the oxo-Mn clusters. The E_m and pK_a changes in different clusters are solely controlled by the classical electrostatic energies between the Mn, the bridging oxygens and the first coordination shell ligands. A valence integer charge is assigned to each fragment that changes charge in the analysis. The DFT input provides cluster geometry and ligand charges that are parameterized in a single state and do not change with the reaction. Yet this simple model does a remarkable job of capturing the experimental E_ms and pK_as for this group of complexes.

Predicted E_ms and pK_as

Complexes 5-8 are well studied.^56,63,70,71 However, due to the intrinsic instability of oxomanganese complexes and other experimental limitations, measurements can not provide a full picture of the electrochemistry of these complexes. Figure 4 and 5 show that there are six E_ms and six pK_as associated with possible transitions in each cluster from the (top, left) di-μ-hydroxo-Mn(III,III) state to the (bottom, right) di-μ-oxo-Mn(IV,IV) state. Of the twelve possible values, only four or five have been measured for each of complexes 5-8. Here, we predict all E_ms and pK_as in these clusters. These values are used to gain a better insight into the manner in which the changes in the ligands or the protonation or redox state change the electron and proton transfer thermodynamics.

The unmeasured values of E_ms and pK_as of the bpy complex 5 (Fig. 4), and the salpn complexes 6-8 (Fig. 5) are predicted in the structures optimized in the Mn(III,IV) state. For comparison, calculations based on the Mn(IV,IV) geometries are also reported in Supporting Information (Table S2). Using both measured and predicted values, the analysis can provide an overview of how changes in redox and protonation states shift subsequent reactions in a complex and how changing the ligands alters the free energy of electron and proton transfer in different complexes (Table 2).

Table 2.

Shifts in E_ms and pK_as induced by changes in the charge distribution of the ligands, protonation states of oxide bridges, or oxidation state transitions in the Mn dimer complexes 5–8.

Shifts due to change in:	pKa(μ-O)	Em(Mn) (V)
• ligand charge distribution
with Cl substituentsa	-0.9±0.7	+0.22±0.03
with NO2 substituentsb	-9.1±1.3	+0.80±0.07
• protonation of μ-Oc	-6.1±0.5	+0.60±0.06
• oxidation of Mnc	-10.6±0.9	+1.01±0.08
• net ligand charge (-2 → 0)d	-13.6±1.4a	+1.68±0.09

Average of appropriate calculated values for complexes 5-8 in ACN using Mn(III,IV) geometries.

^aComplex 7 vs. 6.

^bComplex 8 vs 6.

^cComparison of pK_a or E_m values for complexes 5-8 with different bridging oxygen protonation.

^dComparison of 6 pK_as or 6 E_ms for complex 6 vs 5 in different Mn oxidation states. Data from Figs. 4-5.

Solvent effects on pK_as

Many of the manganese model complexes studied here are unstable in water. Special techniques are required to stabilize the complexes in aqueous solutions, such as the use of buffer solutions (most commonly acetate or phosphate) with an excess of ligand. Therefore, most measurements of E_ms and pK_as have been performed in non-aqueous solutions. For complex 6, experimental pK_as for the bridging oxygens were only measured in ACN solution. pK_as are predicted in water by changing the solvent dielectric constant around the fragments or the cluster from 40 for ACN to 80 for water and changing the reference pK_a,sol for the gedanken, O from value determined in ACN (45.0) to that determined in water (29.8). The 6 calculated pK_as are 6.7±0.9 pH units lower in water than in ACN (supplementary information Table S3). The calculated pK_a shifts are consistent with measurements of other hydrido transition metal complexes that have reported a shift of about 7.5 pH units when comparing pK_as in water and in ACN.⁷² The similarity of the solvent induced pK_a shift found for other transition metal complexes provides support for the predictions using the enhanced MCCE method and gives insight into the crucial role played by the surrounding medium on the acid-base/redox properties of oxomanganese complexes. The ability to approximate how pK_as measured in ACN will shift in water allows clearer comparison with the properties of oxomanganese complexes embedded in aqueous biological environments.

Ligand effects on pK_as and E_ms

Another important question is how the net charge and distribution of charges in the ligands affect the E_ms and pK_as are captured by the method introduced here. For example, comparison of Figures 4 and 5a shows a dramatic increase in the 6 μ-oxo pK_as by 20.2±1.4 pH units when the neutral bpy ligands (5) are exchanged by salpn (with a net charge of - 2) in complex 6. Part of the μ-oxo pK_a shift (6.7 pH units) is due to the change of solvent, as described above. The other 13.6 pH units, however, is caused by the anionic ligands raising the μ-oxo pK_as in the cluster. The ligand charges also affect the redox potentials of the Mn centers that undergo a large change when the bpy ligands (5) are exchanged by the salpn (6) (Figs. 4, 5a). Comparing the 6 E_ms in cluster 5 with those in 6 shows a shift of 1.68±0.09 V. The small standard deviation suggests that the influence of the anionic ligand is similar for all redox and protonation states of these complexes. Knowledge of the magnitude of these shifts is particularly important for understanding biological complexes such as the OEC of PSII, where the ligation of the oxomanganese by several anionic groups, including the carboxylates of Asp and Glu side chains of surrounding amino acid residues, will be expected to modify the thermodynamics of oxidation and deprotonation reactions.⁷³

Ligand substituent groups can also regulate the E_ms and pK_as. In the method used here this influence is accounted for by changing the atomic partial charge distribution on the ligand, which changes the electrostatic potential at the Mn centers and bridging oxides. The three salpn complexes 6–8 have the same ligand net charge yet shows significant polarization effects induced by the electron withdrawing groups in the salpn ligands (Figures 5, 6, Supplementary Information S5-S6). Where there is available data the calculated pK_a and E_ms match the values for these complexes showing the electrostatic potential model can adequately describe the influence of the charge redistribution induced by electron withdrawing substituents. Considering all predicted values, the Cl substitution shifts the μ-O pK_a by -0.9±0.7 pH units and the E_m by +0.22±0.03 V, while NO₂ substitution shifts the pK_a by -9.1±1.3 pH units and the E_m by +0.8±0.07 V.

Figure 6.

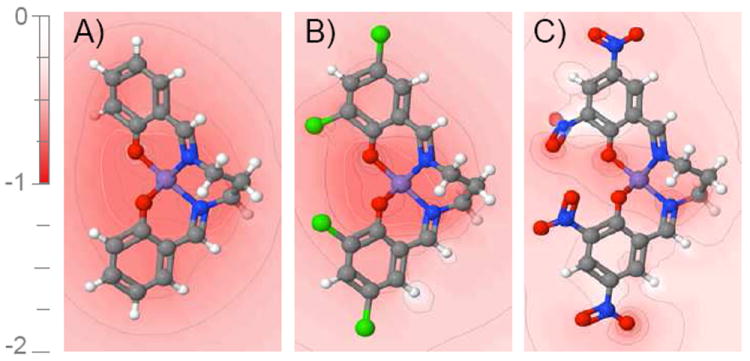
Slices of the DFT electrostatic potential from each ligand in (A) complex 6, (B) 7 and (C) 8 in the plane which contains the axial ligand atoms and is perpendicular to the [Mn₂(μ-O)₂] core (zero-charge Mn atom location shown in purple). The electron-withdrawing substituents Cl and NO₂ move electron density from around Mn to above and below the plane shown here, shifting the redox potential to more positive values (see Supplementary Information S8 for ligand charges and S6 for the correlation between N atom charges and cluster E_m and pK_a).

The E_ms and pK_as in complexes 5-8 shift in a regular manner when the net charge of the complex is changed by protonation or oxidation of the oxygen bridged di-manganese core. For example, protonating an oxide bridge shifts the pK_a of the second μ-O bridge pK_a to be -6.1±0.5 pH units lower than the first one. Each added proton shifts the Mn E_m up by +0.60±0.06 V. Similarly, starting in the Mn(III,III) state, oxidation of the first Mn^III raises the electrostatic potential of the inorganic core, making the oxidation of the second Mn^III +1.01±0.08 V harder. The pK_a of the oxide bridge pK_a shifts by -10.6±0.9 pH units with each Mn oxidation. Remarkably, these changes are accounted for by the changes in formal charges of the Mn and oxide fragments since in the current model neglects changes in the ligand charges or cluster geometry induced by oxidation/protonation state transitions.

Dependence on the input structure

The empirical method presented here is sensitive to the atomic positions in the structure. The E_ms and pK_as for complex 5 were calculated with structures subjected to DFT geometry optimization in the Mn(III,IV) and Mn(IV,IV) states with singly protonated or deprotonated oxo bridges (supplementary information S5, Table S3). Protonation of the μ-oxo bridge increases the Mn(IV)–O bond length by 0.11 Å and the Mn(III)—O by 0.57Å in the Mn(III,IV) structure. In the Mn(IV,IV) structure the Mn(IV)–O bond increases by 0.15 Å. The longer bonds reduce the electrostatic interaction between the oxide bridge and the Mn center and shift the calculated pK_as and E_ms. However, calculations starting with structures optimized in the same redox and protonation state show regular shifts in the pK_as and E_ms. For example protonation of one oxygen bridge increases the calculated pK_a of the second bridge by 12.1±2.7 for the Mn(III,IV) structure and 12.3±2.4 for the Mn(IV,IV) structure. The calculations with Mn(III,IV) structures provide a better match to the experimental data than those carried out with the geometry optimized in the Mn(IV,IV) (Fig. 3a, b) or Mn(III,III) state (data not shown). Since we use the same atomic charge values in all cases, it is the position of the ligand atoms that result from the Jahn-Teller distortion around the Mn^III center(s), captured by the DFT-derived geometries that change when the structures are optimized in different states. Consistent with this picture, the effect of point charge location is most apparent for the neutral ligands of complex 5, where the E_m values are too high when the Mn(IV,IV) structure is used (Fig. 3b, open squares). Thus, in an empirical method such as that used here, good agreement with experiment relies on the use of consistent methods to define the structures, partial charges and reference pK_a,sol and E_m,sol for all complexes.

Thermodynamic coupling in dioxomanganese complexes

The correlated shifts of E_ms and pK_as found by the MCCE analysis (Fig. 3C) shows that the [Mn₂(μ-O)₂] core responds as a unit to changes in electrostatic interactions. This results in a strong correlation between changes in the Mn redox potential and changes in the oxide bridge pK_a in all complexes. The cluster charge can be increased by +1 by either Mn oxidation or cluster protonation. MCCE predicted values shows a correlation of E_ms and pK_as for a given cluster state with a slope of ~83 mV/pKa unit (Fig. 3c). This is in quantitative agreement with experimental studies by Pecoraro and co-workers where a slope of 85 was found.⁷⁰

The underlying changes in protonation and oxidation states compared in Fig. 3c represent independent, uncoupled, processes. Fig. 3c thus analyzes reactions involving a step along the horizontal direction and another one vertically in Figures 4 and 5 (and Supplementary Information S7). The correlation is thus significantly different from the dependence of E_m with pH in PCET mechanisms, as in the reaction:

$$[{\mathrm{Mn}}^{\mathrm{IV}}{(\mathrm{\mu }­\mathrm{O})}_2{\mathrm{Mn}}^{\mathrm{IV}}]+{\mathrm{e}}^{-}+{\mathrm{H}}^{+}\to \leftarrow [{\mathrm{Mn}}^{\mathrm{III}}(\mathrm{\mu }­\mathrm{O})(\mathrm{\mu }­\mathrm{OH}){\mathrm{Mn}}^{\mathrm{IV}}]$$

with an E_m that must change by 59 mV/pH unit.

Thus, PCET correspond to transitions along the diagonal of the same initial and final states. In both sequential and tightly coupled electron and proton transfer reactions deprotonation increases the basicity of the bridge and, therefore, lowers the potential for oxidation of the complex. These mechanisms are thus essential to stabilize high-valent (non-oxidizing) states that can accumulate several oxidation equivalents before engaging in redox reactions.

Potential lessons for proton release with oxidation of the OEC of PSII

Complexes 3 and 5-8 have been constructed as models of the OEC of PSII which is thought to evolve along the catalytic water splitting cycle from the most reduced S₀ state (Mn(III,III,III,IV)) to the S₃ state (Mn(IV,IV,IV,IV)), before forming an oxyl radical species responsible for the O-O bond formation.⁷⁴ The results reported in Figures 4, 5 and Table 2 provide information that can help understand the OEC Mn₄O₅Ca cluster. The analysis of the oxo-manganese clusters shows that the pK_a of oxo bridges shifts by 9 to 10 pH units each time the complex is oxidized, making them good candidates to lose a proton each time the Mn core is oxidized, as long as any bridging oxygens remain protonated.¹⁶ A close coupling between the core loosing protons and electrons is generally consistent with earlier computational models of the OEC that combined DFT and QM/MM methods,^20,23,75,76 and DFT models of the S0 and S1 states. These earlier simulations suggest that the last deprotonation of an OEC hydroxo bridge occurs during the formation of the S₁ state, with two Mn^III and two Mn^IV centers and all bridging oxygens in the μ-oxo form.⁷⁷ The question remains as to whether protons are then lost from a terminal water when going to the S₂ state,²⁰ especially since the proton release during this transition is pH dependent.⁷⁸ HYSCORE experiments do suggest that there are no terminal hydroxo ligands in the S₂ state,⁷⁹ while a recent DFT study suggests that one of the terminal water ligands is deprotonated.²⁷ Notably, the proposed electrostatic valence model will be able to explore the variations of pK_as and E_mS of the OEC as a function of the protonation states of vicinal amino acid residues (e.g. D61, H337, R357) and replacement of cofactors, such as chloride⁸⁰ or calcium. Such applications could shed light on the several structure-function relations in PSII.

CONCLUSIONS

We have documented for the first time the capabilities and limitations of an, enhanced MCCE methodology to characterize proton-coupled electron transfer in oxomanganese complexes, using Monte Carlo sampling of protonation and redox states on the same footing.^80,81 The methodology provides predictions with RMSD of 70 mV for E_ms covering a 1.75 V range, and a 2 pH unit RMSD for pK_as over a 24 pH unit range, without pre-assignment of the microstate at the outset of the calculation as usually done in other techniques, such as standard molecular dynamics, DFT, or QM/MM analysis. The MCCE method, thus, by-passes the exponential scaling problem, due to the large number of possible microstates, and allows for an efficient assessment of the sequence of oxidation and deprotonation state transitions for multicenter redox/acid-base cofactor chelated by Lewis base ligands and surrounded by a cluster or protein environment. The calculations show a remarkable ability of the MCCE methodology to predict shifts in Mn E_ms and pK_as of hydroxo bridges and terminal water ligands in a series of complexes parameterized by geometries and partial atomic charges from quantum chemistry calculations. The E_m and pK_a shifts are modeled solely by the changes in the continuum electrostatic interactions between the Mn and the atoms in their first coordination shell.

Given the success of this simple analysis, the methodology can now be extended and applied to the study of other biologically important Mn complexes such as superoxide dismutase⁸² and the OEC of PSII.^16,83 The reported enhanced MCCE analysis of trends of redox potentials and pK_as across several complexes and solvents, partially validate the classical electrostatic methodology as capable of accounting for changes in the electrostatic potential at the positions of the redox/acidbase constituent fragments. The analysis also provides guidelines for ligand design that should be useful to modulate redox/acid-base transitions.