Genetic and Environmental Variation in Lung Function Drives Subsequent Variation in Aging of Fluid Intelligence

Abstract

Longitudinal studies document an association of pulmonary function with cognitive function in middle-aged and older adults. Previous analyses have identified a genetic contribution to the relationship between pulmonary function with fluid intelligence. The goal of the current analysis was to apply the biometric dual change score model to consider the possibility of temporal dynamics underlying the genetic covariance between aging trajectories for pulmonary function and fluid intelligence. Longitudinal data from the Swedish Adoption/Twin Study of Aging were available from 808 twins ranging in age from 50 to 88 years at the first wave. Participants completed up to six assessments covering a 19-year period. Measures at each assessment included spatial and speed factors and pulmonary function. Model-fitting indicated that genetic variance for FEV₁ was a leading indicator of variation in age changes for spatial and speed factors. Thus, these data indicate a genetic component to the directional relationship from decreased pulmonary function to decreased function of fluid intelligence.

Introduction

With the unprecedented increase in average life expectancy, researchers have focused increasing attention on establishing the etiologies of aging trajectories, particularly for traits that contribute to quality of life such as cognitive and physical functioning. Identifying influences on change and decline with age would enable us to understand what impacts these processes, and thus suggest potential interventions that may enhance the cognitive and physical health of older adults. Many studies have demonstrated relationships between cognitive and physical aging, including the cumulative and interactive effects of health conditions on cognitive performance. Evidence from various approaches points to an important role for physical functioning in cognitive aging. For example, numerous exercise intervention studies document a positive influence of exercise on cognitive function (Colcombe and Kramer 2003; Smiley-Oyen et al. 2008). In addition, population-based studies have documented that pulmonary function is a longitudinal predictor of cognitive function among older adults (Albert et al. 1995; Chyou et al. 1996; Emery et al. 1998) as well as a cross-sectional and longitudinal predictor among middle aged and young adults (Emery et al. 1997; Anstey et al. 2004; Richards et al. 2005). Prior studies have utilized standard indicators of lung function from spirometric assessment to measure pulmonary function. In particular, forced expiratory volume in one second (FEV₁) is the most commonly used indicator of pulmonary function because it provides a readily measured indicator of lung capacity and lung responsivity that reflects over repeated assessments both age-related and pathological changes that may occur in lung functioning. In turn, the influence of pulmonary function on cognitive decline may result from a number of factors including hypoxia, reduced neurotransmitter function, increased systemic inflammatory processes, or possibly a combination of factors. Multiple methods will be required to fully understand the etiology of the relationship between pulmonary and cognitive functioning.

Bivariate dual change score models (DCSM) allow researchers to investigate hypotheses about the temporal dynamics between two variables (McArdle 2001; McArdle and Hamagami 2003; McArdle et al. 2000). Incorporating longitudinal changes in both variables and cross-trait cross-time paths, DCSM allow for the identification of leading indicators of cognitive change: the extent to which changes in one variable impact subsequent changes in a related variable. Recent application of DCSM to the relationship between cognitive and pulmonary function indicated that age changes in pulmonary function precede and drive subsequent age changes in measures of fluid intelligence (Emery et al. 2012). Temporal dynamics is only one step toward understanding etiology. Data from longitudinal twin studies allow researchers to examine the extent to which the relationship between age changes in pulmonary functioning and age changes in cognition result from genetic and environmental factors.

Simplex longitudinal models of genetic and environmental influences on pairs of traits incorporate cross-trait cross-time paths of influence and allow for the identification of new genetic and environmental influences at each wave of data collection (Neale and Cardon 1992). These models are often used in studies of children and young adults because all participants tend to be approximately the same age at each measurement occasion, simplifying the relationship between age and time. Longitudinal studies of aging are often cross-sequential in design: each measurement occasion consists of a cross-sectional sample of older adults (Schaie 1965, 1970). As a result, age and time cannot be equated but must be parameterized separately in the measurement model. In addition, simplex models do not produce estimates of longitudinal trajectories, which are the focus of studies of aging: predictors and causes of age changes. Latent growth curve models (LGCM) can estimate rates of change and can be parameterized as time-based or age-based models, depending on the age range at each measurement occasion (Bryk and Raudenbush 1992; Laird and Ware 1982; McArdle and Anderson 1990). However, application of LGCM to investigations of the relationship between two variables is limited to correlations among intercept and slope parameters (e.g., Deary et al. 2011; Zimprich and Martin 2002) and genetic and environmental decomposition of those correlations. In contrast, biometric DCSM incorporates both the cross-age cross-trait paths of the simplex model and the estimates of longitudinal trajectories of LGCM in a genetically informative model investigating the relationship between two variables (McArdle and Hamagami 2003). For example, in a recent application of biometric DCSM to the relationship between processing speed and cognitive aging, researchers concluded that genetic variance for processing speed was a leading indicator of variation in age changes for components of cognitive functioning (Finkel et al. 2009).

Previous investigation of the etiology of the relationship between pulmonary function and cognitive aging report that correlation between lung function at baseline and cognitive function 6 years later was primarily genetically mediated, particularly for measures of fluid intelligence (Emery et al. 1998). The goal of the current analysis is to incorporate longitudinal twin data on both lung function and cognitive function in a biometric DCSM to examine the extent to which age changes in pulmonary function and age changes in cognitive function result from common genetic and environmental factors. By directly modeling the genetic and environmental decomposition of the lead/lag relationships between two variables, the biometric DCSM can determine whether genetic factors impacting pulmonary function are a leading indicator of variation in aging trajectories for cognitive abilities, genetic factors impacting cognitive abilities are a leading indicator of aging changes in pulmonary function, or a dynamic relationship exists with bidirectional genetic influences. The longitudinal Swedish Adoption/Twin Study of Aging (Finkel and Pedersen 2004) includes measures of cognitive and pulmonary function. Six waves of data collection have been completed for a sample of 808 non-demented individuals with at least one data point and a longitudinal follow-up period of up to 19 years. The cross-sectional age range of the sample at the first wave was 50–88 years, thus the focus of the current analysis is the aging process during the second half of the lifespan. Based on previous results indicating that pulmonary function is a leading indicator of age changes in spatial abilities and processing speed (Emery et al. 2012), we hypothesize that genetic influences on pulmonary function impact the genetic influences on variation in subsequent change in spatial abilities and processing speed.

Method

Participants

Accrual procedures for SATSA have been described previously. In brief, the sample is a subset of twins from the population-based Swedish Twin Registry (Finkel and Pedersen 2004). In-person testing (IPT1) took place in a location convenient to the participants, such as district nurses’ offices, health-care schools, and long-term care clinics. Testing was completed during a single 4-hour visit. The second (IPT2) and third (IPT3) waves of in-person testing occurred at 3-year intervals. IPT did not occur during wave 4; therefore, the next wave of in-person testing is labeled IPT5 and occurred after a 7-year interval (see Finkel and Pedersen 2004). Regular 3-year testing continued after IPT5; therefore, the total time span from IPT1 to IPT7 was 19 years.

Participant data were included from all available time points. Dementia status was determined by clinical diagnosis based on current diagnostic criteria (Gatz et al. 1997), and data were retained in analyses for all available assessments prior to a dementia diagnosis. In total, 808 individuals had cognitive and pulmonary data available from at least one testing occasion. Of those participants, 67 % have data at three or more time points and 12 % participated in all six waves. 59 % of participants were women. Table 1 presents descriptive information for each age interval. Because SATSA is a cohort-sequential design, new participants were added at waves IPT2 through IPT5 and some participants were lost to attrition. Statistical modeling accounts for missing data by giving more weight to participants with more time points of data.

Table 1.

Descriptive statistics for each age interval

Age interval	N	Twin pairs MZ/DZ	Mean age (SD)	Mean spatial (SD)	Mean speed (SD)	Mean FEV1 (SD)
50	89	14/26	51.4 (1.5)	58.1 (10.1)	58.5 (8.6)	2.7 (0.7)
53	165	27/49	54.5 (0.9)	56.9 (9.5)	58.2 (8.2)	2.6 (0.7)
56	200	35/50	57.6 (0.9)	57.3 (9.9)	57.8 (8.2)	2.6 (0.7)
59	233	38/64	60.5 (0.9)	56.3 (10.3)	56.9 (9.5)	2.5 (0.7)
62	299	52/73	63.4 (0.9)	53.9 (10.2)	54.2 (9.3)	2.3 (0.7)
65	346	55/89	66.4 (0.8)	52.6 (9.9)	51.6 (9.4)	2.3 (0.7)
68	329	44/77	69.4 (0.8)	50.5 (10.3)	49.4 (9.1)	2.1 (0.7)
71	303	39/72	72.5 (0.9)	48.7 (9.3)	48.3 (8.6)	2.0 (0.6)
74	251	29/58	75.6 (0.8)	47.8 (9.0)	46.5 (8.9)	1.9 (0.6)
77	186	31/29	78.5 (0.9)	45.6 (9.8)	44.3 (9.6)	1.8 (0.6)
80	127	26/17	81.6 (0.9)	45.3 (9.0)	42.1 (9.8)	1.7 (0.6)
83	59	5/3	84.5 (0.9)	42.7 (6.9)	39.5 (8.4)	1.5 (0.6)
86	26	1/2	87.3 (0.9)	40.6 (7.6)	36.1 (7.3)	1.4 (0.5)

Age interval “50” includes ages 50–52.9

To maintain consistency with the 3-year testing interval and to maximize the age range available for inclusion in the study, data were divided into thirteen 3-year age intervals from age 50 to 85. The data were divided into age intervals such that everyone with data (regardless of IPT) at ages 50–52.9 was included in the first age interval, labeled “50.” Sample sizes within the age intervals are maximized in the middle of the age range (60–80). The data become too sparse (i.e., samples less than 15) after age interval “86” (i.e., after age 88.9) to support statistical modeling; therefore, only data up to age interval “86” were included in these analyses.

Measures

Cognitive performance

Four cognitive domains are represented in the SATSA cognitive test battery (Nesselroade et al. 1988; Pedersen et al. 1992). Because previous analyses (Emery et al. 2012) indicate that lung function is related primarily to measures of spatial and speed, the current analyses focus on these two domains. Block Design (WAIS-R) and Card Rotations assess spatial abilities and Symbol Digit and Figure Identification measure processing speed. Reliabilities for these tests range from 0.82 to 0.96 (Pedersen et al. 1992). Principal components analysis was used to construct latent factors from the individual tests within each domain: spatial and speed. Factor loadings ranged from 0.79 to 0.92. Previous comparisons of factor structure between cohorts and across testing occasions indicate that the factor structure does not vary systematically across age or time (Finkel et al. 2005). To avoid variance in measurement (cf. Wicherts et al. 2004), an invariant definition of factors at each testing occasion was created by standardizing the cognitive measures relative to the respective means and variances at IPT1. Then loadings from the factor analyses conducted at IPT1 were used to construct the spatial and speed factors. For visual interpretation, all factor scores were later transformed to T-scores using factor means and variances from IPT1. Means and standard deviations of T-scores at each wave are included in Table 1.

Pulmonary functioning

Spirometric testing to measure FEV₁ was performed during in-person testing on one of two intercalibrated portable 10-1 dry bellows Vicatest spirometers (Mijnhardt, Bunnik, The Netherlands) with subjects in the seated position and their nasal passages blocked with nose clips. At IPT1 and IPT7 only one trial was collected; during IPT2 through IPT6 two spirometric trials were completed and data from the best trial were used in the present analyses. During the course of the study, it became necessary to change spirometric equipment due to the increasing difficulty of transporting the Vicatest spirometers and the availability of new spirometric equipment that was lighter and easier for the nurses to use. Thus, at IPT3, pulmonary function for 30 % of the subjects was measured using the Vicatest, and the remaining subjects were assessed with a portable ML 330 spirometer (Micor Medical, Kent, United Kingdom). The two spirometers were intercalibrated to ensure consistent measurement. FEV₁ values for both spirometers were expressed in BTPS (body temperature and pressure saturated with water vapor). Mean uncorrected FEV₁ at each testing wave is reported in Table 1. For the purposes of analysis, FEV₁ values were corrected for height and gender and the standardized score was then transformed to T-score metric for ease of interpretation. Because smokers and nonsmokers did not differ significantly on pulmonary functioning in this sample, data were not corrected for smoking status.

Statistical method

Univariate analysis

A univariate biometric DCSM was used to examine genetic and environmental influences on age changes for the cognitive factors and pulmonary function independently. Extensive discussions of the DCSM are available (McArdle 2001; McArdle and Hamagami 2003; McArdle et al. 2004), as well as comparisons of DCSM with LGCMs (Ghisletta and de Ribaupierre 2005; Lövdén et al. 2005). As presented in Fig. 1, the model is based on latent difference scores to create a growth curve based not on performance at one age but on change from one age to the next. Thus, Y50 represents observed performance on measure Y at age 50, with y50 indicating the latent true score and u_y50 signifying error. Error variance (σ_u) is assumed to be constant at each age. Performance at age 53 is a function of both performance at Y50 and of the change in performance that occurred between ages 50 and 53 (Δy53). The focus of the DCSM is to predict changes in the latent trait score (Δy), which are modeled as a function of both constant trends in change across time and a self-feedback component (e.g., added change in the trait given the previous score). Constant change (α) is related to the slope factor (y_s) such that age changes accumulate over time in an additive fashion. Proportional change signifies that the difference between performances at any two adjacent ages is directly proportional to the previous score, through the parameter β. Thus, the model for change in Y at time point t can be written as in Eq. 1.

Fig. 1.

A univariate biometric dual change score model to examine genetic and environmental influences on age changes in Y. Error variance (σ_u) is assumed to be constant at each age; α represents constant change and is related to the slope factor y_s; β represents proportional change. The model includes an estimate for intercept (y₀), mean intercept (μ₀), and mean slope (μ_s). The model includes genetic and environmental effects specific to the intercept (a₀ and e₀) and specific to the slope (a_s and e_s). The paths from a₀ and e₀ to the slope (y_s) generate the decomposition of the correlation between the intercept and slope

$$\Delta y[t]=\text{α}{y}_s+\text{β}y[t-1]$$ (1)

The values of α and β are commonly assumed to be constant across time (although this assumption is testable) and they allow for the generation of a family of curves capturing the trajectories of change with age. In the full DCSM model, α is set to 1 and the parameter β differs from zero to the extent that the longitudinal change is nonlinear. In describing change with age, then, the DCSM estimates four fixed effects: α, β, mean intercept (μ₀), and mean slope (μ_s).

Twin data allow for the decomposition of individual variation (random effects) around the group mean intercept and slope into genetic and environmental components. The variance in any trait can be divided into three separate components: additive genetic effects (V_a), shared rearing environmental effects that serve to make the members of a family more similar (V_c), and nonshared environmental effects including error (V_e). By fitting structural models to the observed MZ and DZ covariance matrices, we can estimate the proportion of total variance accounted for by the variance in genetic factors, shared environment factors, and nonshared environment factors.

To decompose both the individual variation around the mean intercept and slope and the correlation between the intercept and slope, a standard Cholesky model (Neale and Cardon 1992) was implemented (as in McArdle and Hamagami 2003). As shown in Fig. 1, the model includes genetic and environmental effects specific to the intercept (a₀ and e₀) and genetic and environmental effects specific to the slope (a_s and e_s). The paths from a₀ and e₀ to the slope (y_s) generate the Cholesky decomposition of the correlation between the intercept and slope (for simplicity, only additive genetic and nonshared environmental paths are included in the figure).

Bivariate analysis

A bivariate biometric DCSM was used to examine genetic and environmental contributions to the dynamic relationships between age changes in the cognitive factors and pulmonary function (McArdle and Hamagami 2003). The extension of the basic DCSM allows for constant change (α), proportional change (β), and a coupling mechanism (γ) where change in trait X depends on the previous value of Y, and vice versa. The model, presented in Fig. 2, includes time series for two traits, X and Y, with the dynamic interrelationship between changes in the two traits modeled by two additional fixed effects. The new parameters allow the two traits to affect each other in a dynamic way by modeling the effect of Y on subsequent changes in X (γ_yx) and the effect of X on subsequent changes in Y (γ_xy). Thus, the model for the dynamic interaction of changes in X and Y at time point t can be written as in Eqs. 2 and 3,

$$\Delta y[t]={\alpha }_y{y}_s+{\beta }_{y}y[t-1]+{\gamma }_{xy}x[t-1]$$ (2)

$$\Delta x[t]=a_x{x}_s+{\beta }_{x}x[t-1]+{\gamma }_{yx}y[t-1]$$ (3)

so that change in one trait is a time-based function of both itself and another trait. As with the dual change parameters α and β, the coupling parameters (γ_xy and γ_yx) are assumed to be constant over the whole time series.

Fig. 2.

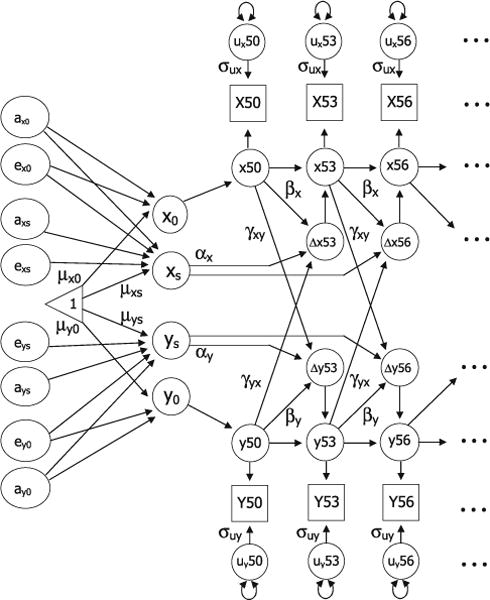
A bivariate biometric dual change score model to examine genetic and environmental influences on the relationship between age changes in two measures (Y and X). Error variance (σ_u) is assumed to be constant at each age within each factor; α_y and α_x represent constant change related to the slope factors y_s and x_s; β_y and β_x represent proportional change in Y and X; cross-trait coupling is indicated by γ_yx and γ_xy. The model includes estimates for intercepts (y₀ and x₀), mean intercepts (μ_y0 and μ_x0), and mean slopes (μ_ys and μ_xs). The model includes genetic and environmental effects specific to the each intercept (a_x0 and e_x0, a_y0 and e_y0) and specific to each slope (a_xs and e_xs, a_ys and e_ys). The paths from a_x0 and e_x0 to x_s and from a_y0 and e_y0 to y_s generate the decomposition of the correlation between the intercept and slope for X and Y

Again, twin data allow us to decompose the individual variation (random effects) around the group mean intercept and slope parameters for each variable. As shown in Fig. 2, the model includes genetic and environmental effects specific to each intercept (a_x0 and e_x0, a_y0 and e_y0) and genetic and environmental effects specific to the slope (a_xs and e_xs, a_ys and e_ys). The paths from a_x0 and e_x0 to x_s and from a_y0 and e_y0 to y_s generate the Cholesky decomposition of the correlation between the intercept and slope for X and Y. Coupling parameters estimate dynamic relationships between variables within individuals. The biometric portion of the model estimates relationships between twins, but within variables. Thus, in the biometric bivariate DCSM, the only paths between variables are the coupling parameters. Model testing is used to determine the impact of the coupling parameters on the estimates of genetic and environmental variance.

It is important to note that one of the fundamental assumptions of DCSM is that data are missing at random (MAR). Without complete mortality data, it is difficult to establish whether the MAR assumption is met, although previous investigations of SATSA data suggest that participants who continue in the study are significantly different from those who drop out (e.g., personality ratings: Pedersen and Reynolds 1998). Of most importance in investigations of aging is to demonstrate that the pattern of missing data does not differ for older and younger participants. Cohort comparisons of missing data (Finkel et al. 2007) indicate that the patterns of participation are fairly similar, although older participants are somewhat more likely (71 %) than younger participants (64 %) to participate in at least 3 time points simply as a result of a greater number of opportunities for participation. At IPT2, IPT3, and IPT5, any twins who had responded to the initial questionnaire and reached age 50 years were invited to participate in SATSA (Finkel and Pedersen 2004).

Both univariate and bivariate biometric DCSM were fit with the structural equation modeling program Mx version 1.66b (Neale et al. 2003), using the variable length datafile option that takes advantage of data from both complete and incomplete pairs. The raw maximum likelihood estimation procedure was used throughout. Hypotheses were tested by comparing model fit indices; nested models were compared using the difference Chi square test obtained by taking the difference between the obtained model fits (−2LL) and testing its significance with the degrees of freedom equal to the difference in the number of parameters of the two models.

Results

Univariate analysis

In the first step of the analysis, the univariate biometric DCSM was fit to cognitive factors and FEV₁ separately, to verify the shape of the change trajectory over age and to provide starting values for the bivariate DCSM model. Parameter estimates (and 95 % confidence intervals) resulting from fitting the full model are presented in Table 2, along with model fit statistics. Estimates of change parameters must be interpreted with caution; consider that the mean slope estimates presented in Table 2 represent only one component of change and can only be interpreted in the context of the proportional change component β. Positive values for β indicate that change accumulates or accelerates with age; in combination with a negative mean slope estimate (μ_s), accelerating decline with age is indicated. Thus, accelerating decline in performance is indicated for the cognitive factors. In contrast, a negative value for β combined with a negative mean slope indicates decelerating decline with age. The value for β for FEV₁ is negative but small and nonsignificant, indicating that in this age range decline in FEV₁ is primarily linear. These trajectories are evident in the estimated longitudinal trajectories for mean cognitive and pulmonary function presented in Fig. 3.

Table 2.

Parameter estimates (and 95 % confidence intervals) from fitting the univariate biometric dual change score model

Parameters	Spatial factor	Speed factor	FEV1
Fixed effects
Mean intercept, μ0	54.98 (53.94, 56.04)	56.95 (55.94, 57.96)	55.24 (54.02, 56.47)
Mean slope, μs	−9.67 (−12.17, −7.34)	−8.06 (−9.74, −6.43)	−0.17 (−2.63, 2.17)
Constant change, α	=1	= 1	= 1
Proportional change, β	0.17 (0.12, 0.22)	0.13 (0.09, 0.16)	−0.02 (−0.06, 0.03)
Random effects
Intercept deviation, σ0
Additive genetic	8.29 (6.63, 9.47)	7.66 (6.00, 8.44)	5.33 (2.13, 7.52)
Shared environment	2.64 (−5.56, 5.56)	0.00 (−4.55, 4.55)	3.41 (−6.07, 6.07)
Nonshared environment	3.26 (2.15, 4.30)	2.93 (1.83, 3.98)	5.93 (4.75, 7.16)
Slope deviation, σs
Additive genetic	0.07 (−0.26, 0.26)	−0.26 (−0.39, 0.39)	0.00 (−0.71, 0.71)
Shared environment	0.00 (−0.21, 0.21)	0.00 (−0.22, 0.22)	−0.16 (−0.59, 0.59)
Nonshared environment	−0.17 (−0.27, 0.27)	0.23 (−0.32, 0.32)	−0.41 (−0.65, 0.65)
Slope on level
Additive genetic	−1.42 (−1.98, −0.91)	−1.00 (−1.31, −0.54)	0.28 (−0.34, 0.69)
Shared environment	−0.56 (−1.16, 1.16)	0.00 (−0.79, 0.79)	−0.34 (−0.63, 0.63)
Nonshared environment	−0.58 (−0.88, −0.22)	−0.46 (−0.73, −0.10)	−0.27 (−0.54, 0.03)
Error deviation, σu	17.45 (16.20, 18.83)	17.67 (16.45, 19.01)	23.55 (21.96, 25.29)

Fig. 3.

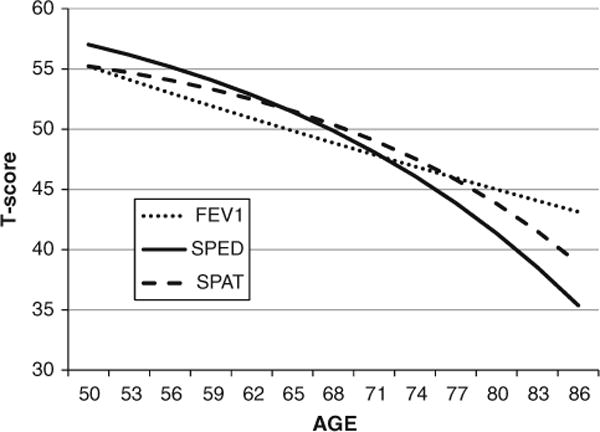
Phenotypic longitudinal trajectories for the SPAT spatial factor, SPED speed factor and FEV₁

Four reduced models were used to test the significance of genetic and environmental contributions to individual variation in the intercept and slope parameters. First, all shared environmental effects were dropped from the models. No significant change in model fit was found, therefore, subsequent models were compared with this reduced AE model. In model 2, genetic influences on the mean intercept were dropped from the model (set a₀ → y₀ = 0). In model 3, genetic influences specific to the slope were dropped from the model (set a_s → y_s = 0). In model 4, genetic influences on the correlation between the intercept and slope were dropped from the model (set a₀ → y_s = 0). The results of univariate model testing are presented in Table 3. Model testing indicates significant genetic influences on the intercept for cognitive factors and FEV₁, but no significant genetic influences specific to the slope. Genetic influences impact the slope parameters for the cognitive factors only through genetic influences on the intercepts via the intercept-slope correlation. No significant genetic influences on longitudinal change in FEV₁ were indicated.

Table 3.

Model-fitting results for univariate biometric dual change score model

Overall misfit (−2LL)
Models	Parameters	Spatial	Speed	FEV1
Full model	15	16,721	17,881	18,696
1. Drop shared env.	12	16,721	17,881	18,697
2. Drop a0 → y0	11	16,898*	18,039*	18,749*
3. Drop as → ys	11	16,722	17,885	18,698
4. Drop a0 → ys	11	16,776*	17,920*	18,697

^*Change in model fit versus model 1 is significant at p < 0.01

Bivariate analyses

Cognitive and pulmonary function are interrelated: FEV₁ correlates 0.38 with the spatial factor and 0.27 with the speed factor. Thus, the focus of the current analysis was bivariate models that allow for the investigation of the impact of genetic and environmental influences on the leading role for pulmonary function in some aspects of cognitive aging. Two dynamic relationships were investigated: FEV₁ as a leading indicator of change in spatial ability and processing speed. Results of testing the primary hypotheses are presented in Table 4. Shared environmental effects were dropped in the first reduced model, and as in the univariate results, there was little impact on model fit. Subsequent models were compared with reduced model 1. Model testing results supported the conclusion that the cognitive factor → FEV₁ coupling parameters (model 2) could be dropped from the model without significantly reducing model fit, whereas dropping the FEV₁ → cognitive factor coupling parameter significantly decreased model fit (model 3). Model 4 verifies that coupling between the two pairs of variables, FEV₁ and spatial or FEV₁ and speed, cannot be eliminated without significantly reducing model fit.

Table 4.

Model-fitting results for bivariate biometric dual change score models

Overall misfit (−2LL)
Models	Parameters	Spatial	Speed
Full model	28	35399	36567
1. Drop shared env.	22	35400	36567
2. Drop γ factor → FEV1	21	35400	36568
3. Drop γ FEV1 → factor	21	35415*	36577*
4. Drop all coupling	20	35418*	36583*

^*Significant change in model fit versus model 1 (p < 0.01)

Parameter estimates resulting from fitting the AE biometric bivariate DCSM (with and without full coupling) to these pairs of variables are presented in Tables 5 (spatial factor) and 6 (speed factor). The addition of the coupling parameter changes the prediction of Δy and Δx: they are now functions of α, β, and γ. Therefore, estimates of α, β mean intercept, and mean slope parameters in the bivariate model may differ from the univariate model results. Significance of parameters in Tables 5 and 6 was tested by dropping each parameter individually and examining the change in model fit; the size of the model precluded calculation of confidence intervals. Although the estimates of γ from FEV₁ to the cognitive factors are small (0.013), model comparisons presented in Table 4 demonstrate the significance of the coupling parameter. Thus, a portion of the genetic influences on change in the spatial and speed factors acts through dynamic coupling with FEV₁.

Table 5.

Parameter estimates from the bivariate biometric dual change score model between FEV₁ and the spatial factor

Parameters	FEV1 Full coupling	Spatial	FEV1 No coupling	Spatial
Fixed effects
Mean intercept, μ0	55.15**	55.22**	55.28**	54.98**
Mean slope, μs	−0.18	−9.19**	−0.10	−9.70**
Constant change, α	=1	=1	=1	=1
Proportional change, β	−0.02	0.14**	−0.02	0.18**
Coupling, γ FEV1 → spatial		0.013**		=0
Coupling, γ spatial → FEV1	0.000		=0
Random effects
Intercept deviation
Additive genetic	6.30**	8.73**	6.35**	8.72**
Nonshared environment	5.92**	3.16**	5.88**	3.16**
Slope deviation
Additive genetic	0.46	0.18	0.46	0.14
Nonshared environment	−0.41	−0.15	−0.42	−0.16
Slope on level
Additive genetic	0.06	−1.36**	0.06	−1.54**
Nonshared environment	−0.27	−0.48**	−0.26	−0.55**
Error deviation, σu	4.85	4.18	4.85	4.18

^**Model comparison indicates parameter is significantly different from zero at p < 0.01

Table 6.

Parameter estimates from the bivariate biometric dual change score model between FEV₁ and the speed factor

Parameters	FEV1 Full coupling	Speed	FEV1 No coupling	Speed
Fixed effects
Mean intercept, μ0	55.25**	57.02**	55.28**	56.94**
Mean slope, μs	0.09	−8.22*	−0.11	−8.05**
Constant change, α	=1	=1	=1	=1
Proportional change, β	−0.03	0.12**	−0.02	0.13**
Coupling, γ FEV1 → speed		0.013**		=0
Coupling, γ speed → FEV1	0.006		=0
Random effects
Intercept deviation
Additive genetic	6.29**	7.74**	6.36**	7.75**
Nonshared environment	6.00**	2.69**	5.88**	2.67**
Slope deviation
Additive genetic	0.47	−0.31**	0.46	−0.29**
Nonshared environment	0.45*	0.21	0.42	0.21
Slope on level
Additive genetic	0.14	−0.96**	0.06	−1.03**
Nonshared environment	−0.25	−0.37*	−0.26	−0.38*
Error deviation, σu	4.85	4.21	4.85	4.20

Model comparison indicates parameter is significantly different from zero at *p<0.05; **p<0.01

The differences in the parameter estimates between the full coupling and no coupling models are subtle and require examination of the accumulating impact of these subtle differences over many age intervals to gauge the full impact of coupling on the cognitive factors. The results of the full and no coupling models were used to estimate the longitudinal trajectories of genetic and environmental variance in the spatial and speed factors, both in the full coupling model and the no coupling model. The resulting trajectories for the spatial factor—both raw variance and proportion of variance—are presented in Fig. 4. The accumulating impact of coupling over age is clear: although genetic variance in spatial ability generally decreases with age, coupling from FEV₁ is supporting less decline in genetic variance and even some increase with age. In parallel, in the full coupling model, less of the variance in the spatial factor is attributed to environmental factors. Thus, genetic variance for FEV₁ is contributing to subsequent genetic variance in the spatial factor. In the absence of coupling with FEV₁, the spatial factor manifests less genetic variance and more environmental variance with increasing age. Trajectories for the speed factor presented in Fig. 5 show the same pattern of results, although the magnitude of the pattern is smaller. For both factors, genetic variance for FEV₁ is contributing to subsequent genetic variance in cognitive performance.

Fig. 4.

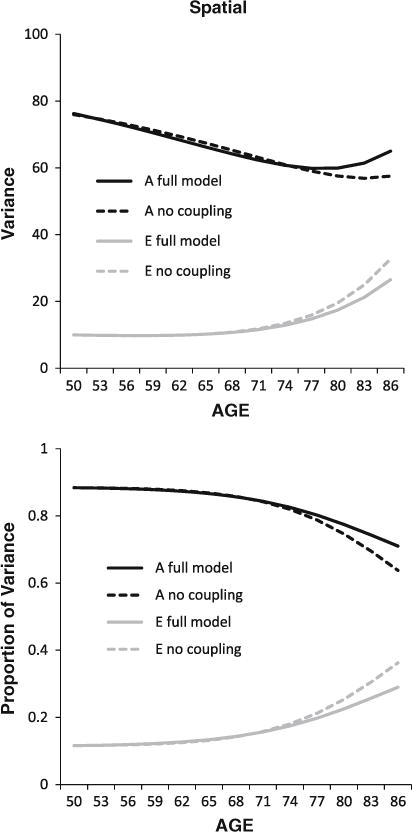
Longitudinal trajectories in total and proportion of genetic (A) and environmental (E) variance for the spatial factor, with and without full coupling with FEV₁

Fig. 5.

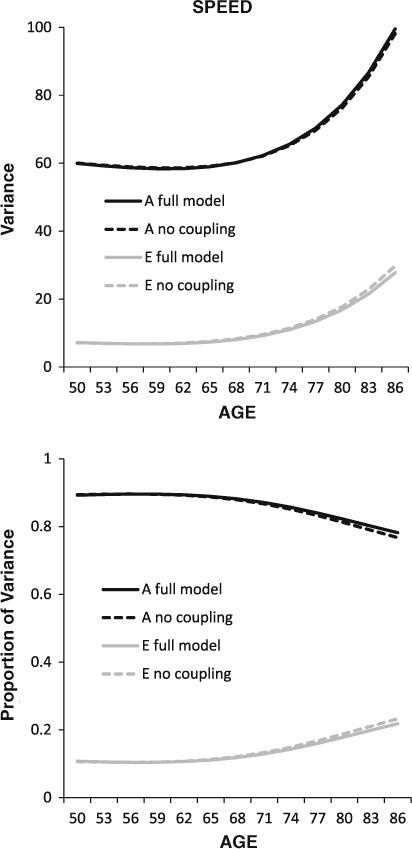
Longitudinal trajectories in total and proportion of genetic (A) and environmental (E) variance for the speed factor, with and without full coupling with FEV₁

Discussion

To test hypotheses about the genetic and environmental influences on the contribution of longitudinal changes in lung function to subsequent changes in fluid intelligence, biometric DCSMs were fit to the cognitive and pulmonary measures in two steps: univariate and bivariate. In the univariate analyses, models were fit to the spatial and speed factors and FEV₁ separately. Model comparisons indicated two general conclusions. First, similar to results from latent growth curve analyses of cognitive data (e.g., McArdle et al. 1998; McGue and Christensen 2001; Reynolds et al. 2002, 2005), model testing indicated significant genetic influences on the intercept and slope for each cognitive factor. Significant genetic influences were also indicated for the intercept of FEV_1; however, no significant genetic influences were found on the rate of change in FEV₁. Second, as is true in most biometric analyses of cognitive aging (for a review see McGue and Johnson 2007), individual variation in late adulthood is explained primarily by additive genetic and nonshared environmental influences; model fitting provided no evidence for correlated or shared environmental effects. The same was true for FEV₁. Although rearing environmental effects make a significant contribution to cognitive abilities during childhood, their impact begins to decline early in adulthood (Plomin et al. 2001).

Application of bivariate DCSMs to the cognitive and pulmonary measures allowed us to address the central hypotheses of genetic and environmental contributions to the temporal dynamics of the relationship between lung function and cognitive aging. Three dynamic relationships were investigated: genetic influences on FEV₁ as a leading indicator of variation in aging trajectories for cognitive abilities, genetic influences on cognitive function as a leading indicator of aging changes in pulmonary function, or a dynamic relationship with bidirectional genetic influences. Given previous investigations of the temporal dynamics between lung function and cognitive aging (Emery et al. 2012) and the genetic contributions to cross-time correlations between lung function and cognition (Emery et al. 1998), we hypothesized that genetic variance in lung function would play a leading role in age changes in spatial abilities and processing speed. Model fitting results supported our expectations by indicating a strong unidirectional coupling between FEV₁ and the cognitive factors. Thus, we can conclude that genetic variance in lung function is a leading indicator of variation in fluid intelligence. Non-shared environmental factors, such as access to physical exercise and health care, also may be important influences on fluid intelligence especially as these non-shared factors interact with genetic factors.

Limitations of these conclusions include the sparse data at either end of the age range, particularly after age 89. Even though the cross-sequential nature of the SATSA design means that older and younger adults have participated in a similar number of measurement waves, attrition and mortality unlikely to be independent of the variables of interest: cognitive and pulmonary function. Attrition rates did not differ by gender, zygosity, or smoking status. More complete data in the oldest portion of the age range, however, may have allowed us to estimate a significant decelerating age change in lung function instead of the nonsignificant trend identified here. That, in turn, may have impacted the etiology of the relationship between lung function and cognitive function. In the current model, the parameters of proportional change within variables (β) and the coupling across variables (γ) were estimated as constant across this age range. Recent analyses indicate that correlations among cognitive variables and genetic components of those correlations are higher in older adults (over age 65) than middle aged adults (Tucker-Drob et al. in press). It is possible, then, that the nature and etiology of the relationship between lung function and cognitive function varies over the second half of the lifespan. Given the computational complexity of the biometric bivariate DCSM, requiring supercomputer facilities to fit the model to the data, this extension of the model was not investigated at this time. Finally, although fluid ability was quantified via two latent factors to maximize stability, the factors do not represent the full range of abilities that are considered representative of fluid intelligence.

A recent genome-wide association study concluded that 51 % of the variance in spatial/fluid cross-sectional performance was accounted for by the thousands of SNPs included in the analysis (Davies et al. 2011). The results of the biometric DCSM analysis reported here suggest that researchers attempting to define the nature of the relationship between these SNPs and fluid intelligence may benefit from focusing their efforts on genetic factors influencing pulmonary function. In fact, we know from previous biometric bivariate DCSM analyses that genetic variance in processing speed drives subsequent changes in fluid intelligence (Finkel et al. 2009). The current analyses indicate that genetic variance in lung function drives subsequent changes in processing speed. Combination of analyses of this nature may allow researchers to begin to piece together the cascade effect of genetic influence as it works through the system: genes influence changes in lung function which impact subsequent changes in processing speed which impact subsequent changes in other aspects of fluid intelligence. Extensive information about genes associated with lung function is available (e.g., Chowdhary et al. 2012). We know that the path from gene product to phenotype is enormously complicated and subject at every stage to environmental influences as well. Combining results from several types of analyses, including DCSM, will bring us closer to understanding the etiology of cognitive functioning and cognitive aging. The significant outcome of the accumulation of subtle effects identified by the DCSM emphasizes the necessity of multiple waves of longitudinal data to fully comprehend the long-term impact of risk and protective factors for cognitive decline.