Modeling the Biomechanical Constraints on the Feedforward Control of Endpoint Stiffness

Abstract

Appropriate regulation of human arm mechanics is essential for completing the diverse range of tasks we accomplish each day. The steady state mechanical properties of the arm most relevant for postural tasks can be characterized by endpoint stiffness, the static forces generated by a limb in response to external perturbations of posture. Endpoint stiffness is directional, resisting perturbations in certain directions more than others. It has been shown that humans can voluntarily control the orientation of the maximum stiffness to meet specific task requirements, although the limits on this control are poorly understood. Both neural and biomechanical factors may limit endpoint stiffness control. The purpose of this work was to quantify the biomechanical constraints limiting the control of stiffness orientation. A realistic musculoskeletal model of the human arm coupled with a model of muscle stiffness was used to explore the range of endpoint stiffness orientations that could be achieved with changes in the feedforward control of muscle activation. We found that this range is constrained by the biomechanics of the neuromuscular system, and by the requirements of the specific task being performed by the subject. These constraints and the sensitivity to experimental conditions may account for some of the discrepancies in the literature regarding the ability to control endpoint stiffness orientation.

I. Introduction

Humans regulate arm mechanics to allow for stable interactions with the environment across a broad range of tasks. Understanding how this regulation occurs is an essential problem in motor control. The steady state mechanical properties of the arm can be characterized by endpoint stiffness, which is the relationship between externally applied displacements of the hand and the steady state forces generated in response [1]. Endpoint stiffness is directional, resisting perturbations in certain directions more than others, and is often represented graphically as an ellipse [1], [2]. The major axis of the stiffness ellipse indicates the orientation of the maximum endpoint stiffness. The ability to modulate the orientation of the maximum stiffness provides a mechanism for tuning arm mechanics to the requirements of a specific task. Experimental studies have shown that humans are able to voluntary control the orientation of maximum stiffness for at least certain tasks, but there are conflicting results regarding the degree of control and how this control varies across different tasks [2–4]. Our hypothesis is that these conflicting results arise at least in part from the biomechanical requirements of the different tasks used to assess endpoint stiffness modulation. Neural and biomechanical factors may constrain the ability to regulate endpoint stiffness orientation.

Neural constraints include the ability or inability to activate muscles independently [5]. Biomechanical constraints pertain to the geometric properties of the musculoskeletal system and the stiffness properties of the muscles within. Biomechanical constraints can be assessed through modeling, but the few modeling studies that have addressed this question either also incorporated neural constraints [4] or used models that did not fully represent the geometric and muscular complexity of the human arm [6].

The purpose of this study was to determine whether the musculoskeletal system of the human arm significantly constrains the ability to regulate endpoint stiffness orientation, and how these constraints vary with the biomechanical requirements of the task. This was accomplished using a realistic musculoskeletal model of the human arm [7] coupled with a scalable model of muscle stiffness [8]. This approach allows us to identify biomechanical constraints on stiffness orientation control separately from those that may also come from neural structures.

II. Methods

A. Modeling

The musculoskeletal model used in this study has two components: a muscle model characterizing muscle short-range stiffness [8], and a realistic musculoskeletal model of the human arm [7].

The muscle short-range stiffness model [8] assumed that the muscle short-range stiffness, K, consisted of two parts of stiffness in series: the tendon stiffness K^t and the muscle fiber stiffness K^m, as shown in (1).

$$K=K^m{K}^t/(K^m+K^t)$$ (1)

The tendon stiffness K^t was defined by generic, dimensionless force-strain curve of tendon [9]. The muscle fiber stiffness K^m was scaled with muscle force by (2) [8], where F^m is the current force generated by the muscle, $l_0^m$ is the optimal muscle fiber length at maximum activation, and γ (23.4) is a dimensionless constant describing the scaling of the short-range stiffness with muscle force.

$$K^m=\gamma F^m/l_0^m$$ (2)

The musculoskeletal model of the human arm [7] used in this study was implemented in SIMM (Musculographics Inc.). The model consisted of 37 arm muscles (or muscle compartments) and 4 kinematic degrees of freedom (elbow flexion/extension and shoulder flexion/extension, abduction/adduction and internal/external rotation). Based on the muscle physiological parameters and moment arms obtained from the arm musculoskeletal model, muscle stiffness K was calculated by (1) and (2), and was then transformed to endpoint stiffness K^e through the coordinate transformations in (3), where K⃗ is short-range stiffness matrix of muscles, K^j is the joint stiffness, θ is the joint angle vector and F⃗^m and F^end are the muscle force and endpoint force vector, respectively. J and G are Jacobians relating motions in joint space to muscle and endpoint space..

$$\begin{array}{l}{K}^j=J^T\overrightarrow{K}J+\frac{\partial J^T}{\partial \theta }{\overrightarrow{F}}^m\\ K^e={\left(G^{-1}\right)}^T\left[K^j-\frac{\partial G^T}{\partial \theta }{F}^{\mathit{end}}\right]G^{-1}\end{array}$$ (3)

B. Graphical representation of endpoint stiffness

Endpoint stiffness K^e can be represented graphically as an ellipse (Fig. 1), which illustrates the directional properties of K^e [1]. The major axis of the ellipse indicates the direction of the maximum endpoint stiffness, while the minor axis indicates the direction of the minimum endpoint stiffness. The endpoint stiffness orientation is defined as the angle between X axis shown in the figure and the major axis of the ellipse. This orientation can be computed using singular value decomposition of the K^e matrix [2]. In addition to orientation, endpoint stiffness is also characterized in terms of the shape (ratio of the minor to major axes) and the area [2].

Fig. 1.

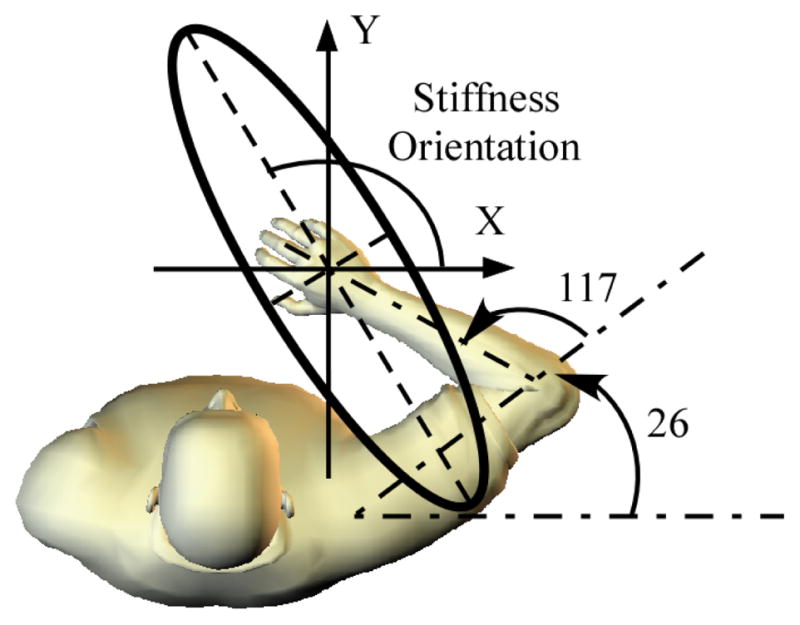
The fixed arm posture in simulating the control of stiffness orientation. Endpoint stiffness orientation was defined as the angle between X axis and the major axis of the ellipse.

C. Model validation

The musculoskeletal model was used to estimate endpoint stiffness across different arm postures in horizontal plane, and the results were compared with experiments in which subjects exerted isometric forces against a rigid manipulator [10]. Three arm postures and 17 endpoint forces were tested in the experimental study. These forces corresponded to 4 equally spaced levels between 7.5% and 30% MVC along the ±X and ±Y directions defined in Fig. 1; stiffness also was measured at rest. Endpoint forces were transformed to joint torques with the Jacobian G, and then joint torques were distributed across muscles by optimization [11]. Once the muscle forces were estimated, endpoint stiffness was estimated with Eqs. (1)~(3).

D. Simulating control of stiffness orientation

The musculoskeletal model was then used to evaluate the biomechanical limits on the range of endpoint stiffness orientations that could be achieved through changes in feedforward activation of the arm muscles. Results were compared to previously published data in which subjects were instructed to rotate the orientation of maximal endpoint stiffness as much as possible in both the clockwise and counterclockwise directions [2]. As in the experiments, endpoint forces in the horizontal plane were required to remain at zero, and postures were fixed (Fig. 1). The endpoint force constraints were implemented by requiring the flexion (Flex) and extension torques about the shoulder and elbow to be zero.

In addition to zero endpoint force, two additional constraints were evaluated. The first constraint assessed the influence of submaximal muscle contractions. The previous experimental trials lasted for approximately 2 minutes [2], making maximum activation in any muscle unfeasible for the entire trial. We evaluated the influence of reduced muscle activation by computing the range of stiffness orientations that could be achieved within full activation and when the maximum activation of all muscles was constrained to be less than 30% of maximum, a value that can be sustained for at least 2 minutes across a range of muscle groups [12]. The second constraint evaluated was the influence of supporting the arm against gravity, as was partially required in the initial experiments [2]. This support required subjects to generate shoulder abduction (Abd) and axial rotation (Rot) torques. To evaluate how these additional torque requirements affect the ability to control stiffness orientation, similar requirements were added to our simulation. These were estimated assuming typical segment masses for an average American adult male (86 kg) [13].

In the simulations, constrained optimization was used to determine the biomechanically feasible range of stiffness orientations given these mechanical constraints. This optimization was used to select the muscle activations that generated the maximum clockwise and counterclockwise rotations of stiffness orientation. The optimization was computed as follows:

$$\begin{array}{l}max(\mathrm{\Delta }\theta )\\ {TQ}_j=\sum _{i=1}^{37}{r}_{ij}\times a_i{F}_{i0}^{m}i=1,\dots ,37;j=1,\dots ,4\\ 0\le a_i\le a_{max}\end{array}$$ (4)

where Δθ is the maximum clockwise or counterclockwise rotations of endpoint stiffness orientation relative to the orientation that resulted with all muscles at rest. $F_{i0}^m$ is the maximum isometric force for ith muscle, r_ij is the moment arm for the ith muscle relative to the jth joint rotation axis (1, 2 and 3 indicate shoulder horizontal flexion, abduction and axial rotation respectively, and 4 indicates elbow flexion), TQ_j is the torque with respect to jth joint rotation axis, a_i is activation of the ith muscle. a_max is the maximum allowed muscle activation, which was set to either 100% or 30%, as described above.

III. Results

Our model accurately characterized how endpoint stiffness changed with changes in voluntary force. One of the 3 tested postures is shown in Fig. 2. The model matched previously collected experimental data well, even though no model parameters were fit to these data. Across all 3 tested postures, the model accounted for 97.19% of the variation in endpoint stiffness orientation. The model also accounted for an average of 93.84% and 84.72% of the variability in ellipse shape and area, respectively. These predictions were robust with respect to changes in model parameters, as determined by a sensitivity analysis. Variations in model moment arms, joint angles and muscle geometry over the full range of plausible changes resulted in orientation changes of less than 10 degrees. Size and shape changes were less than 20%. These results provide evidence that our model is useful for characterizing changes in endpoint stiffness across a range of muscle activation levels.

Fig. 2.

Endpoint stiffness estimation from the model at the central arm position, compared with one previous experimental (Exp) study [10]. Each ellipse is centered at a location proportional to the endpoint force direction and magnitude the subject was exerting.

Using the model, we determined that the control range of endpoint stiffness orientation was indeed constrained biomechanically (Fig. 3). Unconstrained control of stiffness orientation would have allowed for solutions orthogonal to the stiffness estimated for the rest condition (blue, small ellipses). When considering only flexion and extension torques, stiffness orientation could be rotated 21° counterclockwise and 72° clockwise, relative to the orientation of passive endpoint stiffness (Fig. 3A), a control range of 93°. This range decreased substantially when the maximal allowed muscle activations were restricted to 30% of maximum activation, more realistic value for these simulated experiments (Fig. 3B). With this restriction, stiffness orientation could be rotated 19° counterclockwise, and 50° in the clockwise direction. This corresponded to a control range of 69°.

Fig. 3.

Range of stiffness orientations at different levels of maximal muscle activation. Simulations considered a fully supported arm.

The achievable range of endpoint stiffness orientations was further reduced by requiring the model to support the arm against gravity (Fig. 4). These effects were observed only when muscle activations were restricted to 30% of maximum. With this restriction, the control range was decreased from 69° to 41°. For comparison, the control range in the experiments was (30±4°). At the moment, it is not possible to determine whether these small differences are due to the additional presence of neural constraints not included in our model or simply variations in our model that do not reflect the variability of the experimental results. The latter are currently being assessed.

Fig. 4.

Control range of endpoint stiffness from simulations with or without additional supporting torques at the shoulder. Data from one previous experimental study [2] were also shown as comparison.

IV. Discussion

This study examined whether the ability to control the orientation of arm endpoint stiffness is constrained biomechanically. A realistic musculoskeletal model of the human arm coupled with a muscle short-range stiffness model was applied to simulate human’s voluntary control of the endpoint stiffness orientation. We found that biomechanical constraints do exist, and that the extent of these constraints is strongly affected by experimental conditions, such as the muscle activation levels that can be sustained for the duration of an experiment and whether or not the arm is supported against the gravity. Understanding biomechanical constraints is an essential first step in studying additional neural constraints that may influence the ability to regulate endpoint stiffness in a task appropriate manner.

Other studies have also modeled the range of stiffness orientations that should be achievable, but have produced some conflicting results. Flash and Mussa-Ivaldi [14], and Tee et al. [6] demonstrated slightly larger control ranges than the maximum reported here. Neither of these studies, however, explicitly considered muscle properties or the task-dependent biomechanical constraints on the range of orientations that could be achieved. Hence, their predictions represent theoretical limits on the extent of stiffness orientation control, but not how those limits may be influenced by musculoskeletal constraints. Recent work by Tee et al. [15] incorporated more realistic limb geometry in the horizontal plane, but still could not assess the influence of muscle activity and external loads acting outside of this plane. Darainy et al. [4] concluded that control of stiffness orientation was constrained, reporting a number similar to our lowest estimates (~35°). Their model, however, required elbow and shoulder muscles to be activated synergistically, thereby enforcing simulated neural limits on the range of orientations that could be achieved. In contrast, our study focused only on biomechanical constraints, allowing any possible patterns of muscle co-activation, which could have led to a larger control range than those reported by Darainy.

Our results demonstrate that experimental conditions strongly influence the range of stiffness orientations that can be achieved, a finding not previously studied in the literature. Our use of a realistic 3D model allowed us to assess the influence of experimental conditions requiring the activity of muscles acting outside of the horizontal plane, such as those supporting the arm against gravity. Our findings may account for some of the discrepancies noted in the literature, regarding the range of stiffness orientations that could be achieved [2, 3]. The first experimental condition we evaluated was the length of the measurement time. Postural studies using stochastic perturbations [2] required times of up to 2 minutes, which was too long to sustain maximum voluntary contractions. Limiting the extent of muscle activation in our simulations was found to reduce the achievable range of stiffness orientations. Such limits are likely to be less important in studies with short trial times, such as those that assessed stiffness control during reaching [3]. The influence of limiting the maximum muscle activation was greatest when the simulations also were required to support the arm against gravity, as is typical in many experiments [2]. The combined effects of limited muscle activation and gravity compensation reduced the available control range to less than half of what could be achieved without these experimentally related constraints.

It is necessary to point out that our results consider only the steady state activation of muscles. Transient reflexes and voluntary responses to the perturbation may be able to alter the orientation of endpoint stiffness beyond that predicted by our model. This is likely to be especially true for rapid, transient perturbations or continuous perturbations with high bandwidths but low average velocities [16]. Nevertheless, our results clearly describe how the biomechanical properties of the arm limit the degree to which feedforward changes in muscle activation can be used to control endpoint stiffness orientation. Significant deviations from these predictions would suggest contributions from feedback pathways.

In conclusion, our results demonstrated how a realistic musculoskeletal model can be used to explore how biomechanical constraints influence the ability to regulate arm mechanics and whether these biomechanical constraints could cause the conflicting results in different experiments. Differences between our results and experimental findings may provide insight to the neural constraints on stiffness modulation [5] and possibly also the degree to which these constraints may be reduced with appropriate training.