Ionic Strength Effects on Amyloid Formation by Amylin Are a Complicated Interplay between Debye Screening, Ion Selectivity, and Hofmeister Effects

Abstract

Amyloid formation plays a role in a wide range of human diseases. The rate and extent of amyloid formation depends on solution conditions including pH and ionic strength. Amyloid fibrils often adopt structures with parallel, in-register β-sheets, which generate quasi-infinite arrays of aligned side chains. These arrangements can lead to significant electrostatic interactions between adjacent polypeptide chains. The effect of ionic strength and ion composition on the kinetics of amyloid formation by islet amyloid polypeptide (IAPP) is examined. IAPP is a basic 37-residue polypeptide responsible for islet amyloid formation in type 2 diabetes. Poisson–Boltzmann calculations revealed significant electrostatic repulsion in a model of the IAPP fibrillar state. The kinetics of IAPP amyloid formation are strongly dependent on ionic strength, varying by more than a factor of 10 over the range of 20 to 600 mM NaCl at pH 8.0, but the effect is not entirely due to Debye screening. At low ionic strength the rate depends strongly on the identity of the anion, nearly varying by a factor of four and scales with the electroselectivity series, implicating anion binding. At high ionic strength the rate varies by only 8% and scales with the Hofmeister series. At intermediate ionic strength no clear trend is detected, likely because of convolution of different effects. The effects of salts on the growth phase and lag phase of IAPP amyloid formation are strongly correlated. At pH 5.5, where the net charge on IAPP is larger, the effect of different anions scales with the electroselectivity series at all salt concentrations.

Amyloid fibrils are stable fibrous protein aggregates, containing significant cross-beta structure and have been implicated in the pathology of a number of human diseases including Alzheimer’s, Parkinson’s and type 2 diabetes. Proteins that form amyloid can be divided into two broad structural classes: those which adopt a compact well-defined structure in their non-aggregated state and those that are highly flexible and do not fold into a globular structure in their monomeric states, i.e. are natively unfolded. Important examples of the latter class include the Aβ peptide of Alzheimer’s disease and islet amyloid polypeptide (IAPP, amylin), the major component of the islet amyloid associated with type 2 diabetes.

The ability of a polypeptide to form amyloid is dependent on a range of factors; sequences that are rich in hydrophobic amino acids with a high β-sheet propensity, lack prolines and have a low net charge have high amyloidogenic propensity (1–6). Changes in the local environment of a normally soluble polypeptide can trigger and influence the rate of amyloid formation. These factors include changes in pH, temperature, pressure, alterations in the solvent or co-solvent composition, interaction with membranes or components of the extracellular matrix and changes in ionic strength (7–12). The structured regions in amyloid fibrils often adopt parallel in-register β-strand-rich arrangements, thus forming quasi-infinite arrays of identical residues. These in-register arrangements suggest the presence of significant ionic interactions in amyloids (6, 13–15). Ionic strength-dependent studies of amyloid formation have revealed that ions influence the kinetics and thermodynamics of the aggregation process (15–18). The effects differ from protein to protein, the underlying causes of which can be difficult to understand or interpret, in part because as many studies have been restricted to the use of one or only a few salts. Here, we analyze the ability of a wide range of salts to influence amyloid formation by islet amyloid polypeptide at pH 5.5 and 8.0.

IAPP is one of the most amyloidogenic naturally occurring polypeptides and the process of islet amyloid formation is believed to contribute to type 2 diabetes and to the failure of islet cell transplants (19–21). As a monomer, IAPP populates a fluctuating ensemble of conformations with modest local propensity to sample α-helical φ and ψ angles in the N-terminal half to two-thirds of the molecule, but is rich in β-sheet in the amyloid state (22, 23). The 37-residue polypeptide has no negatively charged groups due to the amidation of its C-terminus. There are four potential positively charged groups: the N-terminus, Lys1, Arg11, and His18 (Figure 1). Depending on the protonation state of His18 and the N-terminus, each IAPP molecule carries a +2 to +4 charge at physiological pH. The early stages of IAPP amyloid formation involve oligomerization of the cationic peptide and unfavorable electrostatic repulsion needs to be overcome by other interactions. Growth of the amyloid fibrils involves binding of soluble IAPP to fibril ends and also involves unfavorable electrostatic effects. The kinetics of amyloid formation by IAPP are highly pH-dependent, and are likely modulated by the protonation state of His18 and the N-terminus (15, 24); at low pH the time for amyloid formation is much longer than at neutral pH (15).

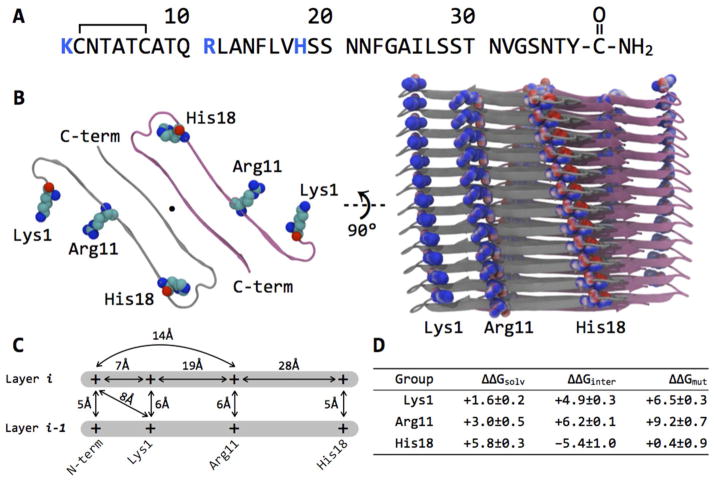
Figure 1.

(A) Primary sequence of human IAPP, with basic residues highlighted in blue. The polypeptide contains a disulfide bridge between residues 2 and 7 and has an amidated C-terminus. At physiological pH, the N-terminus is protonated and charged. (B) A model of the IAPP fiber, adapted from Sawaya and Eisenberg (51). Left, A view down the fibrillar axis (indicated by ●), with only a single layer shown for clarity. A layer consists of two molecules of IAPP, which interact through a dry “steric zipper” interface. With exception of His18 all basic groups are solvent-exposed; in the model of Sawaya and Eisenberg, His18 points inside the core. Right, The proposed supermolecular structure of the IAPP fiber. Twelve layers stacked on top of one another are shown, at an interval of 7.2 Å; the layers are arranged with a super-helical twist. Basic groups are shown in space-filling repserentation, and their heavy atoms are color-coded from red to blue (−20 to +20 k_bT/e_c units) according to the electrostatic potential calculated using APBS (53). The basic groups align with those in the layers above and below, and there is a preponderance of positive charge near the N-terminus. The molecular structures were rendered using VMD (54). (C) A schematic of calculated pairwise distances between the basic groups in the assembled IAPP fibril derived from the MD ensemble. Average distances are given; standard deviations of all measurements are below 2 Å. Two layers are displayed; the fibril continues vertically above layer i and below layer i−1. Please note that the distances are not drawn to scale. (D) Summary of the average Poisson–Boltzmann electrostatic contributions of Lys1, Arg11, and His18 side chains to protein stability. All values are in kcal mol⁻¹.

IAPP is processed in parallel with insulin and stored in the insulin secretory granule (25, 26). Insulin is packaged in a semi-crystalline form in the core of the granule, while IAPP is localized in the so-called “halo” region (27–31). The granule contains high concentrations of Zn²⁺ (20 mM) which is primarily associated with insulin, Ca²⁺ (120 mM), Mg²⁺ (70 mM), HPO₄²⁻ (70 mM) and adenine nucleotides (10 mM), and is thus a relatively high ionic strength environment. (29, 32). IAPP is packaged at protein concentrations which lead to rapid amyloid formation in vitro; thus, there must exist factors which prevent its irreversible aggregation in the granule. pH likely plays a role, since immature granules have a depressed pH of 5.5.

Much of our knowledge of ion-protein interactions is gleaned from studies of soluble globular proteins (33). Quantitative studies of the effect of salts on proteins date back to Hofmeister’s observations in the late 1800’s that different ions salted-out proteins from egg white with varying effectiveness (34). Salts can influence protein stability by specific binding, by altering the properties of the protein-solvent system (Hofmeister effects) and by screening electrostatic interactions (Debye-Hückel effects). At high ionic strengths ions are thought to exert their influence through non-specific clustering around charged protein groups, causing stabilizing charge–charge electrostatic interactions to decrease in strength, referred to as Debye-Hückel screening. In a similar manner, repulsive interactions are screened as well, allowing the forces that govern intermolecular association to predominate. Given that many amyloid fibrils, including those formed by IAPP, contain arrays of like charges, screening effects are likely to stabilize amyloids. So-called Hofmeister effects can also contribute at high ionic strength and arise from the effects of ions on the properties of water (33, 35). The Hofmeister series ranks ions on their ability to precipitate proteins. The effect of different ions can be quantified in a variety of ways; one useful method involves the Jones-Dole B-coefficient, which is a measure of the strength of ion–water interactions normalized to the strength of water–water interactions in bulk solution. Ions with a positive B-coefficient, termed kosmotropes, are strongly hydrated and small, with high charge density; these promote the stability and folding of globular proteins while decreasing protein solubility. Conversely, chaotropes have a negative B-coefficient, are weakly hydrated and “salt-in” proteins. The order with which anions precipitate proteins is as follows:

$${{\text{HPO}}_4}^{2-}>{{\text{SO}}_4}^{2-}>{\text{F}}^{-}>{\text{Cl}}^{-}>{\text{Br}}^{-}>{\mathrm{\Gamma }}^{-}>{\text{SCN}}^{-}$$

F⁻ and Cl⁻ represent the split between kosmotropes and chaotropes, respectively. Although cations can also be ranked according to the Hofmeister series, the effects are often dominated by anions, which are more strongly hydrated and have a greater effect on polarizable molecules. Ions may also specifically interact with charged or polar groups of a peptide, the strength of which is often reflected in the affinity of ions for an ion-exchange resin, the so-called electroselectivity series (36–38). For monovalent ions, the electroselectivity series scales inversely with the Hofmeister series.

We analyzed the distribution of charge–charge interactions in a model of the IAPP fiber and experimentally examined the effect of ionic strength and pH on amyloidogenesis kinetics. We show that increasing the ionic strength of a solution of IAPP monomers significantly increases the rate at which IAPP forms fibrils. The effects were examined at pH 5.5, where IAPP carries a net charge of +4, and at pH 8.0, where the net charge is close to +2, the exact value depending on the pKa’s of His18 and the N-terminus. We chose pH 5.5 because it is comparable to the inner granule pH of β-cells and pH 8.0 because the rate of amyloid formation is less sensitive to small pH changes at this value than it is at pH 7.4. We find that the effects of salts on amyloid formation include more than simple Debye-Hückel screening since significant variation is observed between different anions at constant ionic strength. At pH 8.0 and low ionic strength the ability of an anion to induce fibril formation is dependent on its order in the electroselectivity series, suggesting that ion binding plays a role. As the ionic strength is raised at pH 8.0, the strict dependence on the electroselectivity series disappears, possibly due to competition between Hofmeister and screening effects. However, when only the monovalent ions are considered, we observe linear correlations between the aggregation rates and the Hofmeister and electroselectivity series. At high ionic strength the variation in rate is much smaller than at low ionic strengths and the Hofmeister effect appears to account for the observed inter-anion variation. In contrast, at pH 5.5 the observed effects scale with the anion electroselectivity series at all ionic strengths.

Materials and Methods

Analysis of fibril structures and Poisson-Boltzmann electrostatic calculations

The starting coordinates for MD simulation of the IAPP protofibril were taken from Sawaya et al. The protonation state of His18, as well as the flip states of glutamine or asparagine, were determined with REDUCE (39); since His18 faces into the core of the fibril, it was taken to be uncharged and all copies of His18 were singly-protonated at Nδ. We solvated 24 polypeptide chains (12 layers) in an orthorhombic box (dimensions 106×90×76 Å) containing approximately 18,300 equilibrated TIP3P water molecules using CHARMM (40); the 68,000-atom system was charge-neutralized by adding 72 Cl⁻ ions (220 mM final concentration). To avoid self-interactions in the periodic cell, dimensions of the water box were set such that the solute was 10 Å away from the cell side. Solvation and neutralization steps of the system used a locally-modified solvation input script retrieved from www.charmmtutorial.org.

Isothermal–isobaric (NPT) ensemble molecular dynamics (MD) simulations were carried out with the NAMD 2.6 engine compiled for the IBM Blue Gene/L architecture, using the CHARMM22-CMAP molecular mechanics force field (41, 42). Constant pressure of 1 atm was maintained with the Nosé–Hoover Langevin piston pressure control; simulation temperature was set at 300K. All bonds involving hydrogen atoms were constrained to their equilibrium lengths using the SHAKE algorithm. The simulation time step was set at 2 fs and non-bonded interactions were evaluated every step. We used a cutoff of 12 Å for all Lennard–Jones and short-range electrostatic interactions. Long-range electrostatics were treated using a Particle Mesh Ewald method with a fourth-order interpolation scheme. To minimize edge effects during analysis, distance measurements between basic groups were performed for the two middle stack layers (four chains), and averaged across time to give the final values.

We determined the contributions of side chains to protein stability by solving the linearized Poisson-Boltzmann equation using a multi-grid finite-difference solver distributed with the Integrated Continuum Electrostatics (ICE) software suite (courtesy of B. Tidor), using standard protocols (43). Atomic partial charges were from the CHARMM22-CMAP parameter sets. The dielectric boundary was defined by the molecular surface generated with a 1.4 Å radius probe, and a 2.0 Å ion exclusion layer was used; the surfaces were generated using radii optimized for use in continuum electrostatic calculations (44). The solute and solvent dielectric constants were set to 2 and 80, respectively, at an ionic strength of 145 mM. Boundary conditions were computed using a three-step focusing procedure on a 129³-unit cubic grid, with the molecule first occupying 23%, then 92%, and finally 184% of the grid. At each focusing level boundary conditions were taken from the previous calculation, with Debye-Hückel potentials used at the boundary of the lowest focusing level. The electrostatic contribution of a sidechain at position i to the unfolded state was modeled by its interactions with the (i−1)_carbonyl-(i)-(i+1)_amino “tripeptide” in the absence of any other protein groups; the conformation of the tripeptide was unchanged from that of the fibrillar state. PB calculations were performed on 80 snapshots extracted at 1 ns intervals from the MD ensemble. To minimize edge effects, the PB energetics components were only calculated for the middle two layers (four peptide chains), and averaged to give the final values.

Peptide Synthesis and Purification

IAPP was synthesized on a 0.25 mmol scale using a CEM Liberty Microwave Peptide Synthesizer utilizing 9-fluorenylmethoxycarbonyl (Fmoc) chemistry. All solvents used were ACS grade. The microwave method and the use of Fmoc-protected pseudoproline dipeptide derivatives have been described previously (45, 46). Fmoc amino acids and pseudoproline dipeptide derivatives were purchased from Novabiochem. All other reagents were purchased from Sigma and Fisher Scientific. Use of a 5-(4′-Fmoc-aminomehtyl-3′, 5-dimethoxyphenol) valeric acid (PAL-PEG) resin (Nova biochem) afforded an amidated C-terminus. Residues A8-T9 and L27-S28 were attached to the growing peptide chain as pseudoproline dipeptide derivatives and double coupled. The following residues were also double coupled: N3 through C7, R11, L16, V17, I26, T30 and V32. The peptide was cleaved from the resin through the use of standard trifluoroacetic acid (TFA) methods; ethanedithiol, thioanisole and anisole were used as scavengers. The disulfide bond was formed via incubation in DMSO (47, 48). IAPP was purified via reverse-phase high performance liquid chromatography (RP-HPLC) using a Vydac C18 preparative column. A two buffer system was utilized in which buffer A consisted of 0.045% HCl in H₂O (v/v) and buffer B of 80% acetonitrile and 0.045% HCl in H₂O (v/v). TFA was avoided since small amounts of TFA caninfluence aggregation rates. The purity of the peptide was checked by HPLC using a Vydac C18 analytical column and the identity was confirmed by matrix-assisted laser desorption ionization time-of-flight mass spectrometry (MALDI-TOF MS); observed 3903.9 Da, expected 3903.4. Da.

Fluorescence Assays

All fluorescence assays were performed on a Beckman Coulter DTX 880 Multimode Detector plate reader. Thioflavin-T fluorescence was measured utilizing a 430 nm excitation filter (Beckman Coulter) with a 35 nm bandwidth and a 485 nm emission filter with a 20 nm bandwidth. The assays were performed in a Corning 96-well Non-Binding Surface black plate with a lid and a clear, flat bottom in bottom plate-reading mode. IAPP was prepared by dissolving the peptide in 100% hexafluoroisopropanol (HFIP) to a concentration of 1.58 mM and filtering through a 0.45 μm GHP Acrodisc filter once the peptide was fully dissolved. This solution was lyophilized to remove the HFIP. The lyophilized IAPP was dissolved in 10 mM Tris, pH 8.0 buffer to a stock concentration of 1.58 mM and immediately diluted to a concentration of 32 μM in each salt solution. For the pH 8.0 experiments, 1 M ionic strength salt solutions of Na₂HPO₄, Na₂SO₄, NaSCN, NaI, NaBr, NaCl, NaF, KCl and LiCl were prepared in 10 mM Tris-HCl, pH 8.0. Phosphate is approximately 86% HPO₄²⁻ at this pH. The 1 M salt solutions were diluted to 20, 100, 200, 400, 600 and 800 mM ionic strength solutions using 10 mM Tris buffer and the addition of peptide. The solutions also contained 32 μM thioflavin-T. For the pH 5.5 experiments, salt solutions were prepared as for the pH 8.0 experiments, but in the presence of 10 mM MES buffer, pH 5.5. Phosphate is approximately 98% H₂PO₄⁻ at this pH. The pH was checked after all samples were prepared. Reactions were incubated at 25°C in the plate reader with no agitation. Data points were recorded every 300 s for the first 8 hours and every 900 s thereafter. Data were fit to the sigmoidal curve expression below:

$$r(t)=(m_{1}t+r_1)\alpha +(m_{2}t+r_2)(1-\alpha )$$ (1)

where $\alpha ={(1+e^{\left(\frac{t_{50}-t}{\tau }\right)})}^{-1}$. The fit yields t₅₀, the time at which amyloid formation is 50% complete, as judged by the fluorescence response and the time constant of the transistion, τ, which is related to the apparent rate at t = t₅₀. The constants m₁, m₂, r₁, and r₂ define the baseline slopes and intercepts of the sigmoidal curve in the linear pre- and post-transition regions. The data were fit by allowing the parameters to vary independently. The apparent maximum rate at t = t₅₀, or v_max, is calculated by converting the time constant of the transition t, using the equation

$${\text{v}}_{max}=\frac{{[\text{IAPP}]}_{\text{t}=0}}{4\tau }$$ (2)

where [IAPP]_t=0 is the concentration of IAPP at the start of the reaction (49). The length of the lag phase, t_lag, was calculated using the equation t_lag = t₅₀ − 2τ.

Transmission Electron Microscopy (TEM)

TEM was performed at the University Microscopy Imaging Center at the State University of New York at Stony Brook. 15 μL samples from the end of the kinetic experiments were placed on a carbon-coated 300-mesh copper grid and negatively stained with saturated uranyl acetate.

Results

Analysis of structural models of the IAPP protofibril reveals significant charge repulsion

IAPP is a basic polypeptide with single Lys, Arg and His residues (Figure 1A) and no acidic groups on account of the amidated C-terminus. Depending on the protonation state of the His side chain and the N-terminus, IAPP carries a +2, +3 or +4 charge at the physiological pH of 7.4. In the fibrillar state, IAPP is thought to form in-register, parallel β-sheets. Several models for the supermolecular structure of the IAPP fibril have been proposed. Of these, the solid-state NMR derived models of Tycho and crystallography-derived models of Eisenberg are consistent in their overall geometry (50–52). In these models the protofibfil is composed of two C₂-symmetic stacks of IAPP monomers, with each monomer adopting a “U”-shaped structure containing two β-strands. There are no intrachain backbone hydrogen bonds; instead, each monomer hydrogen-bonds to adjacent neighbors along the fibrillar axis in the same stack (Figure 1B). We adopted the structural model of Sawaya and Eisenberg based on crystallographic studies of short self-complementary IAPP fragments; this model contains more than 50 bimolecular layers, and thus minimizes edge effects, compared to the five-layer solid-state NMR model. Starting with a protofibril fragment composed of 24 IAPP molecules arranged in 12 layers, we generated a conformational ensemble using an 80 ns explicit-solvent all-atom molecular dynamics (MD) simulation and measured the distribution of pairwise distances between the basic groups.

In our fibril model, there are no close charge-charge contacts between two chains belonging to the same layer (Figure 1B). Instead, the closest charge-charge contacts are between layers stacked along the fibrillar axis (Figure 1C). We found that, on average, the side chains of Lys1, Arg11, His18, as well as the N-terminus are within 6 Å away from their counterparts in adjacent layers. Within a layer, the N-terminus and side chain of Lys1 are 7 Å away, and Arg11 is 14 and 19 Å away from the two groups, respectively. His18 is distant from the other basic groups.

Poisson–Boltzmann (PB) calculations revealed that in the protofibril model, both Lys1 and Arg11 reside in a strongly-repulsive electrostatic environment and contribute unfavorably to protein stability. Our approach is to tabulate the desolvation penalty paid by and the interactions made by each side chain (ΔΔG_solv and ΔΔG_inter, respectively). The sum of these two free energy terms yields ΔΔG_mut, which compares the contribution of a side chain relative to its hydrophobic isostere. ΔΔG_mut corresponds to a transformation of “turning on” the charges; thus, a positive value of ΔΔG_mut indicates that a side chain does not compensate in favorable inter- or intra-molecular interactions to overcome its desolvation. The calculations were performed for the sidechains, but not the N-terminus due to the lack of a consistent unfolded-state model. Note that the calculation does include the effect of the N-terminus on the charged side chain. We found that Lys1, Arg11, and His18 paid desolvation penalties of 1.6, 3.0, and 5.8 kcal mol⁻¹, respectively. Lys1 and Arg11 make unfavorable interactions of +4.9 and +6.2 kcal mol⁻¹ with other groups in the fiber, respectively. His18, on the other hand, makes favorable interactions of −5.4 kcal mol⁻¹ with adjacent groups, consistent with the alternating regions of positive and negative electrostatic potential for His18 visible in Figure 1B. Our calculations suggest that both Lys1 and Arg11 significantly destabilize the fibril, and suggest that repulsive interactions involving these groups (as well as the N-terminus) may be reduced in magnitude with increased ionic strength. The effects due to Lys1 are of interest since this residue is outside the core of the β-strand structure, but should still influence fiber stability.

The rate of IAPP amyloid formation depends strongly on ionic strength

We first examined salt-dependent effects at pH 8.0. The kinetics of amyloid formation by IAPP in the presence of various salts were followed by thioflavin-T fluorescence. Thioflavin-T is negligibly fluorescent in the absence of amyloid, but exhibits a significant increase in quantum yield upon binding to amyloid. The aggregation of IAPP can be described by a sigmoidal transition with a well-defined lag phase in which monomers and oligomers dominate the population, followed by a growth phase during which fibrils elongate, and finally, a plateau. The ability of salts to induce the aggregation of IAPP was tested at 20, 100, 200, 400, 600 and 800 mM ionic strength. 10 mM Tris at pH 8.0 was present in all reactions and sodium was used as the counter-ion for all of the anions tested. We chose to perform our experiments at pH 8.0 because minor variations in pH have only a small effect on amyloid kinetics at this pH, but have a significant effect at pH 7.4. Additional experiments were conducted with a set of chloride salts in order to probe the consequences of varying the cation.

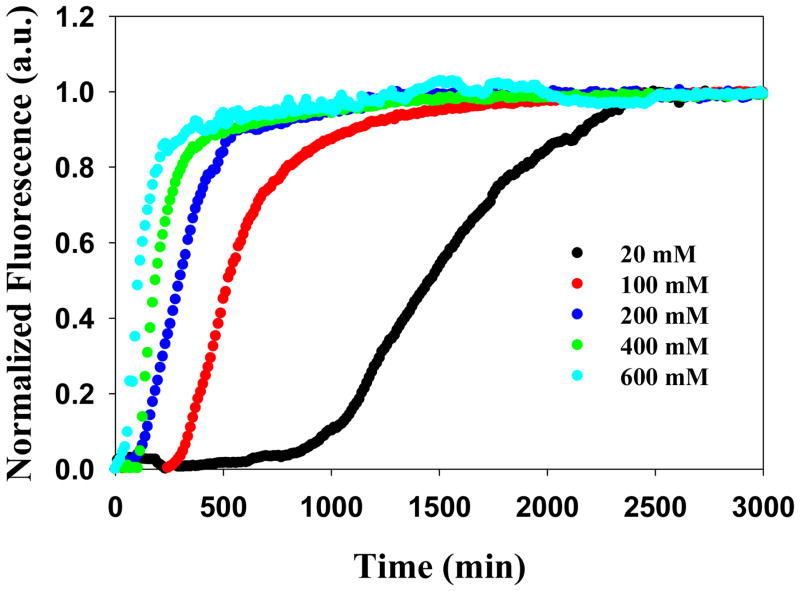
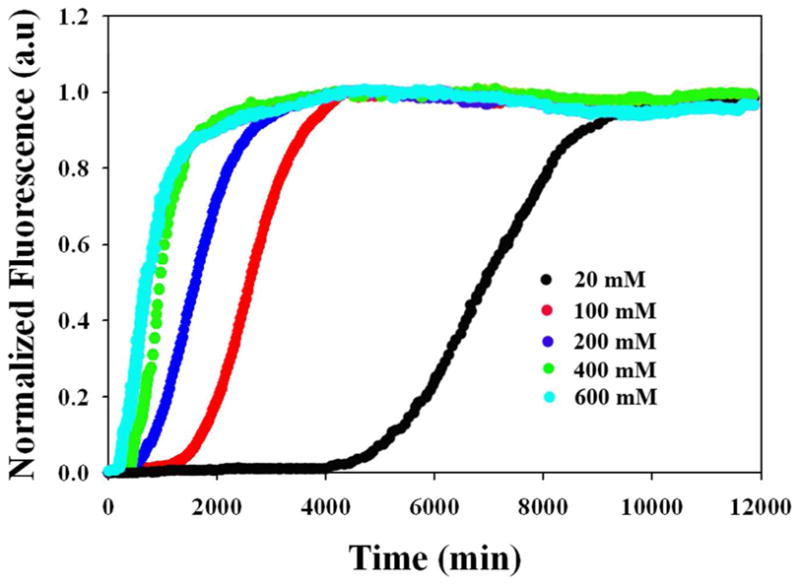
The addition of salt increases the rate at which fibril formation occurs. Figure 2 displays the thioflavin-T kinetic curves for IAPP in the presence of increasing concentrations of NaCl, the weakest chaotropic salt examined. Increasing the NaCl concentration leads to a reduction in the length of the lag phase and a decrease in the value of t₅₀, the time required for the thioflavin-T signal change to reach half its maximal value. At 30 mM ionic strength (20 mM NaCl and 10 mM Tris-HCl) the t₅₀ was 1340 minutes while it was only 130 minutes at 610 mM ionic strength (600 mM NaCl with 10 mM Tris-HCl). Further addition of salt eliminates the lag phase entirely: at 800 mM NaCl fibril formation begins during the dead time of the experiment (data not shown) for nearly all of the anions and kinetic parameters could not be calculated.

Figure 2.

Dependence of the kinetics of amyloid formation on the ionic strength for various concentrations of NaCl at pH 8.0. Plots of thioflavin-T fluorescence intensity versus time are displayed. The concentration of added NaCl ranged from 20 to 600 mM. All experiments were conducted at 25 °C, pH 8.0 and all samples contained 10 mM Tris-HCl. The concentration of IAPP and thioflavin-T were both 32 μM.

The rate of IAPP amyloid formation depends on the choice of anion, but is less dependent on the choice of cation

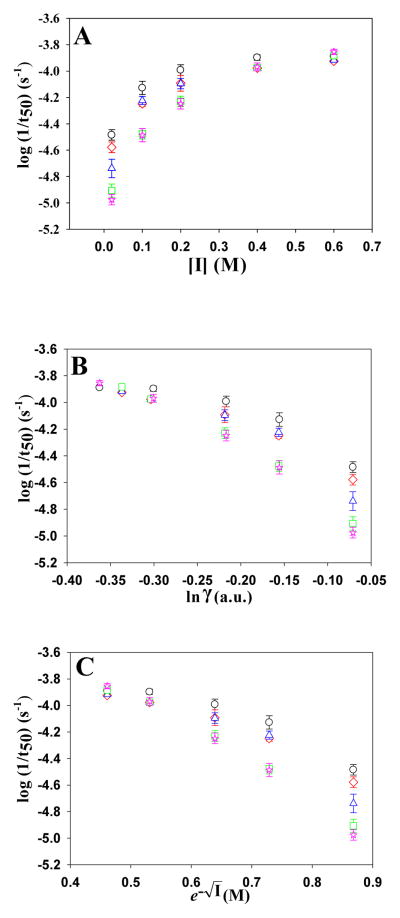
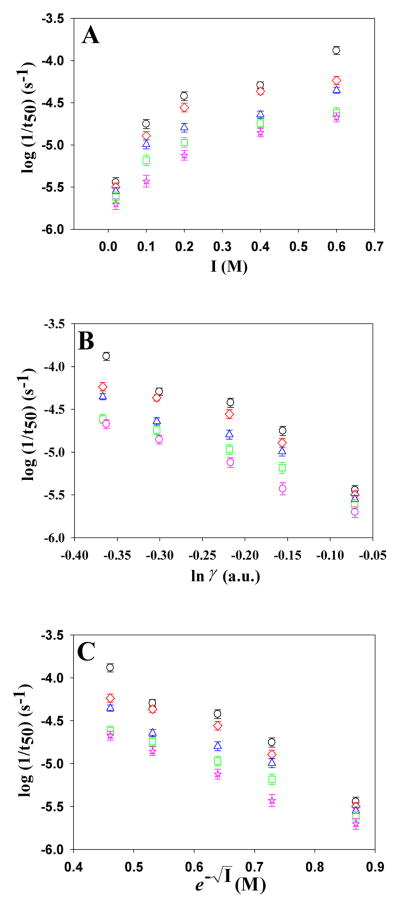
Thioflavin-T fluorescence-monitored kinetic experiments were conducted in the presence of the monovalent anions SCN⁻, I⁻, Br⁻, Cl⁻ and F⁻ and the divalent anions HPO₄²⁻ and SO₄²⁻, with Na⁺ as the counter-ion for all reactions. A plot of log(1/t₅₀) versus the ionic strength (I) from 30 to 610 mM for the monovalent anions SCN⁻, I⁻, Br⁻, Cl⁻ and F⁻ at pH 8.0 is shown in Figure-3a. The kinetics of amyloid formation are complex, involving multiple steps and likely parallel pathways. It is thus difficult, if not impossible, to extract microscopic rate constants from single thioflavin-T curves. We used 1/t₅₀ as a proxy for the rate of amyloid formation and plotted its logarithm since ionic strength effects on protein folding rates are usually analyzed in this fashion. At every concentration tested, all of the salts decreased the t₅₀ of fibril formation compared to buffer. As the ionic strength is increased the rate of amyloid formation increases for all salts and t₅₀ decreased. However, the trend does not follow the form expected if the t₅₀ or log(1/t₅₀) depends solely on electrostatic screening, the Hofmeister effect or direct anion binding. Electrostatic screening has been modeled using the Debye-Hückel limiting law, $ln(\gamma )=\frac{-0.509[z^{+}{z}^{-}]\sqrt{I}}{1+\beta \alpha \sqrt{I}}$ dependence expected for the activity coefficient of an ion, where z is the charge on the ions, I is the ionic strength, a is the effective hydrated radius of the ion and β is an empirical, unitless constant of 0.33. Screening has also been modeled using a relationship that predicts that charge screening should have a e^−√I dependence on ionic strength. The plots of the log(1/t₅₀) versus either e^−√I,or I over the range of ionic are non-linear (Figure-3b and -3c, respectively). The plots are also non-linear if (1/t₅₀) or t₅₀ are plotted instead of log(1/t₅₀). In addition, different ions exert different effects at the same ionic strength. These observations show that ionic strength effects cannot be due to just Debye–Hückel screening.

Figure 3.

Analysis of the dependence of log(1/t₅₀) on ionic strength, I, for the monovalent anions at pH 8.0. The observed values of log(1/t₅₀) are plotted vs. (A) I; (B) ln(γ); (C) e^−√I Black circles, NaSCN; Red diamonds, NaI; Blue triangles, NaBr; Green squares, NaCl; Pink stars, NaF. The error bars represent the apparent standard deviation from three separate kinetic runs.

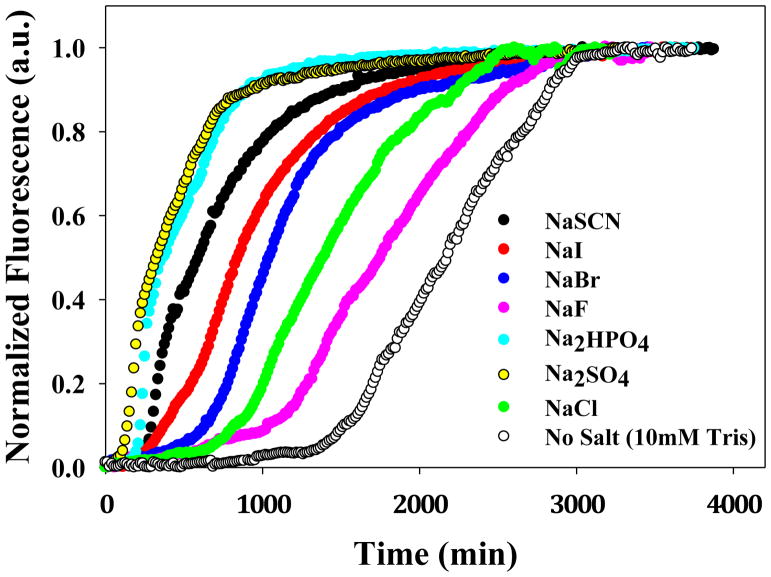
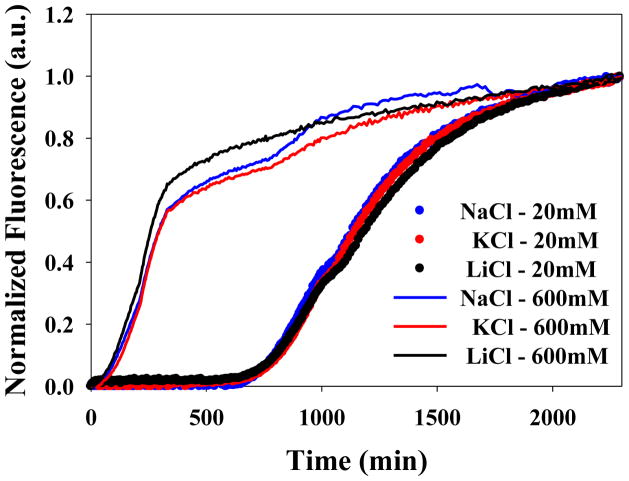
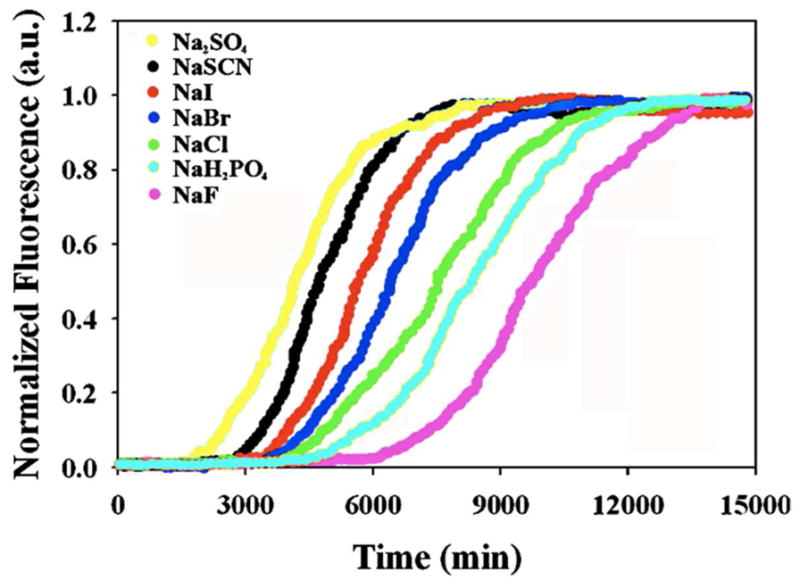
Figure 4 displays the kinetic curves of all the salts at pH 8.0 at 30 mM total ionic strength. All of the salts reduced the lag phase and the t₅₀ of fibril formation compared to buffer alone, but there is significant variation between the different anions. The order with which anions induce amyloid formation by IAPP under these conditions is as follows: SO₄²⁻ > HPO₄²⁻> SCN⁻ > I⁻ > Br⁻ > Cl⁻ > F⁻. The values of t₅₀ ranged from 420 minutes in sulfate to 1,570 minutes in fluoride. The effect of varying the cation (Li⁺, K⁺ and Na⁺) on the kinetics of amyloid formation was also probed at both 30 mM and 610 mM ionic strengths (Figure-5). There is no major difference among the cations tested at both low and high ionic strength.

Figure 4.

Dependence of the kinetics of amyloid formation on the anion identity at 20 mM added salt (30 mM ionic strength) at pH 8.0. Plots of thioflavin-T fluorescence intensity versus time are displayed. All experiments were conducted at 25 °C, pH 8.0 and all samples contained 10 mM Tris-HCl. The concentration of IAPP and thioflavin-T were both 32 μM.

Figure 5.

The identity of the cation has little effect on the kinetics of amyloid formation. Thioflavin-T curves are shown at 20 mM and 600 mM added salt for NaCl, KCl and LiCl. Experiments were conducted at pH 8.0.

At pH 8.0, anionic selectivity is important at low ionic strength and Hofmeister effects are important at high ionic strength

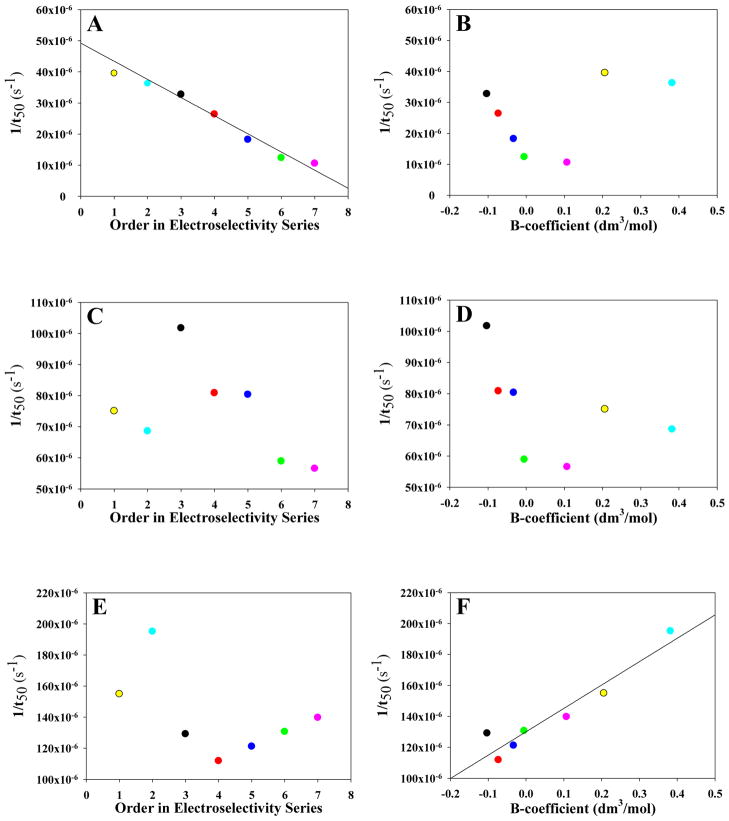
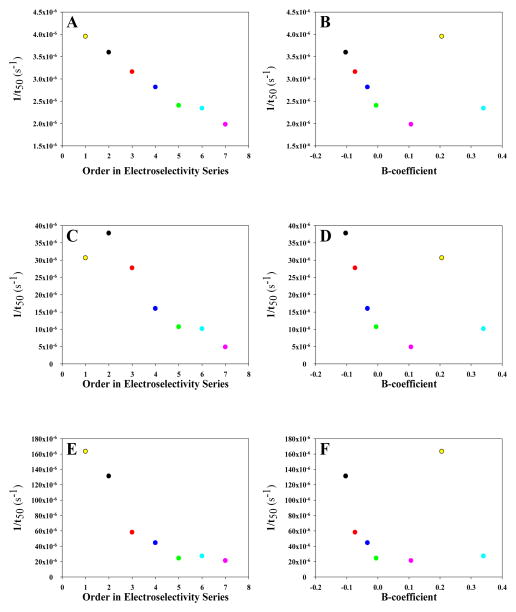
Comparing the rates of fibril formation in the presence of various salts reveals that the different anions influence the rate of IAPP amyloid formation to varying extents. To determine if the effects are dependent on Hofmeister effects or on direct anion binding, the rate of fibril formation (1/t₅₀) was plotted versus either the B-coefficient of each anion, a measure of the Hofmeister effect, or versus the electroselectivity series order. We found that the rate of amyloidogenesis scales inversely with the Hofmeister series at pH 8.0 and the lowest ionic strength for the monovalent salts, while following the order of the electroselectivity series for all anions (Figure 6b and 6a, respectively). As the ionic strength is increased, the strict correlation with the electroselectivity series disappears and no correlation is observed in the plot for 210 mM ionic strength (Figure 6c and 6d) when all anions are considered. The data for 110 and 410 mM ionic strength display a similar lack of direct dependence on either the Hofmeister or electroselectivity series (Supporting Information). The lack of a clear correlation with the Hofmeister effect or the electroselectivity series at intermediate salt concentrations is likely due to the convolution of different effects. At the highest ionic strength, 610 mM, the dependence on the identity of the anion is the opposite of that observed at 30 mM, although the variation is much smaller at high salt than at low salt, varying by only 8%. At 610 mM at pH 8.0, the 1/t₅₀ scales with the B-coefficient of the Hofmeister series for all salts (Figure 6f) and little correlation is observed with the electroselectivity series (Figure 6e). However, when only the monovalent ions are considered, we observe linear correlations between the rate of aggregation and the Hofmeister or electroselectivity series. At intermediate salt concentrations no clear trends are observed. Ion binding will still play a role at high ionic strength, but differences in anion affinity no longer dominate the observed trends.

Figure 6.

The rank order of the effects of different anions on the rate (1/t₅₀) of amyloid formation at pH 8.0 at 20 (A and B), 200 (C and D) and 600 mM (E and F) added salt versus their order in the electroselectivity series (A, C and E) and the Hofmeister series (B, D and F). Note that the vertical axis scale is different for the different ionic strengths. At 20 mM added salt the order of the rate of amyloid formation for the anions scales with their order in the electroselectivity series (A), but not with the Jones–Dole B-coefficient (B). At 200 mM added salt the strictly-linear trend disappears for both the electroselectivity series (C) and Hofmeister series (D), presumably from competing effects between the forces involved from each effect. At high ionic strength, 600 mM added salt, the on amyloid formation scaled with the Hofmeister series (F), but not the electroselectivity series (E). Interestingly, we observe strong linear correlations at all ionic stengths for when only the monovalent salts are considered. Black, NaSCN; Red, NaI; Blue, NaBr; Green, NaCl; Pink, NaF; Yellow, Na₂SO₄; Cyan, Na₂HPO₄. All samples contained 10 mM Tris-HCl in addition to the added salt.

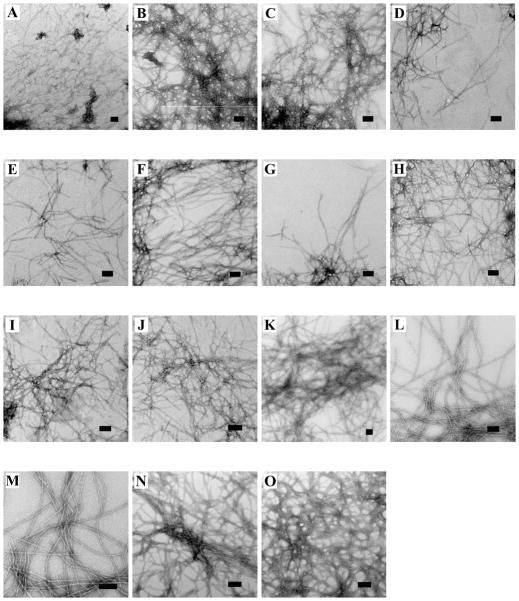
Salts can precipitate proteins into amorphous aggregates as well as into ordered fibrils, hence it is important to confirm that IAPP still forms amyloid under the conditions investigated. Consequently, we used TEM to examine the morphology of the material formed in the presence of each salt at low added salt (30 mM) and high added salt (610 mM). Amyloid fibrils were observed in all cases (Figure 7). There was no significant difference in the morphology at either concentration across the range of anions compared to fibrils formed in buffer alone.

Figure 7.

Salts induce amyloid formation, not amorphous precipitates. All samples were collected at the end of the kinetic assays and contain 10 mM Tris-HCl, pH 8.0. (A) No added salt (B) 20 mM NaSCN, (C) 600 mM NaSCN, (D) 20 mM NaI, (E) 600 mM NaI, (F) 20 mM NaBr, (G) 600 mM NaBr, (H) 20 mM NaCl, (I) 600 mM NaCl, (J) 20 mM NaF, (K) 600 mM NaF, (L) 20 mM Na₂SO₄, (M) 600 mM Na₂SO₄, (N) 20 mM Na₂HPO₄, (O) 600 mM Na₂HPO₄. Scale bar is 100 nm.

At pH 5.5, the rate of IAPP amyloid formation correlates with anionic selectivity at both low and high ionic strength

The rates of fibril formation were also measured at pH 5.5, and we observed a significant dependence of the rate of amyloid formation on ionic strength at this pH. Increasing the NaCl concentration leads to a reduction in both tlag and t₅₀ (Figure 8). At 30 mM ionic strength (20 mM NaCl, 10 mM MES) the t₅₀ was 6,930 minutes and 690 minutes at 610 mM ionic strength (600 mM NaCl, 10 mM MES). The curves are broadly similar to those observed at pH 8.0; however, the rates are significantly slower as judged by comparison to the t₅₀’s at pH 8.0. A plot of the log(1/t₅₀) versus the ionic strength (I) from 30 to 610 mM for the monovalent anions SCN⁻, I⁻, Br⁻, Cl⁻ and F⁻ at pH 5.5 is shown in Figure-9a. All of the salts decreased the t₅₀ of fibril formation compared to buffer at all concentrations tested. The plots of the log(1/t₅₀) versus ionic strength (I), In(γ) or e^−√I from 30 to 610 mM at pH 5.5 for the monovalent salts are non-linear, similar to the plots at pH 8.0.

Figure 8.

Dependence of the kinetics of amyloid formation at pH 5.5 on the ionic strength for various concentrations of NaCl. Plots of thioflavin-T fluorescence intensity versus time are displayed. The concentration of added NaCl ranged from 20 to 600 mM. All experiments were conducted at 25 °C, pH 5.5 and all samples contained 10 mM MES. The concentration of IAPP and thioflavin-T were both 32 μM.

Figure 9.

Analysis of the dependence of log(1/t₅₀) on ionic strength, I, for the monovalent anions at pH 5.5. The observed values of log(1/t₅₀) are plotted vs. (A) I; (B) ln(γ); (C) e^−√I. Black circles, NaSCN; Red diamonds, NaI; Blue triangles, NaBr; Green squares, NaCl; Pink stars, NaF. The error bars represent the apparent standard deviation from three separate kinetic runs.

Similar to the effects observed at pH 8.0, there is significant variation among the salts tested and the t₅₀ of each is decreased in comparison to buffer at the lowest ionic strength, 30 mM (Figure 10). The order with which anions induce amyloid formation by IAPP under these conditions is as follows: SO₄²⁻ > SCN⁻ > I⁻ > Br⁻ > Cl⁻ > H₂PO₄^2–− > F⁻. The values of the t₅₀ range from 4,220 minutes for SO₄²⁻ to 8,410 minutes for F⁻ and follow the electroselectivity series. Note that phosphate is 98% monovalent at this pH and its order in the electroselectivity series shifts to a position between Cl⁻ and F^−. The behavior at pH 5.5 at high salt differs from that at pH 8.0. Unlike at pH 8.0, at high ionic strength the rate of fibril formation at pH 5.5 scales with the electroselectivity series, but not with the B-coefficient (Figure 11). However, the trend with the Hofmeister series and the ionic selection series are similar if phosphate and sulfate are excluded. The trend is the same at intermediate ionic strengths of 110 mM and 410 mM (Supporting Information).

Figure 10.

Dependence of the kinetics of amyloid formation on the anion identity at 20 mM added salt (30 mM ionic strength) at pH 5.5. Plots of thioflavin-T fluorescence intensity versus time are displayed. All experiments were conducted at 25 °C, pH 5.5 and all samples contained 10 mM MES. The concentration of IAPP and thioflavin-T were both 32 μM.

Figure 11.

The rank order of the effects of different anions on the rate (1/t₅₀) of amyloid formation at pH 5.5 at 20 (A and B), 200 (C and D) and 600 mM (E and F) added salt versus their order in the electroselectivity series (A, C and E) and the Hofmeister series (B, D and F). At 20 mM added salt the order of the rate of amyloid formation for the anions scales with their order in the electroselectivity series (A), but not with the Jones–Dole B-coefficient (B). At 200 mM added salt the strictly-linear trend disappears for both the electroselectivity series (C) and Hofmeister series (D), presumably from competing effects between the forces involved from each effect. At high ionic strength, 600 mM added salt, the effect on amyloid formation scaled with the Hofmeister series (F), but not the electroselectivity series (E). Interestingly, we observe strong linear correlations at all ionic stengths for when only the monovalent salts are considered. Black, NaSCN; Red, NaI; Blue, NaBr; Green, NaCl; Pink, NaF; Yellow, Na₂SO₄; Cyan, Na₂HPO₄. All samples contained 10 mM MES.

Discussion

IAPP has no negative charges. Thus, ionic interactions in IAPP should be easier to interpret compared to other amyloidogenic proteins which contain both basic and acidic residues. In this sense, IAPP provides a useful model system. Nonetheless, the analysis presented here reveals a complicated salt-dependence of IAPP amyloid formation. The rate of amyloid formation is significantly accelerated with increasing ionic strength at both pH’s, but the observed trends do not follow a simple relationship based only on Debye screening at either pH 5.5 or at pH 8.0. The t₅₀ values vary by a factor of nearly four at low salt at pH 8.0, depending on the identity of the anion and by a factor of two at pH 5.5. At low salt, anion binding appears to play a role at both pH’s as judged by the dependence on anion identity and its correlation with the electroselectivity series; however, different anion dependencies are observed at pH 5.5 and pH 8.0 as the ionic strength is increased. The anion-dependent effects are much less pronounced at the highest salt concentrations at pH 8.0 and the value of t₅₀ varies by less than 8% amongst all of the anions tested. The t₅₀ no longer scales with the electroselectivity series at high ionic strength at pH 8.0. Anion binding will still occur at high salt concentrations, but the variation between the different ions will be less if saturating concentrations are reached for all ions. The anion is in 18,000-fold excess relative to IAPP at 600 mM ionic strength. In addition, Hofmeister effects will be more important at the higher salt concentrations, and these scale inversely with the electroselectivity series for the monovalent anions. The lack of a clear trend at the intermediate ionic strengths likely reflects competition among these effects. It is important to note that there is still significant variation in the rate with the identity of the anion at pH 8.0 at intermediate ionic strengths, varying by nearly 100%, and these effects should be taken into account when comparing studies conducted using different salts.

In contrast to the behavior observed at pH 8.0, the effects of varying the anion scale with the electroselectivity series for all ionic strengths tested at pH 5.5. The polypeptide has a larger net positive charge at pH 5.5 than at pH 8.0 which will enhance anion binding and this may account for a stronger correlation with the electroselectivity series. The lack of a significant dependence on the cations tested is not surprising since IAPP contains no negatively charged groups and thus cation binding is not expected.

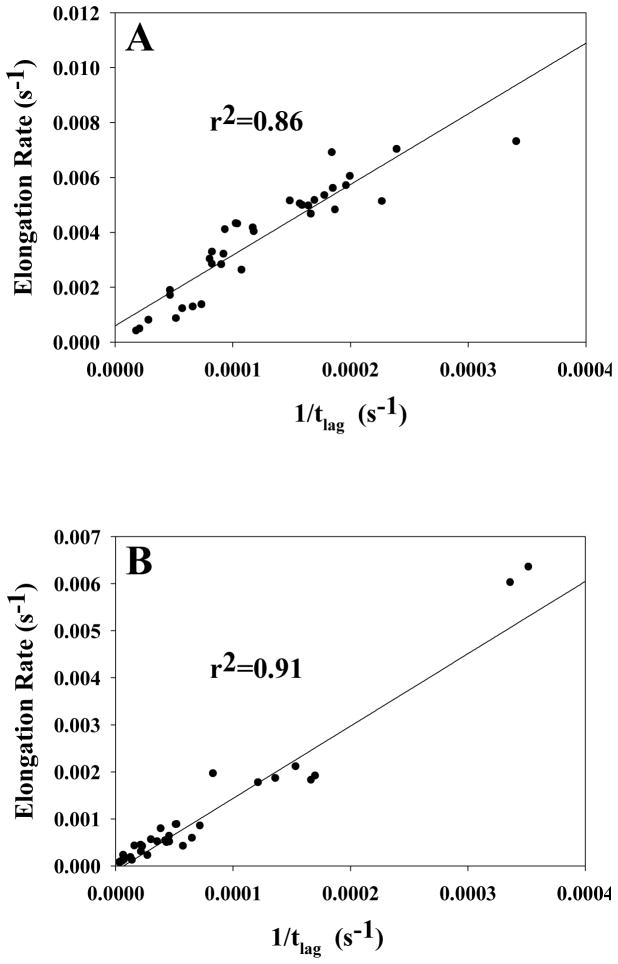
We used the value of t₅₀ in our analysis, which includes contributions from both the lag phase and the growth phase. It is natural to inquire if anions exert different effects on the lag phase and the growth phase. The lag time, t_lag, and the apparent rate at t₅₀ (v_max) which is believed to reflect the elongation rate, can be determined from the sigmoidal fits. We obtain similar results if we compare the effects of anions and ionic strengths on t₅₀, t_lag, or v_max. Plots of 1/t_lag and v_max are included in the B-coefficient for both pH 5.5 and 8.0. The plots at all ionic strengths are very similar to those obtained by plotting 1/t₅₀, indicating that the lag time and elongation rate are sensitive to the same factors that modulate the t₅₀. There is a strong relationship between the effects of different salts on the lag phase and growth phase of amyloid formation by IAPP. The elongation rate, v_max, and the inverse of the lag time are strongly correlated (r²=0.86) at pH 8.0 and an equally strong correlation (r²=0.91) is observed at pH 5.5 (Figure-12). A strong correlation is also observed if the pH 5.5 and pH 8.0 data are plotted together (r²=0.80) (Supporting Information). Such a strong correlation implies that similar effects influence both nucleation events in the lag phase and fibril elongation. This is reasonable since nucleation involves association of charged IAPP monomers and thus has to overcome unfavorable electrostatic effects. The fibril growth phase involves binding of soluble cationic IAPP monomers to the cationic fibrils, and so must also involve unfavorable charge-charge interactions.

Figure 12.

Correlation of the rate at t₅₀, v_max, with 1/t_lag for all anions at all ionic strengths at (A) pH 8.0 and (B) pH 5.5. The kinetic parameters are derived from the thioflavin-T kinetic assays fit to Equation 1. The data are fit to a straight line with an r² of 0.86 (p = 0.03) and 0.91 (p = 0.04) for pH 8.0 and pH 5.5, respectively.

This work highlights the importance of screening electrostatic repulsion that arises from the alignment of positive charges in fibrils during amyloid formation by IAPP. Our analysis also suggests that residues outside the β-sheet core make significant contributions to fiber stability. PB calculations suggest that for IAPP, both the N-terminus and Lys1 contribute to unfavorable electrostatic interactions in the amyloid fiber. This implies that truncated variants of IAPP which are missing the first seven residues may not be perfect models of amyloid formation by the intact polypeptide, despite their experimental convenience. At pH 8.0 specific anion binding is important at low ionic strength and dominates the observed ion dependence. At high salt concentrations at pH 8.0 ion binding will still occur, but the differences between the various ions now scale with the Hofmeister effect. This contrasts with the influence of anions on the kinetics at pH 5.5, where IAPP carries a +4 charge, with two basic residues (Arg11 and His18) in the β-sheet core of the fibril. At pH 5.5 the effects of different anions scale with the electroselectivity series over the entire range of salt concentrations tested. The stronger dependence on anion binding at high salt at pH 5.5 likely reflects the higher net charge of the polypeptide. IAPP is stored in the insulin secretory granule at a moderately high ionic strength at pH 5.5. The data presented herein show that even modest changes in ionic strength accelerate IAPP amyloid formation and highlights the necessity of in vivo mechanisms to prevent irreversible aggregation of IAPP.