Multi-dimensionally encoded magnetic resonance imaging

Abstract

Magnetic resonance imaging typically achieves spatial encoding by measuring the projection of a q-dimensional object over q-dimensional spatial bases created by linear spatial encoding magnetic fields (SEMs). Recently, imaging strategies using nonlinear SEMs have demonstrated potential advantages for reconstructing images with higher spatiotemporal resolution and reducing peripheral nerve stimulation. In practice, nonlinear SEMs and linear SEMs can be used jointly to further improve the image reconstruction performance. Here we propose the multi-dimensionally encoded (MDE) MRI to map a q-dimensional object onto a p-dimensional encoding space where p > q. MDE MRI is a theoretical framework linking imaging strategies using linear and nonlinear SEMs. Using a system of eight surface SEM coils with an eight-channel RF coil array, we demonstrate the five-dimensional MDE MRI for a two-dimensional object as a further generalization of PatLoc imaging and O-space imaging. We also present a method of optimizing spatial bases in MDE MRI. Results show that MDE MRI with a higher dimensional encoding space can reconstruct images more efficiently and with a smaller reconstruction error when the k-space sampling distribution and the number of samples are controlled.

Introduction

The spatial localization of magnetic resonance signals has been commonly achieved by switching orthogonal, linear spatial encoding magnetic fields (SEMs) in order to obtain a bijective mapping between magnetization precession frequencies and spatial locations (1). Specifically, the incremental SEM moment (time integral of the SEM strength) between consecutive data samples and the maximal SEM moment relates to the image field-of-view and the spatial resolution, respectively, based on the Nyquist sampling theorem. This imaging principle has been used to encode, for example, a three-dimensional object within a three-dimensional k-space, each sample of which measures the projection of the object onto one specific three-dimensional spatial harmonic function (2). Spatial encoding using orthogonal linear SEMs has one advantage: when the acquired data satisfy the Nyquist sampling theorem and the data samples lie on a uniform Cartesian grid, images can be reconstructed efficiently and uniquely using the fast Fourier transform algorithm.

As an alternative to linear SEMs, nonlinear SEMs have been used to improve the dynamic range of MR signals (3) and to localize NMR signals without using selective excitation (4). Recently, it has been suggested that parallel imaging techniques using localized gradients (PatLoc) (5) can achieve a higher spatial resolution and reduce peripheral nerve stimulation using nonlinear surface SEM coils and an RF receiver array (6-8). O-space imaging is a different imaging approach using the Z2 SEM together with linear SEMs to reconstruct accelerated images with high spatial resolution (9). One price for using nonlinear imaging SEMs is that the images generally have anisotropic resolution and the image reconstruction becomes more complicated (8,9). The anisotropic spatial resolution in PatLoc and O-space imaging can be improved by utilizing a combination of both linear and nonlinear SEMs in data acquisition (6,7,10). Also, PatLoc image reconstruction can be partially simplified using the iterative time-domain reconstruction based on the conjugated gradient algorithm (7,10).

The SEMs proposed for PatLoc imaging are usually hyperbolic paraboloids (i.e., saddle shapes) (5,6,8). O-space imaging essentially uses paraboloid of revolution (i.e., bowl shapes) for spatial encoding (9). Recently, we found that a PatLoc system with evenly circumferentially-distributed surface SEM coils can generate multipolar, concentric, and even linear SEMs (like the field pattern generated by the linear gradient in a typical MRI scanner) (7,10). The availability of a versatile set of SEMs in a PatLoc system inspired us to explore the possibility of encoding an object into a higher dimensional space. Rather than mapping a q-dimensional object onto a q-dimensional k-space using conventional orthogonal linear SEMs (usually q = 2 or 3 for planar or volumetric imaging), we propose to spatially encode a q-dimensional object onto a p-dimensional space where p > q. This multi-dimensionally encoded (MDE) MRI intuitively allows for more degrees of freedom in encoding an object using spatial basis sets generated from the combination of different SEMs and different RF channels in a coil array.

Here we propose using over-complete spatial basis sets to improve MRI spatial encoding and image reconstructions. We present the theoretical framework to describe multi-dimensional encoded (MDE) MRI, whose local spatial resolution and field-of-view can be quantified by the “local k-space” concept (6). We hypothesize that MDE MRI in a higher dimensional space can represent the object with a smaller error—particularly in accelerated acquisitions—when the k-space distribution and the number of the k-space samples are controlled. Furthermore, we hypothesize that a higher dimensional MDE MRI has a higher encoding efficiency, which can be quantified by the variance of the encoding matrix corresponding to the chosen SEMs and RF coil sensitivities. Without available imaging hardware, we use numerical simulations to study different configurations of the MDE MRI and to investigate how to optimize the design of the SEMs to improve image reconstruction. Parts of this study have been presented previously in the abstract form (11).

Theory

The signal equation for MDE

The MDE MRI signal equation describes the measured signal in terms of the spatial integral of the underlying (unknown) image ρ(r) weighted by both the RF coil sensitivity C_λ(r) of coil λ and the spatial harmonics used for encoding, which are given by the time integral of the SEMs:

$$s(\lambda ,t)=\int c_{\lambda }(\mathbf{\text{r}})\rho (\mathbf{\text{r}})exp(-2\pi j\gamma (\sum _{i=1}^q\underset{\tau =0}{\overset{t}{\int }}{\mathit{\text{SEM}}}_i(\mathbf{\text{r}},\tau )d\tau \left)\right)d\mathbf{\text{r}}\lambda =\text{1}\cdots {\text{n}}_C,$$ [1]

where r represents the spatial location, λ the RF coil channel index, γ the gyromagnetic ratio, and n_c the total number of channels in an RF coil array. SEM_i(r,t) represents the spatial encoding magnetic field i at location r and time t, where t indicates the lapsed time after turning on the i^th SEM and q denotes both the total number of SEMs and also the dimension of the encoding space. It should be noted that using q linear SEMs to map a q-dimensional object makes Eq. [1] degenerate into conventional, Fourier-encoded MRI.

Provided with the SEMs driving by a unit current, the MDE MRI signals can be evaluated at a set of time instants using pre-calculated SEM values tabulated at the desired spatial locations r:

$$s(\lambda ,t_k)=\int c_{\lambda }(\mathbf{\text{r}})\rho (\mathbf{\text{r}})exp(-2\pi j\gamma (\sum _{i=1}^q{\mathit{\text{SEM}}}_i^0(\mathbf{\text{r}})\underset{\tau =0}{\overset{t_k}{\int }}{f}_i(\tau )d\tau \left)\right)d\mathbf{\text{r}}\lambda =\text{1}\cdots {\text{n}}_C.$$ [2]

Here SEM_i⁰(r) represents the i^th spatial distribution of the z-component of the magnetic field generated by a unit current on the SEM coils at location r, p_i(τ) denotes the strength of the i^th normalized SEM at time τ, and t_k indicates the k^th sampling time instant. The moments of SEMs, f_i(τ), parameterized by the amplitude and the evolution time (including polarity) of a SEM can be represented in a q-dimensional encoding space. This encoding space is equivalent to the conventional k-space when only linear SEMs are used. Eq. [2] can be further simplified to describe each spatial basis corresponding to a particular SEM by its spatial pattern SEM_i⁰(r) and its moment ψ_i(t_k):

$$\begin{array}{c}s(\lambda ,t_k)=\int c_{\lambda }(\mathbf{\text{r}})\rho (\mathbf{\text{r}})exp(-2\pi j\gamma (\sum _{i=1}^q\mathbf{(}{\mathit{\text{SEM}}}_i^0(\mathbf{\text{r}}){\psi }_i(t_k)\mathbf{)}\left)\right)d\mathbf{\text{r}}\\ {\psi }_i(t_k)=\underset{\tau =0}{\overset{t_k}{\int }}{f}_i(\tau )d\tau ,\lambda =\text{1}\cdots n_C\end{array}.$$ [3]

Local k-space

Eq. [3] simply describes how signals are generated in MDE MRI, however it gives no explicit information about the size of the FOV and the spatial resolution. Using linear SEMs, the k-space formalism clearly describes the FOV and the spatial resolution in conventional Fourier-encoded MRI. However, in MDE MRI k-space becomes spatially dependent because nonlinear SEMs are used. The concept of the local k-space was also applied to examine the spatial resolution in PatLoc imaging (6). Specifically, similar to conventional MRI, k-space coordinates can be derived for MDE MRI as the partial spatial derivative of the phase accumulated across the product of the normalized SEM_i⁰(r) with the waveform p_i(τ):

$$\begin{array}{c}{k}_x\mathbf{(}{t}_k,\mathbf{\text{r}}\mathbf{)}=\frac{\partial }{\partial x}\{-2\pi \gamma [\underset{\tau =0}{\overset{t_k}{\int }}\sum _{i=1}^q{p}_i(\tau ){\mathit{\text{SEM}}}_i^0(\mathbf{\text{r}})d\tau \left]\right\}\\ =\frac{\partial }{\partial x}\{-2\pi \gamma [\sum _{i=1}^q{\psi }_i(t_k){\mathit{\text{SEM}}}_i^0(\mathbf{\text{r}})\left]\right\}\end{array}$$ [4]

Eq. [4] provides and expression for the k_x coordinate of the k-space data point collected at time t_k for an image pixel located at position r. Similarly, the k_y and k_z coordinates for the k-space data point collected at time t_k for an image pixel located at position r can be derived by calculating the partial derivative with respect to y and z, respectively. Using this location-dependent k-space description, the spatial resolution can be directly derived for each image voxel using SEM_i⁰(r) and its moment ψ_i(t_k) as the conventional Fourier MRI using linear SEMs.

In order to quantitatively evaluate the spatial resolution using the local k-space formalism, we can calculate the mean and the standard deviation of the distance between the optimized k-space data point and the k-space origin at the chosen image pixels across different MDE MRI configurations. Note that in this quantification a distance of 1 in k-space corresponds to a distance of 1/FOV in image space.

Discrete form of the signal equation

Eq. [2] can be converted into a matrix representation to facilitate numerical implementation:

$$\mathbf{\text{s}}=\mathbf{\text{E}}\mathbf{\rho },$$ [5]

where s is the vector consisting of measurement s(λ, t_k) across RF coil channels using individual SEMs with a particular driving current strength, and ρ is the image to be reconstructed. Each row of the encoding matrix E represents a spatial basis function given by the product of the RF coil sensitivity profile and the time integral of the SEMs.

If the measurements are taken at n time points (t_k = t₁ …. t_n), and the final reconstructed image is represented on a grid consisting of m voxels, the size of the encoding matrix E will be (n_c × n) by m. Accordingly, the acceleration rate R of the acquisition can be calculated explicitly:

$$\text{R}=m/n.$$ [6]

It should be noted that the acceleration rate R is defined as a function of the acquired data points m needed to reconstruct a discrete image that satisfies the Nyquist sampling criterion—which is subject to the desired FOV, nominal image resolution, and image matrix.

Encoding efficiency

With sufficient measurements across time and RF coil channels, Eq. [5] is a set of linear equations with an encoding matrix E having more columns than rows. Assuming that the encoding matrix E has no redundancy (rank(E) ≥ m), the image ρ can be reconstructed uniquely using the least squares criteria:

$${\mathbf{\rho }}_{\text{est}}={({\mathbf{\text{E}}}^{\text{H}}\mathbf{\text{E}})}^{-1}{\mathbf{\text{E}}}^{\text{H}}\mathbf{\text{s}}$$ [7]

Importantly, the (co-)variance of the reconstructed image is

$$\text{VAR}({\mathbf{\rho }}_{\text{est}}\text{t})={({\mathbf{\text{E}}}^{\text{H}}\mathbf{\text{E}})}^{-1}.$$ [8]

With n data samples, we define the encoding efficiency η as the inverse of diagonal entries of (E^HE)^-1. The efficiency can be calculated and visualized to provide an image illustrating the spatial distribution of noise present in the reconstruction given a particular encoding scheme:

$$\eta =1/\text{diag}(\mathbf{\text{VAR}}\mathbf{(}{\mathbf{\rho }}_{\text{est}})),$$, [9]

where diag(•) denotes the operation of forming a vector from the entries along a matrix diagonal. A larger value of η denotes a higher efficiency in the encoding. Note that η is jointly controlled by the selected SEMs, their moments ψ_i(t_k), and the RF coil sensitivities C_λ(r). Relative encoding efficiencies between two given MDE configurations, e.g. configuration “A” and configuration “B”, can be quantified by taking a ratio between the two corresponding η values:

$${\eta }^{\text{AB}}={\eta }^{\text{A}}/{\eta }^{\text{B}}.$$ [10]

Note that η_AB is a functional of spatial location, and therefore varies across the image. A η_AB with a value larger than 1 indicates that MDE configuration A is more efficient than configuration B, and therefore configuration A introduces less noise in the image reconstruction. Note that the efficiency metric solely depends on the encoding matrix, which depends on the chosen SEMs and the locations of the multi-dimensional k-space data points. It has nothing to do with the image to be reconstructed.

Note, the efficiency metric η is closely related to the g-factor in parallel imaging (12) but they are distinct: the g-factor is the ratio between two efficiency metrics quantifying how noise is amplified in the parallel imaging reconstruction with respect to the fully sampled non-accelerated acquisitions. In other words, g-factor uses the fully sampled k-space data (regardless of which SEM is used for spatial encoding) as the comparison standard. Thus, it is misleading to use g-factor maps directly to quantify the efficiency of different encoding methods in MDE MRI. Nevertheless, this relative efficiency calculation for comparing MDE configurations is conceptually similar to a g-factor calculation in that it consists of the ratio between two efficiency metrics. In summary, the g-factor and the relative efficiency are both metrics comprised of a ratio of variances. A g-factor map calculation assumes that the two acquisitions under comparison use the same encoding scheme but different amounts of k-space data, whereas the relative efficiency in MDE MRI compares acquisitions using different encoding schemes but the same amount of k-space data.

Methods

Experimental setup and SEMs

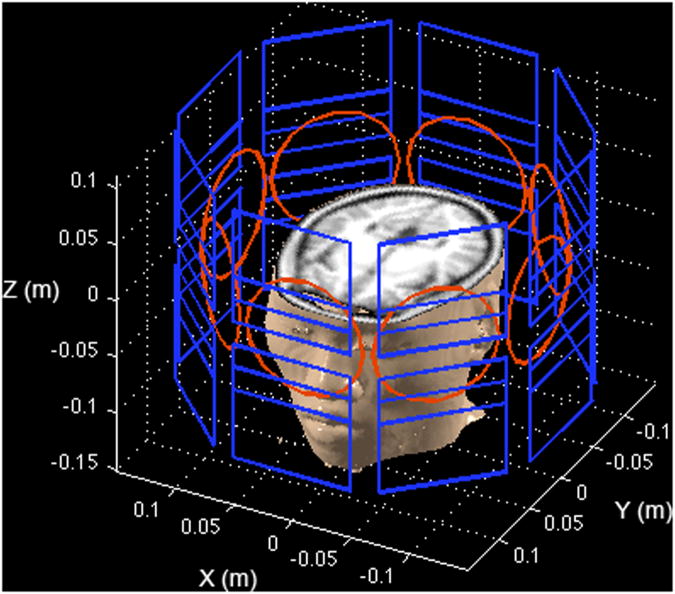
To assess the proposed MDE MRI methodology, we studied MDE MRI performance using numerical simulations because there is no available imaging hardware for experiments. The nonlinear SEMs studied here used eight surface SEM coils with a circumferential geometry, as published previously (5-8). Figure 1 shows the eight-channel surface SEM coils together with eight circular RF coils. The magnetic field generated by each surface SEM coil was calculated using the Biot-Savart law.

Figure 1.

Setup of the simulation. The PatLoc system consisting of eight surface SEM coils are shown in blue. Each element consists of a symmetric pair of planar SEM coils about the x-y plane. There is also an eight-channel RF coil array shown in red. Note that the shown geometry of the coils and the anatomical image are only meant to illustrate the ideas of the acquisition and the experimental setup. They do not match to the exact details of our experimental results.

Previously we reported that the Singular Value Decomposition (SVD) on the collection of B_z's of surface SEM coils can suggest different SEMs configurations (10). These include nearly-linear SEMs, multipolar SEMs, and an O-shape SEM. Figure 2 shows these configurations. These five SEMs were used to construct different configurations of MDE MRI in this study.

Figure 2.

SEMs used for MDE MRI. Five spatial encoding magnetic fields (SEMs) were revealed by the Singular Value Decomposition of the z-component of the magnetic fields generated by PatLoc surface SEM coils. These included a SEM with iso-intensity contours in “O” shapes (O), two linear SEMs (Linear-X and Linear-Y), and two multipolar SEMs (Multipolar-1 and Multipolar-2). The combinations of these five SEMs (Table 1) gave different configurations of MDE MRI.

Specifically, the “G5” configuration uses all five SEMs shown in Figure 2. The “M4” configuration includes two multipolar (Multipolar 1 + Multipolar 2) and two linear SEMs. This configuration was used in our previous study (10) and the 4D-RIO reconstruction (7). The “M2” configuration uses only the two multipolar SEMs (6,8). The “O3” configuration uses the O SEM together with two linear SEMs, similar to O-space imaging (9). The “L2” configuration is the conventional MRI encoding using two linear SEMs. The magnetic field moments corresponding to Linear-X, Linear-Y, O, Multpolar-1, and Multipolar-2 SEMs are denoted as ψ_x, ψ_y, ψ_m1, ψ_m2, ψ_o, respectively. Table 1 lists the SEMs used in these configurations, and the dimension of the encoding is given by q.

Table 1.

MDE MRI configurations used in this study. Based on the SEMs shown in Figure 2, five different SEMs with associated moments ψ_i were studied. Each configuration has different encoding dimension (q).

Configuration	SEMs	ψi(i=1∼q)	q
G5	Linear-X, Linear-Y, Multipolar-1, Multipolar-2, O	ψx, ψy, ψm1, ψm2, ψo	5
M4	Linear-X, Linear-Y, Multipolar-1, Multipolar-2	ψx, ψy, ψm1, ψm2	4
O3	Linear-X, Linear-Y, O	ψx, ψy, ψo	3
M2	Multipolar-1, Multipolar-2	ψm1, ψm2	2
L2	Linear-X, Linear-Y	ψx, ψy	2

Optimizing spatial bases

From Eq. [3], the spatial bases of the MDE MRI are jointly determined by the spatial pattern SEM_i⁰(r) and the corresponding moment ψ_i(t_k). Given the SEM_i⁰(r) and a target object ρ(r), we used the Matching Pursuit algorithm (13) to optimize ψ_i(t_k) with a constraint that the total number of measurements s(λ,t_k) be n. One possibility is to start from ψ_i(t₁) = 0, i =1,…,q (i.e., from the center of the encoding space) for the generation of all SEMs. For measurement k = 2,…,n, n_samp random numbers were generated following an exponential distribution for as ψ_i(t_k) for the i^th SEM (i = 1 …q). All (q)^(n_samp) combinations of ψ_i(t_k) across SEM index i were used to create different spatial bases, each of which corresponded to $exp(-2\pi j\gamma (\sum _{i=1}^m\mathbf{(}{\mathit{\text{SEM}}}_i^0(\mathbf{\text{r}})y_i(t_k)\mathbf{)}\left)\right)$. The target object ρ(r) was projected onto each spatial basis and a projection coefficient was calculated by integrating the spatial basis and the target object over space. Among all (q)^(n_samp) projection coefficients, the spatial basis with the largest projection coefficients was chosen as the optimal basis for measurement k. Then the contribution of the projection with the largest projection coefficient is removed from the remaining signal. This procedure was repeated by incrementing the measurement index k until k = n.

Note that we only optimize the moment of the SEM waveform at each data acquisition point without specifying its actual waveform. For simplicity, we assume that each SEM is turned on instantaneously with a fixed strength over the interval (0, t_k). This assumption is commonly used in phase encoding in conventional MRI.

Based on the prior knowledge that natural images contain more energy in the lower spatial frequencies, we arbitrarily chose a bounded probability distribution function following the exponential distribution (with mean = 1) to generate realizations of ψ_i(t_k) with the maximum and the minimum set to +1 and −1 respectively. This choice was based on the requirements that (i) the central part of the encoding space ψ_i(t_k) should be emphasized, and (ii) the coverage of the k-space should extend far enough to the higher spatial frequency components to ensure sufficient spatial resolution. For example, in a rectilinear Cartesian k-space coordinates system satisfying the Nyquist sampling theorem, ψ_i(t_k) (in the L2 configuration) are uniformly distributed between values +1 and -1. For comparison, we also generated realizations of ψ_i(t_k) using an exponential distribution function with mean = 1/3 to examine the trade-off between spatial resolution and image reconstruction error.

In addition, we chose n_samp = 3 to limit the computational burden: using five SEMs with an image matrix of 128×128 pixels, the search for the optimal bases requires 128×128×53 calculations. This amount of computation requires about 20 hours of compute time on our current workstation (consisting of two quad-core CPU with 16 GB of memory).

Since the moments of the SEMs ψ_i(t_k), (i = 1 …q, k = 1… n) generally are in a higher dimension, we devised a 2D visualization intended to display the 5-dimensional ψ_i(t_k) used in this study (i = 1 …5, Table 1). Specifically, the horizontal and vertical coordinates in this 2D plot represent ψ_x(t_k), and ψ_y(t_k), which are the moments of Linear-X nd Linear-Y SEM, respectively, evaluated at sampling time instant t_k. The red/green/blue color triple of each marker in this plot corresponds to the data at time instant t_k represents the triple of values ψ_o(t_k), ψ_m1(t_k), and ψ_m2(t_k),

• Red(t_k)=1- ψ_o(t_k)/Max(ψ_o(t_k)),

• Green(t_k)=1- ψ_m1(t_k)/Max(ψ_m1(t_k)),

• Blue(t_k)=1- ψ_m2(t_k)/Max(ψ_m2(t_k)),

where Max(ψ_o(t_k)), Max(ψ_m1(t_k)), and Max(ψ_m2(t_k)) are the maximal absolute moment (regardless of the polarity) of the O-SEM, Multipolar-1 SEM, and Multipolar-2 SEM.

Image reconstructions and simulation parameters

Given the SEMs and associated moments, the measurements were synthesized using Eq. [5]. Images were then reconstructed from the synthesized k-space data using the iterative time-domain reconstruction (iTDR) method for the set of SEMs and SEM moments (7,10). The iTDR method is a generalization of the SENSE image reconstruction method for arbitrary k-space trajectories using the conjugate gradient method.

Simulations were based on a two-dimensional (p = 2) high-resolution 3D T1-weighted structural MRI data set. The pulse sequence used to acquire this data was a standard MPRAGE (TR/TE/flip = 2530 ms/3.49 ms/7°, partition thickness = 1.0 mm, matrix = 256 × 256, 256 partitions, FOV = 256 mm × 256 mm). In optimizing MDE MRI acquisition, one axial slice image was selected as the target object ρ(r). Since we are mostly interested if MDE is more efficient in encoding an object for accelerated acquisitions, we studied MDE MRI with 4× and 8× accelerations (see Eq. [6] for the definition of the acceleration rate). We calculated the total reconstruction error as the sum of the absolute value of the difference image between the target object and the reconstruction. In validation tests, we chose a different image slice and simulated the measurements. The reconstruction then used the optimized spatial bases and the calculated reconstruction error. All calculations were implemented by Matlab (Mathworks, Natick, MA, USA) using a 128 × 128 image matrix.

Results

Figure 3 shows the optimized SEM moments ψ_i(t_k) of 4-fold acceleration, each of which corresponded to a data point lying in a multi-dimensional encoding space. The L2 configuration shows rather distributed sampling over the encoding space. In fact, when only linear SEMs are used, the encoding space is equivalent to the k-space in conventional MRI. The M2 configuration used neither Linear-X nor Linear-Y SEM. Thus ψ_i(t_k) are multiple data points lying at the origin of the k-space with different combinations of green and blue colors with different intensities. The O3 configuration shows ψ_i(t_k) with distributed red dots of different intensities. The high intensity red color and a higher density at the center of the encoding space indicate that low spatial frequency components in Linear-X, Linear-Y, and O SEMs contributed significantly to the target image. The optimized ψ_i(t_k) for the M4 configuration are distributed cyan/blue color dots with a higher density at the center of the encoding space. These data points used different blue/cyan color because only green (for ψ_m1) and blue (for ψ_m2) colors were used to represent the moments of the multipolar SEMs. The optimized ψ_i(t_k) for the G5 configuration are multiple color dots. The center of the encoding space has a higher density of the acquisition and their moments are in bright or white colors. Both indicated spatial harmonics of lower frequencies have higher weightings. We found that the optimized L2 trajectory does not have dense distribution around the center of the k-space like the results of O3, M4, and G5 configurations. One potential reason to explain is that the randomization using the exponential distribution is not optimal for the L2 configuration. In the future, the trajectory may be further improved by considering the previously optimized k-space coordinates, rather than considering each data point is independent of others. Thus it can avoid clustered k-space data points, as shown in Figure 3.

Figure 3.

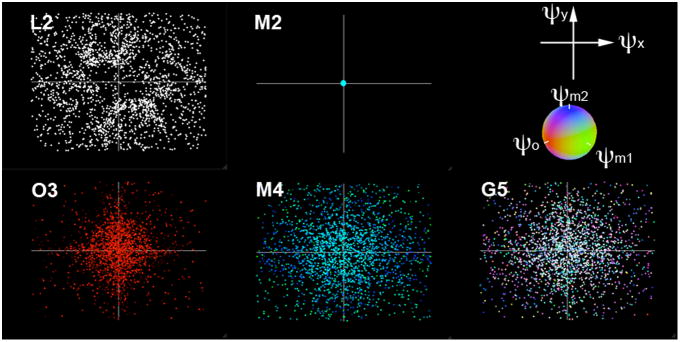
The optimized SEM moments, each of which correspond to a data point in the multi-dimensional encoding space. Due to high dimension, we used the combination of colors and x-y coordinates to represents the encoding data points of MDE MRI for five configurations.

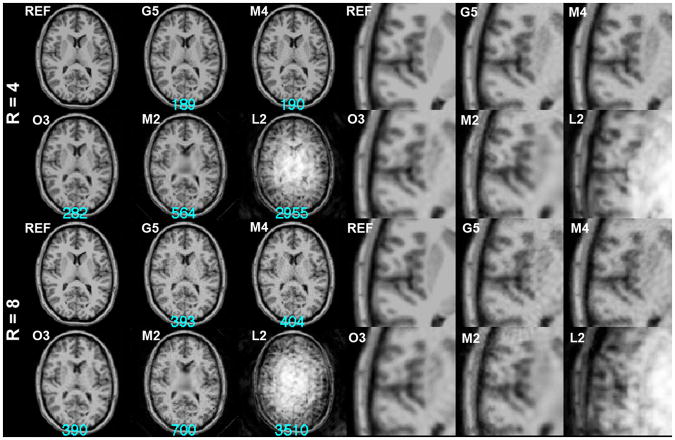
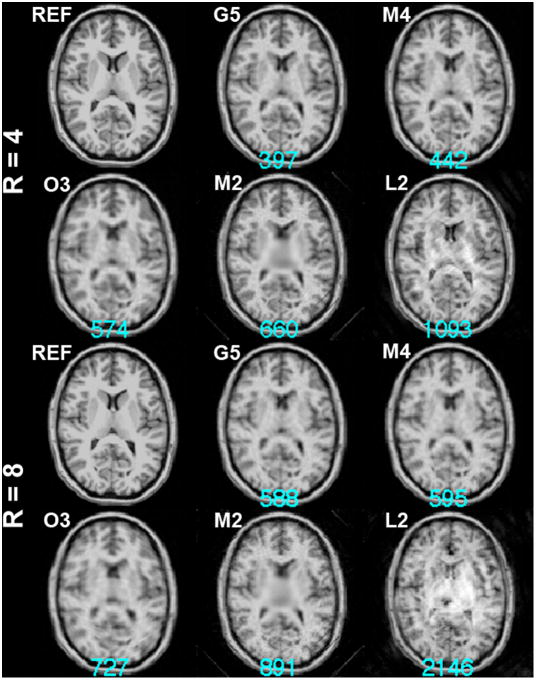
Using the optimized spatial bases, we simulated the acquisition then reconstructed the images for both 4-fold and 8-fold accelerations. Figure 4 shows the reconstructed images using L2, M2, O3, M4, and G5. The largest reconstruction error was found for the L2 configuration with noticeable stripe artifacts over the entire FOV. The M2 configuration also exhibits a high reconstruction error, and the center of the FOV reflects a reduced resolution as a consequence of the ill-conditioning of the SEM and RF encoding in that region. The O3 configuration has an improved reconstruction error, but the reconstructed image is clearly spatially blurred. The M4 configuration generated the reconstruction with a smaller error than the O3 configuration, and areas around the third ventricle in the center of the FOV also show a more clearly defined boundary. Lastly, the G5 configuration had the least reconstruction error and the quality of the image at the cortical and subcortical areas is acceptable.

Figure 4.

4-fold (R=4) and 8-fold (R=8) accelerated MDE MRI reconstructions. Part of the magnified image around the left temporal lobe is shown at the right panel. The k-space data points were optimized by the Matching Pursuit algorithm using an exponential distribution function with mean = 1. The reference image (REF) was shown for comparison. The residual errors of the reconstructions were listed at the bottom of each reconstruction in cyan.

Reconstructions of the eight-fold accelerated acquisitions and part of the magnified left temporal lobe were also shown in Figure 4. Compared to the reconstruction at the four-fold acceleration, the reconstruction errors were considerably larger. Accelerated images show either blurring or patch-like artifacts. The L2 configuration failed to generate reasonable anatomical structures. The reconstruction for the M2 configuration and the O3 configuration exhibit a prominently lower spatial resolution in the FOV center and blurring across the FOV. The reconstruction for the M4 and G5 configurations did not lose spatial resolution but the reconstruction noise was stronger than reconstructions using four-fold accelerated acquisitions. Note that the O3 configuration gave the least reconstruction error, which is marginally smaller than the G5 result.

To further study the spatial resolution, we plotted the local k-space at five image pixel locations for both 4-fold and 8-fold accelerated MDE MRI in Figure 5. The spatial resolution can be qualitatively evaluated by the coverage of the local k-space: a wider coverage corresponds to a higher spatial resolution. The L2 configurations had identical local k-space at all five locations, whereas, in contrast, k-space is spatially invariant in conventional MRI using linear SEMs. The M2 configuration had no spatial resolution at the center of the FOV, where local k-space degenerated to a single point. The spatial resolution improved gradually as the location moved toward the periphery of the FOV. We found that the local k-space plot for M2 is asymmetric. This is likely due to the fact that the target image showing strong vertical boundaries between scalp, skull, and brain parenchyma, particularly at the outer-most location (location 1). These banded structures will promote the use of high spatial harmonics to reduce the residual between the target image and the reconstructed image. The O3 and M4 configurations had improved spatial resolution at the FOV center as the local k-space had a wider coverage. The G5 configuration further improved the spatial resolution at the center and the periphery of the FOV as evidenced by the more distributed local k-space. Quantitatively, the mean and the standard deviation of the distance between optimized k-space data points and the k-space origin were reported in Table 2. Because a longer distance indicates wider coverage of the k-space and thus a higher spatial resolution, these numbers support the finding that the G5/M4 configurations indeed had a higher the spatial resolution, specifically at the FOV center, than MDE MRI using the O3/M2 configurations.

Figure 5.

The local k-space at 5 image pixels, which were indicated by small red boxes at the left. The local k-space had a white box indicating the boundary corresponding to the inverse of the spatial resolution.

Table 2.

The mean and the standard deviation of the distance between local k-space data points to the origin of the k-space at 5 pixels (see Figure 5) in MDE MRI. Distance = 1 corresponds to 1/FOV.

MDE configuration	Pixel location
R = 4	1	2	3	4	5
G5	0.57+/−0.35	0.44+/−0.26	0.33+/−0.19	0.27+/−0.14	0.24+/−0.12
M4	0.57+/−0.35	0.43+/−0.26	0.33+/−0.19	0.27+/−0.14	0.25+/−0.12
O3	0.37+/−0.23	0.30+/−0.18	0.24+/−0.15	0.20+/−0.12	0.19+/−0.11
M2	0.64+/−0.30	0.41+/−0.18	0.25+/−0.11	0.12+/−0.05	0.01+/−0.00
L2	0.73+/−0.26	0.73+/−0.26	0.73+/−0.26	0.73+/−0.26	0.73+/−0.26
R = 8
G5	0.55+/−0.35	0.42+/−0.27	0.32+/−0.20	0.26+/−0.15	0.23+/−0.12
M4	0.57+/−0.35	0.43+/−0.26	0.33+/−0.19	0.27+/−0.15	0.25+/−0.12
O3	0.37+/−0.23	0.30+/−0.18	0.24+/−0.14	0.20+/−0.12	0.18+/−0.11
M2	0.62+/−0.30	0.40+/−0.18	0.24+/−0.11	0.11+/−0.05	0.01+/−0.00
L2	0.68+/−0.25	0.68+/−0.25	0.68+/−0.25	0.68+/−0.25	0.68+/−0.25

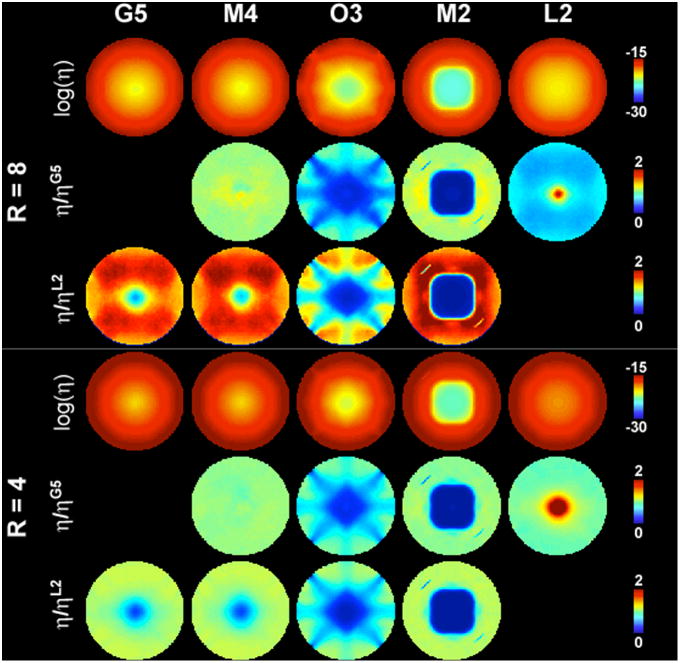
During the optimization of ψ_i(t_k), we did not explicitly enforce the encoding matrix E to be non-redundant. Therefore we calculated the rank of all encoding matrices, and the encoding matrices were all found to be full-ranked. To investigate the noise in the reconstructed MDE MRI, we calculated the encoding efficiency η in order to quantitatively compare different configurations of the MDE MRI. Figure 6 shows maps of the encoding efficiency η. Generally the efficiency is higher at the FOV periphery than at the center of the FOV, regardless of the MDE configurations or the acceleration rate. This spatial distribution is similar to the g-factor maps in parallel MRI: higher efficiency (smaller g-factor) is observed in the FOV periphery and lower efficiency (larger g-factor) in the FOV center, potentially due to the fact that at the FOV center it is both more difficult to use SEMs (due to the smaller B_z gradient found at the center) and to use the RF coil sensitivity (due to the weaker, gradually varying B₁^- fields found at the center) to localize magnetization accurately.

Figure 6.

Maps of the logarithm of the encoding efficiency η for G5, M4, O3, M2, and L2 configurations, the relative efficiency with respect to the G5 configuration, and the relative efficiency with respect to the L2 configuration for 4-fold and 8-fold accelerations.

Note that M2 and O3 configurations show particularly low efficiency. For the same configuration, the high efficiency areas become smaller. In order to compare efficiency of different MDE MRI configurations, we calculated the relative efficiency maps with respect to the G5 and L2 configurations. Note that the color region indicates the distribution with lower efficiency than the chosen comparison standard. Specifically, at R = 8, the M2 configuration had similar efficiency to the G5 configuration; and the O3 and M2 configurations show much lower efficiency at the FOV center. The L2 configuration is not as efficient as the G5 configuration at most locations except at the FOV center. Compared to the L2 configuration, the O3 and M2 configurations had lower efficiency at the FOV center. The locations with a lower efficiency for the M4 and G5 configurations than the L2 configuration is only limited to the very center of the FOV. These characteristics are similar to the results at R = 4 acceleration. Note that the difference between L2 and M4/G5 configurations is smaller at R = 4 than R = 8, mostly at the center of the FOV. Quantitatively, the means η^M4/ η^G5, η^O3/ η^G5, η^M2/ η^G5, and η^L2/ η^G5 are 1.04, 0.57, 0.83 and 0.65 respectively for R = 8. The means η^M4/ η^L2, η^M4/ η^L2, η^O3/ η^L2, and η^M2/ η^L2 are 1.58, 1.64, 0.91, and 1.37 respectively for R = 8. The means η^M4/ η^G5, η^O3/ η^G5, η^M2/ η^G5, and η^L2/ η^G5 are 1.00, 0.68, 0.76, and 1.03 respectively for R = 4. The means η^M4/ η^L2, η^M4/ η^L2, η^O3/ η^L2, and η^M2/ η^L2 are 10, 1.01, 0.71, and 0.81 respectively for R = 4. These results show that spatial encoding using a more dimensions does not necessarily improve the encoding efficiency everywhere in the FOV.

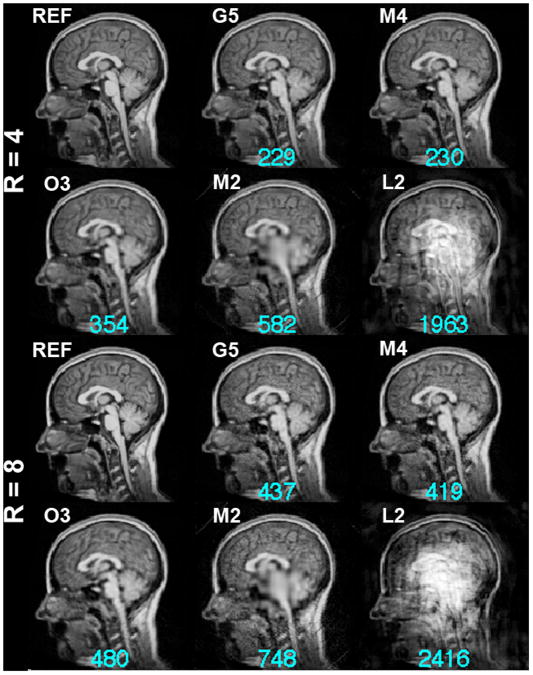
Given a target image ρ(r), we can optimize spatial bases to obtain the reconstruction with the least error with respect to the same given target image. However, in practice, it is more important to know if the optimized spatial bases can better encode an unknown object. To answer this question, we performed a validation test calculating optimized spatial bases generated from one axial slice image and then reconstructing images of different sagittal slice images to examine how well the bases generalize beyond a known imaging slice and, more importantly, whether MDE MRI with a higher dimensional encoding space can yield an improved reconstruction. The results of this validation are shown in Figure 7. Using the 4-fold accelerated acquisitions, the quality of the reconstructed images in this validation was similar to the reconstructions in the basis optimization (Figure 4): the M2 configuration had a prominent loss of spatial resolution around the center of the FOV and the O3 configuration had a blurred reconstruction. The M4 and G5 configurations produced visually similar results, yet the G5 configuration had a marginally smaller reconstruction error. The results of the 8-fold acceleration reconstruction were similar to those in the 4-fold accelerations: the reconstruction error decreased gradually as the number of dimensions in MDE MRI increases. M4 and G5 configurations gave visually similar results yet the M4 configuration had a marginally smaller reconstruction error.

Figure 7.

Validation of the 4-fold (R=4) and 8-fold (R=8) accelerated MDE MRI reconstructions. The reference image (REF), which was not used in optimizing the spatial bases, is shown for comparison. The residual errors of the reconstructions are listed at the bottom of each reconstruction and are shown in cyan.

Figure 8 shows the reconstruction of the G5 configuration using optimized SEM moments ψ_i(t_k) when the mean of the exponential distribution function was set to 1/3. Compared to Figure 4, where reconstructed images using the optimized moments ψ_i(t_k) distributed with an exponential distribution function with the mean = 1, the reconstructions with the mean = 1/3 were of lower spatial resolution for O3, M4, and G5 configurations as the consequence of more low spatial frequency k-space data contained within the image. The associated reconstruction errors were also larger. However, for the L2 configuration, favoring lower spatial frequency components actually improved the reconstruction by producing a smaller reconstruction error. These results illustrate that, depending on the SEM configuration, a lower spatial resolution may be traded-off for a smaller reconstruction error. Additionally, increasing the dimension of the encoding without sufficiently sampling the k-space may not provide accurately reconstructed images.

Figure 8.

4-fold (R=4) and 8-fold (R=8) accelerated MDE MRI reconstructions. The k-space data points were optimized by the Matching Pursuit algorithm using an exponential distribution function with mean = 1/3. The reference image (REF) is shown for comparison. The residual errors of the reconstructions are listed at the bottom of each reconstruction in cyan.

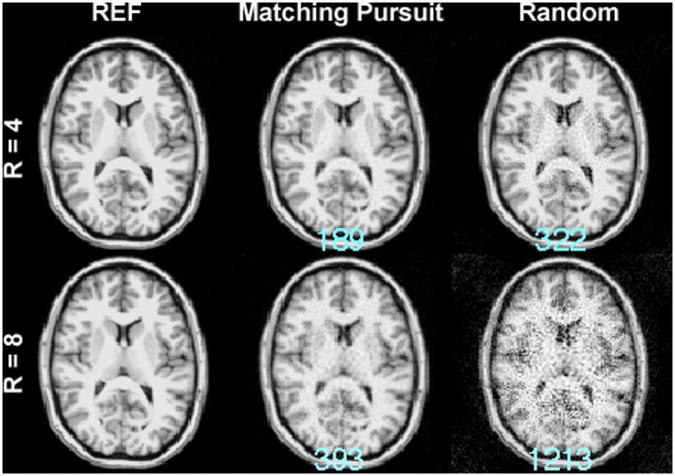
Figure 9 shows the MDE MRI of the G5 configuration with k-space data points generated from one realization of the exponential distribution. Without using the Matching Pursuit algorithm to generate optimized spatial bases, the reconstruction error became 70% (189 vs. 322) or 209% (393 vs. 1213) larger in 4× and 8× accelerated acquisition respectively. This suggests that the ψ_i(t_k) by the Matching Pursuit algorithm is critical to reduce the residuals of the reconstructed image.

Figure 9.

4-fold (R=4) and 8-fold (R=8) accelerated MDE MRI reconstructions with the G5 configuration using the Matching Pursuit algorithm or using one realization of randomized exponential distribution (Random) to obtain k-space data points. The reference image (REF) is shown for comparison. The residual errors of the reconstructions are listed at the bottom of each reconstruction in cyan.

Discussion

This study proposes a framework of using sets of linear and nonlinear SEMs to achieve MRI spatial encoding. We presented the signal equation to encode a q-dimensional object onto a p-dimension space, where p > q. Specifically, we studied p = 2 (the case of a two-dimensional object) with q ranging between 2 and 5. When the image is reconstructed using a constraint of minimizing the l²-norm of the residuals, the efficiency of the MDE MRI can be quantitatively calculated using the encoding matrix. This enables the comparison between different MDE MRI configurations. With a target object, specified dimension in the encoding space, and a set of SEMs for spatial encoding, the Matching Pursuit algorithm (13) can optimize the moments of each SEMs in order to generate spatial bases tailored to the target object. Importantly, the optimized spatial bases in a higher encoding dimension can represent not only the target object but also unknown objects more efficiently and with a smaller reconstruction than encoding the object in lower dimensions when the k-space distribution and the number of samples are controlled. Taken together, our study presents (i) the theoretical framework about the spatial encoding of an object by multiple SEMs, and (ii) an example of optimizing the MDE MRI k-space sampling when the number of the data points is constrained. Our findings are two-fold: a higher dimensional k-space encoding may improve the spatial resolution (Figure 5 and Table 2, local k-space analysis) and the reconstruction error (Figures 4 and 8); and the k-space optimizing is critical in MDE MRI, since a smaller reconstruction error can be obtained from a lower spatial resolution (Figures 4 and 8), and it is not necessarily the case that a higher dimensional encoding will reduce the reconstruction error (Figures 4 and 8).

The MDE MRI directly links the recent PatLoc imaging (5) and O-space imaging (9) approaches as a generalized MRI method using nonlinear and linear SEMs. O-space imaging used the Z2 SEM and two linear SEMs (9). PatLoc imaging used either two multipolar SEMs (5,8) or the combination of two multipolar and two linear SEMs (6,7,10). In fact, MDE MRI provides a generalized formulation for PatLoc imaging regardless of whether the two linear SEMs and two multipolar SEMs are driven simultaneously (6) or sequentially (7,11). With the capability of driving each surface SEM coil independently, all SEMs in PatLoc and O-space imaging can be generated using an array consisting of eight surface SEM coils distributed with azimuthal symmetry. Given the recent demonstration that hardware that can support such configurations has been successfully designed and constructed for animal scanner (14) and human scanner (15), MDE MRI is expected to be feasible. However, it should be noted that the MDE MRI in our simulations were like a ‘single-point’ imaging method, where one phase-encoded read-out was acquired in each RF excitation. Thus in practice, and especially for 3D imaging, long acquisition times may be required to complete all phase encoding steps. Certainly with the chosen phase encoding steps ψ_i(t_k) one may optimize the acquisition schedule to allow multiple read-outs within each RF excitation are desired, as is used in turbo-FLASH or EPI acquisitions.

As the SEMs in MDE MRI include linear SEMs, theoretically the reconstruction can be no worse than what can be achieved by the conventional MRI. This is because the traditional k-space is a sub-space of the encoding space of MDE MRI. Nevertheless, this statement only stands when the k-space is adequately sampled or the k-space data points are all located inside a degenerate, lower dimensional k-space. Nevertheless, the goal of the current evaluation of MDE MRI was to explore if an image can be more accurately and/or more efficiently encoded using different spatial bases generated by SEMs, subject to the same number of k-space data points (thus controlling the image acquisition time and SNR). The efficiency maps (in Figure 6) and reconstructed images using k-space data points following different distribution functions (in Figures 4 and 8) illustrate the importance and the challenges to optimize spatial bases. In fact, even using discrete grids with equal spacing between encoding data points, the number of potential data points in the encoding space ψ_i(t_k) will grow exponentially as the number of the encoding dimension increases. With a fixed amount of measurements, choosing the optimal encoding data points among all candidate data points is computationally intractable. The Matching Pursuit algorithm used in this study is just one approach to mitigate this large combinatorial problem. We used an empirically derived dictionary rather than a complete dictionary. The implication of such an approach is that the results might not be globally optimal (in the sense of minimizing the reconstruction residuals). Yet this is the result of the trading-off between the reconstruction error and the computational efficiency, because the time to search for the most sparse representation of an object using a complete dictionary can be extremely time-consuming. More importantly, without knowing the object apriori, it is practically difficult to choose the spatial bases systematically in order to encode the object with the fewest non-zero basis coefficients using a complete dictionary. It is certainly possible that the Matching Pursuit algorithm misses the globally optimal bases for one particular target image or for a given ensemble of images.

The SEMs used in this study are five dominant SEMs suggested by the Singular Value Decomposition of the collection of B_z generated by each surface SEM coils. In theory, we may further include three additional SEMs available since we are considering an eight-element SEM coil array to explore MDE MRI in an even higher dimension. We did not pursue this due to the concerns regarding the computational complexity. It should be noted that the singular values revealed by SVD have no direct implications on the SEM spatial resolution, which is more closely related to the moments of the SEM, because the spatial basis is the complex exponential with the phase determined by the moment of the product between SEM spatial pattern and its strength. Other decomposition methods may suggest different SEMs. We speculate that different imaging experiments might prefer different SEMs based on appropriate structural and/or functional prior information that might be available for a particular application.

To optimize the moments of the SEMs, we used the prior knowledge that the object to be imaged is dominated by low spatial frequency components. This assumption was used in drawing realizations of candidate SEM moments using an exponential probability distribution function, which provides a higher density around the DC frequency components. Our results, including the validation tests (in Figures 4 and 7), show that the exponential distribution can provide reasonable reconstructions. It should be noted that the distribution of k-space data points can be tuned to trade-off between the ‘accuracy’ (i.e., the size of the reconstruction error) and the spatial resolution. That is, we may emphasize the density of the k-space sampling at lower spatial frequencies in order to reduce the reconstruction error. Our results (Figures 4 and 8) show that MDE reconstructions using an exponential distribution favoring lower spatial frequency components (the mean of the exponential distribution = 1/3) may have a smaller reconstruction error when the k-space sampling distribution and the number of data points were controlled.

The limit of the MDE MRI is closely related to physically feasible SEMs. Given SEMs, the spatial bases are then determined by their moments, which are directly related to the slew rate and the maximum strength of the gradient system as well as the desired spatial resolution and the echo time of the experiment.

The other challenge of MDE MRI is to tailor SEMs and RF coil arrays in order to jointly improve the conditioning of the encoding matrix. This is the same goal of many parallel MRI methods, where the k-space trajectory and RF coil sensitivity maps are jointly optimized to suppress the noise amplification in reconstructions (16).

The potential applications of MDE MRI include imaging experiments exploiting different tissue contrasts. With the optimized bases, we expect that the benefits of MDE MRI are available for both structural and dynamic MRI scans. In addition, based on the reciprocity theory, we expect that RF transmission using MDE MRI may have similar advantages of the transmit SENSE (17): with a higher degree of freedom in controlling the imaging aliasing, MDE MRI may further reduce the SAR limitation in high field MRI to correct B₁ inhomogeneity (18). We will explore this possibility in the near future.