Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Aug 27;3:2512. doi: 10.1038/srep02512

A coevolving model based on preferential triadic closure for social media networks

Menghui Li 1,2,3, Hailin Zou 3,4, Shuguang Guan 1,a, Xiaofeng Gong 2,3, Kun Li 2,3, Zengru Di 5, Choy-Heng Lai 3,4
PMCID: PMC3753589  PMID: 23979061

Abstract

The dynamical origin of complex networks, i.e., the underlying principles governing network evolution, is a crucial issue in network study. In this paper, by carrying out analysis to the temporal data of Flickr and Epinions–two typical social media networks, we found that the dynamical pattern in neighborhood, especially the formation of triadic links, plays a dominant role in the evolution of networks. We thus proposed a coevolving dynamical model for such networks, in which the evolution is only driven by the local dynamics–the preferential triadic closure. Numerical experiments verified that the model can reproduce global properties which are qualitatively consistent with the empirical observations.

Last decade has witnessed the booming of social media websites, suchas YouTube, Facebook, Second Life, Flickr, Epinions, and Twitter, to name just a few, which enable users to upload, disseminate, and share their interesting contents (e.g., photos, videos, or music, etc.), and even make friends with each other forming online communities1,2. These so called social media networks, recording the fingerprints of all participants' activities, provide prototypes of real networked complex systems. It is generally believed that the research in this field will enhance our understandings of the structure of social networks and the patterns of human behaviors3,4,5,6,7,8. Moreover, it also has potential for commercial applications9.

Recently, both theoretical and experimental works have been carried out in analyzing social media networks. For example, Refs. 10 and 11 investigated the dynamics of network visitation and dynamics of online popularity, respectively. Ref. 12 designed online experiments to explore how network structure affects the spread of behaviors. Refs. 13 and 14 studied the relaxation pattern after stimulations in social systems and how attention to novel items propagates and fades. In addition, the collective behaviors among online users under social influence have been studied both theoretically15 and experimentally16,17. These investigations have discovered interesting organization/evolution patterns18,19,20 and correlations21,22 in social media networks.

One of the fundamental issues in the research on networked dynamical systems is to reveal the possible generic laws governing the formation/evolution of networks. In order to obtain better understandings for this issue, the theoretical modelling, especially based on empirical analysis to real data, is of great importance. In the seminal work, Barabási and Albert set up a model, known as BA model after their names later, revealing a general rule in the growth of scale-free networks: the preferential attachment (PA)23. Nevertheless, this model23 and many others4,5,6,7,24 treat the simplest case of networks with only one type of node and one type of link inside. In fact, there exist various real-world complex networks, such as the social media networks, which are characterized by inherent multiplex nodes and multi-relational connections. What are the characteristics of the multi-relations in such systems? How topology and dynamics coevolve? Are there any interaction patterns between topology and dynamics, which essentially lead to universal statistical properties of networks? To obtain deeper insights into these open yet challenging questions in social media networks, a generic dynamical model with multiplex nature is desirable.

In this work, we attempted to set up a model describing the evolution of social media networks. Our model is based on the empirical analysis to the real data of Flickr and Epinions, which are typical social media networks. By analyzing the correlations in the Flickr and Epinions networks, we found that in such networks, the exchange of information, the interaction/influence among users, and the activities of users are essentially within the neighborhood. It is the local dynamical pattern, especially the formation of triadic links, that essentially regulates the whole network to evolve at macroscopic level. Our empirical analysis revealed that the preferential triadic closure could be one possible dynamical origin underlying the PA phenomenon in social media networks. Based on this understanding, we proposed an evolving model starting from two principles: (1) The evolution of network is governed by local dynamics, i.e., the preferential triadic closure; (2) The topology coevolves with the dynamics. This local mechanism in the present model is different from those based on global information in previous works23,24. The validity of our model has been justified by comparison between the results from the model and that from the real data. We think that this work could shed light on the understandings of organization and evolution in networked dynamical systems, and it also could be helpful in certain applications, such as designing efficient strategies for virtual marketing and network marketing, etc.

Results

Analysis to empirical networks

As shown in Fig. 1, Flickr and Epinions are typical dual-component networks which actually represent a broad class of social media networks consisting of users and items such as photos, videos, documents, music, blogs and so on (see Methods for data description and notations). Due to multiplex nodes and multi-relations, social media networks are more complicated than the usual networks involving only one type of node and one type of link. They are also different from the bipartite networks that are special dual-component networks studied previously25,26,27,28. In the following, we report the main findings of our empirical analysis to the Flickr and Epinions networks. Our particular attention is paid to the evolution patterns in these two networks.

Figure 1. Schematic plot of the social media networks, where the items could be photos (as in Flickr), reviews (as in Epinions), videos (as in YouTube), etc.

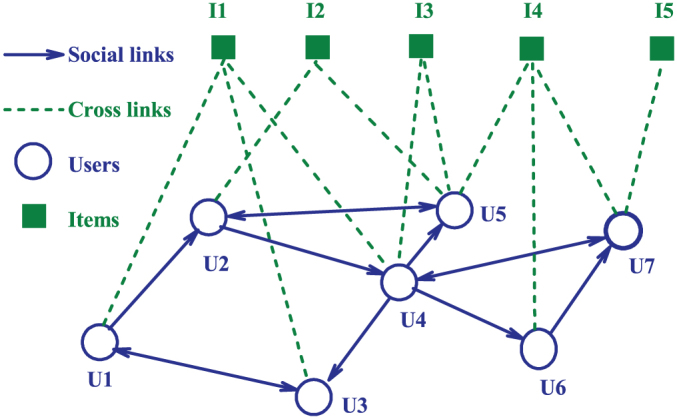
Figure 1

Open in a new tab

In principle, the social links (solid lines with arrowheads) are directional, while the cross links (dashed lines) are not. For these two types of links, we can define four types of degrees (see Methods for the details). For example, U4 in the network has indegree (kin = 2), outdegree (kout = 4), and favorite degree (kf = 2); I4 has popular degree (kp = 3). If the directions of social links are ignored, as we will do in the model, the links among users define the social degree (which is not the direct summation of indegree and outdegree because there is overlap between them for a user). In this case, for example, U4 has social degree (ks = 5) and favorite degree (kf = 2).

Cross correlations

Like many other complex networks, the growth of Flickr and Epinions involves two major factors: adding new nodes and generating new links. In real situations, removing nodes and deleting links also happen, but we neglected them in the present work for simplicity. In particular, we examined the mechanism forming new links because this is the central dynamical process governing network growth. For a growing network, there are several important questions. The first is: How new links are formed based on the current status of the network? To attack this problem, we investigated how generation of new links depends on the existing degrees in network (see Methods for the definitions of various degrees). Specifically, we extended the numerical method measuring PA during network growth29,30 (see Methods for more detail and notations) to calculate the conditional probability, with which a specific type of degree grows with respect to the existing degrees. In this way, the cross correlations among different types of degrees during network evolution can be identified.

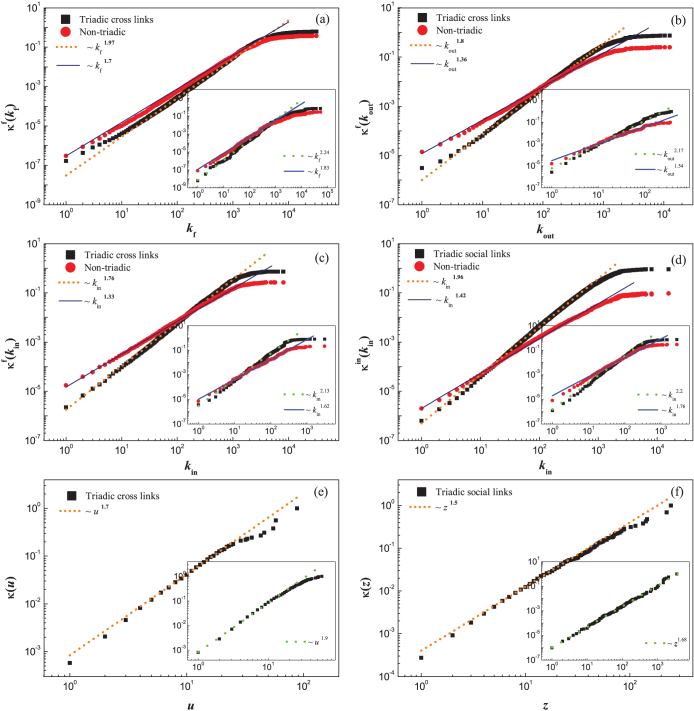
The results of above empirical analysis are illustrated in Figs. 2(a)–2(d) and summarized in Table I. From Fig. 2(a), we can see that the relative probability for a user to build a favorite degree is proportional to the existing favorite degree. Interestingly, as shown in Figs. 2(b) and 2(c), the similar dependence pattern also exists for the outdegree and indegree. Moreover, the approximate linear form of the cumulative functions κ in the double-log scale indicates that the relative probability generating new degree satisfies a power law with respect to the existing degrees, which can be characterized by the positive exponent α as in κ(x) ~ xα+1 with x denoting the degree. Numerical analysis has shown that in the Flickr and Epinions networks the formation of new links correlates with all the existing degrees, i.e., the local topological status. In Table I, we listed all the characteristic exponents α by fitting the κ functions. They are all positive, between 0 and 1.25, confirming the positive correlation pattern in link growth.

Figure 2. The influence of current status on the formation of new links in the Flickr and Epinions (in the insets) networks.

Figure 2

Open in a new tab

(a)–(d) The cumulative functions of relative probability, κf (kf), κf (kout), κf (kin), and κin(kin), respectively, characterizing the cross correlations in the growth of degrees. For example, in (b), κf (kout) plots the cumulative probability for a user to build a new cross link given that his existing outdegree is kout. The exponents are obtained by fitting the curves averaged over different initial t0, and Δt is one day. See the text for the definitions of the triadic and non-triadic links. (e)–(f) Characterizing the localized influence among neighboring users. (e) The cumulative functions of probability for a user to build a cross link to a specific photo (review) given that u of his neighbors have already favorite-marked (commented) it. (f) The cumulative functions of relative probability for a pair of users to build a social link given that they have already shared z favorite photos (reviews). The straight lines are guide to the eye through this paper.

Table 1. Exponents α as in κ(x) ~ xα+1, which characterize the cross correlations in the formation of triadic links and non-triadic links (in the brackets) in the Flickr and Epinions networks. κf and κout describe the relative probabilities of creating new links on the existing degrees, while κin and κp describe the relative probabilities acquiring new links on the existing degrees.
Networks κ(x)\x kf kout kin kp
Flickr κf 0.97 [0.70] 0.80 [0.36] 0.76 [0.33] -
  κout 0.88 [0.31] 0.85 [0.29] 0.73 [0.22] -
  κin 0.90 [0.42] 0.86 [0.34] 0.96 [0.42] -
  κp - - - 0.94 [0.94]
Epinions κf 1.24 [0.83] 1.17 [0.54] 1.13 [0.62] -
  κout 0.87 [0.30] 0.92 [0.45] 0.94 [0.46] -
  κin 1.03 [0.52] 1.25 [0.75] 1.2 [0.76] -
  κp - - - 1.06 [0.43]
Open in a new tab

Local dynamics

The second question regarding network growth is: Are the formed links short-ranged or long-ranged in terms of topological distance? How they depend on the topology? In other words, do users prefer to generate local connections or global connections? To attack this problem, we specially divided the new links into two types: the triadic links and the non-triadic links. If a new link can contribute at least one triangle in the network, it is regarded as a triadic link. Otherwise, it belongs to non-triadic link. It is found that most of new links are triadic links. For example, over 80% social links and over 50% cross links in Flickr18 and over 70% social links and over 60% cross links in Epinions are triadic links. These results show that links with short topological distances are more likely to be established. Moreover, as shown in Figs. 2(a)–2(d) and Table I, the formation of both triadic links and non-triadic links depends on the existing degrees with power law relations. However, the characteristic exponents of the triadic links are significantly larger than that of the non-triadic links, indicating that the local topological structure has more severe influence on the formation of triadic links than on the formation of non-triadic links. This localized growth pattern might be attributed to the specific rules in Flickr and Epinions, where a user usually obtains information from his neighbors and thus has relatively higher probability to connect to one of his second neighbors (neighbor's neighbors), either a user or an item.

On the other hand, more importantly, the above empirical analysis suggests one possible dynamical origin of PA phenomenon: the preferential triadic closure. As we know, it has been a fundamental issue to understand the mechanisms underlying PA since the BA model was successfully proposed31. In the present work, we focused on the possible dynamical origin of PA at microscopic level29. In Figs. 2(a) and 2(d), we have shown that the formation of triadic links can approximately lead to linear PA for degrees kf and kin. In particular, Fig. 2(d) has the exact meaning of PA in previous studies: The probability to acquire a link is proportional to its indegree. In fact, as listed in Table I, the diagonal characteristic exponents α related to triadic links are: 0.97 (1.24), 0.85 (0.92), 0.96 (1.2) and 0.94 (1.06) in the Flickr (Epinions) network, respectively, which are all close to 1. This provides an empirical evidence that the formation of triadic links could be one microscopic dynamical mechanism underlying the linear PA phenomenon.

Influence within neighborhood

The third question regarding network growth is: How a user's behavior is influenced by others, especially his neighbors in the network? To answer this question, we examined the correlations among users' activities within a neighborhood. For example, we calculated the probability for a user to favorite-mark (comment) a specific photo (review) (this will contribute a cross link) given that a certain number of his neighbors have already favorite-marked (commented) it before he does. Fig. 2(e) plots this relation, where the relative probability satisfies a power law with positive exponent about 0.7 (0.9) in the Flickr (Epinions) network. This shows that neighboring users' behaviors of favorite-marking photos (commenting reviews) are strongly correlated. On the other hand, if two users have already shared a large number of favorite photos (reviews), it is highly possible that they have similar appetite or style in photography (product). Thus it is more likely for them to make friends with each other due to the common interest. This correlation has been confirmed in our analysis. As shown in Fig. 2(f), the relative probability for two users, who do not connect to each other before, to become friends increases with the number of favorite photos (reviews) that they have commonly shared. The dependence is also characterized by a power law with exponent about 0.5 (0.68) in the Flickr (Epinions) network. This provides the evidence that common interest is in favor of social connections in these two networks. The above analysis suggests that in these two networks the influence or the interplay among users are typically localized in neighborhood.

Modelling

In this paper we attempted to set up a theoretical model for social media networks. Our primary target is to qualitatively reproduce the main properties observed in the two empirical networks. We have two motivations. Firstly, theoretical modelling is a necessary approach to understand the mechanisms or generic laws governing the evolution of real-world networks. Previously, it has been successfully shown that linear PA can lead to scale-free property32. Nevertheless, there is a deeper and interesting question: Is there any microscopic dynamical origin underlying the phenomenon of PA, which governs the network growth and leads to various statistical properties in real networks? This question has attracted much attention previously24,31,32,33,34, but it is still worthy of further investigation. Secondly, so far, although many models have been proposed to describe the evolution of networked systems4,5,6,7, they mainly dealt with the networks comprising one type of node23,24 or the bipartite networks25,26,27, focusing on the evolution of network topologies4,5,6,7,23,24,25,26,27. In fact, in realistic systems all the network properties should be the natural consequence of the coevolution of both dynamics and topology35.

We then based our modelling on the empirical findings reported in the previous section, i.e., in the Flickr and Epinions networks the main network-involving activities of users, such as searching, sending and receiving information, interacting with each other, and generating new links, are usually limited in the neighborhood. Especially, new links are more likely to be formed between users and their second neighbors, namely, the formation of triadic links is preferential. It is this local dynamical pattern that governs the evolution of network as a whole. Based on this understanding, we made the first guiding principle for our modelling:

• The network evolution should be only driven by local dynamics.

For simplicity, we made the following assumptions in our model: (1) Users and links once join the network, they are never removed; (2) The social links are symmetric, i.e., their directions are ignored; (3) New link connecting existing nodes (not the newly added nodes) is always triadic, i.e., between a user and one of his second neighbors. In this way, the link growth process can be understood as a two-step random walk following the information flow in the network, either via the cross links or via the social links.

In fact, we can consider a model only based on the above principle to describe the evolution of network topology. For example, following the third assumption above, we can assign a user certain probability that is based on the topological information in his neighborhood to form new links. In our study, we have tried several ideas of the existing models to simulate the evolution in social media networks, such as BA model23, growing network with redirection33, distance-dependent preferential attachment model36, connecting nearest-neighbors model37 and so on. The results have shown that considering the topological aspect alone in the modelling will not yield satisfactory properties in the generated network, e.g., the power law exponents are usually larger than 2 in these cases, which is inconsistent with the empirical results in the Flickr and Epinions networks, where the power law exponents are typically less than 2. This urged us to consider the fact that in social media networks dynamics and topology strongly interplay with each other. To obtain a satisfactory description of such networks, we made the second guiding principle for our modelling:

• Both topology and dynamics should coevolve.

However, it is not an easy task to formulate the users' behaviors in real circumstance because they are very complicated due to the inherent diversity of human dynamics. By carefully examining Flickr, Epinions, and LinkedIn, etc, we noticed that users' network-involving activities mainly depend on two factors: the stimuli from their neighbors and their own initiatives. For example, in LinkedIn, once a user updates his profile or connects to a new friend, his friend will automatically receive an email notice from the system, which inspires him to login the website to act accordingly. Of course, even without any notice, a user may also login the website either frequently or occasionally based on his own habit. To describe such behaviors of users, in our model we introduced a state function ϕ(i, t) for each user, where i is the user index and t denotes the time. Physically, it represents the willingness of a user to conduct online activities and it evolves as:

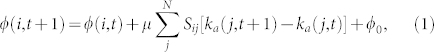graphic file with name srep02512-m1.jpg

where μ and ϕ0 are two parameters; ka(j, t) = ks(j, t) + kf(j, t) is the sum of social degree and favorite degree, i.e., the total degree of user j at time t, which reasonably represents the active level of the user. Note that in our model we neglected the directions of social links, so there are only two types of degrees for users, i.e, ks and kf. In equation (1), the first term at R.H.S. means that the state function is cumulative. The second term at R.H.S. sums up the stimuli received by user i from his neighbors. If his neighbors build new links at time t, his state will be affected at time t + 1, i.e., increasing an amount proportional to the net degree increase of his neighbors. Finally, the third term at R.H.S. simply describes the user's personal initiative by increasing a constant ϕ0 at each time step. To characterize the diversity of users, we randomly set a threshold, e.g., Θi ∈ [40, 4000], for each user. If the state function exceeds the threshold, the user will be activated and has a chance to conduct network-involving events, such as making friends, favorite-marking photos, or uploading photos in analogy to Flickr. Once a user is activated or builds a link, his state ϕ(i, t) will be reset to zero at the next time step. The above modelling, which follows our two guiding principles, though crude, basically imitates users' logins and activities in the social media networks in terms of state function.

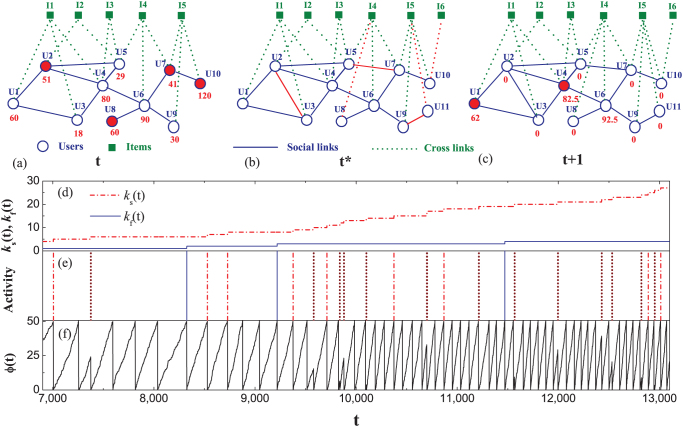
Numerically, the evolution of the model topology obeys the following rules: (1) At the very beginning, the initial network consists of a few users (N0) and items (M0), forming a small random network. The state functions of users evolve according to equation (1). (2) Adding users and items: at every time step, one new user is added and randomly connects a user and one of his favorite items. In the mean time m users are randomly selected from the activated users, and each of them creates one new item. (3) Adding links: at each time step, n users are randomly selected from the activated users, and each of them connects to one of his second neighbors (either user or item) via a two-step random walk if they do not connect each other before. In (2) and (3), if the number of activated users is less than m or n, respectively, the insufficient part can be randomly chosen to complement. A schematic illustration of the above procedure is plotted in Fig. 3, where the state and the topology of the network are shown to coevolve for one step driven by the local dynamics. As shown in Figs. 3(d)–3(f), with the increasing of social degree, the period of the state ϕ(t) for a user could become smaller, which means that those users with larger social degrees are more likely to participate in network-relating events.

Figure 3. Schematic illustration of the coevolution of both topology (a–c), and dynamical states (d–f) in the model.

Figure 3

Open in a new tab

The numeric tags are the values of state functions. (a) The network at time t, where some users (solid) are activated according to their states. (b) One step updating of the network topology, which involves several activities: New user U11 joins and randomly connects to user U9 and one of his favorite item I5; New item I6 is created (uploaded) by activated user U10; The activated users connect to their second neighbors, including friend of friend (e.g., U2 to U3); favorite item of friend (e.g., U8 to I4); and the fan of favorite item (e.g., U7 to U5). (c) At time t + 1, the states of users are updated according to equation (1). The states of activated users at time t are reset to 0, but some nodes are activated again according to their states at time t + 1. (d)–(f) Illustrating the evolution of degrees and state function for a specific user during certain time period in the model. (d) Evolution of the social degree ks(t) and the favorite degree kf(t). (e) The network-involving activities of the user. The dashed dot lines and the dot lines indicate the moments when the user initiatively increases his social degree (e.g., U2 to U3 in (b)), and the moments when the user passively increases his social degree (e.g., U5 was connected by U7 in (b)), respectively. The solid lines represent the moments when the user increases his favorite degree (e.g., U8 to I4 in (b)). (f) Evolution of the state function ϕ(t). Parameters for the model: m = 10, n = 100, μ = 0.5, ϕ0 = 1, Θ ∈ [40, 4000] (uniformly random number), N = 100,000 (the final size of the network).

Numerical verifications

We carried out numerical simulations to validate the model. It has been shown that the model can reproduce the main properties observed in the two empirical networks, for example, the highly skewed distributions of degrees, the long-term temporal correlation, the cross correlations among degrees, the correlation pattern among users' behaviors, etc. In the following, we compared the results of the model with the empirical analysis to the Flickr and Epinions networks.

Degree distributions

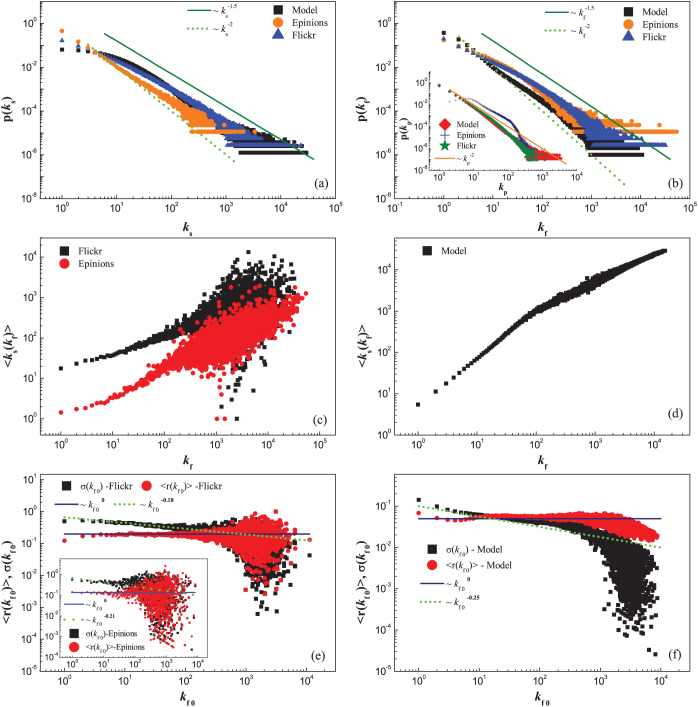
For a complex network, the degree distribution is one of the most important statistical properties. Figs. 4(a) and 4(b) compare the degree distributions of the model with that of the empirical networks. In both cases, the distributions were calculated for the static networks at the final stage. It is shown that all the three types of degrees approximately exhibit power-law scaling, and the distributions in the model are qualitatively consistent with the counterparts of the empirical networks. In particular, the power law exponents for the social degrees and the favorite degree can be less than 2 in certain parameter regimes in the model, which are consistent with the empirical observations in many online social networks38,39,40. If we do not consider the coevolution of dynamics and topology in the model, this property cannot be reproduced.

Figure 4. Comparing the properties of the model network with that of the empirical networks.

Figure 4

Open in a new tab

The model parameters are the same as in Fig. 3. Results are averaged over 10 realizations. Numerical experiments have also been carried out for other parameters, and the results are qualitatively the same. The empirical networks are at the final stage in the data collecting window. In the Flickr network, the total users and photos are about 3.7 × 105 and 1.1 × 107, respectively. 〈kout〉 = 〈kin〉 = 50.9, 〈kf〉 = 91.7, 〈kp〉 = 3.1. In the Epinions network, the total users and reviews are about 8.7 × 104 and 1.2 × 106, respectively, where 〈kout〉 = 〈kin〉 = 9.46, 〈kf〉 = 159.9, 〈kp〉 = 11.8. (a)–(b) The degree distributions. (c)–(d) The correlations between different types of degrees associated with the same users in static network. (e)–(f) Characterizing the mean growth rate r and standard deviation σ for favorite degree. For the model network, t0 = 90,000 and t1 = 100,000. For the empirical networks, t1 is the final day in the data collecting window, and t0 is the date about 90 (400) days before t1 for the Flickr (Epinions) network.

Correlations in static network

For a network inherently characterized by multi-relation links, it is natural to investigate the correlations among different degrees associated with the same nodes. To this end, we calculated the Pearson's correlation coefficients (PCC) between different pairs of degrees at the same nodes. In Fig. 4(c) the correlation between the social degree and the favorite degree is plotted for the empirical networks, where the PCC is about 0.35 (0.69) for the Flickr (Epinions) network, showing that they are correlated to some extent. In Fig. 4(d), the same correlation pattern is found for the model, where the PCC is about 0.90. The quantitative deviation for the PCCs has the following reason: In real system, the formation of cross links are affected by many factors besides the social degree of users, and therefore the PCC is relatively small; In our model, we only considered the influence of social degree on the formation of cross links, so the PCC is larger than that in empirical networks. We have computed all the pairwise PCCs among the four types of degrees of users in the empirical networks. They are: 0.35 (ks vs kf), 0.32 (kout vs kf), 0.4 (kin vs kf), and 0.76 (kin vs kout) for the Flickr; and accordingly 0.69, 0.33, 0.82, and 0.46 for the Epinions. These results confirm that in the two empirical networks, different types of degrees of users are all positively correlated with each other. Our model exhibits qualitatively consistent results. We noticed that some PCCs in the empirical networks are relatively small. They only show that different types of degrees in the network correlate to each other to some extent, but one type of degree cannot fully characterize the other.

Temporal pattern in degree growth

Flickr and Epinions turn out to be very successful commercially. They keep expanding rapidly since foundation. From the viewpoint of network, it is important to investigate the temporal growth pattern of degrees. We considered the growth rate r of a specific type of degree21: r ≡ ln k1/k0, where k could be any type of degree in the empirical networks. k0 = k(t0) and k1 = k(t1) are degrees at time t0 and t1, respectively. By keeping watching on those nodes with degree k0 (at time t0) during period (t0, t1), we can calculate the average conditional growth rate 〈r(k0)〉, and the standard deviation σ(k0). Examples are shown in Fig. 4(e), where the growth rate of kf is almost independent of initial degree kf0. Remarkably, its deviation approximately satisfies a power law scaling: 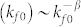Inline graphic, known as the generalized Gibrat's law in economic systems. Particularly, β < 1/2 indicates the nontrivial long-term correlation pattern21. In Fig. 4(f), for instance, we characterized the growth pattern for degree kf in the model, and found that it is well consistent with Fig. 4(e). We further confirmed that this long-term correlation pattern exists in the growth of all types of degrees in the Flickr and Epinions networks. In Table II, we computed the characteristic exponents β(r) and β(σ) for three types of degrees, i.e., ks, kf and kp. Note that in our model only three types of degrees are defined because the directions of social links are neglected. It is found that all the exponents β(σ) are less than 1/2, as observed in economic systems41,42,43,44 and online communication networks21. For comparison, the corresponding characteristic exponents for the model network are also listed in Table II. It is seen that for kf and ks, β(σ) = 0.25 and 0.28, respectively, which are well consistent with the empirical results where β(σ) = 0.18 and 0.23 in Flickr, as well as β(σ) = 0.21 and 0.18 in Epinions, respectively. In our model, for simplicity, we do not define state functions for items, so the increase of kp is basically of random nature. As a consequence, the corresponding β(σ) is approximately 0.5. We emphasize that in the model the values of β(σ) can be influenced by the heterogeneity of threshold parameter Θ. For example, if Θ is set as a constant in the model, β(σ) turns out to be close to 0.5, showing very weak temporal correlation. This, on the other hand, suggests that the diversity of users' behaviors might be one reason for the long-term correlation during network evolution.

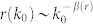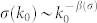Table 2. Exponents β(r) and β(σ) as in Inline graphic and Inline graphic, which characterize the mean degree growth rate r and the standard deviation σ in the evolution of the model network and the empirical networks (Flickr before Epinions in the parentheses). The parameters are the same as in Fig. 3 and Fig. 4.
  kf ks kp
β(r) 0.0 (0.0 & 0.0) 0.05 (0.10 & 0.0) 0.0 (0.0 & 0.0)
β(σ) 0.25 (0.18 & 0.21) 0.28 (0.23 & 0.18) 0.5 (0.17 & 0.2)
Open in a new tab

Cross correlations in the formation of degrees

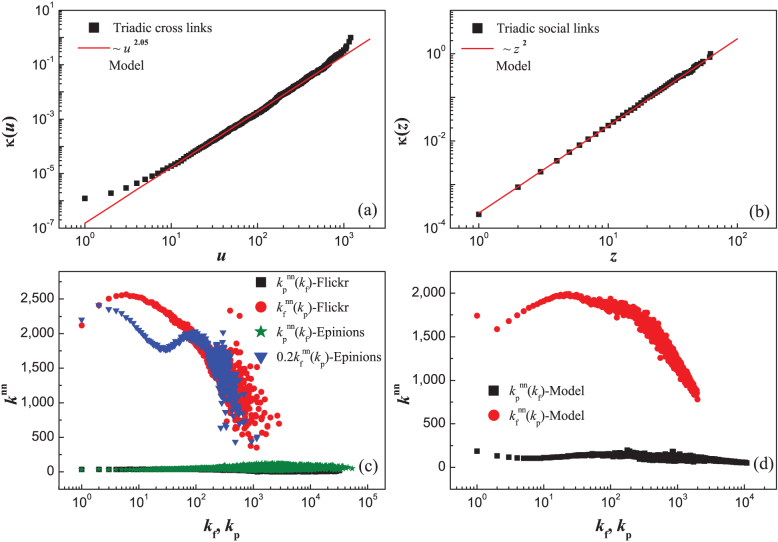
In previous empirical analysis, we have found that in the Flikcr and Epinions networks the probability to build a new link depends on the existing degrees, as shown in Figs. 2(a)–2(d) and Table I. To verify our model, we applied the same analysis and summarized the results in Table III. It is seen that the characteristic exponents α for the model are qualitatively consistent with that for the empirical networks.

Table 3. Exponents α for the model and the empirical networks (Flickr before Epinions in the parentheses). The parameters are the same as in Fig. 3 and Fig. 4.
κ(x)\x kf ks kp
κf 0.95 (0.97 & 1.24) 0.84 (0.79 & 1.16) -
κs 0.85 (0.90 & 0.95) 0.89 (0.84 & 1.10) -
κp - - 0.91 (0.94 & 1.06)
Open in a new tab

Local interaction pattern

In previous empirical analysis, we have revealed that the users' behaviors correlate with each other in the neighborhood, as shown in Figs. 2(e) and 2(f). It is found that the model can reproduce similar correlation patterns for neighboring users, as shown in Figs. 5(a) and 5(b). Since Flickr and Epinions have two types of nodes, it is also important to investigate the correlation between neighboring users and items. To this end, we calculated the average nearest neighbors' degree22. Here the term “neighbors” specially refers to the relation between users and their connecting items. We defined two quantities: the average popular degree of user i's favorite items and the average favorite degree of item λ's fans as

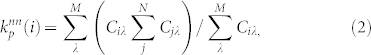graphic file with name srep02512-m2.jpg
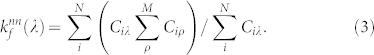graphic file with name srep02512-m3.jpg
Figure 5. Comparing the properties of the model network with that of the empirical networks.

Figure 5

Open in a new tab

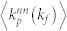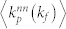(a)–(b) Characterizing the local influence patterns among users in the model, as compared with Figs. 2(e) and 2(f). (c)–(d) Characterizing the correlations between neighboring users and items in the model and in the empirical networks, i.e., Inline graphic and Inline graphic. The parameters for the model are the same as in Fig. 3.

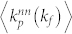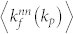Averaging the above two quantities over the whole network gives two functions: Inline graphic and Inline graphic, where the superscript nn denotes “nearest neighbor”. To some extent, they reflect the pattern in users' behaviors in the process of favorite-marking photos (or commenting reviews). Interestingly, it is found that these two quantities exhibit different patterns as shown in Fig. 5(c). 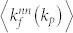Inline graphic positively correlates with kp when it is small (e.g., kp < 10 in Flickr), but the correlation becomes negative when kp is large. This shows that in the Flickr (Epinions) network, the popular photos (reviews) (with large kp) are most favorite-marked (commented) by common users (with small kf). Meanwhile, it is also found that 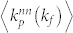Inline graphic approximately keeps constant, indicating that users in the Flickr (Epinions) network do not seem to care about the popularity of photos (reviews) when they favorite-mark (comment) them. This result differs from that in bipartite networks, e.g., the user-movie network, where 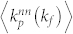Inline graphic is shown to be negatively correlated with kf28. This difference may be due to the different spreading modes of photos (reviews) and movies. For instance, in the user-movie network, a popular Hollywood blockbuster is just like global information that everyone knows, but in the user-photo or user-review networks there is no such counterpart. Instead, in Flickr (Epinions) users mainly favorite-mark photos (comment reviews) based on localized information. In Fig. 5(d), we computed the above two quantities for the model, and found that the model can present similar correlation patterns to the empirical analysis. Moreover, in our model we found the heterogeneity of threshold parameter Θ can also affect the nearest neighbor correlations.

Discussion

In this paper, we first carried out empirical analysis to the Flickr and Epinions networks. Our study revealed both temporal and topological correlation patterns. Especially, it is found that the network growth is essentially governed by the preferential formation of triadic closures. Motivated by the empirical findings, we proposed a coevolving dynamical model that starts from local dynamics, and is able to qualitatively reproduce the main properties observed in the empirical networks. Particularly, to our knowledge, this is the model based on local information which can exhibit: (1) Power law degree distributions with exponents less than 2; (2) Long-term growth pattern of degrees; (3) The nearest neighbors correlations that are consistent with real networks. Based on both empirical analysis and theoretical modelling, we think that the preferential formation of triadic closure could be one dynamical origin governing the evolution in a broad class of social media networks.

We emphasize two major characteristics of the model. First, in the present model, users preferentially generate triadic links based on their state functions, which only involves localized information and interaction. This differs from many previous models, which implicitly require global information23,24. Second, in our model, both dynamics and topology coevolve, which naturally leads to a dynamical network with various correlation patterns. This is also different from many previous models that only considered the evolution of network topology. Due to the ignorance of dynamics, they usually failed to exhibit correlation properties in networks, for example, the long-term correlation in degree growth21. Of course, the preferential triadic closure is only one possible mechanism underlying linear PA phenomenon, which can lead to scale-free properties. Due to the diversity and different nature of complex networks, there might be other microscopic mechanisms governing the network evolution.

It should be pointed out that our model can only reproduce qualitatively consistent results compared with the empirical analysis to real data. We attribute the quantitative mismatch to the simplifications made to set up the model. For example, in our model users are limited to obtain information only from their neighborhoods. Actually, real situations could be much more complicated. Research has shown that although over 80% users make their new friends in their second neighbors and over 50% of users find their favorite photos from their friends in Flickr18, users can access photos through various other channels, including those far from their neighborhoods. For example, by viewing the top-ranking photos or the most downloaded photos provided by the website, users may accordingly build links with large topological distance. These factors will lead to both long distance correlation and multiscale properties in the network. Especially they will affect the statistics of the small degrees. Moreover, the present model produces relatively higher PCC than observations in empirical networks. We think that the performance of the model can be improved by considering more realistic factors analyzed in previous section. All these problems deserve further investigations in the future.

Methods

Data description and notations

Flickr was founded in 2004. As the most famous website sharing photos, currently it has millions of active users and billions of photos. In Flickr, users basically involve three activities: uploading photos, favorite-marking photos and making friends. A user can claim any interesting photos as favorites (called favorites in Flickr). Once he favorite-marks a photo, he will automatically be a fan of this photo and thus in its fan list. Then he can retrieve the information of users in the fan list if he likes. Similarly, a user can unilaterally declare any other users as friends (called contacts in Flickr). For example, when user i declares user j as a friend, user j appears in the friends list of user i, and his profile information, such as his favorite photos and friends, is also available to user i.

The data set for our study is collected by daily crawling Flickr over 2.5 million users from Nov 2, 2006 to Dec 3, 2006, and again daily from Feb 3, 2007 to May 18, 2007. Totally, there are 104 days in the time window for data collection18,45 (http://socialnetworks.mpi-sws.org/). During this period, over 9.7 million new social links are formed, and over 950 thousand new users are observed. In particular, all temporal information for uploaded photos is stamped, including when the owner of a photo uploaded it, and who (and when) marked the photo as favorites, etc. For the purpose of network analysis, here we only considered the users who at least have one favorite photo and one friend. With this constraint, there are about 370 thousand users and 11.1 million photos in the data. Moreover, we assumed that the uploaders have marked their photos as favorite by default.

For analysis purpose, we first mapped the data into a network (referred to as the Flickr network throughout the paper), which is characterized by the dual components and the dual links, as schematically shown in Fig. 1. It has two types of nodes, i.e., N users and M items (photos) totally. Meanwhile, there are also two types of links, i.e., the links among users and the links connecting users and photos. We call them as the social links and the cross links, respectively. In the Flickr network, information can flow either via the social links or the cross links. Note that, in principle, the social links in the Flickr network are directional.

Mathematically, we can use two matrices to characterize the topology shown in Fig. 1. S is an N × N adjacency matrix representing the social links among users, with element Sij = 1 if user i declares user j as his friend, otherwise 0. Note that S is asymmetrical. Similarly, C is an N × M adjacency matrix characterizing the cross links, with element Ciλ = 1 if user i favorite-marks photo λ, otherwise 0. To be specific, we defined the following types of degrees to characterize the multi-relational connections in the Flickr network. Two degrees are related to the cross links: (1) the favorite degree: kf(i) = Σλ Ciλ, i.e., the number of favorite photos marked by user i, and (2) the popular degree kp(λ) = Σi Ciλ, i.e., the number of fans for photo λ, which reasonably represents its popularity extent in the network. Actually, kf and kp are two perspectives of the cross links connecting users and photos. In addition, since the social links in the network are directional, we accordingly defined another two types of degrees as: (3) the indegree: kin(j) = Σi Sij, i.e., the number of users who claim user j as friend, and (4) the outdegree, kout(i) = Σj Sij, i.e., the number of friends claimed by user i. Physically, outdegree and favorite degree together reflect the active level of a user, while the indegree represents the impact of the user. If we do not discriminate the directions of the social links, there are three types of degrees in the network: the popular degree (kp), the favorite degree (kf), and the social degree (ks) that is the number of friends for a user.

Epinions is a product review website established in 1999. In Epinions, users also basically involve three activities: writing reviews about products, commenting reviews and expressing their trust or distrust to other users. Once a user comments a review, he will automatically be in its commenting list. A user can unilaterally declare any other users as trust users or distrust users if he thinks their reviews to be valuable or inaccurate. Trust relationships are publicly accessible in Epinions but not the distrust relationships. The data set of Epinions for our study contains product reviews and review ratings before May 30, 2002, and both trust and distrust relationships before August 12, 200346 (http://www.trustlet.org/wiki/Extended_Epinions_dataset). In particular, all temporal information is available. For the purpose of network analysis, here we only consider the users who at least have one comment and one trust relation before May 30, 2002. With this constraint, there are 87,577 users, 546,883 trust relations, 1,198,115 reviews and 13,668,319 comments. Moreover, we assumed that the review writers have commented their own reviews by default. Apparently, the users, the reviews, trusting users, and commenting reviews in Epinions, just correspond to the users, the photos, making friends, favorite-marking photos in Flickr, respectively. Therefore, these two networks are topologically equivalent. For simplicity and convenience, we did not define another set of notations for the Epinions network. Throughout this paper, we used the same notations defined above for both networks. When necessary, we pointed out their physical implications in their own contexts. For example, in the Epinions network, the popular degree kp and the favorite degree kf specifically refer to the number of users commenting a review and the number of comments given by a user, respectively.

Measuring preferential attachment

In Refs. 29,30, a numerical method is used to measure the preferential attachment (PA) growth of network. Given knowing the temporal order in which the nodes join the network, the essential idea of the method is to monitor to which existing node new nodes connect, as a function of the degree of the old node. We can extend this method to characterize the multi-relational correlations among various degrees in the social media networks such as Flickr and Epinions. We take an example to briefly explain the method as follows: (1) At time t0, we mark the nodes with kout outdegree as “t0 nodes”, denoting their number as C(kout). (2) After the evolution of a period Δt, the favorite degrees of the “t0 nodes” have increased due to the evolution of the network (of course, the other types of degrees also change). We count the favorite degree acquired by the “t0 nodes” as A(kout). Since we divided the newly generated links into two types, i.e., the triadic and non-triadic, we have A(kout) = AT(kout) + AN(kout), where the subscripts T and N denote the two types, respectively. (3) The histogram providing the number of favorite degree acquired by the “t0 nodes” with exact kout outdegree, after normalization, defines a function30:

graphic file with name srep02512-m4.jpg

where, i can be either T or N. It has been proven that if PA mechanism exists, the conditional probability with which the favorite degree grows with respect to the existing outdegree follows a power law:

graphic file with name srep02512-m5.jpg

Numerically, it is convenient to examine the cumulative function of 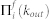Inline graphic, which will also follow a power law, i.e.,

graphic file with name srep02512-m6.jpg

Similarly, the above calculation can be applied to any pair of degrees for kin, kout, kf, and kp.

Author Contributions

M.H.L., H.L.Z., S.G.G., X.F.G., Z.R.D. and C.H.L. designed research and analyzed the data of Flickr; K.L. analyzed the data of Epinions; M.H.L. and S.G.G. performed research and wrote the paper. All authors reviewed and approved the manuscript.

Acknowledgments

We thank A. Mislove for sharing the Flickr database, and P. Massa for sharing the Epinions database. This work is sponsored by the following funding agencies: Science and Technology Commission of Shanghai Municipality under grant No. 10PJ1403300; Innovation Program of Shanghai Municipal Education Commission under grant No. 12ZZ043; and the NSFC under grant No. 11075056 and 11135001. ZRD is supported by NSFC under Grant No. 61174150. This work is partially supported by Temasek Laboratories at National University of Singapore through the DSTA Project No. POD0613356.

References

  1. Kaplan A. M. & Haenlein M. Users of the world, unite! the challenges and opportunities of Social Media. Business Horizons 53, 59–68 (2010). [Google Scholar]
  2. Kietzmann J. H., Hermkens K., McCarthy I. P. & Silvestre B. S. Social Media? get serious! understanding the functional building blocks of Social Media. Business Horizons 54, 241–251 (2011). [Google Scholar]
  3. Borgatti S. P., Mehra A., Brass D. J. & Labianca G. Network analysis in the social sciences. Science 323, 892–895 (2009). [DOI] [PubMed] [Google Scholar]
  4. Albert R. & Barabási A. L. Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97 (2002). [Google Scholar]
  5. Newman M. E. J. The structure and function of complex networks. SIAM Rev. 45, 167–256 (2003). [Google Scholar]
  6. Dorogovtsev S. N. & Mendes J. F. F. Evolution of networks. Adv. Phys. 51, 1079–1187 (2002). [Google Scholar]
  7. Boccaletti S., Latora V., Moreno Y., Chavez M. & Hwang D.-U. Complex networks: structure and dynamics. Phys. Rep. 424, 175–308 (2006). [Google Scholar]
  8. Castellano C., Fortunato S. & Loreto V. Statistical physics of social dynamics. Rev. Mod. Phys. 81, 591–646 (2009). [Google Scholar]
  9. Pitt L. F. & Berthon P. Just when you thought it was safe to go back into the Web: marketing meets web 2.0, Social Media, and creative consumers. Business Horizons 54, 181–183 (2011). [Google Scholar]
  10. Dezsö Z. et al. Dynamics of information access on the web. Phys. Rev. E 73, 066132 (2006). [DOI] [PubMed] [Google Scholar]
  11. Ratkiewicz J., Fortunato S., Flammini A., Menczer F. & Vespignani A. Characterizing and modelling the dynamics of online popularity. Phys. Rev. Lett. 105, 158701 (2010). [DOI] [PubMed] [Google Scholar]
  12. Centola D. The spread of behavior in an online social network experiment. Science 329, 1194–1197 (2010). [DOI] [PubMed] [Google Scholar]
  13. Crane R. & Sornette D. Robust dynamic classes revealed by measuring the response function of a social system. Proc. Natl. Acad. Sci. USA 105, 15649–15653 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Wu F. & Huberman B. A. Novelty and collective attention. Proc. Natl. Acad. Sci. USA 104, 17599–17601 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Onnela J.-P. & Reed-Tsochas F. Spontaneous emergence of social influence in online systems. Proc. Natl. Acad. Sci. USA 107, 18375–18380 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Salganik M. J., Dodds P. S. & Watts D. J. Experimental study of inequality and unpredictability in an artificial cultural market. Science 311, 854–856 (2006). [DOI] [PubMed] [Google Scholar]
  17. Lorenz J., Rauhut H., Schweitzer F. & Helbing D. How social influence can undermine the wisdom of crowd effect. Proc. Natl. Acad. Sci. USA 108, 9020–9025 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Cha M., Mislove A. & Gummadi K. P. A measurement-driven analysis of information propagation in the Flickr social network. Proceedings of the 18th Annual World Wide Web Conference (WWW'09) Madrid, Spain, pp. 721–730 (2009). [Google Scholar]
  19. Szell M., Lambiotte R. & Thurner S. Multirelational organization of large-scale social networks in an online world. Proc. Natl. Acad. Sci. USA 107, 13636–13641 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Gallos L. K., Rybski D., Liljeros F., Havlin S. & Makse H. A. How people interact in evolving online affiliation networks. Phys. Rev. X 2, 031104 (2012). [Google Scholar]
  21. Rybski D., Buldyrev S. V., Havlin S., Liljeros F. & Makse H. A. Scaling laws of human interaction activity. Proc. Natl. Acad. Sci. USA 106, 12640–12645 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Pastor-Satorras R., Vázquez A. & Vespignani A. Dynamical and correlation properties of the internet. Phys. Rev. Lett. 87, 258701 (2001). [DOI] [PubMed] [Google Scholar]
  23. Barabási A. L. & Albert R. Emergence of scaling in random networks. Science 286, 509–512 (1999). [DOI] [PubMed] [Google Scholar]
  24. Papadopoulos F., Kitsak M., Serrano M., Boguñá M. & Krioukov D. Popularity versus similarity in growing networks. Nature 489, 537–540 (2012). [DOI] [PubMed] [Google Scholar]
  25. Newman M. E. J., Watts D. J. & Strogatz S. H. Random graph models of social networks. Proc. Nat. Acad. Sci. USA 99, 2566–2572 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Goldstein M. L., Morris S. A. & Yen G. G. Group-based Yule model for bipartite author-paper networks. Phys. Rev. E 71, 026108 (2005). [DOI] [PubMed] [Google Scholar]
  27. Koskinena J. & Edlingc C. Modelling the evolution of a bipartite network-Peer referral in interlocking directorates. Social Networks 34, 309–322 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Grujić J., Mitrović M. & Tadić B. Mixing patterns and communities on bipartite graphs on web-based social interation. Proceedings of the 16th international conference on Digital Signal Processing, pp. 259–266 (2009). [Google Scholar]
  29. Jeong H., Néda Z. & Barabási A. L. Measuring preferential attachment in evolving networks. Europhys. Lett. 61, 567–572 (2003). [Google Scholar]
  30. Li M., Gao L., Fan Y., Wu J. & Di Z. Emergence of global preferential attachment from local interaction. New. J. Phys. 12, 043029 (2010). [Google Scholar]
  31. Mossa S., Barthélémy M., Stanley H. E. & Amaral L. Truncation of power behavior in “scale-free” network models due to information filtering. Phys. Rev. Lett. 88, 138701 (2002). [DOI] [PubMed] [Google Scholar]
  32. Krapvisky P. L., Redner S. & Leyvraz F. Connectivity of growing random networks. Phys. Rev. Lett. 85, 4629–4632 (2000). [DOI] [PubMed] [Google Scholar]
  33. Krapivsky P. L. & Redner S. Organization of growing random networks. Phys. Rev. E 63, 066123 (2001). [DOI] [PubMed] [Google Scholar]
  34. Kleinberg J. M., Kumar R., Raghavan P., Rajagopalan S. & Tomkins A. S. The web as a graph: measurements, models, and methods. Proceedings of the 5th annual international conference on Computing and combinatorics (Springer-Verlag Berlin), pp. 1–17 (1999). [Google Scholar]
  35. Gross T. & Blasius B. Adaptive coevolutionary networks: a review. J. R. Soc. Interface 5, 259–271 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Li M., Wang D., Fan Y., Di Z. & Wu J. Modelling weighted networks using connection count. New. J. Phys. 8, 72 (2006). [Google Scholar]
  37. Vázquez A. Growing network with local rules: Preferential attachment, clustering hierarchy, and degree correlations. Phys. Rev. E 67, 056104 (2003). [DOI] [PubMed] [Google Scholar]
  38. Mislove A., Marcon M., Gummadi K. P., Druschel P. & Bhattacharjee B. Measurement and analysis of online social networks. Proceedings of the 7th ACM SIGCOMM Conference on Internet Measurement (ACM Press, New York), pp. 29–42 (2007). [Google Scholar]
  39. Xiong F. et al. A dissipative network model with neighboring activation. Eur. Phys. J. B 84, 115–120 (2011). [Google Scholar]
  40. Tang S., Blenn N., Doerr C. & Mieghem P. V. Digging in the digg social news website. IEEE Trans. Multimedia 13, 1163–1175 (2011). [Google Scholar]
  41. Stanley M. H. R. et al. Scaling behaviour in the growth of companies. Nature 379, 804–806 (1996). [Google Scholar]
  42. Plerou V., Amaral L. A. N., Gopikrishnan P., Meyer M. & Stanley H. E. Similarities between the growth dynamics of university research and of competitive economic activities. Nature 400, 433–437 (1999). [Google Scholar]
  43. Matia K., Amaral L. A. N., Luwel M., Moed H. F. & Stanley H. E. Scaling phenomena in the growth dynamics of scientific output. J. Am. Soc. Inf. Sci. Tec. 56, 893–902 (2005). [Google Scholar]
  44. Rozenfeld H. D. et al. Laws of population growth. Proc. Nat. Acad. Sci. USA 105, 18702–18707 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Mislove A., Koppula H. S., Gummadi K. P., Druschel P. & Bhattacharjee B. Growth of the Flickr social network. Proceedings of the 1st Online Social Networks, pp. 25–30 (2008). [Google Scholar]
  46. Massa P. & Avesani P. Trust-aware bootstrapping of recommender systems. Proceedings of ECAI 2006 Workshop on Recommender Systems, pp. 29–33 (2006). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES