Hydrophobic interactions between the voltage sensor and pore mediate inactivation in Kv11.1 channels

Abstract

Kv11.1 channels are critical for the maintenance of a normal heart rhythm. The flow of potassium ions through these channels is controlled by two voltage-regulated gates, termed “activation” and “inactivation,” located at opposite ends of the pore. Crucially in Kv11.1 channels, inactivation gating occurs much more rapidly, and over a distinct range of voltages, compared with activation gating. Although it is clear that the fourth transmembrane segments (S4), within each subunit of the tetrameric channel, are important for controlling the opening and closing of the activation gate, their role during inactivation gating is much less clear. Here, we use rate equilibrium free energy relationship (REFER) analysis to probe the contribution of the S4 “voltage-sensor” helix during inactivation of Kv11.1 channels. Contrary to the important role that charged residues play during activation gating, it is the hydrophobic residues (Leu529, Leu530, Leu532, and Val535) that are the key molecular determinants of inactivation gating. Within the context of an interconnected multi-domain model of Kv11.1 inactivation gating, our REFER analysis indicates that the S4 helix and the S4–S5 linker undergo a conformational rearrangement shortly after that of the S5 helix and S5P linker, but before the S6 helix. Combining REFER analysis with double mutant cycle analysis, we provide evidence for a hydrophobic interaction between residues on the S4 and S5 helices. Based on a Kv11.1 channel homology model, we propose that this hydrophobic interaction forms the basis of an intersubunit coupling between the voltage sensor and pore domain that is an important mediator of inactivation gating.

INTRODUCTION

Kv11.1 channels play an important role in repolarization of the cardiac ventricular action potential and are therefore key regulators of a normal electrical rhythm in the heart (Sanguinetti and Tristani-Firouzi, 2006). Like other voltage-gated potassium (Kv) channels, Kv11.1 channels are comprised of four subunits, each with six transmembrane segments (S1–S6) (Vandenberg et al., 2012). On the periphery of each subunit are the S1–S4 helices, which form the voltage-sensing domain. The central conduction axis of the channel is lined by the four pore domains, formed by the S5 and S6 helices separated by a short pore helix and selectivity filter. Two voltage-regulated gates, located at either end of the pore domain, control the flow of potassium ions through Kv11.1 channels. The activation gate, formed by the intracellular ends of the four S6 segments, is slow to open and close. In contrast, the inactivation gate, formed by the four selectivity filter segments at the extracellular side of the pore, has rapid gating kinetics (Smith et al., 1996; Spector et al., 1996; Wang et al., 2011). These unique kinetics properties make Kv11.1 channels ideally suited for determining the duration of the plateau phase of the cardiac action potential (Vandenberg et al., 2012).

Alterations to the voltage-dependent inactivation gating of Kv11.1 channels can have profound effects on the duration of cardiac repolarization and hence duration of the QT interval on the body surface electrocardiogram. Mutations that shift the voltage dependence of inactivation to more depolarized potentials result in reduced inactivation leading to greater current flow and shorter repolarization intervals (Brugada et al., 2004; Sun et al., 2011), whereas mutations that shift the voltage dependence in the hyperpolarized direction have the opposite effect and result in lengthening of repolarization intervals (Zhao et al., 2009). Both of these scenarios result in a marked increase in the risk of arrhythmias and sudden cardiac arrest.

Although both the activation and the inactivation gates of Kv11.1 channels are voltage regulated, the two gating processes occur over different voltage ranges (Wang et al., 1997) and exhibit different sensitivities to amino acid mutations (Zou et al., 1998; Sanguinetti and Xu, 1999; Piper et al., 2005; Clarke et al., 2006), temperature (Vandenberg et al., 2006), and extracellular [Ca²⁺] (Johnson et al., 1999). Although the first three to four positive charges of the S4 helix have been clearly established as the voltage sensor for Kv11.1 activation (Subbiah et al., 2004; Zhang et al., 2004; Piper et al., 2005), the role of the S4 helix during Kv11.1 channel inactivation is relatively unknown. Even though the two gating processes are quite distinct, there is no reason why the S4 voltage sensor could not undergo two distinct movements and so underlie both functions. The unusual gating kinetics of Kv11.1 channels allows for separation of the rapid open-to-inactivated gating transition from the much slower closed-to-open transition, thereby permitting an examination of the S4 helix contribution to inactivation gating, independent of the S4 helix motion that transfers positively charged residues across the membrane electric field (gating current) and is coupled to activation gate opening.

In a previous study (Wang et al., 2011), we showed that the dynamics of inactivation gating in Kv11.1 channels was amenable to rate equilibrium free energy relationship (REFER) analysis. REFER analysis compares the effect of systematic perturbations to a protein on the free energy changes in kinetic (ΔΔG^‡) and thermodynamic (ΔΔG₀) relationships between two stable end states to gather information on the “structure” of the transition state (Fersht et al., 1992; Fersht, 2004, 2008) and, as a consequence, on the relative timing of domain motions during the transition between two stable end states (Grosman et al., 2000; Cymes et al., 2002; Zhou et al., 2005; Auerbach, 2007; Purohit et al., 2007). When applying REFER analysis to proteins, mutations of individual residues can be used to gain molecular-level detail about the conformational changes taking place (Grosman et al., 2000; Fersht, 2004; Zhou et al., 2005; Purohit et al., 2007; Wang et al., 2011). The slope of a REFER plot, that is the slope of ΔΔG^‡ versus ΔΔG₀, is defined as the Φ-value, and for this reason, in the protein-folding literature REFER analysis is usually referred to as Φ-value analysis (Fersht et al., 1992; Fersht, 2004, 2008). Φ-Values that are between 0 and 1 are indicative of the relative time point at which the mutation perturbed the interconversion between the two stable states, where Φ-values close to 0 indicate that the mutation has affected late steps in the reaction, and Φ-values close to 1 indicate that the mutation perturbed an early step in the reaction (Grosman et al., 2000; Cymes et al., 2002; Zhou et al., 2005; Auerbach, 2007; Purohit et al., 2007; Wang et al., 2011). In our previous study (Wang et al., 2011), we found that mutations to charged residues in the S4 region produced relatively modest perturbations to inactivation gating. In this study, we used REFER analysis to undertake a more comprehensive analysis of the role of the S4 helix during inactivation gating of Kv11.1 channels. Our results show that hydrophobic residues within the S4 domain are crucial in mediating inactivation gating of Kv11.1 channels, independently of the role that the charged residues of the S4 helix play during channel activation.

MATERIALS AND METHODS

Molecular biology and channel expression

Female Xenopus laevis frogs were purchased from Nasco, and all animal procedures were approved by the Garvan and St. Vincent’s Animal Ethics Committee (AEC 08/34, 11/37). Frogs were anaesthetized by immersion in 0.17% wt/vol tricaine, and stage V or VI oocytes were removed via a small (∼7–8-mm) abdominal incision. Oocytes were either mechanically separated using forceps, or lobes of oocytes were digested with 1 mg/ml collagenase A for 2 h, and then stored in ND96 solution (mM: 96 NaCl, 2 KCl, 1.8 CaCl₂, 1 MgCl₂, and 5 HEPES, pH 7.5) supplemented with 10 µg/ml gentamicin and 2.5 mM pyruvate.

Kv11.1 cDNA (provided by G. Robertson, University of Wisconsin-Madison, Madison, WI) was subcloned into a pBluescript vector containing the 5′ untranslated region (UTR) and 3′ UTR of the Xenopus β-globin gene (provided by R. Vandenberg, University of Sydney, Sydney, Australia). Mutations were introduced using the Quikchange method (Agilent Technologies) and confirmed by DNA sequencing. Plasmid DNA was linearized using BamHI-HF (NEB), and the in vitro transcription of cRNA was performed using the mMessage mMachine kit (Ambion). cRNA encoding WT or mutant (mut) Kv11.1 channels was injected into oocytes, which were then incubated at 18°C for 18–72 h before electrophysiological recording of current.

Electrophysiology

Oocytes were impaled with glass capillary micropipettes that had access resistances in the range of 0.3 to 1.0 MΩ. Currents were recorded from oocytes using a Geneclamp500B two-electrode voltage-clamp amplifier interfaced to a PC via a Digidata 1440 (Molecular Devices). Signals were filtered at 2 kHz and digitized at 5–10 kHz. Voltage-clamp protocols are shown as insets in Fig. 1 A. In all protocols, the cells were held at −90 mV before any voltage steps. After each experiment, the offset potential was checked, and if it exceeded ±5 mV, the recordings were discarded. Data acquisition and analysis were performed using pCLAMP (version 10.2; Molecular Devices), Excel (Microsoft) and Prism (version 6; GraphPad) software. All parameter values were calculated as mean ± SEM for n experiments, where n denotes the number of different oocytes studied for each construct.

Figure 1.

Measurement of inactivation kinetics for WT and V535S Kv11.1 channels. (A) Voltage protocols used to measure the rates of onset of inactivation (i) and the rates of recovery from inactivation (ii), with key regions for the measurement of current highlighted in black. (B and C) Representative families of current traces measuring the rates of onset of inactivation (i) and rates of recovery from inactivation (ii) for WT (B) and V535S (C) Kv11.1 channels. Highlighted in bold are current traces at 0 mV (i) and −130 mV (ii) to aid comparison. (D) Chevron plots of the logarithm of the observed rates for onset of (open squares) and recovery from (closed squares) inactivation for WT (i) and V535S (ii) channels, plotted against voltage. Solid black lines are a fit of Eq. 1 (see Materials and methods), whereas the solid gray line in (ii) indicates k_obs,V for WT channels to aid comparison. Dashed lines indicate the derived unidirectional rate constants for the onset of (k_inact,V) and recovery from (k_rec,V) inactivation, with values at 0 mV indicated by arrows. The equilibrium constant for inactivation (K_eq) at 0 mV was calculated by: K_eq,0 = k_inact,0/k_rec,0 (Eq. 2 in Materials and methods).

Kinetic analysis

The first step in performing a REFER analysis is to determine the kinetics of both the forward (open-to-inactivated) and reverse (inactivated-to-open) gating transitions of WT and mutant channels. This is relatively straightforward for Kv11.1 channels because the rapid inactivation gating transitions can be easily separated from the open/closed transitions (Smith et al., 1996; Spector et al., 1996; Wang et al., 2011). Rates of inactivation were measured using a triple-pulse protocol (see Fig. 1 A, i) in which cells were depolarized to +40 mV (or +80 mV for some mutant channels) for 500 ms to activate and inactivate channels, and then stepped to −90 or −110 mV for 10 ms to allow recovery from inactivation, before stepping to voltages in the range of +100 to −60 mV to monitor the onset of current inactivation. A single-exponential function was fitted to the decaying portion of the corresponding current trace (see Fig. 1 B, i). Reverse rates of inactivation gating (inactivated-to-open, k_rec), normally termed “recovery from inactivation,” were measured from two-step voltage protocols in which cells were depolarized to +40 mV (or +80 mV) for 500 ms to activate and inactivate channels, and then stepped to voltages in the range of −40 to −180 mV to allow channels to rapidly reopen before slowly closing (Fig. 1 A, ii). The initial rapid component of the “hooked” tail current at each voltage (depicted by black lines in Fig. 1 B, ii) represents the inactivated-to-open–state transition, whereas the slower component represents the open-to-closed–state transition. Therefore, the faster time constant obtained from a double-exponential function fitted to the hooked tail current represents the rate of recovery from inactivation.

For a bimolecular reaction with voltage-dependent rates, such as Kv11.1 channel inactivation, the observed rate (k_obs) at any particular voltage (V) is equal to the sum of the forward (k_inact,V) and reverse rates (k_rec,V) measured at that voltage:

$$k_{obs,\text{V}}=k_{inact,\text{V}}+k_{\text{rec},\text{V}}.$$ (1)

At 0 mV, k_obs,0 is therefore a combination of k_inact,0 + k_rec,0. However, at very positive voltages, k_rec is extremely small, and hence k_obs ≈ k_inact. Conversely, at very negative voltages, k_inact is extremely small, and so k_obs ≈ k_rec. An extrapolation of the linear portions of k_obs at very positive or very negative voltages (dotted lines in Fig. 1 D) can then be used to derive the unidirectional forward (k_inact,0) and reverse (k_rec,0) rate constants at 0 mV, respectively. A plot of the logarithm of k_obs,V results in a characteristic chevron phenotype (Fig. 1 D, i), indicating a reaction that is dominated by a single transition step (Jackson and Fersht, 1991). The equilibrium constant for inactivation at 0 mV (K_eq,0) was calculated by:

$$K_{eq,0}=k_{\text{inact},0}/k_{\text{rec},0}.$$ (2)

Perturbations to inactivation gating for each mutant were measured as the Δlog(K_eq,0) of the mutant channel compared with WT:

$$\Delta \text{log}\left(K_{\text{eq},0}\right)={\text{log}\left(K_{\text{eq},0}\right)}_{\text{mut}}-{\text{log}\left(K_{\text{eq},0}\right)}_{\text{WT}}.$$ (3)

A positive shift in Δlog(K_eq,0) is equivalent to a hyperpolarizing shift in the voltage dependence of inactivation, whereas a negative shift in Δlog(K_eq,0) is equivalent to a depolarizing shift in the voltage dependence of inactivation. In addition, the limiting slopes of the fits to the chevron plots were used as a direct measure of the voltage dependence of the forward and reverse transition pathways.

For a given mutation, the Φ-value is calculated by comparing changes, versus WT, in the energetics of the transition state (ΔΔG^‡) relative to changes in the free energy difference between the ground states (ΔΔG₀). For a two-state reaction, the transition state energy, ΔG^‡, is given by:

$$\Delta {\text{G}}^{‡}=-\text{RT}.\left(\text{ln}\right(k_{inact})+\text{ln}(\text{A}\left)\right),$$ (4)

where A is the “pre-exponential factor” (Price and Dwek, 1996). The effect of a mutant on the transition-state energy is given by the equation:

$$\Delta \Delta {\text{G}}^{‡}=-\text{RT}.\left(\text{ln}\right(k_{\text{inact},\text{WT}})-\text{ln}(k_{\text{inact},\text{mut}}\left)\right),$$ (5)

i.e., we assume that the mutation does not alter the “pre-exponential factor” for the reaction. Similarly, the effect of a mutant on the equilibrium free energy is given by:

$$\Delta \Delta {\text{G}}_0=-\text{RT}.\left(\text{ln}\right(K_{eq,\text{WT}})-\text{ln}(K_{eq,\text{mut}}\left)\right).$$ (6)

A Φ-value can be calculated from the ratio of the change in the logarithm of the unidirectional forward rate constant, log(k_inact,0), relative to the change in the logarithm of the equilibrium constant, log(K_eq,0):

$$\Phi =\Delta \Delta {\text{G}}^{‡}/\Delta \Delta {\text{G}}_0=\Delta \text{log}\left(k_{\text{inact},0}\right)/\Delta \text{log}\left(K_{eq,0}\right).$$ (7)

The Φ-value calculates to what degree a mutation-induced perturbation in the equilibrium constant for inactivation, which represents the energy difference between the open and inactivated ground states, is caused by a change in the forward transition rate (see Fig. S1). The Φ-value then reflects at what stage during the native reaction pathway the mutated residue experienced a change in its environment, as reflected by the change to the energetics of gating. To derive an accurate Φ-value, a mutation must cause a sufficient perturbation to the equilibrium constant, i.e., the denominator in Eq. 7. We, both previously (Wang et al., 2011) and in Fig. S2 B, and others (Cymes et al., 2002; Fersht and Sato, 2004) have established a Δlog(K_eq,0) of greater than or equal to ±0.5 as the cutoff criterion to derive an accurate Φ-value. Informative Φ-values are those that lie between 0 and 1 (Cymes et al., 2002; Wang et al., 2011), as shown in Fig. S1. There are three scenarios that result in an invalid Φ-value: (1) the mutation affects the transition state but not the ground states (i.e., a catalytic mutation), resulting in an infinite Φ-value (Fig. S1 F); (2) the mutation produces opposite effects on the transition state compared with the equilibrium between the two stable ground states, resulting in a negative Φ-value (Fig. S1 G); and (3) the mutation produces a greater effect on the transition state than on the ground state, resulting in a Φ-value >1 (Fig. S1 H). One benefit to REFER analysis is that these uninformative mutations can be identified because they result in Φ-values that lie outside of the range of 0 and 1. It is, however, also possible that a mutation could affect two or more independent processes that, by coincidence, cancel each other out to give a Φ-value between 0 and 1. Because this coincidental combination is unlikely to occur with a diverse range of mutations at a given residue, a better estimation of the Φ-value is derived from families of mutations at that position (Grosman et al., 2000). The other advantage of using families of mutants is that if a single mutant gives a very different result than that of other mutants at the same residue, it is immediately very obvious (see Fig. S2 A).

Double mutant cycle analysis

To test for an energetic coupling between two residues in different helices, we combined REFER analysis with double mutant cycle analysis. In this approach, individual mutations in the S4 helix, which significantly perturb inactivation (measured as ΔlogK_eq,0 > ±0.5 log units relative to WT), were combined with perturbing mutations in the S5 helix (Ile560, Leu564, or Ile567) or the S5P linker (Asp591). If an energetic coupling exists between two residues, the perturbations caused by the individual mutations (ΔΔG_mut1 and ΔΔG_mut2) would not be additive when combined in the double mutant (ΔΔG_mut1+mut2 < ΔΔG_mut1 + ΔΔG_mut2). Conversely, if the perturbations caused by the two single mutants were additive when combined in the double mutant (ΔΔG_mut1+mut2 = ΔΔG_mut1 + ΔΔG_mut2), the two residues are not energetically coupled.

Mean (X), SEM, standard deviation (S), and number of observations (n) for ΔΔG_mut1 + ΔΔG_mut2 were calculated by summing the corresponding values of Δlog(K_eq,0) from the two individual mutant channels (mut1 and mut2). An unpaired, unequal variance Welch’s t test was used to perform statistical analysis between the measured perturbation caused by the double mutant (ΔΔG_mut1+mut2, termed “X_double”) and the summed values of the two single mutants (ΔΔG_mut1 + ΔΔG_mut2 and X_mut1+mut2). For the statistical test, t-values were calculated as:

$$\text{t}={\text{X}}_{\left(\text{double}\right)}-{\text{X}}_{(\text{mut1}+\text{mut2})}/\mathit{S}({\text{X}}_{\left(\text{double}\right)}-{\text{X}}_{(\text{mut1}+\text{mut2})}),$$ (8)

where the variance (S(X_(double) − X_(mut1+mut2))) was calculated by:

$$S(X_{\left(double\right)}-X_{(mut1+mut2)})=\sqrt{\frac{S{\left(double\right)}^2}{n\left(double\right)}+\frac{S{(mut1+mut2)}^2}{n(mut1+mut2)}}\text{.}$$ (9)

Degrees of freedom (df) was calculated by:

$$\text{df}=({{\text{S}}_{\text{double}}}^2/n_{\text{double}})+({{\text{S}}_{\text{mut1}+\text{mut2}}}^2/n_{\text{mut1}+\text{mut2}})/\left(\right({({{\text{S}}_{\text{double}}}^2/n_{\text{double}})}^2/(n_{\text{double}}-1))+({({{\text{S}}_{\text{mut1}+\text{mut2}}}^2/n_{\text{mut1}+\text{mut2}})}^2/(n_{\text{mut1}+\text{mut2}}-1)\left)\right).$$ (10)

p-Values were calculated using t and df values. P < 0.05 was considered significant.

Voltage dependence of activation

Isochronal activation curves were measured according to standard tail current analysis (Vandenberg et al., 2012). From a holding potential of −90 mV (or −120 mV for some mutants), the membrane potential was stepped to voltages in the range of −60 to +50 mV (the precise range varies from −120 to +100 mV depending on the mutant studied) for 4 s, before a step to −70 mV (or −120 mV) to record tail currents. Tail currents were normalized to the maximum current amplitude (I_max) and fitted with a Boltzmann expression:

$$\frac{I}{I_{max}}={\left[1+e^{\frac{(V_{0.5}-V_t)}{k}}\right]}^{-1},$$ (11)

where I/I_max is relative current, V_0.5 is the voltage of half-current activation, V_t is the membrane potential, and k is the slope factor. Alternatively, data were fitted with the thermodynamic form of the Boltzmann expression:

$$\frac{I}{I_{max}}={\left[1+e^{\frac{(\Delta G_0-z_{g}EF)}{RT}}\right]}^{-1},$$ (12)

where ΔG₀ is the work done at 0 mV, z_g is the effective number of gating charges moving across the membrane electric field (E), F is Faraday’s constant, R is the universal gas constant, and T is the absolute temperature. From Eq. 12 we can calculate the effect of mutations on changes in chemical potential energy:

$$\Delta \Delta G_0=\Delta G_{0,Mut}-\Delta G_{0,WT}.$$ (13)

Homology structure generation

The Kv11.1 homology model, generated using Swiss PdbViewer (Guex and Peitsch, 1997) and optimized using SWISS-MODEL Workspace (Arnold et al., 2006; Bordoli et al., 2009), was based on the crystal structure of a Kv1.2/2.1 channel chimera (Long et al., 2007), according to the sequence alignment shown in Fig. S3.

Online supplemental material

Fig. S1 shows a series of energy diagrams that explain the theory of REFER (Φ-value) analysis when applied to the study of Kv11.1 channel inactivation gating. Fig. S2 demonstrates the variability in Φ-values derived from mutants that perturb Kv11.1 channel inactivation with varying severity. Fig. S3 is a sequence alignment between Kv11.1 and Kv1.2/2.1 channels, which was used to generate our Kv11.1 channel homology model. Table S1 summarizes the kinetic parameters of inactivation for each S4 mutant investigated, and Table S2 summarizes the activation parameters for each S4 mutant investigated. The online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.201310975/DC1.

RESULTS

REFER analysis can be applied to any process where there are two ground states separated by a single dominant transition state, and where the forward and reverse rates can be well described by a single-exponential process (Auerbach, 2007). C-type inactivation gating in Kv11.1 channels is very rapid, so the forward (open-to-inactivated) and reverse (inactivated-to-open) inactivation gating transitions can easily be separated from the much slower activation (closed-to-open) or deactivation (open-to-closed) gating transitions (Smith et al., 1996; Spector et al., 1996; Wang et al., 2011). Although it is possible that Kv11.1 channels may also transition into an inactivated state from a preopen closed state (Kiehn et al., 1999), this transition is likely negligible when compared with the open-to-inactivated transition pathway (Bett et al., 2011). Furthermore, the probability of a closed-to-inactivated transition can be minimized using voltage protocols that ensure that the majority of channels are in the open conformation before initiating inactivation.

The specific voltage protocols used to measure rates of inactivation (k_inact; measured at voltages ranging from −20 to +80 mV) and rates of recovery from inactivation (k_rec; measured at voltages from −60 to −160 mV) are shown in Fig. 1 A, with the resulting currents for WT Kv11.1 channels (Fig. 1 B) or V535S channels (Fig. 1 C) shown below. For WT, the region of current representing the onset of inactivation (Fig. 1 B, i) or the recovery from inactivation (Fig. 1 B, ii) at a given voltage (V) were well described by a single-exponential function and were used to measure k_inact,V and k_rec,V, respectively. A plot of the observed rates (K_obs; see Eq. 1 in Materials and methods) against voltage generates a “chevron” phenotype, which is indicative of a transition dominated by a single step (Fig. 1 D, i). The extremities of each arm of the chevron plot are linear as they reflect the unidirectional rate constants of the forward or reverse transition at the extreme voltages. To calculate an equilibrium constant for inactivation at a single voltage, normally 0-mV (K_eq,0 = k_inact,0/k_rec,0), unidirectional rate constants at each voltage were derived by extrapolation from the linear portion of the relevant arm of the chevron plot (Fig. 1 D, i, dashed lines). After the introduction of a point mutation, V535S, the plot of log(K_obs) against voltage demonstrates a clear depolarizing shift in the voltage dependence of inactivation, which is indicated by a slowing of k_inact,V and a concomitant acceleration of k_rec,V. The resulting logarithm of the equilibrium constant for inactivation is clearly shifted more negative with respect to WT (Δlog(K_eq,0) = −0.91 ± 0.1; n = 7), allowing a Φ-value to be calculated according to Eq. 7 (see Materials and methods). The kinetic properties of Kv11.1 channel inactivation can therefore be exploited to allow its study using REFER analysis.

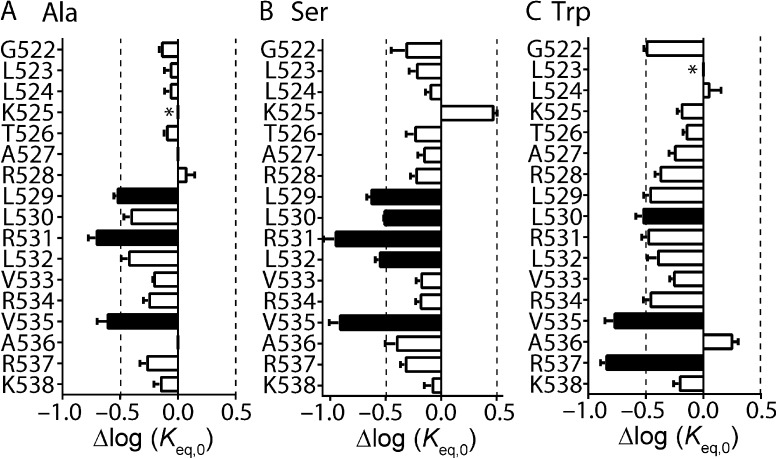
To obtain an accurate estimate of a Φ-value from a REFER plot, one or more mutations of a given residue must cause a sufficient perturbation to the transition pathway. We, both previously (Wang et al., 2011) and in Fig. S2, and others (Cymes et al., 2002; Fersht and Sato, 2004) have established a Δlog(K_eq,0) of greater than or equal to ±0.5 as a reasonable cutoff criterion. Based on these criteria, we used REFER analysis to perform an extensive investigation of the role of the S4 helix during Kv11.1 channel inactivation. To optimize our chances of finding mutant channels within the S4 helix that were amenable to REFER analysis, we performed three separate mutagenesis scans on residues Gly522 to Lys538. Each residue was mutated to alanine (Fig. 2 A), serine (Fig. 2 B), or tryptophan (Fig. 2 C). From these scans, several residues stood out as having at least one mutation with a Δlog(K_eq,0) of greater than ±0.5 log units, namely, L529A/S, L530S/W, R531A/S, L532S, V535A/W/S, and R537W (Fig. 2, closed bars, and Table S1).

Figure 2.

Scanning mutagenesis of the Kv11.1 channel S4 helix. (A–C) Shifts, relative to WT, in log(K_eq,0) values for alanine (A), serine (B), and tryptophan (C) mutagenesis scans of S4 residues spanning from Gly522 to Lys538. Data are presented as means ± SEM for n = 3–20 cells (see Table S1). Dashed lines indicate Δlog(K_eq,0) > ±0.5 log units, which has been shown previously to be the minimum perturbation required to derive an accurate Φ-value (Cymes et al., 2002; Wang et al., 2011). Mutations that fulfill this minimum requirement are indicated by closed bars, whereas mutations with Δlog(K_eq,0) < 0.5 log units are indicated by open bars. *, mutant channels that failed to express or expressed poorly.

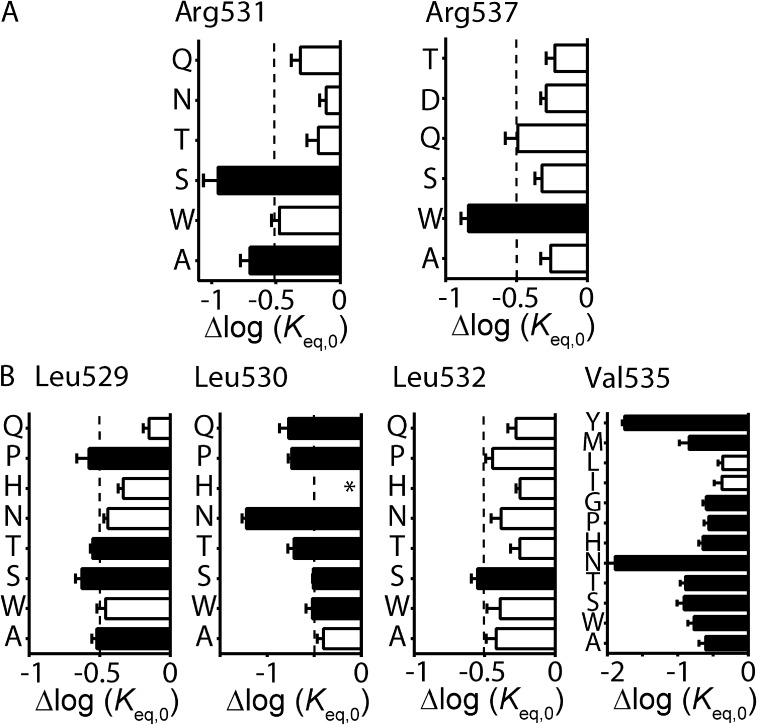
Although it is possible to derive Φ-values from the individual mutant channels listed above (see Table S1), it is important to note that the temporal information they provide is based on the effect of the specific mutation in perturbing the transition pathway, and may not necessarily reflect the role of the native amino acid residue per se. For example, any single mutation could affect two or more different processes that, by coincidence, cancel each other out to give a Φ-value between 0 and 1 (see Materials and methods). However, this type of coincidental combination will not occur with every mutation at that position. Therefore, a better estimation of Φ-values can be derived from plots of log(k_inact,0) versus log(K_eq,0) for a family of mutations at a single residue or region of the channel (Grosman et al., 2000). We therefore interrogated S4 helix residues identified from our scanning mutagenesis in more detail by obtaining families of mutations at each position (Fig. 3). Mutation of charged residues Arg531 (to Gln, Thr, and Asn) or Arg537 (to Gln, Asp, and Thr) did not produce any further mutant channels with adequate perturbations to Δlog(K_eq,0) (Wang et al., 2011, and Fig. 3 A). The relative tolerance of neutral or polar side chains at these positions, as well as at Lys525, Arg528, Arg534, and Lys538 (Table S1 and Wang et al., 2011), suggests that the positively charged side chains are not critical to the inactivation gating transition. We therefore concentrated on the hydrophobic residues: Leu529, Leu530, Leu532, and Val535, which were further mutated to threonine, histidine, proline, asparagine, and glutamine. In the case of Val535, we also mutated this residue to glycine, leucine, isoleucine, methionine, and tyrosine. Perturbations to Δlog(K_eq,0) of greater than ±0.5 log units were observed for several mutant channels at all positions, with the exception of Leu532 (Fig. 3 B). Hydrophobic residues Leu530 and Val535 were particularly sensitive to mutation; i.e., tyrosine, methionine, glycine, proline, histidine, asparagine, and threonine mutations at Val535 all exhibited a Δlog(K_eq,0) of >0.5 log units compared with WT, whereas only the relatively conserved hydrophobic side chains of leucine and isoleucine produced smaller perturbations (Fig. 3 B). The relative intolerance of these hydrophobic residues to mutations that do not maintain their hydrophobic side chain properties indicates their importance in mediating open-to-inactivated transition.

Figure 3.

Families of mutations at important Kv11.1 channel S4 residues. (A and B) Shifts in log(K_eq,0), relative to WT, for families of mutations at charged (A) or hydrophobic (B) residues that were identified as important determinants for inactivation gating from our mutagenesis scans of the S4 helix. Mutations are indicated by single–amino acid code on the y axis. Data are presented as means ± SEM for n = 4–14 cells (see Table S1). Mutations that cause a significant perturbation to inactivation, measured as Δlog(K_eq,0) > ±0.5 log units relative to WT, are indicated by closed bars, whereas mutations with Δlog(K_eq,0) < ±0.5 log units are indicated by open bars. *, mutant channels that failed to express or expressed poorly.

The equilibrium constant represents the energy difference between the open state and the inactivated state (see Fig. S1). Because energy and structure are related, a mutation-induced perturbation to the energetics of gating, observed as a shift in log(K_eq,0), indicates that the amino acid residue experiences a change in environment at a given point during the transition from the open state to the inactivated state. The Φ-value represents the relative time point during the transition at which this change in environment occurs, with Φ-values close to 1 representing a change in environment early in the transition pathway, whereas a Φ-value close to 0 represents a change in environment at a time point closer to the end of the transition. To determine the relative timing of motion for each of the S4 helix hydrophobic residues during the inactivation gating transition, Φ-values were calculated from families of mutations at each position. Plots of log(k_inact,0) versus log(K_eq,0) for all mutants at Leu529 (Φ-value = 0.48 ± 0.10), Leu530 (Φ-value = 0.33 ± 0.07), Leu532 (Φ-value = 0.68 ± 0.08), and Val535 (Φ-value = 0.49 ± 0.02) are shown in Fig. 4 A (i–iv). In addition, a plot of all Leu529, Leu530, Leu532, and Val535 mutants is shown in Fig. 4 B (Φ-value = 0.48 ± 0.03), and a plot of all mutants in the S4 helix is shown in Fig. 4 C (Φ-value = 0.50 ± 0.02). Of the individual hydrophobic residues, only Leu530 produced a Φ-value that was significantly different from the Φ-value derived from the remainder of the S4 mutations (0.33 ± 0.07 for Leu530 vs. 0.52 ± 0.02 for all other S4 mutants; analysis of covariance [ANCOVA]; P < 0.05), suggesting that Leu530 may be involved at a slightly later stage in the open-to-inactivated transition pathway.

Figure 4.

Mutation of S4 residues affects inactivation at a midway point during the transition pathway. (A) REFER plots of the log forward unidirectional rate constant, log(k_inact,0), against the log equilibrium constant, log(K_eq,0), for inactivation, in families of mutations at individual residues: i, Leu529; ii, Leu530; iii, Leu532; iv, Val535. (B and C) REFER plots for all mutations at Leu529, Leu530, Leu532, and Val535 combined (B) or all S4 residue mutations (C). Data are presented as means ± SEM for 3–14 cells. The slope of the linear regression analysis (solid black lines) for each family of mutations represents the Φ-value, as indicated, and can be compared with the slope for all other S4 mutations (solid gray lines). ANCOVA was used to determine statistical significance; *, P < 0.05.

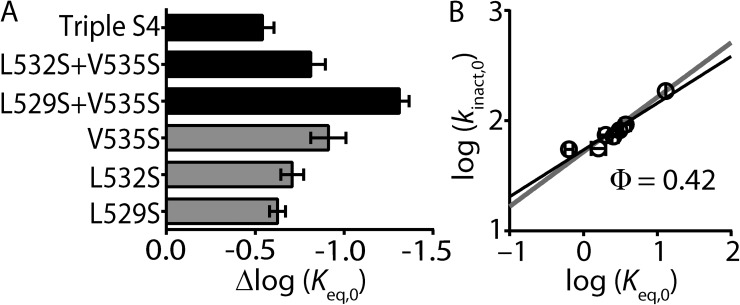
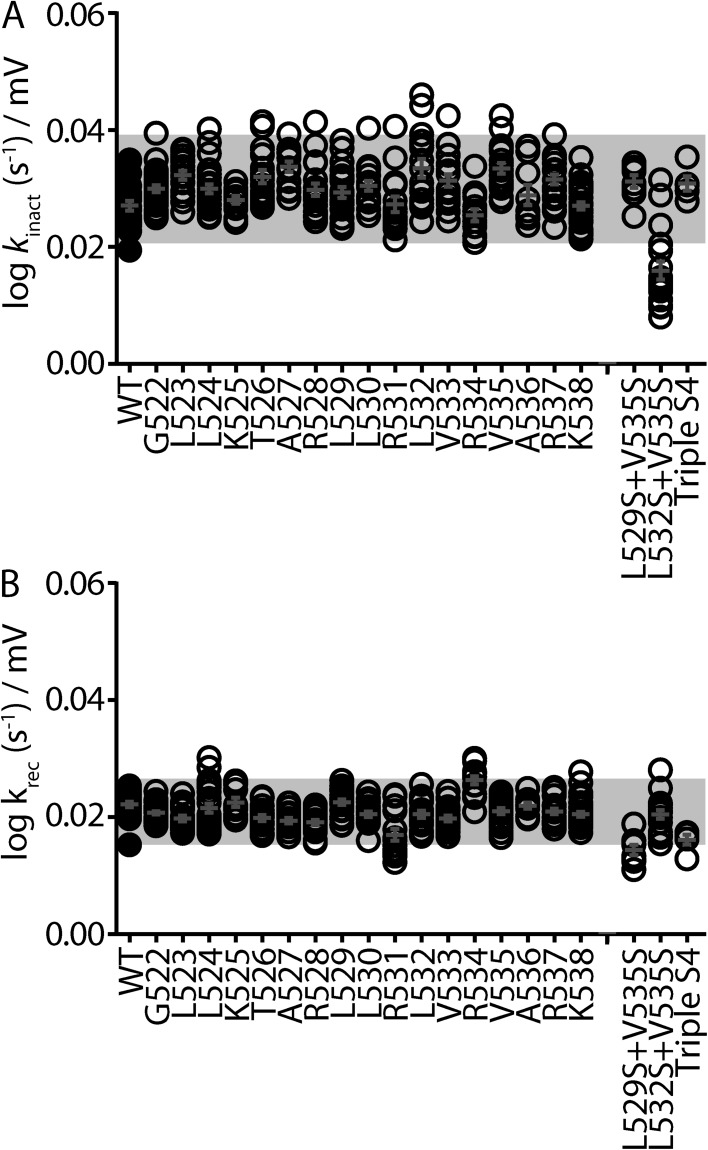
The observation that the slopes of the REFER plots for hydrophobic residues Leu529, Leu532, and Val535 are not significantly different (∼0.5) suggests that this region of the S4 helix moves as a single entity. To test this, we investigated whether combining V535S with either L529S and/or L532S would give additive (expected if motions were independent) or nonadditive (expected for rigid body motions) effects on Δlog(K_eq,0) values. Fig. 5 A shows a bar graph comparing the shifts in log(K_eq,0) of single mutants (V535S, L532S, and L529S), double mutants (L529S + V535S and L532S + V535S), and the triple mutant (L529S+L532S+V535S; Triple S4). Although the Δlog(K_eq,0) was larger for the L529S + V535S double mutant when compared with the single mutations, the increase in Δlog(K_eq,0) was not as large as the sum of the two individual residues combined. Furthermore, neither the double mutant L532S + V535S nor the triple S4 mutant produced Δlog(K_eq,0) values that were significantly different from the largest individual single mutant, V535S (Fig. 5 A). A plot of log(k_inact,0) versus log(K_eq,0) for all combination mutants produced a slope of 0.42 ± 0.07 and was not significantly different from that derived from the S4 helix as a whole (Fig. 5 B). Our data strongly suggests that the face of the S4 helix that encompasses the hydrophobic residues Leu529, Leu532, and Val535 moves as a single entity during inactivation gating of Kv11.1 channels.

Figure 5.

Combinations of S4 mutants do not have additive effects on the energetics of Kv11.1 channel inactivation. (A) Bar graph comparing shifts in log(K_eq,0), relative to WT, for triple S4 mutant (L529S + L532S + V535S), double mutants L532S + V535S and L529S + V535S, and single mutants V535S, L532S, and L529S. Data are presented as means + SEM for 5–18 cells. (B) REFER plot of triple S4 mutant (L529S + L532S + V535S), double mutants L532S + V535S and L529S + V535S, and single mutants V535S, L532S, and L529S. Data are presented as means ± SEM for 5–18 cells. The linear slope (solid black line) indicates a Φ-value of 0.42 and was not significantly different to that derived from all of the individual S4 mutants (Φ = 0.50; P > 0.05 using ANCOVA).

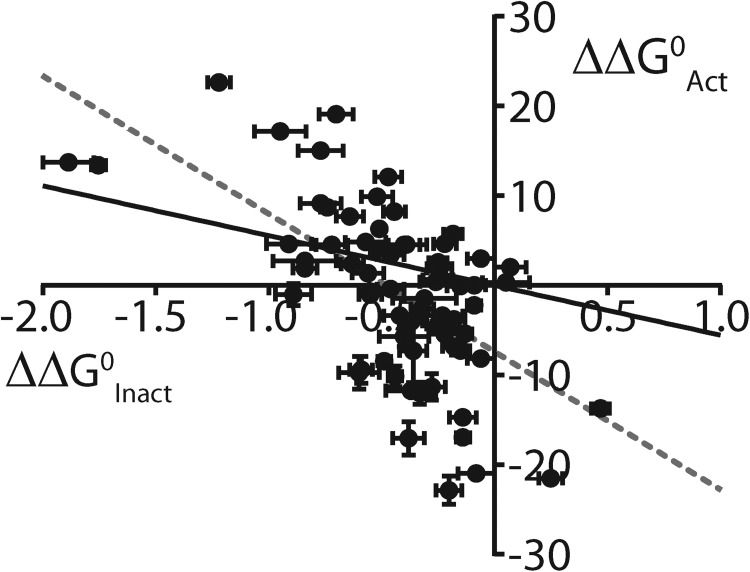
Inactivation of Kv11.1 channels is thought to be intrinsically voltage dependent; i.e., the voltage dependence of inactivation is not directly linked to the voltage dependence of activation (Vandenberg et al., 2012). There are two ways that a mutation can affect the voltage-dependent inactivation of Kv11.1 channels. The first is by altering the chemical free energy change associated with inactivation, i.e., a shift in the equilibrium set point of the voltage dependence (compared with WT), as reflected by a change in log(K_eq,0). The vast majority of point mutations in the S4 helix (66 out of 70; see Fig. 6 and Table S1), and throughout the channel protein (Wang et al., 2011), caused a negative shift in log(K_eq,0), reflecting a depolarizing shift in the voltage dependence of inactivation (i.e., stabilization of the open state). In contrast, the same set of S4 mutations altered the chemical free energy, and hence the voltage dependence, of activation gating in either direction to an approximately equal degree (Fig. 6). Thus, the S4 mutation-induced perturbations to the voltage dependence of inactivation show only a weak correlation (R² = 0.38) with the perturbations to the voltage dependence of activation (Fig. 6), consistent with the notion that the activation and inactivation gating processes are not directly linked.

Figure 6.

Perturbations to inactivation gating and activation gating show poor correlation for S4 residue mutations. Plot comparing perturbations to ΔG⁰, versus WT, of inactivation gating (ΔΔG⁰_Inact, represented by Δlog(K_eq,0)) compared with perturbations to ΔG⁰, versus WT, of activation gating (ΔΔG⁰_Activ; see Materials and methods) for each S4 residue mutation. Solid black line represents linear regression analysis constrained to go through WT, whereas dashed gray line is an unconstrained fit (R² = 0.38).

The second way that a mutation can perturb inactivation is by directly altering the degree of voltage dependence, which can be detected as a change in the slope of the unidirectional forward (inactivation) or reverse (recovery from inactivation) transition rate constants (shown as black lines in Fig. 1 D). Slope values representing the voltage dependence of inactivation (Fig. 7 A) and recovery from inactivation (Fig. 7 B) for all individual S4 residue mutations (to Ala, Ser, and Trp) tested during scanning mutagenesis of the S4 domain all fall within ±2 standard deviations (gray box) of the mean. In other words, none of the individual residue mutations significantly alter the voltage dependence of inactivation gating. It was only when we combined hydrophobic residue mutations (L532S + V535S for the forward rate) and (L529S + V535S and L529S + L532S + V535S for the reverse rate) that we observed modest changes to the voltage dependence of rates of inactivation (Fig. 7). Thus, it is possible that the S4 helix contributes to the voltage dependence of inactivation gating. However, as we only saw significant deviations with combined mutants, we should be cautious in suggesting that S4 plays a direct role. Even with this caveat, it is clear that the role of the S4 helix in inactivation gating is different than the role it plays as the principal voltage sensor for activation gating in Kv11.1 (Subbiah et al., 2004; Zhang et al., 2004; Piper et al., 2005) and other Kv channels (Swartz, 2008).

Figure 7.

Only combinations of S4 mutants alter the voltage sensitivity of Kv11.1 channel inactivation. (A and B) Dot plots showing the linear slope values calculated from the derived unidirectional rate constants (shown as black lines in Fig. 1 D) for the onset of (k_inact; A) and recovery from (k_rec; B) inactivation for groups of mutants (to Ala, Ser, and Trp) at each residue in the S4 domain, as well as the double and triple mutants. Slope values indicate the voltage dependence of the forward (inactivation; A) and reverse (recovery from inactivation; B) gating transitions. The mean of all mutations at each individual residue falls within ±2 standard deviations (gray box) of the mean calculated from all single S4 mutants.

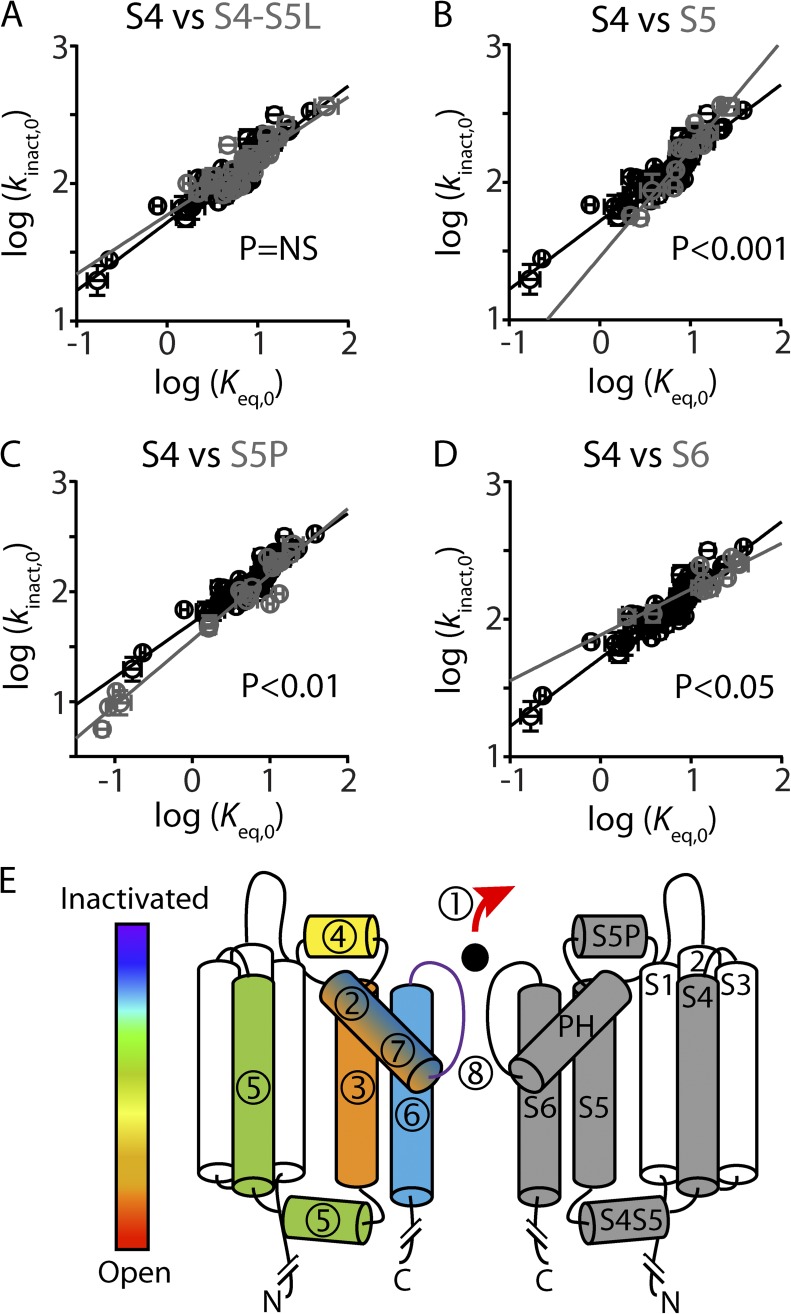
REFER analysis demonstrates that hydrophobic residues within the S4 helix are important determinants for inactivation gating in Kv11.1 channels. The relative timing of the change in environment experienced by the S4 hydrophobic residues during the inactivation gating transition can be determined by comparing the overall Φ-value of ∼0.5 for the S4 helix with Φ-values derived from other domains within the channel protein (Wang et al., 2011), as shown in Fig. 8. The S4 Φ-value was not significantly different from that derived from the internal S4–S5 linker (Φ = 0.43 ± 0.04; P > 0.05; ANCOVA), suggesting that these two domains are coupled during inactivation gating. However, the change in environment experienced by the S4 hydrophobic residues occurs just after a conformational change in the S5 helix (Φ = 0.78 ± 0.07; P < 0.05) and S5P linker (Φ = 0.60 ± 0.03; P < 0.05) but before a conformational change in the S6 helix (Φ = 0.33 ± 0.05; P < 0.05) (Fig. 8).

Figure 8.

Multi-domain model of inactivation gating in Kv11.1 channels. (A–D) REFER plots to compare S4 residue mutations (shown in black) against S4S5 linker (A), S5 (B), S5P linker (C), and S6 (D) residue mutations (shown in gray). ANCOVA shows that the linear regression slope, which represents the Φ-value, was significantly different for the S4 helix compared with the S5, S5P, and S6 helices (P < 0.05), but not the S4–S5 linker. (E) Cartoon showing two opposing subunits of Kv11.1. Segments in the right-hand subunit are labeled S1–S6 and pore helix (PH). Segments in the left-hand subunit are color and number coded, according to derived Φ-values (present study and Wang et al., 2011; Perry et al., 2013), to show the relative sequence of events that occur during the open-to-inactivated gating transition, where red (1) indicates the first step and purple (8) indicates the putative final step. The S4 helix (green, 5), as well as the S4–S5 linker, experience a change in environment shortly after the S5 helix and S5P linker but before the S6 helix. We propose that hydrophobic interactions between the S4 helix and the S5 helix help couple the voltage-sensor domain to the pore domain during the open-to-inactivated gating transition of Kv11.1 channels.

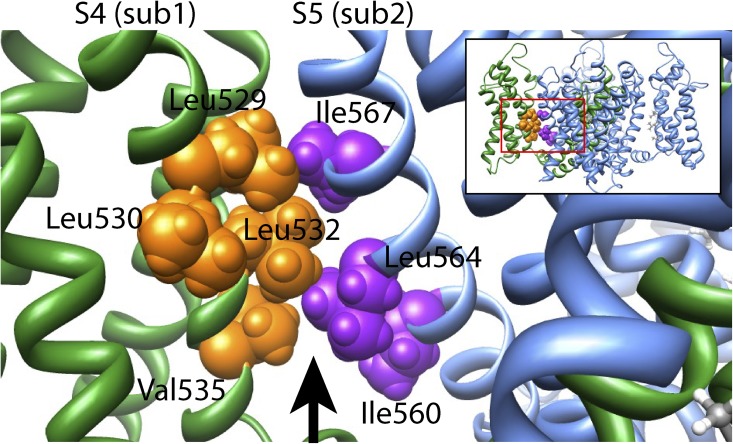
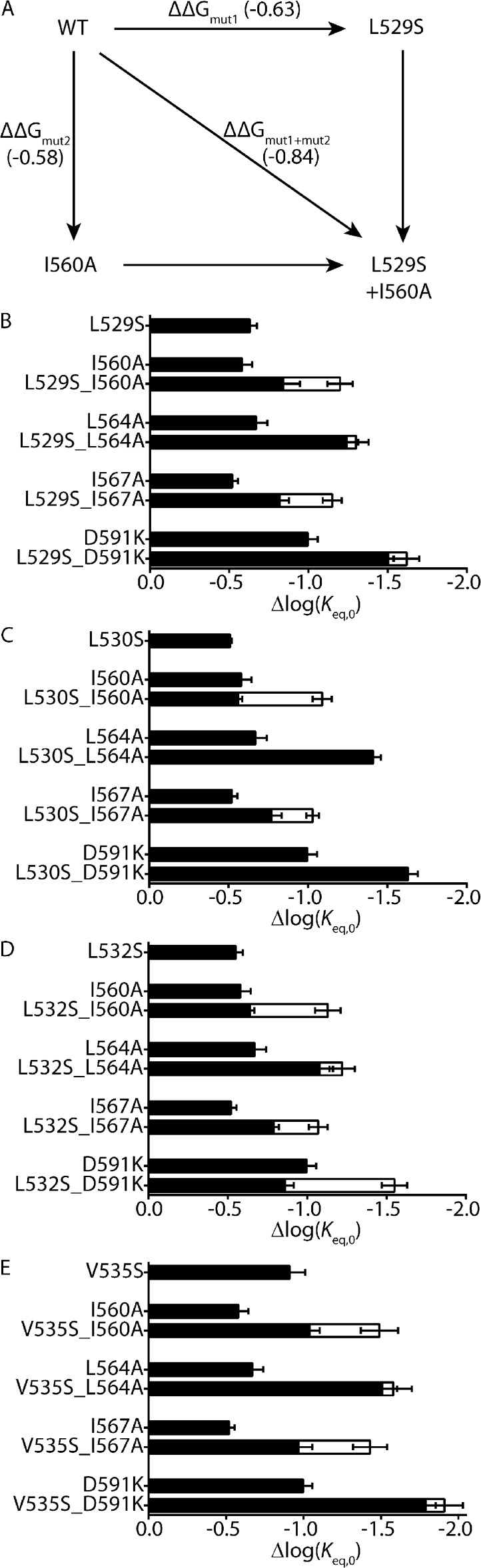
When viewed on a Kv11.1 channel homology model, based on the crystal structure of a Kv1.2/2.1 channel chimera (Long et al., 2007), the side chains of the hydrophobic residues Leu529, Leu532, and Val535 face toward hydrophobic residues on the S5 helix of the neighboring subunit (Fig. 9). This raises the question of whether the S4 helix and S5 helix are energetically coupled via an intersubunit hydrophobic interaction. To experimentally test for an energetic coupling between hydrophobic residues on the S4 helix (Leu529, Leu530, Leu532, or Val535) and hydrophobic residues on the S5 helix (Ile560, Leu564, or Ile567), or a nonhydrophobic residue on the S5P linker (Asp591), we combined perturbing mutations of residues within each helix (Fig. 10). If an energetic coupling exists between two residues, we would predict that the perturbations caused by the individual mutations, measured as Δlog(K_eq,0) relative to WT, would not be additive when combined in the double mutant (i.e., ΔΔG_mut1+mut2 < ΔΔG_mut1 + ΔΔG_mut2; see Materials and methods). Conversely, if the perturbations caused by the two single mutants were additive when combined in the double mutant, the two residues are not energetically coupled (i.e., ΔΔG_mut1+mut2 = ΔΔG_mut1 + ΔΔG_mut2). For example, the schematic in Fig. 10 A represents double mutant cycle analysis between two residues: Leu529 on the S4 helix and Ile560 on the S5 helix. It is clear that the perturbations caused by the two mutations, L529S (ΔΔG_mut1) and I560A (ΔΔG_mut2), are not additive when combined in the double mutant, L529S + I560A (ΔΔG_mut1+mut2). In fact, the ΔΔG_mut1+mut2 of the double mutant is significantly less than the theoretical additive value (ΔΔG_mut1 + ΔΔG_mut2) (Fig. 10 B; P < 0.05; two-tailed Welch’s t test), indicating that Leu529 on the S4 helix and Ile560 on the S5 helix are, at least in part, energetically coupled. Similarly, combining the same S4 helix mutation, L529S, with a different S5 helix mutation, I567A, resulted in a ΔΔG_mut1+mut2, which was significantly less than ΔΔG_mut1 + ΔΔG_mut2 (Fig. 10 B; P < 0.05; two-tailed Welch’s t test), suggesting that these two residues are also energetically coupled. In contrast, combining L529S with either L564A (S5 helix) or D591K (S5P linker) resulted in a ΔΔG_mut1+mut2 ≈ ΔΔG_mut1 + ΔΔG_mut2 (Fig. 10 B; P = NS; two-tailed Welch’s t test), suggesting that Leu529 is not energetically coupled with either Leu564 (S5) or Asp591 (S5P).

Figure 9.

Homology model of the Kv11.1 channel. View parallel to the membrane of an amplified region of a Kv11.1 channel homology model created using the Kv1.2/2.1 chimera crystal structure (Long et al., 2007) as a template, according to the alignment shown in Fig. S3. The amplified region is indicated by the boxed region of the entire four-subunit homology model shown in the inset. Hydrophobic residues on the S4 helix (Leu529, Leu532, and Val535) of one subunit (sub1; shown in green, with residues colored orange) face toward hydrophobic residues on the S5 helix (Ile560, Leu564, and Ile567) of the neighboring subunit (sub2; shown in blue, with residues colored purple). The arrow represents a cavity filled by lipid in the Kv1.2/2.1 crystal structure.

Figure 10.

Double mutant cycle analysis of S4 and S5 helix residues. (A) Schematic showing the principle of double mutant cycle analysis to test for an energetic coupling between Leu529 on the S4 helix and Ile560 on the S5 helix. Perturbations to inactivation, measured by changes in log(K_eq,0) relative to WT, caused by individual mutations, L529S (ΔΔG_mut1) and I560A (ΔΔG_mut2), are compared with the perturbation caused by the double mutant L529S + I560A (ΔΔG_mut1+mut2). Measured Δlog(K_eq,0) values representing ΔΔG_mut1, ΔΔG_mut2, and ΔΔG_mut1+mut2 are shown in parentheses. An energetic coupling between Leu529 (S4) and Ile560 (S5) residues is indicated by ΔΔG_mut1+mut2 being significantly different from ΔΔG_mut1 + ΔΔG_mut2 (P < 0.05; see Materials and methods). (B–E) Double mutant cycle analysis for S4 helix mutations L529S (B), L530S (C), L532S (D), and V535S (E), paired with mutations on the S5 helix (I560A, L564A, or I567A) or S5P linker (D591K). Measured values of Δlog(K_eq,0) for individual or double mutants are shown as closed bars, whereas the theoretical additive values, ΔΔG_mut1 + ΔΔG_mut2, are shown by open bars. Data presented as means ± SEM for 6–14 cells (see Table S1).

In addition to L529S, we also tested three other S4 helix hydrophobic residue mutations: L530S (Fig. 10 C), L532S (Fig. 10 D), and V535S (Fig. 10 E). All show a similar pattern, in that the combinations with the S5 residue mutations I560A or I567A are nonadditive (P < 0.05; two-tailed Welch’s t test), whereas the combinations with the S5 residue mutation L564A, or S5P linker residue mutation D591K, are additive. One exception to this is the combination of L532S (S4) with D591K (S5P linker), which resulted in a nonadditive effect. Although we cannot rule out the possibility that these two residues are energetically coupled, it seems unlikely given their distant spatial proximity in models of the Kv11.1 channel (Tseng et al., 2007; Durdagi et al., 2012). An alternative explanation is that the combination of mutations, L532S + D591K, introduces a non-native interaction or alters the structure of either or both of the two stable end states. Although this is not indicated by an abnormal Φ-value (Φ = 0.75 ± 0.01; n = 10; see Table S1), that is to say outside of the range 0 and 1, it remains possible that the double mutant (L532S + D591K) affects two or more processes that coincidentally cancel each other out to give a Φ-value between 0 and 1.

In general, however, the nonadditive effects of combining S4 helix mutations (L529S, L530S, L532S, or V535S) with S5 helix mutations (I560A or I567A) provide strong evidence for the notion of hydrophobic coupling between the S4 helix and the S5 helix during inactivation gating in Kv11.1 channels. Based on the Kv11.1 channel homology model, we suggest that this energetic coupling is likely to be caused by an intersubunit interaction, which is critical for inactivation gating in Kv11.1 channels.

DISCUSSION

C-type inactivation gating in potassium channels is thought to culminate in a conformational rearrangement of the selectivity filter, which results in the loss of one or more K⁺ coordination sites (Cuello et al., 2010). Recently, we used REFER analysis to show that inactivation of Kv11.1 channels is a complex phenomenon in which a precisely timed sequence of conformational changes in multiple interconnected domains of the channel must occur before reaching the nonconducting stable end state, a process analogous to the opening of a Japanese puzzle box (Fig. 8) (Wang et al., 2011). In the present study, we used REFER analysis to examine the role of the S4 “voltage-sensor” helix during inactivation gating. Our results indicate that in contrast to channel opening, where the positively charged residues within the S4 helix are crucial for “sensing” changes in membrane potential to trigger opening of the S6 activation gate (Subbiah et al., 2004; Zhang et al., 2004; Piper et al., 2005), it is predominantly the hydrophobic residues within the S4 helix that are the crucial molecular determinants for inactivation gating. An overall Φ-value of ∼0.5 indicates that the S4 helix, together with the internal S4–S5 linker, experiences a change in environment after conformational changes in the S5 helix (Φ = 0.78) and S5P linker (Φ = 0.60) but before a conformational change in the S6 helix (Φ = 0.3) (Fig. 8). Based on our Kv11.1 homology model and double mutant cycle analysis data, we propose that intersubunit interactions between hydrophobic residues within the S4 and S5 helices are important determinants of inactivation gating in Kv11.1 channels.

Although we observed perturbations to the energetics of inactivation gating upon mutation of both charged and hydrophobic residues within the S4 helix (Fig. 2), it is clear that the charged residues exhibit greater tolerance to nonconserved side chain replacements than do the hydrophobic residues, at least at positions 530 and 535 (Fig. 3). This finding is initially surprising given the crucial role of the charged residues in mediating the voltage dependence of Kv11.1 channel opening (Subbiah et al., 2004; Zhang et al., 2004; Piper et al., 2005). The voltage-sensor domain, however, is likely to adopt at least three stable conformations: resting, active, and relaxed (Villalba-Galea et al., 2008). The transition from the resting to active conformations is linked to opening of the intracellular channel gate (Swartz, 2008). Our voltage protocols were designed to ensure that the S4 was predominantly in the “active” position before measuring the onset and recovery from inactivation. In this context, it is possible that the hydrophobic S4 residues may contribute to so-called voltage-sensor relaxation. Whether this in turn is coupled to inactivation we cannot determine from our studies and is a source of controversy (Villalba-Galea et al., 2008; Lacroix et al., 2011; Shirokov, 2011). Regardless of whether voltage-sensor relaxation is involved or not, what is clear from our experiments is that the hydrophobic S4 residues are key determinants of the open-to-inactivated transition in Kv11.1 channels.

The voltage dependence of activation and inactivation gating in Kv11.1 channels are clearly separable (Wang et al., 1997; Zou et al., 1998; Johnson et al., 1999; Sanguinetti and Xu, 1999; Piper et al., 2005; Clarke et al., 2006; Vandenberg et al., 2006). Our data indicate a poor correlation between the mutation-induced changes in the equilibrium of inactivation gating compared with that of activation gating (Fig. 6), supporting the notion that the S4 involvement during these two gating transitions involves a quite distinct molecular mechanism. Furthermore, none of the individual S4 residues we mutated directly perturbed the voltage dependence of either the forward or the reverse inactivation gating transitions (Fig. 7), suggesting that the origin of the voltage dependence of inactivation may lie beyond the region of the S4 helix.

REFER analysis provides information regarding the relative time point at which a perturbation affects the native transition pathway of a reaction (Auerbach, 2007) and can be used to infer when the mutated residue or region of the protein was involved in that transition pathway. Previously (Wang et al., 2011), we observed that altering the external concentration of potassium ions gave a Φ-value of ∼1, suggesting that a loss of potassium ions from the selectivity filter is the first step during the inactivation gating transition. Diminishing Φ-values were then observed for families of mutations in the S5 helix (Φ = 0.75), S5P linker (Φ = 0.6), S4–S5 linker (Φ = 0.45), S6 helix (Φ = 0.3), and pore helix (Φ = 0.25). In this context, we can confirm that the S4 helix (Φ = 0.50) experiences a change in environment after the S5 helix and S5P linker but before the S6 helix (Fig. 8). An overall Φ-value of ∼0.5 for the S4 helix was similar to that derived from the internal S4–S5 linker, suggesting that these two domains are coupled during inactivation gating.

Combining three of the S4 hydrophobic residue mutations (Leu529, Leu532, and Val535) produced shifts in log(K_eq,0) that were clearly not additive, suggesting that these residues experience a change in environment at a similar time point. Families of mutations at Leu529, Leu532, or Val535 gave Φ-values that were not significantly different from that derived from the remainder of the S4 domain, whereas the Φ-value derived from Leu530 mutations was significantly smaller (Φ = ∼0.3). This suggests that Leu530 may undergo a change in energetics at a time point closer to that of the S6 domain (Φ = 0.3) than the other S4 residues. According to our homology model (Fig. 9), Leu530 is not in direct contact with the S6 helix but instead faces the S3 helix and/or the lipid membrane. It appears unlikely, therefore, that Leu530 directly interacts with S6 helix residues, but it is entirely possible that the two regions of the channel undergo independent conformational changes at approximately the same time point during the transition pathway. Nevertheless, we suggest that the relatively consistent nature of the Φ-values that we derived from mutations of residues throughout the S4 helix indicates that the majority of the S4 domain, along with the internal S4–S5 helix, experiences a change in environment at the same relative time point during the open-to-inactivated gating transition.

Although REFER analysis provides temporal information about the role of the S4 helix during inactivation gating, it cannot provide a direct indication of the nature of the change in environment experienced by the S4 helix. We therefore used a combination of homology modeling and double mutant cycle analysis to probe the nature of this structural change. Based on our Kv11.1 channel homology model (Fig. 9), we hypothesized that the important hydrophobic residues in the S4 helix face directly toward the S5 helix of the neighboring subunit. Previously, several different types of interactions between the voltage-sensor domain and the pore domain have been suggested in various subtypes of potassium channel. In Kv channels, including Kv11.1, residues at the intracellular end of the S4 helix, together with the S4–S5 linker, interact with residues at the intracellular end of the S6 helices that form the activation gate (Lu et al., 2002; Tristani-Firouzi et al., 2002; Long et al., 2005; Ferrer et al., 2006). This type of interaction is important in coupling the transition of the voltage sensor into the active conformation upon membrane depolarization to the opening of the internal S6 activation gate (Long et al., 2005). A second set of interactions has been proposed between residues at the extracellular ends of the S1 (Long et al., 2005, 2007; Lee et al., 2009; Bocksteins et al., 2011) or S4 helices (Elinder et al., 2001; Neale et al., 2003; Bocksteins et al., 2011) with residues at the extracellular end of the S5 helix of the neighboring subunit. It has been suggested that these interactions could help constrain the voltage sensor to the pore during channel opening (Lee et al., 2009). Lastly, in hyperpolarization-activated KAT1 channels, there is evidence for interactions between two noncharged S4 residues and two residues in the middle of the S5 helix (Lai et al., 2005).

Our double mutant cycle analysis data support the notion of an energetic coupling between hydrophobic residues on the S4 helix (Leu529, Leu530, Leu532, and Val535) and hydrophobic residues on the S5 helix (Ile560 and Ile567) of the neighboring subunit during inactivation gating. However, the number of different side chain mutations tolerated at some of these positions, namely 529 and 532, suggests that these two regions are not tightly packed. Leu529 through Val535 lie within the intracellular half of the S4 helix and, as such, are below the region proposed for the extracellular voltage sensor–pore domain interaction. They are also clearly distinct to the residues at the intracellular end of S4 that have been suggested to form interactions with the intracellular end of S6, i.e., Asp540 with Leu666 (Ferrer et al., 2006). They could, however, be consistent with the midlevel interaction observed in KAT1 channels (Lai et al., 2005). Based on our homology model, it is possible that some of the hydrophobic residues are close enough for a direct hydrophobic interaction, such as Leu529 (S4) with Ile567 (S5), but in other instances, the distance between residues does not support such a notion. In the Kv1.2/2.1 chimera x-ray structure, there is a gap between this region of the S4 helix and the S5 helix of the neighboring subunit that is occupied by lipid (Long et al., 2007). It is conceivable that the replacement of bulky hydrophobic residues with serine affects the interactions between the hydrophobic residues in S4 and S5 with the hydrophobic lipid. The S4 and S5 domains may then be energetically coupled through a shared lipid interaction. It has been shown that gating of Kv channels is influenced by the lipid composition of membranes (Schmidt et al., 2006, 2009). In the case of KvAP channels, Schmidt et al. (2009) showed that the lipid composition influenced multiple gating transitions, with the most dramatic effect observed for rates of recovery from inactivation. Investigation of this hypothesis in Kv11.1 channels will, however, be difficult, as it would require expression of sufficiently large amounts of recombinant protein to allow reconstitution into different lipid bilayers.

Most voltage-gated channels contain several pairs of hydrophobic residues, interspersed between positively charged residues, along the length of the S4 segment (Anselmi et al., 2007; Long et al., 2007; Pless et al., 2011). The highly conserved nature of the S4 hydrophobic residues across all Kv channels (Anselmi et al., 2007; Long et al., 2007; Pless et al., 2011) suggests that the S4 and S5 hydrophobic interaction we propose could be common to all members of the family, rather than being unique to Kv11.1 channels. In fact, it has been suggested that small changes to the degree of hydrophobicity within the S4 helix could alter the extent of packing against the S5 helix, and that this could reflect differences in the kinetics of voltage-sensor motion during channel opening (Anselmi et al., 2007). However, it should be noted that the sequence homology and hydrophobicity of the S5 helix is much less conserved across the Kv family (Shealy et al., 2003; Ju et al., 2009), and that C-type inactivation gating in other Kv channels is not intrinsically voltage dependent (Hoshi and Armstrong, 2013). Because inactivation gating has much slower kinetics than those of channel opening in other Kv channels, it may be difficult to separate these two gating processes sufficiently to test whether hydrophobic residues within the S4 domain play a similar role in mediating selectivity filter gating in other Kv channels. Nevertheless, it is clear that S4 hydrophobic residues are critical mediators of inactivation gating in Kv11.1 channels.