Abstract
A recently developed class of models incorporating the cyton model of population generation structure into a conservation-based model of intracellular label dynamics is reviewed. Statistical aspects of the data collection process are quantified and incorporated into a parameter estimation scheme. This scheme is then applied to experimental data for PHA-stimulated CD4+ T and CD8+ T cells collected from two healthy donors. This novel mathematical and statistical framework is shown to form the basis for accurate, meaningful analysis of cellular behaviour for a population of cells labelled with the dye carboxyfluorescein succinimidyl ester and stimulated to divide.
Keywords: immunology, flow cytometry, cyton models, mathematical and statistical models, label dynamics, parameter estimation, cellular models
1. Introduction
Dating at least as far back as the work of Bell and Anderson [14] in 1967, mathematical models have been proposed which attempt to describe the biophysical processes involved in cell division. These models range in scope and scale from phenomenological descriptions of population growth to mechanistic models of subcellular mechanics. One particularly important class of mathematical models is that in which the behaviours of individual cells are linked in a meaningful way to population-level characteristics. This class of models has applications in quantitative descriptions of the immune system, where the behaviour of individual cells can vary widely across the population but in which the immune response (understood to be the net result of actions of all relevant cells in the system) is much more predictable [45]. In fact, a quantitative description of the ‘cellular calculus’ [25] by which cells send, receive, and respond to intra- and extracellular stimuli is in many respects an open problem in immunology.
In the past, the major limitation of mathematical models linking cellular and population-level behaviour has been the difficulty in obtaining data with which to validate the models. Generally, it is possible to observe the behaviour of a small number of single cells quite carefully in isolation, or to observe a large number of cells in aggregate. More recently, the intracellular dye carboxyfluorescein succinimidyl ester (CFSE) [36] for use in flow-cytometric proliferation assays in vitro has emerged as a powerful experimental technique for the study of dividing cells. Because the dye emits bright, approximately uniform, and long-lasting fluorescent labelling of a population of cells and is approximately evenly partitioned during cell division, the dye provides a useful surrogate for the number of divisions a cell has undergone. Individual cells can be assessed by a flow cytometer, which can simultaneously measure additional properties of cells such as size, internal complexity, cell surface marker expression, levels of cytokine secretion, etc.
When a population of cells is measured, the individual CFSE fluorescence intensity measurements can be placed into a histogram as in Figures 1 and 2. Each ‘peak’ in the histogram represents a cohort of cells having completed the same number of divisions. When such measurements are made sequentially in time, one obtains information on the dynamic response of the population of cells to a stimulus. As such, CFSE-based flow cytometric analysis is a promising tool for the study of cell division and division-linked changes. The ultimate goal for the quantitative analysis of CFSE data (in particular, as it relates to studies of the immune system) is to incorporate fundamental mechanistic modelling of the cellular calculus into a description of population-level behaviour, and thus to obtain a more comprehensive understanding of the immune system, with obvious implications for the study of disease detection, progression, treatment/control, etc. To that end, mathematical modelling provides a quantitative framework with which to analyse and interpret such data.
Figure 1.

Histogram data for CD4T cells from Donor 1 (left) and Donor 2 (right). An initially unimodal distribution of fluorescence intensity becomes multimodal as cells divide asynchronously. By day 5, subsequent generations of cells are no longer detectable as fluorescence resulting from CFSE has been diluted to the level of background autofluorescence.
Figure 2.
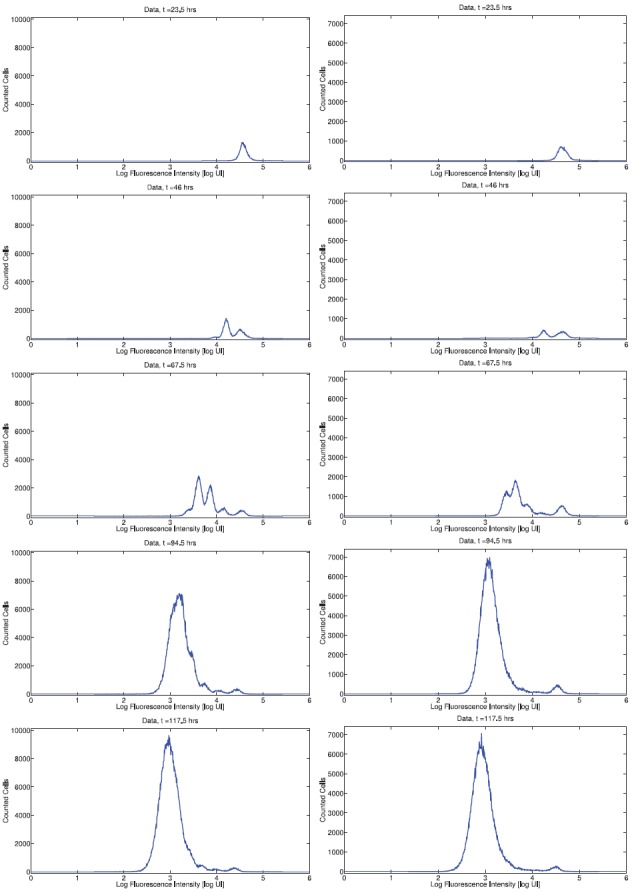
Histogram data for CD8T cells from Donor 1 (left) and Donor 2 (right). An initially unimodal distribution of fluorescence intensity becomes multimodal as cells divide asynchronously. By day 4, subsequent generations of cells are no longer detectable as fluorescence resulting from CFSE has been diluted to the level of background autofluorescence.
A large number of mathematical models (see, e.g. the recent reviews [4,38]) have been proposed with the aim of linking the generation structure (cells per number of divisions undergone) to quantitative descriptions of cellular behaviour (e.g. times to division and death). Most recently [3], a class of mathematical models has been proposed which incorporates the ‘cyton’ model [28,29] of cell division dynamics into a mathematical description of flow cytometry histogram data based upon conservation principles. Here, we revisit this new class of models and provide a more complete discussion of some mathematical properties of the solutions which make them amenable to the fast computational approaches as described in [27]. It is also shown how the new model can be compared with older label-structured models such as those proposed in [13,27,42,47]. Next the data collection process is considered in more detail and a theoretical statistical model is derived. The mathematical and statistical models are then incorporated into a rigorous parameter estimation scheme based upon a weighted least-squares framework and members of the proposed class of mathematical models are compared in terms of their ability to fit the available data.
2. CFSE data
CFSE-based flow cytometry experiments are performed by stimulating CFSE-labelled cells to divide by exposure to either a mitogenic compound or a specific antigen. Cells are then placed into separate wells, one for each measurement to be made. Several protocols exist and can be tailored to the needs of a particular experiment; see, e.g. [36,37,41,49,51]. For the experiment described here, peripheral blood mononuclear cells (PBMCs) from two healthy donors were stained with CFSE and stimulated with the mitogen phytohaemagglutinin (PHA). Measurements were carried out approximately every 24 h for 5 days, beginning 1 day after stimulation.
When a well is selected for measurement, cells are additionally labelled for phenotypic identification by antibodies (anti-CD3T, anti-CD4T, and anti-CD8T cells) tagged with fluorescent markers. These cells are then analysed by flow cytometry, which records the relative brightness of cells in various colours (corresponding to distinct fluorescent markers). Cells of interest can then be identified in the flow cytometry output. For this experiment, we consider CD4 T cells (CD3+, CD4+, and CD8−) and CD8 T cells (CD3+, CD4−, and CD8+). Once these cells are identified, the fluorescence intensity (in the colour channel consistent with CFSE) is analysed for each cell. Because dead cells will disintegrate shortly after death and can be excluded by gating, mainly viable cells are measured by the flow cytometer (the fraction of cells which are dead but not yet disintegrated is assumed to be small).
The population generation structure of the cells at a given measurement time can be visualized by organizing the fluorescence intensity measurements of individual cells into a histogram, as shown in Figures 1 and 2. Because of physical limitations, only a fraction of the cells contained in a selected well are actually analysed by flow cytometry. In order to estimate the total number of cells in the measurement sample, a known number of fluorescent beads are placed in each sample; these beads can be identified and counted in the flow cytometry output and the ratio of beads counted to total beads introduced provides an estimate of the fraction of the sample acquired by the flow cytometer. The histogram profiles obtained from the measured cells can then be normalized by the reciprocal of this quantity.
It is assumed that each well contains an identical population of cells at all times, that the fraction of measured cells is representative of the population of cells in that well, and that the fraction of the total well actually measured is accurately estimated by bead counting (though it is possible to consider errors in bead counts; see Section 4). Under these assumptions, the total mass of CFSE should be conserved in the histogram data. For this reason, the mathematical models proposed to describe CFSE-based flow cytometry data (Section 3) are derived from standard conservation principles (see, e.g. [6]).
A complete discussion of the mathematically relevant aspects of the data collection procedure can be found in [4]. The goal of the mathematical modelling process is to link a mathematical description of cellular division and death processes at the population level to the observed fluorescence intensity profiles as measured by a flow cytometer (Figures 1 and 2). Because each peak in the flow cytometry data represents a cohort of cells having completed the same number of divisions, it is hypothesized that flow cytometry data collected sequentially in time for cells from a single donor will contain sufficient information to analyse the dynamic response of those cells to stimulus. This dynamic response can only be accurately understood in the context of a mathematical model of the biological system, as well as a statistical model linking the mathematical model to the data. Such a model must be able to account for the slow natural loss of CFSE fluorescence intensity over time, the dilution of fluorescence intensity by division, and the asynchronous nature of cellular division and death processes.
3. Mathematical modelling of CFSE data
We begin by summarizing a partial differential equation model structured by (continuous) fluorescence intensity and (discrete) division number which has been proposed to describe histogram data from CFSE-based proliferation assays [13,27,42,47]. We then summarize a new class of models incorporating cyton dynamics into a label-structured framework and consider several different versions of the cyton model at greater length. Finally, the role of cellular autofluorescence is briefly considered.
3.1. Previous label-structured model
Let ni(t, x) be the structured density (cells per unit of fluorescence intensity) of a cohort of cells having completed i ≥ 0 divisions at time t and with x units of fluorescence intensity resulting from induced CFSE (that is, ignoring the contributions of cellular autofluorescence). It is assumed that this fluorescence is directly proportional to the mass of CFSE within a cell, and thus can be treated as a mass-like quantity. These cells are assumed to divide with time-dependent exponential rate αi(t) and die with time-dependent exponential rate βi(t). Then the entire population of cells can be described by the system of partial differential equations
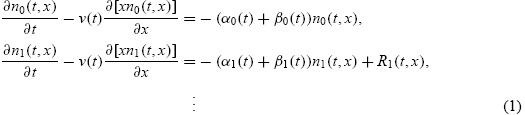 |
The recruitment terms describe the symmetric division of CFSE upon mitosis and are given by Ri(t, x) = 4αi − 1(t)ni − 1 (t, 2x) for i ≥ 1; the form of these recruitment terms arises naturally from the derivation of the above system of equations from conservation principles [47]. The advection term describes the rate of loss of fluorescence intensity (resulting from the turnover of CFSE), which is assumed to depend linearly on the fluorescence intensity x with time-dependent rate function v(t). This follows the convention of [27], and includes exponential loss (v(t) = c) and Gompertz decay (v(t) = ce−kt) as special cases. The loss of CFSE has been observed to be very rapid during the first 24 h after initial labelling and much slower thereafter [13,47]). Thus, when data are collected in the first 24 h, it is more accurate [11] to describe the rate of loss of fluorescence intensity with a time-varying rate (e.g. Gompertz decay). Such rates are consistent with the sequence of chemical reactions known to occur during the labelling process [18]. If data are not collected in the first day after labelling with CFSE (as in the data collected for this report) then, as we shall see below, exponential decay is sufficient. For the remainder of this report, we assume v(t) = c.
The initial conditions for the model (1) are
for x ≥ 0. Note that a no-flux condition at x = 0 is naturally satisfied by the form of the advection term provided ni(t, 0) is finite (so that the flux term is well defined) for all i and for all t ≥ 0. The solution of Equation (1) can be computed by the method of characteristics [47]. Alternatively, the following characterization of the solution is given in [42].
Proposition 3.1
The solution to Equation (1) can be factored as
The functions Ni(t) indicate the number of cells having completed i divisions at time t and satisfy the weakly coupled system of ordinary differential equations
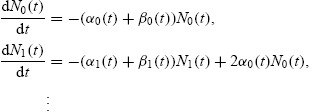 |
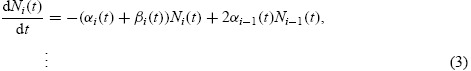 |
with initial conditions N0(t0) = N0, Ni(t0) = 0 for all i ≥ 1. The functions ni(t, x), describe the distribution of CFSE within a generation of cells. Each satisfies the equation
for x ≥ 0 with initial condition
Again, the no flux condition at x = 0 is trivially satisfied by the form of the advection term. Note that, by definition,
We remark that the form of the equations presented above is slightly different from that considered in [13] as here we initially neglect considerations of autofluorescence. The formulation above follows the work of Hasenauer et al. [27] and allows for a more intuitive formulation of the model, as well as the fast numerical techniques discussed below and in the appendix. The system above is derived in terms of the fluorescence intensity resulting only from induced CFSE; the experimentally measured fluorescence intensity is the sum of this quantity and the cellular autofluorescence which results from the light absorption and emission properties of intracellular molecules. Let ñi(t, 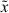 ) be a structured density for cells having completed i divisions at time t with measured fluorescence intensity
) be a structured density for cells having completed i divisions at time t with measured fluorescence intensity 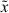 . While the measured fluorescence intensity
. While the measured fluorescence intensity 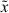 is given by the sum of the induced fluorescence x and the cellular autofluorescence, this latter quantity may vary from cell to cell in the population. As such, given the solutions ni(t, x) for i ≥ 0 to Equation (1), one computes the densities ñi(t,
is given by the sum of the induced fluorescence x and the cellular autofluorescence, this latter quantity may vary from cell to cell in the population. As such, given the solutions ni(t, x) for i ≥ 0 to Equation (1), one computes the densities ñi(t, 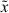 ) using the convolution integral [27,42]
) using the convolution integral [27,42]
where p(t, ζ) is (for fixed time t) a probability density function describing the distribution of autofluorescence in the population (see [13,40,47] and Section 3.4). Fast approximation techniques for the convolution (5) have been demonstrated in [27] and the references therein. These techniques are summarized in the appendix.
3.2. New class of label-structured models
While the model (1) for computing population label structure has been shown to accurately fit experimental data [13], it lacks a certain intuitive appeal in that the ‘time-dependent exponential rates’ of division and death, αi(t) and βi(t), are not explained in biologically relevant terms (e.g. times to division and death). An alternative to the mathematical model (3) is the cyton model for division dynamics [28,29] which relates the number of cells in a population directly to probability distributions describing times at which cells divide or die. The cyton model is motivated by the assumption of independent regulation by the cellular machinery of times to division and death. Using the definition of Ni(t) above, the cyton model is described by the set of equations
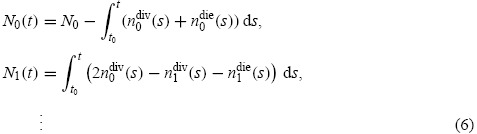 |
where nidiv(t) and nidie(t) indicate the rates (cells per hour) at which cells (having already undergone i divisions) divide and die, respectively, at time t. For undivided cells, let φ0(t) and ψ0(t) be probability density functions describing the distribution from which the times to division and death, respectively, are drawn. Let F0, called the initial progressor fraction, be the fraction of undivided cells which would hypothetically divide in the absence of any cell death. (It is assumed that in each generation, non-progressing cells may die according to the probability density function ψi(t), but may not divide.) Then, under the assumptions of the cyton model, it follows that
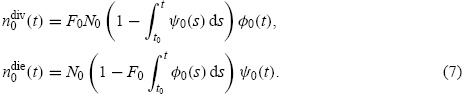 |
Similarly, one can define probability density functions φi(t) and ψi(t) for times to division and death (measured in hours since completion of the (i − 1)th division), respectively, for cells having undergone i divisions, as well as the progressor fractions Fi of cells which would complete the ith division in the absence of cell death. Then the cell division and death rates are computed as
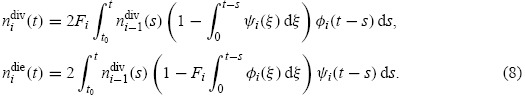 |
Given the success of the cyton model in describing cell dynamics, as well as the experimental evidence supporting it [4,28,29], the cyton model has been incorporated into a label-structured framework [3] similar to Equation (1). The mathematical ideas rely heavily upon the separability of the model solution (Proposition 3.1) originally demonstrated by Hasenauer and co-workers [27,42]. Let ni(t, x) be a structured density as before. Consider the system of partial differential equations
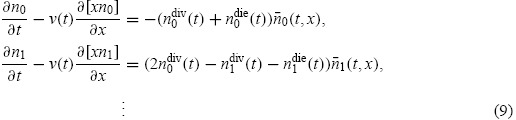 |
with initial conditions specified as for Equation (1). The terms ni(t, x) are described as in Equation (4). This system of equations incorporates the cyton model (6)–(8) for cell population dynamics into a label-structured framework for use with histogram data. We remark that Equation (9) corrects a typographical error in [3], where the factors ni(t, x) were missing from the right side of the equations.
Proposition 3.2
The solution of Equation (9) is
where the quantities Ni(t) satisfy Equation (6) and ni(t, x) satisfy Equation (4).
Proof
The proof follows immediately by the direct substitution of the stated solution into Equation (9). Working with the left side of Equation (9) for the ith equation,
which is exactly the right side of Equation (9). For the purposes of this proof, it is assumed that n−1div = 0 so that the equations for n0(t, x) are well defined. It is easy to check that the initial and boundary conditions for Equation (9) are satisfied by the above solution.
Given the densities ni(t, x) computed according to Equation (9), one can compute the densities ni(t, 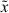 ) via the convolution (5) as before. Much like the original model (1), the new model (9) can be fit directly to histogram data from CFSE-based experiments and is highly accurate [3]. Significantly, the new model describes the dynamics of a dividing population of cells in intuitive terms (i.e. probability distributions of times to divide and die). This is the primary advantage of the new class of models over the previous modelling framework. Similarly, while the cyton model has been widely used to analyse cell count data obtained from CFSE data (e.g. through a deconvolution process; see [4]), the new class of models can be fit directly to CFSE histogram data. As a result, the class of models is less dependent upon peak separation or a high frequency of cells which respond to stimulus. Moreover, the fit of the model to data can be assessed in a statistically rigorous manner (see Section 4).
) via the convolution (5) as before. Much like the original model (1), the new model (9) can be fit directly to histogram data from CFSE-based experiments and is highly accurate [3]. Significantly, the new model describes the dynamics of a dividing population of cells in intuitive terms (i.e. probability distributions of times to divide and die). This is the primary advantage of the new class of models over the previous modelling framework. Similarly, while the cyton model has been widely used to analyse cell count data obtained from CFSE data (e.g. through a deconvolution process; see [4]), the new class of models can be fit directly to CFSE histogram data. As a result, the class of models is less dependent upon peak separation or a high frequency of cells which respond to stimulus. Moreover, the fit of the model to data can be assessed in a statistically rigorous manner (see Section 4).
Although the motivation for this model formulation is clear (combining cyton and label dynamics in a division-dependent compartmental model) the form of the new model is complex, describing the population densities ni(t, x) in terms of yet another set of density functions, n i(t, x). A simple reformulation shows that the new class of models is consistent with the mass-conservation principles of the old label-structured model. Moreover, this reformulation shows how the two model forms can be related and directly compared.
Recall the definitions of ni(t, x), Ni(t), and ni(t, x) given in Proposition 3.2. Note that
and
Thus the quantities ni(t, x) can be considered as probability density functions for the distribution of CFSE in cells having divided i times at time t. When considering cell death, the mathematical terms nidie(t)ni(t, x) in Equation (9) reflect the tacit assumption that the rate at which cells die (ndie(t)) is independent of the label distribution ni(t, x) of those cells. Moreover,
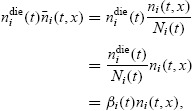 |
with
which is exactly the same form as Equation (1). Similar statements hold true for the rates of dividing cells and the terms αi(t) in Equation (1) if Fi of Equations (7) and (8) equal 1 for all i. For 0 < Fi < 1, then this is a more complex issue and indeed is the subject of some of our current efforts. This fact can be used as the basis for a quantitative comparison of the two model formulations, as well as to give physical / biological meaning to the time-dependent exponential rates αi(t) and βi(t) used previously to describe cell division and death.
3.3. The Cyton class of models
It follows from the form of Equations (6)–(9) that the generation structure of the population (cells per division number) is completely determined by the functions φi(t) and ψi(t) and the progressor fractions Fi. To motivate the form of the functions φi(t) and ψi(t), define the random variable Tidiv to be the time required for a progressing cell to complete the ith division, with the clock starting from the completion of the (i − 1)th division. (That is, the random variables Tidiv are defined in the temporal reference frames of the individual cells.) Similarly, define the random variables Tidie to be the time required for a newly divided cell to die. The cyton model is built from the premise that these two random variables are independent. Upon the completion of the ith division (orupon activation, for i = 0), every cell realizes a new value for Tidiv and Tidie; whichever realization is smaller determines the eventual fate of the cell. The functions φi(t) and ψi(t) are the probability density functions for Tidiv and Tidie, respectively (which are assumed to be common for all cells having completed i divisions).
Experimental evidence suggests that the functions φi(t) and ψi(t) canbe heuristically described by lognormal probability density functions [28,29]. Thus for all t > 0,
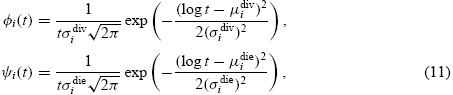 |
where the parameters μidiv and σidiv represent the means and standard deviations of the natural logarithms of the random variables Tidiv (and similarly for Tidie). Since it is more intuitive to discuss the means and standard deviations of the random variables Tidiv and Tidie directly (as opposed to the means and standard deviations of their logarithms) these quantities are easily defined in terms of the parameters μidiv, μidie, σidiv, and σidie:
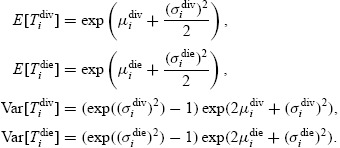 |
For the basic cyton model, it is standard (following the work [28,29]) to assume that the random variables Tidiv are identically distributed for all i ≥ 1 and that the random variables Tidie are identically distributed for all i ≥ 1. These distributions may be different from the corresponding random variables for undivided cells (i = 0). Thus
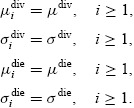 |
It is also assumed that Fi = 1 for all i ≥ 1 in the basic cyton model.
Of course, any number of generalizations of the basic cyton model is possible. For instance, following [28], the fractions Fi can be defined in terms of a division destiny. Among the cells which are activated to divide (F0N0 of them), let pi be the probability that a cell (or its progeny) ceases to be activated after completing i divisions and define the cumulative probabilities
(Note that we must have ci → 1 as i → ∞.) It follows that the progressor fractions (for i ≥ 1) are
 |
Rather than estimate the progressor fractions Fi (or the probabilities pi) independently, we follow the approach suggested in [28] and assume that the probabilities pi can be described as a discrete normal density function defined on the nonnegative integers. Thus the values of the probabilities pi (and the progressor fractions Fi) are uniquely determined by the mean Dμ and the standard deviation Dσ of a discrete normal distribution. This assumption has been shown to be consistent with experimental data [28] and has the beneficial effect of reducing the total number of parameters of the mathematical model.
We can now define the division destinies in terms of the progressor fractions (12). The division destiny di is defined to be the fraction of cells out of those cells in the original population which would have proceeded through exactly i divisions in the absence of any cell death. These quantities are computed as
It should be noted that this definition does not make any assumptions regarding the exact lineage of cells (which cannot be determined from flow cytometry data) so that the progeny of a single cell are not assumed to all undergo the same number of divisions. Rather, one can consider a fractional number of precursors. For example, consider a single cell which divides once, after which one of the two daughter cells divides again. Then there are three cells in the total population, and the division destinies are d0 = 0, d1 = ⅓, and d2 = ⅔. Though counterintuitive for a single cell, division destinies provide an indication of the number of divisions undergone averaged over the population of precursors.
Following the work presented in [3], one may also generalize the death rate mechanism for undivided cells to incorporate a separate set of behaviours forunactivated cells. In particular, it can be assumed that a fraction pd of such cells will remain dormant and neither divide nor die during the experiment. The remaining fraction (1 − pd) will die with some exponential rate β which is independent of the death-rate distribution of activated cells. It follows that the probability density function describing cell death for undivided cells is
It should be noted that this generalization changes the interpretation of the random variable T0die and its relationship to the parameters μ0die and σdie in the sense that the parameters μ0die and σ0die describe the statistical properties of progressing cells only.
While the more complex death rate function (14) was found to accurately describe a CFSE data set in [3], the data sets collected for this manuscript differ in that the first measurement was taken approximately 24 h after stimulation by PHA (as opposed to immediately following stimulation). As a result, the initial condition for the mathematical model represents only those cells which have not died in the first 24 h after stimulation. It seems reasonable to hypothesize that such cells are unlikely to die at subsequent measurement times. Thus an additional possibility is ψ0(t) = 0 for all t. (This ψ0(t) is not a proper probability density function, but is sufficient to describe the intended behaviour. Equivalently, one could assume the function ψ0(t) has a large mean and small variance so that the support of the density function is effectively limited to a region beyond the final measurement time.)
Finally, we consider one possible generalization of the density function for time-to-first-division for progressing cells. If there are multiple subpopulations (e.g. naive vs. memory cells) contained within the population under study, the density φ0(t) may be multimodal. For simplicity, we consider a bimodal density function which is a weighted sum of two lognormal distributions,
where f ∊ [0,1] is a weighting parameter.
The possible model parameterizations considered in this report are summarized in Table 1.
Table 1.
List of the possible cyton model parameterizations considered in this report. These models are compared (in terms of their ability to describe experimental data sets) in Tables 3 and 4.
| Model | Description | Parameters (cyton only) |
|---|---|---|
| Model 1 | Basic cyton model; Equations (11), Fi = 1 for all i ≥ 1 | 9 |
| Model 2 | Basic cyton model plus division destiny according to (12) | 11 |
| Model 3 | Basic cyton model, but with Equation (14) for undivided cell death | 11 |
| Model 4 | Basic cyton model, but with no undivided cell death (ψ0(t) = 0) | 7 |
| Model 5 | Combine models 2 and 3 | 13 |
| Model 6 | Combine models 2 and 4 | 9 |
| Model 7 | Model 1, but with Equation (15) for undivided cell division | 12 |
| Model 8 | Model 2, but with Equation (15) for undivided cell division | 14 |
| Model 9 | Model 3, but with Equation (15) for undivided cell division | 14 |
| Model 10 | Model 4, but with Equation (15) for undivided cell division | 10 |
| Model 11 | Model 5, but with Equation (15) for undivided cell division | 16 |
| Model 12 | Model 6, but with Equation (15) for undivided cell division | 12 |
3.4. Distribution of cellular autofluorescence
To this point we have considered a class of models based on the cyton modelling framework which describe the dynamic population generation structure for dividing cells. This class of models has been incorporated into a label-structured partial differential equation model derived by considering the CFSE in a mass-conservation framework. As discussed previously, once the structured densities ni(t, x) (in terms of the fluorescence x resulting from CFSE) have been constructed, these quantities must be related to the measured fluorescence intensity  (which includes the contribution of cellular autofluorescence) via the convolution (5). Autofluorescence is the result of the absorption and emission properties of molecules which are naturally found within all cells and is present even in the absence of an added fluorescent label. Mean autofluorescence is known to increase as cells are activated to divide [1], probably as a result of the production of additional intracellular components associated with increased metabolic activity within the cell. Thus the notation of Equation (5) explicitly includes the time-dependence of the autofluorescence density function, p(t, ζ). Because these intracellular molecules are partitioned among daughter cells during cell division, the distribution of autofluorescence can be intuitively considered as a growth and fragmentation process, which is known to produce skew-right density functions such as the lognormal density function [26]. In fact, it has been shown [13] that the distribution of autofluorescence in the population can be well-approximated using a lognormal density function, and thus can be characterized by its mean and its variance. This observation has been used as the basis for approximation techniques to the convolution (5) [27].
(which includes the contribution of cellular autofluorescence) via the convolution (5). Autofluorescence is the result of the absorption and emission properties of molecules which are naturally found within all cells and is present even in the absence of an added fluorescent label. Mean autofluorescence is known to increase as cells are activated to divide [1], probably as a result of the production of additional intracellular components associated with increased metabolic activity within the cell. Thus the notation of Equation (5) explicitly includes the time-dependence of the autofluorescence density function, p(t, ζ). Because these intracellular molecules are partitioned among daughter cells during cell division, the distribution of autofluorescence can be intuitively considered as a growth and fragmentation process, which is known to produce skew-right density functions such as the lognormal density function [26]. In fact, it has been shown [13] that the distribution of autofluorescence in the population can be well-approximated using a lognormal density function, and thus can be characterized by its mean and its variance. This observation has been used as the basis for approximation techniques to the convolution (5) [27].
To test the assumption of lognormality, a portion of PBMCs from each donor were set aside and stimulated with PHA but never labelled with CFSE. Thus the measured fluorescence distribution of these cells (represented in histogram form) can be used to approximate the density function p(t,ζ) representing the actual population distribution of autofluorescence. This autofluorescence data are depicted for the two donors and cell types in Figures 3 and 4. To assess the lognormal approximation, we used two parameter estimation schemes to construct lognormal density functions from the autofluorescence data. The first method is the method of moments, in which the exact mean and variance of the measured cells was computed and a lognormal curve was constructed with the same mean and variance. (In the figures, the resulting lognormal density function has been scaled by the number of cells in the data to facilitate comparison.) The second method is to use least squares to estimate the scale, mean, and variance of a lognormal density function.
Figure 3.
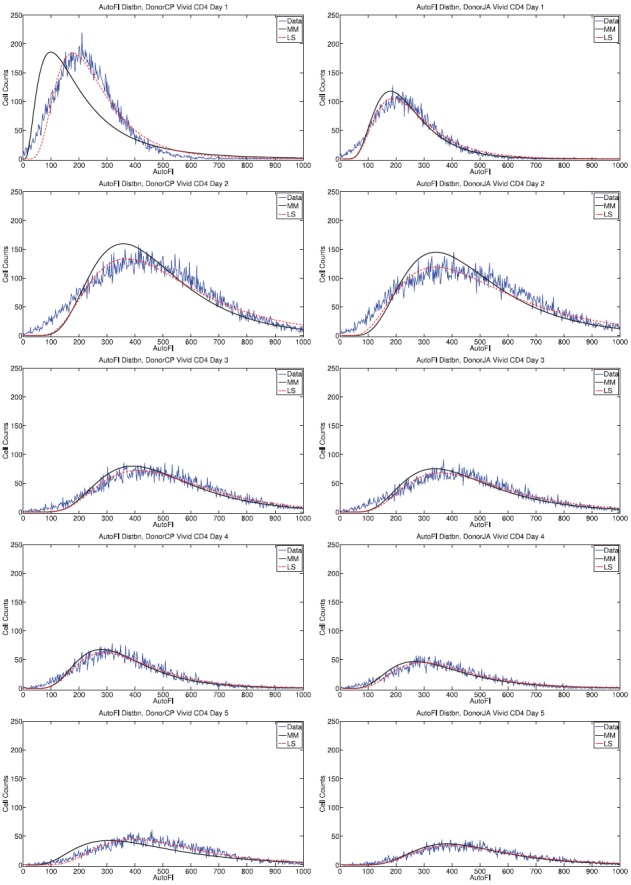
Measured autofluorescence distributions in comparison to fitted lognormal curves for Donor 1 (left) and Donor 2 (right) for CD4T cells. The least-squares fit to data is visually better than the fit obtained by the method of moments (MM), though the difference is small and becomes less noticeable at later measurement times. This pattern is more noticeable for CD4T cells (here) than for CD8T cells (Figure 4).
Figure 4.
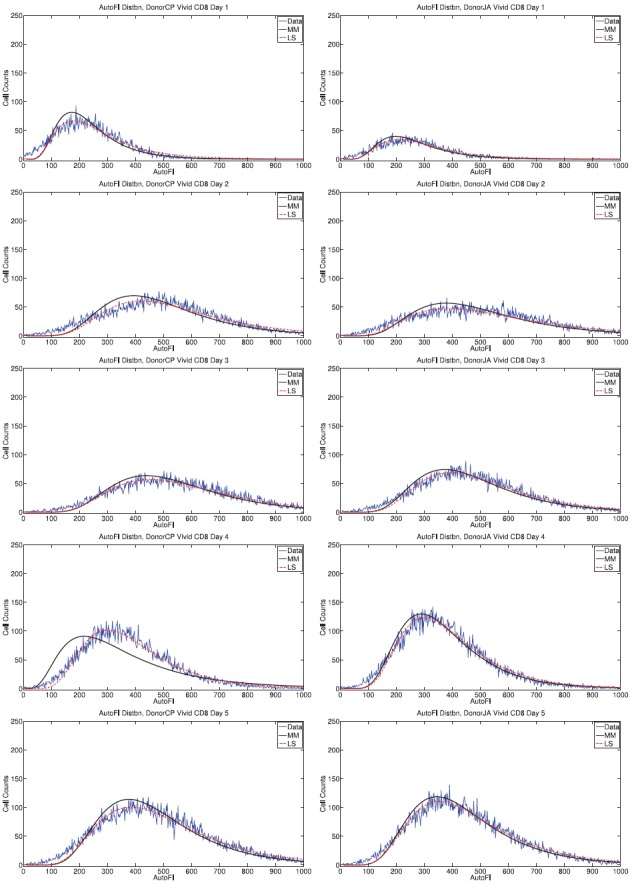
Measured autofluorescence distributions in comparison to fitted lognormal curves for Donor 1 (left) and Donor 2 (right) for CD8T cells. The least-squares fit to data is visually better than the fit obtained by the method of moments (MM), though the difference is small.
Though the autofluorescence data are not perfectly lognormal, the assumption is fairly accurate for both cell types and both donors. For CD4 T cells, the lognormal approximation becomes more accurate as time progresses. This is consistent with the existence of an initial transient distribution of autofluorescence which corresponds to the quiescent state of the cells at the start of the experiment; as cells are activated to divide, the lognormal (or at least skew-right) distribution emerges possibly as a result of growth and division processes [26]. For CD8 T cells, the validity of the approximation does not change much in time.
Significantly, the statistical moments of the autofluorescence distribution are observed to change in time (Figure 5). This is particularly true for the mean. The significant increase in mean autofluorescence between 24 and 48 h is known to be associated with cellular activation. Though the increase is large, it is of little consequence for mathematical modelling because the contribution of autofluorescence to the fluorescence intensity measurements is very small (less than 1%) for undivided cells. The decrease in autofluorescence as measured at approximately t = 96h is more problematic as some cells will have completed multiple divisions by that time; the cause of the decrease is unknown. It is possible that a change in instrument settings between the two measurement days could account for this effect. Yet this seems unlikely as comparable changes are not observed in the data collected for cells labelled with CFSE (Figures 1 and 2). Another possibility is nutrient depletion; by the third day of the experiment, the cells begin to run out of the nutrients originally placed in culture and these must be replaced. Nutrient depletion could cause activated cells to die or return to a quiescent state.
Figure 5.
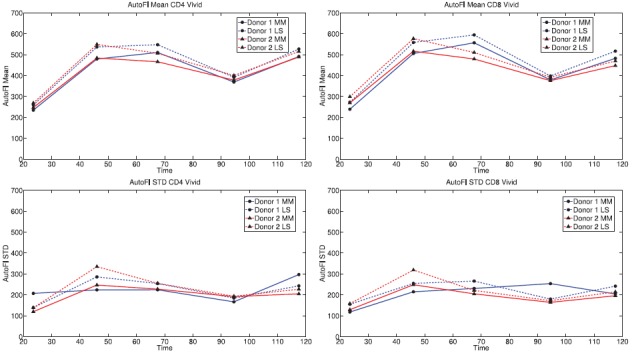
Top: Mean autofluorescence as estimated by the method of moments (solid lines) and least squares (dashed lines). Bottom: Standard deviation as estimated by the method of moments (solid lines) and least squares (dashed lines). Data shown for CD4T cells (left) and CD8T cells (right). Mean autofluorescence is observed to increase significantly in the first two days of the experiment, an effect which is known to be the result of cellular activation. The cause of the decrease in mean autofluorescence at approximately 96 h is unknown; nutrient depletion is one hypothesized cause.
Based upon these observations, the population distribution of autofluorescence can be accurately described as a lognormal density function at each measurement time. Thus
where the parameters μxa(t) and σxa(t) are related to the mean and standard deviation of the autofluorescence distribution (at time t) by the formulas
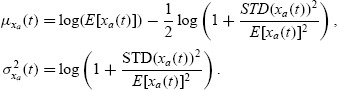 |
In the context of parameter estimation for the mathematical model (9), we consider two frameworks. The first is to use the method of moments (as above) with the autofluorescence data to compute E[xa(t)] and STD(xa(t)); these values will then be considered fixed while the remaining parameters of the mathematical model are determined by using least squares to fit the data in Figures 1 and 2 (see Section 4). The second method is to ignore the time-dependence of the distribution and assume E[xa(t)] = E[xa], STD(xa(t)) = STD(xa). The values of E[xa] and STD(xa) are estimated in a least-squares framework as described in Section 4, and these estimated values can be compared to the values returned by the method of moments. One could also attempt to parameterize and estimate a function p(t, ζ) which is time-dependent. This is a more complex estimation problem and is unlikely to be identifiable; therefore we do not consider it here.
4. Statistical modelling of CFSE data
Models similar to those discussed in Section 3 have previously been shown to accurately describe population generation structure as measured by flow cytometry [3]. However, the statistical properties of the measurement process have not been nearly as carefully considered. A major limitation of the current modelling framework lies not in the mathematical model itself but rather in the statistical model which links the mathematical model to the data. An accurate statistical model is of vital importance for the consistent estimation of model parameters, as well as the unbiased estimation of confidence intervals around those parameters [5–7,10,19,44]. Additionally, an accurate statistical model is necessary for the rigorous comparison of different model parameterizations and generalizations [2,9,16] and the optimal design of experiments [8].
To this point, we have discussed a class of mathematical models which combine the cyton modelling framework of [28,29] with the label and division structured population models of [13,27,42,47] to describe CFSE data. Given several members of this class of models (see, e.g. Table 1) there is a need to compare the mathematical models on a quantitative basis in order to identify which model provides the ‘best’ (in an appropriate sense) description of an underlying experimental data set. Several techniques based upon information theory [16] or asymptotic properties of least-squares estimators [2,9,24] have been developed for this purpose. In all cases, the techniques are premised upon an accurate statistical model which links the mathematical model to the collected data.
Mathematical descriptions of CFSE data have generally described numbers of cells per generation as estimated from histogram data, rather than the histogram data itself. As such, little consideration has been given to the statistical model which generates the histogram data. In their likelihood estimation framework, Hyrien and Zand [31] propose that the marginal probability density of each datum is normally distributed, and that the variance of this normal distribution is constant for all data points. Least-squares estimators, though not restricted to any parametric class of probability density functions, have also generally assumed a constant variance error model [3,11–13,34,35,47]. However, it has been shown that such an assumption does not accurately describe the variance as observed in actual data sets [12,13,47]. Another common error model for least-squares estimation, in which the variance of each data point is assumed to be directly proportional to the square of the model value at that point (a constant coefficient of variance model) has also been hypothesized, but was again observed to be inaccurate [12,13,47]. Here, we revisit the discussion of [47, Chapter 4] to consider the probabilistic aspects of the actual experimental process itself and derive a hypothetical statistical model from a theoretical basis. This statistical model is then incorporated into a weighted least-squares estimation scheme and several computational algorithms are proposed.
4.1. Theoretical statistical model
Define the structured densities ñi(t, 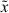 ) (in terms of measured fluorescence intensity) for cells having completed i divisions as in Section 3. Then the structured density for the entire population of cells is
) (in terms of measured fluorescence intensity) for cells having completed i divisions as in Section 3. Then the structured density for the entire population of cells is
Because CFSE histogram data are most commonly represented using abase 10 logarithmic scale, we define the change of variables z = log10(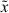 ) to arrive at
) to arrive at
which gives the structured density (measured in cells per base 10 log unit intensity) for the entire population of cells at time t. Let Nkj be a random variable representing the number of cells measured at time tj with log-fluorescence intensity in the region [zk, zk + 1). The goal of the statistical model is to link the structured density 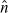 (t, z) to the data random variables Nkj in a manner that is consistent with the statistical properties of the random variables Nkj. Moreover, in the experimental process, the quantities Nkj are not directly measured. Rather, only a fraction of the contents of each measurement well are acquired by the measurement apparatus. In order to account for this discrepancy, a known number of beads (which can be identified and counted in the flow cytometry output) are contained within each sample to be measured. By comparing the number of beads acquired to the number of beads known to be in the tube, one is able to estimate the fraction of the sample acquired.
(t, z) to the data random variables Nkj in a manner that is consistent with the statistical properties of the random variables Nkj. Moreover, in the experimental process, the quantities Nkj are not directly measured. Rather, only a fraction of the contents of each measurement well are acquired by the measurement apparatus. In order to account for this discrepancy, a known number of beads (which can be identified and counted in the flow cytometry output) are contained within each sample to be measured. By comparing the number of beads acquired to the number of beads known to be in the tube, one is able to estimate the fraction of the sample acquired.
Let 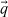 be the vector of parameters of the mathematical model (that is,
be the vector of parameters of the mathematical model (that is, 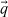 contains the parameters necessary to describe the cyton dynamics as well as the parameters describing the label loss function v(t) and the autofluorescence distribution p(t, ζ)) so that we may rewrite
contains the parameters necessary to describe the cyton dynamics as well as the parameters describing the label loss function v(t) and the autofluorescence distribution p(t, ζ)) so that we may rewrite 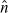 (t, z) =
(t, z) = 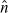 (t, z;
(t, z; 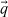 ). In order to derive an error model for the histogram data we first make the common assumption that the model is correctly specified so that the structured population density
). In order to derive an error model for the histogram data we first make the common assumption that the model is correctly specified so that the structured population density 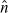 (t, z;
(t, z; 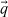 0) (where
0) (where 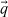 0 is a hypothetical ‘true’ parameter) perfectly describes the population of cells. Let Ni(t) be defined as in Equation (6) and let N(t) = ΣNi(t). That is, N(t) is the total number of cells in the population at time t. Define
0 is a hypothetical ‘true’ parameter) perfectly describes the population of cells. Let Ni(t) be defined as in Equation (6) and let N(t) = ΣNi(t). That is, N(t) is the total number of cells in the population at time t. Define
It follows that pj(z) is a probability density function. Let Sj be the number of cells of interest (e.g. CD4T cells) sampled at measurement time tj. Then one can consider the sample of Sj cells (of interest) to be taken without replacement from the total population of N(tj) cells; the fluorescence intensity of the sampled cells is subject to the sampling density pj(z). It should be carefully noted that there are numerous steps required to separate the cells of interest from the actual culture of cells passing through the cytometer; see, e.g. 4], Section 2]. References to the total number of cells N(t), and the number of sampled cells Sj are understood to refer only to the specific cells of interest in the experiment. For the moment, we make the additional assumption that these two numbers are exact and are not subject to any errors (systematic, experimental, or otherwise) caused by gating, etc.
Let B be the total number of beads (in each sample tube) which are used to quantify the fraction of the population of cells which is measured at time tj and let bj be the ‘true’ number of beads passing through the cytometer. By this, we mean the exact number of beads which would pass through the cytometer if the measured culture were perfectly homogeneous, etc. It follows that
Now consider the kth histogram bin [zk,zk + 1). The number of cells in the whole population which are contained in this bin is
Let Mkj be a random variable representing the number of cells (out of the sampled population) counted into the kth bin. Because the measurement process represents a sampling without replacement, it follows that Mkj is described by a hypergeometric distribution,
That is, Sj cells are sampled without replacement from a population containing a total of N(tj) cells, of which I[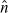 ](tj, zk;
](tj, zk; 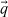 0) are of interest. We make the following assumptions regarding the measurement process:
0) are of interest. We make the following assumptions regarding the measurement process:
Then it can be shown [23] that 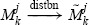 , where
, where
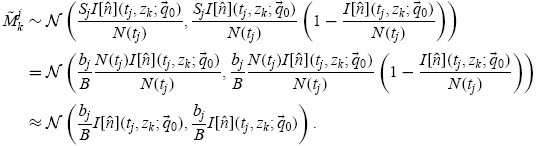 |
The final approximation is valid provided I[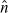 ](tj, zk;
](tj, zk; 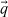 0) ≪ N(tj), which is a perfectly reasonable assumption (Table 2).
0) ≪ N(tj), which is a perfectly reasonable assumption (Table 2).
Table 2.
Summary of notation for the statistical model.
| Notation | Description |
|---|---|
| ñ(t, z) | Log-transformed label-structured density |
| N(t) | Total number of cells in the population at time t |
| pj(z) | Probability density function from which cells are sampled |
| Sj | Number of cells sampled at time tj |
| B | Total number of beads originally placed into each well |
| bj | ‘True’ number of beads counted by the cytometer at time tj |
I[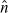 ](tj, zk; ](tj, zk; 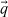 0) 0) |
‘True’ number of cells from the total population belonging in the kth histogram bin at time tj |
| Mkj | Random variable representing the number of cells counted into the kth histogram bin at time tj |
| bj | Actual number of beads counted by the flow cytometer (a realization of bj) |
| Nkj | Random variable resulting when Mkj is scaled by the ratio B/ j j
|
| njk | The actual data, a realization of Njk |
| λj | Random variable representing the bead count error ratio bj/ j j
|
It can easily be shown that the first assumption regarding the measurement process is accurate provided bj/B ≪ 1, which again is reasonable (the ratio is typically less than 0.1). This assumption is necessary to ensure that the sampling (without replacement) process is conducted in a such a way that the ratio of cells of interest to total cells is approximately constant during the measurement. The assumption is unusual in that it places a restriction on the total amount of data which can be collected. The second assumption regarding the measurement process bounds the probability that a cell belongs to a particular bin away from zero and one (although this assumption is not strictly necessary in some cases [33]). In practice, this assumption is only violated when I[ñ(tj, zk;  0)] ≈ 0.
0)] ≈ 0.
Finally, when the measurements are actually taken, a certain number of beads  j are actually counted. We would certainly hope that
j are actually counted. We would certainly hope that  j ≈ bj; however, we can think of
j ≈ bj; however, we can think of  j as a realization of some random variable (which may or may not be an unbiased estimator of bj, depending upon any systematic error that might occur in obtaining bead counts from flow cytometry data). To obtain the histogram data which is actually used to calibrate the mathematical model, one scales the sampled cell counts Mjk by the inverse of the fraction of the total population actually sampled (as estimated by the number of counted beads
j as a realization of some random variable (which may or may not be an unbiased estimator of bj, depending upon any systematic error that might occur in obtaining bead counts from flow cytometry data). To obtain the histogram data which is actually used to calibrate the mathematical model, one scales the sampled cell counts Mjk by the inverse of the fraction of the total population actually sampled (as estimated by the number of counted beads  j). Thus the data may be represented by the random variable
j). Thus the data may be represented by the random variable
It follows that
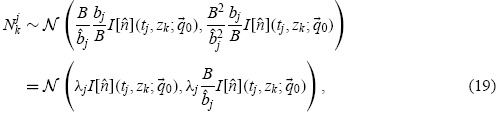 |
where we have defined λj = bj/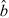 j. The quantities λj in effect represent a ‘scaling error’ and are sufficient to explain the apparent violation of conservation principles often noticed in flow cytometry data (see, e.g. 11],20,32]; the problem is discussed at greater length in [47, Chapters 1,4]).
j. The quantities λj in effect represent a ‘scaling error’ and are sufficient to explain the apparent violation of conservation principles often noticed in flow cytometry data (see, e.g. 11],20,32]; the problem is discussed at greater length in [47, Chapters 1,4]).
From Equation (19), one sees that the variance of the data is not constant (as is the case for data described by constant variance models), nor does it scale with the square of the magnitude of the model (as is the case for data described by constant coefficient of variance models), see [6, Chapter 3]. Rather, the variance grows linearly with the magnitude of the model solution. This relationship has been shown to accurately describe CFSE data [9,47], and we can use this relationship to establish a parameter estimation framework.
4.2. Parameter estimation
The goal of the parameter estimation problem is to find an estimate for the parameter 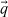 0 which is assumed to generate the data (neglecting model misspecification). In the above statistical model, we must also estimate the nuisance parameters
0 which is assumed to generate the data (neglecting model misspecification). In the above statistical model, we must also estimate the nuisance parameters 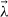 = {λj}. Given a collection of random variables Njk distributed according to Equation (19), one may define the estimators
= {λj}. Given a collection of random variables Njk distributed according to Equation (19), one may define the estimators
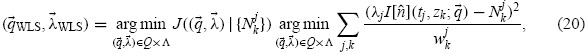 |
where the weights are chosen in a manner that accounts for the assumed reliability of each measurement (see below). Experimental data are considered as a set of realizations njk of the random variables Nkj; these are used to obtain the estimates
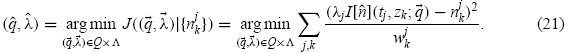 |
We see that the cost functional J, and thus the estimators, depends upon the data random variables Njk and thus on the statistical model (19). In order for the estimators  WLS and
WLS and  WLS to be asymptotically optimal, the weights wjk must be chosen to match the variance of the random variables njk
43],44],
WLS to be asymptotically optimal, the weights wjk must be chosen to match the variance of the random variables njk
43],44],
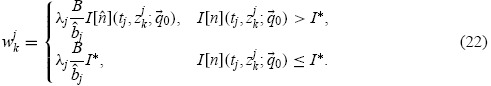 |
The cutoff value I∗ > 0 is determined by the experimenter so that the resulting residuals appear random. In the work that follows, I∗ = 200. The values of B and 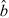 j are known from the experiment. Notice that the computation of the weights (22) depends upon the value of the ‘true’ parameter
j are known from the experiment. Notice that the computation of the weights (22) depends upon the value of the ‘true’ parameter 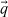 0 as well as on the nuisance parameters
0 as well as on the nuisance parameters 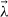 . As a result, one must use an iterative estimation procedure [6,19].
. As a result, one must use an iterative estimation procedure [6,19].
Traditionally, it has been assumed that λj = 1 for all j 3],11–13,35] – that is, that there is no scaling error. While this assumption is obviously violated by some data sets [11,20,32,47] it is not clear that the incorporation or omission of the nuisance parameters will have a significant effect on the estimation of parameters. In practice, the nuisance parameter vector must be estimated in conjunction with the model parameter vector in a two-stage process. Unfortunately, two-stage estimation may cause some parameters of the mathematical model to become unidentifiable (or, at the very least, the variance of the estimators for certain parameters may increase dramatically). For this report, it will be assumed that λj = 1 for all j and the nuisance parameters will not be estimated. As will be seen in Section 5, the available data are well-described by the mathematical model even under this simplified assumption. We consider the following estimation algorithm:
-
(1)Set ℓ = 0. Obtain an initial estimate (the ordinary least-squares estimate) by solving Equation (21) with λ = (1, …, 1) and wkj = 1 for all j and k,
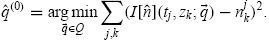
-
(2)
Compute the weights wjk for each j and k according to Equation (22) with
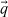 0 replaced by
0 replaced by 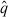 (0) and with
(0) and with 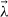 = (1,…, 1);
= (1,…, 1); -
(3)
At iteration ℓ, compute
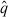 ℓ according to Equation (21) with the current weights, and with
ℓ according to Equation (21) with the current weights, and with 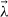 = (1,…,1);
= (1,…,1); -
(4)
Update the weights again according to Equation (22), now with
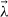 0 replaced by
0 replaced by 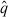 (ℓ) (and
(ℓ) (and 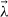 = (1,…, 1) still); increment ℓ;
= (1,…, 1) still); increment ℓ; -
(5)
Repeat steps 3 and 4 until convergence is obtained.
5. Results
Twelve models of cyton dynamics are considered in Table 1 and two methods of estimating the statistical moments of the autofluorescence distribution(s) as proposed in Section 3.4 are used. In order to determine which of these model formulations best describes the available data, we need mathematical tools for rigorous model comparison. These tools are explored in Section 5.1 and a best-fit model is selected. The fit of this model to the data, as well as the statistical model of the data, are then discussed. Finally, the dynamic responsiveness of the cells from the experimental data is analysed.
5.1. Model comparison
From Section 3.3, it is clear that some of the models of cyton dynamics are refinements of other models (in the sense that the more complex model includes all possible solutions of the simpler model). For instance, the basic cyton model (Model 1) can be considered as a refinement of a cyton model for which it is assumed ψ0(t) = 0 (Model 6). This is because, for appropriate choices of the parameters E[T0die] and STD[Tdie0], Model 1 is exactly equivalent to Model 6. In such a case, it is clear that the more complex model must result in a minimized cost functional at least as low as that of the simpler model; yet the more complex model has more parameters, and one must consider the possibility of overparameterization against this decrease in the least-squares cost. To this end, results from the asymptotic theory of least-squares estimators can be extended [9] to weighted least-squares estimators such as Equation (20).
Assume (without loss of generality) that the nuisance parameters 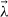 are known. Let
are known. Let 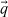 WLS be defined, as above, as the minimizer over the admissible parameter space Q of the least-squares cost function
WLS be defined, as above, as the minimizer over the admissible parameter space Q of the least-squares cost function 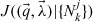 . Now define
. Now define 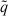 WLS to be the minimizer of
WLS to be the minimizer of 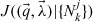 over the restricted parameter set QH, where QH = {q ∊ Q|Hq = h} for some linear function H of rank r and a vector h of size r × 1. (For nonlinear restrictions on the parameter space, a locally equivalent condition can be derived from the first order linearization of the nonlinear constraint; see [9].) In such situations, the model comparison problem can be recast as one of hypothesis testing. Consider the null and alternative hypotheses,
over the restricted parameter set QH, where QH = {q ∊ Q|Hq = h} for some linear function H of rank r and a vector h of size r × 1. (For nonlinear restrictions on the parameter space, a locally equivalent condition can be derived from the first order linearization of the nonlinear constraint; see [9].) In such situations, the model comparison problem can be recast as one of hypothesis testing. Consider the null and alternative hypotheses,
Then under fairly general conditions (see [9]) and assuming the null hypothesis is true, the test statistic
(where n is the total number of data points) is asymptotically a chi-square random variable with r degrees of freedom, Un ∼ χ2(r). Thus given the data {njk} as realizations of the random variables njk, one obtains a realization un of Un which can be used to assess the likelihood that the decrease in cost associated with the unrestricted parameter space is the result of chance (see [6, Section 3.5]). The complete conditions under which Un is asymptotically distributed as a chi-square random variable, as well as a proof of the result, can be found in [9] and the references therein.
For comparison among models which are not refinements, one can use information theoretic criteria such as Akaike's Information Criterion (AIC). From Equation (19), it follows that the scaled residuals
 |
are independent and normally distributed with constant variance (for all k and j). Then the AIC, which is the expected value of the relative Kullback–Leibler distance for a given model [16], is
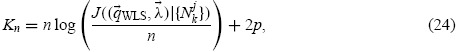 |
where p is the dimension of the space Q for the particular model of interest. Because Kn provides information regarding the relative Kullback–Leibler distance, AIC values have meaning only in comparison to one another. The model which results in the lowest AIC value is the most likely model for the particular data set being investigated. We note that a direct comparison of the costs (in Tables 3 and 4) may not be reasonable due to the fact that the AIC values also must take into account the numberp of parameters estimated in a given model (see Equation (24)). A derivation of the AIC as well as numerous examples can be found in [16].
Table 3.
Minimized weighted least-squares costs 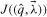 for various cyton model parameterizations (see Table 1). Autofluorescence estimated as a time-invariant lognormal density function by least-squares fit to data.
for various cyton model parameterizations (see Table 1). Autofluorescence estimated as a time-invariant lognormal density function by least-squares fit to data.
| CD4T Cells |
CD8T Cells |
|||
|---|---|---|---|---|
| Donor 1 | Donor 2 | Donor 1 | Donor 2 | |
| Model 1 | 6.0547 × 104 | 11.812 × 104 | 7.9383 × 104 | 20.348 × 104 |
| Model 2 | 5.4212 × 104 | 5.1257 × 104 | 2.8669 × 104 | 4.5650 × 104 |
| Model 3 | 6.0344 × 104 | 11.812 × 104 | 8.2439 × 104 | 20.348 × 104 |
| Model 4 | 6.1677 × 104 | 11.863 × 104 | 7.9383 × 104 | 20.348 × 104 |
| Model 5 | 5.4212 × 104 | 5.1257 × 104 | 2.7963 × 104 | 4.5651 × 104 |
| Model 6 | 5.4212 × 104 | 5.1257 × 104 | 2.8670 × 104 | 4.5650 × 104 |
| Model 7 | 4.3175 × 104 | 9.4856 × 104 | 6.1827 × 104 | 18.761 × 104 |
| Model 8 | 3.4376 × 104 | 4.2341 × 104 | 2.8038 × 104 | 3.9553 × 104 |
| Model 9 | 4.4006 × 104 | 9.5017 × 104 | 6.0628 × 104 | 19.563 × 104 |
| Model 10 | 4.3196 × 104 | 9.4931 × 104 | 6.2538 × 104 | 18.761 × 104 |
| Model 11 | 3.4375 × 104 | 4.2346 × 104 | 2.8004 × 104 | 3.9551 × 104 |
| Model 12 | 3.4376 × 104 | 4.8931 × 104 | 2.8038 × 104 | 3.9554 × 104 |
Table 4.
Minimized weighted least-squares costs 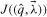 for various cyton model parameterizations (see Table 1). Autofluorescence estimated using the method of moments at each measurement time.
for various cyton model parameterizations (see Table 1). Autofluorescence estimated using the method of moments at each measurement time.
| CD4T Cells |
CD8T Cells |
|||
|---|---|---|---|---|
| Donor 1 | Donor 2 | Donor 1 | Donor 2 | |
| Model 1 | 7.1255 × 104 | 14.302 × 104 | 8.5425 × 104 | 23.068 × 104 |
| Model 2 | 5.8092 × 104 | 5.4022 × 104 | 3.9701 × 104 | 5.8327 × 104 |
| Model 3 | 7.1097 × 104 | 14.313 × 104 | 8.4900 × 104 | 23.503 × 104 |
| Model 4 | 7.2613 × 104 | 14.344 × 104 | 8.5434 × 104 | 23.068 × 104 |
| Model 5 | 5.8092 × 104 | 5.4020 × 104 | 3.9709 × 104 | 5.8309 × 104 |
| Model 6 | 5.8092 × 104 | 5.4041 × 104 | 3.9701 × 104 | 5.8327 × 104 |
| Model 7 | 4.3392 × 104 | 11.098 × 104 | 6.7689 × 104 | 20.965 × 104 |
| Model 8 | 3.3741 × 104 | 4.4724 × 104 | 3.7443 × 104 | 5.2944 × 104 |
| Model 9 | 4.3418 × 104 | 11.098 × 104 | 6.8680 × 104 | 20.952 × 104 |
| Model 10 | 4.3392 × 104 | 11.098 × 104 | 6.7689 × 104 | 20.965 × 104 |
| Model 11 | 3.3741 × 104 | 4.4730 × 104 | 3.7436 × 104 | 5.2944 × 104 |
| Model 12 | 3.3741 × 104 | 4.4724 × 104 | 3.7443 × 104 | 5.2944 × 104 |
With these tools, we are now ready to compare the models suggested in Sections 3.3 and 3.4. The minimized costs J((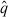 WLS,
WLS, 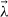 j)) for each donor, cell type, and model are summarized in Tables 3 and 4. Table 3 contains the results when the autofluorescence distribution is assumed to be time-invariant and its statistical moments are estimated within the least-squares framework summarized in Section 4; Table 4 contains the results when the autofluorescence distribution is estimated at each measurement time using the method of moments.
j)) for each donor, cell type, and model are summarized in Tables 3 and 4. Table 3 contains the results when the autofluorescence distribution is assumed to be time-invariant and its statistical moments are estimated within the least-squares framework summarized in Section 4; Table 4 contains the results when the autofluorescence distribution is estimated at each measurement time using the method of moments.
Of the 12 models of cyton dynamics considered, Model 12 is generally selected as the best model. The only exception is for Donor 2 CD4 T cells when estimating a time-invariant autofluorescence distribution using least squares. In this case, Model 8 is narrowly selected by the AIC (K = 9525.77 compared to K = 9525.98), although AIC differences less than 2 are generally not considered significant [16]. On the other hand, the model comparison test statistic (Model 8 is a refinement of Model 12) is un = 5.7992, so that one would reject the null hypothesis (Model 12) only at confidences less than 87.82%, which is lower than typical thresholds for hypothesis testing. Thus the results for this particular data set are ambiguous. It should be acknowledged that Model 8 and Model 12 are quite similar (Model 8 is the generalization of Model 12 allowing for undivided cell death), so that the distinction between the two is quite small. It seems safe to consider Model 12 to be the most parsimonious model of the data for both donors and for both cell types.
A comparison of the two methods of treating autofluorescence is not straightforward. On one hand, the minimized costs given in Tables 3 and 4 are directly comparable in the sense that the costs do not include any measure of cost associated with the autofluorescence data, whether or not that data are used. On the other hand, the estimation of a time-invariant autofluorescence distribution does not make any use of the autofluorescence data. From this perspective the two methods of describing autofluorescence are associated with distinct collections of data, even if the histograms of interest (e.g. those shown in Figures 1 and 2) are the same. It is also not clear whether the failure of the minimized cost functionals to reflect the costs associated with the autofluorescence data is a strength or a weakness of the current approach. When such data are available (as it is here) it seems that it would make for a useful comparison. However, the collection of such data requires additional experimental setup, and these data itself are only interesting to the extent that it helps to describe the dynamics of cellular division and death as observed in the histogram profiles of labelled cells.
Comparing the two approaches strictly in terms of accuracy in describing the histogram profiles of labelled cells (that is, comparing the minimized costs in Tables 3 and 4), the results depend upon cell type. For CD8 T cells, there is a clear advantage in describing the autofluorescence distribution as time-invariant and estimating the moments of the distribution in a least-squares framework. For CD4 T cells, the results are less clear. For Donor 1, there is a very small improvement (among the more accurate models) in using the method of moments to estimate the autofluorescence distribution. For Donor 2, the method of moments works best for Model 12, but not for Model 8 (which is the AIC-selected model when autofluorescence is estimated by least squares). Again, the difference is very small. The analysis presented in the remainder of this document is based on results obtained with Model 12 with a time-invariant autofluorescence distribution estimated in a least-squares framework.
5.2. Analysis of the mathematical and statistical models
The fit of the mathematical model to data for both donors is summarized in Figures 6 (CD4 T cells) and 7 (CD8 T cells). The figures show the best-fit model solution of the mathematical model in comparison to the data; the shaded region indicates the expected level of ‘noise’ in the data as a result of the measurement process. That is, if the calibrated mathematical model were perfectly specified (E[Njk] = I[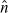 ](tj, zk;
](tj, zk; 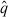 )), the data would oscillate randomly around the model solution. Since the data are assumed to be normally distributed (see Section 4), the 4 standard deviation region highlighted should contain 99.9% of the data points.
)), the data would oscillate randomly around the model solution. Since the data are assumed to be normally distributed (see Section 4), the 4 standard deviation region highlighted should contain 99.9% of the data points.
Figure 6.

Calibrated model with CD4T cell data for a particular set of triplicates from Donor 1 (left) and Donor 2 (right). Shaded regions indicated a 4 standard deviation confidence region computed according to the theoretical statistical model (19), assuming the model is correctly specified.
Overall, the fit to data is good. For Donor 1 CD4 T cells, the estimated mean and standard deviation of the autofluorescence distribution are E[xa] = < 372.42, STD[xa] = 220.08. For Donor 2 CD4 T cells the estimates are E[xa] = 543.76, STD[xa] = 251.90. For CD8T cells the estimates are E[xa] = 658.35, STD[xa] = 319.79 and E[xa] = 542.76, STD[xa] = 271.25, for Donors 1 and 2, respectively. These numbers are within reason when compared to measured autofluorescence data (Figure 5).
The primary shortcoming of the statistical model is the assumption of correct specification, i.e. E[Njk] = I[ ](tj, zk;
](tj, zk;  ). There are clearly instances in Figures 6 and 7 where the data are not centred around the mathematical model, indicating that the mathematical model is systematically in error. As a result, the shaded regions do not contain 99.9% of the data points. From one perspective, this shortcoming of the statistical model is entirely mathematical – if an improved mathematical model were available, then it is possible that the assumption of correct specification would be accurate. Alternatively, it is possible to consider a more general statistical model which directly considers the effects of misspecification, for instance by assuming an autoregressive error structure [24]. This may provide a more accurate measure for model comparison in the absence of a more accurate mathematical model.
). There are clearly instances in Figures 6 and 7 where the data are not centred around the mathematical model, indicating that the mathematical model is systematically in error. As a result, the shaded regions do not contain 99.9% of the data points. From one perspective, this shortcoming of the statistical model is entirely mathematical – if an improved mathematical model were available, then it is possible that the assumption of correct specification would be accurate. Alternatively, it is possible to consider a more general statistical model which directly considers the effects of misspecification, for instance by assuming an autoregressive error structure [24]. This may provide a more accurate measure for model comparison in the absence of a more accurate mathematical model.
Figure 7.
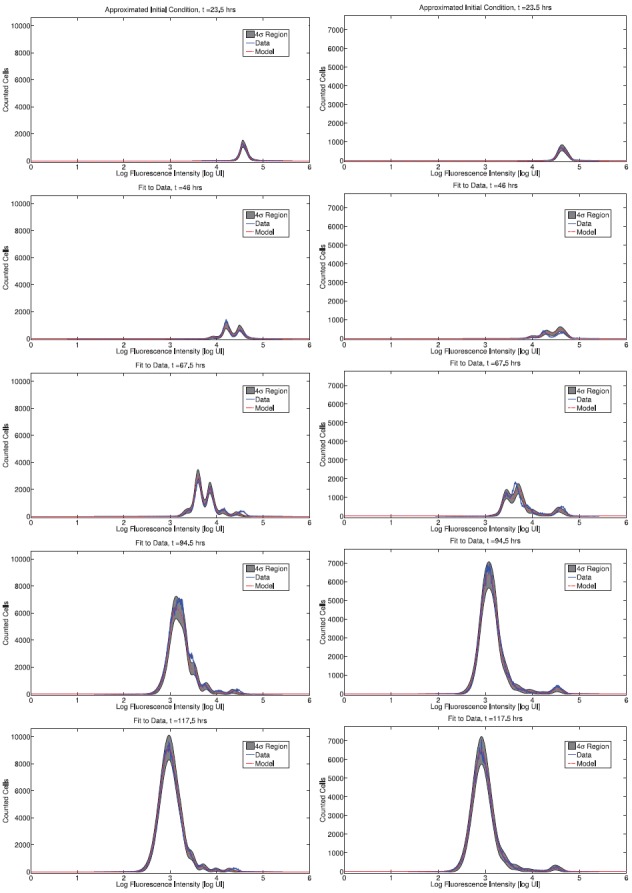
Calibrated model with CD8 cell data for a particular set of triplicates from Donor 1 (left) and Donor 2 (right). Shaded regions indicated a 4 standard deviation confidence region computed according to the theoretical statistical model (19), assuming the model is correctly specified.
It is also assumed in the statistical model that Var[Nkj] ∝ I[ ](tj, zk;
](tj, zk;  ). Traditionally, the accuracy of this assumption is examined by residual plots [6, Chapter 3]. For instance, the modified residuals (23) should be randomly distributed when plotted against the magnitude of the model solution. However, this analysis is premised upon the assumption of correct specification, and thus cannot be performed here. For other data sets, it has been shown that the statistical model presented in this document does accurately describe the variance in CFSE-based flow cytometry data [9,47].
). Traditionally, the accuracy of this assumption is examined by residual plots [6, Chapter 3]. For instance, the modified residuals (23) should be randomly distributed when plotted against the magnitude of the model solution. However, this analysis is premised upon the assumption of correct specification, and thus cannot be performed here. For other data sets, it has been shown that the statistical model presented in this document does accurately describe the variance in CFSE-based flow cytometry data [9,47].
In spite of these shortcomings, it should be emphasized that the fit of the model is quite good for both donors and cell types. As such, we proceed to analyse the dynamic responsiveness of the measured cells in the current modelling framework.
5.3. Analysis of dynamic responsiveness
From the calibrated mathematical model, one can compute the probability density functions φi(t) and ψi(t) from which the times to divide and die are assumed to be drawn in the cyton model of cell division. One can also summarize the division destiny of each population of cells. These are summarized graphically in Figure 8 for CD4 T cells and Figure 9 for CD8 T cells.
Figure 8.
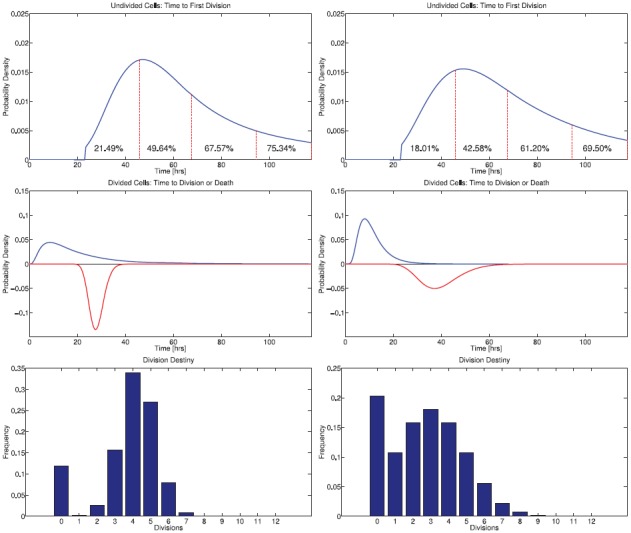
Comparison of estimated CD4 T cell division dynamics between Donor 1 (left) and Donor 2 (right). Top: Probability density function φ0(t) for time to first division for initially undivided CD4 T cells, scaled by the initial progressor fraction F0 of activated cells. Percentages indicate the fraction of undivided cells which will have entered their first division by the next measurement time (vertical dashed lines). On average, cells for Donor 1 complete their first division more rapidly than those for Donor 2; cells from Donor 1 are also more likely to have divided in response to stimulus before the end of the experiment. CD4T cells from both donors are estimated to respond more slowly and in greater frequency than CD8 T cells (compare Figure 9). However the total CD 8 T cell response for Donor 1 is greater than the CD4T cell response while the total CD4 and CD8 responses are comparable for Donor 2. Middle: Probability density functions for time to subsequent division or time to die (inverted) for CD4 T cells having completed at least one division. Cells from Donor 2 divide slightly more rapidly and more synchronously than those from Donor 1. Bottom: Division destiny, indicating the average number of divisions undergone by cells initially in the population (at t = t0). The fraction of cells with division destiny equal to zero estimates the relative abundance of cells which will not become activated to divide.
Figure 9.
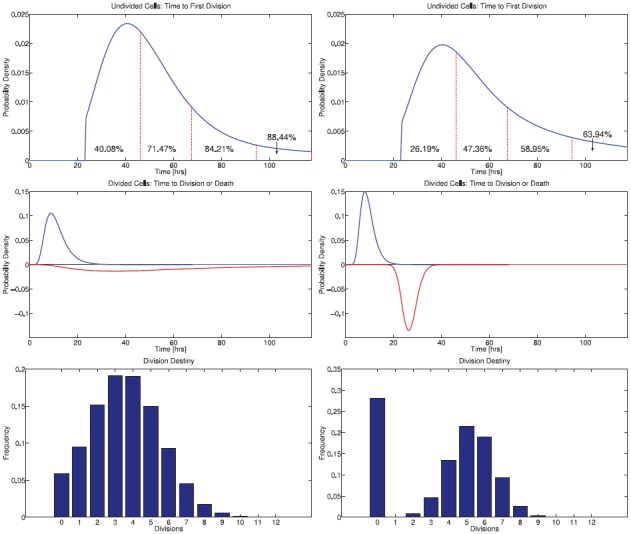
Comparison of estimated CD8 T cell division dynamics between Donor 1 (left) and Donor 2 (right). Top: Probability density function φ0(t) for time to first division for initially undivided CD8 T cells, scaled by the initial progressor fraction F0 of activated cells. Percentages indicate the fraction of undivided cells which will have entered their first division by the next measurement time (vertical dashed lines). On average, cells for Donor 1 complete their first division more rapidly than those for Donor 2 and cells from Donor 1 are more likely to have divided in response to stimulus before the end of the experiment. Middle: Probability density functions for time to subsequent division or time to die (inverted) for CD8 T cells having completed at least one division. Cells from Donor 2 divide slightly more rapidly and more synchronously than those from Donor 1. Bottom: Division destiny, indicating the average number of divisions undergone by cells initially in the population (at t = t0). The fraction of cells with division destiny equal to zero estimates the relative abundance of cells which will not become activated to divide.
Notice that the cytons  0(t) have been truncated to the left at t = t0 = 23.5. This is because no information is available before the first measurement time; the assumption that the density functions
0(t) have been truncated to the left at t = t0 = 23.5. This is because no information is available before the first measurement time; the assumption that the density functions  0 can be described by a weighted sum of lognormal densities does not require that the support of
0 can be described by a weighted sum of lognormal densities does not require that the support of  0 be contained in the region t ≥ t0, so this condition must be additionally imposed (see the appendix). This gives the impression in Figures 8 and 9 that some fraction of cells will begin to divide immediately following the first measurement time. Though this may be true, it is beyond the capabilities of the current modelling framework to determine. This is because the estimated parameters are only unique up to the numbers of cells predicted to divide and die between measurement times. In other words, if {tj} is a collection of measurement times, the model provides meaningful estimates of the quantities
0 be contained in the region t ≥ t0, so this condition must be additionally imposed (see the appendix). This gives the impression in Figures 8 and 9 that some fraction of cells will begin to divide immediately following the first measurement time. Though this may be true, it is beyond the capabilities of the current modelling framework to determine. This is because the estimated parameters are only unique up to the numbers of cells predicted to divide and die between measurement times. In other words, if {tj} is a collection of measurement times, the model provides meaningful estimates of the quantities
the fraction of cells from the initial population estimated to have completed the first division between measurement times tj and tj + 1. These quantities (converted to percentages) are superimposed on the graphs of the curves F0φ0(t) in Figures 8 and 9. Thus, although the current modelling framework does not provide information regarding when cells will begin to divide it does provide meaningful information on the distribution of times to first division. Unsurprisingly, this information is constrained by the frequency at which the population is measured.
We see that CD4 T cells from Donor 1 reach their first division more rapidly and in greater quantity than CD4T cells from Donor 2. By the end of the experiment, 75.34% of the initial population of CD4 T cells from Donor 1 had divided in response to stimulus, compared to 69.50% for Donor 2. CD8 T cells from Donor 1 likewise respond more rapidly and in greater quantity than those from Donor 2. By the end of the experiment, 88.44% of the initial population of cells from Donor 1 had divided, while only 63.94% of those from Donor 2 had divided. Comparing CD4 T cells and CD8 T cells within the same donor, we observe that CD8 T cells complete their first division more quickly than CD4 T cells.
For cells having already completed at least one division, CD4 T cells from Donor 1 are estimated to divide more slowly and with greater variation across the population (E[Tidiv] = 21.2, STD[Tidiv] = 19.5) compared with those from Donor 2 (E[Tidiv] = 11.3, STD[Tidiv] = 5.7). Similar behaviour is observed for CD8T cells (E[Tidiv] = 11.2, STD[Tidiv] = 4.6 for Donor 1; E[Tdiv] = 94, STD[Tidiv] = 3.0 for Donor 2).
The analysis of cell death is complicated by several factors. While the cyton density functions φi and ψi are assumed to be identical for i ≥ 1 (that is, for all cells having divided at least once), the fraction Fi of progressing cells varies from one generation to the next according to Equation (12). The fraction of cells which are non-progressors dies according to the density function ψi, but will not divide. Thus the division destiny for the population of cells must be taken into account when interpreting cell death. Simultaneously, even among cells which would be progressors, cell death is a possibility if that cell's time-to-die (sampled according to the density ψi is less than time-to-divide (sampled according to the density φi).
Based upon the densities φi and ψi (i ≥ 1) in Figures 8 and 9 and ignoring division destiny, it would appear that cells from Donor 1 (both CD4T and CD8T) are more likely to die relative to cells taken from Donor 2. Yet when the numbers of dying cells are computed (Figure 10), we find that this hypothesis holds for CD4 T cells (cells from Donor 1 are slightly more prone to die) but completely fails for CD8T cells. When division destiny is taken into account, we see that CD4T cells from Donor 1 are estimated to have a much narrower division destiny than CD4 T cells from Donor 2. As a result, fewer cells progress to high division number (i ≥ 6), and these non-progressors begin to die. The result is that more cells are observed with high division number for Donor 2, and the expansion of the population of cells over the course of the experiment is greater for Donor 2. For CD8T cells, the estimated division destiny for Donor 2 is narrow but has a high mean. Coupled with the faster rate of division (middle-right panel, Figure 9), we see that most CD8T cells from Donor 2 proceed through large number of divisions, after which the population has reached its division destiny and the size of the population reaches a maximum before cells begin to die.
Figure 10.
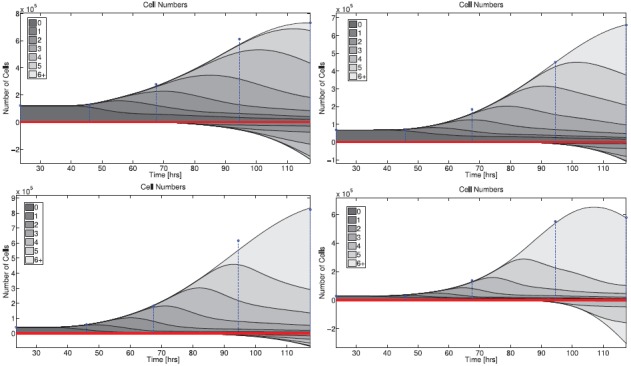
Cell numbers and population generation structure for CD4T cells (top) and CD8T cells (bottom) for Donor 1 (left) and Donor 2 (right). Shaded areas represent model generated numbers while dots represent experimental data values. Total numbers of dead cells (with generation structure) are shown inverted. Note that the numbers of dead cells are cumulative and does not reflect any decrease in numbers of dead cells which would be associated with disintegration. While it is difficult to determine the numbers of dying cells from cyton graphics alone (Figures 8 and 9), one can clearly compare the relative frequency of cell death between donors and cell types using these reconstructions of the population behaviour. For both donors and cell types, cell death is estimated to be negligible until 3–4 days after stimulation (not considering any cells which die before the first measurement is taken). After this time, most cells appear to have reached their division destinies (see Figures 8 and 9, bottom) after which time they begin to die.
Thus, in effect, division destiny imposes a limit on the degree to which a population of cells can expand in response to stimulus. For CD4T cells from Donor 1, the population appears to have reached its maximum expansion just as the experiment ends, expanding by a total factor of 6.01 (ratio of maximum population size to initial size). For CD4T cells from Donor 2, the expansion factor at the end of the experiment is 9.75 and still rising. For CD8T cells, Donor 1 expands by a factor of 20.88 (and rising) by the end of the experiment, while for Donor 2 the population expanded by a factor of 23.55 before it began to contract.
Therefore we see that the cytons φi and ψi provide meaningful information regarding the times at which cells will divide or die, but this information must be carefully interpreted with respect to division destiny. This can be accomplished by reconstructing the population generation structures for viable and dead cells (as in Figure 10). Then, one can make deductions concerning the viability of the populations of cells by analysing the numbers of cells as described above.
6. Concluding remarks
In this document, we have described and analysed a recent class of mathematical models which combines the cyton model of population generation structure with a mass-conservation model of label dynamics. Unlike previous label-structured models, the new class of models describes the processes of cellular division and death in intuitive terms which are relatable to important biological features. Significantly, because the new models can be fit directly to CFSE histogram data, it is possible to consider the statistical properties of such data. From these properties and under mild assumptions, a statistical model of the data has been derived and incorporated into a least-squares parameter estimation framework. Using this framework, various models selected from the new class of models were fit to experimental data and compared. The best-fitting model has been observed to accurately describe the behaviour of both CD4 T cells and CD8 T cells acquired from two healthy donors and stimulated to divide with PHA.
Of those models tested, the selected model (Model 12) features a bimodal distribution of times to first division and ignores cell death for undivided cells. From the distribution of times to first division, it is possible to compute the fraction of cells completing the first division between each set of measurements. Distributions for cell division and death for cells having already completed at least one division are assumed to be described by lognormal density functions. Though the best-fit mathematical model is observed to be accurate, there is some room for improvement. To this end, the modelling framework presented here is readily generalizable; any distributions of times to divide and/or die which admit density functions can be tested. Moreover, because the mathematical solution is separable (see Proposition 3.2) the cyton model of population generation structure can be replaced by any other model of cellular dynamics with a sufficiently similar form (e.g. branching process models [22,32,38,39]). It is possible that the model may be improved further by amore detailed consideration of the effects of cellular autofluorescence and the changes of the autofluorescence distribution over time.
The primary shortcoming of the statistical model is the assumption that the model is correctly specified; otherwise, the statistical model has been previously shown to correctly account for the variance in histogram data [9,47]. Thus, for a sufficiently accurate mathematical model, the statistical model of CFSE data presented here can be incorporated into a model comparison framework so that alternative mathematical descriptions of cell division can be tested in a manner that is statistically rigorous. However, the lack of inclusion of model misspecification in the statistical model suggests that to use this statistical model for computation of confidence intervals via either asymptotic theory or bootstrapping may not be appropriate. Moreover, the statistical model given by Equation (19) is
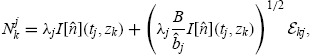 |
where ℰkj ∼  (0, 1), was derived by considering a single histogram bin at a single time. The statistical model results from repeating this derivation for each histogram bin at each measurement time. However, in this derivation, the dependence of the cell counts (and thus the probabilities) on additional factors has been completely ignored. The model values I[
(0, 1), was derived by considering a single histogram bin at a single time. The statistical model results from repeating this derivation for each histogram bin at each measurement time. However, in this derivation, the dependence of the cell counts (and thus the probabilities) on additional factors has been completely ignored. The model values I[ ](tj, zk) will depend strongly on the set of bins [zk, zk + 1) used for the histogram data. It can be readily seen that the level of noise in the data (relative to the magnitude of the data) increases as the number of bins increases. Conversely, as fewer bins are used, the data are effectively ‘smoothed out’ or averaged and some smaller features of the population data may be lost. Thus there seems to be some optimal number of bins to use to represent the histogram data. On one hand, this possibility could be assessed by trial and error on the number of histogram bins. Alternatively, the statistical model might be analysed and/or generalized to explicitly incorporate the dependence of the statistical model on the number of histogram bins, and more importantly, the dependence of parameter confidence intervals on the number of histogram bins. Finally, the statistical model makes the simplifying assumption that the numbers of cells counted into each distinct histogram bin represents an independent (from the other bins) process. But this is not true, for if Sj cells are measured at time tj, then we must have the identity ∑kMkj. Thus the random variables representing the numbers of cells Njk = B/
](tj, zk) will depend strongly on the set of bins [zk, zk + 1) used for the histogram data. It can be readily seen that the level of noise in the data (relative to the magnitude of the data) increases as the number of bins increases. Conversely, as fewer bins are used, the data are effectively ‘smoothed out’ or averaged and some smaller features of the population data may be lost. Thus there seems to be some optimal number of bins to use to represent the histogram data. On one hand, this possibility could be assessed by trial and error on the number of histogram bins. Alternatively, the statistical model might be analysed and/or generalized to explicitly incorporate the dependence of the statistical model on the number of histogram bins, and more importantly, the dependence of parameter confidence intervals on the number of histogram bins. Finally, the statistical model makes the simplifying assumption that the numbers of cells counted into each distinct histogram bin represents an independent (from the other bins) process. But this is not true, for if Sj cells are measured at time tj, then we must have the identity ∑kMkj. Thus the random variables representing the numbers of cells Njk = B/ jMjk in the total population counted into distinct bins are not independent. So, for various reasons we cannot expect to be able to compute standard errors or confidence bounds for the estimated parameters in an unbiased manner [6,7].
jMjk in the total population counted into distinct bins are not independent. So, for various reasons we cannot expect to be able to compute standard errors or confidence bounds for the estimated parameters in an unbiased manner [6,7].
The work presented here demonstrates how the current modelling framework can be used as a basis for comparison between multiple donors and/or cell types. There are two primary limitations for such comparisons. First, while a comparison among donors and/or cell types may focus on the differences in estimated moments and/or cyton density functions (such as those shown in Figures 8 and 9), the information contained within these estimated distributions is limited to the chosen modelling framework. Thus, for instance, one cannot determine the time at which cells first begin to divide only from this information. Of course, more complex models can be incorporated into the current modelling framework if knowledge of this information should prove necessary. Second, there has not been (to our knowledge) a comprehensive study of the biological and experimental variability inherent in the measurement process. In other words, it is not known how the behaviour of cells from a single donor may vary from day to day (if multiple blood samples are acquired) or from sample to sample (even if acquired at the same time).
Because the Malthusian cell proliferation and death rates of [11,12] are not necessarily compatible with a requirement of minimum cell cycle times, we have here incorporated and used the cyton models of Section 3.3. As noted above (see Equation (10)) this new formulation is compatible with time-dependent Malthusian death rates βi(t) (and in some cases with time-dependent Malthusian proliferation rates αi(t)). However, several other generalizations of the proliferation and death rate terms are immediately available.
One might consider, for example, the addition of a second structure variable (say, volume or physiological age [15]), which could be used to enforce a minimum cell cycle time by requiring that cells progress from some size V to 2V before dividing, at which point two cells of size V are produced. However, in the absence of additional observations, it is unclear what parameters (e.g. average rate of growth, or the structure variable V) could be estimated from CFSE histogram data. Video microscopy measurements by Hawkins et al. [30] indicate that average cell size may be division dependent, and this may complicate the inclusion of volume structure. Biologically, it is expected that apoptosis occurs only at particular checkpoints in the cell cycle (particularly if external ‘kill signals’ are absent), so that a generalization to volume structure (or any other surrogate for cell cycle position or physiological age [15]) may permit a more accurate description of cell death. Still, it is unclear what information might be available when considering only CFSE histogram data. It is possible that the forward scatter (FSC) of laser light might be used as some sort of observable surrogate for cell size, but additional work will be necessary to investigate this hypothesis. However, a more promising approach may involve use of recently developed fluorescence microscopy data (such as the fluorescent ubiquitination-based cell cycle indicator in [15]) to estimate probability density functions representing durations of cell cycle phases.
Ideally, cell cycle parameters (as represented in the cyton model) can be related back to more physically/experimentally meaningful parameters such as the type and strength of stimulation, which may, in turn, require the translation of certain molecular pathways within individual cells into mathematical equations/expressions. Recent work has indicated that the mechanisms responsible for cell proliferation and death may be mutually dependent upon a common molecular pathway [21,46]. As more data become available, we hope to examine how the estimated parameters change under various experimental conditions, with an eye toward additional constitutive relationships linking molecular and/or subcellular functions to population dynamics [17]. In this context, it seems necessary to consider the extent to which these functions and/or pathways are inherited. Evidence suggests that closely related cells exhibit strong correlation in times to divide and some correlation in times to die, and that this correlation tends to decrease with the number of divisions undergone [30]. Cells with a common precursor may also share a common division destiny [30], which can be altered by stimulation conditions [48]. While computed cell numbers are relatively unaffected provided correlation is limited to cells having undergone the same number of divisions [22,30,32], correlation between subsequent division of cells can alter the dynamics predicted by a mathematical model [50]. For large populations, this effect seems negligible, but may play an important role in vivo where only a small number of responding cells can trigger an immune response [50]. As noted above, branching process models have been formulated to account for various levels of correlation, and these models may be incorporated into the compartmental model framework as described above.
In spite of the limitations discussed above, the proposed mathematical and statistical framework represents a positive step toward a more comprehensive model of cellular division as measured by flow cytometry. The flexibility of the class of mathematical models combined with the probabilistic treatment of the data collection process allows for a rigorous comparison between competing descriptions of cellular behaviour. As such, this framework can help to test biological hypotheses and serve as a bridge between cellular-level events and population-level observations. This framework can also be used to study the optimal design of experiments; thus it may be possible to identify measurement times which minimize the size of the blood sample required while maximizing the information one can obtain. In the future, it will be possible to analyse cellular behaviour for donors in a variety of clinical states and thus to develop a more complete understanding of infectious disease, immunosuppressive drug actions, etc.
Acknowledgements
This research was supported in part by Grant Number NIAID R01AI071915-10 from the National Institute of Allergy and Infectious Diseases, in part by the Air Force Office of Scientific Research under grant number AFOSR FA9550-12-1-0188, in part by the National Science Foundation under Research Training Grant (RTG) DMS-0636590, and in part by grant SAF2010-21336 from the Spanish Ministry of Science and Innovation. The authors are grateful to several referees for a number of helpful comments.
Appendix 1. Comments on numerical methods and code
The computational algorithm for the model (9) is an extension (accounting for the incorporation of cyton dynamics) of the algorithm originally proposed by Allgöwer et al. [27]. Because the solution is factorable (Proposition 3.2), it is possible to compute the population generation structure (Ni(t), for i ≥ 0 and t ≥ 0) independently, and then to use this information to compute the population label structure (ñi(t), 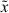 ), for i > 0, t ≥ 0, and x ≥ 0). Naively, one could compute the functions Ni(t) numerically and the functions ni(t, x) either numerically or exactly (depending on the form of the function v(t)). One then obtains the densities ni(t,x) by Proposition 3.2 and the densities ñi(t,x) by the convolution integral (5). However, this naive approach is computationally intensive as a result of the convolution. As shown in [27], there is a more efficient method. We first discuss the overall computational scheme for the construction of the population label structure, followed by a detailed algorithm for the computation of the population generation structure.
), for i > 0, t ≥ 0, and x ≥ 0). Naively, one could compute the functions Ni(t) numerically and the functions ni(t, x) either numerically or exactly (depending on the form of the function v(t)). One then obtains the densities ni(t,x) by Proposition 3.2 and the densities ñi(t,x) by the convolution integral (5). However, this naive approach is computationally intensive as a result of the convolution. As shown in [27], there is a more efficient method. We first discuss the overall computational scheme for the construction of the population label structure, followed by a detailed algorithm for the computation of the population generation structure.
A.1. Computation of population label structure
Assume one has already computed the functions Ni(t). The solutions ni(t, x) of Equation (4) can be obtained using the method of characteristics,
Now, assume (for the moment) that the initial label density in the population is lognormally distributed with parameters μ0 and σ0 so that
forx > 0. Inserting this definition into Equation (A1),
 |
where
In other words, if the initial label density is lognormally distributed, then the distribution of CFSE (that is, the distribution of fluorescence intensity resulting from CFSE) will be lognormally distributed at all times, with parameters μi(t) and σ0. Now, assume more generally that the initial condition can be written as a convex combination of lognormal density functions
This assumption is not overly restrictive and the initial condition (see the measurements collected on Day 1 in Figures 1 and 2) can be well approximated by such a series. Then by the principle of superposition, Proposition 3.2, and Equations (17) and (A2),
where μik(t) is given as above. To account for the contributions of cellular autofluorescence, we have from Equation (5)
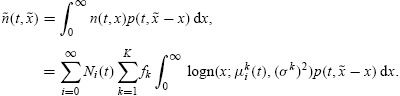 |
By assumption, p(t, ζ) is itself a lognormal density function and the integral above (for each pair of values (i, k)) is the convolution of two lognormal density functions, which can be accurately approximated by a lognormal density function having a mean and variance which is the sum of the means and variances of the two density functions in the convolution (see [27] and the references therein). In other words
where
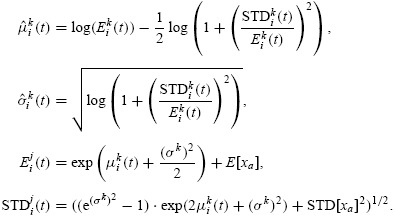 |
Thus, given the population generation structure Ni(t), the values {fk}, {μk}, and {(σk)2} which represent the initial condition Φ(x), and the parameters E[xa] and STD[xa] describing the distribution of autofluorescence, one can very quickly construct the solutions ñ(t, 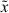 ) using Equation (A3). Significantly, this approximation to the solution does not involve any discretization in the structure variable (x or
) using Equation (A3). Significantly, this approximation to the solution does not involve any discretization in the structure variable (x or 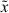 ) so that solutions can be evaluated cheaply even on a very fine mesh in the structure variable. We find, in agreement with [27], that this method of approximation increases computational speed by several orders of magnitude over other methods of solution [13].
) so that solutions can be evaluated cheaply even on a very fine mesh in the structure variable. We find, in agreement with [27], that this method of approximation increases computational speed by several orders of magnitude over other methods of solution [13].
Once the label-structured densities ñi(t,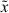 ) have been obtained, we must compute the cell counts I[
) have been obtained, we must compute the cell counts I[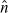 ](tj,zk;
](tj,zk; 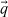 ) according to Equation (18). The values ñ(t,
) according to Equation (18). The values ñ(t, 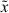 ) can be computed very cheaply and efficiently by Equation (A3) so that a large number of evaluations of ñ(t,
) can be computed very cheaply and efficiently by Equation (A3) so that a large number of evaluations of ñ(t, 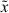 ) can be used in the approximation of the integral operator I[
) can be used in the approximation of the integral operator I[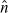 ](tj, zk;
](tj, zk; 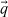 ) with no adverse effect on computational time. For the results presented in this manuscript, the values I[
) with no adverse effect on computational time. For the results presented in this manuscript, the values I[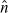 ](tj,zk;
](tj,zk; 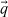 ) have been approximated using two point Gauss–Legendre quadrature on each interval [zk, zk + 1].
) have been approximated using two point Gauss–Legendre quadrature on each interval [zk, zk + 1].
A.2. Computation of population generation structure
We now discuss a computational scheme for a general cyton model, given by Equations (6)–(8). Assume φi(t) and ψi(t) are known functions of time for all i ≥ 0. Given initial and final measurement times t0 and tf, as well as a time step size h, define the number of time steps
and the time grid points
For eachj, the values 0(tj) and ψ0(tj) can be precomputed for each i ≥ 0 and stored in vectors of size (N + 1). Similarly, the values 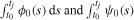 can be precomputed and stored in vectors. The integration can be efficiently carried out using two-point Gauss–Legendre quadrature on each subinterval of size h. We have generally found h = 1 to be a sufficiently small time step. The results in this document were all obtained with h = 0.25. Because precomputation is cheap, computation of the terms
can be precomputed and stored in vectors. The integration can be efficiently carried out using two-point Gauss–Legendre quadrature on each subinterval of size h. We have generally found h = 1 to be a sufficiently small time step. The results in this document were all obtained with h = 0.25. Because precomputation is cheap, computation of the terms 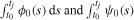 using a higher order rule (e.g. Gauss-Legendre quadrature) allows for a larger value of h than would otherwise be acceptable.
using a higher order rule (e.g. Gauss-Legendre quadrature) allows for a larger value of h than would otherwise be acceptable.
When the functions φ0(t) and ψ0(t) are parametric density functions (as is the case in this document), it is possible that a portion of the support of the functions lies in the half line t < t0. In order for the cyton model to function properly, it must be true that  for all i ≥ 0. Since one does not have any information about the behaviour of the population of cells prior to t = t0, the simplest method of resolving this problem is to truncate (on the left) the functions φ0(t) and ψ0(t) at t = t0. Thus, we can define
for all i ≥ 0. Since one does not have any information about the behaviour of the population of cells prior to t = t0, the simplest method of resolving this problem is to truncate (on the left) the functions φ0(t) and ψ0(t) at t = t0. Thus, we can define
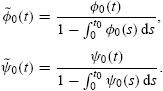 |
If one of the denominators above is zero, we define 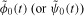 to be identically zero. We will simply refer to φ0(t) and ψ0(t) without tildes, although it should be understood that the functions have been appropriately scaled.
to be identically zero. We will simply refer to φ0(t) and ψ0(t) without tildes, although it should be understood that the functions have been appropriately scaled.
Given the precomputed vectors above, one can compute the quantities n0div(tj) and n0die (tj) according to (7) for each j. These equations can be computed for all values of j simultaneously using a single element-wise vector multiplication. From the quantities n0div (tj) and n0die (tj), one can obtain N0(tj) using the trapezoidal rule.
Next, we can define an additional vector of time values, sj = tj for all j = 1, …,(N + 1). Then the values of ϕi(tj − sk), ψi(tj − sk), 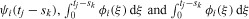 can be precomputed for i ≥ 1 and stored in an array of size (N + 1) × (N + 1). To do so efficiently, one can simply compute
can be precomputed for i ≥ 1 and stored in an array of size (N + 1) × (N + 1). To do so efficiently, one can simply compute  (and similarly for ψi) where
(and similarly for ψi) where  j = tj − t0 for each j and store these quantities in a vector; the (j, k) entry of each array is the (j − k + 1) entry of the corresponding vector, or is zero if j − k + 1 < 1. Note that in this document, φi(t) and ψi(t) are identical for all i ≥ 1, so that only 4 arrays are required to store these precomputed values.
j = tj − t0 for each j and store these quantities in a vector; the (j, k) entry of each array is the (j − k + 1) entry of the corresponding vector, or is zero if j − k + 1 < 1. Note that in this document, φi(t) and ψi(t) are identical for all i ≥ 1, so that only 4 arrays are required to store these precomputed values.
Given these precomputed vectors, one can compute (recursively on i) the values nidiv(tj) and ndie(tj) according to Equation (8) for each j. Again, these values can be computed for all values ofj simultaneously by carefully vectorizing the resulting operations. The terms ni − 1div in Equation (8) are vectors of size (N + 1), which can be replaced by an (N + 1) × (N + 1) array where each row is the vector of values ni − 1div(tj). Then Equations (8) can be computed using element-wise matrix multiplication, followed by quadrature (using the trapezoidal rule) over values of sk. From the quantities nidiv (tj) and nidie(tj), one can obtain Ni(tj) using the trapezoidal rule.
A.3. Inverse problem/parameter estimation
Given the forward solution constructed as described in the previous subsections, this information must be incorporated into a computational scheme for the optimization problem (21). This optimization is carried out using the BFGS algorithm as implemented in the Matlab routine fmincon. Computations were carried out on a Dell Optiplex 990, running an Intel Core i7-2600 (4 × 3.4 GHz) with 2 × 4BGRAM (1333 MHz). The inverse problem took an average of 6.41 min.
References
- [1].Aubin J.E. Autoflouresecence of viable cultured mammalian cells. J. Histochem. Cytochem. 1979;27:36–43. doi: 10.1177/27.1.220325. [DOI] [PubMed] [Google Scholar]
- [2].Banks H.T., Fitzpatrick B.G. Springer Lecture Notes in Biomath. Vol. 81. Berlin: Springer-Verlag; 1989. Inverse Problems for Distributed Systems: Statistical Tests and ANOVA, Proceedings of the International Symposium on Mathematical Approaches to Environmental and Ecological Problems; pp. 262–273. LCDS/CSS Report 88-16, Brown University, July 1988. [Google Scholar]
- [3].Banks H.T., Thompson W.C. A division-dependent compartmental model with cyton and intracellular label dynamics. Int. J. Pure Appl. Math. 2012;77:119–147. CRSC-TR12-12, North Carolina State University, May 2012. [Google Scholar]
- [4].Banks H.T., Thompson W.C. Mathematical models of dividing cell populations: Application to CFSE data. J. Math. Model. Nat. Phenom. 2012;7:24–52. CRSC-TR12-10, North Carolina State University, April 2012. [Google Scholar]
- [5].Banks H.T., Thompson W.C. Least squares estimation of probability measures in the Prohorov metric framework Center for Research in Scientific Computation Tech Rep, CRSC-TR12-21. North Carolina State University, Raleigh, NC, November, 2012.
- [6].Banks H.T., Tran H.T. Mathematical and Experimental Modeling of Physical and Biological Processes. Boca Raton, FL: CRC Press; 2009. [Google Scholar]
- [7].Banks H.T., Davidian M., Samuels J., Sutton K.L. Chowell G., Hyman M., Bettencourt L. M. A., Castillo-Chavez C. Chapter 11 in Mathematical and Statistical Estimation Approaches in Epidemiology. Berlin: Springer; 2009. An inverse problem statistical methodology summary; pp. 249–302. CRSC-TR08-01, North Carolina State University, January 2008. [Google Scholar]
- [8].Banks H.T., Holm K., Kappel F. Comparison of optimal design methods in inverse problems. Inv. Prob. 2011;27:075002. doi: 10.1088/0266-5611/27/7/075002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Banks H.T., Kenz Z.R., Thompson W.C. An extension of RSS-based model comparison tests for weighted least squares. Int. J. Pure Appl. Math. 2012;79:155–183. CRSC-TR12-18, North Carolina State University, August 2012. [Google Scholar]
- [10].Banks H.T., Kenz Z.R., Thompson W.C. A review of selected techniques in inverse problem nonparametric probability distribution estimation. J. Inv. Ill-posed Problems. 2012;20:429–460. Special issue on the occasion of the 80th anniversary of the birthday of M.M. Lavrentiev. [Google Scholar]
- [11].Banks H.T., Sutton K.L., Thompson W.C., Bocharov G., Doumic M., Schenkel T., Argilaguet J., Giest S., Peligero C., Meyerhans A. A new model for the estimation of cell proliferation dynamics using CFSE data. J. Immunol. Methods. 2011;373:143–160. doi: 10.1016/j.jim.2011.08.014. doi:10.1016/j.jim.2011.08.014. CRSC-TR11-05, North Carolina State University, Revised July 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Banks H.T., Sutton K.L., Thompson W.C., Bocharov G., Roose D., Schenkel T., Meyerhans A. Estimation of cell proliferation dynamics using CFSE data. Bull. Math. Biol. 2011;70:116–150. doi: 10.1007/s11538-010-9524-5. CRSC-TR09-17, North Carolina State University, August 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Banks H.T., Thompson W.C., Peligero C., Giest S., Argilaguet J., Meyerhans A. A division-dependent compartmental model for computing cell numbers in CFSE-based lymphocyte proliferation assays. Math. Biosci. Eng. 2012;9:699–736. doi: 10.3934/mbe.2012.9.699. CRSC-TR12-03, North Carolina State University, January 2012. [DOI] [PubMed] [Google Scholar]
- [14].Bell G., Anderson E. Cell growth and division I. A mathematical model with applications to cell volume distributions in mammalian suspension cultures. Biophys. J. 1967;7:329–351. doi: 10.1016/S0006-3495(67)86592-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Billy F., Clairambault J., Delaunay F., Feillet C., Robert N. Age-structured cell population model to study the influence of growth factors on cell cycle dynamics. Math. Biosci. Eng. 2013;10:1–17. doi: 10.3934/mbe.2013.10.1. [DOI] [PubMed] [Google Scholar]
- [16].Burnham K.P., Anderson D.R. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. 2nd ed. New York: Springer; 2002. [Google Scholar]
- [17].Burroughs N.J., van der Merwe P.A. Stochasticity and spatial heterogeneity in T-cell activation. Immunol. Rev. 2007;216:69–80. doi: 10.1111/j.1600-065X.2006.00486.x. [DOI] [PubMed] [Google Scholar]
- [18].Choi A., Huffman T., Nardini J., Poag L., Thompson W.C., Banks H.T. Quantifying CFSE label decay in flow cytometry data. Appl. Math. Lett. 2013;26:571–577. doi: 10.1016/j.aml.2012.12.010. doi:10.1016/j.aml.2012.12.010. CRSC-TR12-20, North Carolina State University, December 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Davidian M., Giltinan D.M. Nonlinear Models for Repeated Measurement Data. London: Chapman & Hall; 2000. [Google Scholar]
- [20].DeBoer R.J., Ganusov V.V., Milutinovic D., Hodgkin P.D., Perelson A.S. Estimating lymphocyte division and death rates from CFSE data. Bull. Math. Biol. 2006;68:1011–1031. doi: 10.1007/s11538-006-9094-8. [DOI] [PubMed] [Google Scholar]
- [21].Dowling M.R., Milutinovic D., Hodgkin P.D. Modelling cell lifespan and proliferation: Is likelihood to die or to divide independent of age? J. R. Soc. Interface. 2005;2:517–526. doi: 10.1098/rsif.2005.0069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Duffy K., Subramanian V. On the impact of correlation between collaterally consanguineous cells on lymphocyte population dynamics. J. Math. Biol. 2009;59:255–285. doi: 10.1007/s00285-008-0231-x. [DOI] [PubMed] [Google Scholar]
- [23].Feller W. An Introduction to Probability Theory and its Applications. I. New York: Wiley; 1971. [Google Scholar]
- [24].Gallant A.R. Nonlinear Statistical Models. New York: Wiley; 1987. [Google Scholar]
- [25].Gett A.V., Hodgkin P.D. A cellular calculus for signal integration by T cells. Nat. Immunol. 2000;1:239–244. doi: 10.1038/79782. [DOI] [PubMed] [Google Scholar]
- [26].Goh S., Kwon H.W., Choi M.Y., Fortin J.Y. Emergence of skew distributions in controlled growth processes. Phys. Rev. E. 2010;82:061, 115. doi: 10.1103/PhysRevE.82.061115. [DOI] [PubMed] [Google Scholar]
- [27].Hasenauer J., Schittler D., Allgöwer F. Analysis and simulation of division- and label-structured population models: a new tool to analyze proliferation assays. Bull. Math. Biol. 2012;74:2692–2732. doi: 10.1007/s11538-012-9774-5. [DOI] [PubMed] [Google Scholar]
- [28].Hawkins E.D., Hommel M., Turner M.L., Battye F., Markham J., Hodgkin P.D. Measuring lymphocyte proliferation, survival and differentiation using CFSE time-series data. Nat. Protoc. 2007;2:2057–2067. doi: 10.1038/nprot.2007.297. [DOI] [PubMed] [Google Scholar]
- [29].Hawkins E.D., Turner M.L., Dowling M.R., van Gend C., Hodgkin P.D. A model of immune regulation as a consequence of randomized lymphocyte division and death times. Proc. Natl. Acad. Sci. 2007;104:5032–5037. doi: 10.1073/pnas.0700026104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Hawkins E.D., Markham J.F., McGuinness L.P., Hodgkin P.D. A single-cell pedigree analysis of alternative stochastic lymphocyte fates. Proc. Natl. Acad. Sci. 2009;106:13457–13462. doi: 10.1073/pnas.0905629106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Hyrien O., Zand M.S. A mixture model with dependent observations for the analysis of CFSE-labeling experiments. J. Amer. Statist. Assoc. 2008;103:222–239. [Google Scholar]
- [32].Hyrien O., Chen R., Zand M.S. An age-dependent branching process model for the analysis of CFSE-labeling experiments. Biol. Direct. 2010;5 doi: 10.1186/1745-6150-5-41. Published Online. doi:10.1186/1745-6150-5-41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Lahiri S.N., Chatterjee A., Maiti T. Normal approximation to the hypergeometric distribution in nonstandard cases and a sub-Gaussian Berry-Esseen theorem. J. Statist. Plann. Inference. 2007;137:3570–3590. [Google Scholar]
- [34].Luzyanina T., Roose D., Bocharov G. Distributed parameter identification for a label-structured cell population dynamics model using CFSE histogram time-series data. J. Math. Biol. 2009;59:581–603. doi: 10.1007/s00285-008-0244-5. [DOI] [PubMed] [Google Scholar]
- [35].Luzyanina T., Roose D., Schenkel T., Sester M., Ehl S., Meyerhans A., Bocharov G. Numerical modelling of label-structured cell population growth using CFSE distribution data. Theor. Biol. Medical Model. 2007;4 doi: 10.1186/1742-4682-4-26. published online. doi:10.1186/1742-4682-4-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Lyons A.B., Parish C.R. Determination of lymphocyte division by flow cytometry. J. Immunol. Methods. 1994;171:131–137. doi: 10.1016/0022-1759(94)90236-4. [DOI] [PubMed] [Google Scholar]
- [37].Lyons A.B., Hasbold J., Hodgkin P.D. Flow cytometric analysis of cell division history using diluation of carboxyfluorescein diacetate succinimidyl ester. a stably integrated fluorescent probe, Methods Cell Biol. 2001;63:375–398. doi: 10.1016/s0091-679x(01)63021-8. [DOI] [PubMed] [Google Scholar]
- [38].Miao H., Jin X., Perelson A., Wu H. Evaluation of multitype mathemathematical models for CFSE-labeling experimental data. Bull. Math. Biol. 2012;74:300–326. doi: 10.1007/s11538-011-9668-y. doi:10.1007/s11538-011-9668-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Nordon R.E., Ko K.-H., Odell R., Schroeder T. Multi-type branching models to describe cell differentiation programs. J. Theor. Biol. 2011;277:7–18. doi: 10.1016/j.jtbi.2011.02.006. [DOI] [PubMed] [Google Scholar]
- [40].Quah B.J.C., Parish C.R. New and improved methods for measuring lymphocyte proliferation in vitro and in vivo using CFSE-like fluorescent dyes. J. Immunol. Methods. 2012;379:1–14. doi: 10.1016/j.jim.2012.02.012. [DOI] [PubMed] [Google Scholar]
- [41].Quah B., Warren H., Parish C. Monitoring lymphocyte proliferation in vitro and in vivo with the intracellular fluorescent dye carboxyfluorescein diacetate succinimidyl ester. Nat. Protoc. 2007;2:2049–2056. doi: 10.1038/nprot.2007.296. [DOI] [PubMed] [Google Scholar]
- [42].Schittler D., Hasenauer J., Allgöwer F. A generalized modelfor cell proliferation: Integrating division numbers and label dynamics. pp. 165–168. Proceedings of the Eighth International Workshop on Computational Systems Biology (WCSB 2011), Zurich, Switzerland, June 2011.
- [43].Seber G.A.F., Lee A.J. Linear Regression Analysis. Hoboken, NJ: Wiley; 2003. [Google Scholar]
- [44].Seber G.A., Wild C.J. Nonlinear Regression. Hoboken, NJ: Wiley; 2003. [Google Scholar]
- [45].Subramanian V.G., Duffy K.R., Turner M.L., Hodgkin PD. Determining the expected variability of immune responses using the cyton model. J. Math. Biol. 2008;56:861–892. doi: 10.1007/s00285-007-0142-2. [DOI] [PubMed] [Google Scholar]
- [46].Terrano D.T., Upreti M., Chambers T.C. Cyclin-dependent kinase 1-mediated Bcl-xL/Bcl-2 phosphorylation acts as a functional link coupling mitotic arrest and apoptosis. Mol. Cell. Biol. 2010;30:640–656. doi: 10.1128/MCB.00882-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Thompson W.C. Partial differential equation modeling of flow Cytometry data from CFSE-based proliferation assays. Ph.D. Dissertation, Dept. of Mathematics, North Carolina State University, Raleigh, December, 2011.
- [48].Turner M.L., Hawkins E.D., Hodgkin PD. Quantitative regulation of B cell division destiny by signal strength. J. Immunol. 2008;181:374–382. doi: 10.4049/jimmunol.181.1.374. [DOI] [PubMed] [Google Scholar]
- [49].Wallace P.K., Tario J.D., Jr., Fisher J.L., Wallace S.S., Ernstoff M.S., Muirhead K.A. Tracking antigen-driven responses by flow cytometry: monitoring proliferation by dye dilution. Cytom. A. 2008;73:1019–1034. doi: 10.1002/cyto.a.20619. [DOI] [PubMed] [Google Scholar]
- [50].Wellard C., Markham J., Hawkins E.D., Hodgkin PD. The effect of correlations on the population dynamics of lymphocytes. J. Theor. Biol. 2010;264:443–449. doi: 10.1016/j.jtbi.2010.02.019. [DOI] [PubMed] [Google Scholar]
- [51].Witkowski J.M. Advanced application of CFSE for cellular tracking. Curr. Protoc. Cytom. 2008;44:9.25.1–9.25.8. doi: 10.1002/0471142956.cy0925s44. [DOI] [PubMed] [Google Scholar]



