Combining hidden Markov models for comparing the dynamics of multiple sleep electroencephalograms

Abstract

In this manuscript we consider methods for the analysis of populations of electroencephalogram (EEG) signals during sleep for the study of sleep disorders using hidden Markov models (HMMs). Notably, we propose an easily implemented method for simultaneously modeling multiple time series that involve large amounts of data. We apply these methods to study sleep disordered breathing (SDB) in the Sleep Heart Health Study (SHHS), a landmark study of SDB and cardiovascular consequences. We use the entire, longitudinally collected, SHHS cohort to develop HMM population parameters, which we then apply to obtain subject-specific Markovian predictions. From these predictions we create several indices of interest, such as transition frequencies between latent states. Our HMM analysis of EEG signals uncovers interesting findings regarding differences in brain activity during sleep between those with and without SDB. These findings include stability of the percent time spent in HMM latent states across matched diseased and non-diseased groups and differences in the rate of transitioning.

1 Introduction

In this manuscript we introduce extensions of hidden Markov models (HMMs) for the analysis of the Fourier power spectrum of the electroencephalogram (EEG) during sleep. The two key accomplishments of the manuscript are as follows: first, we introduce a method of combining (Dirichlet) HMMs that is specifically designed for populations of time series and second, we give a detailed HMM analysis of electroencephalogram data recorded during a full montage sleep study conducted in the home setting. In this analysis, we compare parameters from the population-level model between a well matched subset of subjects with and without sleep disordered breathing (SDB). Thus, we develop a method for the application of HMMs in complex epidemiological studies, as well as illustrate the methods on a unique data set created to study an important public health issue.

The application under study involves SDB and its potential correlation with cortical activity. Human sleep and its physiological and health correlates comprise extremely complex biological phenomena. Rather than being simply inert, sleep is a highly dynamic process. In children, sleep has been shown to be instrumental in physical and cognitive development. Sleep is also crucial for memory consolidation and immune system repair. Research in sleep continues to unravel the crucial role that sleep plays in health and well being [1]. SDB is a chronic condition whereby subjects have repeated either complete (apneas) or partial (hypopneas) collapses of the upper airway during sleep. SDB has been shown to have a number of health consequences such as: daytime sleepiness, increased risk for motor vehicle accidents, incident hypertension, cardiovascular disease, stroke, and mortality [2].

Electrophysiological measures are an objective means to characterize cortical electrical activity in the brain during sleep. The electroencephalogram, along with a battery of other biological signals, is collected as part of the overnight polysomnogram (PSG). In clinical and research settings, the PSG is used to characterize sleep quality and assess the presence of various disorders, such as SDB. The suite of biological signals of the PSG are also used in concert by physicians for visual classification into sleep state hypnogram data, which constitute a single, discrete-time, discrete-state process. We focus entirely on the EEG signal, and consider the Fourier transform of the raw signal in thirty second bins. We further summarize the Fourier transform by considering the power in bands of the spectrum, thus simultaneously focusing on the core components of the signal of interest and greatly alleviating computational concerns. Such bands have been established as key components of the EEG signal and are important for understanding the overnight dynamics of sleep brain activity and any possible alternation due to disease or behavior. Some example analyses investigating correlates of sleep-EEG spectrum include: Crainiceanu et al. [3], Di et al. [4] and Zhang et al. [5].

After preprocessing the EEG signal we employ HMMs on the spectral band powers. HMMs comprise two components: an unobserved (hidden) Markov chain and an observed state–dependent process. Each realization of the latter is assumed to be generated by one of N distributions as determined by the state of an N-state Markov chain. The realizations are assumed to be conditionally independent, given the states. For comprehensive accounts of the theory of HMMs see Cappé et al. [6] and Zucchini and MacDonald [7]. The application of hidden Markov models to EEG spectrum data is natural, since sleep in humans and many other species is often characterized by sleep states. In humans, sleep is visually classified into light sleep (Stage I and II), deep sleep (slow wave sleep) and rapid eye movement (REM) sleep. Such sleep stage hypnogram data have been well studied in the clinical/medical and statistical literature [8–20]. The present investigation does not focus on visually classified sleep stage data, other than as partial motivation for using latent states via HMMs to study sleep EEG behavior. Hence, our use of the term “state” always refers to latent nominal classifications estimated via HMMs, not realizations of sleep stages, as it is used in the medical literature. Further motivation for HMMs in this setting is given by the fact that EEG spectrum data show high autocorrelation, which HMMs elegantly address. As argued by Zhong and Ghosh [21], the raw EEG signal can be well modeled by HMMs. The general benefits of using HMMs in the context of EEG classification have also been discussed by Penny and Roberts [22]. In the context of sleep staging, such an approach has been taken previously in Flexer et al. [23], but with different objectives than those of the current investigation. Those authors attempt to reproduce the visually scored hypnogram via automated scoring, which is distinct from the goals of the current manuscript.

Our model represents an alternative way for summarizing the dynamics of sleep, in particular for populations of EEG time series. There are, in principle, several different ways to extend HMMs to the case of longitudinal data; the most popular such approaches can be viewed as particular cases of so-called mixed HMMs as defined by Altman [24]. Mixed HMMs can incorporate subject-specific covariates and/or random effects. These models aim at capturing heterogeneity across subjects. MacDonald and Zucchini [25], Wang and Puterman [26] and Bartolucci et al. [27] incorporated subject-specific covariates in their models. While the use of subject-specific covariates provides an elegant and easily implementable approach for dealing with heterogeneous subjects, it requires that suitable covariates are available. HMMs incorporating random effects were considered for example by Seltman [28], Zucchini et al. [29] and Schliehe-Diecks et al. [30]. HMMs that involve random effects are particularly attractive due to their flexibility and parsimony in terms of parameters. In addition, they are relatively easy to interpret in many applications. However, their implementation is very demanding in terms of computational effort; in the case of R random effects, the likelihood function is given by an R-fold integral which, in general, cannot be evaluated directly. Our application comprises large amounts of data and numbers of model parameters, and there is no obvious means of how to employ subject-specific covariates; mixed HMMs thus do not seem suitable for our problem. Thus, we propose a different modeling strategy using a combination of population and subject-specific parameters. This approach is relatively easy to implement and interpret while being very flexible. No primacy claims are made with regard to inventing a new class of models – instead we consider a combination of subject-specific HMMs and impose some constraints on the parameters across subjects. This improves interpretability while making inferential approaches computationally feasible.

2 Description of the data set

The Sleep Heart Health Study (SHHS) is a landmark study of sleep, sleep disorders and their cardiovascular correlates [31]. In this study, over six thousand subjects underwent in-home polysomnography with measurements of the EEG during sleep. Approximately four thousand subjects had a repeat polysomnogram four years after the baseline sleep study. In this analysis, we restrict ourselves to 102 carefully matched subjects with and without SDB.

Matching is appealing, as the data are observational and epidemiologic confounding of the disease effect is of concern. The number of subjects in the SHHS dataset motivating this manuscript allow for well populated, well selected sub-groups for the desired comparisons. To assess the independent effects of SDB on sleep structure, strict exclusion criteria were employed and included prevalent cardiovascular disease, hypertension, chronic obstructive pulmonary disease, asthma, coronary heart disease, history of stroke, and current smoking. For the purpose of this analysis, we will examine subjects with moderate to severe SDB as assessed by a respiratory disturbance index (RDI) of at least 30 events/hour. Subjects without SDB, were identified as those with an RDI < 5 events/hour. Propensity score matching was utilized to balance the SDB and non-SDB groups on demographic factors and to minimize confounding [32]. Subjects with SDB were matched with those without SDB on the factors of age, BMI, race, and sex. Race and sex were exactly matched, while age and BMI were matched using the nearest neighbor Mahalanobis technique, so that matches had to be within a Mahalanobis distance (caliper) of 0.10, with multiple matches within the caliper being settled by random selection [33].

The resultant match was 51 pairs (M = 102 individuals) that met the strict inclusion criteria outlined above and exhibiting very low standardized biases, a vast improvement on the imbalance of BMI between diseased and non-diseased groups from previous work on the same data [20]. Selecting two groups that are polar opposites of each other in SDB severity and both isolated from comorbidities increases the appropriateness of attributing results to the independent effects of SDB on sleep continuity. The composition of the matched groups is displayed in Table 1.

Table 1.

Demographic covariates and sleep variables, means of the two groups. All measures are not significantly different (RDI is different by design).

Variable	SDB	no-SDB	p-value
RDI (events/hour)	40.532	2.114	0.000
BMI (kg/m2)	30.275	30.247	0.972
Age (years)	61.804	61.804	1.000
Race (% white)	92.160	92.160	1.000
Sex (% male)	66.667	66.667	1.000
Total Sleep Time (min.)	351.397	357.466	0.593
% Total Sleep Time asleep	81.941	83.364	0.743

The sleep EEG was processed in Matlab (Mathworks) as follows. Separately for each of two nodes per subject, the signal was separated into non-overlapping 30 second bins. The fast Fourier transform was applied to each bin. Band pass filters were applied to separate the signal into four bands: δ (up to 4 Hz), θ (4 – 7 Hz), α (8 – 12 Hz) and β (12 – 30 Hz). The Fourier coefficients were squared and summed to obtain the spectral power within each band. For each 30 second bin the raw powers were then normalized by dividing individual band power by the sum of power over the δ, θ, α and β bands, resulting in proportions of the total power represented by each band. Therefore, the processed observations are points on the unit 4-simplex for each 30 second epoch, as the normalized power in each band is a positive number between 0 and 1 and the sum of the normalized power in the four bands is equal to 1. The distance between the two EEG leads was 2 cm on the scalp, and given the high correlation between the two nodes, we decided to analyze only one of the two resulting series. Normalizing the spectrum was performed for a variety of reasons, including alleviating inter-subject variability. Further descriptions of EEG processing for this data set can be found in Crainiceanu et al. [3]. A repeat polysomnogram was made for 60 out of the 102 individuals, such that for the others only observations from one night are available. For individual m (m= 1,…,M), we denote the number of observations available in night i (i =1,2) by T_m,i. The average total number of observations available per individual is 1711 (the minimum number is 798, the maximum number is 2526).

3 Model description and estimation method

3.1 Introducing the combination of HMMs

For each time instant t, the vector of observations is an element of the unit 4-simplex

$${\mathrm{\Delta }}_4=\{(x_1,x_2,x_3,x_4)|x_i\ge 0,\sum _i{x}_i=1\}\subset {ℝ}^4.$$

Here x₁, x₂, x₃ and x₄ represent the proportions of the δ−, θ−, α− and β−waves, respectively, as obtained from the fast Fourier transforms of the EEG data. The Dirichlet distribution $𝒟(\mathrm{\lambda }),\mathrm{\lambda }=({\mathrm{\lambda }}_1,{\mathrm{\lambda }}_2,{\mathrm{\lambda }}_3,{\mathrm{\lambda }}_4)\in {ℝ}_{+}^4,$ with density

$$f_{\mathrm{\lambda }}(\mathbf{x})=f_{\mathrm{\lambda }}(x_1,x_2,x_3,x_4)=\frac{\mathrm{\Gamma }({\sum }_{i=1}^4{\mathrm{\lambda }}_i)}{{\prod }_{i=1}^4\mathrm{\Gamma }({\mathrm{\lambda }}_i)}{x}_1^{{\mathrm{\lambda }}_{1^{-1}}}{x}_2^{{\mathrm{\lambda }}_{2^{-1}}}{x}_3^{{\mathrm{\lambda }}_{3^{-1}}}{x}_4^{{\mathrm{\lambda }}_{4^{-1}}},$$

is a convenient and flexible model to describe random samples from Δ₄. In particular, D(λ) is a member of the exponential family, has finite dimensional sufficient statistics and is often used as a prior to the multinomial distribution [34]. Expectation and standard deviations of the marginal distributions of 𝒟(λ) are ${\mu }_i=𝔼(x_i)=\frac{{\mathrm{\lambda }}_i}{s}$ and ${\sigma }_i^2=\text{Var}(x_i)=\frac{{\mu }_i(1-{\mu }_i)}{s+1},$ where s≔λ₁+λ₂+λ₃+λ₄. Thus, a Dirichlet distribution with a fixed mean µ = (µ₁,µ₂,µ₃,µ₄) can account for different levels of variability using a parameterization of the type D (c · λ) and varying the positive scalar c. The parameter s – sometimes called concentration parameter – is a measure of how concentrated the distribution D(λ) is around its mean; the larger s, the less dispersed on Δ₄ are the observed values.

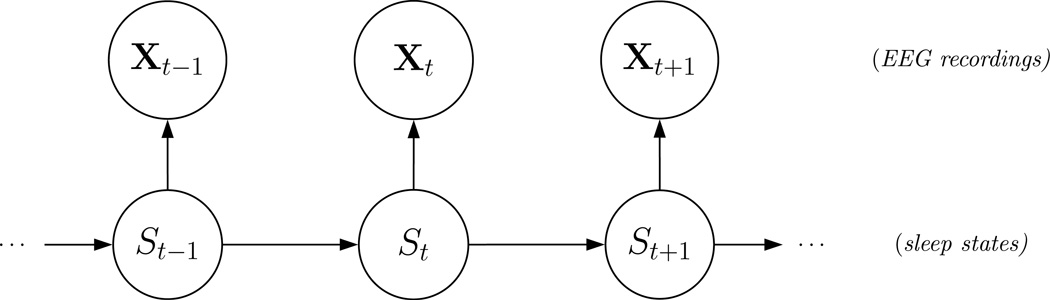
To model the EEG spectral data using Dirichlet distributions, consider a hidden Markov model with N-state (hidden) homogeneous Markov chain {S_t}_t=1,2,… and (observed) state-dependent process {X_t}_t=1,2,…. The dependence structure of the model (for a single individual) is displayed in Figure 1 in a directed acyclic graph. A question of interest concerns the choice of the number of states N. We discuss this in detail in Section 4.3.3.

Figure 1.

Dependence structure of an HMM for a single individual.

The Markov chain is assumed to be of first order, i.e.

$$\mathbb{P}(S_t=S_t|S_{t-1}=s_{t-1},S_{t-2}=s_{t-2},\dots )=\mathbb{P}(S_t=S_t|S_{t-1}=s_{t-1}).$$

Moreover, given the current state, the distribution of X_t is assumed to be conditionally independent of previous observations and states, i.e.

$$\mathbb{P}({\mathbf{X}}_t={\mathbf{x}}_t|{\mathbf{X}}_{t-1}={\mathbf{x}}_{t-1},{\mathbf{X}}_{t-2}={\mathbf{x}}_{t-2},\dots ,S_t=s_t,S_{t-1}=s_{t-1},\dots ,)=\mathbb{P}({\mathbf{X}}_t={\mathbf{x}}_t|S_t=s_t).$$

We summarize the probabilities of state switches in the (N × N)–transition probability matrix (tp.m.) given by B = (b_ij) (for i,j = 1,…,N) where b_ij = ℙ(S_t = j | S_t−1 = i).

For the given time series of spectral band power proportions, we propose to use $\{𝒟(\mathrm{\lambda })|\mathrm{\lambda }\in {ℝ}_{+}^4\}$ as approximating family of distributions for the state-dependent process {X_t}_t=1,2,…. We then have N different Dirichlet distributions D (λ⁽ⁿ⁾), n = 1,…,N – one for each state of the Markov chain – and the current state of the Markov chain (the ‘sleep state’) determines which of these distributions is selected:

$${\mathbf{X}}_t|S_t=n~𝒟({\mathrm{\lambda }}^{(\mathrm{n})}).$$

If the underlying Markov chain is stationary, then the marginal distribution of the HMM at each time t is given by

$$\mathbb{P}({\mathbf{X}}_t=\mathbf{x})=\sum _{n=1}^N{\pi }_n{f}_{{\mathrm{\lambda }}^{(n)}}(\mathbf{x}),$$

where π = ℙ(S_t = 1,…S_t = N) is the stationary distribution of {S_t}. This shows that the observable part of the HMM, {X_t}, is a finite mixture. It is a dependent mixture due to the influence of the Markov chain.

We want to employ HMMs to analyze and quantify the stochastic properties of the trajectory of the EEG spectral data during sleep with regard to underlying latent, or hidden, state processes. Furthermore, we want to compare these properties between groups of subjects with and without SDB. Fitting a separate HMM to each individual would substantially limit our ability to compare results across subjects or groups of subjects, because the Dirichlet distribution parameters and thus the EEG states would have different interpretations (which would make the individual-specific models essentially incommensurable). Thus, our methods differ substantially from standard HMM methods, where the interest centers on estimating and quantifying the underlying HMM in an individual time series. Here, we are concerned with populations of time series. As pointed out in the introduction, HMMs incorporating random effects are computationally too demanding to apply them to a data set as complex as ours. Instead, we consider the following combination of HMMs, where we assume that the Dirichlet parameters are variable across states but fixed across subjects and that the transition probabilities across states are subject-specific. The common Dirichlet parameters serve an analogous purpose as the common criteria of the polysomnography signals in manual determination of sleep states.

Fixing the state-dependent parameters across individuals enables us to compare different individuals in terms of the different Markov chains resulting from the HMM fits. Conditional on a particular state n, the distribution of {X_t}_{t =1,2,…} for different individuals is identical, what differs is the stochastic structure of the succession of states. Questions of interest regarding the state sequence of an individual include: i) how much time on average is spent in a particular latent state? ii) what is the expected total number of state changes per hour? iii) what is the expected number of transitions between particular states? At the population level, these questions investigate variations around population norms and differences between sub-populations (diseased and nondiseased groups). We will return to these questions in the course of the evaluation of the results in Section 4.

3.2 Parameter estimation for the proposed combination of HMMs

Fitting the combination of HMMs using numerical maximization of the joint likelihood is infea-sible. For the 102 subjects selected from the SHHS, the number of parameters under stationarity would be N · (N – 1) · 102 + 4 · N (where the first term corresponds to the Markov chain parameters and the second term to the Dirichlet distribution parameters); 1,240 for a basic model with N = 4 states. An additional difficulty is the large size of the data set, which contains roughly 170,000 observations. We also anticipate that the size and complexity of data sets with similar structure will increase dramatically in the future. The amount of data, but most of all the high dimensionality of the parameter space – with the associated danger of not finding the global maximum of the likelihood – seriously hinder standard HMM fitting approaches, both direct numerical likelihood maximization and the expectation-maximization algorithm (but see the discussion of an EM approach in the conclusions).

To circumvent these problems we consider the following pragmatic two-stage approach to model fitting. In Stage I we calibrate the Dirichlet parameters which will be fixed in Stage II to fit HMMs to all individuals. This strategy partitions the infeasible maximization problem into several relatively simple maximization problems, each of them involving a small number of parameters. The calibration of the Dirichlet parameters in Stage I is carried out by fitting an independent mixture of N Dirichlet distributions to the observations from all individuals (5·N – 1 parameters). By first considering independent rather than dependent mixtures (i.e. HMMs), the complexity of the problem is reduced substantially. This approach is likely to yield estimators similar to those that would be obtained from the HMM fit considering all parameters simultaneously (for more details see Sections 4.1 and 4.2). In Stage II the Dirichlet parameters are fixed and only the Markov chain parameters, i.e. the entries of the t.p.m. B, are estimated for each individual (N . (N – 1) parameters for each individual). This makes the entire approach computationally feasible.

In Stage I the likelihood to be maximized is a product of probability density functions of a mixture distribution:

$$ℒ({\mathrm{\lambda }}^1,\dots ,{\mathrm{\lambda }}^{(N)},{\mathrm{\gamma }}_1,\dots {\mathrm{\gamma }}_N)=\prod _{m=1}^M\prod _{i=1}^2\prod _{t=1}^{T_{m,i}}\sum _{n=1}^N{\mathrm{\gamma }}_n{f}_{{\mathrm{\lambda }}^{(n)}}({\mathbf{X}}_t^{(m,i)}),$$ (1)

where ${\mathbf{x}}_t^{(m,i)}$ denotes the vector of observed proportions of δ-, θ-, α- and β-waves for individual m at time t in night i, and γ_ndenotes the weights of the Dirichlet distribution associated with state n. The observations originate from a set of individuals (see 4.3.1 for more details), and for each individual from two separate overnight recordings of the EEG. Clearly the ordering of observations does not play any role in the likelihood computation. The likelihood given by (1) is maximized over the mixture component weights γ_i (With the constraint γ₁+…+γ_N = 1) and the Dirichlet parameter vectors ${\mathrm{\lambda }}^{(n)}\in {ℝ}_{\ge 0}^4,n=1,\dots ,N.$

In Stage II the likelihood to be maximized for individual m is

$$ℒ({\mathbf{B}}^{(m)})={\pi }^{(m)}\mathbf{P}({\mathbf{x}}_1^{(m,1)}){\mathbf{B}}^{(m)}\mathbf{P}({\mathbf{x}}_2^{(m,1)}){\mathbf{B}}^{(m)}{·}_{\dots }·{\mathbf{B}}^{(m)}\mathbf{P}({\mathbf{x}}_{T_{m,1}}^{(m,1)}){\mathbf{1}}^t·{\pi }^{(m)}\mathbf{P}({\mathbf{x}}_1^{(m,2)}){\mathbf{B}}^{(m)}\mathbf{P}({\mathbf{x}}_2^{(m,2)}){\mathbf{B}}^{(m)}{·}_{\dots }·{\mathbf{B}}^{(m)}\mathbf{P}({\mathbf{x}}_{T_{m,2}}^{(m,2)}){\mathbf{1}}^t,$$ (2)

where

$$\mathbf{P}({\mathbf{x}}_t^{(m,i)})≔\text{diag}(f_{{\mathrm{\lambda }}^{(1)}}({\mathbf{x}}_t^{(m,i)}),\dots ,f_{{\mathrm{\lambda }}^{(N)}}({\mathbf{x}}_t^{(m,i)})),$$

${\mathbf{B}}^{(m)}=(b_{ij}^{(m)}),i,j=1,\dots ,N,$ denotes the t.p.m. of the Markov chain for individual m, and 1 is a row vector of ones. The vector of probabilities π^(m) = (π₁^(m),…, π_N^(m)) is the solution to the linear system π^(m)B^(m) = π^(m) subject to ${\sum }_i{\pi }_i^{(m)}=1$, i.e. the stationary distribution of the fitted Markov chain, associated with individual m. The likelihood given by (2) is maximized only over the parameters of the underlying hidden Markov chain of the model; the parameters at the observation level, i.e. the Dirichlet parameters λ⁽ⁿ⁾, are fixed at the values obtained in Stage I.

Likelihood maximization in Stage I and II cannot be carried out analytically and a numerical maximization algorithm was used instead. Note that the estimators for the Dirichlet parameters are not the MLEs for the combination of HMMs. However, the estimates can be very informative (see the results of the model fitting in Sections 4.1 and 4.2). Model fitting was carried out using R. Both likelihood expressions, (1) and (2), are easy to compute and the parameters can be estimated using numerical maximization. The risk of finding a local rather than the global maximum was addressed by trying several different randomly chosen initial starting points (50 in Stage I, and four in Stage II for each individual). Maxima were not accepted before being identified by different sets of initial values. We applied the unconstrained minimization algorithm nlm(), which required transformation from a constrained to an unconstrained maximization. Techniques to deal with this problem are standard. For instance, in the combination of HMMs the Dirichlet parameters ${\mathrm{\lambda }}_k^{(n)}$ have to be positive, but the parameters ${\eta }_k^{(n)}=\text{log}{\mathrm{\lambda }}_k^{(n)}$ are unconstrained. We thus reparametrize the model in terms of unconstrained “working parameters” and then maximize the likelihood with respect to those parameters. Approximate confidence intervals for the “natural parameters”, e.g.${\mathrm{\lambda }}_k^{(n)}$, can be obtained by first estimating confidence intervals or the working parameters from the inverse of the estimated information matrix, and then applying the inverse transformations, back to the natural parameter space, to the interval boundaries for the working parameters. In the two-stage approach confidence intervals for the Dirichlet parameters are obtained in Stage I, while those for the Markov chain parameters are obtained in Stage II. If the true model is indeed a combination of HMMs, than the model fitted in Stage I of the two-stage method is incorrect, such that in particular the validity of resulting confidence intervals for Dirichlet parameters needs to be checked (e.g., using simulation experiments).

4 Fitting the combination of HMMs to sleep EEG data

We now fit the combination of HMMs to simulated data and to the sleep EEG data acquired at the SHHS. We begin by looking at a simple four-subject example which is supposed to illustrate the (SHHS) data and to compare the proposed estimation method to the conventional maximum likelihood approach (Section 4.1). Section 4.2 provides more insights into the performance of the proposed estimation method by applying it in a simulation study. Subsequently, Section 4.3 discusses the model fitting results for the whole set of matched pairs as described in Section 2 (i.e. 102 subjects).

4.1 An illustrative and method-comparative example

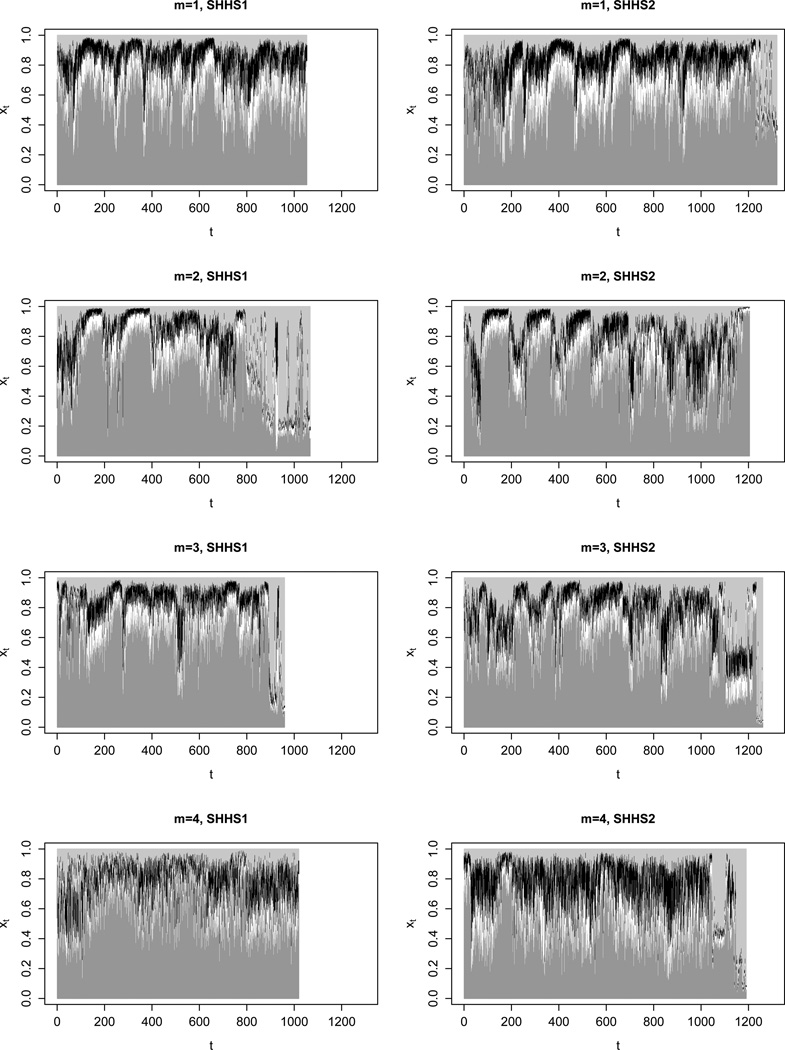
Figure 2 displays the EEG spectral power proportions of the δ-, θ-, α- and β-bands that were observed in the SHHS for four subjects (two with SDB and two without SDB, and in each case for two nights). Each time t refers to a 30-second interval.

Figure 2.

Observations of four subjects acquired at SHHS1 (initial polysomnogram) and SHHS2 (repeat polysomnogram, four years later); dark gray segments: δ-band spectral power prop., white segments: θ-band spectral power prop., black segments: α-band spectral power prop., light gray segments: β-band spectral power prop..

The combination of HMMs was fit to these data in two different ways, 1) by maximizing the joint likelihood and 2) by using the two-stage approach as described in Section 3.2. Table 2 compares: i) the computational time needed to perform the model fits; ii) the estimated Dirichlet parameters λ⁽ⁿ⁾ and the associated 95% confidence intervals (with n denoting the associated state of the Markov chain); iii) the associated expected spectral band power proportions µ⁽ⁿ⁾; and iv) the stationary Markov chain distributions for the four subjects, i.e. π^(m), m = 1,2,3,4 (where m refers to the subjects).

Table 2.

Four-state combination of HMMs fitted 1) via maximization of the joint likelihood and 2) via the two-stage approach for four subjects.

	Joint likelihood				Two-stage
Comp. time (Hrs.)	71.3				3.2
Log-likelihood	40438.34				40367.95
	Dirichlet parameters				Dirichlet parameters
	${\mathrm{\lambda }}_1^{(n)}$	${\mathrm{\lambda }}_2^{(n)}$	${\mathrm{\lambda }}_3^{(n)}$	${\mathrm{\lambda }}_4^{(n)}$	${\mathrm{\lambda }}_1^{(n)}$	${\mathrm{\lambda }}_2^{(n)}$	${\mathrm{\lambda }}_3^{(n)}$	${\mathrm{\lambda }}_4^{(n)}$
state n = 1	44.7	5.6	4.0	2.3	48.5	5.9	4.3	2.5
(95%-c.i.)	(42.7;46.8)	(5.3;5.8)	(3.9;4.2)	(2.2;2.4)	(46.1;50.9)	(5.6;6.1)	(4.1;4.5)	(2.4;2.6)
state n = 2	10.6	4.5	5.9	4.7	10.3	4.7	6.0	4.9
(95%-c.i.)	(10.2;10.9)	(4.3;4.7)	(5.6;6.1)	(4.5;4.9)	(9.8;10.7)	(4.5;4.9)	(5.7;6.3)	(4.7;5.1)
state n = 3	35.5	9.2	7.8	5.0	35.4	9.2	7.9	5.2
(95%-c.i.)	(34.0;37.1)	(8.7;9.6)	(7.5;8.1)	(4.8;5.2)	(33.7;37.2)	(8.7;9.6)	(7.6;8.3)	(5.0;5.4)
state n = 4	2.7	1.0	0.9	5.7	3.4	1.2	1.0	8.4
(95%-c.i.)	(2.5;3.0)	(1.0;1.1)	(0.8;1.0)	(5.3;6.2)	(3.1;3.7)	(1.1;1.3)	(0.9;1.1)	(7.5;9.4)
	Expected band power prop.				Expected band power prop.
	δ	θ	α	β	δ	θ	α	β
state n = 1	0.79	0.10	0.07	0.04	0.79	0.10	0.07	0.04
state n = 2	0.41	0.18	0.23	0.18	0.40	0.18	0.23	0.19
state n = 3	0.62	0.16	0.14	0.09	0.61	0.16	0.14	0.09
state n = 4	0.26	0.10	0.08	0.56	0.24	0.08	0.07	0.60
	Stationary state prob.				Stationary state prob.
	${\pi }_1^{(m)}$	${\pi }_2^{(m)}$	${\pi }_3^{(m)}$	${\pi }_4^{(m)}$	${\pi }_1^{(m)}$	${\pi }_2^{(m)}$	${\pi }_3^{(m)}$	${\pi }_4^{(m)}$
subject m = 1	0.19	0.27	0.50	0.03	0.19	0.25	0.52	0.03
subject m = 2	0.30	0.28	0.30	0.12	0.30	0.28	0.31	0.11
subject m = 3	0.24	0.20	0.44	0.12	0.24	0.19	0.45	0.12
subject m = 4	0.19	0.49	0.24	0.08	0.19	0.47	0.27	0.06

As pointed out above, method 1) (conventional ML estimation) is infeasible for large populations. The two-stage method is feasible for very large populations and is substantially faster already for smaller populations. Moreover, the second step of the method can be implemented in parallel, as each subject fit can be done on a different processor. This makes our two-stage method scalable to essentially any number of subjects using parallel computing. As can be seen in Table 2, the two-stage method yields reasonable results in the sense that they are close to those obtained by joint maximization of the likelihood. In particular, the expected spectral band power proportions differ by at most 0.04 (β-waves in state 4, which here is the least frequented state, i.e., the one with least observations in the sample). These findings indicate that the two-stage method provides reasonable estimates in cases where both the joint likelihood and the two-stage approaches are feasible.

Most of the Dirichlet parameter estimates are found to be higher when using the two-stage approach than when using conventional ML estimation. We believe that this is because the latter approach takes into account the autocorrelation of the sequence, whereas the two-stage approach neglects it. For example, assume that a couple of successive observations strongly suggest that they are associated with the same underlying state, except that one of the observations (somewhere in the middle of the sequence) is an outlier. If that underlying state is relatively persistent (i.e., if it is associated with a relatively high self-transition probability), then the conventional ML procedure may try to accommodate the outlying observation within that state by estimating a higher variance of the corresponding Dirichlet distribution than the two-stage method does (and a higher variance of the Dirichlet distribution can be achieved by lower Dirichlet parameters), since the two-stage procedure would be more likely to assign the outlying observation to a different state.

The fit to the four-subject example indicates that the fitted hidden Markov chains have different characteristics across subjects. Indeed subject 1 (healthy) spends about half of the night in state 3, whereas for example subject 4 (diseased ) spends only about a fourth of the night in that state. Section 4.3 will concentrate on the quantitative analysis of such differences for a large population containing 51 healthy subjects paired to 51 sleep apneics.

4.2 A simulation study

In order to better evaluate the performance of the two-stage estimation method we conducted a simulation study. We simulated from the model for sleep EEG outlined in Section 3.1, generating T = 800 observations – each drawn from one of N = 2 possible Dirichlet distributions as selected by an underlying Markov chain – for each of M = 4 individuals. To these four time series we then fitted the combination of HMMs by 1) maximizing the joint likelihood (conventional ML) and 2) using the two-stage approach. This exercise was repeated 500 times, and the comparison of the two methods is based on point and interval estimates of the Dirichlet parameters. We decided to simulate from a model with two (sleep) states only because more states would make the joint fitting method (MLE) too time-consuming for a simulation study (but see the web-based supporting material for another simulation study which considers more states). We provide detailed results only for the state-dependent distributions to focus on the first stage of the two-stage method. The second stage is expected to perform very well when the first stage parameters are well estimated.

For each of the 500 simulation runs we used Dirichlet distributions with parameter vectors λ⁽¹⁾ = (4,3,2,1) and λ⁽²⁾ = (1,2,3,4) for states 1 and 2, respectively. For each run and individual the diagonal entries of the t.p.m. of the underlying two-state Markov chain were drawn from a uniform distribution on [0.85,0.95]. This choice was made to allow for different state-switching dynamics for different individuals. The diagonal entries were chosen to be large, such that the independent mixture model fitted in Stage I is the wrong model because it neglects the high within-subject autocorrelation.

Table 3 provides the following summary statistics for the estimates of the Dirichlet parameters: sample means of the estimates, sample standard errors of the estimates, coverage proportions of the associated 95% confidence intervals, and mean absolute deviation between estimates obtained via conventional ML and those obtained via the two-stage method. Confidence intervals were obtained based on the Hessian of the log-likelihood for the parameter estimates. All confidence intervals, both those obtained using conventional ML and those obtained using the two-stage method, have coverage proportions close to the desired value 0.95. There is also no indication of bias for either of the two methods. For both methods, the estimates of the Markov chain parameters also showed no indication of bias, with the standard deviations of the estimates being marginally higher in the case of conventional ML estimation (likely due to the uncertainty in the Dirichlet parameter estimates being neglected in Stage II of the two-stage method). These results indicate that the two-stage method is a sensible way of reducing the computational burden when fitting HMMs to multiple time series. The only notable effect of using the simpler procedure was slightly higher standard errors of the estimators for the Dirichlet parameters; as a consequence, the resulting CIs were also slightly wider. In several other simulation scenarios we found similar results (not shown). In particular, the two-stage method also yielded unbiased estimates and valid coverage in a scenario with N = 5 states and parameter as estimated in Sections 4.3.1 and 4.3.2 below – see the web-based supporting material to this manuscript.

Table 3.

Summary statistics for the Dirichlet parameter estimates in the simulation study.

		state n = 1				state n = 2
Para.	Meth.	ME	SE	CC	MAD	ME	SE	CC	MAD
${\mathrm{\lambda }}_1^{(n)}$	MLE	4.003	0.101	0.936	0.049	11 1.000	0.024	0.956	0.004
	2-stage	4.002	0.119	0.938		1.000	0.025	0.956
${\mathrm{\lambda }}_2^{(n)}$	MLE	3.000	0.075	0.930	0.030	2.004	0.047	0.956	0.013
	2-stage	2.999	0.085	0.936		2.005	0.050	0.952
${\mathrm{\lambda }}_3^{(n)}$	MLE	2.003	0.048	0.944	0.012	3.005	0.071	0.952	0.030
	2-stage	2.003	0.050	0.952		3.005	0.080	0.950
${\mathrm{\lambda }}_4^{(n)}$	MLE	1.000	0.024	0.948	0.004	4.011	0.094	0.960	0.049
	2-stage	1.000	0.025	0.954		4.012	0.114	0.950

Columns in the table are: Para. = parameter, Meth. = applied estimation method, ME = mean estimate, SE = standard error of estimates, CC = coverage proportion of confidence intervals, MAD = mean absolute deviation between estimates obtained by the two different methods.

4.3 Results for matched subset of the SHHS

In this section we use the proposed two-stage method to fit the combination of HMMs to the whole population of matched pairs (i.e. to M = 102 subjects). We provide the results and interpretations using N = 5 states for the Markov chain. (Section 4.3.3 discusses this choice and the associated consequences.)

4.3.1 Stage I — Calibrating the state-dependent distributions

In this first stage, the state-dependent parameters are estimated by fitting an independent mixture of N = 5 Dirichlet distributions to the EEG data. The first task was to choose the calibration sample, i.e. the set of individuals to which the mixture is to be fitted. We chose all individuals, including those with SDB, to avoid potential biases induced by their patterns. However, the parameters may be substantially different in the two populations. To address this potential problem we repeated Stage I for the healthy and diseased subjects separately. The EEG recordings from both nights made in the SHHS were taken into account. In Table 4 the estimated Dirichlet parameters and the associated expected spectral band power proportions for the diseased and non-diseased subgroups, as well as for the whole group, are displayed.

Table 4.

Estimated Dirichlet parameters, associated expected spectral band power proportions of δ-, θ-, α- and β-waves and concentration parameters for healthy and diseased subgroups.

Whole population
state	Diri. parameter vector λ(n)				δ	θ	α	β	s(n)
n=1	76.29	07.99	04.62	02.47	0.83	0.09	0.05	0.03	091.37
n=2	68.83	14.18	08.81	04.24	0.72	0.15	0.09	0.04	096.06
n=3	07.80	04.87	06.08	03.90	0.34	0.21	0.27	0.17	022.65
n=4	25.20	08.74	06.85	04.13	0.56	0.19	0.15	0.09	044.92
n=5	00.83	00.57	00.56	01.00	0.28	0.19	0.19	0.34	002.96
Healthy subgroup
state	Diri. parameter vector λ(n)				δ	θ	α	β	s(n)
n=1	75.59	08.03	04.53	02.44	0.83	0.09	0.05	0.03	090.59
n=2	77.96	16.36	09.89	04.43	0.72	0.15	0.09	0.04	108.43
n=3	06.81	04.46	05.56	03.51	0.33	0.22	0.27	0.17	020.36
n=4	24.20	08.40	06.35	03.84	0.57	0.20	0.15	0.09	042.79
n=5	00.73	00.52	00.49	01.03	0.26	0.19	0.18	0.37	002.76
Diseased subgroup
state	Diri. parameter vector λ(n)				δ	θ	α	β	s(n)
n=1	83.99	08.55	04.97	02.59	0.84	0.09	0.05	0.03	100.09
n=2	55.27	11.01	07.43	03.86	0.71	0.14	0.10	0.05	077.58
n=3	09.39	05.41	06.78	04.47	0.36	0.21	0.26	0.17	026.05
n=4	29.04	10.33	08.32	04.88	0.55	0.20	0.16	0.09	052.57
n=5	01.01	00.65	00.67	01.00	0.30	0.19	0.20	0.30	003.33

The two group analyses led to similar results. The largest difference in the state-dependent expected spectral band powers can be observed for state 5, probably because it is the least frequented state (see the discussion of the sleep architecture below), which leads to unstable estimates. The variances of the fitted Dirichlet distributions are quite different for the different states. The lowest concentration parameter s⁽ⁿ⁾ was estimated for state 5 (2.76 for the healthy and 3.33 for the diseased subgroup). This could be an indication that the make-up of this sleep state differs largely across individuals. Indeed, a model with fixed Dirichlet parameters across individuals would try to capture this heterogeneity by estimating a small concentration parameter. As the two fits led to similar results, we will subsequently use the parameters estimated from the set of all individuals.

4.3.2 Stage II — Individual state switching probabilities

After fixing the Dirichlet parameters at the values obtained from the calibration fit performed above, we fitted a five-state Dirichlet HMM for each of the 102 individuals. Of interest is the stochastic structure of the resulting Markov chains, which we analyze in two different ways. First, we discuss sleep architecture by looking at the stationary distributions of the Markov chains. Second, we analyze the estimated transition probabilities using the resulting expected frequencies of transitions.

Sleep architecture

We start by investigating the stationary distributions π^(m), m = 1,…,102, which provide the estimated average proportions of time spent in the different states by each subject. In the following the indices m = 1,…,51 correspond to the healthy individuals while those with the indices m = 52,…,102 correspond to the diseased ones (and the matched pairs are (1,52), (2,53), …, (51,102)). We obtain

$${\overline{\pi }}_{\mathit{\text{healthy}}}≔\frac{1}{51}\sum _{m=1}^{51}{\pi }^{(m)}\approx (0.141,0.218,0.178,0.373,0.090)$$

and

$${\overline{\pi }}_{\mathit{\text{diseased}}}≔\frac{1}{51}\sum _{m=52}^{102}{\pi }^{(m)}\approx (0.127,0.208,0.178,0.400,0.087).$$

Thus, according to the fit of the combination of HMMs, the EEG-derived sleep architecture, i.e. the average proportion of time the individuals spend in the different HMM states, is similar for healthy and diseased subjects. This confirms findings of papers dealing with sleep architecture analyses based on the hypnogram [17, 20]. The most frequented HMM state is state 4 in which about 37 – 40% of the night is spent. The least frequented HMM state is state 5 in which about 9% of the night is spent.

The stationary distributions of the individuals show sizeable variation. Indeed, in each of the states 1–4 almost all individuals have stationary probabilities substantially larger than zero, i.e. > 0.01 (the only exception being one diseased individual who, according to the fitted model, never switches to state 3). State 5 is visited very infrequently by some individuals. Indeed, for 19 individuals (eight healthy and eleven diseased) the stationary probability of being in state 5 was estimated to be less than 0.01. We emphasize that our analyses do not consider night-to-night variation within an individual, but rather variation within a night and variation across individuals.

Expected number of transitions

We also analyze the state transition probabilities. The expected number of transitions of individual m from state i to state j in a series of T observations is equal to [29]

$$𝔼\{t_{ij}^{(m)}(T)\}=(T-1){\pi }_i^{(m)}{b}_{ij}^{(m)}.$$

Table 5 displays the averaged values of the expected numbers of transitions per hour, from state i to state j, for the two groups of interest (healthy and diseased individuals), i.e.

$$\frac{1}{51}\sum _{m=1}^{51}𝔼\{t_{ij}^{(m)}(120)\}\text{and}\frac{1}{51}\sum _{m=52}^{102}𝔼\{t_{ij}^{(m)}(120)\},$$

for i, j = 1,2,3,4,5.

Table 5.

Averaged expected numbers of transitions per hour for healthy and diseased individuals.

Healthy subgroup
	to state
from state	1	2	3	4	5
1	13.30	1.66	0.59	1.08	0.15
2	2.01	19.94	0.16	3.74	0.07
3	0.38	0.08	17.63	2.83	0.25
4	0.98	4.19	2.42	36.74	0.10
5	0.12	0.05	0.37	0.05	10.12
Diseased subgroup
	to state
from state	1	2	3	4	5
1	9.68	2.71	0.65	1.90	0.15
2	3.05	17.32	0.18	4.21	0.03
3	0.39	0.05	17.48	2.96	0.36
4	1.86	4.69	2.43	38.41	0.17
5	0.11	0.02	0.50	0.07	9.61

Summing up the off-diagonal elements from the tables yields the averaged expected total numbers of cross-state transitions:

$$\sum _{i,j\in \{1,2,3,4,5\},i\ne j}\frac{1}{51}\sum _{m=1}^{51}𝔼\{t_{ij}^{(m)}(120)\}=21.27(\text{healthy subgroup}),$$

and

$$\sum _{i,j\in \{1,2,3,4,5\},i\ne j}\frac{1}{51}\sum _{m=52}^{102}𝔼\left\{t_{ij}^{(m)}(120)\right\}=26.50(\text{diseased subgroup}).$$

Not considering the group averages, and instead applying a two-sided Welch’s t-test to the (51) pairwise differences, yields a p-value of 0.0005, indicating that there is strong evidence of difference in the average expected number of cross-state transitions between the diseased and healthy groups.

In summary, diseased individuals tend to switch significantly more often between various states. Most of the switches occur between states 2 and 4, followed by the switches between states 1 and 2. The most striking difference between the groups is in the number of switches between states 1 and 2, which occur about 57% more often in the diseased group.

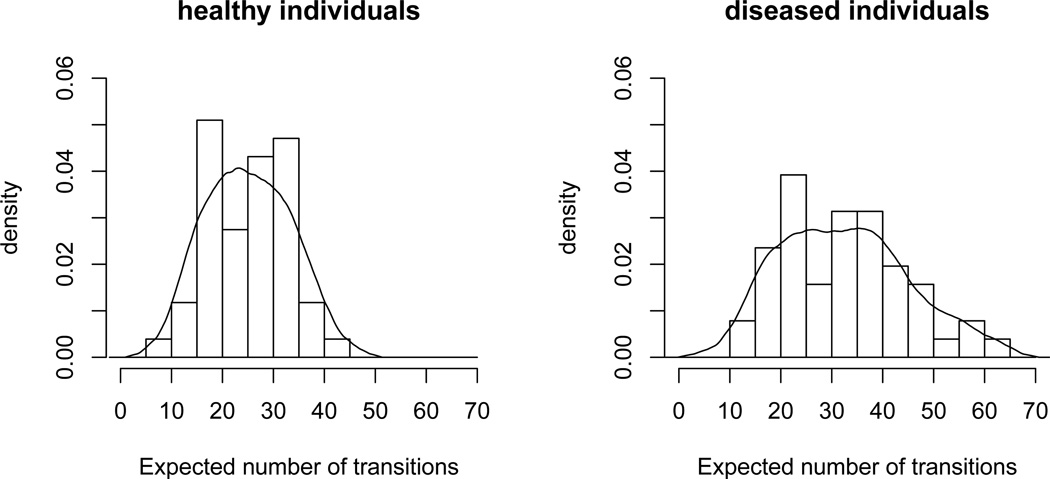
Not captured by this analysis of the group averages is the heterogeneity within the groups. Although the difference between the average expected numbers of cross-state transitions is substantial, there are large fluctuations within the groups. This can be seen in Figure 3, where histograms and kernel density estimators of the expected numbers of cross-state transitions per individual, i.e. the values

$$\sum _{i,j\in \{1,2,3,4,5\},i\ne j}𝔼\{t_{ij}^{(m)}(120)\},m=1,\dots ,102,$$

separated in the groups of healthy and diseased individuals, are displayed. The apparent substantial heterogeneity in the state switching behavior, both across groups and within groups, underlines the need for using individual-specific Markov chains in the suggested combination of HMMs.

Figure 3.

Histogram and kernel density estimator (kde) for the expected total number of cross-state transitions. Bandwidths for the kde were obtained via cross-validation (4.0 and 4.7 in the cases of healthy and diseased subjects, respectively), and the Epanechnikov kernel was used.

The plot does not suggest that the distribution for the set of diseased individuals is simply shifted. Instead, according to this plot about four-fifths of the diseased individuals do not show an anomalously high number of cross-state transitions: only for 11 (17) out of 51 diseased individuals the expected number of cross-state transitions exceeds the empirical 99%-quantile (95%-quantile) of the corresponding numbers obtained for the healthy individuals. There seems to be a subgroup in the diseased group of diseased individuals leading to the strong difference observed.

4.3.3 Number of states

We have shown results for a combination of HMMs with five states each. This number is in agreement with the sleep states stipulated by the American Academy of Sleep Medicine (AASM) manual from 2007 (REM, wake and Non-REM stages I-III). In the light of the possibility that classical sleep staging is playing a key role in the determination of the HMM states, both models with five and six states seem reasonable. One might conjecture that the simpler layout possibly corresponds to the decomposition in three Non-REM states plus waking and REM, while the six-state model considers a fourth Non-REM state, as stipulated in the standard manual for scoring of sleep stages [35].

Because our choice is arbitrary, it is interesting to investigate the differences in results between the five- and the six-state model. Table 6 provides the expected band power proportions associated with the states obtained in the combination of HMMs with five and six states each, respectively.

Table 6.

Expected band power proportions in the combination of HMMs with five and six states; in each case the estimates were obtained using the two-stage method.

5-state model
state	expec. band power prop.
n	δ	θ	α	β
1	0.83	0.09	0.05	0.03
2	0.72	0.15	0.09	0.04
3	0.34	0.21	0.27	0.17
4	0.56	0.19	0.15	0.09
5	0.28	0.19	0.19	0.34

6-state model
state	expec. band power prop.
n	δ	θ	α	β
1	0.84	0.09	0.05	0.02
2	0.72	0.15	0.09	0.04
3	0.36	0.21	0.26	0.17
4	0.56	0.21	0.15	0.09
5	0.26	0.20	0.19	0.35
6	0.68	0.09	0.10	0.12

All states of the fitted five-state HMM combination are altered only slightly when moving to the six-state model, and all main conclusions obtained for the five-state model remain practically unchanged when assuming six states (results not shown). The additional inclusion of a sixth state simply provides a more detailed distinction between different sleep characteristics.

5 Conclusions

In this manuscript we considered a combination of HMMs which can easily and conveniently be fitted using a novel two-stage fitting process. The method is easy to use and scales up well to large studies. Numerical studies demonstrate good agreement between our ad hoc fitting method and full maximum likelihood, while also demonstrating large scale decreases in computing time.

Via simulations we have in particular demonstrated that the two-stage method performs well in the scenario represented by the SHHS (see the web-based supporting material to this manuscript). In potential cases where simulation experiments indicate unsatisfactory behavior of the Dirichlet parameter estimators based on Stage I of the two-stage method, we recommend considering the option of additionally running an EM algorithm, using the estimates obtained from the two-stage method as initial values. An EM algorithm for the suggested combination of HMMs would involve – in each iteration – 1) applying the forward-backward algorithm to obtain the conditional probabilities of all states and pairs of consecutive states, given the current parameter estimates and the observations (the E step; note this can be applied to each subject separately, such that parallelization is possible), and 2) computing the new estimates of the initial state distributions and transition probability matrices from those conditional probabilities, and a numerical maximization to obtain the new estimates of the Dirichlet parameters (the M step).

We have not implemented EM in this work for two reasons: first, given the good performance of the two-stage method in the conducted simulation studies, there seems to be no need to additionally grapple with the complexity of an EM algorithm. Compared to EM, the crucial advantages of the two-stage method clearly are computational speed and its accessibility to users. In particular, it will usually be straightforward to apply the two-stage method in other (similar) HMM settings, whereas any EM approach is likely to involve nontrivial modifications whenever the structure of the model is altered. Second, in scenarios with high-dimensional parameter spaces, in general neither EM nor standard numerical maximum likelihood will stand alone, since extremely good starting values need to be available. Such starting values can relatively easily yet objectively be obtained via the two-stage approach. Thus, our simple method can be a very useful tool even in cases where MLEs are desired. For these reasons we decided to focus exclusively on the two-stage method in the present manuscript.

We applied the suggested combination of HMMs to a novel study of sleep and its correlates. Our results confirm findings based on visual inspection of sleep hypnograms, despite being based entirely on the EEG signal. We found that the percentage of time spent in HMM-derived EEG states is equivalent across carefully matched diseased (sleep apnea) and non-diseased subgroups. That is, subjects with SDB, despite repeated arousals during the night, manage to obtain a consistent percentage of time spent in sleep states (generally defined) as subjects without SDB.

However, we also identified interesting differences in the transitions between states. Specifically, we identified and quantified differences in the (HMM-derived) state transition rates between diseased and non-diseased subjects as well as the variability in these transition processes. These differences confirm results based on hypnograms [17, 20]. However, our approach is entirely automated, does not require human scoring, and requires only the processed EEG signal.

In summary, HMMs are useful to extract features and study sleep phenomena for epidemiological studies. Given the utility of the proposed models, important future research would include covariate adjusted and nonhomogeneous variations of the model. In particular the latter issue is important, since brain activity during sleep can depend on the time of night through Circadian and other processes. Also assuming more flexible distributions for the duration of stay in particular states is likely to improve the fit; corresponding extensions are straightforward to apply since corresponding models can be framed as HMMs [36]. Variations incorporating random effects could also be worthwhile, provided that the computational burden can be decreased. The semiparametric approach proposed by Maruotti and Rydén [37] might offer a way forward in that direction.