Mechanism of activation of elongation factor Tu by ribosome: Catalytic histidine activates GTP by protonation

EF-Tu is an essential GTPase involved in loading aminoacyl-tRNA substrates into the A site of the ribosome with high fidelity during each round of translation elongation. Here, various mechanisms for GTPase activation are explored using high-level quantum chemical/molecular mechanical simulations. These studies find the most likely mechanism for catalysis to depend on direct involvement of His85 in the catalytic reaction with minor contributions from the rRNA. This mechanism is likely conserved for related translational GTPases.

Abstract

Elongation factor Tu (EF-Tu) is central to prokaryotic protein synthesis as it has the role of delivering amino-acylated tRNAs to the ribosome. Release of EF-Tu, after correct binding of the EF-Tu:aa-tRNA complex to the ribosome, is initiated by GTP hydrolysis. This reaction, whose mechanism is uncertain, is catalyzed by EF-Tu, but requires activation by the ribosome. There have been a number of mechanistic proposals, including those spurred by a recent X-ray crystallographic analysis of a ribosome:EF-Tu:aa-tRNA:GTP-analog complex. In this work, we have investigated these and alternative hypotheses, using high-level quantum chemical/molecular mechanical simulations for the wild-type protein and its His85Gln mutant. For both proteins, we find previously unsuggested mechanisms as being preferred, in which residue 85, either His or Gln, directly assists in the reaction. Analysis shows that the RNA has a minor catalytic effect in the wild-type reaction, but plays a significant role in the mutant by greatly stabilizing the reaction’s transition state. Given the similarity between EF-Tu and other members of the translational G-protein family, it is likely that these mechanisms of ribosome-activated GTP hydrolysis are pertinent to all of these proteins.

INTRODUCTION

The elongation factor Tu (EF-Tu) protein is a crucial component in protein synthesis. It forms a ternary complex with amino-acylated tRNAs (aa-tRNAs) and GTP and delivers them to the A site of the ribosome for interaction with mRNA. When the correct codon–anticodon recognition occurs between tRNA and mRNA, the ribosome stimulates GTP hydrolysis by EF-Tu, releasing EF-Tu:GDP and Pi and leaving the aa-tRNA behind. EF-Tu by itself has a very low GTPase activity and it is only when it has the appropriate interactions with the ribosome that hydrolysis occurs (Rodnina 2009).

It is known that a histidine in the switch II region of EF-Tu (His85 in Thermus thermophilus, and His84 in Escherichia coli) is crucial for catalysis. This residue is also strictly conserved in other members of the translation-factor family (Bourne et al. 1990, 1991), which, together with the similarities in their structures and ribosome-binding modes (Dever et al. 1987; Moazed et al. 1988; Holmberg and Nygård 1994) suggests a common mechanism by which the ribosome activates GTP hydrolysis in all these proteins.

Despite much work, the mechanism of ribosome-induced hydrolysis of GTP by EF-Tu remains uncertain. Recently, an important step forward in the understanding of this process occurred with the publication of a medium-resolution X-ray crystallographic structure of the ribosome:EF-Tu:aa-tRNA:GTP structure in its active conformation by Voorhees et al. (2010). The active site of this complex is shown in Figure 1. As a result of their analysis, these workers proposed a mechanism in which His85 acts as a general base by abstracting a proton from the catalytic water molecule, which then attacks the γ-phosphate of GTP. This proposal caused some controversy, and alternatives based upon both experimental and theoretical evidence were suggested by a number of groups including Liljas et al. (2011) and Adamczyk and Warshel (2011).

FIGURE 1.

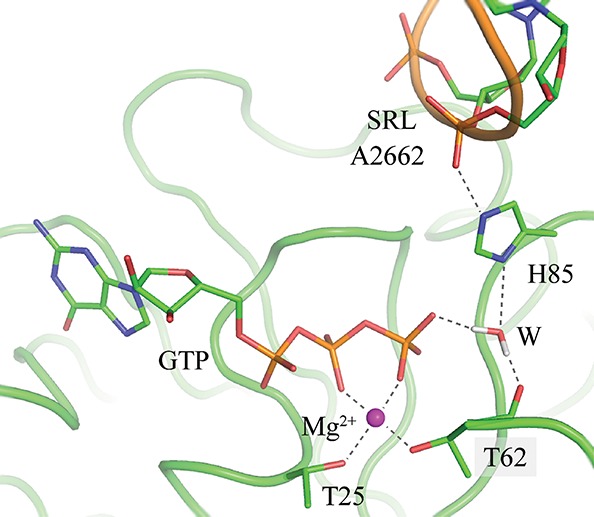
The active site pocket of the ribosome:EF-Tu:GTP complex.

Due to the doubt surrounding the mechanism and the importance of the reaction, we decided to look at the various proposals in the literature and to investigate other possibilities using molecular simulation techniques. We used molecular dynamics (MD) free energy simulations to determine the protonation states of residues that might be implicated in the reaction and high-level hybrid quantum chemical (QC)/molecular mechanical (MM) potentials in conjunction with a nudged-elastic-band reaction-path-finding algorithm to map out energy profiles. We studied both the wild-type protein and its His85Gln mutant, for which experimental data exist (Scarano et al. 1995; Zeidler et al. 1995), and also analyzed the role that the ribosome plays in the catalysis.

The outline of this study is as follows. First, we present the results that were obtained, then we conclude, and in Materials and Methods we describe in detail the simulation approaches that were used.

RESULTS

His85 protonation free-energy simulations

A necessary preliminary to studies of mechanism is the determination of the protonation states of residues that might be implicated in the reaction, as these can have a profound effect on the mechanisms and energetics that are found (Warshel and Naray-Szabo 1997). Those of most residues were straightforward to deduce, but there was some uncertainty about the δ-protonation of His85 in the ribosome complex, which is crucial for reaction. To resolve this, we utilized MD free-energy simulations (Sham et al. 1997; Simonson et al. 2004; Aleksandrov et al. 2007) to calculate the free energy of protonation from the thermodynamic cycle shown in Figure 2. To effect the protonations of the histidine in solution and in the ribosome complex, we performed a series of MD simulations in which the neutral and charged forms of His85 were reversibly transformed in both directions. This technique has no adjustable parameters and has been shown to give good results for acid/base reactions when standard biomolecular force fields are used despite the systematic errors that might arise, for example, by the neglect of electronic polarization (Simonson et al. 2004).

FIGURE 2.

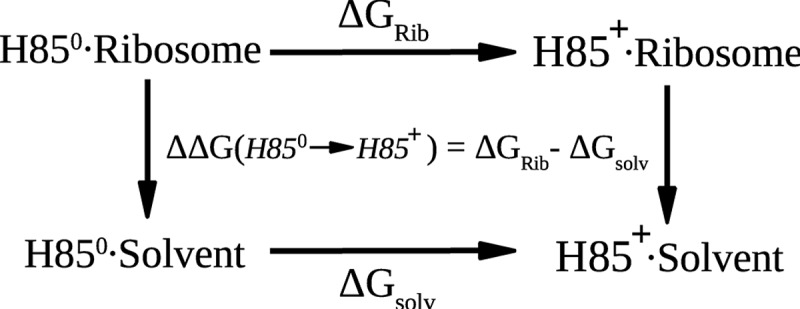
The thermodynamic cycle used to calculate the protonation free-energy difference for His85 in the ribosome complex and in solution. Horizontal legs represent the protonation of His85 on its δ nitrogen, either in the ribosome (above) or in solution (below). The MD free-energy simulations follow the horizontal legs.

The computed free energies in solvent and in the protein with the CHARMM force field are 13.4 (±0.8) and −0.7 (±2.5) kcal/mol, respectively, which gives a protonation free energy for His85 in the ribosome of 14.1 (±2.5) kcal/mol. The value of 8.0 (±0.7) kcal/mol obtained with the AMBER force field is smaller, but in qualitative agreement with the CHARMM value. Both of these free energies clearly favor the biprotonated form of His85 in the ribosome.

The large stabilization of a positively charged His85 may be understood by the interactions that it has with GTP via the water molecule that participates in hydrolysis and with the phosphate group of A2662 of the 23S rRNA. Further support for the biprotonated state comes from the observation that the position of the histidine during the free-energy MD simulations is in much better agreement with the crystal structure when it is charged. In the latter, the distance between the γ-phosphate of GTP and the Nδ of His85 is 4.6 Å, whereas in the simulations, the average distances are 5.0 and 7.9 Å with biprotonated and neutral His85, respectively. The longer distance in the neutral form is because the water molecule nearest to the Nδ of His85 prefers to hydrogen bond with the phosphate of GTP and the backbone carbonyl group of T62. As a result, His85 departs from its crystal position by rotating around its Cα–Cβ bond, so that its deprotonated Nδ can interact with solvent. The presence of a charged His85 contrasts with the neutral His85 that was hypothesized from the crystallographic analysis (Voorhees et al. 2010), but agrees with the predictions of the calculations of Adamczyk and Warshel (2011).

Hybrid potential simulations of the catalytic reaction

Wild-type protein

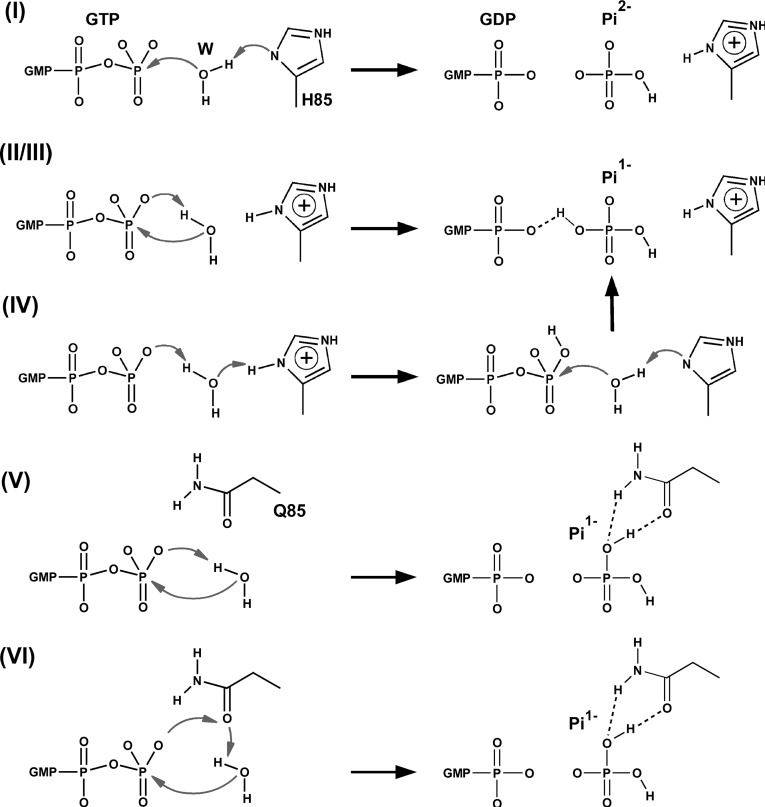
We studied four mechanisms. Schematics of these are shown in Figure 3, and the energies of pertinent intermediates (Ints) and transition states (TSs) in Table 1. Mechanism I requires a neutral His85 and corresponds to that proposed by Voorhees et al. (2010), based on an analysis of the crystal structure. It is also essentially the same mechanism as the one investigated by Grigorenko et al. (2008) in their simulation study of the GTP hydrolysis catalyzed by EF-Tu in the absence of the ribosome. In the first step of mechanism I, His85 takes a proton from the water molecule, and the resulting hydroxide attacks GTP to give a product state consisting of His85⁺ and Pi²⁻. The barrier for this step is 20.6 kcal/mol, but the products are very high in energy, being only 1.0 kcal/mol more stable than the transition state (TS). Proton transfer occurs readily, with essentially no barrier, to give the His85⁰/Pi⁻ pair with an energy 4.0 kcal/mol above the initial reactants. This latter proton transfer is explained by the repulsion of the GDP³⁻ and Pi²⁻ species in the product state, which favors protonation of the phosphate. It is interesting to note that in the study by Grigorenko et al. (2008) the barrier to reaction was much lower, at 10.8 kcal/mol, and the products were more stable than reactants by 5.0 kcal/mol. These differing values reflect the very different environments within which the reaction occurs, but may also depend on the lower level of QC theory that was used in the calculations.

FIGURE 3.

Schematics of the mechanisms investigated in the hybrid potential QC/MM simulations. I–IV correspond to the wild-type protein and mechanisms, V–VI to the His85Gln mutant. Mechanism I is that proposed by Voorhees et al. (2010), whereas mechanism II was suggested by Liljas et al. (2011) and by Adamczyk and Warshel (2011). Mechanism III (data not shown) is a variant of mechanism II, in which His85 is in its neutral state. Mechanism V is equivalent to mechanisms II and III, but for the His85Gln mutant. Mechanisms IV and VI are the mechanisms proposed in this work for the wild-type and mutant proteins, respectively.

TABLE 1.

Energies of intermediate and transition state structures from the proposed mechanisms of GTP activation for the wild-type (I–IV) and mutant (V–VI) proteins

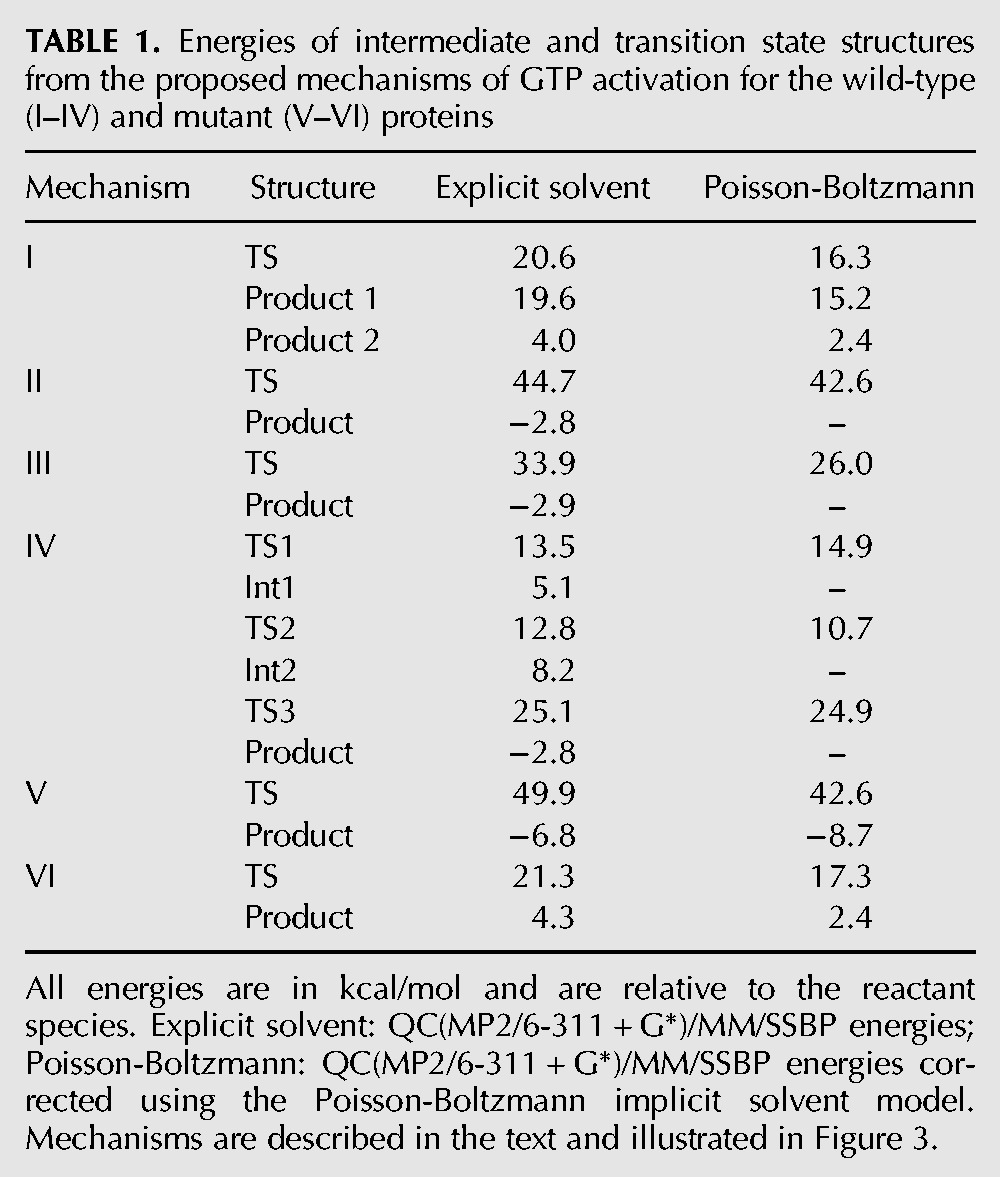
Mechanism II, in contrast to mechanism I, involves a charged His85. It was proposed by Adamczyk and Warshel (2011) based upon their simulations with an empirical valence bond potential, and also hypothesized by Liljas et al. (2011). It involves transfer of a proton from the hydrolytic water to the phosphate, followed by hydroxide attack on the terminal phosphate of GTP, to give GDP and Pi⁻. We computed the energy barrier for this reaction to be 44.7 kcal/mol and found no stable intermediate. In the TS, hydroxide is formed, but the bond between it and the phosphate is not yet established. The high-energy barrier for the reaction is explained by the need to bring two negative species together.

Mechanism III is the same as mechanism II, except that we take His85 to be in its neutral state. The reaction paths are very similar, except that the absence of the proton results in a lower barrier of 33.9 kcal/mol, although this is still very high.

The last mechanism we studied, mechanism IV, was one in which His85 assists in the reaction. In the first step, the histidine donates its Nδ proton to the terminal phosphate of GTP via the hydrolytic water molecule. The energy barrier for this step is 13.5 kcal/mol, which is lower than the experimental estimate for the energy barrier of the complete reaction (Daviter et al. 2003), and the product is 5.1 kcal/mol less stable than the reactants. No conformational changes were observed for this step, which only affects the disposition of protons in the system.

In the second step of the reaction, the hydroxyl group of the terminal phosphate of GTP reorients to a position where it interacts with the oxygen that links GTP’s β- and γ-phosphates. The barrier for this step was 7.7 kcal/mol, and the rearranged products are 3.1 kcal/mol higher in energy than those resulting from the initial proton transfer.

In the third and final step of the reaction, the water molecule gives its proton to His85 and attacks the phosphate of GTP in a concerted fashion with a computed energy barrier of 16.9 kcal/mol. This value is in reasonable agreement with the experimental upper-bound for the reaction of ∼14 kcal/mol (Daviter et al. 2003). The hydrogen transferred to the phosphate in the first step helps to stabilize the TS for this step by creation of a hydrogen bond to the β-phosphate, whereas in the product state it is shared between GDP and Pi. It is interesting to note that this step of the reaction is equivalent to mechanism I, in which His85 acts as a general base, except that the GTP is protonated.

Mutant protein

For the His85Gln mutant, we considered a number of mechanisms. The first, denoted mechanism V, is equivalent to mechanism II of the wild-type and to that proposed by Adamczyk and Warshel (2011). The computed barrier for this reaction is 49.9 kcal/mol with explicit solvent, and 42.6 kcal/mol with implicit solvent, both of which are clearly too high.

After this, we investigated mechanisms involving a second water molecule in the active site as these have been reported by Martín-García et al. (2012) to be pertinent for glutamine-assisted GTP hydrolysis in HRAS. To do this, we placed a second water in the active site near Gln85 and the γ-phosphate of GTP and performed short MD simulations of 10 psec in length. However, all simulations resulted in Gln85 being pushed out of the catalytic site by the second water molecule, indicating that only a single water molecule is present, as in the wild-type complex.

Finally, we found a viable mechanism, mechanism VI, that is assisted directly by Gln85. In it, Gln85 acts as a relay for the excess proton of the catalytic water in its transit to the oxygen of the γ-phosphate. In the transition state for this single-step process, the distances between this proton and the Oε1-Gln85 and O3γ atoms are 1.02 and 1.96 Å, respectively, whereas the equivalent distances in the products are 1.53 and 1.03 Å, respectively. The computed barrier for this mechanism is 21.3 kcal/mol with explicit solvent and 17.3 kcal/mol with implicit solvent. These numbers are in reasonable agreement with the experimental estimate, which indicates that this mutation leads only to a small reduction in the rate of GTP hydrolysis (Scarano et al. 1995; Zeidler et al. 1995).

Catalytic role of the RNA

The ribosomal residue A2662 has been postulated to have various roles in the reaction (Hausner et al. 1987; Bilgin and Ehrenberg 1994; Daviter et al. 2003; Rodnina 2009; Schmeing et al. 2009). To analyze its electrostatic influence, we performed calculations on the structures previously obtained for the preferred mechanisms’ critical points, but with the atomic charges of A2662 set to zero. The resulting values are given in Table 2.

TABLE 2.

Energies of selected intermediate and transition state structures from mechanisms IV (wild-type) and VI (mutant) of GTP activation

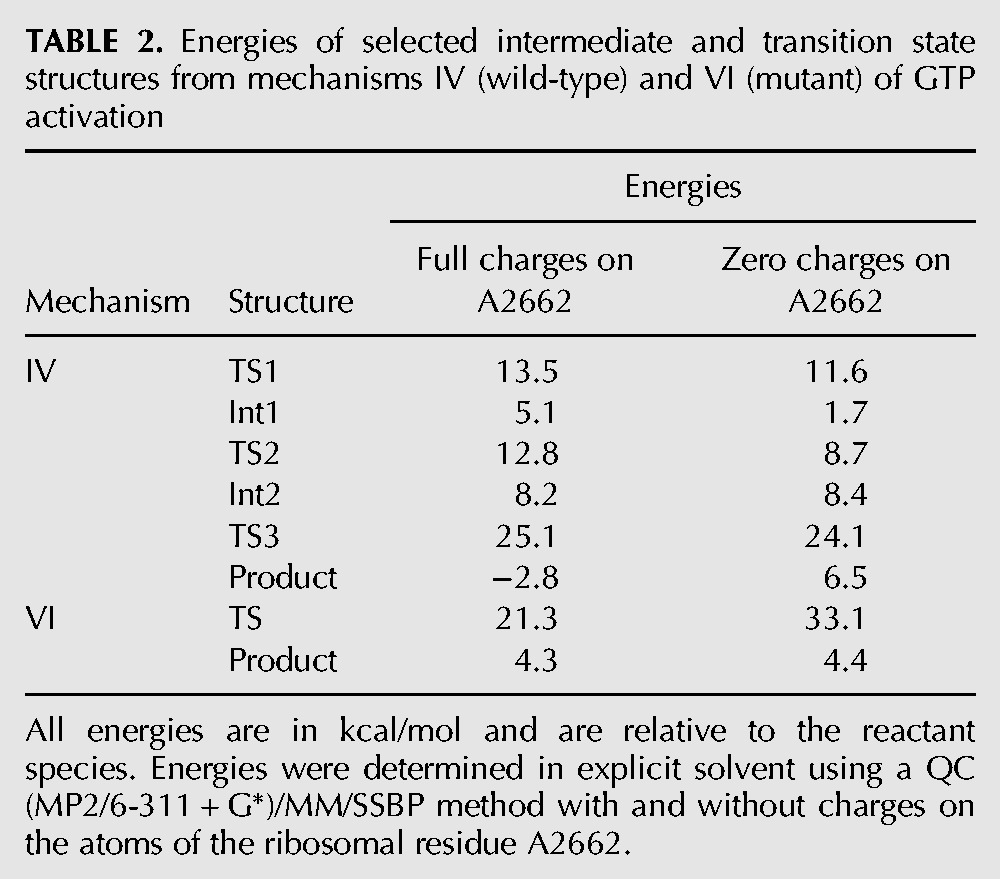
For mechanism IV of the wild-type protein, it can be seen that a charged A2662 actually increases the barriers for all of the steps in the reaction, although sometimes only slightly. It also increases the energy of the first intermediate and decreases the energy of the products. The increase in the energy of TS1 is due to the strong interaction between the negative phosphate of A2662 and the positive His85, whereas in TS3 the re-establishment of a biprotonated His85, which is favored by A2662, is counterbalanced by the unfavorable shift of the negative Pi product toward the negative phosphate of A2662. Overall, therefore, it appears that A2662 does not play a significant direct role in catalysis in the wild type, but instead contributes in an indirect way by correctly positioning His85 for reaction.

In contrast, the RNA appears to have a critical stabilizing effect on the transition state of mechanism VI in the mutant, thereby rendering the reaction feasible. This can be understood because Gln85 interacts with the two negative phosphates of A2662 and GTP, which help stabilize the protonated glutamine residue in the transition state.

A2662 belongs to the sarcin–ricin loop (SRL), whose role in GTP hydrolysis is unclear. Mutations in this loop definitely reduce GTPase activity, but this has been hypothesized to be the result of the misaligned binding of Ef-Tu in the mutants (Sanbonmatsu 2006). Our simulations do not allow us to comment on the latter directly, but they do support the notion that misalignment would reduce the rate of GTP hydrolysis, due to the energetic influence of A2662 and the importance of having it in the correct position to orient His85.

CONCLUSIONS

In this work we have studied the mechanism of GTP hydrolysis catalyzed by the ribosome:EF-Tu:aa-tRNA complex with both wild-type and mutant EF-Tu proteins. This reaction initiates release of EF-Tu from the ribosome:aa-tRNA complex and thereby plays a crucial role in protein synthesis. To investigate it, we used state-of-the-art simulation techniques, including free-energy MD simulations and high-level QC/MM hybrid potentials in conjunction with a nudged-elastic-band reaction-path-finding algorithm.

For the wild-type protein, our free-energy MD simulations strongly suggest that the important active site residue, His85, is in its biprotonated form in the ribosome:EF-Tu:aa-tRNA complex. Nevertheless, in our reaction path calculations, we examined a number of existing mechanistic proposals in which His85 was in its neutral as well as its cationic form. The favored mechanism with a neutral His85 was mechanism I, which was proposed by Voorhees et al. (2010) from an analysis of their crystal structure. Of the mechanisms with a protonated His85, we found the suggestion of Adamczyk and Warshel (2011), mechanism II, to be very unfavorable with an energy barrier of over 40 kcal/mol. Instead, we were able to locate a three-step route, mechanism IV, in which His85 actively assists in the reaction. It does this by first denoting its Nδ proton to the terminal phosphate of GTP via the hydrolytic water molecule. There is then a rearrangement of the proton’s position within the GTP, followed by attack of the catalytic water on GTP’s γ-phosphate and a concomitant reprotonation of the histidine. This last step, which is equivalent to mechanism I apart from the protonated GTP, has the highest energy barrier along the path with a value of 16.9 kcal/mol. This is in reasonable agreement with the experimental upper-bound for the reaction of ∼14 kcal/mol (Daviter et al. 2003).

In addition to the wild-type protein, we also studied the reaction in the His85Gln mutant, as experimentally this has been determined to have only a slightly reduced rate of GTP hydrolysis (Scarano et al. 1995; Zeidler et al. 1995). From their simulations of the mutant, Adamczyk and Warshel (2011) proposed mechanism V, which is the equivalent of mechanism II in the wild type. However, as in that case, we computed the energy barrier to be unfeasibly high. As an alternative, we found mechanism VI, which is much more favorable. In it, the proton that is lost from the catalytic water as it attacks GTP transits via the amide oxygen of Gln85 before protonating the γ-phosphate.

Our preferred mechanisms, IV and VI, are different from previous proposals in the literature and, significantly, also from each other. In both, residue 85, either His or Gln, is directly implicated in the chemical steps, but otherwise they follow different routes, indicating that the protein has considerable plasticity in being able to catalyze the same reaction. This is underlined by our analysis of the energetic role that the ribosomal residue A2662 plays, which shows that it has little direct effect on mechanism IV but is critical in rendering mechanism VI feasible. Given the similarity between EF-Tu and other members of the translational G-protein family, it is likely that the mechanisms of ribosome-activated GTP hydrolysis that we have elucidated here are of general relevance.

To terminate, we note that it might be possible to test experimentally the preferred mechanism that we find by targeting the first step of the reaction in which His85 donates its hydrogen. This could be done by introducing mutations in the local environment of His85 that increase its pKa, rendering the first step of the reaction less favorable, and so interfere with GTP hydrolysis. On the other hand, if the reaction followed a self-assisted pathway, without the direct participation of His85, such mutations should have no effect on the overall rate of GTP hydrolysis. The identification of such mutations and the corresponding experimental validation we leave for future studies.

MATERIALS AND METHODS

Molecular dynamics simulations

The crystal structure of the elongation factor Tu in complex with the ribosome was taken from the Protein Data Bank, entries 2XQD and 2XQE (Voorhees et al. 2010). Protonation states of histidines were assigned by visual inspection. The simulations included protein residues within a 24 Å sphere, centered on the GTP binding site. In addition to crystal waters, a 26 Å sphere of water was overlaid and waters that overlapped ribosome, crystal waters, the Mg ion, or GTP were removed. Two additional water molecules, which coordinate the Mg ion in the apo EF-Tu complex were placed by superimposing the GTP molecules of these two structures. Throughout the molecular dynamics (MD) simulations, protein atoms between 20 and 26 Å from the sphere’s center were harmonically restrained to their experimental positions. Simulations were done with the SSBP solvent model (Beglov and Roux 1994; Simonson 2000), which treats the region outside the 26 Å sphere as a uniform dielectric continuum with a dielectric constant of 80. Newtonian dynamics was used for the innermost region, within 20 Å of the sphere’s center, and Langevin dynamics for the outer part of the sphere, with a temperature bath at 292 K. The CHARMM27 force field was used for the protein and RNA (Mackerell et al. 1998; Foloppe and MacKerell 2000) and the TIP3P model for water (Jorgensen et al. 1983). Electrostatic interactions were computed without any cutoff, using a multipole approximation for distant groups (Stote et al. 1991). Calculations were done with the CHARMM program (Brooks et al. 2009).

The mutant His85Gln protein was set up in a similar way to the wild-type, except that the glutamine residue had to be positioned in place of the histidine. This was done by superimposing the GTP ligands of the EF-TU:Ribosome and RasGap systems (PDB entry 1WQ1) (Scheffzek et al. 1997) and extracting the appropriate glutamine residue, Gln61. MD simulations for the resulting system were then run for 1 nsec. The position of Gln85 remained stable throughout with hydrogen bonds between its amide group and the γ-phosphate of the GTP ligand and the phosphate of the ribosomal residue A2662, and between its amide oxygen and the catalytic water molecule.

Alchemical MD free-energy simulations

To determine the protonation state of the catalytic residue His85, we performed molecular dynamics free energy (MDFE) simulations (Sham et al. 1997; Simonson et al. 2004) using the thermodynamic cycle shown in Figure 2. The MDFE method follows the horizontal legs of the cycle. Protonated histidine is reversibly transformed into its deprotonated form during a series of MD simulations and the corresponding work is derived from a thermodynamic integration formula (Simonson 2001; Aleksandrov et al. 2010). For the lower leg of the thermodynamic cycle, we simulated methyl-imidazole in solution, which served as the reference molecule, whereas for the upper leg we simulated a portion of the ribosome complex. Both the ribosome and the solution transformations were modeled as rearrangements of atomic charges on the imidazole group. See references Simonson et al. (2004) and Aleksandrov et al. (2007) for details. The systems were solvated in a 70 Å box of water, and periodic boundary conditions were imposed so that the entire box was replicated periodically in all directions. All long-range electrostatic interactions were computed efficiently by the particle mesh Ewald method (Darden 2001), and the appropriate number of sodium counterions were included to render the system electrically neutral. MD simulations were performed at constant room temperature and pressure, after 200 psec of thermalization. The CHARMM27 force field was used for the protein and RNA (Mackerell et al. 1998; Foloppe and MacKerell 2000) and the TIP3P model for water (Jorgensen et al. 1983). As a check of the dependence of the results on the force field, calculations were also repeated with the AMBER99 force field for the protein and nucleic acid (Cornell et al. 1995). Simulations in both cases were done with the NAMD (Phillips et al. 2005) and CHARMM programs (Brooks et al. 2009).

During the MDFE simulations, the energy function can be expressed as a linear combination of terms associated with the neutral and protonated forms of His85:

(1)

in which λ is a coupling parameter and U₀ represents interactions between parts of the system other than the histidine. The free-energy derivative with respect to λ has the form:

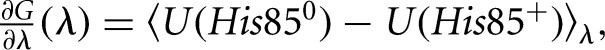(2)

where the brackets indicate an average over the MD trajectory with the energy function U(λ) (Simonson 2001). We gradually mutated His85⁺ into His85⁰ by changing λ from zero to one. The successive values of λ were: 0.001, 0.01, 0.05, 0.1, 0.2, 0.4, 0.6, 0.8, 0.9, 0.95, 0.99, and 0.999. The free-energy derivatives were computed at each λ value from a 100-psec MD simulation or window. The last 80 psec of each window were used for averaging. A complete mutation run corresponded to 12 windows and 1.2 nsec of simulation.

Thirty-four runs were performed (17 from His85⁺ to His85⁰ and 17 for the reverse transformation), giving a total simulation time of >40 nsec. The uncertainty was calculated as the standard deviation of the individual runs obtained in each direction (Aleksandrov et al. 2010). This extended simulation length was necessary to correctly sample the important degrees of freedom and to obtain a low statistical uncertainty.

Hybrid potential simulations

For the hybrid potential QC/MM calculations, the ribosome:EF-Tu:GTP complex was partitioned between QC and MM regions as depicted in Figure 4. The QC region had 32 atoms, comprising the GTP, Mg cation, the sidechain of His85, and the hydrolytic water molecule, and the MM region had 7510 atoms. Single-point calculations on the optimized structures were also done with an enlarged QC region that, in addition to the original QC atoms, contained Lys24 and the residues coordinating the Mg cation, namely, Thr25, Thr62, and two water molecules. The larger QC region contained 67 atoms and was electrically neutral. The mutant protein partitioning was the same as that of the wild type, but with His85 replaced by glutamine.

FIGURE 4.

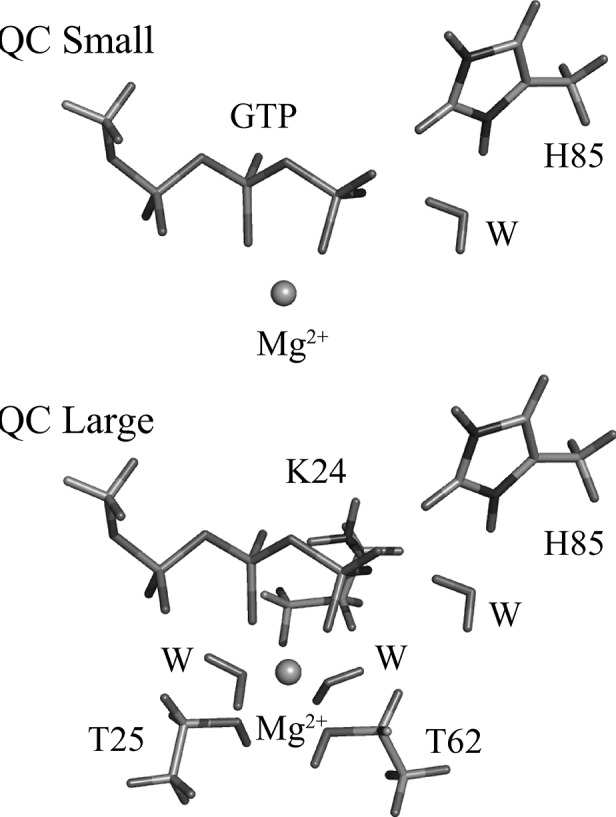
The small and large QC regions used in the hybrid potential QC/MM reaction path simulations.

The CHARMM27 force field was used for the MM region (Mackerell et al. 1998; Foloppe and MacKerell 2000) and a density functional theory (DFT) method for the QC region with the BLYP functional and Ahlrichs’s split valence basis with polarization functions (Gill et al. 1992; Schäfer et al. 1992). Single-point calculations on the optimized structures were done with the MP2 method and the larger 6-311 + G* basis set with polarization and diffuse functions on all atoms except hydrogen. B3LYP DFT calculations were also done with the larger basis and QC region, but were very similar to the MP2 results (within 1–2 kcal/mol) and so are not discussed here. We note that high-level DFT and MP2 methods with large basis sets, such as the ones used here, have previously been shown to be essential for a correct description of reactions involving substitution and elimination about a phosphate group (Marcos et al. 2010).

All geometry optimizations and reaction path calculations were performed with the DFT-QC/MM potential. To include the system beyond the explicit 24 Å sphere, we used our recent QC/MM implementation of the stochastic solvent boundary potential (Aleksandrov and Field 2011), which treats the region outside the explicit sphere as dielectric continuum, and includes its effect in the self-consistent field procedure (SCF).

The starting coordinates of the complexes were taken after 200 psec of MD simulation on the systems described in the Materials and Methods. The QC(DFT)/MM calculations were performed with the pDynamo software (Field 2008), whereas the QC(MP2)/MM computations were carried out with pDynamo and its interface to the ORCA program (Neese 2008). No truncation or cut-off was used to calculate nonbonding interactions. The reaction path was optimized with the nudged elastic band (NEB) method (Aleksandrov and Field 2012) implemented in pDynamo. The utility of the NEB method is that it does not require a predefined set of reaction coordinate variables and makes no assumptions as to how the reaction proceeds. The only bias in the calculation comes from the structures utilized in the starting guess for the NEB pathway.

Poisson-Boltzmann solvation free energy calculations

To estimate the electrostatic contribution to the solvation free energy we used the Poisson-Boltzmann (PB) implicit solvent model. The contribution was obtained by subtracting the electrostatic free energies of the complex computed with a high dielectric constant for solvent and a dielectric constant of one. The electrostatic potential was calculated by numerically solving the PB equation using a cubic grid and a finite-difference algorithm (Brooks et al. 2009). The calculations were done at physiological ionic strength with a solvent dielectric constant of 80. For the solute dielectric constant, the value of 1 was used since structural reorganization is accounted for in the NEB algorithm. For the PB calculations all water molecules were removed except for the two water molecules that bind the Mg cation, the water participating in hydrolysis, and the two waters interacting directly with the β- and γ-phosphates of GTP. CHELPG (Breneman and Wiberg 1990) charges computed with the B3LYP/6-311 + G* DFT method were used for the atoms in the QC region and CHARMM27 charges for those in the MM region.