A proposal for augmenting biological model construction with a semi-intelligent computational modeling assistant

Abstract

The translational challenge in biomedical research lies in the effective and efficient transfer of mechanistic knowledge from one biological context to another. Implicit in this process is the establishment of causality from correlation in the form of mechanistic hypotheses. Effectively addressing the translational challenge requires the use of automated methods, including the ability to computationally capture the dynamic aspect of putative hypotheses such that they can be evaluated in a high throughput fashion. Ontologies provide structure and organization to biomedical knowledge; converting these representations into executable models/simulations is the next necessary step. Researchers need the ability to map their conceptual models into a model specification that can be transformed into an executable simulation program. We suggest this mapping process, which approximates certain steps in the development of a computational model, can be expressed as a set of logical rules, and a semi-intelligent computational agent, the Computational Modeling Assistant (CMA), can perform reasoning to develop a plan to achieve the construction of an executable model. Presented herein is a description and implementation for a model construction reasoning process between biomedical and simulation ontologies that is performed by the CMA to produce the specification of an executable model that can be used for dynamic knowledge representation.

1 Introduction

The biomedical research community faces a challenge manifest as the discrepancy between an increasing amount of basic mechanistic knowledge about biological processes and the inability to effectively translate that mechanistic knowledge into clinically effective therapeutics. The divergence between basic science knowledge and the delivery of effective therapeutics was noted by the United States Food and Drug Administration in a 2004 report: “Innovation or Stagnation: Challenge and Opportunity of the Critical Path to New Medical Products,” where, despite increasing expenditures on basic science research, there was a downward trajectory in terms of the number of new therapies that reached the bedside (USFDA 2004). This is the essence of the translational dilemma in biomedical research, and appears to be particularly evident when investigating systems diseases, where there are disturbances of internal system-level regulatory mechanisms, such as cancer, autoimmunity, diabetes and sepsis. We suggest that there are fundamental process issues present in the biomedical research workflow that lead to the current translational dilemma. Characterization and identification of these process issues are a necessary step in the rational development of strategies to address the translational dilemma.

1.1 The roots of the translational dilemma

A recent review has examined the roots of the translational dilemma (An 2010) and a summary of its assertions is below:

As primarily an applied science, the ultimate goal of biomedical research is to identify and affect control on biological systems moving between states of health and disease. Effecting control requires an approximation of mechanistic causality, as planned interventions must have their basis in some imputed causal mechanism. Identification of correlative relationships do not amount to identifications of causality, therefore a means of testing causality must be incorporated into any knowledge-expansion process. Since the complete and comprehensive description of a biological system is impossible (i.e. a putative solution based on just obtaining more data will not suffice), a more efficient means of evaluating the sufficiency of the current state of knowledge must be established, where sufficiency is defined as establishing enough trust in a presumptive mechanistic hypothesis such that the hypothesis is useful in designing a means of control. The biomedical research community is in a situation where the balance of the scientific method (conversion of observations/data into patterns/hypotheses via correlation leading to testing of presumptive causality via experiment) has dramatically shifted towards the correlative component. The advent of the high throughput data environment has led to an increasing range of possible explanatory hypotheses, while the ability to evaluate those hypotheses through testing remains a time consuming, linear task. As such, where establishing correlation has become parallelized, testing causality remains a serial process. Adding to the challenges posed by this situation are the hierarchical organization and multi-scale nature of biological systems, resulting in epistemological boundaries to human intuition and synthesis, such that mechanistic hypotheses cannot be merely aggregated to obtain system-level behavior. The overall process of biomedical research is therefore limited in both (1) the breadth of hypothesis testing (throughput problem) and (2) complexity of hypotheses (multi-scale problem). These issues point to the need to enhance representation and examination of mechanistic hypotheses to facilitate the identification and evaluation of plausible solutions. Automation aimed at augmenting the rate-limiting steps of the scientific process is therefore a reasonable strategy for the future. More specifically, the need to represent the dynamics of a putative hypothesis and the imputed paths of causality within that hypothesis is greatly enhanced by the use of computational modeling and simulation (M&S) as a means of instantiated, dynamic knowledge representation. Furthermore, the need to provide a scalable solution means that this use of M&S must be augmented via semi-automation of the simulation-creation workflow. Advancing the process of dynamic biological knowledge representation involves: (1) formalizing the expression of biomedical knowledge, (2) being able to tie those representation formats to a classification of M&S methods and approaches, and (3) doing so in a manner that limits the intellectual overhead of non-computer experts among the biomedical research community, which in essence requires the proposed process to generate executable code for simulations. Restated, developing scalable dynamic knowledge representation involves leveraging existing biomedical knowledge representation achieved through ontologies, linking knowledge thus represented with M&S methods to produce dynamics, and semiautomating the process by which this transfer occurs. In the following sections we will deal with each of these steps.

1.2 Biomedical ontologies

Ontologies are knowledge classification systems that provide a structured vocabulary and taxonomy for a particular scientific domain. The benefits of such classification systems include: providing organizational structure to an established corpus of knowledge, allowing a contextual placement of existing and new research, allowing navigation within a particular domain and identification of intersections of knowledge, providing a frame of reference with respect to existing and new terminology, and providing a knowledge base amenable to automated inference with respect to expanding relationship structure. Ontologies emphasize class-structures, properties and taxonomic relationships between the constitutive concepts within the domain. The Web Ontology Language (OWL) and the Resource Description Framework (RDF) currently specify the descriptive capacity of ontologies. This descriptive capacity generally consists of a collection of facts and axioms that define the knowledge about classes, properties and individuals in the ontology. Ontology development methods have expanded into the area of bioinformatics, and as such biomedical ontologies follow these conventions. Bio-ontologies are currently found in an online repository, BioPortal (http://bioportal.bioontology.org), which is managed by the National Center for Biomedical Ontologies (NCBO) (http://www.bioontology.org). The NCBO has ongoing development of computational and bioinformatics tools to increase the utility of bio-ontologies for the biomedical community at large. Additionally, the OBO Foundry (http://www.obofoundry.org) is a collaborative project that is focused on establishing principles for biomedical ontology development with the goal of growing a group of interoperable ontologies to be used in the biomedical arena; a substantial number of the ontologies found in BioPortal originate from the OBO Foundry.

However, despite their usefulness, ontologies/bio-ontologies have a significant limitation in terms of their expressiveness given the goal of evaluating the dynamic behavior of mechanistic hypotheses. Current ontologies generally utilize a limited predicate set focused on classifying objects, concepts and relationships between them, allowing logical inference and proof of the internal consistency of a statement, but not being able to represent any of the dynamic consequences associated with that relationship. Therefore, there is a critical need to expand the predicate expressiveness to “actions” or “functions” to allow the expression of rules necessary to generate dynamics. To some degree, terms corresponding to these function predicates already exist in BioPortal ontologies, but they exist as adjectives that can be applied to other noun-concepts in the various ontologies. For instance, in the Gene Ontology there is class called “Molecular_Function” (GO:0003674) that lists a series of possible functional roles for molecules, such as “Enzyme Regulator Activity” (GO:0030234). However, this in the form of an adjective, and would need to be converted into its verb form in order to be used in a rule. For example, such a rule might be “Compound A modulates the activity of Enzyme B.” The ability to express a rule would require a concatenation of terms from different ontologies, and also may require some transformation of the form of the ontological term. There is already some recognition of these limitations of OWL in the area of Semantic Web research, with ongoing development in languages such as Rule Markup Language (RuleML) (http://www.ruleml.org) and Semantic Web Rule Language (SWRL) (http://www.w3.org/Submissions/SWRL/). The need to use rules to instantiate dynamics moves knowledge representation towards the realm of modeling and simulation (M&S).

1.3 Ontologies in modeling and simulation

As in the biomedical arena, there is interest in the use of ontologies in the area of M&S, particularly in terms of the development and use of ontology-driven M&S (Yilmaz 2007; Miller et al. 2004; Petty and Weisel 2003; Fishwick and Miller 2004; Benjamin et al. 2006). The advantages of an ontology-driven approach can be seen in the development of M&S standards for interoperability, modularity, use of legacy codes/models and federated simulation (Benjamin et al. 2006). The key concept underlying these projects is that of composability: the ability to select and assemble simulation components in various combinations to meet specific simulation use goals (Benjamin et al. 2006; Petty and Weisel 2003). Performing simulation composition is recognized as a dynamic process that evolves during the course of a research/experimental program (Yilmaz 2007), an important realization in terms of addressing the translational challenge. There has also been significant work on the development of ontologies for M&S methods, such as the Discrete-event Modeling Ontology (DeMO) proposed and developed by Miller and Fishwick (Miller et al. 2004; Fishwick and Miller 2004; Silver et al. 2011). DeMO is a “classical” ontology that relies upon a hierarchical “IS/A” class-subclass organizational structure. This allows the application of automated inference methods on DeMO knowledge structures, as is possible with bio-ontologies, but also means that the dynamic expressiveness of a M&S structure within DeMO is limited. However, utilizing the concept of composability along with the domain-specific knowledge in a M&S ontology allows the creation of computational objects that can effectively capture dynamics.

1.4 Ontology concatenation for dynamic knowledge representation

As noted above limitations of the expressiveness of OWL and existing ontologies are based in the inability of current ontologies to express rules. Rules form the basis for instantiating mechanistic relationships, and the ability to express rules forms the key step in moving from static knowledge representation to dynamic knowledge representation. Expressing rules requires extending predicate logic systems to statements that denote functions or actions. This will allow the statements to be converted to dynamic models and simulations, fulfilling a critical role in the use of modeling in biology in overcoming the Translational Dilemma. Due to the complexity of the relationships in biology and the uncertainty with respect to its constitutive statements the importance of a biological model requires not only an assessment of its internal consistency (veracity) but also its mapping to the real world (validity). A biological conceptual model based on a purely logical formalism does not have sufficient expressiveness to assess the application of that conceptual model to the real world: the internal “correctness” of the logical formalism (“true/false”) does not provide enough information to correlate to real world measurements. Since the expression of functional/actionable predicate relationships within an ontology is not possible using OWL, we propose the concatenation of knowledge components from biomedical ontologies using function-representing structures from M&S methods. A key point to this proposal is that while an ontology of M&S methods is limited in its expressiveness to relational predicate statements, the domain knowledge associated with each M&S object/class contains, by necessity given the nature of the M&S domain, a formal description of the simulation method (see DeMO) and therefore becomes the core data for the formal system used to generate the dynamic model. It should be noted that a logical model can be constructed that operates upon either a relational predicate or functional/actionable predicate statement (i.e. a computer program that utilizes the syntax of the statement as a data structure). We propose to use the logical inference capability of a formal system to augment the ability of researchers to operate in the real world. The key to this argument has to do with the different realms between the operations of logic and determinations of “truth” within the knowledge structure, and the relationship between the relationship structure and the real world (validity). Herein we identify a series of formats and protocols to facilitate the process of dynamically composing simulations such that a computational agent can be developed to exercise those protocols.

1.5 Prior work in computational discovery of scientific knowledge

The past few decades has seen increasing research in the computational discovery of scientific knowledge (Džeroski et al. 2007). While originally envisioned as the development of computer systems that could produce new scientific discoveries on par with a human scientist (Langley 2000), the field has grown to encompass creativity processes and computational augmentation of the scientific method both with and without the involvement of the human scientist, i.e. human-in-the-loop and human-out-of-the-loop. Initial research led to the distinction between scientific knowledge structures and scientific activities. Scientific knowledge structures constitute the primary products of the scientific endeavor and consist of taxonomies (or ontologies), laws and theories. Scientific activities are the formation and revision of those scientific knowledge structures, and those activities typically utilize intermediate knowledge structures such as models and experiments to aid in the task. Computational creativity attempts to expand beyond the artificial intelligence problem-solving paradigm, with its well-defined goals and algorithms to achieve them, into an artifact-generating paradigm that incorporates cognitive aspects of creativity and social and cultural interactions (Colton et al. 2009; Chen et al. 2009; Shneiderman 2007). Computational creativity goes beyond scientific discovery to include other creative tasks such as writing poems and jokes, composing music and painting pictures. Computational augmentation of the scientific process focuses upon those intermediate knowledge structures to increase productivity and effectiveness of the primary scientific activities. Through development of computer tools, example augmented tasks include generation and evaluation of models (Yilmaz and Hunt 2011; Bridewell et al. 2006), design of experiments (Zytkow et al.1992), aggregation and management of scientific knowledge (Antezana et al. 2009; Rzhetsky et al. 2000), and construction of scientific workflows (Goecks et al. 2010; Hull et al. 2006; Linke et al. 2011). The research presented in this article falls in the latter category of computational augmentation, specifically the automation of constructing computational models from biological knowledge.

Computational discovery is a daunting task, and for that reason much research has concentrated on the manipulation of well-defined formal structures such as mathematical statements (Montano-Rivas et al. 2010), mathematical equations (Krishnamurthy and Smith 1994; Atanasova et al. 2006), and logic programs (Zupan et al.2007; Karp 2001). Consequently, there has been considerable advance in artificial intelligence algorithms to perform deductive, inductive (Colton and Muggleton 2006; Montano-Rivas et al. 2010; King et al. 2007) and abductive (Prendinger and Ishizuka 2005; Zupan et al. 2007) reasoning for scientific discovery, heralding the day of the robot scientist (King et al. 2009). Furthermore, data mining and machine learning have introduced a new parallel paradigm where patterns are discovered from large data sets, leading to an explosion of bioinformatic tools to analyze and manage the data produced from high-throughput biology experiments and accumulated in biological databases. However, while artificial intelligence approaches have succeeded for some disciplines, such as mathematics and physics where the underlying axioms and physical laws are well established, they have been less successful for biological discovery because the underlying laws that govern the behavior of biological phenomena at higher organizational scales above the physical scale, such as cells, tissues, organisms and ecosystems, are poorly understood. These organizational scales tend to require symbolic versus equation-based representations, and those systems that have been implemented have focused on biochemical reaction networks that draw upon decades worth of knowledge in molecular biology and operate using the physical laws of chemistry (Karp 2001; Calzone et al. 2006; Curti et al. 2004).

Alternatively, our objective is to provide hypothesis evaluation across these multiple organizational scales, and we maintain the human-in-the-loop as part of discovery process because of the invaluable contribution provided by human intuition. To reduce the computer/programming expertise threshold for the researcher we utilize a near-natural language representation for biological knowledge that allows hypotheses to be expressed in the concise way that scientists expect. While this might make the model construction task more difficult for the semi-intelligent agent, we consider this an advantageous approach because it alleviates the problem with many existing systems whereby the biologist must translate their knowledge into an intermediate modeling language. Our approach draws upon artificial intelligence research but instead of attempting to automate discovery, we augment the scientist’s own capability to evaluate hypotheses through modeling and simulation by facilitating the translation of biological knowledge into computational models. While we recognize that in the future a more comprehensive computational augmentation tool would include aiding in the evaluation of models (Yilmaz and Hunt 2011; Bridewell et al. 2006), design of experiments (Zytkow et al. 1992), and construction of scientific workflows (Goecks et al. 2010; Hull et al. 2006; Linke et al. 2011), we assert that computational augmentation of hypothesis representation and instantiation is a necessary step towards these future goals. Therefore, in the next section, we discuss the translation process from biological conceptual models into computational/mathematical model specifications in more detail and demonstrate our method with two biological case studies.

2 Model construction

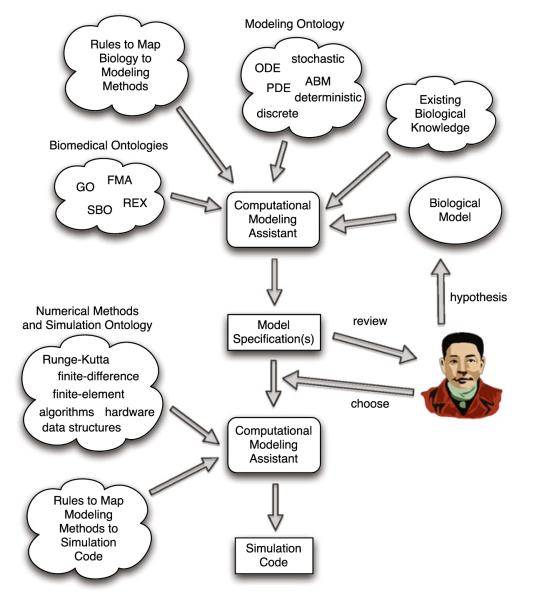
A critical step in developing a robust and scalable solution to the translational dilemma is facilitating the adoption of dynamic computational modeling as a means of knowledge representation within the general biomedical research community. However, at this point in time, the threshold for the average biomedical researcher to engage in computational and mathematical modeling remains prohibitive. The process of transforming biological knowledge and data into computational models requires specific expertise acquired through extensive training and experience. However, we suggest that certain aspects of the modeling process can be characterized algorithmically and then embedded into computational agents to semi-automate model construction. We suggest that the general adoption of M&S-enhanced hypothesis instantiation/evaluation can be aided by the development of software entities that we term a Computational Modeling Assistant (CMA). We propose the CMA as a software tool that augments biological model construction by integrating biological knowledge, computational modeling methodology, and expert-derived rules for mapping biological concepts to modeling methods. Figure 1 gives an overview of the information flow for the interactions between the researcher and the CMA.

Fig. 1.

Overview of workflow and interaction between researcher, computation modeling assistant (CMA) and various ontologies and knowledge databases

The CMA is intended to be agnostic to any specific modeling method, providing possible alternatives using multiple methods as different abstractions of the same biological concept. This latter point is a significant issue, as different aspects of a biological model may be best represented with different simulation methods, resulting in an increasing recognition of the importance of being able to construct hybrid biological models.

2.1 Biological Example #1

To demonstrate how our proposed CMA would be used to instantiate and explore hypotheses for a biological mechanism, we consider as an initial example the formation of the stratified mucus layer in the human colon.

2.1.1 Gut mucus stratification

Many epithelial layers produce and maintain a mucus layer that acts as an additional barrier between the epithelium and the external or luminal environment. In the human colon, epithelial goblet cells secrete mucus that forms a stratified structure composed of an inner “tight” mucus layer and an outer “loose” mucus layer (Johansson et al. 2010). The outer mucus layer is the habitat of the gut bacteria flora while the inner mucus layer is attached to the epithelial cells and is normally devoid of bacteria, thus providing a protective layer to prevent contact between bacteria and the epithelial cells. It is not known how the inner mucus layer is converted into the outer mucus layer, but it is known to be under host control (versus caused by bacteria) because both layers form in bacteria-free mice. Also, mucus conversion is an active chemical process performed by a molecule released by the epithelial cells, as there are no cells in the mucus layer and conversion is inhibited in the inner layer.

We consider a hypothesized mechanism whereby epithelial cells release one or more morphogens that form a spatial gradient where conversion is inhibited near the cells and activated further away from the cells, resulting in the stratified mucus layers. For our biological model, we consider two unknown genes A and B. Inside a cell, the proteins for A and B are bound together into a protein complex AB that is secreted from the cell. AB diffuses in the extracellular space and decays back into the A and B proteins at some rate. Protein A then converts mucus from the tight to loose form, while protein B decays. We formalize our biological model into a set of near-natural language statements that have been annotated with their corresponding bio-ontology term (Gene Ontology (GO), Systems Biology Ontology (SBO), Foundational Model of Anatomy Ontology (FMA), and Physico-chemical Process Ontology (REX)) to produce the enriched communicative biological model given below:

1. goblet cell [GO:0005623] has [GO:has_part] muc2 gene [SBO:0000243].

2. Muc2 gene is transcribed [SBO:0000183] into muc2 mRNA [SBO:0000278].

3. Muc2 mRNA is translated [SBO:0000184] into muc2 protein [SBO:0000252].

4. goblet cell [GO:0005623] has [GO:has_part] A gene [SBO:0000243].

5. A gene is transcribed [SBO:0000183] into A mRNA [SBO:0000278].

6. A mRNA is translated [SBO:0000184] into A protein [SBO:0000252].

7. goblet cell [GO:0005623] has [GO:has_part] B gene [SBO:0000243].

8. B gene is transcribed [SBO:0000183] into B mRNA [SBO:0000278].

9. B mRNA is translated [SBO:0000184] into B protein [SBO:0000252].

10. Goblet cell secretes [GO:0046903] muc2 protein into extracellular space [GO:0005615].

11. A protein and B protein bind [SBO:0000177] to form AB complex [SBO:0000296].

12. Goblet cell secretes AB complex into extracellular space.

13. Extracellular AB complex diffuses [REX:0000122].

14. Extracellular AB complex disassociates [SBO:0000180] into extracellular protein A and B.

15. Extracellular A protein diffuses [REX:0000122].

16. Extracellular B protein diffuses [REX:0000122].

17. Extracellular A protein decays [SBO:0000179].

18. Extracellular B protein decays [SBO:0000179].

19. Extracellular muc2 protein forms inner mucus layer [GO:0070702].

20. Extracellular A protein cleaves [SBO:0000178] extracellular muc2 protein.

21. Cleaved extracellular muc2 protein forms outer mucus layer [GO:0070703].

22. Colon epithelium [FMA:Epithelium_of_colon] is a 2D plane of cells.

2.1.2 Intelligent agent composition

The CMA utilizes and leverages developments in formal knowledge representation through the use of ontologies in biology and M&S by using an intelligent-agent approach based upon a logical framework. It performs automated reasoning to aid in the construction of a computational model (and ultimately simulation code), treating model construction as a planning task where the goal is translating a conceptual biological model into simulation code. The plan is divided into two parts: constructing the model specification and producing the simulation code. As illustrated in Fig. 1, construction of the model specification requires the integration of numerous knowledge databases and ontologies. The researcher hypothesizes a conceptual biological model in a near-natural language format such as demonstrated for gut mucus stratification. This model is then supplemented with a database of existing biological knowledge. Ontologies for biology and modeling concepts are then used with a knowledge base of mapping rules to produce one or more model specifications.

The CMA produces multiple model specifications corresponding to alternative modeling methods. For example, one specification might be for a continuous deterministic model, while another may be a discrete stochastic model. The researcher reviews those model specifications and chooses one or more for the CMA to produce simulation code. This decision is based upon various factors: availability of certain types of biological data, prior knowledge about the behavior of the biological system and level of modeling detail. More than one model specification can be chosen, maybe to compare the different models and determine whether the extra complexity in one model over another is required for the particular biological problem of interest. This is one reason why the human cannot be completely taken out of the loop: because as all models are abstractions of reality, only the researcher has the intuition to assess the usefulness of one model abstraction versus another for the biology being studied.

Given a chosen model specification the CMA can produce simulation code using an ontology of numerical and simulation methods and logical rules to map the model specification into code using particular methods. Here too there may be multiple choices for implementation, though these choices are primarily concerned with stability and performance issues. While these are important issues, we do not explore them further in this article.

2.1.3 Maude logical framework

We implement our system using Maude (Clavel et al. 2007). Maude is a logical framework based on rewriting logic that is simple yet expressive. It provides capabilities such as reflection and formal verification beyond other logical frameworks such as CLIPS or Prolog. These additional capabilities are useful for the CMA as it can provide alternative models and analyze the knowledge database for inconsistencies or gaps.

2.1.4 Biological knowledge representation

Three pieces of biological knowledge need to be represented within Maude in order for the CMA to operate: a list of biomedical ontologies, existing biological knowledge and the conceptual biological model to be instantiated. In order for ontological knowledge representations to be operated on by Maude, ontology data types need to be translated into Maude structures. Towards this end, we translate ontological terms into Maude sorts while the ontology’s IS/A hierarchy is represented by Maude subsorts. Maude sorts correspond to types in programming language theory, so this provides us with customized ontology-derived data types for representing and reasoning about the entities and processes in the biological and M&S knowledge.

The biological knowledge is represented as a series of biological statements whereby the nouns and verbs of the statement are defined according to their ontology term and thus a Maude sort. Figure 2 shows how statement #2 is represented in Maude. The biological entities, muc2-gene and muc2-mRNA, are defined as constant instances of the Maude sorts “gene” and “messenger RNA.” The biological process of transcription is defined as a “transcribe” operator on a “gene” and a “messenger RNA,” and is used to represent a biological statement. Lastly, the biological statement that the muc2-gene is transcribed into muc2-mRNA is stated. Maude supports polymorphism for operators so another transcribe operator could be defined that operates on “pre-messenger RNA,” thus allowing for mRNA processing and alternative splicing to be defined. This flexibility allows multiple levels of biological detail with the appropriate level of abstraction chosen automatically by the types of biological statements.

Fig. 2.

Biological statement #2 from the gut mucus stratification model represented in the Maude language as a set of operators

The diffusion operator shows how the IS/A ontology hierarchy is utilized. While transcription is clearly defined as operating on a gene, many different biological entities can diffuse, thus the “diffuse” operator is defined for the general “material entity” sort as can be seen in Fig. 3. The biological statement that “A-protein[e] (extracellular A protein) diffuses” is valid because “A-protein[e]” IS/A “polypeptide chain” IS/A “information macromolecule” IS/A “macromolecule” IS/A “material entity,” according to the biomedical ontologies.

Fig. 3.

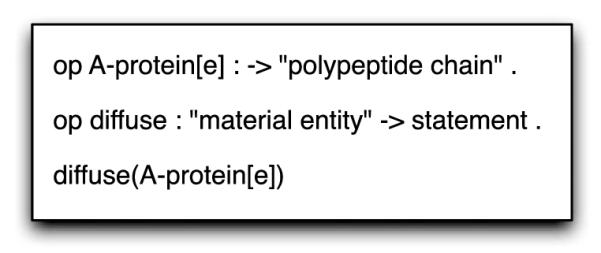
Subsort hierarchy identifying the biological entity A-protein[e] as a material entity

All of the biological statements are thus represented in Maude as logical statements as shown in Fig. 4. As shown, these logical statements would correspond to a set of facts that are asserted as true in other logic systems like CLIPS or Prolog. However, Maude allows for richer expression than propositional logic as in those logic systems, and the statements are closer to first-order logic that have been argued as a more appropriate representation for scientific discovery (King et al. 2007), though Maude is also capable of supporting higher-order logics. This current model lacks some of the biological knowledge about goblet cells and their spatial arrangement in an epithelium layer, which we consider in future work. Maude considers certain biological statements invalid due either to incorrect specification of the biological statement, or because Maude lacks a proper definition of the biological process or entity.

Fig. 4.

Biological model expressed as a set of Maude logical statements

2.1.5 Modeling knowledge representation

The modeling ontology is translated into Maude sorts and subsorts just as with the biomedical ontologies. However the breadth of modeling ontologies is limited in comparison to the biomedical ontologies; therefore we have had to extract this knowledge from published M&S literature. Existing ontologies such DeMO and the Ontology of Physics for Biology (OPB) offer starting points, but accurate and detailed characterization of modeling methods require specific descriptions of mathematical entities such as variables, functions, arithmetic, derivatives, etc. Standards such as OpenMath (http://www.openmath.org) and MathML (http://www.w3.org/Math/) provide some formalization of mathematical knowledge but there are still many challenges related to attempts to catalog mathematical methods that are beyond the scope of this paper. For our current work with the CMA, we have focused on building up a small but sufficient ontology of common modeling methods. This work will continue over time to incorporate additional methods into a more complete ontology.

2.1.6 Mapping rules

Transformation of biological knowledge into a model specification is described by a set of Maude rewrite rules that take one or more biological statements and produce a modeling specification statement. The rules are specific to both the biological statement and the modeling method used to represent the biology. It is these rules that encapsulate the expert knowledge of modelers and the process of model construction.

A set of rewrite rules for the biological functions of transcription, translation, degradation, binding, dissociation, secretion and diffusion can be seen in Fig. 5. These specific rules produce a specification for a continuous model using ordinary differential equations (ODE) or partial differential equations (PDE). Each left-hand side of the rule matches a biological statement and the right-hand side of the rule appends a model specification statement. For the transcribe rule which has two components of the gene (G) and the resultant RNA (R), an ODE is specified for variable R with a Hill function in the variable G. The secrete rule is more complicated with four components of the source molecule (A), source spatial context (CA), the resultant secreted molecule (B), and the resultant spatial context (CB). The secrete rule results in two ODEs added to the model specification, one for the source molecule A and one for the resultant secreted molecule B. The diffusion rule is of interest because it shows that when a molecule diffuses then an ODE is not sufficient, and it becomes a PDE for that molecule variable. These rules all use generic functions like hillFunction, linearFunction, bindFunction, etc., and these can be specified in more detail elsewhere which allow for different and alternative dynamics to be modeled.

Fig. 5.

Maude rewrite rules that describe how various biological statements are translated into a continuous deterministic (ODE and PDE) model specification. Variables such A, B, C, S and M are declared as specific Maude sorts related either to the biological model or the modeling method

The flexibility of Maude rewrite rules allows for complex transformations to be described. There could be situations whereby the method required for two biological statements together is different from either of those biological statements modeled in isolation. These situations typically arise at the interfaces between modeling methods such as with hybrid models that integrate continuous and discrete methods. For example, if a cell secretes a molecule into the extracellular space, then there is an interface between the cell model and the extracellular spatial model that describes how variables in the cell model relate the context of the secrete operation to variables in the extracellular spatial model. If the cell or the extracellular space were specified as individual models, then there would be no need for an explicit representation of the interface between the two models. Rewrite rules can be generated that describe how the interface between different modeling methods should be performed, and those rules can be specialized for a particular biological process. For the secrete operation in Fig. 5, the rules describe a continuous model, so both the cell and the extracellular space are coupled by variables in a set of ODEs.

2.1.7 Model specification construction

There are numerous techniques for computational modeling of biological phenomena. Broad categories include continuous versus discrete and deterministic versus stochastic. Multiple categories can often represent the same biology. For example, molecular interactions can be modeled with ordinary differential equations, a continuous deterministic description, or with stochastic chemical kinetics, which is a discrete stochastic description. As the CMA develops a plan for the specification of the biological model these different modeling techniques correspond to alternative plans: thus there is not a single representation of the biological model but rather numerous potential representations. The CMA provides these alternatives to the researcher such that one or more can be chosen for implementation.

Construction of the model specification is designed as a planning task. The initial state of the task is the set of Maude logical statements representing the conceptual biological model as in Fig. 4. The goal state is a model specification where all of the statements from the conceptual biological have been accounted for in the list of potential computational models. Planning fails if there are one or more biological statements that could not be transformed into a modeling method. This could be due to the lack of a mapping rule for that particular biological entity or process into a M&S method. The CMA uses the Maude search command to find all possible solutions to complete model specifications from the initial biological statements. The search command uses a standard breadth-first search as an inference algorithm that selects mapping rewrite rules to be applied to the set of Maude logical statements, and incrementally constructs the model specification as each mapping rewrite rule is applied. The algorithm creates a state transition graph where goal states correspond to complete model specifications, and a path from the initial state to a particular goal state is the sequence of mapping rewrite rules for transforming the conceptual biological model into a model specification. While Maude uses breadth-first search as the standard algorithm, its meta-level reflection capabilities allow strategies to be defined that control the rewriting inference process. Such strategies are written as part of a mapping rewrite rule, and though they are not required for the examples presented in this article, the CMA can use strategies for high-order reasoning that cannot be performed with first-order logical inference. Furthermore because the exact sequence of rules can be recovered, this enables an explanatory description to be provided to the user about how the biological model was transformed into a computational model, which might be useful for pedagogical or debugging purposes. For the biological model given in Fig. 4, the CMA produces the model specification show in Fig. 6. This model specification is composed of eight ODEs and three PDEs represented by these equations:

$$\begin{array}{cc}\hfill \frac{d\left[\mathit{muc}{2}_{\mathit{mRNA}}\right]}{\mathit{dt}}& =H\left(\mathit{muc}{2}_{\mathit{gene}}\right)\hfill \\ \hfill \frac{d\left[\mathit{muc}2\right]}{\mathit{dt}}& =H\left(\mathit{muc}{2}_{\mathit{mRNA}}\right)-S\left(\mathit{muc}2\right)\hfill \\ \hfill \frac{d\left[A_{\mathit{mRNA}}\right]}{\mathit{dt}}& =H\left(A_{\mathit{gene}}\right)\hfill \\ \hfill \frac{d\left[A\right]}{\mathit{dt}}& =\left(A_{\mathit{mRNA}}\right)-B(A,B)\hfill \\ \hfill \frac{d\left[B_{\mathit{mRNA}}\right]}{\mathit{dt}}& =H\left(B_{\mathit{gene}}\right)\hfill \\ \hfill \frac{d\left[B\right]}{\mathit{dt}}& =H\left(B_{\mathit{mRNA}}\right)-B(A,B)\hfill \\ \hfill \frac{d\left[\mathit{AB}\right]}{\mathit{dt}}& =B(A,B)-S\left(\mathit{AB}\right)\hfill \\ \hfill \frac{d\left[\mathit{muc}{2}_E\right]}{\mathit{dt}}& =S\left(\mathit{muc}2\right)\hfill \\ \hfill \frac{d\left[A_E\right]}{\mathit{dt}}& ={\nabla }^2{A}_E+D\left(\mathit{AB}\right)-k_1{A}_E\hfill \\ \hfill \frac{d\left[B_E\right]}{\mathit{dt}}& ={\nabla }^2{B}_E+D\left(\mathit{AB}\right)-k_2{B}_E\hfill \\ \hfill \frac{d\left[{\mathit{AB}}_E\right]}{\mathit{dt}}& ={\nabla }^2{\mathit{AB}}_E+S\left(\mathit{AB}\right)-D\left({\mathit{AB}}_E\right)\hfill \end{array}$$

where H, S, B and D are the hillFunction, secreteFunction, bindFunction and dissociateFunction functions.

Fig. 6.

Model specification produced by CMA for gut mucus stratification model

2.1.8 Model parameters

In our example for gut mucus stratification, the model specification uses generic names for various interaction functions such as hillFunction, bindFunction, etc. However, these functions can be defined in more detail, allowing the CMA to perform additional modeling and simulation capabilities. For example, the CMA could query the number and type of parameters required for each function. That list of parameters could be passed to another process that executes parameter sweeps for the simulation. Likewise, the CMA could query existing biological knowledge to find experimentally determined values such as transcription rates, degradation rates, diffusion rates, etc. to be used as initial values for those parameters.

2.1.9 Simulation code

The final step for the CMA is to produce simulation code that can be executed from the model specification. Here the CMA utilizes an ontology categorizing various numerical and simulation methods along with a set of mapping rules to transform the model specification into simulation code using specific numerical methods. There has been even less effort devoted to formalizing such numerical and simulation method knowledge into a machine-readable format, and we are not aware of any existing ontologies with this information.

Just as with construction of the model specification, multiple numerical methods can be applied for the simulation of the same model. These alternatives are typically concerned with computational and stability issues. They play less of a role regarding interpretation and analysis of the biological model, but they are important for insuring the simulation produces valid results. For example, a Runge-Kutta 4th-order method could provide greater stability and a larger time step over the basic Euler method, though it may have a greater computational cost. CMA might be able to analyze the parameter values for the model, looking for order of magnitude scale differences that indicate a stiff system, thus requiring more stable methods to be used. Furthermore, CMA could take advantage of information about the hardware, thus producing simulation code that is geared towards a specific computing environment whether it be a single computer, multi-core processor, parallel MPI cluster, or a GPU. While this scalability across hardware platforms is not gained for free, over time as the knowledge database of numerical and simulation methods increases, more of this capability can be provided in an automated fashion.

2.1.10 Alternative hypotheses

One advantage of using an approach such as the CMA is the increased throughput gained by the ability to easily pose and investigate alternative hypotheses. With our gut mucus stratification model, we can consider a slight modification to our model that still utilizes the mechanism of morphogen gradients. In this alternative hypothesis, A and B are secreted by the cells individually, and protein A diffuses faster than protein B. Extracellular protein A and B form a complex AB which then decays. Proteins A and B also decay at some rate, and protein A converts mucus from tight to loose form as before. The idea behind this model is that the AB complex binding prevents protein A from converting the mucus near the cells, but the faster diffusion rate of protein A means it accumulates in greater concentration than protein B further from the cells, thus allowing mucus conversion to occur. This alternative model would remove statements 11–14 from the original hypothesis, and add the following statements.

1. Goblet cell secretes [GO:0046903] A protein into extracellular space [GO:0005615].

2. Goblet cell secretes [GO:0046903] B protein into extracellular space [GO:0005615].

3. Extracellular A protein and B protein bind [SBO:0000177] to form AB complex [SBO:0000296].

4. 4. Extracellular AB complex decays [SBO:0000179].

The CMA could readily generate a new model specification and simulation code for this alternative hypothesis. Furthermore, the CMA could carry over parameter values and choices made regarding the original model specification and implementation methods to the alternative model, thus ensuring a close correspondence and effective comparison of the results predicted by the two simulations. By reducing the degree of implementation detail required, the CMA allows the researcher to maintain focus at the level of the biological model during the course of exploring model possibility-space. This type of computational augmentation of the hypothesis evaluation stage would facilitate the parallelization of identifying plausible mechanisms and aid in reducing the process bottleneck present in biomedical research.

2.1.11 Biological Example #2

Having described the general process by which the CMA can semi-automate the translation of a biological model into a computational one, we present another example that uses a different target M&S method. In this case, the biological model being transformed is that of an intracellular pathway that involves receptor activation, signal transduction, gene transcription and protein synthesis. While many pathways of this sort have been modeled using ODEs, in the interest of demonstrating the capabilities of the CMA we choose a discrete alternative, Petri nets, to the deterministic continuous ODE. Petri nets are a graph-based modeling formalism that has been used for mathematical modeling of molecular pathways and networks, and are a popular means of capturing stochastic and qualitative dynamics from such pathways (Chaouiya 2007; Goss and Peccoud 1998). For our example we will use a virulence factor activation pathway found in the bacteria, Pseudomonas aeruginosa.

2.1.12 Virulence activation in Pseudomonas aeruginosa by the host immune response

The bacterial species P. aeruginosa is a gram negative bacillus that is one of the most dangerous bacteria in terms of hospital acquired infection (Obritsch et al. 2005). P. aeruginosa is noted for its ability to develop resistance to antibiotics as well as activate a series of virulence mechanisms causing it to change from a relatively benign species to a dangerous one. P. aeruginosa is normally found in the colon of healthy humans, being one of the multitude of microbial species that reside in the human intestinal tract. Under normal healthy circumstances, there is no adverse consequence resulting from the presence of P. aeruginosa in the host colon. However, recently P. aeruginosa virulence expression has been identified as responding to host tissue factors released by the gut in response to physiologic stresses seen in hospitalized patients, such as immune activation (Wu et al. 2005). For purposes of our example for the CMA we will focus on the sensing of host immune response factor, interferon-γ (IFN-γ), and the subsequent virulence pathway activated in response to bacterial binding of IFN-γ. It has been identified that in P. aeruginosa, the immune mediator, interferon-γ induces the expression of virulence factors that in turn reduce host defenses (Wu et al. 2005). IFN-γ binding to outer bacterial membrane receptor OprF activates the expression of PA-I lectin, a compound secreted by P. aeruginosa that attacks the connections between intestinal epithelial cells, leading to breakdown of gut barrier defenses and allowing potential bacterial invasion. Up regulation of the transcription factor RhlI during exposure to IFN-γ represents an intermediate step between the molecular signaling and gene activation (the target regions being identified as Lux box for the promoter gene region and LecA as the coding gene region) leading to the production of PA-I lectin.

Using the same, near-natural language syntax described previously above, the biological model of the immune activation of PA-I production is as follows:

1. Pseudmonas is a bacteria

2. Pseudomonas has OprF [VO:0012360]

3. OprF [VO:0012360] is a receptor [SBO:000024]

4. Interferon-γ bind to [SBO:0000177] OprF [VO:0012360] to form Interferon-γ - OprF-complex [SBO:0000179]

5. Interferon-γ -OprF-complex decays

6. Interferon-γ is a ligand [SBO:0000280]

7. Pseudomonas has Rh1RI

8. Rh1RI is a transcription factor [GRO:TranscriptionFactor]

9. Interferon-γ -OprF-complex is a stimulator [SBO:0000459] of Rh1RI

10. Pseudomonas has Lux box

11. Lux box is a gene regulatory region [SBO:0000369]

12. Rh1RI bind to [SBO:0000177] Lux box to form Rh1RI-Lux box-complex

13. Rh1RI-Lux box-complex disassociates into Rh1RI and [SBO:0000177] Lux box

14. Pseudomonas has LecA

15. LecA is a gene [SBO:0000243]

16. Rh1RI-Lux box-complex positively regulates transcription [GRO:PositiveRegulationOfTranscriptionByTranscriptionActivator] of LecA

17. LecA is transcribed [SBO:0000183] into PA-I lectin mRNA

18. PA-I lectin mRNA is translated [SBO:0000184] into PA-I lectin

19. PA-I lectin mRNA decays

20. Pseudomonas secretes [GO:0030528] PA-I lectin into extracellular compartment [GO:0005615].

2.1.13 Mapping rules and model specification creation

As in the process delineated above, the virulence pathway biological model was presented to the CMA, translated into a set of Maude logical statements, and then the application of the Maude logical rewrite rules shown in Fig. 7 produced a Petri net model. The resulting model is shown in Fig. 8.

Fig. 7.

Maude rewrite rules that describe how various biological statements are translated into a Petri net model specification. Variables such A, B, C G, TG, S and M are declared as specific Maude sorts related either to the biological model or the modeling method

Fig. 8.

Petri net model specification produced by CMA for the Pseudomonas aeruginosa virulence activation pathway. The Petri net model is composed of a set of variables for the biological entities (places in Petri net formalism) and a set of transition rules. The transitions consist of pre-conditions, post-conditions, and a rate function currently defined as constantFunction. The initial state is defined outside of the model specification

It should be noted that an additional output of this process was an error statement:

“polypeptide chain” entities “OprF,” “interferon-gamma,” “RhlRI,” has no “translate”

This statement resulted from the fact that some of the entities listed in the biological model did not have a rule leading to their production. However, rather than considering this error statement as rendering the biological model invalid, these entities would be presented back to the researcher as variables in the model that require initialization values; i.e. the input values for simulation execution.

The above model specification can be described in standard notation for biochemical rules:

PA-I-lectin-mRNA	→	∅
PA-I-lectin-mRNA	→	PA-I-lectin-mRNA + PA-I-lectin
PA-I-lectin	→	PA-I-lectin[e]
interferon-OprF-complex	→	∅
interferon-OprF-complex	→	interferon-OprF-complex + RhlRI
RhlRI-Lux-box-complex	→	Lux-box + RhlRI
OprF + interferon-gamma	→	interferon-OprF-complex
Lux-box + RhlRI	→	RhlRI-Lux-box-complex
lecA + RhlRI-Lux-box-complex	→	lecA + RhlRI-Lux-box-complex + PA-I-lectin-mRNA

As with the gut mucus model example, the conversion of the base Petri net model into simulation code would involve a selection by the researcher among a set of subcategories of Petri nets based on their specific properties, such as deterministic or stochastic, and the characteristics of the system under study. Furthermore, as described in Example #1, the CMA could also have generated an ODE model of the virulence activation pathway; in practice, the biological model of virulence activation would have been inputted into the CMA and both a Petri net and an ODE model (among, perhaps, other types) would be generated, each with suggested parameters based on the requirements of the particular modeling method, and the researcher would select one or the other (or perhaps even both) based on the initialization data available or the desired dynamics to be investigated. Additionally, future development of the CMA would include the capability to parse the biological model and determine which components of the model would be suitably represented with deterministic methods (such as signal transduction) and which components would be best represented with stochastic approaches (such as gene binding and activation), resulting in a hybrid method model.

3 Summary

In this paper we present a description of how a semi-intelligent computational agent can augment the process of computational biological model construction by utilizing bio-medical and M&S ontologies to generate simulation code for dynamic knowledge representation. We suggest that the use of a CMA can aid in addressing the current throughput issues facing the biomedical research community regarding hypothesis instantiation, verification and validation. As noted above, the eventual goal of the computational solution to the Translational Dilemma will require the expansion of the CMA’s planning and analysis capabilities to include model behavior assessment, anomaly identification, suggesting alternative hypotheses/solutions and the design of putative experiments to evaluate these new hypotheses, and scientific workflows (Hull et al. 2006; Zytkow et al. 1992; Yilmaz and Hunt 2011; Bridewell et al. 2006; Linke et al. 2011; Goecks et al. 2010). However, achieving these goals will require biological knowledge to be in a formal, computable format such that a wide range of machine learning, model checking, automated inference and AI-planning methods can be employed. Therefore, the current developmental focus of the CMA is on the necessary first step of enhancing the conversion of biological knowledge into the computational and mathematical formal structures that would allow for the development and implementation of these capabilities. As such the CMA represents a potentially robust and scalable strategy for enhancing the utilization of dynamic computational models by the general biomedical research community via semi-automation of the specification-mapping work associated with computational model development. By utilizing the meta-programming capabilities of the Maude system, specifically related to its rewriting logic and reflection properties, the CMA leverages ongoing development in bio-ontologies, formal knowledge representation and M&S methods to facilitate the generation of simulation code. It is important to recognize that while the overall translational goal cannot be achieved using only logic-based systems, the implementation of computational models using logical inference can aid in achieving the greater research goal of instantiating conceptual models. Treating the steps of the model construction process as a planning task can improve the modularity, robustness and scalability of knowledge integration through the introduction of a new class of meta-programming semi-intelligent computational agents. This would allow the focusing of future development on the CMA’s inference instruction set. Given its role as a “translator” between biological models and M&S methods, future research can be targeted at advancing the CMA’s capabilities and expressiveness while maintaining interoperability with established but ongoing development in the areas of formal semantics/knowledge representation and M&S methods. From the biological side, future development of the CMA would include the ability to read and integrate models expressed in XML and Resource Description Framework (RDF) compatible formats (Cuellar et al. 2003; Hedley et al. 2000; Bullivant et al. 2001; Hucka et al. 2003). This would allow leveraging of existing model repositories expressed in those markup languages being used to standardize model sharing in the biomedical community, such as Systems Biology Markup Language (SBML) (Hucka et al. 2003) and Cell Markup Language (CellML) (Cuellar et al. 2003). Development from the M&S community has a bit farther to go, though OpenMath and MathML may provide the initial steps toward cataloging M&S methods in a computable form. We believe that the process automation advances offered by the CMA will lead towards the development of cyber-environments providing scalable high-throughput hypothesis evaluation.

Biography

Scott Christley is an Associate Professor of Surgery at the University of Chicago and the President of the Swarm Development Group. He has for over 11 years been involved in the use of agent-based modeling to address the translational challenge in biomedical research, specifically in the use of agent-based modeling for dynamic knowledge representation, and integration of bioinformatics methods.

Gary An is a Research Associate in the Department of Surgery at the University of Chicago. He has over 20 years of experience in software design and development, and 6 years experience developing computational methods for simulating biological systems.