Oxygen Consumption Rates of Bacteria under Nutrient-Limited Conditions

Abstract

Many environments on Earth experience nutrient limitation and as a result have nongrowing or very slowly growing bacterial populations. To better understand bacterial respiration under environmentally relevant conditions, the effect of nutrient limitation on respiration rates of heterotrophic bacteria was measured. The oxygen consumption and population density of batch cultures of Escherichia coli K-12, Shewanella oneidensis MR-1, and Marinobacter aquaeolei VT8 were tracked for up to 200 days. The oxygen consumption per CFU (Q_O2) declined by more than 2 orders of magnitude for all three strains as they transitioned from nutrient-abundant log-phase growth to the nutrient-limited early stationary phase. The large reduction in Q_O2 from growth to stationary phase suggests that nutrient availability is an important factor in considering environmental respiration rates. Following the death phase, during the long-term stationary phase (LTSP), Q_O2 values of the surviving population increased with time and more cells were respiring than formed colonies. Within the respiring population, a subpopulation of highly respiring cells increased in abundance with time. Apparently, as cells enter LTSP, there is a viable but not culturable population whose bulk community and per cell respiration rates are dynamic. This result has a bearing on how minimal energy requirements are met, especially in nutrient-limited environments. The minimal Q_O2 rates support the extension of Kleiber's law to the mass of a bacterium (100-fg range).

INTRODUCTION

Heterotrophic bacterial respiration constitutes 50% to 90% of ocean community respiration (1) and plays a critical role in the recycling of organic carbon in all natural environments (2). Despite this importance, respiration remains poorly quantified in ocean models of metabolism, gas exchange, and carbon mass balances (3). This uncertainty in heterotrophy makes it difficult to predict when areas of the ocean will be sources or sinks of CO₂ (4). Microbial community ecosystem behavior is ultimately a function of auto- and heterotrophic relationships; hence, understanding the biogeochemical contribution of heterotrophic bacteria at the single-cell level is necessary for making predictions of how ecosystems will respond to global change (5). Extracting this information is difficult. Efforts are being made with single-cell observatories designed to trap cells in microwells and monitor their consumption of oxygen over time using optical techniques (6, 7). Field-based approaches involve modeling oxygen pore water profiles in marine sediments and dividing oxygen consumption rate by cell numbers (8). A more frequently employed method for analyzing cellular respiration rates is to determine bulk oxygen uptake (consumption) rates (OUR), using either batch or continuous cultures with large populations of microbes. The average cellular respiration rate is calculated by normalizing OUR to population size. Most studies of this nature determine respiration rates while cells are growing (9–14). In the rare cases where respiration was measured after cells exited exponential-phase growth (15, 16), respiration rates dropped significantly—presumably as the cells became increasingly nutrient limited. The decline in oxygen consumption rates with time in both studies suggests that continuation of the experiments could have yielded a lower oxygen consumption rate. Batch cultures of bacteria can survive without the addition of fresh nutrients for periods of months (17) or even years (18, 19) by utilizing strategies such as cryptic growth (20–23) and expression of the growth advantage in stationary phase, or GASP, phenotype (24–31). The GASP phenotype is characterized by the appearance of spontaneous mutations conferring novel activities, including alternative metabolic processing, which results in mutants of increased relative fitness. Therefore, we studied how adaptations to starvation, cryptic growth, and the emergence of GASP mutants affect respiration rates. The goal of this study was to compare respiration rates for bacteria in a nutrient-abundant state versus a nutrient-limited state through a much longer time range than previously measured.

Oxygen consumption rates, CFU, counts of respiring cells, and counts of live (L) and dead (D) cells were measured over a 200-day time series in batch cultures of Escherichia coli K-12 strain ZK126 (32), Shewanella oneidensis MR-1 (33, 34), and Marinobacter aquaeolei VT8 (35). These strains were selected for analysis because of their diverse range of metabolic capabilities and because two of these bacterial genera, Shewanella and Marinobacter, are found in marine systems (Table 1). Our results are discussed in the context of environmental oxygen consumption rates in marine sediments and in terms of how cell survival strategies and evolution during starvation affect respiration.

Table 1.

Characteristics of bacterial strains used in this study cultured in LB/5 media at 24°C^a

Strain	Metabolic description	Fermentation	μmax (h−1)	Kb (CFU ml−1)	DP	QO2(max)b (μmol O2 CFU−1 day−1)	OUR(max) (μmol O2 ml−1 day−1)	QO2(min)b (μmol O2 CFU−1 day−1)	OUR(min) (μmol O2 ml−1 day−1)
Escherichia coli K-12	Facultative anaerobe	Mixed acid	0.42 ± 0.02	8.8 ± 0.2	44	−6.7 ± 0.2	10	−9.6 ± 0.7	0.09
Shewanella oneidensis MR-1	Facultative anaerobe	Nonfermenting	0.35 ± 0.06	8.5 ± 0.2	4	−6.5 ± 1.8	25	−7.9 ± 1.0	0.07
Marinobacter aquaeolei VT8	Facultative mixotrophic iron oxidizer	Mixed acid	0.30 ± 0.08	8.9 ± 0.5	17	−6.3 ± 1.2	2.2	−8.9 ± 0.5	0.06

^aμ_max is the maximum growth rate observed during the initial growth phase. K is the maximum population size. DP is the approximate day of the onset of death phase. Q_O2(max) and Q_O2(min) refer to maximum and minimum oxygen consumption rates per CFU measured. OUR(max) and OUR(min) refer to the maximum and minimum levels of oxygen consumption per volume. μ_max, K, and Q_O2 and their associated 90% confidence intervals are derived from Fig. 1 regressions. OUR values are from direct measurements.

^bValues are reported as log₁₀.

Finally, the history of respiration studies versus organism size includes the well-studied “Kleiber's law” (36), which describes the relationship between animal body mass and metabolic rate at rest. The small body mass of the heterotrophic bacteria used in this study affords an opportunity to test if the Kleiber law can correctly predict metabolic rates for some of the smallest known organisms.

MATERIALS AND METHODS

Experiments were conducted using three bacterial strains: Escherichia coli K-12 strain ZK126, Shewanella onedeisis MR-1, and Marinobacter aquaeolei VT8 (Table 1). Bacterial incubations and analyses were performed in a temperature-controlled room set to 24 ± 1°C. This room was kept dark except for short periods of sample manipulation. Water pretreated by reverse osmosis was used throughout the study and was further purified (Millipore) to >18.0 M Ω/cm and sterilized for 20 min at 121°C in an autoclave (STERIS Corporation). The medium used in all experiments was Luria-Bertani Lennox broth (EMD Biosciences) diluted to 1/5 the original concentration (LB/5), resulting in a final concentration of 1 g liter⁻¹ NaCl. Culture flasks were foil capped and orbitally shaken at 120 rpm.

Four different experiments performed with various culture volumes, sampling frequencies, durations, and analyses are reported here: a high-frequency sampling experiment, a low-frequency sampling experiment, a visualization experiment, and a long-term experiment.

(i) High-frequency sampling experiment.

Experimental cultures (250-ml flasks with 100 ml of LB/5) were inoculated with 2 μl of overnight cultures of E. coli, MR-1, or M. aquaeolei grown from frozen stocks. E. coli and MR-1 were analyzed for population density (CFU ml⁻¹) approximately daily for 25 days, while M. aquaeolei was analyzed for 20 days.

(ii) Low-frequency sampling experiment.

Cultures were initiated as described above, except 1-liter flasks with 500 ml of LB/5 were used. E. coli and MR-1 cultures were analyzed for CFU and OUR (tube respirometer; see below) with a sampling frequency of approximately every 3 to 5 days for 61 days of incubation; M. aquaeolei was analyzed on days 1.2, 3.2, 32, and 37.

(iii) Visualization experiment.

Two cultures of E. coli were initiated exactly as described for the low-frequency sampling experiment. Cultures were analyzed for CFU, OUR (tube respirometer), cell size, and numbers of respiring cells, live cells, and dead cells with a sampling frequency of approximately every 3 to 5 days for 78 days.

(iv) Long-term experiment.

Three replicates of E. coli, MR-1, and M. aquaeolei were initiated as described above, except 250-ml flasks with 75 ml of LB/5 were used. Cultures were analyzed for CFU and OUR using a capillary respirometer (see below) with a sampling frequency of ∼5 to 10 days, starting after 20 days of incubation and continuing to day 200. Evaporative loss was monitored monthly by weight. When water loss exceeded 5%, it was replaced with sterilized water purified to >18.0 M Ω/cm.

(v) Oxygen consumption analysis.

The OUR of culture subsamples was measured with either a tube or capillary respirometer; both detect the dissolved oxygen (DO) concentration of a solution with a 50-μm-diameter Clark-type oxygen microsensor (Unisense, Denmark). The sensor was calibrated daily using the two end values as standards. Zero μM was achieved by scrubbing a 1 g liter⁻¹ NaCl solution of all DO by either supersaturating the solution with sodium sulfite or vigorously bubbling the solution and maintaining the headspace with nitrogen gas. Atmospheric oxygen saturation was achieved by allowing a solution of 1 g liter⁻¹ NaCl to exchange with the atmosphere with gently stirring for >12 h. The microsensor response to saturation was translated to DO concentration values using salinity-temperature-solubility tables provided by Unisense (37).

The tube respirometer used 400 μl of culture transferred into a sterile borosilicate glass test tube (VWR, Radnor, Pennsylvania) (6 by 50 mm [outer diameter by length]). Samples were continuously stirred with a Teflon-coated stir bar (VWR) (2 by 7 mm). If the sample DO concentration was initially below 200 μM, oxygen was injected into the respirometer by bubbling the sample with atmospheric air (delivered via a sterile needle) until the concentration reached >250 μM. When the initial DO concentration was >250 μM, the tube was sealed by layering 200 μl of white light mineral oil (Mallinckrodt, St. Louis, MO) over the sample. Stirring the sample did not disturb the mineral oil layer. The oxygen concentration in the tube respirometer was logged at intervals of 5 to 10 s with Profix (Unisense) computer software. The change in DO concentration with time was fitted with a linear regression after an equilibration period of 20 to 30 min (examples are provided in the supplemental material). The linear regression generates a negative slope (m) which is a function of two terms, m = (−OUR + LR), where OUR is the oxygen uptake rate (in μmol ml⁻¹day⁻¹) and LR is the leak rate (in μmol ml⁻¹day⁻¹). To establish the rate of oxygen leakage into the tube respirometer system, the increase of the DO concentration in a solution of 1 g liter⁻¹ NaCl was measured. This solution was scrubbed of all DO with N₂ gas before loading into the respirometer (the rest of the setup was identical to that described above for tube respirometer samples). Based on the increase of the DO concentration with time, three linearly approximated LRs (<210, 210 to 240, and 240 to 265 μM = 0.8 ± 0.3, 0.06 ± 0.03, and 0.02 ± 0.004 μmol ml⁻¹ day⁻¹, respectively; see the supplemental material) were established for the typical concentration ranges measured for samples. Our criterion for detectable oxygen uptake rate data was that the measured slope had to be 3× greater than the leak rate.

The capillary respirometer used approximately 15 μl of the culture transferred into a sterile closed-bottom borosilicate glass capillary tube (Kimble Chase, Vineland, NJ) (1.5 by 20 mm [diameter by length]) via syringe injection. Following the addition of the sample, 5 to 15 μl of mineral oil was layered over the sample via syringe. To dampen temperature fluctuations, the capillary tube was suspended in a water bath. The oxygen microsensor was inserted into the capillary tube to a depth of 3 mm below the oil/sample interface. These samples were not stirred. About 30 min following the insertion of the microsensor (to allow for electrode equilibration with the new solution), the DO concentration was logged for over 1 h and fitted with a linear regression. OUR was calculated based on the slope of the linear regression, corrected for LR, in the same manner as described for the tube respirometer. All slopes measured were linear, with r² > 0.85. The capillary respirometer required a more elaborate equation for LR than the tube respirometer because the capillary oil layer thicknesses differed from sample to sample (because it was difficult to consistently add the same amount of oil via needle injection to each sample). To establish the rate of oxygen leakage into the capillary respirometer, the increase in oxygen concentration of a 1 g liter⁻¹ NaCl solution (scrubbed of oxygen with N₂ gas) was measured over time with a setup identical to that described above. The relationship between LR (in μmol ml⁻¹ day⁻¹) and mineral oil layer thickness (Ω, in vertical mm) was determined as follows:

$$\mathrm{L}\mathrm{R}=(0.105)[e^{-0.275(\mathrm{\Omega })}];r^2=0.88$$

This equation applied to a DO range of 240 to 265 μmol liter⁻¹ and to oil coverage from 7 to 20 mm thick. To correct for the absence of stirring, a relationship between stirred and unstirred standards (covering a 240 to 265 μM DO concentration range) was determined as follows:

$$m_{\mathrm{C}\mathrm{S}}=(1.935)(m_{\mathrm{N}\mathrm{S}})-0.085;r^2=0.99$$

where m_CS is the corrected slope (in μmol O₂ ml⁻¹ day⁻¹) and m_NS is the nonstirred slope (in μmol O₂ ml⁻¹ day⁻¹). This correction was applied to all m_NS values greater than 0.044 μmol ml⁻¹ day⁻¹.

(vi) CFU analysis.

The number of cells capable of forming a colony was determined (in CFU) with the drop plate method (38). A dilution series was created of 1:10 dilutions with a final dilution of 10⁻⁸. Triplicate drops (10 μl each) of the eight dilutions were dispensed onto LB/5 1.5% agar petri dishes (100 by 15 mm). Drops were allowed to dry by evaporation, plates were incubated at 24°C, and the numbers of colonies per spot were determined. The detection limit of this method is 1,000 CFU ml⁻¹. Based on equation 8 of Herigstad et al. (38), the standard deviation of CFU values is calculated to be ∼10%. This calculation was confirmed by comparing the reproducibilities of the CFU values of replicate drops (data not shown).

(vii) Microscopic visualization analyses.

We used an Eclipse Ti-E microscope (Nikon, Melville, NY) equipped with a mercury lamp and appropriate filters to produce images of cells. Drift in the fluorescence intensity of the microscope was monitored at each session by imaging fluorescent polystyrene MultiSpeck multispectral microspheres (Invitrogen, Carlsbad, CA) (4.0 μm diameter) under a fluorescein isothiocyanate (FITC) HYQ filter (excitation, 460 to 500 nm; emission, 510 to 560 nm). Measured fluorescence was normalized to these standard microsphere emissions.

(viii) Cell size analysis.

E. coli cultures of the visualization experiment were analyzed for cell size. Formaldehyde (2% [vol/vol])-fixed cells mixed with fluorescent polystyrene MultiSpeck multispectral microspheres (4.0 μm diameter) were wet mounted on a glass slide (7 μl of sample under a 22-by-22-mm glass coverslip) and imaged using ×400 magnification phase-contrast (PC) microscopy. Cell lengths and widths were determined by comparisons to fluorescent microspheres of known size with the assistance of the measuring tools of ImageJ version 1.43u software (39). The error bars reported (see Table S1 in the supplemental material) represent the standard deviation of 10 to 20 cells measured per time point.

(ix) PC cell counts.

A 7-μl volume of culture medium containing cells was wet mounted, and multiple fields of view (FOV) per slide were photographed using ×200 magnification. For each FOV analyzed on the microscope, a phase-contrast (PC) image was captured (exposure, 6 to 12 ms). The same FOV was used to capture a fluorescent image. This allowed fluorescent image counts (discussed below) to be normalized to the number of PC cells present. PC images were processed in ImageJ software (39). First, the image was converted into a binary black and white format with the “Threshold” command set to the default algorithm that is based on an iterative isodata algorithm. This sets a threshold at the average of the average black and average white values (40). Once the data are converted to binary intensities, any objects larger than 0.8 μm² containing a pixel brighter than the threshold were scored as representing a cell using the “Analyze Particles” command. The “Analyze Particles” command scans the image for an edge, selects the region inside the edge (the cell), assigns a score to the region, fills the region with the background (to prevent recounting), and moves to the next edge.

(x) Respiring-cell-count analysis.

The dye RedoxSensor Green (Invitrogen) was used for staining and imaging cells for analysis of the E. coli cultures of the visualization experiment for determining respiring-cell counts (RG). RedoxSensor Green is a stain that fluoresces (excitation, 490 nm; emission, 520 nm) when reduced and is therefore an indicator of bacterial reductase activity and changes in electron transport chain function (41). Staining included a 10-min incubation of 0.5 ml of cells at room temperature with 0.5 μl of RedoxSensor Green reagent (1 mM solution in dimethyl sulfoxide). Following incubation, samples were immediately fixed with formaldehyde (2% [vol/vol]). A volume of 7 μl of the stained and fixed cells was wet mounted on a glass slide, and multiple FOVs were imaged with phase-contrast and fluorescence microscopy using an FITC HYQ filter (excitation, 460 to 500 nm; emission, 510 to 560 nm) with mercury lamp illumination. The background (approximated as the image mode pixel intensity) of each image was subtracted, and the images were scaled to a microsphere fluorescence standard. A series of brightness thresholds were applied to the normalized images, and any objects larger than 0.8 μm² and containing a pixel brighter than the threshold were scored as representing cells. The initial brightness threshold applied was 400 normalized gray-scale units (ĝ), and each subsequent threshold was increased by 100 units until the image maximum intensity was reached. Fluorescent-cell counts were normalized to a percentage of the PC count generated on the same FOV. To determine the percentage of cells present within a specific ĝ interval, each threshold percentage had the next (higher) threshold percentage subtracted from it. This generated a percentage of PC cells respiring for each 100-ĝ interval. The value reported for a particular interval represented an average of 5 to 13 FOVs. The standard deviations of the FOV percentages are reported. Interval percentages determined to be outliers (95% certain with Grubb's test [42]) were not included in the average or standard deviation reported. The final interval includes all cells brighter than 9,800 ĝ.

(xi) L and D cell count analysis.

The E. coli cultures of the visualization experiment were analyzed for live (L) and dead (D) cell counts by staining cells with a combination of SYTO 9 and propidium iodide (PI) (Invitrogen). SYTO 9, a green fluorescent nucleic acid stain (excitation, 485 nm; emission, 498 nm), is membrane permeative. PI, a red fluorescent nucleic acid stain (excitation, 490 nm; emission, 520 nm), is not membrane permeative and can enter the cell only if the membrane is damaged. In the presence of PI, SYTO 9 fluorescence is quenched. Cells that stain green are considered “live” cells, while those that stain red are considered “dead” cells even though they still contain nucleic acid. Staining included incubating 0.5 ml of cells at room temperature (10 min) with 0.25 μl of SYTO 9 reagent (5 mM solution in dimethyl sulfoxide [DMSO]) and 0.5 μl of PI reagent (20 mM solution in DMSO) followed by fixation with formaldehyde (2% [vol/vol]). A 7-μl volume of cells was wet mounted, and multiple fields per slide were imaged using ×200 magnification phase-contrast and fluorescence microscopy with a microscope fitted with an FITC HYQ filter (excitation, 460 to 500 nm; emission, 510 to 560 nm) to visualize live cells and then a tetramethylrhodamine isothiocyanate (TRITC) HYQ filter (excitation, 530 to 560 nm; emission, 590 to 650 nm) to visualize dead cells. Images were corrected for background and scaled to microsphere intensity in the same manner as described for the respiring-cell-count analysis. Objects larger than 0.8 μm² and brighter than a threshold of 1,800 ĝ, when stained with SYTO 9, were scored as L. Objects larger than 0.8 μm² and brighter than a threshold of 1,500 ĝ, when stained with PI, were scored as D.

RESULTS

(i) Population density.

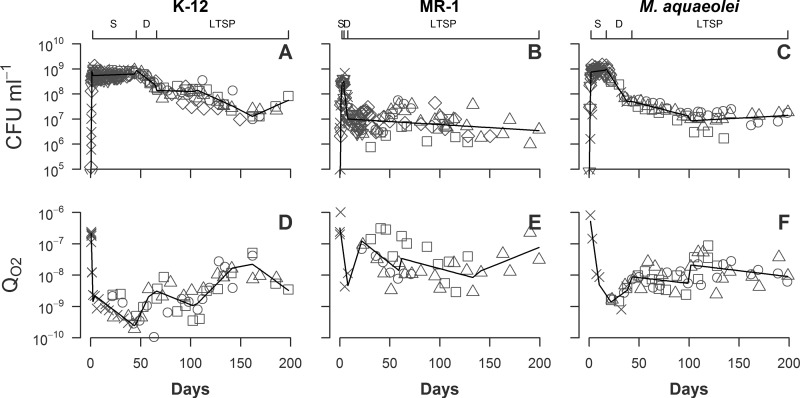
All three bacterial cell populations displayed the bacterial life cycle in all five phases, the lag, exponential, stationary, death, and long-term stationary phases (Fig. 1). E. coli reached a maximum density of 8.7 × 10⁸ CFU ml⁻¹ after 3 days. This strain remained stable in stationary phase at 4 to 8 ×10⁸ CFU ml⁻¹ for 55 days and then declined by 78% to 1.3 ×10⁸ over the next 20 days. Following this decline, the population stabilized again for ∼40 days at ∼1.5 × 10⁸ CFU ml⁻¹ and then declined from day 115 to 165 by another 90% to 1.6 ×10⁷. Over the final 30 days of the time series, E. coli CFU ml⁻¹ increased by a factor of 5, growing to a final density of 8.3 × 10⁷.

Fig 1.

Density (CFU ml⁻¹) and Q_O2 (μmol O₂ CFU⁻¹ day⁻¹) of K-12 (A and D), MR-1 (B and E), and M. aquaeolei (C and F) replicates grown for up to 200 days (diamonds, inverted triangles, x marks, squares, circles, and triangles represent different experiments). n = 6 replicates for panels A to C; n = 4 replicates for panels D to F. Solid lines representing segmented linear regressions of combined replicate data are provided to help define trends. The upper x axes identify segments of the stationary phase (S), death phase (D), and long-term stationary phase (LTSP) for each strain.

MR-1 reached a maximum density at 4.2 × 10⁸ CFU ml⁻¹ by 3 days, after which the population experienced an acute death phase, declining 99% over 14 days to ∼4 × 10⁶ CFU ml⁻¹. From this day onward, MR-1 cultures experienced large CFU fluctuations but showed an overall decline to a density of 2.4 ×10⁶ CFU ml⁻¹.

M. aquaeolei populations reached a maximum density of 1.4 × 10⁹ CFU ml⁻¹ after 13 days. The stationary phase lasted 19 days at ∼1 × 10⁹ and then declined 93% over 16 days to 6.8 ×10⁷. After day 35, M. aquaeolei populations continued to slowly decline by 87% over 80 days. From day 115 onward, the population density stopped declining and fluctuated at ∼2 × 10⁷ CFU ml⁻¹.

Population density patterns, while strain specific, are highly reproducible across replicate cultures (Fig. 1). These general population density patterns for the three strains are qualitatively similar but with significant differences in the timing and magnitude of the transitions.

(ii) Specific oxygen consumption.

The maximum value of oxygen consumption per CFU (Q_O2) for E. coli, 2.4 × 10⁻⁷ μmol O₂ CFU⁻¹ day⁻¹, was obtained during exponential phase (Fig. 1). The minimum value of 3.3 × 10⁻¹⁰ μmol O₂ CFU⁻¹ day⁻¹ occurred at the end of stationary phase (day 45). During a death phase between days 45 and 75, Q_O2 increased by a factor of 10, stabilizing at ∼1 × 10⁻⁹ for the next 40 days. During a second death phase between days 115 and 165, Q_O2 increased by a factor of 10. From day 165 to the end of the time series, Q_O2 declined to a value of 3.5 ×10⁻⁹ μmol O₂ CFU⁻¹ day⁻¹.

The Q_O2 for MR-1 reached a maximum of 1.0 × 10⁻⁶ μmol O₂ CFU⁻¹ day⁻¹ during exponential phase and then a minimum of 2.9 × 10⁻⁹ μmol O₂ CFU⁻¹ day⁻¹ by the end of stationary phase (day 3). By day 35, where population density was at a minimum, Q_O2 had increased to 7 × 10⁻⁸ μmol O₂ CFU⁻¹ day⁻¹. Between days 35 and 75, MR-1 Q_O2 declined by a factor of 7 to 1.0 × 10⁻⁸. For the remainder of the time series, Q_O2 generally increased to a final value of ∼1 × 10⁻⁷ μmol O₂ CFU⁻¹ day⁻¹. This rate is 1/10 the value measured during exponential growth.

M. aquaeolei reached a maximum of 8 ×10⁻⁷ μmol O₂ CFU⁻¹ day⁻¹ during exponential phase and a minimum of 1.7 × 10⁻⁹ μmol O₂ CFU⁻¹ day⁻¹ by the end of stationary phase (day 25). During the initial rapid death phase (days 25 to 50), Q_O2 increased by a factor of 2. During the subsequent slower decline in population density, there was a corresponding slow but steady increase in Q_O2 to ∼3 × 10⁻⁸. The cell numbers and Q_O2 values generally stabilized after day 115.

Oxygen consumption patterns are highly reproducible across replicate cultures but are species specific in terms of timing and magnitude of change (Fig. 1). For each species, there is a very large decline in respiration rate from exponential to stationary phase. The longer a species remains in stationary phase, the lower the Q_O2. However, Q_O2 increased for each species after the death phase.

(iii) Cell size.

Changes in respiration rates could be due to a variety of factors, including changes in cell size. Many bacterial species are known to shift in shape from rod-shaped bacilli to more spherical coccoid cells during stationary phase (43). To examine changes in cell morphology, the average cell volume (V) and surface area (SA) of the low-frequency-sampling experimental populations of E. coli, MR-1, and M. aquaeolei were calculated (see Table S1 in the supplemental material). Based on visual analysis, the cells were described as either spherical or rod shaped and their length (L) and width (D) were measured. SA and V were calculated by assuming rod-shaped cells to be cylinders with hemispheres on each end. E. coli cells changed in shape from rod to sphere between day 1 and day 4. The cells maintained a spherical shape for the remainder of the experiment. The changes in shape and size over the 61-day analysis did not result in a consistent change in the SA/V ratio (the largest deviation from the starting SA/V ratio was 26%). MR-1 cells transitioned in shape from rod to spherical between days 26 and 33. This change in shape increased cellular volume by over 300% and resulted in a ∼50% drop in the SA/V ratio. M. aquaeolei cells changed from rod to spherical shape by day 6 to 7. This change in shape caused an increase in volume of 26% and a change in the SA/V ratio of less than 9%.

(iv) Fluorescent-cell counts.

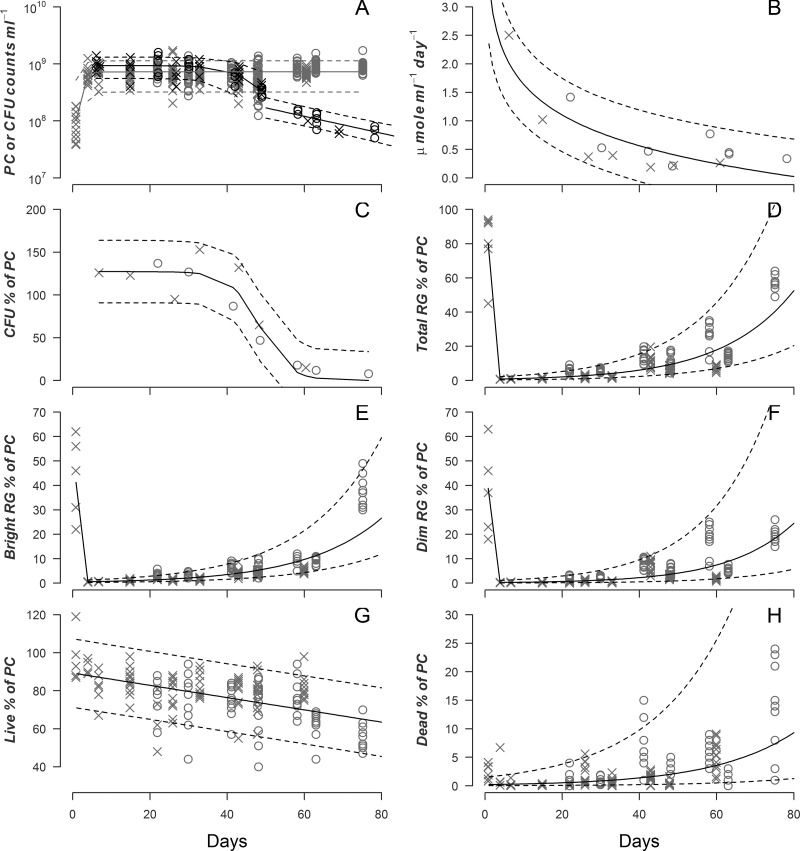
Another possible explanation for a change in the respiration rate of a population could be the divergence of the cells into subpopulations with different metabolic states. To test this, CFU, oxygen uptake rate (OUR), phase-contrast (PC) imaging of cells, the number of respiring cells (RG), the number of live cells (L), and the number of dead cells (D) were determined for duplicate cultures of E. coli for up to 76 days (Fig. 2). The PC counts increased during exponential phase but then stayed stable for the remainder of the experiment (Fig. 2A). OUR declined ∼85% over the first 25 days and then maintained a steady value of ∼0.4 μmol ml⁻¹ day⁻¹ (Fig. 2B). The PC data do not indicate a death phase; thus, CFU declines as a fraction of PC during death phase, around day 45 (Fig. 2C).

Fig 2.

Population dynamics of E. coli cells of two replicate cultures (open circles and x marks) over 80 days. (A) Phase-contrast (PC) counts (gray symbols) and sigmoid regression (gray lines). Data represent CFU (black symbols) and segmented regression (sigmoid and then exponential; black lines). (B) μmol O₂ consumed per ml of culture per day and exponential regression (black lines). (C) CFU percentage of PC and sigmoid regression (black lines). (D) Percentage of PC staining as respiring and exponential regression (black lines). (E) Percentage of PC staining as highly respiring and exponential regression (black lines). (F) Percentage of PC staining as dimly respiring and exponential regression (black lines). (G) Percentage of PC staining as live and linear regression (black lines). (H) Percentage of PC staining as dead and exponential regression (black lines). Dashed lines indicate 90% prediction intervals. For panels A and D to H, data points represent counts or percentages calculated for a specific field of view (FOV), with 5 to 13 FOVs counted.

Essentially all cells were respiring during exponential phase (Fig. 2D), but this fraction decreased to <10% during stationary phase. After the onset of death phase, the fraction of total cells respiring increased steadily, attaining a value of 60% by day 76. These patterns were similar for all respiring cells for both the highly respiring cells (Fig. 2E) and those cells that showed the minimal response to the respiration green stain (Fig. 2F).

The fraction of all cells that stained as live was ∼100% during exponential phase and underwent a slow decline thereafter (Fig. 2G). The fraction of live cells by day 76 was ∼70%.

This trend was reversed for the fraction of cells staining as dead, with initial amounts near 0% and an increase to about 7%.

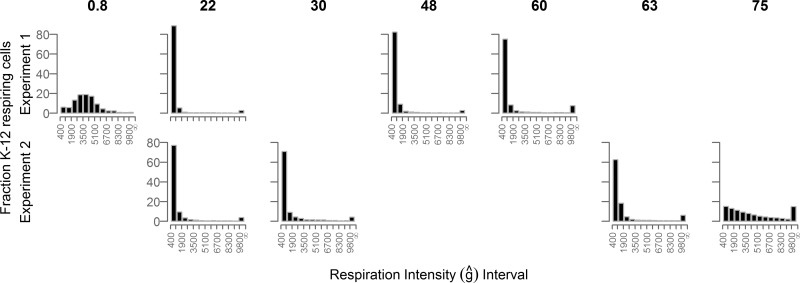
Cells fluorescing in the presence of RG were binned by their fluorescence into intensity intervals (Fig. 3). The cell count per bin was normalized to the total RG counts made using the same field of view. This generated a histogram of the percentage of RG cells respiring at specific respiration intensity intervals (total of all binned interval percentages = 100). Histograms were created for specific time points during the 76-day incubation, and this plot shows the evolution of respiration intensity over this period.

Fig 3.

Percentage of phase-contrast-visualized K-12 cells (y axis) respiring at specific respiration intensity intervals (x axis). The respiration intensity intervals have a width of 800 normalized fluorescent units (ĝ). Numbers above the plots indicate days since inoculation.

Initially, the RG percentages produced a broad “bell curve” distribution centered around 3,600 ĝ and spanning a range of about 5,000 ĝ. By day 22, the population distribution changed dramatically. Of the total cells fluorescing, over 80% were in the dimmest interval above the detection limit (400 to 1,200 ĝ). The distribution of cell brightness was narrow, skewed to the low values, and reduced to less than 0.5% by the 1,300- to 1,400-ĝ interval. However, the final interval, which included all cells brighter than 9,800 ĝ, contained 3% of the population. This distribution pattern was roughly maintained through day 60 to 63 with two notable exceptions. First, the narrow distribution of cells centered in the low-intensity bins widened slightly by day 63. Second, the highest bin percentage increased with time. By day 75, the dim-cell percentage distribution had reduced to <20% and the brightest interval contained 15% of the fluorescent population.

DISCUSSION

(i) Changes in respiration rate over time.

In this study, three different species of heterotrophic bacteria were analyzed. Each organism has evolved a unique suite of metabolic capabilities resulting in species-specific growth patterns when the organisms are cultured under identical conditions (Table 1). It has previously been established that LB broth has a limited supply of carbon relative to other required nutrients (44). Since all components of LB/5 broth are diluted equally, it can be inferred that cultures grown in LB/5 are carbon limited at the termination of growth phase. Despite different lengths of stationary phase and differences in the timing and magnitude of death phase, the three species showed similar progressions for adapting population density levels to the transition from carbon abundance to carbon limitation (Fig. 1).

In all cases, the highest oxygen demand per cell occurred during exponential growth and the lowest oxygen demand occurred at the end of stationary phase. The longer a cell spent in stationary phase, the lower the oxygen consumption rates per cell. All three species in this study experienced a death phase, and in all cases, during the death phase, oxygen demand per CFU increased. There was a trend during LTSP toward increasing oxygen demand per CFU with time although cell numbers were holding steady or declining. For MR-1, the Q_O2 after 200 days was within 10% of the maximum oxygen consumption rate measured during exponential-phase growth.

One explanation for the Q_O2 increase during the death phase is that cells were utilizing nutrients liberated from dead cells, a phenomenon referred to as cryptic growth. For MR-1, a population increase occurred even after death phase. If a burst of cryptic growth were the only change occurring after death phase, then it would be expected that the respiration rates would return to previous minimum values once the liberated nutrients were consumed. This was not observed; Q_O2 increased to higher values after the death phase for all three strains.

Q_O2 has been defined in this study as the population respiration rate normalized by the population CFU. This definition assumes equal contributions by all CFU to the population respiration rate. While this hypothesis is supported for log phase and early stationary phase (45), it may not hold true through death phase and into LTSP.

One factor that may influence Q_O2 is the change in size and shape of a cell during LTSP. It is well established that bacterial cells decrease in length in response to starvation (45). A range of cell lengths (1.5 to 3.6 μm) were measured, with each species showing a 50% decline in cell length during the first 61 days of the time series compared to the length seen at the time that the largest changes in Q_O2 were observed (see Table S1 in the supplemental material). However, the change in cell length cannot fully account for the 25-to-800-fold change observed in Q_O2 during the same period (Table 2). If respiration rates were limited by oxygen diffusion across the surface of the cell, then Q_O2 would track the cell surface area-to-volume ratio, which changed by only, at most, 54%. Respiration is thus not directly linked to surface area diffusion control.

Table 2.

CFU decline compared to Q_O2 increase for cultures transitioning from stationary phase to long-term stationary phase^a

Strain	SP			LTSP			CFU ml−1 ratio (SP/LTSP)	QO2 ratio (LTSP/SP)
	Day	log10 (CFU ml−1)	log10 (QO2)	Day	log10 (CFU ml−1)	log10 (QO2)
Escherichia coli K-12	39	8.8 ± 0.1	−9.5 ± 0.4	67	8.1 ± 0.2	−8.5 ± 0.4	4 ± 2	9 ± 4
Shewanella oneidensis MR-1	4.5	8.5 ± 0.1	−7.6 ± 0.8	22.5	7.0 ± 0.4	−6.9 ± 0.6	34 ± 2	5 ± 10
M. aquaeolei	10	8.9 ± 0.2	−8.3 ± 0.5	43	7.7 ± 0.1	−8.1 ± 0.3	16 ± 2	2 ± 4

^aCFU ml⁻¹ and Q_O2 (μmol O₂ CFU⁻¹ d⁻¹) values are from Fig. 1. Uncertainties are as explained in the text. SP, stationary phase; LTSP, long-term stationary phase.

Given that previous work has shown that under long-term stationary-phase growth conditions, subpopulations of cells exist that can grow while others remain static or may die, another important consideration is whether the population of respiring cells is physiologically homogeneous or heterogeneous. For a homogenous population, the elevation of LTSP Q_O2 over time would be indicative of a true change in individual cell respiration rates across the population. Under the homogenous assumption, there are two primary explanations for why cellular respiration rates would elevate during LTSP. The first is that mutant strains have out-competed and displaced their ancestor cells and thereby converted the cells in the population to a respiration rate different from that of their ancestors. A second possible explanation is that a density-induced signaling agent may be controlling cellular respiration rates such that the LTSP Q_O2 increases with the decline in population density over time. Researchers have noted that respiration can be density dependent in yeast and, to a lesser extent, bacteria (46); this density dependence has also been observed in soil samples (47). It is not conclusive from their results if the density dependence is due to an endogenous or exogenous factor, but these authors speculate that it could be the result of negative feedback from carbon dioxide buildup.

Populations of bacteria can be heterogeneous due to cell differentiation, mutation, and/or random fluctuations in gene expression (48). If this heterogeneity leads to a few “superbreather” cells present in a larger population that are not respiring and a vast majority of cells that are not consuming oxygen and are dying, then a decrease in the population density through the death phase would be expected to scale linearly with the increase of Q_O2. For MR-1 and M. aquaeolei, the magnitude of the population decline does not account for the increase of Q_O2; the change of CFU is not equal to the change in Q_O2 (Table 2). This is also true for K-12; however, for this species, the ratio has enough uncertainty to accommodate a 1:1 ratio in these terms. These data suggest that the respiration rate of the population is likely not driven by a few respiring bacteria but that the presence of superbreather cells is worth investigating further.

Another possible heterogeneous community configuration would be that all respiring cells in the culture do not form colonies upon plating. It has been documented that stressed populations of bacteria can form “viable but nonculturable” (VBNC) cells that do not yield CFU (49, 50). These cells cannot form a colony, but they still show signs of active metabolism (51). The formation of VBNC cells occurs in many species of bacteria with a range of environmental stressors, including starvation. If VBNC cells are forming during LTSP, this would suggest that at least part of the increase in Q_O2 observed is the result of an undercounting of the number of respiring cells.

The use of respiration reporter stains (Fig. 2) demonstrates that the populations of respiring cells are indeed dynamic. For example, after E. coli cells enter death phase (∼day 55), the CFU percentage of PC counts declines. However, the fraction of live cells relative to PC counts remains constant over this time interval. This is evidence that cells remain viable but unable to replicate during death phase. There is also heterogeneity in the intensity of respiring cells. The fraction of cells respiring begins to increase after day 55. Neither PC counts nor CFU counts are a good proxy for either live or respiring cell numbers within a batch culture after the population has experienced a death phase. These data are consistent with observations that minimum Q_O2 values occur during stationary phase when the number of CFU cells is high but the number of cells scoring as respiring is a small fraction of the CFU (Fig. 2). The increase in Q_O2 following the death phase involves the decline in CFU relative to respiring-cell counts.

Histograms of respiration intensity show that the majority of cells were initially weakly respiring (Fig. 3). Upon death phase (∼55 days), the CFU decline 99% but the population of cells staining as live drops only 20%. Additionally, the proportion of cells respiring increases by 40% (Fig. 2) and the distribution of the respiration intensity broadens into higher intervals (Fig. 3). From day 22 to day 75, the percentage of the brightest interval (9,800 − ∞ ĝ) increased from <3% to 15%. This highly respiring subset of cells may indicate the emergence of a different physiological strategy for cells to cope with the stress of starvation. Both the observation that VBNCs are forming and the emergence of a highly respiring subset of cells explain why Q_O2 values increase after the death phase (Table 3).

Table 3.

Oxygen consumption rates normalized with different cell-counting techniques^a

Replicate	Day	μmol O2 count−1 day−1 × 10−10
		CFU	PC	BRG	DRG	Live
1	6	27	34	5,065	11,267	42
	15	12	14	643	2,181	21
	27	5	5	359	505	7
	33	4	6	383	1,180	8
	43	3	4	89	53	4
	49	6	4	106	154	5
	61	26	4	71	199	5
2	22	12	17	442	650	22
	30	6	7	219	328	9
	42	8	7	109	88	9
	49	7	3	54	65	4
	58	52	9	100	51	12
	63	40	5	49	95	7
	78	47	4	10	19	6

^aCell-counting techniques included CFU, phase-contrast (PC), brightly fluorescing cells stained with RedoxSensor Green (B_RG), dimly fluorescing cells stained with RedoxSensor Green (D_RG), and cells indicating a living status (Live) under conditions of Live/Dead staining. All measurements were performed concurrently with oxygen consumption measurement on the days indicated for K-12 replicate cultures.

(ii) Laboratory results compared with environmental results.

With the exception of bloom periods, natural bacterial populations spend the majority of their existence in a nongrowing state of starvation for a specific nutrient (52). From modeling geochemical gradients, it has been determined that some fraction of the bacterial population living in a nutrient-limited environment, e.g., at a depth of 1,600 m below the sea floor (53) underlying water depths exceeding 4,500 m, maintains an active metabolism (8, 54–57). These sedimentary bacterial communities have some traits similar to those of our batch cultures; they are heterotrophic, may have had a single or small initial input of reduced material, and may be a closed system in terms of electron donors but not electron acceptors. To place the laboratory respiration rate data from this study in context with respiration in natural settings, our results are compared with three environmental data sets (Table 4).

Table 4.

Oxygen consumption rates from this study compared to environmental sediment data^a

Sample strain, species, or reference	Site	Oceanic setting	QO2(min) (μmol O2 cell−1day−1)
K-12	Laboratory	N/A	4 × 10−10
MR-1	Laboratory	N/A	8 × 10−9
M. aquaeolei	Laboratory	N/A	2 × 10−9
58	Patton Escarpment	Eutrophic	2 × 10−9
56	South Pacific Gyre	Oligotrophic	6 × 10−13 to 3 × 10−11
8	North Pacific Gyre	Oligotrophic	3 × 10−13 to 3 × 10−12

^aLaboratory values were calculated from measured oxygen consumption and CFU counts. Values for the sample from reference 58 were determined from geochemical modeling and sediment cells counts. Values for the samples from references 56 and 8 are as reported.

The Patton Escarpment, a site off the southern California continental slope at a depth of ∼3,500 m, lies under seasonally productive waters. Oxygen consumption rates at this site were modeled from in situ oxygen concentration profiles (58), which were converted to gradients in flux (59) and then converted to oxygen consumption rates by examining interval differences in flux. These rates were normalized to sediment cell counts provided by Reimers (58). We note that normalizing to total cell numbers is not the same as using viable counts (as CFU). Sediment counts may include dead cells, and therefore any specific oxygen consumption rates likely represent a lower limit. The average value at the Patton Escarpment site is most similar to the minimum Q_O2 value for M. aquaeolei and is even greater than the minimum value for E. coli. This might imply that the microbes at the Patton Escarpment are experiencing nutrient limitation similar to stationary-phase batch culture cell levels.

Another site, the South Pacific Gyre (SPG) sediment, lies beneath the most unproductive (oligotrophic) waters on Earth and experiences a much lower rate of sediment and organic carbon accumulation than the Patton Escarpment site. Oxygen consumption rates were also determined from pore water concentration profiles and also normalized to sediment cell counts (56). The natural population rates obtained from the South Pacific Gyre are several orders of magnitude lower that the values obtained in this study.

The difference between the natural population respiration rate and those obtained in batch cultures is further exemplified in comparing our data to that of Røy et al. (8) for the North Pacific Gyre. This was also a study of deep Pacific Ocean sediments, and oxygen demand per cell was derived, as with D'Hondt et al. (56), by geochemical modeling of the oxygen consumption rate and dividing by cell numbers. The lowest respiration rate values obtained by Røy al. (8) are 2 to 4 orders of magnitude lower than the values for oxygen demand per CFU obtained in our experiments (Table 4). Our laboratory observations of a strong cellular respiration response to the nutrient status of the environment may help explain the low rates obtained in natural settings. The rates obtained in 200-day batch experiments are most similar to rates obtained from oceanic sediments of relatively high organic carbon inputs but excess oxygen supply (Patton Escarpment), perhaps a natural site that more closely resembles the batch culture conditions. Rates of cellular oxygen consumption at the most oligotrophic oceanic sites appear to be several orders of magnitude lower than the LTSP rates obtained in the laboratory. It is possible that there are few cells respiring at the SPG site relative to the number of cells counted (see Table 3). It is also possible that the cells at the South Pacific Gyre, possibly the most nutrient-limited cells on the planet, are exhibiting extreme starvation physiology not observed in 200-day batch experiments. However, both the cell enumeration technique and the actual distribution of respiration intensity among surviving cells are key to understanding the significance of these low rates.

(iii) Kleiber's law.

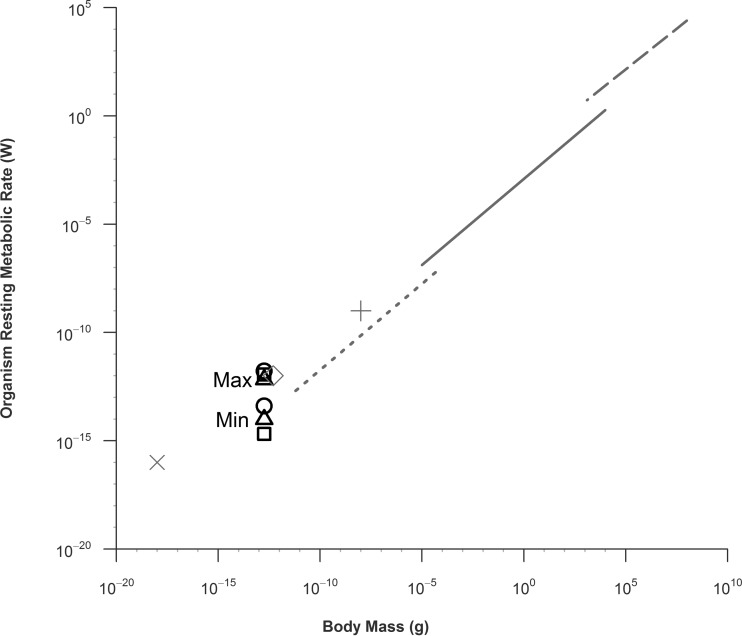
The history of respiration studies includes the well-studied Kleiber's law (36), which describes the relationship between animal body mass and metabolic rate at rest (W = M^b where W is watts, M is mass of the organism body, and b = 0.75). In 1960, this classic power law relationship was expanded to include “eukaryotic unicells” (60). There has been extensive discussion in the literature concerning many aspects of Kleiber's law (61–69). However, no heterotrophic bacteria, which have a mass on the order of hundreds of femtograms (70), have been described in terms of the Kleiber relationship. Their small body mass affords an opportunity to test if Kleiber's law can correctly predict metabolic rates for some of the smallest known organisms.

The results of comparisons of the minimum metabolic rates of the three species studied here to the resting rates of other organisms expand the whole organism mass/metabolic scaling relationship (36) an order of magnitude beyond the eukaryotic unicellular data set (Fig. 4). To make this comparison, the bacterial OUR were converted to watts (W) using the ideal gas law (22.4 liters = 1 mol gas) and 1 ml of O₂ = 20 J energy (66). Bacterial mass was estimated from published values for cell dry weight (69). The original Kleiber data set (36) was expanded and temperature corrected (60, 64). Cytochrome oxidase, coupled mitochondrion, and mammalian cell data from cardiac myocyte data were added to the plot to provide a more complete comparison (71).

Fig 4.

Metabolic rates in watts (W) and body masses (g) of bacteria from this study compared to other organisms. Maximum and minimum values for K-12 (squares), MR-1 (circles), and M. aquaeolei (triangles) are indicated. The symbol width represents the approximate body mass confidence interval. Unicellular organism (dotted line), ectotherm (solid line), and homeotherm (dashed line) metabolic rates are adapted from Hemmingsen (60). Cardiac myocyte cytochrome oxidase molecule (gray X), cardiac myocyte mitochondrion (gray diamond), and cardiac myocyte cell (gray cross) rates from are from West et al. (71). The organization of this figure is based on reference 64.

Bacterial respiration rates during the stationary phase are concordant with the Kleiber law trend. These data extend the trend to a lower body mass (∼10⁻¹⁵ kg) than previously reported. Our data also show that the range of bacterial respiration rates is >3 orders of magnitude, which is much greater than that of other organisms.

Summary and conclusions.

The pattern of Q_O2 (μmol O₂ CFU⁻¹ day⁻¹) has been documented for three species of facultative anaerobic heterotrophic bacteria, E. coli K-12, S. oneidensis MR-1, and M. aquaeolei VT8, incubated in batch cultures of carbon-limited medium for up to 200 days. Patterns are consistent in all species; high rates of oxygen consumption (2 × 10⁻⁷ to 1 × 10⁻⁶ μmol O₂ CFU⁻¹ day⁻¹) are found during exponential growth. The lowest rates (2 × 10⁻¹⁰ to 3 × 10⁻⁹ μmol O₂ CFU⁻¹ day⁻¹) are found in late stationary phase. After the death phase, Q_O2 increases in all species. The increase in Q_O2 for MR-1 over 200 days of LTSP brings its respiration rate per CFU to 10% of the value obtained during nutrient-replete exponential-growth phase.

However, a critical aspect of this analysis has been the documentation of the emergence of potentially VBNC cells. After a species-specific length of time in stationary phase, a significant fraction of the cells no longer form CFU, and yet the community respiration rate persists at surprisingly high values. The population becomes structured such that CFU do not represent the entire population of respiring cells, which explains the elevated LTSP Q_O2 values observed. Population restructuring includes the redistribution of respiration intensities. An exponentially growing population has a normal distribution of cell respiration intensities. Upon the shift to stationary phase, the population of cells becomes dominated by low respiration activity, with a minority subpopulation of cells respiring at very high rates. As death phase and LTSP proceed, the population of high-respiring cells increases. It appears that, with more time spent under nutrient stress conditions, the population shifts to or selects for highly respiring cells.

Minimum Q_O2 values were compared to cellular rates of oxygen uptake in ocean sediment environments. Laboratory-determined rates are comparable to those calculated for cells within the sediment from a continental slope margin (Patton Escarpment) but are 1 to 4 orders of magnitude higher than those calculated for cells within sediment from oligotrophic, open ocean sites. The failure to find rates similar to those seen with deep-ocean-sediment environments may indicate that hoping to draw a meaningful conclusion from a comparison between rates from a 200-day experiment and from sediment that is thousands of years old is unrealistic. The very low rates for the deep-sediment cells suggest either that extreme physiological states exist (in reaction to nutrient limitation) that have not yet been observed in the laboratory or that the assumption (used in rate calculations) that all cells in the deep-sediment environment are respiring equally is false. Our results strongly support the latter statement. The possibility remains that a small fraction (10% to 0.01%) of environmental cells are respiring at a rate similar to the (minimal) Q_O2 values calculated in our experiments.

Finally, Q_O2 values were converted to metabolic rates and used to test the validity of Kleiber's law for bacteria. The minimal Q_O2 rates support the extension of Kleiber's law to the mass of a bacterium (100-fg range).

Starving bacteria form complex and dynamic subpopulations of viable and respiring cells. These results complicate estimation of per-cell metabolic activity with both laboratory rates and in situ geochemical rates. The nutrient status of the environment and subpopulation formation must be considered when studying starving microbial populations.