Abstract
Dielectrophoretic field-flow fractionation (DEP-FFF) has been used to discriminate between particles and cells based on their dielectric and density properties. However, hydrodynamic lift forces (HDLF) at flow rates needed for rapid separations were not accounted for in the previous theoretical treatment of the approach. Furthermore, no method was developed to isolate particle or cell physical characteristics directly from DEP-FFF elution data. An extended theory of DEP-FFF is presented that accounts for HDLF. Using DS19 erythroleukemia cells as model particles with frequency-dependent dielectric properties, it is shown that the revised theory accounts for DEP-FFF elution behavior over a wide range of conditions and is consistent with sedimentation-FFF when the DEP force is zero. Conducting four elution runs under specified conditions, the theory allows for the derivation of the cell density distribution and provides good estimates of the distributions of the dielectric properties of the cells and their deformability characteristics that affect HDLF. The approach allows for rapid profiling of the biophysical properties of cells, the identification and characterization of subpopulations and the design of optimal DEP-FFF separation conditions. The extended DEP-FFF theory is widely applicable and the parameter measurement methods may be adapted easily to other types of particles.
Keywords: Particle sorting, Cell discrimination, Membrane capacitance, Cell biophysical properties
Introduction
Dielectrophoresis1;2 (DEP) is a well known electrokinetic phenomenon that scales ideally for the microscale manipulation and characterization of particles. DEP trapping3–10 has often been applied to the separation of particles and cells but. its discrimination is limited6;10. To solve this, dielectrophoretic field-flow fractionation (DEP-FFF) was developed11–15. The DEP force positions particles in a hydrodynamic flow profile according to their dielectric properties and they are carried through the channel at characteristic heights and speeds, with dissimilar particle types emerging separated in time and/or space. DEP-FFF and other DEP approaches have been demonstrated in many potential applications. In biology and medicine these include separating blood cell subpopulations6;16, purifying and enriching stem cell harvests17–20, capturing parasitized cells from blood21–23, and isolating circulating tumor cells from cancer patients24. Non biological applications include characterizing and processing nano particles25–28, characterizing thin film coatings on particles29, the detection of environmental toxicants30;31 and of pathogens in water32;33, the characterization of minerals34;35, and mineral beneficiation36. DEP-FFF provides greater discrimination than sedimentation-FFF37–40 because it exploits both particle and buffer dielectric properties.
Despite its higher discrimination, an adequate theory describing DEP-FFF has not been presented, preventing the derivation of particle properties from their elution times. Thus cell biophysical properties could not be derived for basic research and the design of new separation protocols was partly empirical. In this article, the theory of DEP-FFF is extended to include hydrodynamic lift effects and to show how, through appropriate steps, particle density, dielectric, and deformability parameters may be derived from elution characteristics. The focus here will be on mammalian cells not only because urgent medical applications await but also because cells form excellent test particles showing distributions in density and deformability as well as in frequency-dependent dielectric properties.
Theoretical Background
Field-flow fractionation (FFF) is a family of methods that exploits the laminar hydrodynamic flow profile in a thin channel to drive the separation of different particle types41–43. Particles are positioned in the flow profile by counterbalancing forces that depend on the particle properties. For mammalian cells, two FFF modes are of importance, namely the steric mode in which some forces result from contact with the channel floor, and the hyperlayer mode in which floor interactions are negligible. The focus of this article is the hyperlayer mode. Typically, the flow velocity profile at low Reynolds numbers is parabolic and the velocity at height h is
| (1) |
where v̇0 = 6v0/H is the shear rate at the flow channel floor and v0 = F/(HW) is the mean fluid velocity. F is the flow rate and H and W are the channel height and width.
Torque, wall, and lateral forces on a particle of radius R modify its velocity from that of the eluate at a given height and empirical equations for its velocity vp have been derived from experimental data 44;45 of the form:
| (2a) |
| (2b) |
In DEP-FFF, the height at which a particle moves through the channel depends on the balance of DEP, sedimentation and HDL forces:
| (3) |
The sedimentation force is , where ρp and ρs are the densities of the particle and eluate, respectively, and g is the acceleration due to gravity.
In earlier DEP-FFF studies, flow rates were kept low enough that the HDLF was thought to be negligible. These low flow rates resulted in long elution times. Furthermore, mammalian cells left in suspension for more than 1000 seconds changed behavior 24, suggesting cell dielectric alterations were occurring. Shorter elution times required faster, HDLF-inducing, flow rates. Several workers have considered HDLF effects and identified contributions from wall effects, particle rotation, and particle deformation46 and rigidity47. Abkarian and Viallat48 showed that lift forces on deformable lipid vesicles, the only particles for which definitive HDLF-shape correlations have been reported, depended on the geometry of the vesicles according to the relationship
| (4) |
Here η is the dynamic viscosity of the eluate and F(ν) is a dimensionless hydrodynamic geometry function (0 < F(ν) < 1) that increases with increasing deviation from particle sphericity. Both particle shape and deformability can contribute to F(ν)49. To describe HDLF effects in cells, which are more complex than solid particles and lipid vesicles, it is helpful to indicate explicitly the shape S and mechanical flexibility M contributions to the geometry function:
| (5) |
When the DEP force is zero, a balance of HDLF and sedimentation forces alone determines the particle transport in hyperlayer FFF:
| (6) |
giving
| (7) |
Eqs. 1, 2a, or 2b, as appropriate, may be used to calculate the height h at which particles moved through the channel from their elution times. For example, Eq. 1 for h ≪ H, gives
| (8) |
for an elution time Telute from a channel of length L. Regression may be used to fit this or Eqs. 2a and 2b to the data. The unknowns are particle F(S, M) and density ρp. Small changes in vesicle geometry led to large changes in F(ν)48 so that F(S, M) is expected to reflect differences in the geometry of different particle types sensitively. Because most harvested mammalian cells (including the DS19 cells used as model particles here) relax to a spherical shape in non-shear conditions, F(S, M)can be expected to depend most significantly on cell deformability in the FFF shear field so that F(S, M) → F(M).
The vertical component of the DEP force that controls the height of particles in the FFF channel may be written11
| (9) |
where Re[fCM(f)] is the real part of the Clausius-Mossotti factor describing the dielectric polarization of the particles in the DEP medium of dielectric constant εs. ε0 is the permittivity of free space and V is the AC voltage of frequency f used to energize the DEP electrodes. p(f) allows for voltage drop resulting from electric polarization at the DEP electrode-liquid interface, and q(h) describes how the DEP field falls with height above the channel floor11.
In general, fCM(f) depends on the complex permittivities of the particle and the eluate, and , respectively, that account for frequency-dependent dielectric and conductivity characteristics,
| (10a) |
Re[fCM (f)] ranges from −0.5 for non-conducting particles with a dielectric constant much less than the eluate to +1 for particles with a conductivity and/or dielectric constant much greater than the eluate. The properties of fCM (f) for cells has been the subject of numerous papers50–54. Intact cells having a cytoplasmic conductivity much higher than the suspending medium and an intact membrane barrier function are repelled from high electric field regions at low DEP frequencies(Re[fCM (fsmall)] → −0.5), attracted to them at high frequencies below ~5 MHz (Re[fCM(flarg e)] → +1), and exhibit null DEP response at an intermediate crossover frequency f0 (Re[fCM (f0)] = 0). In this case51;54–56
| (10b) |
Once f0 has been determined, a dielectric model may be applied to extract biophysical information including the cell membrane capacitance and conductivity, revealing cell membrane area and ion permeability57. In DEP-FFF the condition Re[fCM (fsmall)] → −0.5 provides maximum DEP levitating force, and Re[fCM (flarge)] → +1) provides maximum DEP attractive force towards the channel floor.
The factor 0 ≤ p(f) ≤ 1 corrects for voltage drop at the electrode-eluate interface due to electrode polarization11.. The complex polarization impedance at the interface may be approximated in terms of an effective polarization resistance Rpol and polarization capacitance Cpol11;58–60 as
| (11) |
The impedance of the bulk suspending medium can be written
| (12) |
where Rbulk and Cbulk result from the conductivity (σs) and permittivity (εs ε0) of the eluate in the channel. For an electrode array comprised of plain, parallel, interdigitated electrode elements having equal width and spacing s, the “lumped” area of electrode connected to each pole of the signal generator is WL and the effective spacing of these lumped electrodes is 2s, giving
| (13a) |
| (13b) |
The interface and bulk eluate impedances form a voltage divider for the AC signal applied to the electrode array, giving the proportion of voltage acting in the eluate as11
| (14) |
Lastly, the DEP field of a plain parallel interdigitated electrode array falls off exponentially with height above the DEP-FFF channel floor11,
| (15) |
Substitution of all these expressions into Eq. 3 gives a non-linear equation that lacks an analytical solution but is amenable to numerical simulations and fitting.
Experimental
To test the theory and demonstrate isolation of particle parameters from elution data, experiments were conducted using DS19 erythroleukemia cells61. These were convenient because their growth in suspension culture allowed a fresh aliquot to be used for every run, ensuring consistency. Cells were grown in RPMI medium (Cellgro, Mediatech, Monassess, VA USA) with 10% fetal bovine serum (Atlanta Biochemicals, Atlanta, GA, USA). To maintain consistent dielectric properties, cells were harvested in exponential growth at a density of 106 mL−1 two days after seeding. Viability, determined by trypan blue dye exclusion, was at least 98%.
For each run, a 1 mL aliquot of cells was washed in 10 mL of DEP buffer, centrifuged at 300 g × 10 min, decanted, and resuspended in 300 μL of DEP buffer. 30 μL of this cell suspension was diluted with 250 μL of DEP buffer and injected, via septum, into the DEP-FFF channel. The sample occupied the first 5% of the chamber length and contained ~105 cells. This volume avoided significant elution peak broadening and the cell concentration was low enough to avoid cell-cell dielectric interactions 24. Cells settled for eight minutes with the flow and DEP field off. Then the fluid flow and the DEP field were activated. Eluting cells were counted using a Laser Particle Counter (PC 2400 D, ChemTrac Systems, Norcross, GA, USA). In all experiments, the eluate buffer consisted of an aqueous solution of 9.5% ultra pure sucrose (S7903, Sigma-Aldrich), 0.01% dextrose (Fisher D-19), 0.1% pluronic F-68 (P-1300, Sigma-Aldrich), 0.1% bovine serum albumen, 10 mM phosphate buffer pH 7.0, 0.1 mM Ca acetate, 0.5 mM Mg acetate and 100 units per mL of catalase. The eluate conductivity was adjusted to 30 mS.m−1 with KCl using a conductivity meter (EC M 19101-00, Cole-Parmer Instruments, Vernon Hills, IL, USA).
The DEP-FFF flow channel was 0.6 mm high × 25 mm wide × 300 mm long and had a floor covered with a flex-circuit, interdigitated 50 μm wide gold on copper electrodes spaced 50 μm apart on a Kapton substrate as described previously20;24. 3000 electrode elements ran widthwise across the chamber with alternate elements connected to 2 bus lines energized by a signal generator. This could deliver sinusoidal signals from 1 kHz to 2 MHz and up to 10 V peak to peak at a maximum current of 3 A RMS20;24. All experiments conducted here used a 2.8 V peak to peak signal monitored by an HP 54601A oscilloscope. Eluate was delivered by a pulseless gear pump (Ismatec, Glattbrugg, Switzerland) via a 0.2 μm inline filter (MediaKap-2, Spectrum Laboratories, Rancho Dominguez, CA).
The factor p(f) in Eq. 14 was determined by measuring the AC current through the electrode array as a function of frequency, allowing Zpol (f) to be calculated. Provided the electrode array was maintained in good condition (i.e. no growth of biofilm and no use of corrosive cleaning agents), p(f) remained constant. The DEP scaling factor A(s) in Eq. 15 was determined by running calibration experiments in which the elution times of 10 μm diameter polymer beads (PC06N ρ = 1062 kg.m−3, BB01N ρ = 1200 kg.m−3, Bangs Laboratories, Fishers, IN) were measured as a function of DEP voltage. This parameter remains fixed for the chamber and electrode configuration. Based on the stability of p(f) and the fixed A(s), the DEP field inside the channel remained well defined for several months of electrode use and could be verified using the beads.
Testing the DEP-FFF Theory
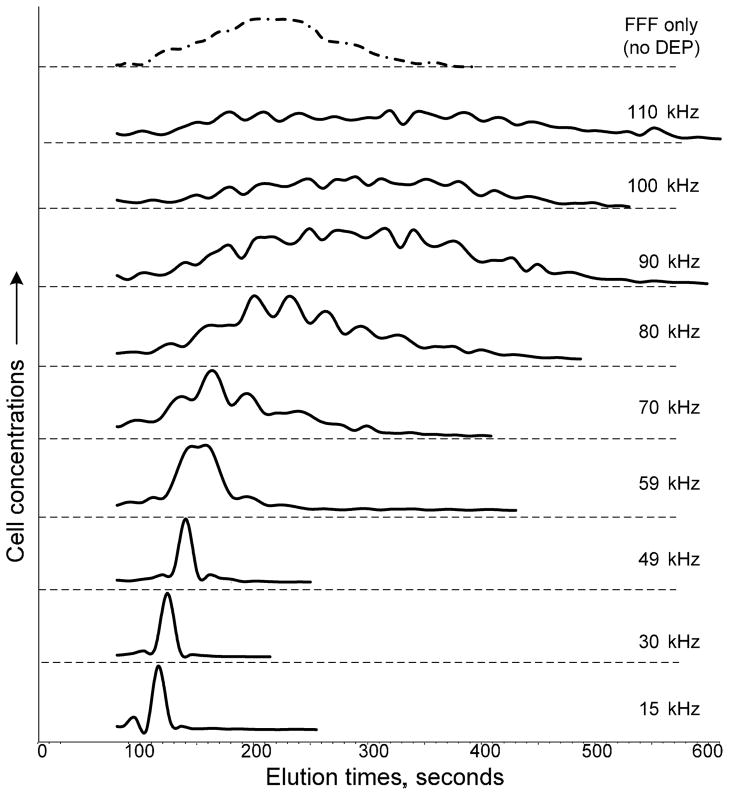
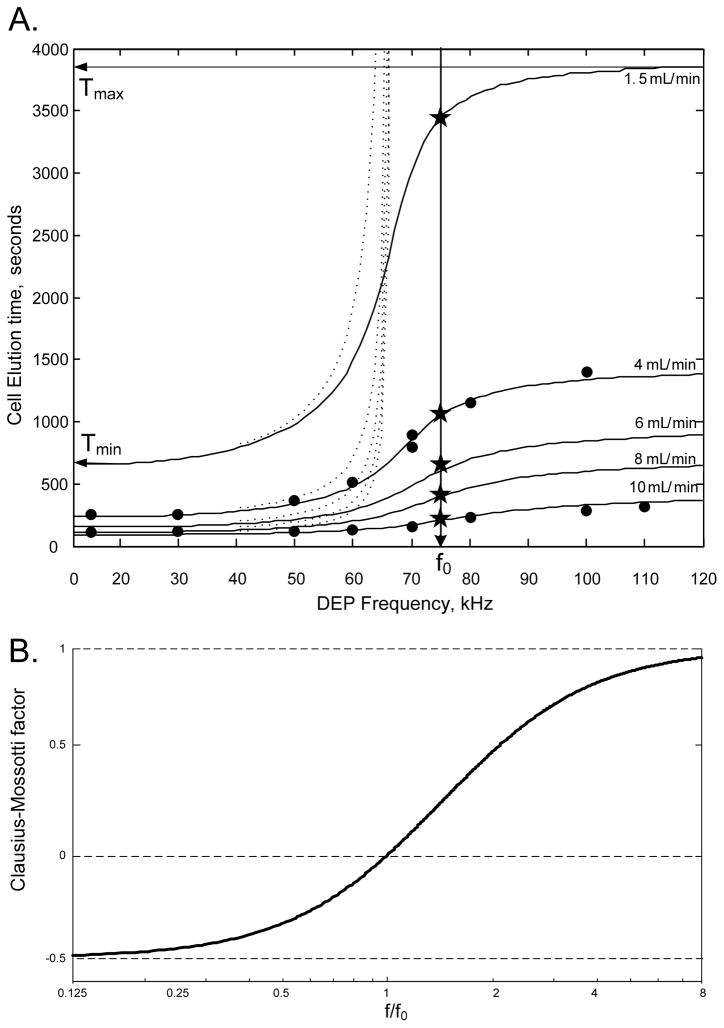
DS19 elution profiles were measurements as a function of DEP frequency at a flow rate of 10 mL.min−1 (wall sheer rate v̇0 = 95 sec−1)(Fig. 1). Peak elution times for these profiles and for similar ones obtained at a flow rate of 4 mL.min−1 (v̇0 = 13 sec−1), are plotted as a function of the DEP frequency in Fig. 2A (solid circles). Clearly, the cell elution times are influenced by the frequency-dependent DEP force embodied in the Clausius-Mossotti factor (Fig. 2B). The plots in Fig. 2A were analyzed to determine the height h at which the DS19 cells traversed the channel. Because h was unknown, it was unclear whether Eq. 2a or 2b was appropriate. Instead a blended function was used:
Fig. 1.
Elution profiles of DS19 cells at a flow rate of 10 mL.min−1 (wall sheer rate v̇0 = 95 sec−1) for FFF (no DEP field) and for DEP at different fixed frequencies. Above the crossover frequency (74 kHz) the elution profiles spread out and the peaks become ill-defined.
Fig. 2.
(A) Relationship between the DEP-FFF elution time and frequency for DS19 cells (●) for different flow rates. At the crossover frequency f0 the DEP force is zero and elution times correspond to those measured by conventional sedimentation-FFF (★). Solid lines show simulated elution characteristics based upon the analysis given in the text. Dotted lines show elution characteristics predicted by earlier theory that ignored hydrodynamic lift. (B) The Clausius-Mossotti factor reveals the relative DEP force experienced by cells as a function of DEP frequency. The influence of this on cell elution characteristics is evident in (A).
This was considered appropriate because Eq. 2a overestimates cell velocity at large h, Eq. 2b overestimates cell velocity at small h, and the two equations coincide at an intermediate height.
The Nelder-Meade simplex algorithm was used to minimize the error function for the n data points plotted in Fig. 2 using fminsearch (MATLAB, The MathWorks, Natick, Massachusetts) under the conditions in Table 1. The derived parameters were the effective cell density ρp = 1058 kg.m−3, hydrodynamic lift geometry function F(M) = 0.12 and cell crossover frequency f0 = 74 kHz. Solid lines at 10 mL.min−1 and 4 mL.min−1 in Fig. 2A show this fit. Elution characteristics calculated for 1.5, 6 and 8 mL.min−1 (v̇0 = 76, 57 and 14 sec−1) are also shown.
Table 1.
Parameters used for deriving the best fit of Eq. 3 to frequency-dependent elution time data for DS19 cells (Fig. 2) and for calculations of the mapping characteristics between elution profiles and cell biophysical characteristics as described in the text.
| Parameter | Value | Units | Explanation |
|---|---|---|---|
| fstart | 160 × 103 | Hz | Sweep start frequency |
| fend | 15 × 103 | kHz | Sweep end frequency |
| Tsweep | 600 | s | Sweep time |
| R | 7.5 × 10−6 | m | Cell radius |
| g | 9.81 | m.s−2 | Acceleration due to gravity |
| H | 600 × 10−6 | m | Channel height |
| W | 25 × 10−3 | m | Channel width |
| L | 300 × 10−3 | m | Channel length |
| V | 1.42 | V | Applied DEP volts p-p |
| η | 1.002 × 10−3 | N.s.m−2 | Dynamic viscosity of water at 20°C |
| σs | 30 × 10−3 | S.m−1 | Eluate conductivity |
| S | 50 × 10−6 | m | Electrode element width and spacing |
| F | 4 and 10 | mL.min−1 | Flow rate |
| Rpol | 0.375/(L × W) | Ω.Hz½ | Frequency-dependent electrode polarization resistance |
| Cpol | 11.3 × L × W | F. Hz½ | Frequency-dependent electrode polarization capacitance |
| Rbulk | 8s/(σs × L × W) | Ω | Bulk resistance of eluate on DEP electrode |
| Cbulk | 690 × L × W/(8* s) | pF | Bulk capacitance of DEP electrode |
| ρp | 1058* | Kg.m−3 | DS19 cell density |
| f0 | 74* | kHz | DS19 cell crossover frequency |
| F (Mcyt, Mmem) | 0.11* | dimensionless | DS19 HDLF geometric scaling function |
Values derived from the best fit of the DEP-FFF theory.
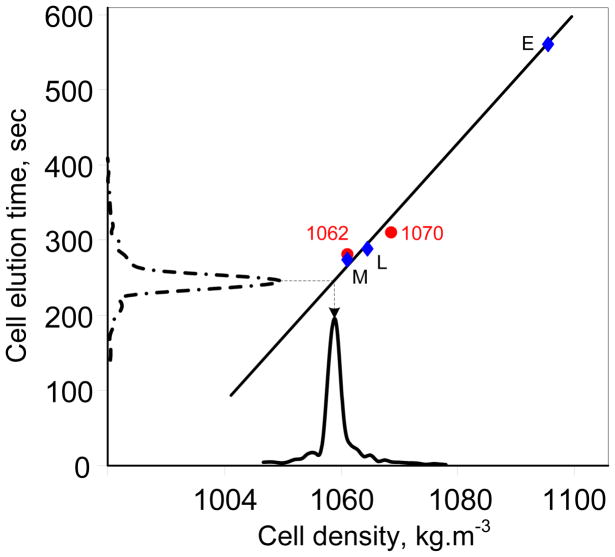
Because Re[fCM (fsmall)] → −0.5, the DEP force reaches its maximum levitating value at low frequency and cells have minimum elution time Tmin. DS19 cells are >20 μm above the channel floor under these conditions and HDLF becomes negligible. Therefore, the cell density can be calculated directly from the elution time as the DEP force is known when Re[fCM (f)] = −0.5. Fig. 3 shows the expected relationship between elution time and density, which is almost linear under the conditions here. Peak elution times were measured for beads having densities of 1062 and 1070 kg.m−3 and for monocytes (M), lymphocytes (L), and erythrocytes (E) (densities 1063, 1071 and 1096 kg.m−3, respectively). These data coincide with the predicted elution-density relationship in Fig. 3 and provide independent verification. Using this relationship, the elution profile for DS19 plotted along the time axis of Fig. 3 is mapped to its density distribution along the abscissa.
Fig. 3.
Relationship between cell elution time and cell density for DEP-FFF at 15 kHz. Symbols represent measured elution times for beads of 1062 and 1070 kg.m−3, and for monocytes (M), lymphocytes (L), and erythrocytes (E). The solid line shows the calculated responses expected from the theory under the experimental conditions (Table 1). The cell density distribution can be derived by mapping the elution profile using the calculated response. The elution profile for DS19 cells at 15 kHz shown along the time axis is mapped to the corresponding cell density distribution along the density axis.
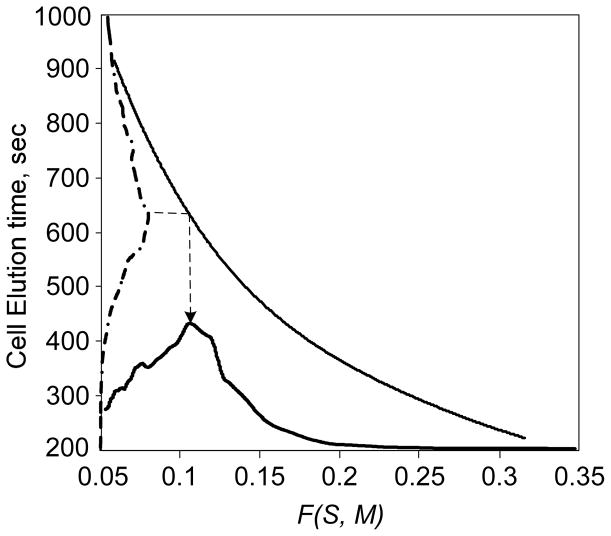
The FFF elution profile (no DEP) depends on the balance of cell sedimentation and HDLF. Using the cell density derived above, a mapping from the FFF profile to the corresponding F(M) distribution can be established as shown in Fig. 4. The FFF elution profile for DS19 is plotted along the time axis of Fig. 4 and the corresponding geometry function distribution is shown on the abscissa. This distribution peaks at F(M) = 0.11, a value close to the value found for the most rigid of the vesicles examined by Abkarian and Viallat48.
Fig. 4.
Relationship between cell elution and the cell hydrodynamic geometry function calculated from the theory is shown by the solid curve using the density peak data from Fig. 3. Using this relationship, the cell elution distribution for DS19 under sedimentation-FFF conditions can be mapped to the corresponding hydrodynamic geometry function distribution.
By definition, cells should not experience a DEP force at their crossover frequency (f0 = 74 kHz). Peak cell elution times for sedimentation FFF (no DEP) were measured at flow rates of 1.5, 4, 6, 8 and 10 mL.min−1 and plotted as stars on the line at 74 kHz in Fig. 2A. These data coincide with the intersections of the calculated DEP-FFF characteristics and the 74 kHz line. This verifies that the theory accounts correctly for HDLF effects and is consistent with sedimentation FFF40;43.
Efficient Isolation of Cell Parameters from DEP-FFF Data
Fig. 2A shows cells approach not only a limiting elution time, Tmin for f ≪ f0 but also a limiting elution time Tmax when f ≫ f0. For a channel of length L, the cell velocity will vary between the limits Vmax = L/Tmin and Vmin = L/Tmin if the frequency is swept over a sufficiently wide range. To exploit this, we used field programming40;62;63 and swept the frequency from 160 kHz to 15 kHz over 600 seconds during a DEP-FFF run.
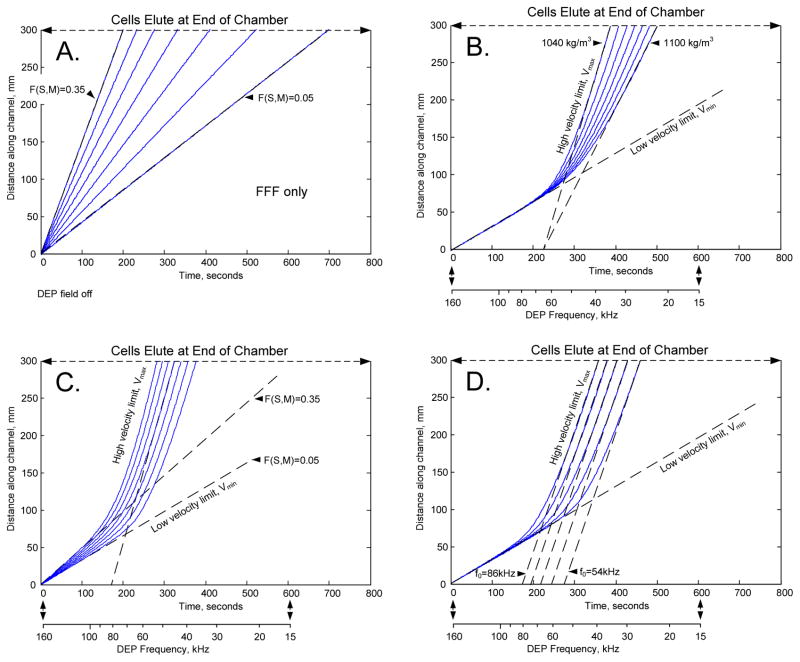
To derive f0 from a swept-frequency elution profile, it is helpful to consider cell transits inside the DEP-FFF channel under different conditions. Fig. 5 A shows conventional FFF for different values of F(M). Panels B, C and D show transit behavior during frequency sweeps. The frequency starts well above f0 and DEP pulls cells towards the electrodes where they move at Vmin. As time progresses, the frequency passes through f0 and the velocity increases as DEP starts to levitate cells into faster-moving fluid. Eventually, the frequency becomes low enough that the DEP force is maximally levitating and cell velocity approaches Vmax.
Fig. 5.
Simulations of the progression of a cell through a DEP-FFF channel under different experimental conditions. (A) With no DEP field, cells move by conventional sedimentation-FFF at a height determined by the balance of sedimentation and HDLF effects. Changes in the hydrodynamic geometry function F(S, M) impact the height and corresponding velocity with which cells travel. (B – D) Simulations of cell progress during a logarithmically-programmed sweep of the DEP field frequency from 160 kHz to 15 kHz over 600 seconds. At short times the DEP frequency greatly exceeds the cell crossover frequency f0 and cells move at minimum velocity Vmin. Later, cells move faster as the swept frequency passes through f0. At still longer times the DEP frequency has fallen far below f0, and cells moves at maximum velocity, Vmax. (B) Increasing the cell density ρp decreases the maximum velocity Vmax but leaves Vmin unchanged. (C) Increasing the hydrodynamic geometry function F(S, M) increases Vmin but leaves Vmax unchanged. (D) Increasing the crossover frequency f0 leaves Vmax and Vmin unchanged, but increases the time at which the transition of the velocities occurs.
Fig. 5A shows that, under FFF conditions, smaller F(M) results in shorter elution times. For swept frequencies, the cell density controls Vmax without altering Vmin (Fig. 5B). Fig. 5C shows that F(M) controls Vmin without significantly changing Vmax. Finally, Fig. 5D shows that changing f0 keeps Vmin and Vmax unaltered but modifies when cells begin to levitate. If Vmin and Vmax are known then the time at which f0 is reached can be calculated from the elution time.
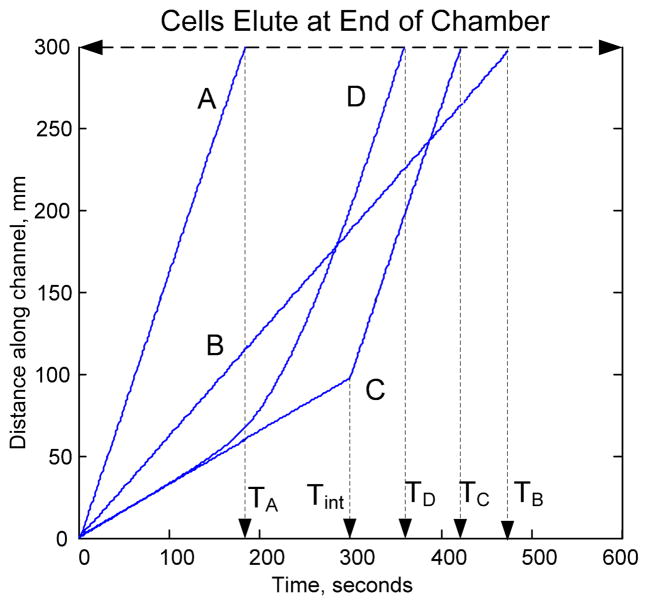
With this knowledge, the cell parameters may be derived efficiently from a set of four DEP-FFF runs as shown in Fig. 6.
Fig. 6.
Cell biophysical properties may be derived from four independent measurements. A shows the displacement of cells through the DEP-FFF channel as a function of time under the influence of a low frequency DEP field. The frequency is set low enough that the cells attain maximum levitation and so their resulting velocities reflect their density. B the conventional sedimentation-FFF elution profile is measured with the DEP field off. C the DEP frequency is maintained far above the anticipated crossover frequency of the cells for a period Tint and then switched to the low frequency used for Run A. Cells travel at minimum velocity under the influence of hydrodynamic lift forces until the frequencies switch. D shows cell behavior during a 600 second sweep from 160 kHz to 15 kHz.
DEP-FFF is conducted at a fixed frequency f ≪ f0 and cells elute at maximum velocity Vmax. The elution profile is mapped directly to the cell density distribution (as in Fig. 3);
FFF is conducted (no DEP). Using the density from run A, the FFF profile is mapped to the F(M) distribution (as in Fig. 4);
The DEP-FFF frequency starts fixed at f ≫ f0 and cell velocity is Vmin. Elution would be extremely slow with the risk of cell dielectric properties changing in the eluate. To avoid this, after an intermediate time Tint, the DEP frequency is switched to f ≪ f0 (as in Run A) to rapidly elute the cells. Vmin is calculated from the elution time TB knowing Tint and Vmax from Run A.
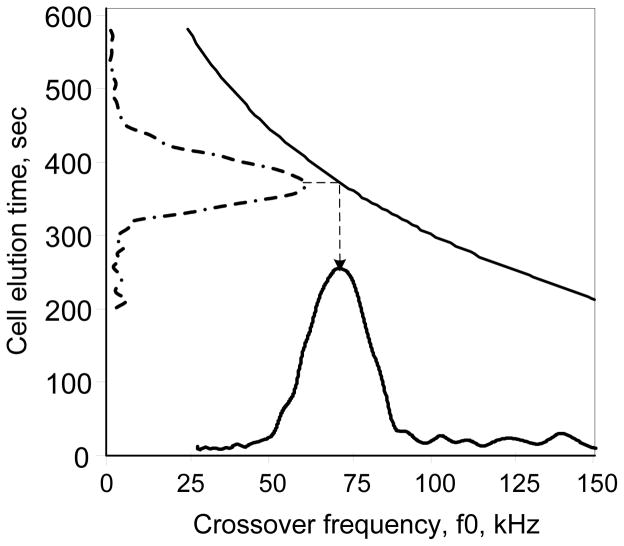
The DEP-FFF frequency sweeps from well above the crossover frequency to well below it. Cell velocity is tangential to Vmin early in the run and tangential to Vmax late in the run (Fig. 5D), allowing the time at which the frequency was equal to the crossover frequency to be calculated from the elution time TD, maximum velocity Vmax from Run A and minimum velocity Vmin from Run C. A mapping from the swept frequency cell elution profile to the corresponding DEP crossover frequency distribution can be obtained as shown in Fig. 7 for DS19.
Fig. 7.
Relationship between cell elution time and cell crossover frequency f0 calculated for a cell density of 1054 kg.m−3 and a hydrodynamic geometry function of 0.11 (solid line). The elution profile for DEP frequency swept from 160 to 15 kHz, is shown on the elution time axis. The corresponding cell crossover frequency distribution is shown on the abscissa.
Discussion
DEP-FFF elution profiles depend upon particle density, dielectric properties and deformability. Existing theory11 ignored HDLF and predicted particles would be trapped when the net DEP and sedimentation forces pulled them to the floor. The dotted lines in Fig. 2A show simulations for that theory and those do not describe any of the data.
The new theory fits the DEP-FFF data over a range of conditions and is consistent with sedimentation FFF. It allows derivation of effective values for cell density, f0, and deformability from elution profiles. By exploiting high frequency and low frequency DEP limits, population distributions of the cell parameters are derived through mappings in Figs. 3, 4 and 7, using only 4 runs of a few hundred seconds each.
The results show that low frequency DEP-FFF elution provides a rapid, microfluidic approach for measuring particle densities and separating them accordingly. As long as Re[fCM (f)] → −0.5, such density distributions are obtained with no assumptions. The densities for DS19 cells (Fig. 3) are narrowly distributed around 1058 kg.m−3.
The F(M) and f0 distributions were obtained by mappings that assume distributions upstream in the calculations do not broaden the derived distributions. This is valid only if the cell density and geometry profiles are sufficiently narrow. Using Fig. 5 to gauge DS19 distribution broadening, the narrow density range (Fig. 3) resulted in negligible broadening of F(M) (Fig. 4), while the density and F(M) distributions together broadened the f0 distribution by approximately 4 kHz in Fig. 7. Such broadening effects might be reduced significantly through deconvolution64;65, though interdependencies between cell density, cell geometry factor and f0 could impact the validity of this method.
The DS19 F(M) profile (Fig. 4) varies from ~ 0.05 to ~0.125 with a tail extending to 0.25. A value of 0.05 indicates significant rigidity, while a value of 0.125 corresponds to the least flexible of the vesicles reported by Abkarian and Viallat48. The DS19 cultures were asynchronous and cell membrane and cytoskeletal structural differences during the cell cycle are expected to be reflected within the deformability distribution. Similarly, cell membrane capacitance and conductivity changes during the cell cycle66;67 should be reflected within the cell crossover frequency distribution (Fig. 7). Now that the parameter distributions can be measured by the methods provided here, these and other structure-function relationships can be studied by synchronizing cells and examining cell cycle changes, for example. By using DEP-FFF as a front end to a flow cytometer17;68 or high throughput molecular profiler, such relationships can be resolved within mixed cell populations and correlated with molecular profiles. Thus, cell biophysical parameters could be interpreted using appropriate models in the literature to provide insights into underlying cell morphology, physiology, structure-function, metabolic, proteomic and gene expression relationships.
DS 19 cells are complex particles because they exhibit distributions in density, flexibility and in frequency-dependent dielectric properties. For particle types having frequency-independent properties, frequency sweeping is not required. For insulating particles, density and F(S, M) could be deduced from runs A and B alone. For semiconducting particles, run A combined with two or more runs B conducted at different eluate conductivities would allow density, F(S, M) and conductivity to be deduced. The method is more problematical for conducting particles because Re[fCM (f)] = +1 for all frequencies. In that case, DEP and sedimentation forces would need to be balanced against HDLF during a voltage sweep and particle density would have to be deduced indirectly.
Conclusions
Previous treatments of DEP-FFF did not take into account HDLF effects or provide methods to derive particle properties from elution characteristics. The theory presented here accounts for HDLF and describes the DEP-FFF elution data over a wide range of conditions. The theory was used to profile cell density, deformability and membrane capacitance distributions of cell populations. Using this approach, the identification of cell subpopulations having different biophysical characteristics and the rapid measurement of changes induced by external agents is enabled. The ability to derive cell properties explicitly will permit design of optimal conditions for isolating target cell subpopulations by DEP-FFF. With minor modifications, the methods presented here can be adapted to a wide range of particle characterization applications.
Acknowledgments
This work was supported by grants from NIH (R33 CA88364-01) and from the Kleberg Center for Molecular Markers. I am grateful to Jamileh Noshari for cytology and constant support, to Tom Anderson for patient fabrication and experimentation and to William Spencer for help preparing this article.
Reference List
- 1.Chen CS, Pohl HA. Ann N Y Acad Sci. 1974;238:176–85. doi: 10.1111/j.1749-6632.1974.tb26787.x. [DOI] [PubMed] [Google Scholar]
- 2.Pohl HA, Crane JS. Biophys J. 1971;11:711–27. doi: 10.1016/S0006-3495(71)86249-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Aldaeus F, Lin Y, Amberg G, Roeraade J. J Chromatogr A. 2006;1131:261–66. doi: 10.1016/j.chroma.2006.07.022. [DOI] [PubMed] [Google Scholar]
- 4.Aldaeus F, Lin Y, Roeraade J, Amberg G. Electrophoresis. 2005;26:4252–59. doi: 10.1002/elps.200500068. [DOI] [PubMed] [Google Scholar]
- 5.Cui HH, Lim KM. Langmuir. 2009 doi: 10.1021/la803761f. [DOI] [PubMed] [Google Scholar]
- 6.Gascoyne PR, Vykoukal J. Electrophoresis. 2002;23:1973–83. doi: 10.1002/1522-2683(200207)23:13<1973::AID-ELPS1973>3.0.CO;2-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gielen F, deMello AJ, Cass T, Edel JB. J Phys Chem B. 2009;113:1493–500. doi: 10.1021/jp808897g. [DOI] [PubMed] [Google Scholar]
- 8.Huang JT, Wang GC, Tseng KM, Fang SB. J Ind Microbiol Biotechnol. 2008;35:1551–57. doi: 10.1007/s10295-008-0459-x. [DOI] [PubMed] [Google Scholar]
- 9.Jen CP, Chen TW. Biomed Microdevices. 2009;11:597–607. doi: 10.1007/s10544-008-9269-1. [DOI] [PubMed] [Google Scholar]
- 10.Becker FF, Wang XB, Huang Y, Pethig R, Vykoukal J, Gascoyne PR. Proc Natl Acad Sci USA. 1995;92:860–64. doi: 10.1073/pnas.92.3.860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Huang Y, Wang XB, Becker FF, Gascoyne PR. Biophys J. 1997;73:1118–29. doi: 10.1016/S0006-3495(97)78144-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wang XB, Yang J, Huang Y, Vykoukal J, Becker FF, Gascoyne PR. Anal Chem. 2000;72:832–39. doi: 10.1021/ac990922o. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wang XB, Vykoukal J, Becker FF, Gascoyne PR. Biophys J. 1998;74:2689–701. doi: 10.1016/S0006-3495(98)77975-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Yang J, Huang Y, Wang XB, Becker FF, Gascoyne PR. Anal Chem. 1999;71:911–18. doi: 10.1021/ac981250p. [DOI] [PubMed] [Google Scholar]
- 15.Markx GH, Pethig R. Biotechnol Bioeng. 1995;45:337–43. doi: 10.1002/bit.260450408. [DOI] [PubMed] [Google Scholar]
- 16.Yang J, Huang Y, Wang XB, Becker FF, Gascoyne PR. Biophys J. 2000;78:2680–89. doi: 10.1016/S0006-3495(00)76812-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Huang Y, Yang J, Wang XB, Becker FF, Gascoyne PR. J Hematother Stem Cell Res. 1999;8:481–90. doi: 10.1089/152581699319939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Stephens M, Talary MS, Pethig R, Burnett AK, Mills KI. Bone Marrow Transplant. 1996;18:777–82. [PubMed] [Google Scholar]
- 19.Talary MS, Mills KI, Hoy T, Burnett AK, Pethig R. Med Biol Eng Comput. 1995;33:235–37. doi: 10.1007/BF02523050. [DOI] [PubMed] [Google Scholar]
- 20.Vykoukal J, Vykoukal DM, Freyberg S, Alt EU, Gascoyne PR. Lab Chip. 2008;8:1386–93. doi: 10.1039/b717043b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gascoyne P, Pethig R, Satayavivad J, Becker FF, Ruchirawat M. Biochim Biophys Acta. 1997;1323:240–52. doi: 10.1016/s0005-2736(96)00191-5. [DOI] [PubMed] [Google Scholar]
- 22.Gascoyne P, Mahidol C, Ruchirawat M, Satayavivad J, Watcharasit P, Becker FF. Lab Chip. 2002;2:70–75. doi: 10.1039/b110990c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gascoyne P, Satayavivad J, Ruchirawat M. Acta Trop. 2004;89:357–69. doi: 10.1016/j.actatropica.2003.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gascoyne PR, Noshari J, Anderson TJ, Becker FF. Electrophoresis. 2009;30:1388–98. doi: 10.1002/elps.200800373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kim Y, Hong S, Jung S, Strano MS, Choi J, Baik S. J Phys Chem B. 2006;110:1541–45. doi: 10.1021/jp055110c. [DOI] [PubMed] [Google Scholar]
- 26.Lapizco-Encinas BH, Rito-Palomares M. Electrophoresis. 2007;28:4521–38. doi: 10.1002/elps.200700303. [DOI] [PubMed] [Google Scholar]
- 27.Mattsson M, Gromov A, Dittmer S, Eriksson E, Nerushev OA, Campbell EE. J Nanosci Nanotechnol. 2007;7:3431–35. doi: 10.1166/jnn.2007.830. [DOI] [PubMed] [Google Scholar]
- 28.Peng H, Alvarez NT, Kittrell C, Hauge RH, Schmidt HK. J Am Chem Soc. 2006;128:8396–97. doi: 10.1021/ja0621501. [DOI] [PubMed] [Google Scholar]
- 29.Techaumnat B, Takuma T. Journal of Applied Physics. 2004;96:5877–85. [Google Scholar]
- 30.Pui-ock S, Ruchirawat M, Gascoyne P. Anal Chem. 2008;80:7727–34. doi: 10.1021/ac801095p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ratanachoo K, Gascoyne PR, Ruchirawat M. Biochim Biophys Acta. 2002;1564:449–58. doi: 10.1016/s0005-2736(02)00494-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Archer GP, Betts WB, Haigh T. Microbios. 1993;73:165–72. [PubMed] [Google Scholar]
- 33.Quinn CM, Archer GP, Betts WB, O’Neill JG. Lett Appl Microbiol. 1996;22:224–28. doi: 10.1111/j.1472-765x.1996.tb01148.x. [DOI] [PubMed] [Google Scholar]
- 34.GOOSSENS K, VAN BIESEN L. International Geoscience and Remote Sensing Symposium IEEE-IGARSS. Washington (USA): 2009. pp. 999–1003. [Google Scholar]
- 35.Deinega YF, Lobastova AV, Solodkaya LN, Ratushnyak VV. Chemistry and Technology of Fuels and Oils. 1992;28:20–22. [Google Scholar]
- 36.Lungu M. International Journal of Mineral Processing. 2006;78:215–19. [Google Scholar]
- 37.Chianea T, Assidjo NE, Cardot PJ. Talanta. 2000;51:835–47. doi: 10.1016/s0039-9140(99)00335-5. [DOI] [PubMed] [Google Scholar]
- 38.Kassab JR, Cardot PJ, Zahoransky RA, Battu S. J Chromatogr B Analyt Technol Biomed Life Sci. 2005;826:8–16. doi: 10.1016/j.jchromb.2005.06.020. [DOI] [PubMed] [Google Scholar]
- 39.Lautrette C, Cardot PJ, Vermot-Desroches C, Wijdenes J, Jauberteau MO, Battu S. J Chromatogr B Analyt Technol Biomed Life Sci. 2003;791:149–60. doi: 10.1016/s1570-0232(03)00229-0. [DOI] [PubMed] [Google Scholar]
- 40.Metreau JM, Gallet S, Cardot PJ, Le MV, Dumas F, Hernvann A, Loric S. Anal Biochem. 1997;251:178–86. doi: 10.1006/abio.1997.2271. [DOI] [PubMed] [Google Scholar]
- 41.Caldwell KD. Anal Chem. 1988;60:959A–71A. doi: 10.1021/ac00168a001. [DOI] [PubMed] [Google Scholar]
- 42.Giddings JC. Science. 1993;260:1456–65. doi: 10.1126/science.8502990. [DOI] [PubMed] [Google Scholar]
- 43.Caldwell KD, Compton BJ, Giddings JC, Olson RJ. Invest Ophthalmol Vis Sci. 1984;25:153–59. [PubMed] [Google Scholar]
- 44.Goldman AJ, Cox G, Brenner H. Slow viscous motion of a sphere parralel to a plane. Chemical Engineering Science. 22:637–660. 1-1-0067. Ref Type: Generic. [Google Scholar]
- 45.Williams PS, Koch T, Giddings JC. Chemical Engineering Communications. 1992;111:121–47. [Google Scholar]
- 46.Qing D, Schimpf ME. Anal Chem. 2002;74:2478–85. doi: 10.1021/ac0200318. [DOI] [PubMed] [Google Scholar]
- 47.Tong X, Caldwell KD. J Chromatogr B Biomed Appl. 1995;674:39–47. doi: 10.1016/0378-4347(95)00297-0. [DOI] [PubMed] [Google Scholar]
- 48.Abkarian M, Viallat A. Biophys J. 2005;89:1055–66. doi: 10.1529/biophysj.104.056036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Mader MA, Vitkova V, Abkarian M, Viallat A, Podgorski T. Eur Phys J E Soft Matter. 2006;19:389–97. doi: 10.1140/epje/i2005-10058-x. [DOI] [PubMed] [Google Scholar]
- 50.Pethig R, Jakubek LM, Sanger RH, Heart E, Corson ED, Smith PJ. IEE Proc Nanobiotechnol. 2005;152:189–93. doi: 10.1049/ip-nbt:20050040. [DOI] [PubMed] [Google Scholar]
- 51.Goater AD, Pethig R. Parasitology. 1998;117(Suppl):S177–S189. doi: 10.1017/s0031182099004114. [DOI] [PubMed] [Google Scholar]
- 52.Marszalek P, Zielinsky JJ, Fikus M, Tsong TY. Biophys J. 1991;59:982–87. doi: 10.1016/S0006-3495(91)82312-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Chan KL, Gascoyne PR, Becker FF, Pethig R. Biochim Biophys Acta. 1997;1349:182–96. doi: 10.1016/s0005-2760(97)00092-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Jones TB. IEEE Eng Med Biol Mag. 2003;22:33–42. doi: 10.1109/memb.2003.1304999. [DOI] [PubMed] [Google Scholar]
- 55.Pethig R, Jakubek LM, Sanger RH, Heart E, Corson ED, Smith PJ. IEE Proc Nanobiotechnol. 2005;152:189–93. doi: 10.1049/ip-nbt:20050040. [DOI] [PubMed] [Google Scholar]
- 56.Pethig R, Markx GH. Trends Biotechnol. 1997;15:426–32. doi: 10.1016/S0167-7799(97)01096-2. [DOI] [PubMed] [Google Scholar]
- 57.Marszalek P, Zielinsky JJ, Fikus M, Tsong TY. Biophys J. 1991;59:982–87. doi: 10.1016/S0006-3495(91)82312-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Mirtaheri P, Grimnes S, Martinsen OG. IEEE Trans Biomed Eng. 2005;52:2093–99. doi: 10.1109/TBME.2005.857639. [DOI] [PubMed] [Google Scholar]
- 59.Schwan HP. Ann Biomed Eng. 1992;20:269–88. doi: 10.1007/BF02368531. [DOI] [PubMed] [Google Scholar]
- 60.Schwan HP. Biophysik. 1966;3:181–201. doi: 10.1007/BF01191612. [DOI] [PubMed] [Google Scholar]
- 61.Gascoyne PR, Becker FF. J Cell Physiol. 1990;142:309–15. doi: 10.1002/jcp.1041420213. [DOI] [PubMed] [Google Scholar]
- 62.Plockova J, Chmelik J. J Chromatogr A. 2006;1118:253–60. doi: 10.1016/j.chroma.2006.03.124. [DOI] [PubMed] [Google Scholar]
- 63.Williams PS, Giddings JC. J Chromatogr. 1991;550:787–97. doi: 10.1016/s0021-9673(01)88582-4. [DOI] [PubMed] [Google Scholar]
- 64.Li Y, Lacey ME, Sweedler JV, Webb AG. J Magn Reson. 2003;162:133–40. doi: 10.1016/s1090-7807(03)00055-7. [DOI] [PubMed] [Google Scholar]
- 65.Bonnot G, Febvay G. Anal Biochem. 1995;224:354–63. doi: 10.1006/abio.1995.1051. [DOI] [PubMed] [Google Scholar]
- 66.Huang Y, Wang XB, Gascoyne PR, Becker FF. Biochim Biophys Acta. 1999;1417:51–62. doi: 10.1016/s0005-2736(98)00253-3. [DOI] [PubMed] [Google Scholar]
- 67.Kim U, Shu CW, Dane KY, Daugherty PS, Wang JY, Soh HT. Proc Natl Acad Sci USA. 2007;104:20708–12. doi: 10.1073/pnas.0708760104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Cardot P, Battu S, Simon A, Delage C. J Chromatogr B Analyt Technol Biomed Life Sci. 2002;768:285–95. doi: 10.1016/s1570-0232(01)00609-2. [DOI] [PubMed] [Google Scholar]