Quality by Design: Scale-Up of Freeze-Drying Cycles in Pharmaceutical Industry

Abstract

This paper shows the application of mathematical modeling to scale-up a cycle developed with lab-scale equipment on two different production units. The above method is based on a simplified model of the process parameterized with experimentally determined heat and mass transfer coefficients. In this study, the overall heat transfer coefficient between product and shelf was determined by using the gravimetric procedure, while the dried product resistance to vapor flow was determined through the pressure rise test technique. Once model parameters were determined, the freeze-drying cycle of a parenteral product was developed via dynamic design space for a lab-scale unit. Then, mathematical modeling was used to scale-up the above cycle in the production equipment. In this way, appropriate values were determined for processing conditions, which allow the replication, in the industrial unit, of the product dynamics observed in the small scale freeze-dryer. This study also showed how inter-vial variability, as well as model parameter uncertainty, can be taken into account during scale-up calculations.

INTRODUCTION

Freeze-drying typically is used to recover an active pharmaceutical ingredient from an aqueous solution. As the process can be carried out at low temperatures, it makes possible to avoid damage to molecules that, in most cases, are highly heat sensitive. In a standard freeze-drying cycle, first the product is frozen, and then the surrounding pressure is decreased in order to promote ice sublimation (primary drying). As a part of water does not freeze, but is bound to the product, product temperature is increased after the end of primary drying in order to promote water desorption (secondary drying). This study focuses on primary drying as it is widely considered the most critical stage.

During primary drying processing conditions, namely pressure in the drying chamber and temperature of the heat transfer fluid, have to be defined accurately in order to preserve the product quality. Various critical quality attributes are relevant to freeze-dried products, e.g., the stability of the active pharmaceutical ingredient, the reconstitution time, the cake appearance, etc.… All these quality targets can be expressed in terms of maximum value for the product temperature that should not be exceeded during freeze-drying cycle. For example, if the critical quality attribute is the cake appearance, the critical product temperature corresponds to the collapse temperature for amorphous products, or the eutectic temperature for crystalline products. If two or more critical quality attributes are considered, the critical temperature for the product is the lowest value among the various critical temperatures identified. In this perspective, a suitable cycle can be obtained by means of an extended experimental investigation carried out with laboratory equipment, or by using model-based tools such as the SMART^TM Freeze-Dryer (1), the LyoDriver (2,3) or model predictive control systems (4–6). These tools provide the optimal cycle with few runs. Recently, design space was proposed as a valid alternative to the above tools for cycle development. Design space can be obtained by means of extended experimental investigation (7), where the number of experiments can be reduced drastically by combining statistical design of experiments and mathematical modeling (8), or by using process simulation (9–14).

Once the cycle has been developed in a lab-scale unit, this cycle should not be transferred to a production unit without modifications. In fact, this approach does not guarantee that the product has the same thermal history both in lab-scale and in production scale freeze-dryers. This difference may be due to various factors, which are well known to every freeze-drying practitioner and have recently been discussed in literature (15–18). Some of these factors are listed below:

• Variations in pressure in the drying chamber depend on freeze-dryer geometry (19);

• The nucleation temperature can vary with environmental conditions in the manufacturing area (20);

• Temperature of the heat transfer fluid can vary with the equipment, although the same set-point value is used (21,22);

• Rate of heating and cooling for the heat transfer fluid may vary with the equipment used (21,22);

• Different freeze-dryers may show variations in radiative heat between shelves and chamber walls, because of different values of view factor and surface emissivity (23);

• In laboratory and production freeze-dryers, the condenser may impart a different resistance to mass transfer (e.g., because of a different configuration, internal vs. external condenser), or show a different capability to remove vapor and control pressure inside the drying chamber (24).

In the past, various solutions were proposed to scale-up a cycle. The simplest one is based on trial and error (25). This approach requires expertise and leads to non-optimal cycles. A valid alternative to this method is the development of a robust cycle, which is not necessary to modify when scaled-up to manufacturing equipment (16). If the design space is used to develop the cycle, a “robust” design space can be defined, e.g., by using statistical tools (26). A true scale-up of a freeze-drying cycle can only be obtained by mathematical modeling. Kramer et al. (27) proposed a simple method, which can be applied if the temperature of heat transfer fluid is maintained constant during primary drying, and variations in product resistance to vapor flow between lab and production units are negligible. Fissore and Barresi (28) proposed a more sophisticated method for both scale-up and process transfer, which can also manage variations in product resistance during primary drying and between dryers, as well as batches with heterogeneous drying behavior and parameter uncertainty. They also tested the suitability of their approach by mathematical simulations.

If model-based tools are employed for the design and scale-up of a cycle, a suitable (and robust) model has to be used; this model should entail few parameters which can easily be measured by using inexpensive sensors, both in lab-scale and production equipment. Furthermore, limitations posed by manufacturing freeze-dryers have to be accounted for, e.g., plant availability for testing.

This paper deals with the problem of scaling up freeze-drying cycles from lab-scale to manufacturing equipment. The most critical parameters for scale-up and process transfer are identified, and the ability of predictive modeling to facilitate this operation (17,28) is discussed. The problem of scale-up is presented for a real case in industry, which is the freeze-drying of small molecules in a lab freeze-dryer and in two different industrial units. The main issues related to the application of the method proposed by Fissore and Barresi (28), as well as to the determination of model parameters, are discussed and effective solutions are provided.

MATERIALS AND METHODS

Mathematical Model

In order to be suitable for the design and scale-up of a freeze-drying cycle, a mathematical model should reliably describe the dynamics of the process, the time required by calculations should be short, and model parameters should be few and easy to be measured. In this work, the model proposed by Velardi and Barresi (29) and used by Fissore et al. (10) for design space calculation is used, as it can accurately describe process dynamics in a wide range of processing conditions and involves only two parameters, namely an effective heat transfer coefficient between shelf and product (K_v) and an overall resistance to vapor flow (R_p).

Determination of Model Parameters

The parameter K_v can be determined by means of various methods, e.g., the tunable diode laser absorption spectroscopy (30,31) or by the pressure rise test technique (32–36). Both methods supply the average value of K_v for the batch as a whole, while any information is given about how K_v varies with vial position. This information can be obtained by the gravimetric method, which can be applied to both lab-scale and production units (37). In industrial equipment, the use of wireless sensors can facilitate operations as these sensors are compatible with the restrictions posed by automatic loading systems (38,39). For all these reasons, in this paper, the above method is used for the thermal characterization of the vials.

In order to scale-up a cycle, as the value of K_v of a specific vial can vary between different freeze-dryers, this value has to be determined in both lab-scale and production units. The sequence of operations required is listed below:

• Determine the value of K_v for a batch of vials in the small equipment. The measurement is carried out at a given value of pressure and by using the gravimetric method;

• Classify vials into various groups by their position on the heating shelf;

• Calculate the average value of K_v for each vial group, as well as its variance. This measurement is performed at a precise value of pressure, which is fixed a priori and is then used during primary drying, unless its local variation in the larger apparatus is so significant to require the knowledge of pressure dependence for K_v. If this is not the case, the heat transfer coefficient has to be measured only at the operating pressure used; therefore only two gravimetric runs have to be carried out, one in the lab-scale freeze-dryer and one in the production unit.

• If the pressure is modified during the cycle, or the design space is used for cycle development, repeat the above points for (at least) other two values of pressure. Then, for each group of vials, determine the coefficients C₁, C₂, and C₃ which describe the pressure dependence for K_v (37):

  $$K_v={\left(\frac{1}{C_1+\frac{C_2{P}_c}{1+C_3{P}_c}}+\frac{s_{\mathrm{glass}}}{{\lambda }_{\mathrm{glass}}}+\frac{1}{k_s}\right)}^{-1}$$ 1

  The above coefficients are determined by the regression of experimental values for K_vvs. P_c.

• As shown by Pisano et al. (13), C₁ is the only parameter in Eq. (1) which cannot be calculated theoretically, as it depends on the contact between the shelf surface and the bottom of the vial. Furthermore, the uncertainty of C₂ and C₃ gives a minor contribution to the final value of K_v with respect to the uncertainty of C₁. For all these reasons, we assume that C₁ is the only factor responsible for the uncertainty of K_v which is thus expressed in terms of variance of C₁.

• If C₂ and C₃ are not affected by the type of freeze-dryer used, the value of C₂ and C₃ determined for the lab-scale freeze-dryer can also be used for the large scale unit. Therefore, the determination of K_vvs. P_c for the production unit requires only one gravimetric test, which is used to calculate the average value (and the variance) of C₁ for each group of vials.

The overall resistance to vapor flow can be expressed by a nonlinear function of the thickness of the dried layer:

$$R_p=R_{p,0}+\frac{P_1{L}_{\mathrm{dried}}}{1+P_2{L}_{\mathrm{dried}}}$$ 2

where R_p,0, P₁, and P₂ are determined by regression of experimental values for R_pvs. L_dried. In this study, the experimental values of R_pvs. L_dried were estimated by the pressure rise test technique combined with a modified version of the Dynamic Parameters Estimation algorithm (36). A weighing device combined with miniaturized radio-controlled thermometer, which measures the product temperature, can also be used to determine the values of R_pvs. L_dried and, as shown by Fissore et al. (14), the results obtained agree with estimations supplied by the pressure rise test technique. This weighing device is suitable especially for production units where limitations to the use of the pressure rise test technique are common.

Cycle Design

In this study, the design space technique was used to identify an appropriate combination of chamber pressure and temperature of the heat transfer fluid satisfying specific product quality attributes. For this purpose, the procedure proposed by Fissore et al. (10) was used as it is the only method which gives the evolution of the design space during primary drying and can also account for parameter uncertainty. Furthermore, the approach proposed by Pisano et al. (13) was used in order to take into account that the heat transfer coefficient varies with the position of the vial in the array.

The calculation of the design space is based on pre-defined quality targets, which influence the critical quality attributes of the final product, e.g., activity and stability of the active pharmaceutical ingredient (API), reconstitution time, cake appearance, and residual moisture content. These targets are usually expressed in terms of maximum value for the product temperature, which is the maximum temperature above which an undesired phenomenon occurs. For the formulation investigated, the critical temperature (to be used during the design space calculation) was the temperature of the dried cake collapse, as no loss of the API activity was observed at temperatures well above the collapse value. In addition to the residual water content and the macroscopic integrity of the final product, the activity and the stability of the API are key parameters to be assessed. However, this study focuses on the process, thus the analysis of the API stability is beyond the scope of the present work. For this reason, the macroscopic integrity of the freeze-dried product is the only critical quality attribute assessed in the analysis.

The calculation of the design space can also manage an upper bound on the vapor flow rate to be trapped by the condenser. However, for the three freeze-dryers used in this study, this bound was never active, as the condenser capacity was far higher than the highest value of sublimation rate that can be reached respecting the product-imposed constraint.

Cycle Scale-Up

As vials can be classified into various groups on the basis of their position on shelf, the first step to scale-up a cycle is the selection of an appropriate group of vials which is used as reference for the calculations. The method proposed by Fissore and Barresi (28) can be used to scale-up the cycle. If the product resistance to vapor flow is not affected by the type of equipment, the activities needed by the above method are listed below:

• Develop a cycle in a lab-scale freeze-dryer (denoted as unit A) by using the design space (as in the case shown here) or an automatic procedure.

• Use of mathematical modeling to calculate the evolution of the product temperature (T_B and T_i) and of the thickness of the frozen layer (L_frozen) in freeze-dryer A for the above cycle. At each time instant t, i.e., for each value of T_fluid,1, the values of L_frozen, T_i and T_B for the product in freeze-dryer A (denoted as L_frozen,A, T_i,A and T_B,A) are thus known.

• Measure the value of K_v (at the operating pressure used during primary drying) for freeze-dryer B and select the reference vial group to be used for cycle scale-up. If chamber pressure is modified during drying, measure the values of K_vvs. P_c for freeze-dryer B.

• At each time instant t, the temperature of the heat transfer fluid in freeze-dryer B (T_fluid,B) is calculated in order to reproduce the product state obtained in freeze-dryer A (L_frozen,A, T_i,A and T_B,A) on freeze-dryer B (L_frozen,B, T_i,B and T_B,B). For this purpose, the equation proposed by Fissore and Barresi (28) is used:

  $$T_{\mathrm{fluid},B}=\frac{K_{v,B}\left(\frac{1}{K_{v,B}}+\frac{L_{\mathrm{frozen},A}}{k_{\mathrm{frozen}}}\right)T_{B,A}+T_{i,A}}{K_{v,B}\left(\frac{1}{K_{v,B}}+\frac{L_{\mathrm{frozen},A}}{k_{\mathrm{frozen}}}\right)-1}$$ 3

  which relates the temperature of the heat transfer fluid in equipment B directly to the state (temperature and/or thickness) of the frozen product, whose evolution has to be the same observed when the original cycle is used in equipment A. In Eq. (3) the value of K_v for the reference vial group has to be used.

• The above calculations are repeated for any time instant, until ice sublimation is completed. In this way, a new cycle is defined for freeze-dryer B.

A cycle scaled-up by using the above procedure can reproduce on the industrial freeze-dryer the temperature profile and drying time of the reference vials which were observed in the lab-scale unit. Furthermore, as the drying behavior of a batch of vials is heterogeneous, the same mathematical model used for the cycle scale-up is employed to calculate product dynamics when the new cycle is used in freeze-dryer B for all the vial groups previously identified. This analysis aims to check whether or not product temperature remains below its limit value for all the vials, as well as to estimate the drying time.

If product resistance is different for the freeze-dryer A and B, the above algorithm can still be used, but the target for scale-up is to reproduce in freeze-dryer B either the temperature profile or the sublimation flux observed in freeze-dryer A. Details on this aspect are given by Fissore and Barresi (28). A different configuration of the condenser (external vs. internal condenser) can also lead to variations in the resistance to mass transfer. The algorithm can still manage this situation, provided that the overall resistance to mass transfer (given by the contribution of both product and equipment) was determined for both laboratory and production units.

Finally, if parameter uncertainty is known, mathematical modeling can be used to calculate the probabilistic distributions of maximum product temperature and drying time in both freeze-dryer A and B.

Equipment and Instrumentations

Experiments were carried out in three different pieces of equipment:

• A.A laboratory scale freeze-dryer (LyoBeta 25^TM by Telstar, Terrassa, Spain) that comprises a vacuum-tight chamber (volume = 0.2 m³) equipped with four shelves (area of a heating shelf = 0.16 m²), a separate condenser (maximum ice capacity = 40 kg) and a vacuum pump to evacuate non-condensable gases. The system is equipped with appropriate components and sensors to control processing conditions. In particular, the pressure inside the drying chamber is monitored by capacitance (Baratron type 626A, MKS Instruments, Andover, MA, USA) and thermal conductivity gauges (Pirani type PSG-101-S, Inficon, Bad Ragaz, Switzerland), while the temperature of the heat transfer fluid is measured by PT100 sensors. The refrigeration system can reach a minimum temperature of 193 K in the condenser and 218 K in the drying chamber shelves, and perform an average cooling/heating rate of 1 K min⁻¹. The temperature of the product is monitored by T-type miniature thermocouples with 0.5 mm diameter wire (Tersid S.p.A., Milano, Italy), but can also be estimated by a computer-based system that uses the pressure rise test technique.
• B.A pilot-scale freeze-dryer (Lyovac FCM 40-D, GEA Process Engineering, Columbia, MD, USA) that comprises a vacuum-tight chamber (volume = 1.15 m³) equipped with six shelves (area of a heating shelf = 0.56 m²), a separate condenser (maximum ice capacity = 120 kg) and a group of vacuum pumps to evacuate the non-condensable gases. The cooling/heating system uses a diathermic fluid (i.e., silicon oil) for the drying chamber shelves and direct expansion of cryogenic gases in the condenser coils. To carry out basic controls for pressure and temperature, the dryer is equipped with capacitance (Baratron type 626A, MKS Instruments, Andover, MA, USA) and thermal conductivity gauges (Pirani type PSG-101-S, Inficon, Bad Ragaz, Switzerland), as well as PT100 sensors. The refrigeration system can reach a minimum temperature of 183 K in the condenser and 208 K in the drying chamber shelves, and perform an average cooling/heating rate of 0.9 K min⁻¹. The temperature of the product is instead monitored by T-type thermocouples (Tersid S.p.A., Milano, Italy) and using a wireless communication system based on radio signals (39).
• C.An industrial scale freeze-dryer (Lyovac FCM 500-D, GEA Process Engineering, Columbia, MD, USA) that consists of a drying chamber with 15 shelves (area of a heating shelf = 2.7 m²), a separate condenser (maximum ice capacity: 600 kg) and a group of vacuum pumps to evacuate the non-condensable gases. Processing conditions are monitored by a capacitance pressure sensor (Baratron type 621C, MKS Instruments, Andover, MA, USA) and PT100 sensors. The refrigeration system can reach a minimum temperature of 183 K in the condenser and 208 K in the drying chamber shelves, and perform an average cooling/heating rate of 0.9 K min⁻¹.

The various freeze-dryers have different load configurations. In fact, if experiments are carried out in freeze-dryer A or B, vials are surrounded by a metal band, which introduces an additional contribution to heat transfer (because of heat conduction through the band), but shields edge-vials from side-wall radiation. Nevertheless, radiative heat is still transferred to edge-vials from the metal band, but its contribution to the energy balance of the system is limited as the temperature of the radiative surface is low. Instead, in freeze-dryer C vials are trapped between two lateral guides that do not shield edge-vials from side-radiation.

The effect of the load configuration on critical process parameters may be remarkable; therefore a cycle developed in a lab-scale unit may need to be adjusted in order to obtain the same drying time and product temperature profile in a production unit. The size and geometry of drying chamber may modify gas flow dynamics (and thus the resistance of the equipment to vapor flow), as well as the view factor for radiative heat transfer. Furthermore, emissivity of surfaces involved in radiative heat transfer can be different, although this was not the case investigated. Finally, during the cycle scale-up, the nucleation temperature and, thus, the resistance of the product to vapor flow can vary with the environmental conditions in the manufacturing area.

Case Study

The problem of cycle scale-up for a parenteral product is discussed. The product being dried is a proprietary pharmaceutical formulation (with 9.4% w/w of active pharmaceutical ingredient and 1.8% w/w of sodium hydroxide), which contains small molecules sensitive to high temperatures. A fixed volume (i.e., 1.5 mL) of this solution was filled in glass tubing vials (internal diameter = 21.95 mm; thickness at the vial bottom = 1.41 mm; vial volume, 17 mL), which were loaded directly on shelves and arranged in clusters of hexagonal arrays. Figure 1 shows a schematic of vial arrangement for the three freeze-dryers used. As shown in Fig. 1, vials can be classified by their position on the shelf into three different groups: (1) vials at the edge, (2) on the second row and (3) in the central part of the batch (37). A further refinement may be introduced to further classify vials of group 1 into various subgroups, as they can be radiated by different walls of the chamber, or receive heat by conduction through the metal band. For the sake of simplicity, in this study we have gathered all edge-vials in only one group, while potential inter-vial variability was included in parameter uncertainty. Only for freeze-dryer B, edge-vials were classified in two subsets (i.e., 1a and 1b) because the observed variance was very high.

Fig. 1.

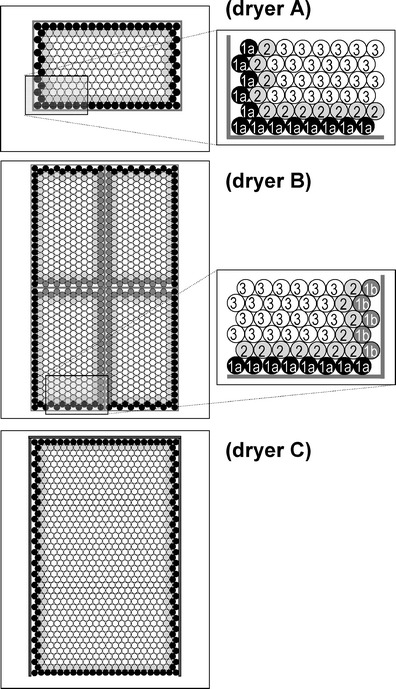
Vial groups as classified by their position on the shelf: group 1 (1a: filled black circle, 1b: filled dark-gray circle), 2 (filled light-gray circle), and 3 (open circle)

After vial load, the product was frozen at T_fluid = 223 K. An annealing step was introduced during the freezing phase, during which product temperature was maintained above its glass transition value (i.e., 238 K) for about 1 h. In this study, all the runs were carried out with non-GMP conditions.

During primary drying, operating conditions were set according to the final scope of the test. For example, if the objective of the test was to determine the relationship between R_p and L_dried, T_fluid, and P_c were appropriately set in order to maintain the product temperature below its limit value and hence preserve the structure of the cake. By contrast, if the objective of the test was to determine the values of K_vvs. P_c for the vial used, experiments were carried out using de-ionized water (Milli-Q RG, Millipore, Billerica, MA) and higher temperature for the shelf. In addition, in order to evaluate the pressure dependence of the heat transfer coefficient, the test was carried out at different values of P_c in the range of 5–20 Pa. Afterward, as the design space of the formulation shows that the optimal pressure (as that value at which the rate of sublimation has the highest value) is lower than 20 Pa, the range of pressure utilized is sufficient for the scope of the work. By contrast, if the design space showed that the optimal pressure was higher than 20 Pa, the gravimetric test would be carried out at P_c higher than 20 Pa.

The maximum temperature at which the formulation can be processed was instead measured by a differential scanning calorimeter (DSC type Q200, TA Instruments, New Castle, DE, USA), where samples were frozen at 213 K and, then, heated at 10 K min⁻¹ up to room temperature. The entire analysis was carried out in inert atmosphere. The limit product temperature was determined also by cryo-microscope (type BX51, Olympus Europa, Hamburg, Germany).

The morphology of metalized freeze-dried samples was examined by using a Scanning Electron Microscope (FEI, Quanta Inspect 200, Eindhoven, The Netherlands) at 15 kV and under high vacuum, while the structure of freeze-dried powders was assessed by means of X-ray diffraction. The X-ray powder diffraction patterns were collected by a Philips PW1710 diffractometer using CuKα radiation and a graphite secondary monochromator.

RESULTS

Characterization of Heat Transfer

The heat transfer coefficient of a specific vial can vary with the load configuration of the freeze-dryer, as well as with its position on shelf. Depending on vial position, as said before, vials were classified into three different categories (see Fig. 1): (1) vials at the edge, (2) on the second row and (3) in the central part of the batch. The values of K_vvs. P_c for the three groups of vials were measured by the gravimetric procedure. These results were analyzed by Eq. (1), where parameters C₁, C₂ and C₃ were obtained by regression of experimental values. The results of this analysis are shown in Table I. It must be reminded that the pressure dependence of K_v has to be known only if the cycle is developed using the design space technique and the value of pressure has to be optimized, or if the pressure is modified during drying. By contrast, if P_c is fixed a priori and is not modified during the cycle, the value of K_v has to be measured only at the operating pressure used.

Table I.

Parameters of Eq. (1) Needed for the Calculation of K _v vs. P _c. (C ₂ = 2.15 J s⁻¹ m⁻² K⁻¹ Pa⁻¹, C ₃ = 0.04 Pa⁻¹)

Equipment	Group of vials	$C_1\pm {\sigma }_{C_1}$, J s−1 m−2 K−1
A	1	10.12 ± 1.19
	2	4.71 ± 1.67
	3	3.17 ± 1.50
B	1a	8.36 ± 1.52
	1b	4.78 ± 2.15
	2	4.14 ± 2.58
	3	3.88 ± 1.88
C	1	8.11 ± 1.01
	2	4.43 ± 1.72
	3	3.75 ± 1.20

If the batch is surrounded by a metal band (this is the case of dryer A and B), a further refinement can be introduced for group 1 in order to distinguish between vials in contact and not in contact with the metal band. However, in this study, the conduction through the metal band was limited; therefore edge-vials were not divided into two groups. Nevertheless, if the freeze-dryer B is used, vials of group 1 can still be distinguished between vials 1a and 1b. Vials 1a are in contact with the external border, which is radiated by chamber walls, while vials 1b are in contact with the internal border, which is shielded from chamber walls radiation but receives heat by conduction through the border of the contiguous frame. For the case study here investigated, experiments confirmed that the heat transfer coefficient for vials 1b was lower than that of vials 1a, see Table I.

As already described by Ref. (37), a simple and effective way to express the uncertainty, and/or variability, of K_v is to assume that the only source of uncertainty is the parameter C₁. This uncertainty was expressed as variance of this parameter and, thus, in order to evaluate it, the distribution curve for C₁ was calculated from the experimental distribution of K_v by using Eq. (1) and the values of C₂ and C₃ shown in Table I. An example of results is given in Fig. 2, which refers to vials 3 processed in freeze-dryers A, B, and C.

Fig. 2.

Distribution of the parameter C ₁ for vials of group 3 in freeze-dryer A, B, and C

Characterization of Mass Transfer

The freeze-dried product was analyzed by X-ray diffraction in order to obtain basic information about its solid structure. This analysis showed that the freeze-dried product is completely amorphous without any crystalline structure embedded. Therefore, the limit temperature for the frozen product was assumed to be a few degrees higher than the temperature of glass transition (40), which was determined by differential scanning calorimetry analysis. In fact, for the formulation used, the glass transition temperature was 238 K, while the collapse temperature observed by cryo-microscope was 240 K. However, it must be noted that the difference between glass transition and collapse temperature becomes larger as protein concentration increases (41).

Various freeze-drying cycles were carried out in order to determine the relationship between the resistance to vapor flow and the thickness of the dried layer. In order to maintain the temperature of the product below its limit value during primary drying, the temperature of heat transfer fluid was adjusted by an automatic control system (2), while chamber pressure was maintained constant (P_c = 8 Pa). The value of R_pvs. L_dried as estimated by the pressure rise test technique is displayed in Fig. 3 (graph a, void symbols). R_p sharply increased in the first part of the drying (i.e., L_dried < 1 mm), then it continued to increase but more slowly. This trend is clear evidence of the presence of a more compact layer at the top surface of the dried product, which was confirmed by scanning electron microscope analyses (data not shown).

Fig. 3.

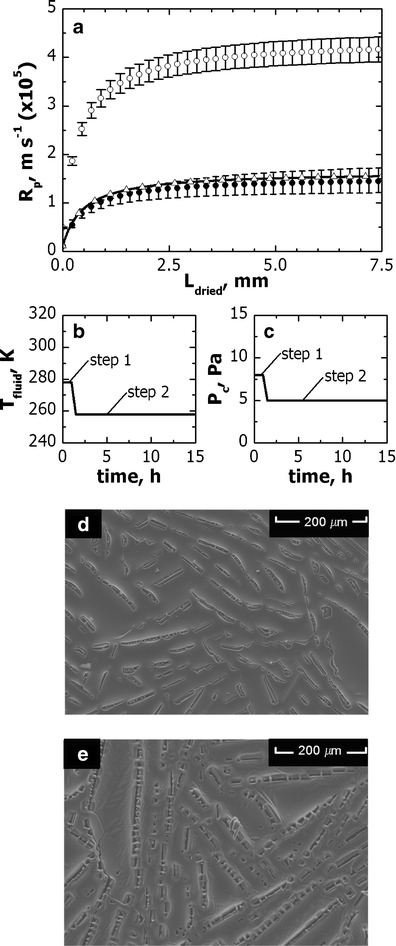
a Values of R _p vs. L _dried for the proprietary formulation used, if it is processed in freeze-dryer A with the one- (R _p,2, filled black circle) and two-step cycle (R _p,1, open circle). The value of R _p,2 for freeze-dryer C is also displayed (solid line, open upright triangle). Processing conditions for the two-step cycle are shown: b temperature of the heat transfer fluid and c chamber pressure. The structure of the top surface of the freeze-dried product as observed by scanning electron microscopy is shown for d the one- and e the two-step cycle

A second test was carried out, where more aggressive heating was used at the beginning of the drying in order to facilitate the crust cracking; then, the temperature of the heat transfer fluid was lowered in order to maintain the product temperature below its limit value. The above cycle made it possible to dramatically increase the maximum value for vapor flow rate (0.8 vs. 0.3 kg h⁻¹ m⁻²) and bring the product temperature above its limit value within the first hour of drying. Figure 3 (graphs b and c) shows that this approach produced larger and more numerous holes on the top surface of the cake, which offered a lower resistance to vapor flow (graph a). It is not yet clear which phenomenon is at the basis of the crust cracking. On the one side, it can be due to a partial collapse of the material and, on the other side, to mechanical shocks caused by high vapor flow rates.

Once the values of R_pvs. L_dried had been measured experimentally, Eq. (2) was used to describe the above dependence and model parameters R_p,0, P₁ and P₂ were obtained by regression of experimental values. The results of this analysis are shown in Table II. As expected, the value of R_p,0 is lower in case of crust cracking (i.e., case #2).

Table II.

Parameters of Eq. (2) Needed for the Calculation of R _p vs. L _dried With (case #2) or Without (case #1) Crust Cracking

Parameter	case #1	case #2
R p,0, m s−1	4.90 × 104	1.13 × 104
P 1, s−1	9.50 × 108	2.74 × 108
P 2, m−1	2.45 × 103	1.92 × 103

Capability of the Condenser

The condenser capability was compared for the three freeze-dryers in terms of ratio of the condenser surface area to the shelf surface area (24). As shown in Table III, this ratio is similar for the three units investigated; despite freeze-dryer C is 12 times larger than freeze-dryer B, and 60 times larger than freeze-dryer A. As already observed by Kuu et al. (24), these results suggest similar condenser capabilities for the three freeze-dryers. It must also be observed that “sink conditions” were never exceeded for the condenser, as the load of ice to be sublimated was lower than 10% of condenser ice capacity, even when the freeze-dryer is full-loaded. Therefore, during the cycle scale-up, the resistance to vapor flow was not modified because of different condenser capability.

Table III.

Geometrical Properties of the Condenser for the Three Freeze-Dryers Used in This Study

Properties	A	B	C
Capacity of the condenser, kg	40	120	600
Surface area of the condenser, m2	0.38	2.00	25.00
Surface area of the shelves, m2	0.64	3.35	40.50
Ratio between condenser and shelf surface area	0.59	0.60	0.62

Development of a Freeze-Drying Cycle via Design Space

Primary drying was carried out in two steps; first, the product was heated above its limit temperature for one hour. In this way, the vapor flow rate was high enough (i.e., J_w = 0.8 kg h⁻¹ m⁻²) to promote formation of cracks on the crust, which allow the reduction in the mass transfer resistance. To facilitate this phenomenon, the product has to be heated up above its glass transition temperature so that the mobility of the structure is sufficiently high. Of course, this operation can produce the product collapse. However, this phenomenon is limited to the already dried product which, within the first hour of drying, corresponds to a thin layer (less than 0.5 mm thickness) close to the top surface of the product. Afterward, the temperature of the heat transfer fluid was lowered in order to maintain the product temperature for edge-vials below T_max, as these vials had the highest value of K_v and therefore can easily be damaged by product overheating. This temperature was determined using the design space of edge-vials (data not shown). The two-step cycle used was: (step 1) from t = 0 to t = 1 h, P_c = 8 Pa and T_fluid = 278 K; (step 2) from t = 1 h until the completion of ice sublimation, P_c = 5 Pa and T_fluid = 258 K. Of course, processing conditions for step 1 exits the design space for all the vial groups within 1 h since the beginning of drying. It must also be noted that here the chamber pressure is modified during drying; therefore in order to scale-up the cycle, the pressure dependence for K_v has to be known.

When step 1 was not used, the value of R_pvs. L_dried dramatically increased (see Fig. 3) and hence the maximum value of T_fluid, which can maintain the product temperature below its limit value for a given value of P_c, was lower. Differences in T_fluid between one- and two-step cycles were more marked as pressure increased, see Fig. 4. Although the above variations in the temperature of heat transfer fluid seem negligible (less than 3 K), their impact on drying time is important, up to about 6 h which corresponds to a reduction in drying time of 20%.

Fig. 4.

Differences in the maximum value of T _fluid (top graph) and drying time (bottom graph) between the one- and two-step cycle shown in Fig. 3 (graphs b and c). These results were obtained at L _dried/L = 99%

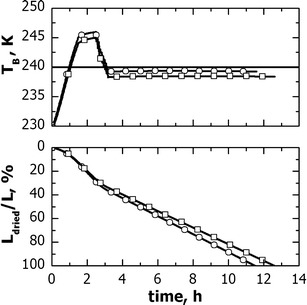
Figure 5 shows an example of freeze-drying cycle carried out using the above two-step cycle. As expected, the product temperature of both edge and central vials was below the limit value only in the second part of the drying. However, visual inspections of end product confirmed that step 1 did not compromise the final product quality. Furthermore, the reduction in R_pvs. L_dried (caused by step 1) was confirmed by the pressure rise test technique estimations. The drying time (as measured by the comparison of Pirani and Baratron signals) was 18 h. This result agrees with the drying time for vials of group 3 estimated by mathematical modeling (see vertical line in Fig. 5) as the time at which L_dried/L is 1.

Fig. 5.

Example of freeze-drying cycle for the proprietary formulation processed in freeze-dryer A. Evolution of a temperature of the heat transfer fluid and chamber pressure, b Pirani–Baratron pressure ratio and model estimations of L _dried/L, and c product temperature measured through thermocouples in vials of groups 1 (edge-vial) and 3 (central vial). The vertical line indicates the sublimation end-point as predicted by the mathematical simulation

Scale-Up of a Freeze-Drying Cycle

Mathematical modeling is used to predict the evolution of T_i, T_B and L_dried when the above two-step cycle is employed in freeze-dryers B and C. Calculations were carried out using the same value of R_pvs. L_dried for both freeze-dryers. This assumption is justified by the fact that the differences in cooling rate and degree of super-cooling are small between the freeze-dryers used. Experiments confirmed this hypothesis, e.g., the degree of super-cooling was −11.5 ± 0.6°C for freeze-dryer A and −11.9 ± 0.7°C for freeze-dryer B. It must be reminded that tests were carried out with non-GMP batches. Figure 6 shows an example of results, which refers to edge-vials as they are used as reference group in the subsequent analysis. In both freeze-dryers, product temperature overcame its limit value within the first hour of drying, afterwards it was below T_max. Furthermore, in freeze-dryer B, T_B was constantly lower than the value observed in the freeze-dryer A, while the drying time was 0.8 h longer. However, the total cycle time was not modified, because this time is decided by central vials which had almost the same value of K_v in both freeze-dryers.

Fig. 6.

Evolution of (top graph) the product temperature and of (bottom graph) the thickness of the dried layer for vials of group 1, which were processed in freeze-dryer (open circle) A and (open square) B using the processing conditions of Fig. 5

In order to replicate the product dynamics observed for freeze-dryer A in freeze-dryer B, Eq. (3) was used. This algorithm requires the definition of the vial group to be used as reference during cycle scale-up. In this study, the cycle being scaled-up was developed for freeze-dryer A using as design criterion T_B < T_max for all the vials of the batch. In order to obtain the same result in freeze-dryer B, edge-vials have to be used as reference as they had the highest value of K_v and hence the highest product temperature. Therefore, T_fluid was adjusted in order to replicate the temperature profile of vials of group 1 for freeze-dryer A in vials of group 1a for freeze-dryer B. Figure 7 (graph a) compares the original and the scaled-up cycle.

Fig. 7.

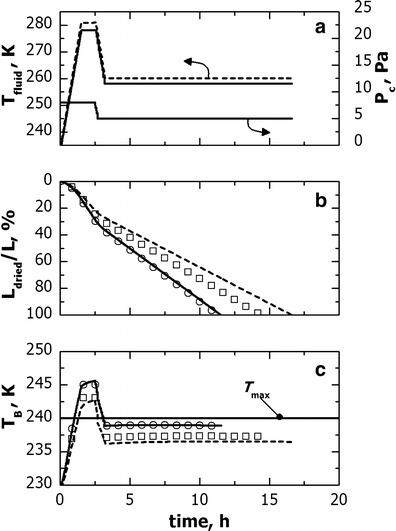
Comparison between the freeze-drying cycles developed with freeze-dryer A (solid line) and scaled-up in a freeze-dryer B (dashed line). In the cycle scale-up, vial of group 1 for freeze-dryer A and group 1a for freeze-dryer B were used as reference vials. The evolution of (graph b) L _dried and (graph c) T _B for vial 1 (solid line, open circle) and 3 (dotted line, open square) is also shown for both (lines) the original cycle and (symbols) the cycle scaled-up in freeze-dryer B

The batch of vials is not uniform; therefore the various vial groups identified in Fig. 1 show different drying behaviors. Consequently, in order to check the suitability of the new cycle for the entire batch of vials, mathematical modeling was used to predict the product dynamics of the various vial groups in freeze-dryer B. An example of results is shown in Fig. 7. Here, the comparison is given for groups 1 (or 1a for freeze-dryer B) and 3, as the same conclusions obtained for group 3 are valid for group 2 (and 1b for freeze-dryer B). As expected, freeze-dryer A and B showed similar product dynamics for edge-vials (i.e., group 1 and 1a), while the product dynamics for group 3 was different. As shown in graph b and c, central vials showed the highest product temperature in freeze-dryer B and as a consequence the drying time was shorter in freeze-dryer B. This result was predictable as the value of K_v was not modified passing from equipment A to B, and the scaled-up cycle involves the highest temperature for the heat transfer fluid. An example of application of the above scaled-up cycle to a manufacturing freeze-dryer is given in Fig. 8.

Fig. 8.

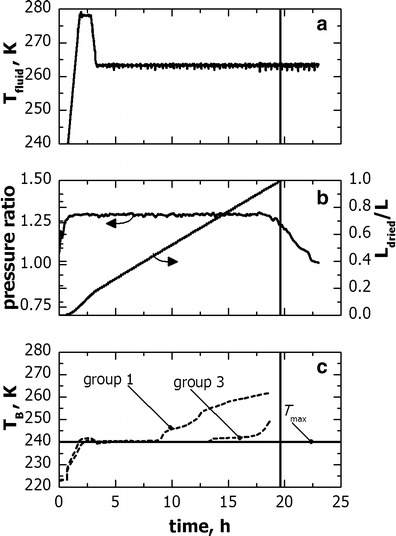
Example of freeze-drying cycle for the proprietary formulation used in freeze-dryer B. Processing conditions were obtained by scale-up in freeze-dryer B of the cycle developed with freeze-dryer A. Evolution of a temperature of the heat transfer fluid, b Pirani–Baratron pressure ratio and model estimations of L _dried/L, and c product temperature as measured through thermocouples. The vertical line indicates the sublimation end-point as predicted by pressure ratio signal

In the following part, the above analysis is carried out for the same case study but also including parameter uncertainty in scale-up calculations. For this purpose, the standard deviation for C₁ was defined for each group of vials on the basis of experimental observations (see Table I), while the standard deviation of parameter P₁ (of Eq. (2)) was set to 10% according to what observed in Fig. 3. As shown by Fissore et al. (14), the values of K_v and R_p for a batch of vials could be described by normal distributions, which were calculated using the mean and the standard deviation above shown. Because of parameter uncertainty, the drying time and the product temperature are distributed around an average value, which is specific of the group of vials used. Fig. 9 compares the cumulative distribution of the drying time for the original cycle in freeze-dryer A and the scaled-up one in freeze-dryer B. As expected, the distribution curves of vials of group 1 are similar in equipment A and B, since their dynamics was used as reference for the cycle scale-up. On the contrary, central vials show significantly different distributions of the drying time. As these vials determine the duration of the drying, the total drying time has to be modified during the cycle scale-up. As shown in Fig. 9, for the case study investigated the cycle was 2 h longer after scale-up.

Fig. 9.

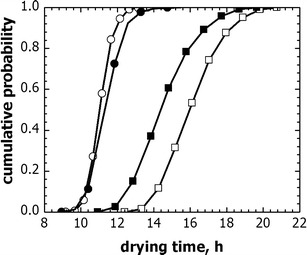
Cumulative distribution of drying time for vial 1 (circle) and 3 (square) when: (void symbols) the original cycle is used in freeze-dryer A, and (filled symbols) the scaled-up cycle is used in freeze-dryer B

A similar comparison can be done when the original cycle is scaled-up from freeze-dryer A to C. However, as the values of K_vvs. P_c and R_pvs. L_dried are similar for freeze-dryer B and C, the scaled-up cycle for freeze-dryer C should be similar to what obtained for freeze-dryer B. This hypothesis was confirmed by Fig. 10 which shows an example of freeze-drying cycle carried out in the industrial unit (freeze-dryer C), where processing conditions were scaled-up (from the cycle developed with the lab unit) using the algorithm proposed in this paper.

Fig. 10.

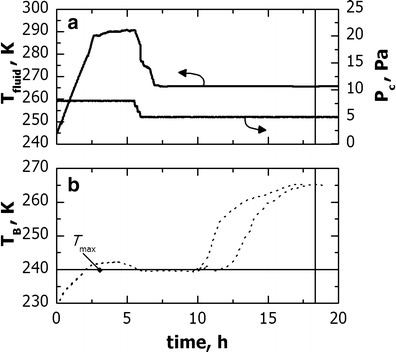
Example of freeze-drying cycle for the proprietary formulation used in freeze-dryer C. Processing conditions were obtained by scale-up in freeze-dryer C of the cycle developed with freeze-dryer A. Evolution of a temperature of the heat transfer fluid and chamber pressure, and c product temperature as measured through thermocouples. The vertical line indicates the sublimation end-point as predicted by the product temperature response

Finally, Fig. 11 shows how the scaled-up cycle is modified when the original cycle is transferred from freeze-dryer A to B using group 1b as reference vials. These vials had a lower value of K_v than vials of group 1a, therefore the scaled-up cycle could involve higher temperature for the heat transfer fluid. The product quality was preserved for all the vials of the batch, apart from vials of group 1a, and the drying time was 5 h shorter.

Fig. 11.

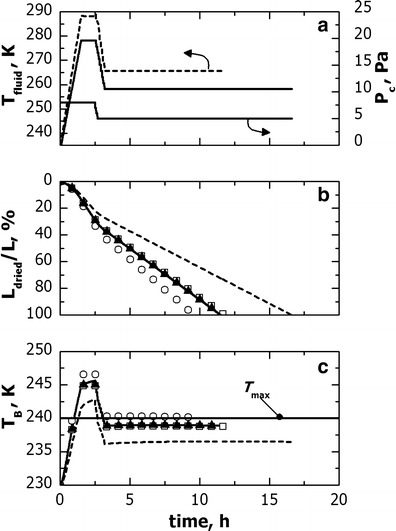
Comparison between the freeze-drying cycles developed in freeze-dryer A (solid line) and scaled-up in freeze-dryer B (dashed line). In the cycle scale-up, vial 1 for freeze-dryer A and 1b for freeze-dryer B were used as reference vials. The evolution of (graph b) L _dried and (graph c) T _B for vial 1 (solid line, 1a: open circle, 1b: filled upright triangle) and 3 (dotted line, open square) is also shown for both (lines) the original cycle and (symbols) the cycle scaled-up in freeze-dryer B

DISCUSSION

Design space was used to optimize the primary drying, for both product quality and drying time, of a parenteral product processed in a small scale freeze-dryer. In this study, the optimal processing conditions were determined looking for the best combination of T_fluid and P_c which maximizes the vapor flow rate and maintains product temperature below its limit value for all the vials of the batch. However, this constraint was not respected at the beginning of the drying, when product temperature was intentionally brought above T_max in order to promote the formation of cracks on the top surface of the product.

Afterward, we coped with the problem of scale-up of the above freeze-drying cycle in a production freeze-dryer. This operation is necessary as the two freeze-dryers showed different product dynamics (see Fig. 6) when the same processing conditions were used. This behavior was due to differences in K_v of edge-vials between the two units. This result was predictable, as the contribution of the radiative heat and conduction through the metal band (if present) can vary with the type of equipment used, because of differences in load configuration, emissivity of radiative surfaces, and dryer geometry. Furthermore, vials loaded on different shelves can be exposed to different processing conditions (19,42) because of a different position of the spool. As this phenomenon is more common in industrial apparatus, the analysis of the heat transfer coefficient in freeze-dryers B and C was extended to various shelves. Unlike what asserted by Rasetto et al. (19), in the production unit here investigated the value of K_v did not change with shelf position or, however, was within the range of variability of each group. Furthermore, variations in R_pvs. L_dried between the freeze-dryers used were within the range of uncertainty observed in the lab-scale unit. As a confirmation of this statement, Fig. 3 shows a fairly good agreement between the values of R_p measured in freeze-dryer A (by the pressure rise test technique) and estimated in freeze-dryer C (by best fitting of the experimental data). A similar good agreement was also observed (data not shown) between the value of R_pvs. L_dried estimated in freeze-dryer A and B, although the clean room classification was different for the various freeze-dryers used. Therefore, despite in a production freeze-dryer, parenteral solutions can undergo different freezing conditions from those observed for a lab-scale freeze-dryer; these differences did not significantly modify the resistance to vapor flow. In addition, if the value of R_p is different for the various freeze-dryer investigated (e.g., because of different degrees of super-cooling), the algorithm proposed by Fissore and Barresi (28) for cycle scale-up can still be used provided that the above modification is taken into account during calculations. If this is the case, the target of the scale-up is still to replicate in the large scale unit the temperature profile observed in the small scale one although this operation can produce a variation in drying time.

Figure 7 (graph a) shows how processing conditions have to be modified when the cycle developed in freeze-dryer A is scaled-up in freeze-dryer B. As edge-vials had the highest K_v in freeze-dryer A, the scaled-up cycle can be carried out at higher temperature for the heat transfer fluid although vials 1a were used as reference for freeze-dryer B. The new cycle permits the replication in freeze-dryer B of the temperature profile of edge-vials in freeze-dryer A, while the drying time was shorter. This last result was predictable as drying time is decided by central vials which showed similar values of K_v in the two freeze-dryers, see Fig. 9. Experimental runs of Figs. 5 and 8 confirmed the above results. A similar behavior was also observed when the cycle was scaled-up in the largest unit (i.e., freeze-dryer C), see the experimental cycle shown in Fig. 10.

Vials of group 1 were divided into two subsets (see Fig. 1) which had different values of K_v. Consequently, the scaled-up cycle varied significantly with the group of edge-vials used as reference. Figure 11 shows the freeze-drying cycle obtained using group 1b as reference for scale-up. As expected, when group 1b is used as reference, the temperature of the heat transfer fluid was higher than that obtained when group 1a is used as reference (see Fig. 7) and, hence, the drying time was shorter. However, product quality was not guaranteed for the entire batch of vials, as group 1a overcame its limit temperature. It follows that if the final goal is to preserve the product quality for the entire batch of vials, scale-up should be performed using as reference those vials that might more easily be damaged by product overheating and, thus, group 1a.

For cycle scale-up, it is not necessary to classify edge-vials into two groups, but they can be collected in only one group, which is characterized by an average K_v and an appropriate variance. Then, in order to guarantee product quality for the entire batch, the original cycle has to be scaled-up using edge-vials as reference.

As an alternative, we can scale-up the cycle using central vials as reference. In this manner, the drying time is unchanged between the two freeze-dryers; obviously, this result can be obtained only if the resistance to vapor flow is not modified passing from one unit to another. This approach guarantees product quality only for central vials. Nevertheless, the fraction of edge-vials decreases with the dryer size and increases with the vial diameter. For the vials used in this study, edge-vials constitute about 30% of the entire batch for dryer A and less than 10% for dryer C. In order to profit from the reduction in drying time, edge-vials can be substituted with empty vials.

CONCLUSION

This study shows how an effective procedure can be used for scaling up a freeze-drying cycle developed for a lab-scale freeze-dryer in a production unit. The sensors used to estimate model parameters are now available for both lab-scale and manufacturing apparatus.

A freeze-drying cycle can be scaled-up in different ways depending on the final purpose. For example, a cycle can be scaled-up for both product quality and drying time, or only for product quality. The latter approach leads to a new cycle which guarantees the product quality for all the vials of the batch, but can require a different time to complete ice sublimation with respect to what observed for the original cycle. Fundamentally, the same approach can be used for both scaling up and transferring a cycle from a freeze-dryer to another. However, it must be noted that the scale-up procedure can be avoided if the design space approach is used to develop the cycle directly in the production unit (43). This approach makes it possible to transfer not only a specific cycle, but the entire design space which gives a full view of the set of processing conditions compatible with the constraint on product temperature. In addition, this approach can account for the specific inter-vial variability of the second freeze-dryer.

In theory, the scale-up algorithm presented in this paper can also be used to calculate the new cycle when the fill volume is modified, or a different type of container is used (e.g., tubing vs. molded vials). Of course, in order to carry out the calculations, the new system has to be characterized in terms of mass and heat transfer coefficients.

List of symbols

C₁

Parameter used in Eq. (1), in joule per square meter per second per kelvin

C₂

Parameter used in Eq. (1), in joule per square meter per second per kelvin per pascal

C₃

Parameter used in Eq. (1), in per pascal

K_v

Overall heat transfer coefficient between the heating fluid and the product, in joule per square meter per second per kelvin

k_frozen

Thermal conductivity of the frozen layer, in joule per kelvin per second per meter

k_s

Heat transfer coefficient between the technical fluid and the shelf, in joule per second per kelvin per square meter

L

Total product thickness, in meter

L_dried

Dried layer thickness, in meter

L_frozen

Thickness of the frozen layer, in meter

P₁

Parameter used in Eq. (2), in per second

P₂

Parameter used in Eq. (2), in per meter

P_c

Chamber pressure, in pascal

R_p

Resistance to vapor flow, in meter per second

R_p,0

Parameter used in Eq. (2), in meter per second

s_glass

Thickness of the wall at the bottom of the glass vial, in meter

T_i

Temperature of the product at the interface of sublimation, in kelvin

T_B

Temperature of the product at the bottom of the vial, in kelvin

T_max

Maximum allowable product temperature, in kelvin

ΔT_fluid

Variation in the maximum value for the temperature of the heating fluid, in kelvin

T_fluid

Temperature of the heating fluid, in kelvin

Δt_d

Variation in the drying time, in kelvin

t

Time, in second

Greeks

λ_glass

thermal conductivity of the glass, in joule per second per meter per kelvin

Abbreviations

API

Active pharmaceutical ingredient

GMP

Good manufacturing practice