Abstract
Background
It is thought that genes with similar patterns of mRNA expression and genes with similar functions are likely to be regulated via the same mechanisms. It has been difficult to quantitatively test these hypotheses on a large scale because there has been no general way of determining whether genes share a common regulatory mechanism. Here we use data from a recent genome wide binding analysis in combination with mRNA expression data and existing functional annotations to quantify the likelihood that genes with varying degrees of similarity in mRNA expression profile or function will be bound by a common transcription factor.
Results
Genes with strongly correlated mRNA expression profiles are more likely to have their promoter regions bound by a common transcription factor. This effect is present only at relatively high levels of expression similarity. In order for two genes to have a greater than 50% chance of sharing a common transcription factor binder, the correlation between their expression profiles (across the 611 microarrays used in our study) must be greater than 0.84. Genes with similar functional annotations are also more likely to be bound by a common transcription factor. Combining mRNA expression data with functional annotation results in a better predictive model than using either data source alone.
Conclusions
We demonstrate how mRNA expression data and functional annotations can be used together to estimate the probability that genes share a common regulatory mechanism. Existing microarray data and known functional annotations are sufficient to identify only a relatively small percentage of co-regulated genes.
Background
It is axiomatic in functional genomics that genes with similar mRNA expression profiles are likely to be regulated via the same mechanisms [1,2]. This hypothesis is the basis for almost all attempts to use mRNA expression data from microarray experiments to discover regulatory networks. Several investigators have provided indirect evidence for this hypothesis by clustering genes according to their mRNA expression profiles and then showing that genes in a cluster often share common upstream sequence motifs [3-5]. Ideker et al detailed examples of genes known to be regulated by a common transcription factor where the expression profiles of the co-regulated genes were highly correlated [6]. Despite supporting evidence and some known examples, the link between co-expression and co-regulation has not been directly tested or quantified on a large scale. Doing so would solidify the theoretical basis for using mRNA expression data to identify regulatory networks. It would also be useful, in a practical sense, for investigators to know what level of expression similarity was required for genes to have a certain probability of having a common regulatory mechanism.
It has been difficult to measure or analyze the relationship between co-expression and co-regulation previously because there has been no "gold standard" for determining whether or not two genes are regulated by a shared transcription factor. Recently however, Lee et al described a genome wide binding analysis in which they quantified the in vivo binding of known S. cerevisiae transcription factors to the promoter sequence of almost all known yeast open reading frames (ORFs) [7]. Though by no means fully complete or accurate, their data greatly increase our knowledge of transcriptional regulation in yeast and provide the needed quantitative measure of the likelihood that two given yeast ORFs are bound by the same transcription factor. In vivo transcription factor binding is not precisely equivalent to being regulated by the same transcription factor. The overlap is considerable, however, and shared transcription factor binding is likely to be a good proxy for co-regulation.
In this paper, we use publicly available microarray data in combination with the transcription factor binding data from Lee et al to investigate and quantify the link between co-expression and co-regulation. In particular, we combine this data to estimate the probability that two genes are bound by a common transcription factor as a function of the correlation between the expression profiles of the two genes. We also develop a more general measure of similarity in regulatory mechanism and relate this to similarity in mRNA expression.
Other investigators have shown that genes with similar functions frequently have similar patterns of mRNA expression [8-10]. Here, we also investigate the link between functional similarity and likelihood of being bound by the same transcription factor. Finally, we combine expression data with functional annotation in an attempt to develop a better predictive model of co-regulation.
Results and discussion
Co-expression and co-regulation
We downloaded all publicly available micorarray data for S. cerevisiae from the Stanford Microarray Database [11,12]. We then downloaded Lee et al's transcription factor binding data from their website [13]. We restricted our analysis to those genes in the microarray data set which had at least one transcription factor which bound upstream of the gene according to the binding data. This left us with data on 2284 genes across 611 arrays.
To measure similarity in expression we calculated the pairwise correlation coefficient between the mRNA expression profiles of all genes in our data set. Initially, there were 2,607,186 gene pairs in our analysis. If both genes in the pair shared the same promoter region, we excluded the pair from the analysis. After excluding these gene pairs, there were 2,606,473 gene pairs. For each pair of genes we also determined if there was a common transcription factor which bound to the promoter region of both genes. Figure 1 shows the observed fraction of gene pairs which share a common transcription factor binder as a function of the correlation between the expression profiles of the two genes. The figure demonstrates that genes with strong, positively correlated expression profiles are much more likely to be bound by a common transcription factor than genes with less strongly correlated expression profiles. This effect is present, however, only at relatively high correlation coefficients. In order for two genes to have a 50% chance of sharing a common regulator, the correlation between their expression profiles must be 0.84. There were 168,994 pairs of genes which had a common transcription factor binder, but only 5,419 (3.2%) of these pairs had a correlation greater than 0.84.
Figure 1.
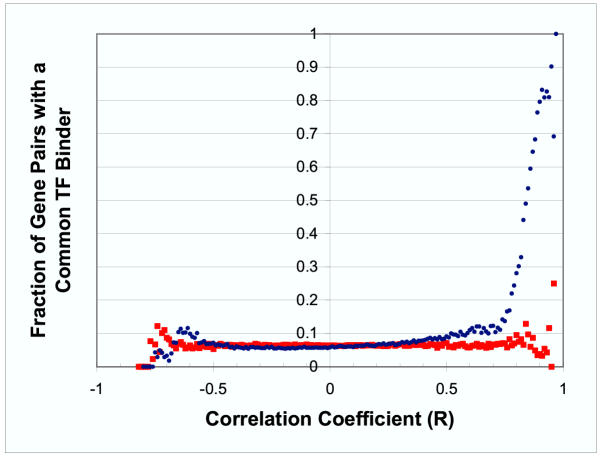
Fraction of Gene Pairs Sharing a Common Transcription Factor Binder vs. Correlation Coefficient In this figure each point represents a ratio – the denominator is the number of gene pairs where correlation in expression profile is between x and x+.01 and the numerator is the number of those gene pairs that share a common transcription factor. The actual yeast data is represented by blue ● and the control data (where the mapping between genes and promoters is permuted) by red ■. The observed fraction of gene pairs sharing a common transcription factor increases when the correlation between the expression profiles of the two genes is high.
As a control, we randomly permuted the mapping between genes and their promoter regions. As Figure 1 shows, when the analysis described above was repeated using this permuted data, there was no relationship between correlation in expression profile and shared transcription factor binding. We also performed two additional permutation tests. For the first of these, we permuted the relationship between transcription factors and their target genes. For the second additional permutation test, we randomly permuted the expression profiles for each gene. No relationship between correlation in expression profile and shared transcription factor binding was seen when either of these additional permutations of the data was used in the analysis (data not shown). These controls provide evidence that the relationship between correlation and shared transcription factor binding observed in actual yeast data is extremely unlikely to be due to chance alone. Instead, it is a result of the co-regulatory mechanisms that do exist in yeast.
We also defined a measure of regulatory closeness, c(X,Y), which was designed to capture more distant regulatory relationships between genes. c(X,Y) is inversely proportional to the path length between genes X and Y in a graph where nodes represent genes and edges are drawn between each transcription factor and the genes to which it binds (see Methods). If two genes (X and Y) are regulated by two different transcription factors, but both of those transcription factors are regulated by the same transcription factor, then c(X,Y) will be high. Figure 2 shows a plot of c(X,Y) versus correlation coefficient. Like Figure 1, this graph also suggests that co-expressed genes are likely to share common regulatory mechanisms. When this broader measure of co-regulation is used, the effect is apparent at less extreme correlation coefficients and also appears to be present for strong, negative correlations. A similar relationship is not seen when permuted data is used in the analysis. Note that when the mapping between genes and their promoter regions is permuted, the natural regulatory network of transcription factors is perturbed and c(X,Y) tends to be smaller for any given correlation in expression profiles. This same effect is also seen when the relationship between transcription factors and their target genes is permuted.
Figure 2.
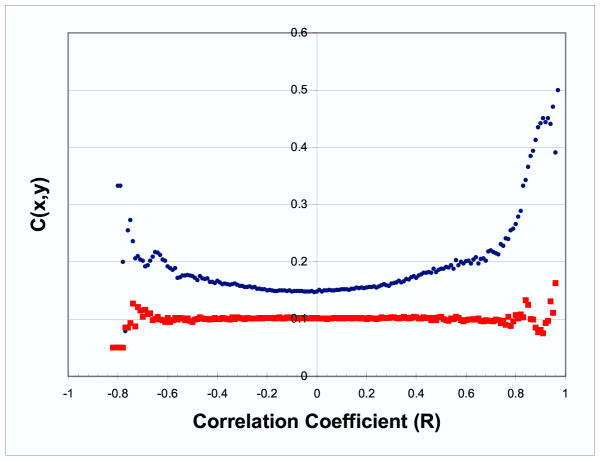
Regulatory Closeness vs. Correlation Coefficient Each point shows the mean regulatory closeness for gene pairs whose correlation in expression profile is between x and x+.01. The actual yeast data is represented by blue ● and the control data (where the mapping between genes and promoters is permuted) by red ■. The mean regulatory closeness c(X,Y) increases with the absolute value of the correlation between the expression profiles of genes X and Y.
The above analysis included all genes in the data set, regardless of whether or not the genes themselves were transcription factors. We also looked specifically at the situation where one gene in the pair was a transcription factor. Ideker et al published examples of cases where the mRNA expression profiles of a transcription factor and the genes it regulated were strongly correlated [6]. In our analysis, we did not observe that the correlation between two genes tended to be higher than average if one of the genes was a transcription factor which regulated the other gene. In fact, a strong correlation between a gene X and transcription factor A was more likely to be explained by the presence of transcription factor B which bound both A and X (data not shown).
Our analysis used data from 611 microarrays covering a wide variety of experimental conditions. In many cases, however, researchers have much smaller and more limited data sets. To investigate how the link between co-expression and co-regulation depended on the number and type of experiments in the data set we repeated the above analyses using only selected subsets of the microarray data. We created subsets by randomly selecting experiments and also by choosing experiments related to either cell-cycle, starvation or the stress response. We chose to examine cell-cycle, starvation and stress related experiments because they provided relatively large data sets and because they have been well studied in the past [14-16]. By choosing different threshold correlation coefficient levels above which gene pairs are predicted to have a shared transcription factor binder, different levels of sensitivity and specificity can be obtained. For each data subset, we chose a threshold correlation coefficient r such that 75% of all gene pairs whose correlation in expression profile was greater than r had a shared transcription factor binder. We then determined what percentage of the total number of gene pairs sharing a common transcription factor had a correlation in expression profile greater than r. To state this in a different way, we evaluated the sensitivity of expression data for detecting shared transcription factor binding when positive predictive value was held constant at 75%.
Figure 3 shows how r and sensitivity vary as a function of the number of microarray experiments in the mRNA expression data. The analysis illustrates several important points. First, as the number of microarrays in a data set decreases, a higher threshold correlation coefficient is required to achieve a given positive predictive value. Second, performance in finding pairs of genes with shared transcription factors initially improves as the number of microarray experiments increases, but this effect levels off after approximately 100 microarrays are used. Third, randomly selected data sets composed of arrays spanning a diversity of experimental conditions are more informative overall than similarly sized data sets relating to a single experimental condition.
Figure 3.
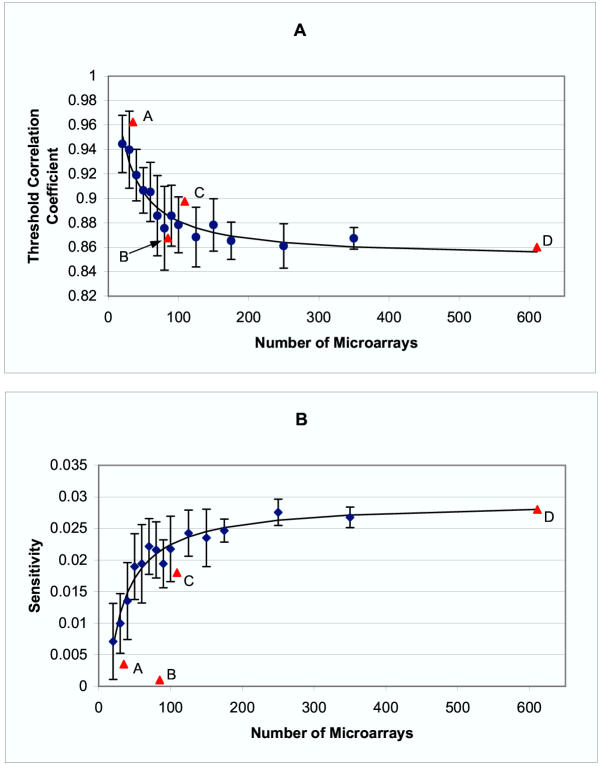
Threshold Correlation Coefficient and Sensitivity vs. Number of Microarrays Labeled data points represent selected subsets as follows: A – starvation, B – cell cycle, C – stress response, D – all data. All other data points, marked by blue ●, indicate the mean value for 10 randomly selected data sets of the given size. The bars show one standard deviation. The curves shown are fit using only the randomly chosen subsets. A) The threshold correlation coefficient r, chosen such that 75% of all gene pairs with correlation greater than r share a common transcription factor, decreases as the number of microarrays increases. B) Sensitivity (the ratio of the number of gene pairs which both share a common transcription factor and have an expression correlation greater than r to the total number of gene pairs which share a common transcription factor) when threshold correlation is chosen such that positive predictive value is 75%, increases with the number of microarrays used up to a limit of 2.8%. Random sets of microarrays showed greater sensitivity for finding gene pairs bound by a common transcription factor than predetermined sets of microarrays.
Functional similarity vs. co-regulation
One major difficulty in testing the hypothesis that functionally similar genes are likely to be co-regulated is the problem of defining functional similarity. There is no commonly accepted methodology for doing this. Here we used the Gene Ontology (GO) classification system [17] to define two measures of functional similarity. For our first measure of functional similarity, which we termed the minimum node count method, we determined for each GO term how many genes in our data set were annotated with that GO term. We termed this the node count for a GO term. For our purposes, a gene was considered to be annotated with a given GO term if it was directly annotated with the term or if it was annotated with a descendent of that term. Then for each pair of genes we found all GO terms that were annotated to both genes in the pair and determined the node count for each GO term. We took the smallest node count as our measure of functional similarity. Small minimum node counts thus represented significant functional similarity while gene pairs with larger minimum node counts were less similar functionally. As examples, the GO term "microtubule binding" had a node count of 5, while the GO term "binding" had a node count of 443.
For our second measure of functional similarity, we defined GO term levels. Level 1 GO terms were defined as terms whose distance from the root of the ontology was 1 (for example, direct child terms of "molecular function"). Using this method, "microtubule binding" is a level 5 GO term, while "binding" is a level 1 GO term. Two genes were considered to have matching level 1 GO terms if they each were annotated with a GO term that was a descendent of the same level 1 term. Levels 2 through 8 were similarly defined to represent increasingly similar levels of function.
Figure 4 shows the fraction of gene pairs that share a common transcription factor binder as a function of minimum node count. Figure 5 is similar, but uses GO term levels instead of minimum node count as the measure of functional similarity. Both of these measures are only proxies for true functional similarity. Although small node counts generally reflect significant functional similarity, the minimum node count method is misleading when large numbers of functionally similar genes are annotated with the same GO term. The ribosomal genes are an example of this, and these genes account for many of the outliers in Figure 4. Functional similarity as defined by GO term level is also problematic in that it is highly dependent on the complexity and depth of annotation in each ontology. Figure 5b appears to suggest that the molecular function ontology is more useful for identifying co-regulated genes than the biological process ontology. However, this is likely due to the fact that higher level GO terms in the biological process ontology are generally broader and more inclusive than terms at the corresponding level of the molecular function ontology (as is suggested by the number of gene pairs which match at each level in the two ontologies). As an example, consider the level 1 GO term "cellular process" from the biological process ontology. Knowing that two genes are both involved in a "cellular process" is unlikely to provide much information about the regulation of the two genes. Nevertheless, despite the inherent flaws in each of these measures of functional similarity, use of either measure shows that genes with similar functional annotations tend to share common regulatory mechanisms.
Figure 4.
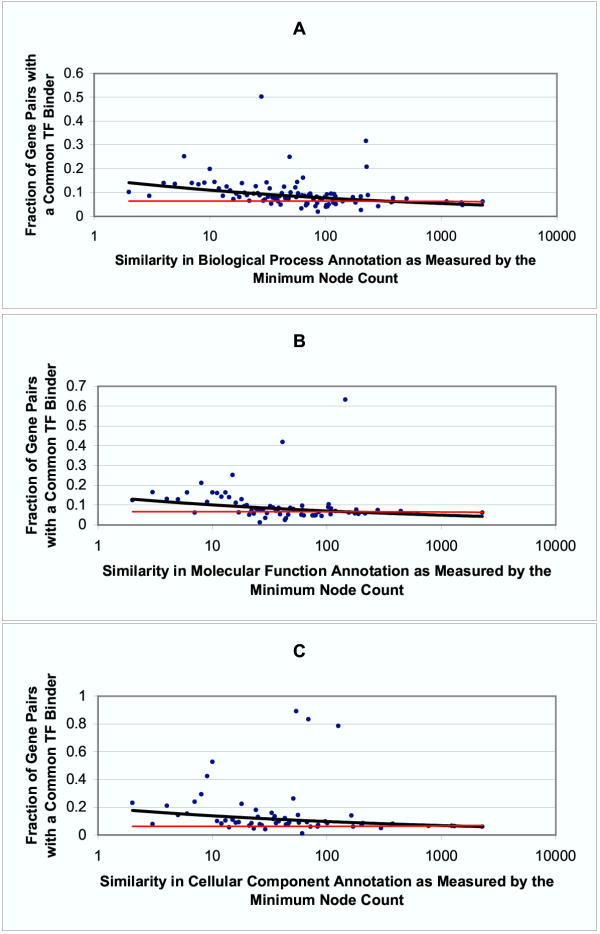
Co-regulation vs. Functional Similarity as Defined by Minimum Node Count A, B and C were created using the biological process, molecular function and cellular component ontologies, respectively. The dark black lines are fit using the actual yeast data (individual data points represented as blue ●). The thin red lines are fit using data where the mapping between genes and their promoters is permuted. For clarity, the individual data points representing permuted data are not shown. For each of the three ontologies, the fraction of gene pairs sharing a common transcription factor binder increases as functional similarity increases (i.e. as the minimum node count decreases).
Figure 5.
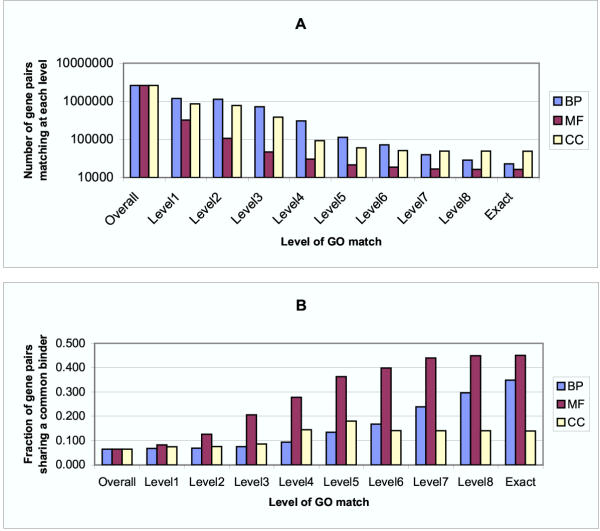
Co-regulation vs. Functional Similarity as Defined by Level of GO Term Match BP, MF and CC refer to the biological process, molecular function and cellular component ontologies, respectively. A) The number of gene pairs which have matching GO terms decreases as the strictness of the required match increases. B) The fraction of gene pairs sharing a common transcription factor binder increases as the level of functional similarity increases, particularly for the BP and MF ontologies.
The above analysis, which shows an association between functional annotation and regulatory mechanism, suggests that functional annotations can be useful in identifying co-regulated genes. This conclusion is confounded by the fact that knowledge of regulatory mechanisms may (and almost certainly does to at least some extent) influence functional annotation. If functional annotation was solely a reflection of existing knowledge about regulatory mechanisms, we would still observe an association between functional annotation and regulatory mechanism even though functional annotation would not be useful for identifying novel co-regulated genes. One of the limitations of our study is that we are not able to exclude this effect. Doing so would require an assessment of gene function which was unbiased by existing knowledge of regulatory mechanisms. As far as we know, such an assessment of gene function does not exist. We suspect, however, that the functional annotations from Gene Ontology do contain a significant amount of other information not based on prior knowledge of regulatory mechanisms. To the extent that this is true, the observed association between functional annotation and regulatory mechanism is indicative of the utility of functional annotations in identifying co-regulated genes.
Using co-expression and functional similarity to predict co-regulation
Figures 6 and 7 show how likely two genes are to be co-regulated, as estimated by the fraction of gene pairs sharing a common transcription factor binder, when correlation in expression profile and functional similarity are both taken into account. Both figures suggest measures of similarity in expression and function provide independent information about similarity in regulatory mechanism. Functional annotations are particularly helpful in identifying co-regulated gene pairs when there is an intermediate level of correlation (i.e. 0.5 < r < 0.8) between expression profiles. Genes with this level of pairwise correlation in expression are likely to share a common transcription factor binder only if they have similar functional annotations. As discussed in the previous section, our study may overestimate the utility of functional annotation to the extent that functional annotations merely reflect existing knowledge of regulatory mechanisms.
Figure 6.
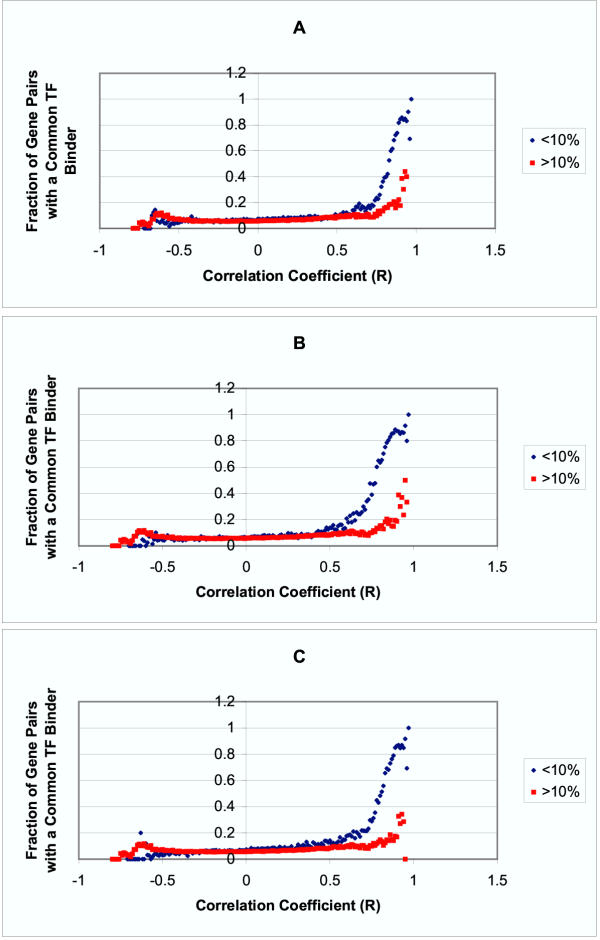
Co-regulation vs. Co-expression and Functional Similarity as Defined by Minimum Node Count A, B and C were created using the biological process, molecular function and cellular component ontologies, respectively. For each of the three ontologies, the gene pairs are divided into two groups – those with minimum node counts less than the 10th percentile and greater than the 10th percentile. At higher levels of correlation in expression profile, gene pairs with greater functional similarity are more likely to share a common transcription factor binder.
Figure 7.
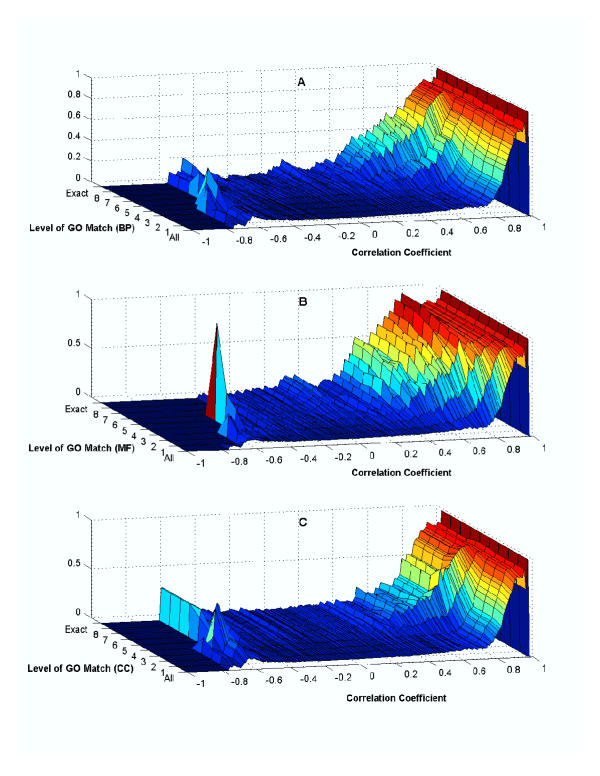
Co-regulation vs. Co-expression and Functional Similarity as Defined by Level of GO Term Match A, B and C were created using the biological process, molecular function and cellular component ontologies, respectively. For each of the three ontologies, the fraction of gene pairs sharing a common transcription factor binder is shown as a function of both correlation in expression profile and the level of GO term match.
Conclusions
Our study demonstrates that if two genes have highly correlated expression profiles, there is likely to be a common transcription factor which binds to the promoter regions of both genes. Given that common transcription factor binding is expected to be a good proxy for co-regulation, our study provides strong support for the widely held supposition that co-expressed genes are likely to be co-regulated. In S. cerevisiae, two genes have a 50% chance of having a common transcription factor binder if the correlation between their expression profiles is equal to 0.84. This threshold allows the identification of approximately 3.2% of all gene pairs which share a common binder. It remains to be seen how these numbers change in other species, but they should sound a cautionary note to those using less similar expression profiles in an attempt to identify co-regulated genes. Many commonly used clustering methodologies will link genes on the basis of relatively weak similarities in expression which, based on the results of our study, are unlikely to correlate with direct co-regulation. This may be one explanation for the limited success of many attempts using clustering techniques to identify co-regulated genes.
Success in using expression data to identify genes with shared transcription factor binders is also crucially dependent on the number and type of experiments in the expression data. While more data is better, our study suggests that the marginal benefit to additional microarrays is small after approximately 100 microarrays are used. Diversity in the type of experiment is particularly important and increasing the breadth of experimental conditions covered is likely to significantly increase the power of mRNA expression data to predict patterns of co-regulation.
Using mRNA expression data to identify co-regulated genes is currently the focus of many research groups. Most of the methodologies for identifying co-regulated genes using microarray data are fundamentally based on pairwise measures of expression similarity. Our study provides an estimate of the performance in finding genes with shared transcription factor binders of one very commonly used pairwise measure of expression similarity, the Pearson correlation coefficient. We also show how known functional annotations can potentially be used to create a better predictive model of co-regulation. This study will hopefully give investigators using related methodologies better insight into which computationally predicted interactions are likely to be real and make it easier to decide which results are worthy of further biological investigation.
The use of genome wide binding data and the technique we describe for quantititatively evaluating the success of a method for identifying co-regulated genes are broadly applicable. We encourage other investigators to similarly evaluate the performance of any proposed methodologies. This will greatly facilitate evaluation and comparison of these methodologies.
Methods
Microarray data
As of mid April 2003, the Stanford Microarray Database contained the results of more than 600 microarray experiments on S. cerevisiae conducted by multiple different investigators under a wide variety of experimental conditions. If the same ORF appeared more than once on a given array, the mean value was used. Spots flagged as unreliable in the database were excluded from the analysis. If a gene or array had more than 20% of its values missing or flagged as unreliable, that gene or array was also excluded from the analysis. The log (base 2) R/G normalized ratio of sample to control was used as the measure of mRNA expression. Median centering was performed over the arrays. All of the above are default or commonly used options implemented directly through the Stanford Microarray Database interface. After applying these filters, we had data for 6156 ORFs across 611 arrays. We further restricted our analysis to ORFs which had at least one transcription factor which bound upstream according to Lee et al's binding data. This left us with data on 2284 ORFs.
Binding data
The binding data from Lee et al contained information on 6270 yeast genes. Each yeast gene was mapped to one of 4532 distinct promoter regions. The binding data consisted of a binding score for each combination of the 4532 promoter regions with the 106 transcription factors whose binding they were able to characterize. Following Lee et al, we considered that a transcription factor bound to a promoter region if its binding score was less than 0.001. Lee et al estimated that this cutoff would identify about two thirds of all transcription factor-promoter interactions and would have a false positive rate of 6–10% [7].
Permuted data and controls
As a control, we permuted the mapping between genes and their promoter regions. The analysis was redone using this permutation of the binding data and the results are displayed as a control in our figures. We also repeated our analysis using two other permuted data sets. For each gene X, the 106 transcription factors bound to the promoter region of X with binding score Bi (with i ranging from 1 to 106). We randomly permuted the Bi for each gene X. For the second additional control, we permuted the expression values Xk (with k ranging from 1 to 611) for each gene X.
Calculating positive predictive value and sensitivity
It is necessary to choose a threshold correlation coefficient r in order to define positive predictive value and sensitivity. Let A be the number of gene pairs where correlation in expression profile is greater than r, B be the number of gene pairs that share a common transcription factor binder and C be the number of gene pairs that both share a common transcription factor binder and have a correlation in expression profile greater than r. Then positive predictive value is C/A and sensitivity is C/B. Note that Figure 1 is not a graph of positive predictive value because each point (x,y) represents only those gene pairs where r = x, as opposed to r > x.
Measuring similarity in expression profile
For each pair of genes, we calculated the Pearson correlation coefficient between the genes' mRNA expression profiles as follows:
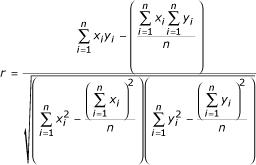
Individual arrays were only used in the calculation if the expression values for both genes were non-missing. We chose to use the Pearson correlation coefficient because it is one reasonable and widely used similarity metric, though other choices were possible.
Functional annotation
We obtained Gene Ontology (GO) annotations for each yeast ORF from the Saccharomyces Genome Database [18]. Each ORF was assigned one or more GO terms from each of the biological process, molecular function and cellular component ontologies.
Defining regulatory closeness
Our measure of regulatory closeness was motivated by a desire to capture the relationship between genes that, while not directly regulated by the same transcription factor, still shared a common regulatory mechanism. In order to do this, we constructed a graph where each gene (including transcription factors) was a node. Edges were drawn between a transcription factor and a gene if the transcription factor bound to the gene. The regulatory closeness of genes X and Y was defined to be c(X,Y) = 1/d where d was the length of the shortest path between two genes. Each edge was counted as having a length of one. As an example, consider the situation where transcription factor A bound to gene X and transcription factor B bound to both gene Y and to transcription factor A. In this example, c(X,Y) = 1/3. If there was no path between genes X and Y, c(X,Y) was defined to be zero. For computational reasons, we also defined c(X,Y) to be zero if d was greater than 20.
Defining similarity in function
For each GO term A we defined a node count N(A) and a level L(A). The node count N(A) was set equal to the number of genes in our data set that were annotated with GO term A or one of its descendents. L(A) was defined as the shortest distance from A to the root of the ontology (where the distance between a parent and a child GO term was defined to be 1). For each gene X we found the set A(X) such that A(X) contained all GO terms that X was annotated with directly and their ancestors. Then for each gene pair (X,Y) we found the intersection of A(X) and A(Y). Our first measure of functional similarity, the minimum node count, was defined as the smallest node count of the GO terms in the intersection of A(X) and A(Y). For our second measure of similarity, based on GO term levels, we defined X and Y as having a level Q match if one of the GO terms in the intersection of A(X) and A(Y) had level Q.
As an example of the minimum node count method suppose gene X is annotated with the following GO terms (where each term is a descendent of the previous term): molecular function->binding->amino acid binding->glutamate binding, and gene Y is annotated with: molecular function->binding->amino acid binding->glycine binding. Suppose further that there are 2283, 504 and 121 genes annotated with molecular function, binding and amino acid binding, respectively. Then the minimum node count for X and Y would be 121.
As an example of GO term levels suppose that gene X is annotated with: biological process->physiological processes->metabolism->carbohydrate metabolism->carbohydrate catabolism, and gene Y is annotated with biological process->physiological processes->metabolism->carbohydrate metabolism->carbohydrate biosynthesis. X and Y have matching level 1, 2 and 3 GO terms – but do not have a matching level 4 GO term.
Authors' contributions
DJA conceived the study, performed the bioinformatical analysis and drafted the manuscript. ISK guided the study and coordinated the project. AJB guided the study and helped with the analyses. All authors read and approved the final manuscript.
Acknowledgments
Acknowledgements
The authors would like to thank all of the researchers who made publicly available the data used in this study. This work was made possible in part by funding from NIH grants R01 DK060837, K12 DK063696-01, U01HL066582 and 5TI5 LM07092.
Contributor Information
Dominic J Allocco, Email: allocco@chip.org.
Isaac S Kohane, Email: isaac_kohane@harvard.edu.
Atul J Butte, Email: atul_butte@harvard.edu.
References
- Schulze A, Downward J. Navigating gene expression using microarrays–a technology review. Nat Cell Biol. 2001;3:E190–5. doi: 10.1038/35087138. [DOI] [PubMed] [Google Scholar]
- Altman RB, Raychaudhuri S. Whole-genome expression analysis: challenges beyond clustering. Curr Opin Struct Biol. 2001;11:340–7. doi: 10.1016/S0959-440X(00)00212-8. [DOI] [PubMed] [Google Scholar]
- Brazma A, Jonassen I, Vilo J, Ukkonen E. Predicting gene regulatory elements in silico on a genomic scale. Genome Res. 1998;8:1202–15. doi: 10.1101/gr.8.11.1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tavazoie S, Hughes JD, Campbell MJ, Cho RJ, Church GM. Systematic determination of genetic network architecture. Nat Genet. 1999;22:281–5. doi: 10.1038/10343. [DOI] [PubMed] [Google Scholar]
- Wolfsberg TG, Gabrielian AE, Campbell MJ, Cho RJ, Spouge JL, Landsman D. Candidate regulatory sequence elements for cell cycle-dependent transcription in Saccharomyces cerevisiae. Genome Res. 1999;9:775–92. [PMC free article] [PubMed] [Google Scholar]
- Ideker T, Thorsson V, Ranish JA, Christmas R, Buhler J, Eng JK, Bumgarner R, Goodlett DR, Aebersold R, Hood L. Integrated genomic and proteomic analyses of a systematically perturbed metabolic network. Science. 2001;292:929–34. doi: 10.1126/science.292.5518.929. [DOI] [PubMed] [Google Scholar]
- Lee TI, Rinaldi NJ, Robert F, Odom DT, Bar-Joseph Z, Gerber GK, Hannett NM, Harbison CT, Thompson CM, Simon I, Zeitlinger J, Jennings EG, Murray HL, Gordon DB, Ren B, Wyrick JJ, Tagne JB, Volkert TL, Fraenkel E, Gifford DK, Young RA. Transcriptional regulatory networks in Saccharomyces cerevisiae. Science. 2002;298:799–804. doi: 10.1126/science.1075090. [DOI] [PubMed] [Google Scholar]
- Wu LF, Hughes TR, Davierwala AP, Robinson MD, Stoughton R, Altschuler SJ. Large-scale prediction of Saccharomyces cerevisiae gene function using overlapping transcriptional clusters. Nat Genet. 2002;31:255–65. doi: 10.1038/ng906. [DOI] [PubMed] [Google Scholar]
- Brown MP, Grundy WN, Lin D, Cristianini N, Sugnet CW, Furey TS, Ares M, Jr, Haussler D. Knowledge-based analysis of microarray gene expression data by using support vector machines. Proc Natl Acad Sci U S A. 2000;97:262–7. doi: 10.1073/pnas.97.1.262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisen MB, Spellman PT, Brown PO, Botstein D. Cluster analysis and display of genome-wide expression patterns. Proc Natl Acad Sci U S A. 1998;95:14863–8. doi: 10.1073/pnas.95.25.14863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gollub J, Ball CA, Binkley G, Demeter J, Finkelstein DB, Hebert JM, Hernandez-Boussard T, Jin H, Kaloper M, Matese JC, Schroeder M, Brown PO, Botstein D, Sherlock G. The Stanford Microarray Database: data access and quality assessment tools. Nucleic Acids Res. 2003;31:94–6. doi: 10.1093/nar/gkg078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanford Microarray Database http://genome-www5.stanford.edu/MicroArray/SMD
- Transcriptional Regulatory Networks in Saccharomyces cerevisiae http://web.wi.mit.edu/young/regulator_network/ [DOI] [PubMed]
- Spellman PT, Sherlock G, Zhang MQ, Iyer VR, Anders K, Eisen MB, Brown PO, Botstein D, Futcher B. Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol Biol Cell. 1998;9:3273–97. doi: 10.1091/mbc.9.12.3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gasch AP, Spellman PT, Kao CM, Carmel-Harel O, Eisen MB, Storz G, Botstein D, Brown PO. Genomic expression programs in the response of yeast cells to environmental changes. Mol Biol Cell. 2000;11:4241–57. doi: 10.1091/mbc.11.12.4241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gasch AP, Werner-Washburne M. The genomics of yeast responses to environmental stress and starvation. Funct Integr Genomics. 2002;2:181–92. doi: 10.1007/s10142-002-0058-2. [DOI] [PubMed] [Google Scholar]
- Ashburner M, Ball CA, Blake JA, Botstein D, Butler H, Cherry JM, Davis AP, Dolinski K, Dwight SS, Eppig JT, Harris MA, Hill DP, Issel-Tarver L, Kasarskis A, Lewis S, Matese JC, Richardson JE, Ringwald M, Rubin GM, Sherlock G. Gene ontology: tool for the unification of biology. The Gene Ontology Consortium. Nat Genet. 2000;25:25–9. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saccharomyces Genome Database http://www.yeastgenome.org/


