Deciphering the global organization of clustering in real complex networks

Abstract

We uncover the global organization of clustering in real complex networks. To this end, we ask whether triangles in real networks organize as in maximally random graphs with given degree and clustering distributions, or as in maximally ordered graph models where triangles are forced into modules. The answer comes by way of exploring m-core landscapes, where the m-core is defined, akin to the k-core, as the maximal subgraph with edges participating in at least m triangles. This property defines a set of nested subgraphs that, contrarily to k-cores, is able to distinguish between hierarchical and modular architectures. We find that the clustering organization in real networks is neither completely random nor ordered although, surprisingly, it is more random than modular. This supports the idea that the structure of real networks may in fact be the outcome of self-organized processes based on local optimization rules, in contrast to global optimization principles.

The architecture of real complex systems lies between order and disorder, although its precise location is quite difficult to determine. Disorder in complex networks is manifested by the small-world effect¹ and a highly heterogeneous degree distribution², both properties commonly present in real complex networks³,⁴. Order is, on the other hand, manifested by the presence of triangles –or clustering– representing three point correlations in the system. Indeed, the very concept of order is typically related to the existence of a metric structure in the system which, from the network perspective, is captured by clustering, the smallest network motif able to encode the triangle inequality. Yet, unlike the small-world effect and the heterogeneity of nodes' degrees, clustering is not an emergent property spontaneously generated by paradigmatic connectivity principles such as preferential attachment and, therefore, calls for specific mechanisms for explaining its emergence, thus giving important insights into the nature of network formation and network evolution.

However, the effects of clustering on the structural and dynamical properties of networks have not yet been conclusively elucidated. In fact, several studies have reported apparently contradictory results concerning the effects of clustering on the percolation properties of networks and little is known on its effects on dynamical processes running on networks⁵,⁶,⁷,⁸,⁹,¹⁰,¹¹. This is further hindered by the technical difficulties of any analytical treatment. Indeed, the presence of strong clustering invalidates, in general, the “locally tree-like” assumption used in random graphs, leaving little room for any theoretical study. In an effort to overcome these problems, a new class of clustered network models has been proposed⁷,⁸,⁹,¹⁰,¹¹,¹²,¹³,¹⁴. These are based on the idea of introducing clustering in the network by means of cliques of different sizes. While different models have different rules to match these cliques to close the network, they all are based on the same principles used in the classical configuration model to generate random graphs with a given degree sequence. In this way, the resulting clustered graph is embedded in another graph that is locally tree-like, thus allowing for an analytical treatment. With these approaches, it is possible to generate networks with a given degree distribution P(k) and degree-dependent clustering coefficient 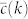, defined as the average fraction of triangles attached to nodes of degree k.

While this is indeed a fair approach to the problem, triangles generated by these models are arranged in a very specific way, with strong correlations between the properties of adjacent edges. In some sense, we can consider this class of models as generators of maximally ordered clustered graphs. At the other side of the spectrum, we can define an ensemble of maximally random clustered graphs such that correlations among adjacent edges are the minimum needed to conform with the degree-dependent clustering coefficient, but no more. These two types of models define –in a non-rigorous way– two extremes of the phase space of possible graphs with given P(k) and 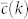. A simple question arises then: where are real networks positioned in this phase space? To give an answer to this question, we need to go beyond the local properties of networks and to study their global organization. In this paper, we study the global structure of clustering in real networks and compare them with the global structure of clustering induced by the two types of models with identical local properties. More specifically, we analyze the organization of real and model networks into m-cores, defined as maximal subgraphs with edges participating in at least m triangles, that is able to distinguish between hierarchical and modular architectures. Interestingly enough, real networks tend to be closer to maximally random clustered graphs, although clear differences are evident.

Results

In this paper, we analyze three real paradigmatic networks from different domains: the Internet at the Autonomous System level¹⁵, the web of trust of the Pretty Good Privacy protocol (PGP)¹⁶, and the metabolite one-mode projection of the metabolic network of the bacterium E. coli¹⁷. However, the results obtained here also hold for a wide spectrum of systems (See Supplementary Information for the analysis of a larger set of systems). We first describe their random counterparts, namely, maximally ordered and maximally random clustered graphs with the same degree distribution and clustering spectrum.

Network models

One of the best clique-based models to generate maximally ordered clustered networks is the one introduced by Gleeson in⁹. In this model, nodes belong to single cliques and are also given a number of connections outside their cliques. Then, cliques are considered as super-nodes, each with an effective degree given by the sum of all the external links of the members of the clique, and connected using the standard configuration model. The input of the model is the joint distribution γ(c, k), defined as the probability that a randomly chosen node has degree k and belongs to a clique of size c. Both the degree distribution and the degree-dependent clustering coefficient are related to function γ(c, k). Therefore, by properly choosing its form, it is possible to match the desired degree distribution and clustering. Note, however, that since we start with cliques and not nodes, the number of nodes and their actual degrees are not fixed a priori. As a consequence, in finite heterogeneous networks, there may be some unavoidable discrepancies between real and random versions of the network. Hereinafter, we denote this model as “clique-based model” (CB).

On the other hand, we generate maximally random clustered networks as an ensemble of exponential graphs¹⁸ with Hamiltonian

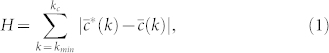where k_min and k_c are the minimum and maximum degrees of the network, 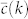is the target degree-dependent clustering coefficient and 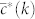is the one corresponding to the current state of the network. Starting from a given real network and after an initial randomization, this Hamiltonian is minimized by means of simulated annealing coupled to a Metropolis rewiring scheme until the current clustering is close enough to the target one (see Methods Section for further details). Here we use two different rewiring schemes. In the first one¹⁹, degrees of nodes are preserved after each single rewiring event but correlations between the degrees of connected nodes are either destroyed or, in the case of very heterogeneous networks, brought down to the level of the structural ones²⁰,²¹. In the second scheme²², rewiring events preserve both the degree distribution and the joint degree-degree distribution of connected nodes, P(k, k′), so that degree-degree correlations are fully preserved. Hereinafter, we denote these models as “maximally random models” (MR). We would like to stress that, even though there are many models of exponential random graphs generating clustered graphs²³,²⁴,²⁵, none of them reproduces the actual clustering spectrum as a function of node degree. In this sense, our maximally random model gets closer to real networks.

Notice that none of the random models used in this paper enforces global connectivity of the network in a single connected component. Therefore, the number of disconnected components and the size of the giant (or largest) component must be considered as predictions of the models, which can be readily compared to those of real networks. In Table 1, we show this comparison with the networks analyzed in this paper. Quite remarkably, in the case of the Internet, MR models predict the existence of, basically, a single connected component, as it is also observed in the real network. On the other hand, the CB model generates a very large number of disconnected components and a giant component significantly smaller than the real one. Even more surprising are the results for the PGP web of trust. The real network is fragmented into a large number of small components whereas its giant component occupies around 18% of the network. All models generate a similar number of disconnected components. However, the relative size of the giant component is very well reproduced by MR models, whereas the CB model predicts a giant component twice as large. In the case of the metabolic network of the bacterium E. coli, all models predict the existence of a single connected component, in good agreement with the real network.

Table 1. Statistics of real networks and their random counterparts. N is the number of nodes, E is the number of edges, C is the average clustering coefficient averaged only over nodes with degrees k ≥ 2. We also show the number of disconnected components (clusters) and the relative size of the giant component. Error bars are computed as the standard deviation of the corresponding metric as obtained from a sample of 10 network realizations. Figures without errors did not show any significant difference between different samples.

	N	E	C	# of clusters	Giant component
Internet	23752	58416	0.61	3	99.98%
Internet clique-based model	23800 ± 200	50000 ± 10000	0.62 ± 0.01	2200 ± 400	(75 ± 4)%
Internet random	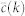23752	58416	0.61	16 ± 4	(99.84 ± 0.06)%
Internet random	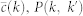23752	58416	0.61	4 ± 1	(99.96 ± 0.02)%
PGP	57243	61837	0.50	16221	18.65%
PGP clique-based model	62000 ± 1000	57200 ± 200	0.506 ± 0.005	13700 ± 200	(37 ± 1)%
PGP random	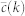57243	61837	0.487 ± 0.001	15550 ± 60	(21.3 ± 0.4)%
PGP random	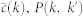57243	61837	0.493 ± 0.001	15810 ± 20	(22.3 ± 0.3)%
E. Coli	1010	3286	0.48	2	99.8%
E. Coli clique-based model	1010 ± 40	3300 ± 700	0.51 ± 0.01	7 ± 3	(97.9 ± 0.6)%
E. Coli random	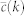1010	3286	0.48	2.2 ± 0.9	(99.7 ± 0.3)%
E. Coli random	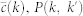1010	3286	0.48	7 ± 2	(98.2 ± 0.6)%

Revealing network hierarchies: k-cores and m-cores

Real heterogeneous networks are typically hierarchically organized. One of the most useful tools to uncover such hierarchies is the k-core decomposition²⁶. Given a network, its k-core is defined as the maximal subgraph such that all nodes in the subgraph have at least k connections with members of the subgraph. This defines a hierarchy of nested subgraphs, where the 1-core contains the 2-core, which in turn contains the 3-core and so on until the maximum k-core is reached. Nodes belonging to the k-core but not to the (k + 1)-core are said to have coreness k. Real networks often show a deep and complex k-core structure, as made evident by tools such as LaNet-vi²⁷. However, even though clustering has been shown to induce strong k-core hierarchies⁵, the k-core per se does not include any information about clustering and, thus, cannot discriminate well between two networks with different global organization of clustering but with the same clustering coefficient.

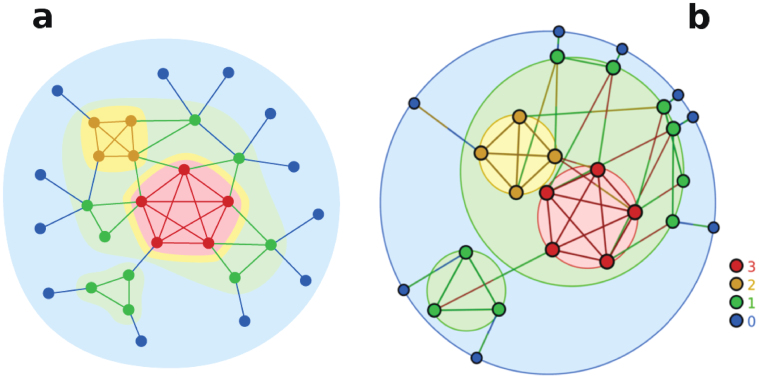
To overcome this problem, the concept of k-core has been remodeled to account for clustered networks. A key ingredient throughout the paper is the concept of edge multiplicity m, defined as the number of distinct triangles going through an edge²⁸,²⁹,³⁰. All edges belonging to a clique of size n have identical multiplicity n − 2 whereas an edge connecting two cliques has zero multiplicity. Therefore, strong correlations between the multiplicities of adjacent edges indicate that triangles are arranged in a clique-like fashion whereas a weaker correlation indicate a random distribution of triangles. It is therefore clear that, in order to uncover the global organization of triangles in a network, it is necessary to understand the organization of the multiplicities of their edges. This can be achieved with the m-core, defined as the maximal subgraph such that all its edges have, at least, multiplicity m within it. This concept was developed in³¹,³² under the name of k-dense decomposition. The edges in a k-dense graph have multiplicity m = k − 2. Because of this, we prefer the notion of m-core, which is directly related to the multiplicity: an edge belongs to the m-core if its multiplicity within the m-core is, at least, m. A node belongs to the m-core if at least one of its edges belongs to it. A node belonging to the m-core but not to the (m + 1)-core is said to have m-coreness m. As in the case of the k-core, the m-core defines a set of nested subgraphs whose properties informs us about the global organization of triangles in the graph. The left plot in Fig. 1 shows an example of a simple network and its m-core structure.

Figure 1. m-cores decomposition and its visualization.

The example network in (a) is colored according to the m-coreness of nodes and edges. Nodes and edges colored in blue belong to the m0-core but not to the m1-core. Nodes and edges colored in green belong to the m1-core but not to the m2-core, etc. The same structure is represented in (b) with the visualization tool described in the main text. The outermost circle in blue represents the m0-core, with nodes of m-coreness 0 located in its perimeter. The m1-core –which is contained within the m0-core– is fragmented in two disconnected components, which are represented as two non-overlapping circles within the outermost one and with nodes of m-coreness 1 located in their perimeters. The larger of these two components is further fragmented in two disconnected components representing the m2-core and m3-core. The angular positions of nodes in each circumference are chosen to minimize the angular separation with their neighbors in different layers. Notice that in this representation, each edge is colored with two colors, corresponding to the colors of the m-coreness of the nodes at the end of the edge but in reverse order. In this way, it is possible to visualize easily connections between different layers. See27 for further details of the visualization.

In the case of the k-core, the internal average degree within each subgraph grows as k is increased. As a consequence, it is very unlikely that the (k + 1)-core is fragmented in different components if the k-core is connected. Therefore, the main interest of the k-core decomposition is focused on the size of the giant k-core and the maximum coreness of the system. The situation is completely different in the case of the m-core. This is so because of a weaker correlation between m-coreness of a node and its degree³³. In fact, the m-core decomposition is able to distinguish between a strong hierarchical structure –when m-cores do not fragment into smaller components– from a highly modular architecture –when m-cores are always fragmented. In this case, the quantities of interest are, besides the size of the giant m-core and the maximum m-coreness, the number of components as a function of m.

Figures 2, 3, and 4 show a comparison of the k-core and m-core decompositions between real networks and their random equivalents. As it can be observed in the top plots of these figures, all models do a reasonably good job at reproducing both the k-core structure and the distribution of edge multiplicities, even though MR models are clearly better than the CB one. However, there are important differences in the m-core decompositions. While both versions of MR models reproduce well the giant m-core, the maximum m-coreness, and the number of components as a function of m of all the studied networks, the CB model overestimates the size and number of components in the case of the Internet and underestimates the size of giant m-cores in the PGP web of trust. In the case of the metabolic network, MR models reproduce well its entire m-core structure. The CB model, on the other hand, does not capture well the m-core decomposition. Even though the CB network is originally connected, it fragments into a large number of disconnected components already at the m1-core and keeps fragmenting at each level almost up to the largest m-core, which is also three times larger than the real one.

Figure 2. Measuring hierarchies in real and random networks.

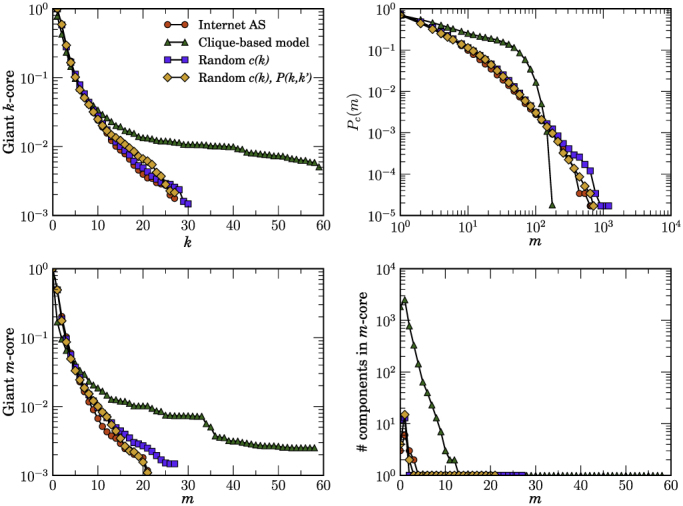
Comparison of the k-core and m-core decompositions between the real Internet AS network, the clique based model, and maximally random models. “Random c(k)” stands for the maximally random model with a fixed degree distribution and clustering spectrum c(k). “Random c(k), P(k, k′)” stands for the maximally random model that preserves also the degree-degree correlation structure of the real network. The top left plot shows the relative size of the giant k-core as a function of k. Top right plot shows the complementary cumulative distribution of edge multiplicities. Bottom left plot shows the relative size of the giant m-core as a function of m. Finally, the bottom right plot shows the number of components in the m-core as a function of m.

Figure 3. Measuring hierarchies in real and random networks.

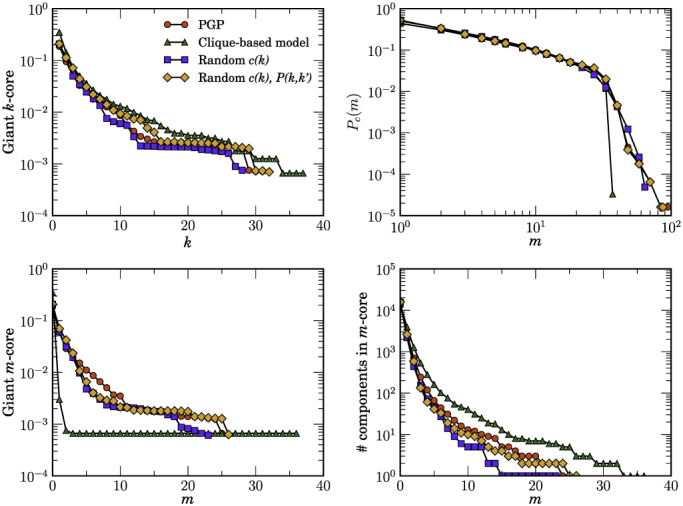
The same as in Fig. 2 but for the PGP web of trust.

Figure 4. Measuring hierarchies in real and random networks.

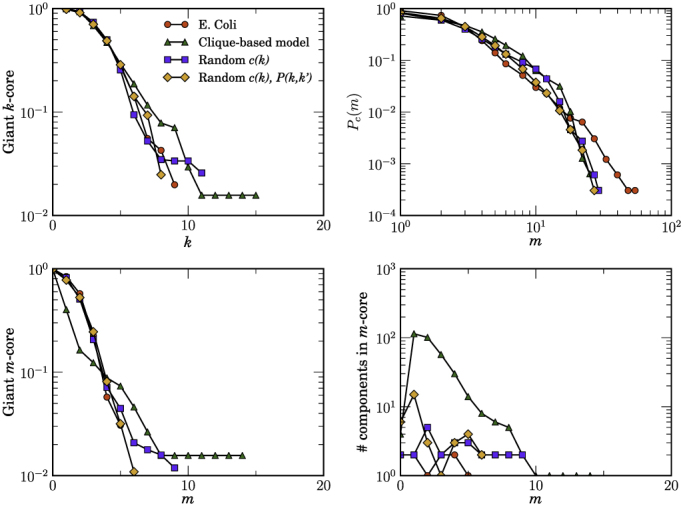
The same as in Fig. 2 but for the E. Coli metabolic network.

m-core visualization

The m-core decomposition is actually much richer and complex than what Figs. 2, 3, and 4 show. Certainly, the m-core decomposition can be represented as a branching process that encodes the fragmentation of m-cores into disconnected components as m is increased. The tree-like structure of this process informs us about the global organization –for instance hierarchical vs. modular– of clustering in networks. To visualize this process we use LaNet-vi 3.0, a modified version of LaNet-vi, originally designed to visualize the k-core structure of a network²⁷, but now extended to include the m-core decomposition. We have made our code publicly available to the scientific community on SourceForge³⁴. In short, the old LaNet-vi tool evaluates the coreness of all nodes of the network and arranges them in a plane following the hierarchy induced by the k-cores, so that nodes with high coreness are placed at the center of the figure whereas nodes with lower coreness are located around nodes with higher coreness in an onion-like shape. The major modification in LaNet-vi 3.0 with respect to the visualization mode in the previous version concerns the representation of disconnected components. If the network forms a single connected component, nodes with m-coreness 0 are arranged in the outermost circle of the representation. Whenever the m1-core is fragmented into several components, these are arranged in separate and non-overlapping disks within the circle of m-coreness 0, with nodes of m-coreness 1 placed at the edge of their corresponding disk. The process is repeated for each disconnected component with the m2-core, m3-core, etc., until the maximum m-coreness present in the network is reached. The size of each disk is proportional to the logarithm of the number of nodes in the component. In this way, it is possible to visualize simultaneously all the information encoded in the m-cores so that different networks can be easily compared (see the right plot in Fig. 1 for a simple example). When the original network is already fragmented (like in the PGP web of trust, for instance), we first proceed to arrange disconnected components in non overlapping disks within the outermost disk, that in this case does not have any node in its perimeter.

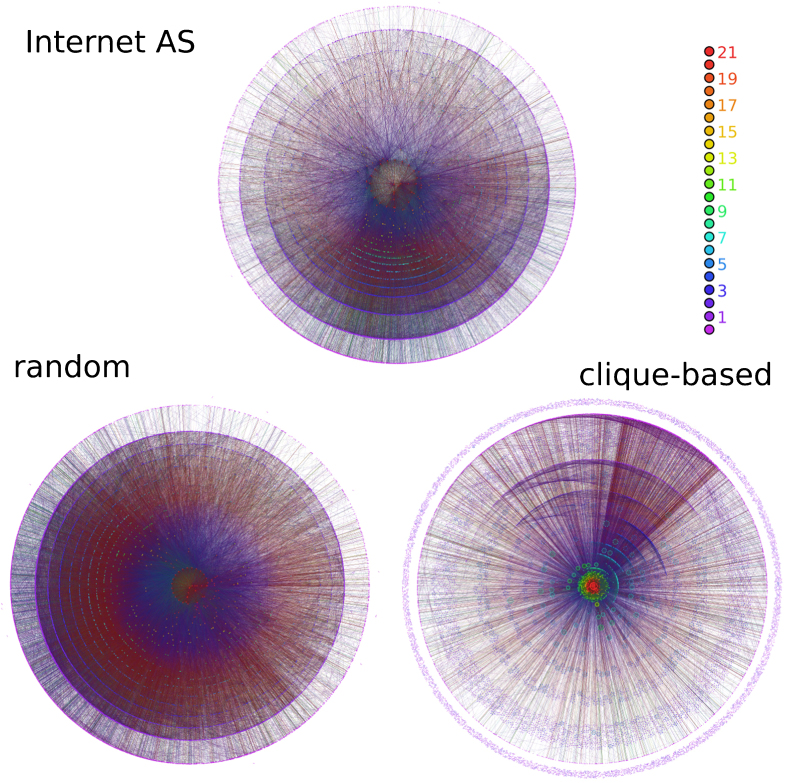
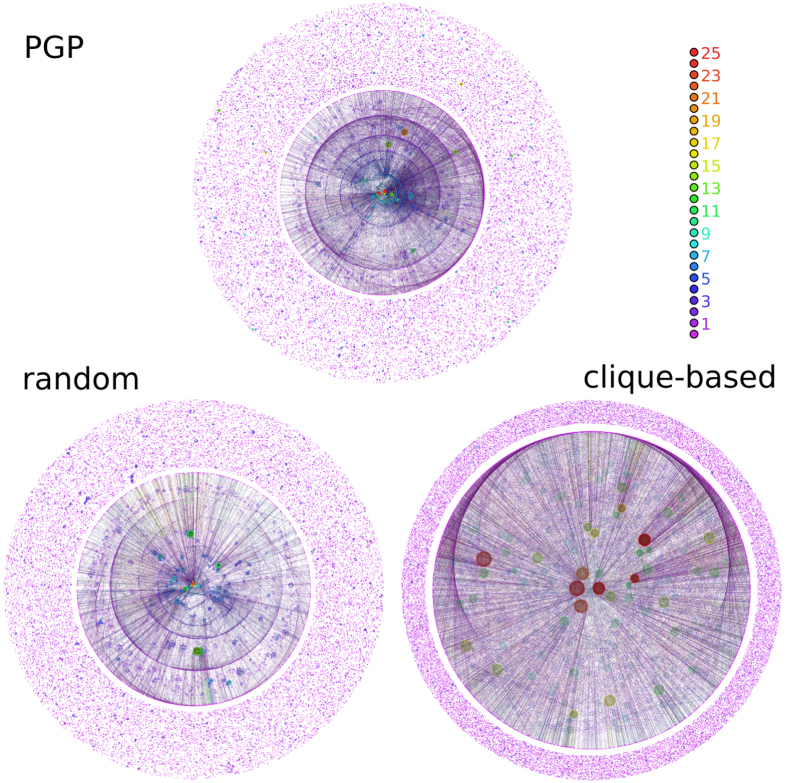
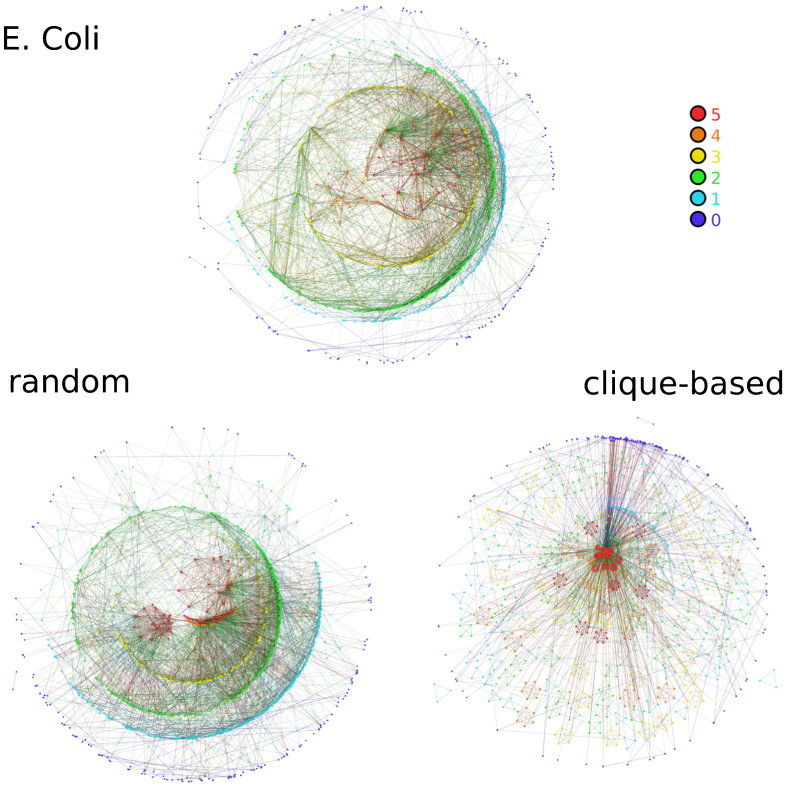
Figures 5, 6, and 7 show the visualization of m-cores of real networks and their random equivalents (visualizations of MR models are shown only for P(k) preserving rewiring). In the case of the Internet graph, the m-core visualization reveals a strongly hierarchical structure, where each layer is contained within the previous layer and where connections are mainly radial, with nodes with low m-coreness connected to nodes with higher m-coreness and very few connections between nodes in the same layer. Interestingly, this type of structure is also revealed in recent embeddings of the Internet graph into the hyperbolic plane¹⁵. This structure is very well reproduced by MR models, as it can be seen in the left bottom plot of Fig. 5, but not by the CB model, which generates a highly modular and non-hierarchical structure. The case of the web of trust of PGP is particularly interesting. Figure 6 reveals a mixture of a modular structure, with a strong fragmentation for all values of m –as one would expect for a social network–, and a hierarchical structure, revealed by the existence of a persistent giant m-core and a large number of layers. Again, this structure is very well reproduced by MR models whereas the CB model generates a very flat modular structure without any hierarchy. Finally, the metabolic network is also strongly hierarchical, although due to the small network size the number of layers is relatively small. MR models reproduce very well its structure whereas the CB model does not generate any hierarchy.

Figure 5. Visualizing m-cores.

m-core decomposition of the Internet AS network and its random versions. The MR version shown on the bottom left plot of the figure corresponds to the “Random c(k)” model, that is, with the rewiring scheme that does not preserves degree-degree correlations. The latter case is always closer to the real network. The color code is determined by the real network and kept the same in its random versions. However, layers in random networks above the maximum m-coreness of the real network are colored all in red. Maximum m-coreness for the MR and CB models are 27 and 58, respectively.

Figure 6. Visualizing m-cores.

The same as in Fig. 5 for the PGP network and its random versions. Maximum m-coreness for the MR and CB models are 23 and 36, respectively.

Figure 7. Visualizing m-cores.

The same as in Fig. 5 for the E. Coli metabolic network and its random versions. Maximum m-coreness for the MR and CB models are 9 and 14, respectively.

Discussion

The results presented in this paper indicate that, in agreement with previous studies³⁵,³⁶, the degree distribution P(k) and clustering spectrum 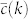are the main contributors to the global organization of the majority of real networks, which are close to maximally random once these properties are fixed. This supports the idea that most real networks are the result of a self-organized process based on local optimization rules, in contrast to global optimization principles, that yield a hierarchical organization that cannot be reproduced by maximally ordered clustered models. Besides, the strong clustering observed in real networks, supports also the idea that such local principles are related to a similarity measure among nodes of the network that can be quantified by an underlying metric structure¹⁵,¹⁷,³⁷,³⁸,³⁹,⁴⁰. On the other hand, global optimization principles are necessarily present, for instance, in power grids, where they induce topologies that are very different from what one would expect at random. This is made evident by its m-core decomposition (see Supplementary Information). In this case, even thought the m-core structure is not very deep, it is very different from any of the random models, which generate highly unstructured m-cores. Therefore, the m-core decomposition along with its visualization tool can help us to find the true mechanisms at play in the formation and evolution of real networks.

Methods

Maximally random clustered networks

Maximally random clustered networks are generated by means of a biased rewiring procedure. We use two different rewiring schemes. In the first one, two different edges are chosen at random. Let these connect nodes A with B and C with D. Then, the two edges are swapped so that nodes A and D, on the one hand, and C and B, on the other, are now connected. We take care that no self-connections or multiple connection between the same pair of nodes are induced by this process. This rewiring scheme preserves the degree distribution of the original network but not degree-degree correlations. In the second rewiring scheme, we first chose an edge at random and look at the degree of one of its attached nodes, k. Then, a second link attached to a node of the same degree k is chosen and the two links are swapped as before. Notice that this procedure preserves both the degree of each node and the actual nodes' degrees at the end of the two original edges. Therefore, the procedure preserves the full degree-degree correlation structure encoded in the joint distribution P(k, k′). Both procedures are ergodic and satisfy detailed balance.

Regardless of the rewiring scheme at use, the process is biased so that generated graphs belong to an exponential ensemble of graphs 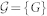, where each graph has a sampling probability P(G) ∝ e^−βH(G), where β is the inverse of the temperature and H(G) is a Hamiltonian that depends on the current network configuration. Here we consider ensembles where the Hamiltonian depends on the target clustering spectrum of the real Network 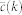as

where 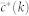is the current degree-dependent clustering coefficient. We then use a simulated annealing algorithm based on a standard Metropolis-Hastings procedure. Let G′ be the new graph obtained after one rewiring event, as defined above. The candidate network G′ is accepted with probability

otherwise, we keep the graph G unchanged. We first start by rewiring the real network 200E times at β = 0, where E is the total number of edges of the network. This step destroys the clustering coefficient of the original network. Then, we start an annealing procedure at β₀ = 50, increasing the parameter β by a 10% after 100E rewiring events have taken place. For each 100E rewires of a given β we compute which fraction of the proposed rewires with ΔH ≠ 0 are accepted. If this ratio is smaller than a certain parameter, generally set to 5 · 10⁻⁵, we stop the process.

Computing m-cores

To compute m-cores efficiently, we develop a new approach, different from the one in³¹,³². We first map the original graph G into a hypergraph G*, where edges in G become vertices in G* and where each triangle in the original graph is mapped into an edge (a 3-tuple) in G*. Then, by noticing that the degree of a vertex v* in G* equals the number of triangles associated to the original edge in G, it is possible to obtain the m-core just by computing the k-core of the same level in G*. The complete description can be found in the Supplementary Information.

Author Contributions

P.C., M.A.S. and M.B. designed research; M.A.S. proposed the use of m-cores and M.G.B. and J.I.A.H. developed a fast algorithm to compute it; P.C. developed the graph generators; P.C., M.G.B. and J.I.A.H. developed the visualization tool M.B. wrote the manuscript; all authors analyzed data, discussed the results, and reviewed the manuscript.

Supplementary Material

Supplementary Information

Supplementary Information