Receiver Operating Characteristic (ROC) Curve Analysis for Medical Diagnostic Test Evaluation

Abstract

This review provides the basic principle and rational for ROC analysis of rating and continuous diagnostic test results versus a gold standard. Derived indexes of accuracy, in particular area under the curve (AUC) has a meaningful interpretation for disease classification from healthy subjects. The methods of estimate of AUC and its testing in single diagnostic test and also comparative studies, the advantage of ROC curve to determine the optimal cut off values and the issues of bias and confounding have been discussed.

Evaluation of diagnostic tests is a matter of concern in modern medicine not only for confirming the presence of disease but also to rule out the disease in healthy subjects. In diagnostic test with dichotomous outcome (positive/negative test results), the conventional approach of diagnostic test evaluation uses sensitivity and specificity as measures of accuracy of test in comparison with gold standard status (1). In situation where the test results are recorded in ordinal scale (e.g. 5 ordinal scale: "definitely normal", "probably normal", "uncertain", "probably abnormal", "definitely abnormal") even or the test results are reported on continuous scale, the sensitivity and specificity can be computed across all the possible threshold values (2-4). So, the sensitivity and specificity vary across the different threshold and the sensitivity is inversely related with specificity (1-4). Then, the plot of sensitivity versus 1-Specifity is called receiver operating characteristic (ROC) curve and the area under the curve (AUC), as an effective measure of accuracy has been considered with a meaningful interpretations (5). This curve plays a central role in evaluating diagnostic ability of tests to discriminate the true state of subjects, finding the optimal cut off values, and comparing two alternative diagnostic tasks when each task is performed on the same subject (5-7). Pubmed search reveals that this analysis has been used extensively in clinical epidemiology for the assessment of diagnostic ability of biomarkers (e.g. serum markers) and imaging tests in classification of the diseased from the healthy subjects (7-11). This predictive model is also commonly used to estimate the risk of any adverse outcome based on the patient’s risk profile in medical researches. This article provides a full review of the advantage of ROC curve, measures of accuracy that use the ROC curve and their statistical behaviours, the issues of bias and confounding in ROC analysis.

Conventional Analysis of Diagnostic Test Data

Conventionally, a standard way of describing the accuracy of a diagnostic test is the two-by-two table. This is performed when the test results are recorded as dichotomous outcomes (positive/negative results). As table 1 shows, the column represents the true status of disease state that is assessed without errors by gold standard.

Table 1.

Frequencies of test outcome for n₁ patients with disease and n₂ patients without disease

Diagnostic test result	Disease status
	Present	Absent
Total	n1=a+c	n2=b+d
Positive Negative	a (TP) c (FN)	b (FP) d (TN)

Summary Indices of Test Performance

TPF=True Positive Fraction (Sensitivity)= TP/ (TP+FN)= a/(a+c)

FNF=False Negative Fraction (1-Sensitivity)= FN/ (TP+FN)= c/(a+c)

TNF=True Negative Fraction (Specificity)= TN/ (TN+FP)= d/(b+d)

FPF=False Positive Fraction (1-specificity)= FP/ (TN+FP)= b/(b+d)

PPV=Positive Predicted Value=TP/(TP+FP)=a/(a+b)

NPV=Negative Predicted Value=TN/(TN+FN)=d/(c+d)

This standard may be another test but more expensive diagnostic method or invasive method but more accurate or combination of tests may be available in clinical follow up, surgical verification, autopsy, biopsy or by a panel of experts (6, 11). The row of table 1 represents the dichotomous outcome of test results. From the frequency of test results among patients with and without disease based on gold standard, one can derive the probability of a positive test result for patients with disease (i.e. the conditional probability of correctly indentifying the diseased subjects by test-- sensitivity or true positive fraction-TPF) and the probability of negative test results for patients without disease (i.e. the conditional probability of correctly identifying non-diseased subjects by test -- specificity or true negative fraction-TNF). The positive predicted values (PPV) and the negative predicted values (NPV) are the two other indices that are useful in clinical practice when test results are available for the clinicians. The PPV is defined as the probability of disease for positive test results and the NPV is also defined the probability of being healthy for negative test results. Although, these two measures are useful for clinical decision, these are influenced by the prior prevalence of disease in population. PPV is elevated with a higher prevalence of disease while the NPV decreases with a higher prevalence (12).

The PPV and NPV can also be calculated from Bayes’ theorem using the estimates of sensitivity and specificity and the prior probability of disease (or prevalence of diseased in population) before the test is applied. The PPV and NPV are calculated through the posterior probability of the diseased after the test results are known. Let p denotes the prevalence of the diseased in population and Sen and Spe in the sensitivity and specificity of diagnostic test, then the PPV and NPV are formulated using Bayes’ theorem as follows:

PPV=p× Sen / [p ×Sen+ (1-p) ×Spe] and NPV= (1-p) ×Spe / [p×(1-Sen)+(1-p) ×Spe]

Thus, one calculates the PPV and NPV if one knows the sensitivity, specificity and pre-test probability of the diseased in population (i.e. prevalence). These two indices are influenced by the prevalence of disease. When disease prevalence is high the PPV increases and the NPV decreases.

The conventional diagnostic test indexes (sensitivity and specificity) can be combined into a single index as likelihood ratio (13). The likelihood ratio is defined as the ratio of two density functions of test results conditional in diseased and non-diseased subjects. The positive LR of test (LR⁺) is nothing more than the ratio of sensitivity to 1-sepecificity.

${\mathrm{LR}}^{+}=\frac{\mathrm{pr}[\mathrm{T}+\mathrm{│}\mathrm{D}+]}{\mathrm{pr}[\mathrm{T}+\mathrm{│D}-]}=\frac{\mathrm{sensitivity}}{1-\mathrm{specificity}}$

The LR⁺ is ranged from 0 to infinity. The worst case is LR⁺=0. This happens when sensitivity becomes close to 0. The largest value of LR⁺ occurs when specificity tends to be close to 1 and sensitivity also to be close to 1. Thus the higher value of LR⁺ has a greater information value for diagnostic test. On the other hand, the negative likelihood ratio (LR^-) is the ratio of probability of negative test in diseased to non diseased. This is also the ratio of 1-sensitivity to specificity.

${\mathrm{LR}}^{-}=\frac{\mathrm{pr}[\mathrm{T}-\mathrm{│\; D}+]}{\mathrm{pr}[\mathrm{T}-\mathrm{│D}-]}=\frac{1-\mathrm{sensetivity}}{\mathrm{specificity}}$

The lower (i.e close to 0) LR^- has a greater information values of a negative test. The larger value of LR^- has lower information values. Therefore, the total information content of a diagnostic test can be summarized either its LR⁺ or its LR^-. The Bayesian analysis combines the data of the likelihood ratio of test and prior odds of disease in order to obtain the posterior odds of disease among positive and negative test results (13). Posterior odds of disease=likelihood ratio × prior odds of disease

Conventional analyses consider the sensitivity and the specificity of a diagnostic test as the primary indices of accuracy since these indices are considered to be independent of the prior probability of disease. However, using a single sensitivity and a single specificity as measures of accuracy is problematic since these measures depend on a diagnostic criterion (i.e. cut-off) for positivity which is often chosen arbitrarily (14, 15). For example, one observer may choose a lenient decision criterion and the other may choose a stringent decision criterion for positivity. ROC analysis circumvents this arbitrariness.

Background and Rationale of ROC Analysis

ROC analysis originated in the early 1950's with electronic signal detection theory (16). One of the first applications was in radar, to separate observer variability from the innate delectability of signal. Psychologists also adapted ROC methodology into psychology in the early 1950's in order to determine the relationship between properties of physical stimuli and the attributes of psychological experience (sensory or perceptual) (17). The task of observers is to detect a weak signal in the presence of noise; e.g. whether the "signal" was caused by some sensory event.

The applications of ROC methodology in diagnostic radiology and radionuclide imaging date back to the early 1960's. The first ROC curve in diagnostic radiology was calculated by Lusted (1960) who re-analyzed the previously published data on the detection of pulmonary tuberculosis and showed the reciprocal relationship between the percentage of false positive and of false negative results from the different studies of chest film interpretations (18). Since then, several authors have used ROC methodology to diagnostic imaging systems. The work of Dorfman and Alf (1968) was a pioneering step toward objective curve fitting and the use of computerized software in ROC analysis (19). An automated program of maximum likelihood approach under binormal assumption was developed in 1968. Since then, several new methodologic developments have been implemented in programs such as ROCFIT, CORROC, ROCPWR, and LABROC, developed by Metz at the University of Chicago for analysis of ROC data. They are available in the public domain (20).

During the past four decades, ROC analysis has become a popular method for evaluating the accuracy of medical diagnostic systems. The most desirable property of ROC analysis is that the accuracy indices derived from this technique are not distorted by fluctuations caused by the use of arbitrarily chosen decision criteria or cut-offs. In other words, the indices of accuracy are not influenced by the decision criterion (i.e. the tendency of a reader or observer to choose a specific threshold on the separator variable) and/or to consider the prior probability of the "signal" (16). The derived summary measure of accuracy, such as the area under the curve (AUC) determines the inherent ability of the test to discriminate between the diseased and healthy populations (21). Using this as a measure of a diagnostic performance, one can compare individual tests or judge whether the various combination of tests (e.g. combination of imaging techniques or combination of readers) can improve diagnostic accuracy.

Basic Principles of ROC Analysis

ROC analysis is used in clinical epidemiology to quantify how accurately medical diagnostic tests (or systems) can discriminate between two patient states, typically referred to as "diseased" and "nondiseased" (16, 17, 21, 22). An ROC curve is based on the notion of a "separator" scale, on which results for the diseased and nondiseased form a pair of overlapping distributions (1). The complete separation of the two underlying distributions implies a perfectly discriminating test while complete overlap implies no discrimination. The ROC curve shows the trade off between the true positive fraction (TPF) and false positive fraction (FPF) as one change the criterion for positivity (1, 22).

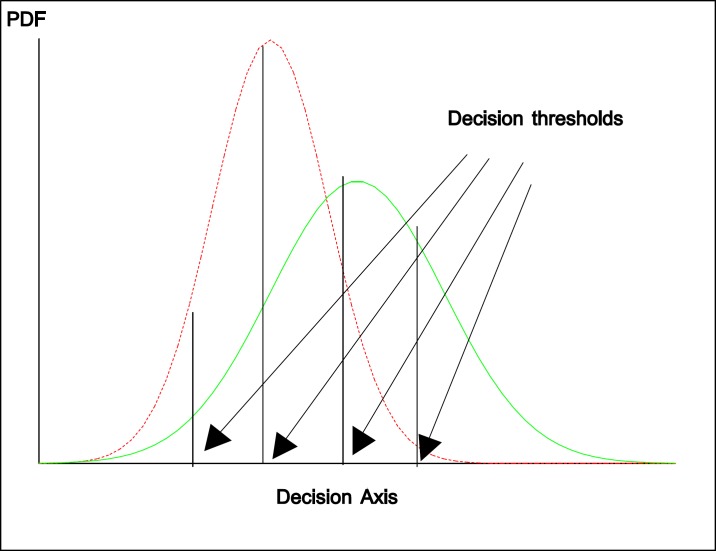
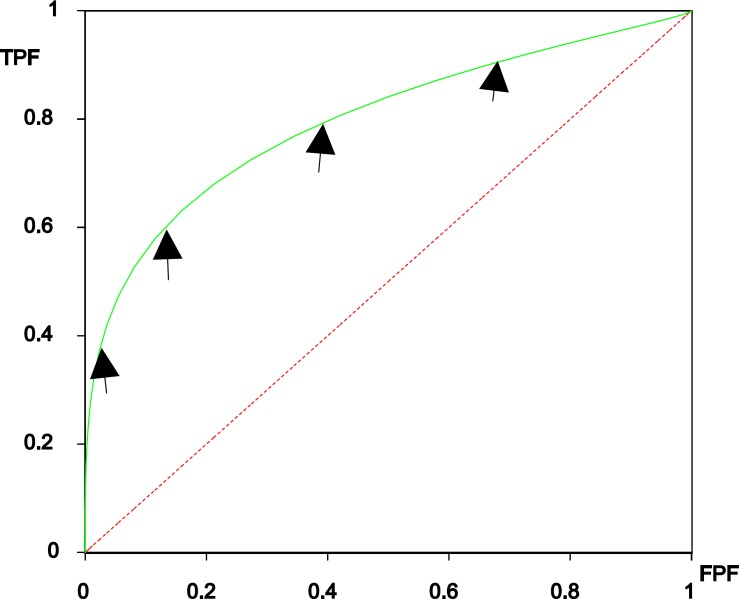
Figure 1 show the two overlapping distributions with four thresholds used and figure 2 is the corresponding ROC curve and the arrows on the curve show ROC operating points. Derived indices, such as the area under the entire curve (AUC), the TPF at a specific FPF, or the partial area corresponding to a clinically relevant range of FPF (5, 23-25), are the most commonly used to measure diagnostic accuracy. Here, we briefly discuss the concept of ROC curve and the meaning of area under the curve.

Figure 1.

The two overlapping distributions (binormal model: probability density function-PDF) for diseased (right site) and nondiseased (left side) and four different decision threshold

Figure 2.

ROC curve derived from two overlapping distributions in Figure 1

Concept and Interpretation of ROC Curve

The concept of an ROC curve is based on the notion of a "separator" (or decision) variable. The frequencies of positive and negative results of the diagnostic test will vary if one changes the "criterion" or "cut-off" for positivity on the decision axis. Where the results of a diagnostic system are assessed based on subjective judgement, the decision scale is only "implicit". Such a decision variable is often called a "latent" or unobservable variable.

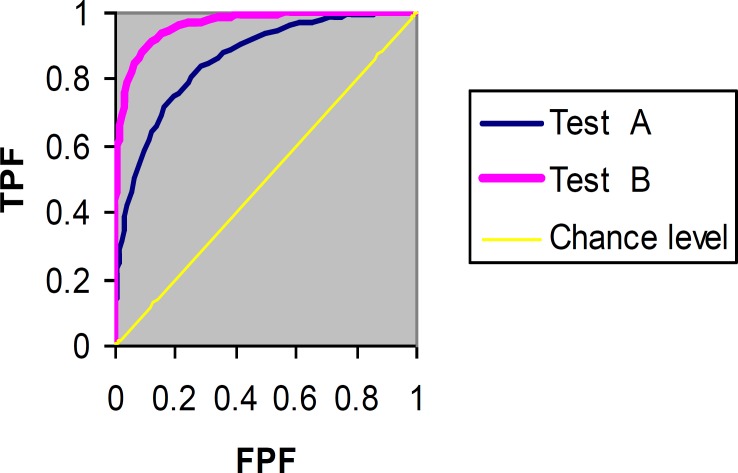
The plot of TPF (sensitivity) versus FPF (1-specificity) across varying cut-offs generates a curve in the unit square called an ROC curve. ROC curve corresponding to progressively greater discriminant capacity of diagnostic tests are located progressively closer to the upper lefthand corner in "ROC space" (figure 3 shows test B has a greater discriminate capacity than test A). An ROC curve lying on the diagonal line reflects the performance of a diagnostic test that is no better than chance level, i.e. a test which yields the positive or negative results unrelated to the true disease status. The slope of an ROC curve at any point is equal to the ratio of the two density functions describing, respectively, the distribution of the separator variable in the diseased and nondiseased populations, i.e. the likelihood ratio (26, 27). A monotonically increasing likelihood ratio corresponds to a concave ROC curve (16, 17). The area under the curve (AUC) summarizes the entire location of the ROC curve rather than depending on a specific operating point (1, 5). The AUC is an effective and combined measure of sensitivity and specificity that describes the inherent validity of diagnostic tests (7).

Figure 3.

ROC curves of two diagnostic tasks (test A versus test B)

As an example of real data of breast cancer study that was reported recently by Hajian-Tilaki et al. (12), the calculation of sensitivity and specificity of various cut-off values of body mass index (BMI) for predicting of breast cancer are given in table 2 and shows that sensitivity and specificity has an inverse relationship (12). As an illustration, the corresponding empirical ROC curve was drawn in figure 4 by a nonparametric method using SPSS software (AUC=0.79, 95% confidence interval: 0.74-0.84, p<0.001). This curve and the corresponding AUC show that BMI as a biomarker has predictive ability to discriminate breast cancer from normal subjects.

Table 2.

An example of real data showing sensitivity and specificity at various cut- off points of BMI for detection of breast cancer

Cut-off values of BMI (kg/m2)	Breast cancer (n=100)		Normal subjects (n=200)		Sensitivity	Specificity
	True positive (TP)	False negative (FN)	False positive (FP)	True negative (TN)
18 20 22 24 26 28 30 32 34 36 38 40	100 100 99 95 85 66 47 34 21 17 7 1	0 0 1 5 15 34 53 66 79 83 93 99	200 198 177 117 80 53 27 17 14 6 4 1	0 2 23 83 120 147 173 183 186 194 194 199	1.0 1.0 0.99 0.95 0.85 0.66 0.47 0.34 0.21 0.17 0.07 0.01	0.0 0.01 0.115 0.415 0.60 0.735 0.865 0.915 0.93 0.97 0.98 0.995

Indices of Accuracy

Several indices of accuracy have been proposed to summarize ROC curves (1, 5, 13). Based on these indices, statistical tests have been developed to compare the accuracy of two or more different diagnostic systems. We will review briefly the three important commonly used indices, AUC, partial area, TPF_FPF, and their statistical properties. These indices can be estimated both parametrically and nonparametrically. The area under the curve (AUC), as a one-dimensional (uni-dimensional) index, summarizes the "overall" location of the entire ROC curve. It is of great interest, since it has a meaningful interpretation. The AUC can be interpreted as the probability that a randomly chosen diseased subject is rated or ranked as more likely to be diseased than a randomly chosen nondiseased subject (5). This interpretation is based on nonparametric Mann-Whitney U statistics that is used in calculating AUC (5). The other interpretation is the average value of sensitivity for all the possible values of specificity. Such an index is especially useful in a comparative study of two diagnostic tests (or systems). If two tests are to be compared, it is desirable to compare the entire ROC curve rather than at a particular point (1). The maximum AUC=1 means that the diagnostic test is perfect in the differentiation between the diseased and nondiseased. This happens when the distribution of test results for the diseased and nondiseased do not overlap. AUC =0.5 means the chance discrimination that curve located on diagonal line in ROC space. The minimum AUC should be considered a chance level i.e. AUC=0.5 while AUC=0 means test incorrectly classify all subjects with diseased as negative and all subjects with nondiseased as positive that is extremely unlikely to happen in clinical practice.

Partial Area Index: Despite the meaningful interpretation and statistical properties of AUC, it may still be argued that a large part of the area arises from the right side of the unit square where the high false positive fraction is of no clinical relevance. Thus, one may be adding noise when using the area index to compare the two different diagnostic systems. Also, two ROC curves with the same area may cross, but one may have higher TPF than another in the clinically relevant range of FPF. In this situation, a partial area under the curve corresponding to a clinical relevant FPF is recommended as an index of choice (25, 28- 30).

TP fraction for a given FP fraction: A true positive fraction (TPF) for a given false positive fraction (FPF), termed TPF_FPF for short, is one natural index of accuracy (23). One may be interested in comparing the performance of two tests at a given FPF for clinical reasons, especially in a case where two ROC curves cross. The areas under the curves may be equal but in a clinical range of interest the FPF for one test may be superior to that of the other. Also, TPF_FPF can easily be applied and it is readily understood. However, the main criticism of TPF_FPF as an index of accuracy is that the different investigators may not report the estimates of TPF at the same FPF. If so, the two TPF from the different investigators of the same test may not be comparable.

Advantage of ROC Curve Analysis and Optimal Cut-off Value

ROC curve analysis has several advantages (31-36). First, in contrast to single measures of sensitivity and specificity, the diagnostic accuracy, such as AUC driven from this analysis is not affected by decision criterion and it is also independent of prevalence of disease since it is based on sensitivity and specificity. Second, several diagnostic tasks on the same subjects can be compared simultaneously in a ROC space and the methods also developed to consider the covariance between two correlated ROC curve (6, 37). Third, one can easily obtain the sensitivity at specific FPF by visualizing the curve. Forth, the optimal cut- off value can be determined using ROC curve analysis (26). In determining optimal cut off values, at least three methods have been proposed (7, 26, 32, 33, 35). The two methods give equal weight to sensitivity and specificity with no ethical, cost and prevalence constraints (7). The first method uses the square of distance between the point (0, 1) on the upper left hand corner of ROC space and any point on ROC curve ie. d²= (1-TPF)²+ FPF²=(1-sensetivity)²+ (1-specificty)². In order to obtain the optimal cut off points, the square of this distance is minimized. In other words, one can calculate this distance for each cut off point in order to find the optimal cut- off value. The second method called Youden index uses the maximum of vertical distance of ROC curve from the point (x, y) on diagonal line (chance line). In fact, Youden index maximizes the difference between TPF (sensitivity) and FPF (1-sepicificity): Youden Index=TPF-FPF= Sensitivity+ Specificity -1. Thus, by maximizing Sen + Spec aross various cut-off points, the optimal cut- off point is calculated. The third method incorporates the financial costs for correct and false diagnosis and the costs of further work up for diagnosis. In fact, the consequence of each possible test outcome is ascertained to their costs and combining ROC analysis with utility-based decision theory can be used to determine the optimal cut point (26). For example, given a disease with low prevalence and high cost of false positive diagnosis, the cut-point may be chosen at higher value to maximize specificity while for a disease occurring at high prevalence and missing diagnosis has a serious fatal consequences, a lower cut-point value would be selected to maximize sensitivity.

Testing of accuracy index (AUC) of a single diagnostic test

Suppose clinical researcher may wish to test the accuracy (AUC) of a single diagnostic test as unknown parameter with a pre-specified value of AUC₀. Thus, the null and alternative hypotheses are: H₀: AUC=AUC₀ versus H₁: AUC ≠ AUC₀. With normal approximation of asymptotic properties of AUC, the Z-score under H₀ is as follows:

Z=$\frac{\widehat{\mathrm{AUC}}-{\mathrm{AUC}}_0}{\mathrm{SE}(\widehat{\mathrm{AUC})}}$

where $\widehat{\mathrm{AUC}}$ and its standard error can be estimated either parametric (binormal model) or purely nonparametric approaches. Hanley and McNeil showed that AUC has a meaningful interpretation as Man- Whitney U-statistics and thus, U-statistics is a nonparametric estimate of AUC. In addition, they proposed exponential approximation of SE of nonparametric AUC (5). Delong et al. also developed a nonparametric methods of SE of AUC (37). The DeLong’s method of components of U-statistics and its SE has been well illustrated by Hanley and Hajian-Tilaki in a single modality of diagnostic test (38).

In testing, if the absolute observed value of Z-score is greater than its critical value at 95% confidence level (i.e. |Z_obs|> 1.96), then the null hypothesis would be rejected and its p-value can be calculated by Z- distribution using observed Z- score. Obviously, one can test AUC with any prespecified value for example testing AUC with chance level (AUC=0.5). SPSS software allows to depict ROC curve in unit square space by trapezoidal rule (i.e. nonparametric method) and nonparametric estimate of AUC and its SE and 95% confidence interval and the p-value for testing AUC=0.5 versus AUC ≠0.5 are calculated as well.

Testing the Accuracy in comparative study of two diagnostic tests

In comparative diagnostic studies in the context of ROC analysis, as an example, an investigator has a plan to compare the accuracy of MRI and CT in detecting abnormality. The accuracy of these two diagnostic tests are usually calculated on the same subjects (i.e. each subject undergoing two alternative diagnostic tasks) for the purpose of the efficiency of design. Let us suppose AUC₁ and AUC₂ are the accuracy of MRI and CT respectively. The null and aletrnative hypothesis H₀: AUC₁ =AUC₂ versus H₁: AUC1≠ AUC2.

Using the normal approximation under the null hypothesis, the Z-score is as follows

 $\mathrm{Z}=\left(\right(\mathrm{AUC})\mathrm{ ̂\_1}-(\mathrm{AUC}\left)\mathrm{ ̂\_2}\right)/\mathrm{SE}\left(\right(\mathrm{AUC})\mathrm{ ̂\_1}-(\mathrm{AUC}\left)\mathrm{ ̂\_}\right(2\left)\right)$

Where

$\mathrm{SE}\left({\widehat{\mathrm{AUC}}}_1-{\widehat{\mathrm{AUC}}}_2\right)=\mathrm{Var}\widehat{\mathrm{AUC1}}+\mathrm{Var}\left(\widehat{\mathrm{AUC2}}\right)-2\mathrm{cov}(\widehat{\mathrm{AUC1}},\widehat{\mathrm{AUC2}})$

$\mathrm{Cov}\left(\widehat{\mathrm{AUC1}},\widehat{\mathrm{AUC2}}\right)=\mathrm{r\; SE}\left(\widehat{\mathrm{AUC1})}\mathrm{SE}\right(\widehat{\mathrm{AUC2})}$

where r and SE denote the correlation between two AUC’s and standard error of each AUC. If the two diagnostic tests are not examined on the same subjects, obviously the two estimated AUC’s are independent and the covariance term would be zero. The SE ($\widehat{\mathrm{AUC1})}$ and SE$\widehat{\left(\mathrm{AUC2}\right)}$ can be estimated using Hanley and McNeil formula (5) but it does not give the covariance between the two$\widehat{\mathrm{AUCs}}$. However, the advantage of Delong method is that the covariance between two correlated AUC can be estimated from its components of variance covariance matrix as well (37). In addition, the CORROC software as developed by Metz et al. also provide the correlation and thus, the covariance between the two correlated AUC’s is in the parametric approach (20, 39).

Spectrum and Bias

The defects in designing of diagnostic studies concern spectrum and bias. Spectrum means to what extend the range of patients or controls be adequate. A broad spectrum of case and control are required to evaluate the accuracy of specificity and a broad spectrum for accuracy of specificity. For example, the case should be recruited with pathologic spectrum both for the local and metastatic and extend the histology. Thus, the clinical spectrum of disease should include varying degrees of severity. The second type of design defect is bias. The bias leads in a falsely low or high sensitivity/specificity and thus results in a falsely low or high AUC. The bias in diagnostic assessment has been manifesting in different ways. For example, work up bias means the results of work up has been affected by extensive subsequent “work up” i.e. further diagnosis procedure leads to the increase of the chance of diagnosis. Non-blind design (i.e. the person makes a decision and interpretation of test results) is aware of the status of case and control when the test result is in a matter of subjectivity. Incorporating bias means the test results are actually incorporated as a part of evidence used to make diagnosis (13, 40).

Confounding Issues

In designing a diagnostic study, a covariate incorporates a role of confounder if it has been associated with both disease status and test results (41). For example, if the distribution of age is incomparable between case and control and age is associated with test results, then age could be a confounder. The confounder leads the location of ROC curve deviates from its true location in ROC space. Thus, it results over or under estimate in ROC diagnostic accuracy. Restriction and matching in design and using adjustment methods in statistical analysis help that confounding be prevented. For example, if age is a confounder, then stratified ROC curve with age (<60 years and ≥60 years) and combining the stratum specific AUC with some weighing approach yields a valid estimate of AUC. An attempt has been focused for covariate adjustment by regression model in ROC analysis, but the approach was not used widely in medical literature perhaps because of lack of availability of software by clinicians in the literature of diagnostic test evaluation (42). ROC analysis is also involved with several other methodological aspects, such as model selection to derive ROC curve, the choice between parametric and nonparametric approaches, multiple reader variations in subjective interpretations, presence of errors in gold standard assessment or even the absence of gold standard and the methods for adjusting confounding. The interesting readers are referred to some published articles in this context (43-50).

In summary, despite the fantastic feature of ROC analysis in diagnostic test evaluation and the meaningful interpretation of AUC and its asymptotic properties, a proper design with broad spectrum of case and control and avoidance of bias and control for confounding are necessary for a valid and reliable conclusion in the assessment of performance of diagnostic tests. Spectrum and bias should be considered with careful consideration in study design while confounding can be controlled in analysis as well. While the adjustment of confounding is widely used in etiologic studies in epidemiology, a little attention has been focused for the control of confounding in ROC analysis of medical published diagnostic studies.