Network representations and methods for the analysis of chemical and biochemical pathways

Abstract

Systems biologists increasingly use network representations to investigate biochemical pathways and their dynamic behaviours. In this critical review, we discuss four commonly used network representations of chemical and biochemical pathways. We illustrate how some of these representations reduce network complexity but result in the ambiguous representation of biochemical pathways. We also examine the current theoretical approaches available to investigate the dynamic behaviour of chemical and biochemical networks. Finally, we describe how the critical chemical and biochemical pathways responsible for emergent dynamic behaviour can be identified using network mining and functional mapping approaches.

Introduction

Determining the minimal chemical interactions underlying dynamic behaviour of biochemical systems is a major task of modern systems biology.¹ Many studies have shown that the dynamic behaviour of biochemical systems is driven by the underlying network structure as well as small subnetworks of interacting components, known as network motifs.^2-6 To perform such studies, it is necessary to translate chemical and biochemical mechanisms into a network representation.

A network representation of chemical reactions is an abstraction. It facilitates analysis of reaction dynamics, especially in very large networks, and permits doing so without use of sophisticated computational techniques and resources. There are a number of network analysis methods^{7, 8} and motif detection tools^9-11 available in the literature to investigate the dynamic behaviour of biochemical systems. However, determining the true dynamic behaviour of a biochemical system, and the network motifs controlling these dynamics, remains a challenge. The results of network analysis methods and motif detection tools are dependent upon the network representation adopted for the biochemical system under investigation. Moreover, mainstream methods for motif identification rely implicitly on assumptions that may be incorrect for certain biochemical systems.^12-14

In this review, we present a detailed discussion of network representations of chemical and biochemical reactions. We illustrate how the four most common network representations convey different aspects of reaction mechanisms and illustrate which representations sacrifice information for practical advantage. We present a critical discussion of network methods for analysis of the dynamic properties of chemical and biochemical pathways. We also discuss current approaches available for the identification and selection of network motifs as well as provide a discussion of their limitations. Finally, we illustrate how the critical chemical and biochemical pathways responsible for emergent dynamic behaviour are identified using network mining and functional mapping approaches in the systems biology literature.

Reaction kinetics describe dynamic behaviour of interacting chemical species

A complex reaction mechanism can be represented by a set of elementary chemical reactions which are easily translated into mathematical terms using physicochemical relationships. The schematic representation of reactions captures the interactions between reacting species and products. For example, the homo-dimerisation of species to synthesise species is represented schematically by:

$$A+A\stackrel{k}{\to }B$$ (1)

In this chemical equation, there is a local chemical interaction between two species of A that produces species B with a reaction rate k[A]². In this expression k is a rate constant. The rate of consumption of species A - governed by the law of mass action - is represented in mathematical terms as an ordinary differential equation (ODE) of the form:

$$\frac{\mathrm{d}A}{\mathrm{d}t}=-2k{\left[A\right]}^2$$ (2)

The negative reaction rate implies that the concentration of A, denoted [A], declines over time; the reaction rate will increase as [A] increases. Using the law of mass action, the reaction dynamics depend on the rate constants, reactant concentrations, and molecularity.

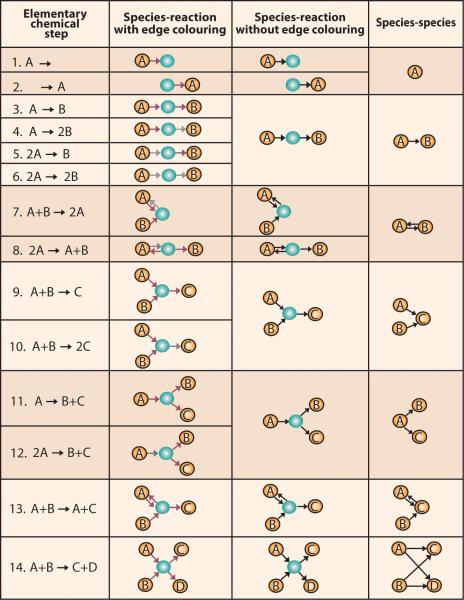
In chemistry, elementary steps represent chemical equations that have uni- and/or bimolecular reactants and products (Fig. 1, first column). A reaction mechanism is composed of a set of elementary steps, each representing an actual molecular event.

Fig. 1. The three most common network representations of elementary chemical steps.

In the first fourteen, realistic elementary chemical steps between two species are shown. The elementary steps are represented as species-reaction networks with edge colouring in the second column. Species-reaction networks with edge colouring provide a one-to-one relationship between chemical steps and network representations. In the third column, species-reaction networks without edge colouring reduce the number of network representations by losing stoichiometric information. The reduction in the number of networks introduces ambiguity in the network representation. Species-species networks reduce further the number of network representations by representing multiple chemical steps with the same network presentations (fourth column). In the species-reaction networks, orange nodes represent species and green nodes represent pathways. In species-reaction networks with edge colouring (second column), a red arrow represents a stoichiometry of one while a grey arrow represents a stoichiometry of two. In the species-reaction network without edge colouring (third column) and the species-species network (fourth column), the black arrows present connections regardless of stoichiometry.

Overall reactions (e.g., 3A → B) summarise reaction mechanisms that describe several elementary steps (e.g., A + A → 2A + A → B). Network representations and network analysis tools¹⁵ can provide powerful approaches for investigating reaction dynamics associated with both elementary steps and overall reactions.

Network representations of biochemical systems

Networks are comprised of nodes connected by edges. In graph theory, networks are often represented with weighted edges. The systems biology definition of a network is broader and includes a variety of graphs.¹⁶ The nodes in a network generally represent biochemical components. Some examples include: genes and proteins in a transcription network; substrates, enzymes, and products in a metabolic network; and amino acids in a network representation of a folding protein. Interactions between components are represented by edges connecting the nodes. Examples include: activation of gene expression by a protein; product formation via a substrate and an enzyme; and electrostatic interactions between nodes in an amino acid network. Chemical or biochemical networks are static representations of the dynamic interactions of different species that occur in time and space. There are four commonly used network representations, which are widely used to investigate chemical or biochemical reactions: species-reaction with edge colouring, species-reaction without edge colouring, species-species, and species-interaction networks.

Species-reaction networks

Species-reaction networks are often used to represent overall chemical reactions. They contain two types of nodes and have either single or multiple edges (see Fig. 1). The edges can be directed or undirected.³ In these networks, one type of node is used to represent chemical species while the other type is used to represent interaction between species. Edges connect species and interaction nodes. Species-reaction networks are bipartite graphs where two nodes of the same type are never connected directly. Edges connect reacting species nodes to interaction nodes. Interaction nodes are then connected to newly produced species nodes. These network representations are advantageous because edge colouring captures molecularity of the reactants (Fig. 1, second column). In other words, species-reaction networks provide a one-to-one representation of the reaction when edge colouring is employed to capture the molecularity of interacting species. For large reaction mechanisms, this network representation can be difficult to implement and is computationally expensive to analyse. This issue can be resolved by representing the networks without edge colouring (Fig 1, third column). The removal of edge colouring can produce ambiguous network representations. For example, the same species-interaction network without edge colouring is obtained for elementary steps 3, 4, 5, and 6 (Fig. 1, first and third column). Thus while the representation gains computational feasibility, information is lost during translation. Whether the model remains suitable without edge colouring depends on whether the sacrificed information, in this case molecularity, is relevant to the application at hand.

Species-species networks

Species-species networks are commonly used to represent metabolic and transcription pathways.^{6, 17} These networks have one type of node representing chemical species (see Fig. 1, last column). They have directed or undirected edges representing interactions between species. In metabolic networks, species-species networks are called substrate networks because they describe enzyme catalysed reactions where only the substrate and product are shown in the network representation. Species-species networks contain less chemical information than species-reaction networks. As a consequence, complex biochemical pathways are much simpler to write as species-species networks. The simplification again occurs at the cost of introducing ambiguity into reaction representations. As can be seen in Fig. 1 (last column), the majority of elementary steps are represented by the same species-species network. This indistinguishability problem is also observed in the mathematical representation of chemical and biochemical reactions.¹⁸ In the case of species-species networks, the indistinguishability is the result of losing the node representing the interaction between chemical species. For example, elementary chemical reactions 7 and 8 (in Fig. 1), have unique representations using species-reaction networks (with and without edge colouring) but are represented by the same two-node species-species network.

Species-interaction networks

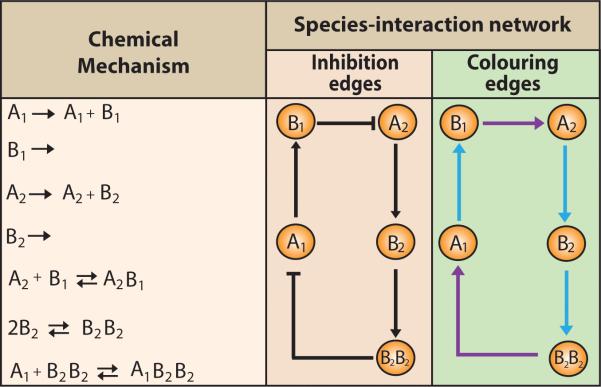
Finally, species-interaction networks are commonly used to represent protein-protein interactions (Fig. 2). A species-interaction network is comprised of one type of species node and multiple types of edges representing different interaction types. Protein-protein interaction networks have two types of edges, inhibition (Fig. 2, second column, blunt arrowheads) and activation (Fig. 2, second column, broad arrowheads), which describe the relationships between the protein nodes. The nonlinear dynamics of biochemical pathways arises from activation or inhibition feedback cycles in which the output of a pathway is not proportional to its input.¹ Species-interaction networks simplify complex inhibition or activation mechanisms into edge representations. The graphical representation of edges can be achieved by adopting different colours for each type of interaction. For example, in Fig. 2, last column, blue edges represent activation and purple edges represent inhibition. Like species-species networks, the species-interaction networks can also provide ambiguous representations. Additionally, it is difficult to represent complex mechanisms composed of numerous elementary steps via this approach. In the case of biochemical pathways, species-interaction networks can represent upstream or downstream indirect interactions between two species as direct relationships.

Fig 2. Representation of a mechanism using two species-interaction networks.

In the first column, a mechanism is represented through several elementary steps. In the second column, the species-interaction network representation shows the inhibition and activation interactions of the mechanism. Note that multiple pieces of information are missing from the species-interaction network with inhibition edges: the stoichiometry of the B₂ dimerization, the self-loops, and the degradation of B₁ and B₂. In the third column, species-interaction network representation using edge colouring of the mechanism is shown. Both species-interaction network representations are identical. The difference lies in the edge representation. In the species-interaction network with edge colouring, the purples edges represent inhibition and blue edges represent activation.

The above network representations do not provide explicit information about reaction rates. This makes it difficult to analyse the dynamic behaviour of chemical and biochemical pathways. However, in the next section we describe how existing network analysis methods can be used to investigate the dynamic behaviour of networks without prior knowledge of the reaction rates.

Network analysis methods for investigating the dynamic behaviour of chemical and biochemical systems

Biologists and biochemists have used mathematical modelling to analyse the properties of chemical and biochemical reaction networks for quite some time. Dynamical systems theory can be used to investigate behaviour of models by analysing the linear stability of steady states (or equilibrium points). If it is possible to identify all steady states and determine their linear stability, then model behaviour around steady state can be characterised.¹⁹ In the mathematical literature, a model with more than two steady states is known as multistable.²⁰ If the stability of steady states cannot be determined, models capable of exhibiting multiple steady states are known as multistationary dynamical models.²¹ In general, the nonlinear differential equations governing chemical and biochemical systems are difficult – if not impossible – to solve analytically. Therefore numerical methods are required to investigate the dynamic behaviour of chemical and biochemical systems.²² Steady states can be estimated using algebraic topology methods, such as homotopy.²³ These methodologies often require an educated guess for the values of model parameters, as well as access to high performance computing facilities to carry out an extensive search of the model's parameter space. In the absence of model parameter values, network analysis methods exist for investigating the dynamic behaviour of chemical and biochemical systems.

In recent years the focus of dynamical system and network analysis approaches has been to investigate the design principles of complex networks of genes and proteins.^{1, 24, 25} Special attention has been paid to the identification of the two- or three-node subnetwork cycles, referred as motifs, which appear frequently in mechanisms associated with certain biochemical functions.^{1, 26, 27} In these approaches, a motif's functionality can be analysed using mathematical modelling and dynamical systems theory.²⁶ Since complex networks contain many species and motifs, a significant portion of systems biology research is aimed at analysing models using combinations of network feedback cycles. In this section, we discuss a variety of methods for analysing networks with single or multiple feedbacks that are capable of exhibiting complex dynamic behaviour, such as oscillations, Turing instability, or bistability.

There are two primary approaches for studying network dynamics that also identify criteria for the existence of multiple stable steady states using species-reaction networks with edge colouring: Stochiometric Network Analysis (SNA)^{4, 28} and Chemical Reaction Network Theory (CRNT)^{2, 29}. It should be noted that, in the mathematical literature, edge colours are replaced by edge weights that correspond to stoichiometric coefficients. This encoding simply makes computational analysis more tractable.

Stochiometric Network Analysis

SNA identifies a minimal set of reactions capable of exhibiting multiple steady states (multistability) or oscillations within a large chemical reaction mechanism.^{28, 30} In this way, SNA allows for the reduction of a complex network into a smaller (but often still large) set of interactions underlying system-wide behaviour. In general, applying SNA theory involves first isolating the core set of network interactions underlying the system-wide steady state behaviour, and second, assessing the reduced set of interactions for criteria necessary for multiple steady states. Through application of the SNA methodology, the chemical and biochemical complexity is reduced without loss of system-wide dynamic behaviour. SNA theory is most applicable to reactions with mass action kinetics represented by species interaction networks with colour edges (see Fig. 1, Column 2).

A similar theory to SNA was independently developed by A. Ivanova.^{31, 32} In this case, mass-action kinetics reactions are again represented by species-reaction networks with edge colouring (or equivalently the directed edges are weighted by the stoichiometric coefficients). A feedback cycle in a network is a subnetwork where each species node is the beginning and end of a path. The path may not always follow the direction of edges and, in the case of a species-reaction network, the cyclic path contains an equal number of reaction nodes because between any two species nodes lies a reaction node. If two species in a species-reaction network interact at a reaction node, we refer to it as a consumed species path (○→●←○); and, if a species is produced in an elementary step by another species, we refer to this combination of species and edges as a produced species path (○→●→○). A cycle in a species-reaction network is then constructed by consumed or produced species paths. Based on the number of consumed species paths, a cycle presents a positive feedback if it contains an even number of consumed species paths (see Fig. 3, 1a and 1b). A cycle represents a negative feedback if it contains an odd number of consumed species paths (see Fig. 3, 2a and 2b). It has been shown that the existence of a positive feedback cycle is a necessary condition for multistability in different network representations.^{20, 21} Moreover, in the SNA theory and the theory of A. Ivanova, this multistability condition is further generalised to the existence of a subnetwork of species-disjoint cycles and edges (different cycles and edges contain different species) with an odd number of positive cycles. We will refer to this type of subnetwork as a critical subnetwork since its existence in a species-reaction network is necessary for the corresponding dynamic model to display multistability.

Fig 3. Representation of positive and negative feedback cycles using species-reaction network without edge colouring.

Positive and negative feedback cycles in species reaction networks are constructed by consumed species paths (○→●←○) and produced species paths (○→●→○). A positive feedback cycle has an even number of consumed species paths (1a and 1b) and a negative feedback cycle has an odd number of consumed species paths (2a and 2b). Note that the direction of the arrows in the consumed species paths is ignored.

One disadvantage of the theory developed by A. Ivanova is that mass conservation of all species is required in order to apply the technique. Mincheva and Roussel³³ removed this requirement using bifurcation theory arguments. Additionally, they showed that the existence of a critical subnetwork of species-disjoint cycles that does not contain all species can indicate that the dynamical model is capable of oscillations.

Many models in cell and developmental biology assume spatially homogenous concentrations of the biochemical species. However, cells can be viewed as reactors that are not well stirred since some biochemical species diffuse differently between different cellular compartments.³⁴ Moreover, spatial diffusion processes are important for the proper functioning of cell and developmental systems. For example, they are essential for polarity and pattern formation in morphogenesis. The first mathematical model of pattern formation was proposed by Alan Turing in 1952. It has been shown that Turing patterns develop when a stable spatially homogenous steady state, in the absence of diffusion, becomes unstable in the presence of diffusion.³⁵ This type of phenomena associated with instabilities of a steady state induced by diffusion is referred to as Turing instability. Remarkably, the existence of the same type of critical subnetwork – as in the case of oscillations – is necessary for the dynamic model with diffusion to exhibit Turing patterns.³⁶

Biochemical models with time delays are used for modelling genetic networks containing subsystems that are too complex to be explicitly included in the model. Transcription and translation processes are prevalent examples. Additionally, transport, diffusion, and signal transduction processes can also introduce time delays in biochemical dynamics.^{37, 38} Moreover, many models of biochemical systems can reproduce experimentally observed oscillations only if the delays are included in the model. If a steady state of a delay-differential model is stable when the delays are zero, and there exist positive values of the delays for which the steady state becomes unstable, then delay-induced oscillations occur. Usually the reason for delay-induced oscillations is related to the existence of a negative feedback cycle.³⁹ The necessary condition for mass action kinetics models with time delays to exhibit delay-induced oscillations is generalised to the existence of a subnetwork of species-disjoint cycles and edges containing an odd number of feedback cycles, of which an odd number are negative.⁴⁰

Chemical Reaction Network Theory

CRNT also uses a mathematical approach to determine relationships between species-reaction networks with edge colouring and dynamic behaviour of mass action kinetics reactions.^{2, 29} One application of CRNT is to exclude networks that do not have the capacity for multiple positive steady states. In the context of CRNT, if a species-reaction network with edge colouring and undirected edges is employed, complex pairs (c-pairs) are defined as pairs of species “entering” (with respect to the chemical reaction) the same reaction node. By determining the number of c-pairs in a feedback cycle, we can classify cycles as even cycles containing an even number of c-pairs and odd cycles containing an odd number of c-pairs. Even and odd cycles are similar to the positive and negative cycles, respectively, as defined in SNA theory. CRNT theory allows for the exclusion of multistable networks by checking for the following network conditions: if all stoichiometric coefficients equal one and all cycles are odd, or if no two even cycles contain exactly one common edge of a c-pair (following Craciun et al.³ no two even cycles split a c-pair), then the network is not multistable for any parameter values of the rate constants. On the other hand, if the latter condition is violated, i.e., if two even cycles split a c-pair, then the reaction has the capacity for multistability.³ CRNT is implemented in the software Chemical Reaction Network Toolbox.⁷ This toolbox can be used to determine if a chemical reaction with mass action kinetics has the capacity for multistability. In some cases, the Toolbox will often provide example parameter values for a multistable network.

An advantage of CRNT is that it can be used to exclude networks that do not have the capacity for multistability regardless of parameters. This is often useful when analysing large numbers of networks, e.g. when enumerating possible reaction mechanisms (of some chosen size) underlying a chemical or biochemical system with observed multistable dynamics. By employing CRNT to exclude networks without the capacity for multiple positive steady states, one can significantly reduce the search space of possible multistable networks.³⁰ SNA and CRNT can identify networks capable of multistability in the absence of kinetic rate parameters. This useful identification capability has a caveat however. In most cases, the networks can only be identified as capable of multistability. It is much more difficult to identify specific steady states. Another disadvantage of CRNT and SNA is the exclusion of steady states with zero coordinates. In chemical and biochemical systems, it is quite possible that a component (e.g. a protein) could be completely depleted (e.g. degraded) from a system resulting in a stable steady state value of zero. Additionally, the mathematical theory underlying SNA and CRNT is sophisticated and rigorous, making it non-trivial to implement. Fortunately, software tools implementing these theories are available. Thus these network analysis approaches are accessible to scientists with expertise elsewhere than the mathematical theory.^{7, 8} As mentioned above, CRNT toolbox⁷ in some cases identifies kinetic rate parameters necessary to obtain multiple stable steady states. Overall, these tools provide a powerful way to investigate system-wide behaviour within a species-reaction network.

Examples of network feedback cycles critical for the dynamic behaviour of biochemical and biological systems

The theories discussed above are by no means exhaustive. We now select some examples to illustrate how positive or negative feedback cycles within complex networks have the capacity to display complex dynamic behaviours in biological systems. Some biochemical pathways exhibit a switch-like behaviour characterised by a sudden shift in the concentration of a species from low concentration to high concentration. One type of dynamic behaviour that can describe this phenomenon is bistability. In a bistable switch network, the system will have two stable steady states that are separated by a third unstable steady state.¹⁹ Depending on where the system begins (the initial condition), its solution may end up in one of the stable steady states. A simple example of a bistable switch is given by a network containing a positive feedback cycle (see Fig. 3, 1a and 1b) of two mutually activating or inhibiting interactions. In both cases, the positive feedback cycle can create a biological switch where the cellular response abruptly starts to decrease after an initial increase (one-way switch) and possibly increase again (toggle switch).²⁶ Examples of switch behaviour identified in biological systems include apoptosis (one-way switch)⁴¹ and the lac operon in bacteria (toggle switch).⁴²

Oscillations are another type of ubiquitous dynamic behaviour in biochemical networks.^{24, 43} Mathematical models have been used to study oscillations in calcium signalling,⁴⁴ glycolysis,⁴⁵ cAMP,⁴⁶ and in circadian rhythms.⁴⁷ Both positive and negative feedback cycles as well as their combinations can generate oscillations in biochemical networks. In the simplest case, oscillations can also be generated by self-activation, which is a positive feedback cycle from a species back to itself, also known as autocatalysis. Self-activation may be responsible for oscillations in glycolysis.⁴⁸ Examples of negative feedback oscillators in biological systems include circadian rhythms,⁴⁷ MAPK cascade²⁵ and NFΚB.⁴⁸

The subnetworks discussed so far primarily consist of a single two- or three-species positive or negative feedback cycles that participate as components of complex networks. However, in reality more complicated feedback mechanisms are frequently found in biochemical or biological systems. For example, the Cdk network that regulates the cell cycle can be decomposed into three simpler modules - the G1/S and G2/M modules, which are switches that arise from a positive feedback cycle, and the M/G1 module, which is an oscillator that arises from a three-species negative feedback cycle.^{49, 50} The oscillatory response curves created by the three-species negative feedback cycle interact with the bistable motif of the G2/M module generating a large amplitude periodic curve that is maintained until the cell size becomes too large. At this stage, the period of the oscillations drops dramatically and the cell divides into two.²⁶ CDK1 cell cycle oscillations in Xenopus are another example of a biochemical network with multiple feedback cycles.⁵¹ In this system, the oscillatory network contains both a negative and a positive feedback cycle. The negative feedback cycle creates the oscillations, while the role of the positive feedback cycle is to adjust the oscillation frequency without changing the amplitude. Another important advantage of the two-cycle network of CDK1 cell cycle in Xenopus, in comparison to a single-cycle network (containing only a negative cycle), is its robustness, i.e., the two-cycle network oscillates over a broader range of parameter values than the single-cycle network.⁵¹ This result highlights the importance of investigating bistability, oscillations, and other important dynamic behaviour as an aggregation of feedback cycles rather than a single feedback cycle.

The biological role of multiple feedback cycles in biochemical networks is still under investigation. In the example of oscillations in the cell cycle⁵¹ discussed above, the negative cycle is sufficient to create the oscillations while the role of the positive feedback cycle is to adjust the period. Some studies on circadian rhythms suggest that single-cycle models are not as robust or sensitive⁵² as multiple-cycle models.^{53, 54} Combinations of other subnetwork such as feedforward cycles associated with the detection and adaptation of network signals, or combinations between feedforward and feedback cycles, are yet to be studied.⁵⁵ The connections or the coupling between the feedback cycles and other subnetworks are also not thoroughly understood and are a matter of further research. In the next section, we discuss approaches for identifying network motifs. These motifs are associated with subnetwork cycles that constitute critical dynamic functions.

Mining for motifs in chemical and biochemical reaction networks

As we previously mentioned, motifs are subnetwork cycles which appear frequently in mechanisms associated with certain biochemical functions.^{1, 26, 27} A network motif is identified as a connected, induced subgraph that appears significantly more frequently than would be expected in a similar random network (e.g., the same number of nodes and edges). Since the number of possible subgraphs increases dramatically as the size of the subgraph increases, most research to date has focused on searching for subgraphs of two to four nodes.

Two methods are commonly used for identifying subgraphs as network motifs. The first method identifies motifs as the subgraphs occurring above a certain frequency threshold in similar networks.⁵⁶ A problem with this approach is that the higher frequency of a subgraph does not imply function.⁵⁷ Moreover, this approach does not provide a statistical significance level for the identification of a motif.

The second method is the normalised z-score of Milo et al.,⁵⁷ which identifies subgraphs as overrepresented or underrepresented motifs if they have z-scores values greater or less than zero, respectively. Normalised z-score permits a statistical comparison of a particular motif across different networks. It requires the generation of a set of physically realistic randomized networks for comparison, which can be difficult.⁵⁸ The use of normalised z-score has some drawbacks. The normalised z-score implicitly assumes that motif frequencies are distributed normally and candidate motifs are independent. Picard et al.¹³ found that the assumption of normally distributed motif frequencies is not always valid. Some networks exhibit motifs frequencies with a Poisson distribution.^{13, 59} The normalised z-scores are also dependent on network size as motif sizes increase.⁵⁷ Furthermore, empirical analysis of metabolic networks shows that motifs are dependent for a given set of random similar networks due to clusters and hierarchy in the structure of motifs.¹⁴

Despite its limitations, the mainstream approach to identifying network motifs is the normalised z-score method. However, if the assumption of normality is not tested properly in the networks under investigation it is unclear if normalised z-score has the capacity to differentiate effectively between spurious subnetworks and network motifs of true statistical significance. This is an active area of research in the network science community.

Motifs do not necessarily represent unique chemical reactions

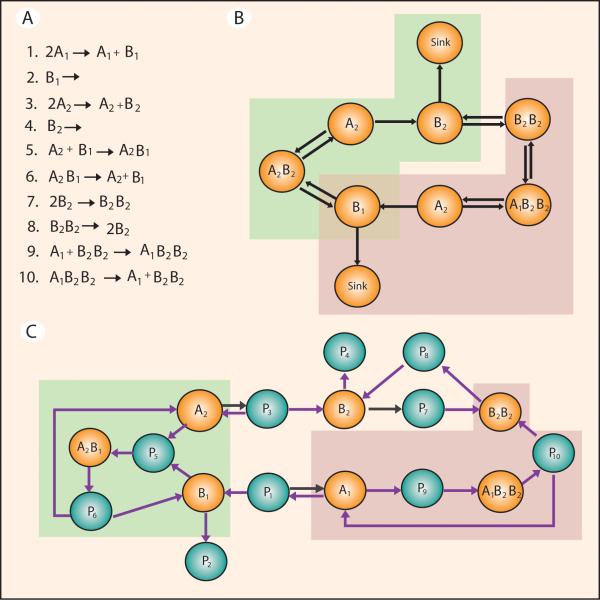
In practical terms, motifs are simple patterns of interactions between small numbers of species molecules. Therefore the chemical information contained in a motif depends on the network representation used for its pictorial representation. We can illustrate this point using a mechanism of gene regulation (see, Fig. 4A) with the capacity of exhibiting switch-like behaviour.⁶⁰ We represent the reaction mechanism in two forms: species-species network (Fig. 4B) and a species-reaction network with edge colouring (Fig. 4C).

Fig. 4. Identification of over-represented network motifs in a gene regulation mechanism.

Over-represented motifs are identified for two distinct network representations. FANMOD¹⁰ was used to mine networks for motifs using a random background of 1000 networks using local constraints. Nodes and reaction labels are provided but are not considered during motif mining. The overrepresented motifs are calculated using the normalized z-score.⁵⁷ (A) A mechanism of gene regulation with the capacity of exhibiting switch-like (bistable) behaviour is composed of ten elementary reactions. (B) Species-species network representation of the mechanism shown in A. Orange nodes represent species, and the black arrows represent interactions regardless of their stoichiometry. Motifs were mined using node colouring to generate random network background. The green and pink boxes highlight the chemical reactions represented by the two occurrences of the motif with the highest normalized z-score. (C) Species-reaction with edge colouring network representation of mechanism shown in A. Motifs were mined using edge colouring to generate random network background. Orange nodes represent species and green nodes represent interactions. Purple and black arrows represent reaction stoichiometry of 1 and 2, respectively. The green and pink boxes highlight the sets of reactions represented by the two occurrences of the motif with the highest normalized z-score.

The species-reaction network with edge colouring (Fig. 4C) is a one-to-one representation of the original gene regulation mechanism molecularity containing seven species nodes and ten reaction nodes. We mined the network for motifs of five nodes. A total of 68 overrepresented motifs were identified (motif mining approach is explained in the legend of Fig. 4). The highlighted subnetworks in Fig. 4C (green and pink blocks) represent a single motif with the highest normalised z-score (0.58). This five node motif appears twice in the network represented in Fig. 4C. It also appears an average of 0.86 times across a set of 1000 random networks with the same number of nodes and edges. Although the five node motif is the same for both coloured blocks, it represents two different sets of chemical reactions in each coloured block: reactions 5 and 6 (green block) and reactions 9 and 10 (pink block). Therefore it is always important to draw a clear distinction between a network motif and the chemical reactions it can represent.

In the case of the species-species network representation (Fig. 4B) for the mechanism of gene regulation under consideration (Fig 4A), it is not possible to draw a direct relationship between motifs and reactions. Nine motifs of size five nodes were identified as overrepresented in this network. The motif of size five with the highest normalised z-score (0.38) appears twice in the original network (highlighted in green and pink blocks). However, the overrepresented motif is not represented by a unique set of the chemical reactions. The motif in the pink block represents six reactions (1, 2, 5, 6, 7, and 8), while the motif in the green block represents four reactions (3, 4, 5, and 6). As we discussed before, the lack of a unique relationship between motif and chemical reactions in species-species networks is typical of this network representation.

The significantly overrepresented motifs identified in this subsection could have some functional significance in networks. In Fig. 4C, the overrepresented motifs with the highest normalised z-scores (green and pink boxes) are remarkably are bistable critical subnetworks. The motif coloured in green in Fig. 4C contains the critical subnetwork consisting of the positive feedback cycle (A₂B₁ → P₆ → B₁ → P₅) and the edge (A₂ → P₅) as well as the critical subnetwork consisting of the positive feedback cycle (A₂ → P₅ → A₂B₁ → P₆) and the edge (B₁ → P₅). We are not surprised by this result, because the network is a representation of a mechanism of gene regulation with the capacity of exhibiting switch-like behaviour.⁶⁰ However, in most of the cases, it is not possible to draw a direct relationship between a significantly overrepresented represented motif and a biochemical function. Mapping motifs to function is an active area of research in the chemical and systems biology community. In the next section we discuss some of the advances made in this area, and present network enumeration approaches which have been successfully applied to explore motifs in large network spaces.

An approach to explore the network space to map motifs to function

The fact that motifs are observed significantly more frequently than would be expected in a similar random network suggests an evolutionary origin. However, the higher frequency of a motif in a network does not necessarily imply that the motif is associated with a particular biochemical function.^61-65 A network motif could be a vestigial structure of the biochemical evolution of organisms.⁶⁶ To determine if a motif is associated to a function in a large space of chemical and biochemical networks, it is necessary to use both network analysis and motif mining methods.

In general systems biologists have typically mapped function to motifs on a case-by-case basis.^{1, 26} A limitation of this approach is that there could be an unidentified motif which could be associated to a particular function, but remains to be discovered. Moreover, this approach is ineffective for exploring a large network space.

With the advent of high-performance scientific computing, it is now possible to search through a large space of networks. Nowadays scientists are computationally generating a large space of possible biophysical-chemical realistic pathways,⁶⁷ and then testing them for their potential to exhibit particular biochemical functions.^{56, 60, 68-71} In this approach, scientists are asking: what are the possible networks that can exhibit a particular behaviour? Once the networks capable of exhibiting a specific behaviour are enumerated, relationships between structural network motifs and biochemical function can be systematically mapped (see, Fig. 5). The mapping is generally carried out by mining motifs in the networks capable of exhibiting the specific behaviour under investigation. This approach is known as network enumeration analysis.⁵⁵

Fig 5. Representation of a network enumeration approach to map network motifs to function.

In the first step, a large space of biophysical-chemical realistic pathways are generated computationally, and represented as networks. The goal is to investigate the network motifs responsible for the function z. The network space is expected to be composed of numerous network of distinct functions. In the second step, networks are selected by determining those capable of exhibiting the function z. The section can be made by analysing the network dynamics using dynamical system theory, or network analysis methods (such as CRNT). Once the networks capable of exhibiting function z are enumerated, the mapping between network motifs and the function z is carried out by mining motifs in the enumerated networks (third step). The motif responsible for the function z in all networks can be selected from the motifs with the highest normalised z-score across all enumerated networks.

In principle it is theoretically possible to generate a large number of biophysical-chemical realistic networks and exhaustively explore the parameter space of each network for a specific biochemical behaviour. However, evaluating each network is too computationally expensive to be practical. Consequentially, researchers have been adopting approximations to render motif mapping to biochemical functions in networks computationally feasible. In general, two compromises are adopted to make the calculations computationally feasible within reasonable timescales. The first compromise is limiting the size of networks to three nodes. In three-node networks, the first node corresponds to the signal or input, the second node is an intermediate, and the third node is the response or output.^{26, 70} This makes the network search-space computationally tractable as there are just over 16,038 possible architectures to explore.⁵⁵ The second compromise is limiting the exploration of the parameter space for all networks. In a three-node network, each node has several parameters which depend on the rate equations used to represent the governing behaviour of the network. If a node represents a substrate in an enzyme catalysed reaction, the parameters can be the substrate concentration, maximum velocity, Michaelis-Menten constant, Hill coefficient, or the enzyme activation coefficient. The common strategy is analysing each network by exploring 10,000 combinations of parameters within physiologically realistic range⁵⁵ using the Latin hypercube sampling method.⁷² These two simplifications have been successfully used to infer motifs observed in real biochemical pathways for switch-like (bistable) behaviour,⁵⁶ biochemical oscillations,⁶⁸ and perfect adaptation⁷⁰ in biochemical pathways. Biochemical pathways exhibiting perfect adaption transiently respond to a stimulus and then reset back to their original steady state. Perfect adaption is observed in many homeostatic and sensory systems.

Of course, the coarse-graining approximations made during the implementation of network enumeration analysis have some caveats. Limiting the analysis to three-node networks is a drop in the bucket given the combinatorial explosion of networks that is imaginable. It remains to be explored if the analysis of three-node networks can provide a comprehensive understanding of the networks motifs responsible for creating complex biochemical functions. On the other hand, the function of biochemical pathways may greatly vary with the rate equations and its parameters values. Therefore, there is always the risk that the sparse parameter sampling misses important emergent dynamic behaviour to map motifs to function. One way to determine if the parameter search has been exhaustively sampled is to evaluate the robustness of each network. In this context, the robustness of a network is defined as the fraction of the sampled parameters for which the network can perform the studied function above a certain threshold.⁵⁵ The analysis of the network robustness can provide a probability of finding the studied behaviour within the sampled parameter space.

It is possible to carry out an enumeration analysis to map network motifs to biochemical function in a free parameter manner. CRNT can be used to map the dynamic behaviour of mass action kinetics reactions and species-reaction networks with edge colouring. Recently Siegal-Gaskins et al.⁶⁰ determined the capacity for bistability of 40,680 simple gene regulatory networks (GRNs) that can be formed by two transcription factor-coding genes and their associated proteins. They found that ~90% of their GRN could exhibit bistable behaviour for a given set of parameters. The majority of the bistable network could only be identified as bistable through an original subnetwork-based analysis using CRNT. Interestingly only 11 of the 36,771 bistable networks identified lose bistability by the removal of any network reaction or node. These minimal networks were composed of three to eight node motifs which were essential for the bistable behaviour. In each one of the 11 minimal bistable networks, a positive or negative feedback loop played a critical role in controlling the bistable behaviour.

Remarkably, the mapping of network motifs to biochemical function through the network enumeration analysis suggests that there is unique and limited number of network motifs responsible for each type of dynamic behaviour in biochemical pathways.^{1, 55} These studies suggest that it may be possible to determine many different ways biochemical reactions can be configured to produce the emergent functional responses characteristic of cellular and physiological systems.

Conclusions and future challenges

During the past 40 years, network theory has been employed to analyse chemical reaction systems and biochemical pathways. Network representations of molecular interactions between chemical species facilitate the use of sophisticated analytical and numerical techniques developed by network theoretical approaches.

A crucial question that arises upon translating chemical and biochemical interactions into a network representation is whether the representation is accurate and whether any information is lost. In this critical review, we discussed the four most prevalent network representations for chemical and biochemical reactions: species-reaction with edge colouring, species-reaction without edge colouring, species-species, and species-interaction networks. We also discussed which representations introduce ambiguity during translation and why these losses of information can be advantageous in some instances. The representations themselves have distinct properties and different methods of representing the same information can be advantageous for distinct practical applications. Species-reaction networks with edge colouring provide the most accurate representation of elementary reaction steps (see Fig. 1, second column). This network representation is the ideal to describe and investigate the properties of reactions following mass action kinetics. However, the most widely used network representation is the species-species network. It is frequently employed to investigate the large organisational properties of genetic, protein, and metabolic networks.^{17, 73-76} The popularity of species-species network representation lies in its simplicity: chemical species are represented by nodes which are directly or indirectly connected to other species with edges. The trade-off for this simplicity is ambiguity since distinct types of molecular interactions (see Fig. 1, fourth column) generate identical representations.

Given the direct relationship between network representation and mass action kinetics in species-reaction networks with edge colouring, two methods – Stochiometric Network Analysis and Chemical Reaction Network Theory – have been widely used to investigate the dynamic behaviour of chemical and biochemical systems. These two methods allow identification of clearly distinct critical subnetwork classes capable of exhibiting specific dynamic behaviour, such as oscillations and bistability. However, the appearance of critical subnetwork classes in large chemical and biochemical networks is not sufficient to determine a dynamical function. Network dynamics can exhibit qualitatively different functions in distinct regions of the parameter space.⁶⁶ Therefore, one of the challenges in the identification of critical subnetworks with functional classes is determining the region of the parameter space that corresponds to distinct function(s). The most common strategy to determine the regions of the parameter space capable of exhibiting certain dynamical functions is sampling the network dynamics using large combinations of parameters.

We further discussed network enumeration approaches to map specific dynamical functions in large network spaces to simpler modules – known as network motifs. The theoretical analysis of the network space using network enumeration approaches suggest that there are certain networks motifs enriched in biochemical networks that are necessary for exhibiting regulatory functions, such as oscillations, or bistable switches. The results of these theoretical studies are supported by the experimental observations in biological pathways,^{1, 26} and synthetic biology reconstructions.⁷⁷ These studies suggest that there are some organisational principles in biochemical networks which could allow us to systematically organise network motifs in functional modules in the future.⁵⁵ An interesting challenge is investigating whether network motifs can be considered as modules that can be used to build more complex dynamical functions.⁵ A related fundamental problem is investigating whether a network motif remains functional when linked to other complex modules in large biological networks.

In practical terms, the systematic exploration of the network space to map motifs to biochemical function in biological networks may be of great utility in medicine, the pharmacology industry, and the nascent field of synthetic biology. A key to controlling disease is understanding the underlying mechanisms responsible for modulating the biochemistry of the health state and what mechanisms, such as blocking the expression of malfunctioning proteins, will yield desired functional changes. The approaches presented in this critical review also have potential for investigating the underlying network of the disease state, thereby facilitating treatment strategies to modulate network dynamics and restore function.