Mathematical modelling in nuclear medicine

Abstract

Modern imaging techniques can provide sequences of images giving signals proportional to the concentrations of tracers (by emission tomography), of X-ray-absorbing contrast materials (fast CT or perhaps NMR contrast), or of native chemical substances (NMR) in tissue regions at identifiable locations in 3D space. Methods for the analysis of the concentration-time curves with mathematical models describing the physiological processes and the appropriate anatomy are now available to give a quantitative portrayal of both structure and function: such is the approach to metabolic or functional imaging. One formulates a model first by defining what it should represent: this is the hypothesis. When translated into a self-consistent set of differential equations, the model becomes a mathematical model, a quantitative version of the hypothesis. This is what one would like to test against data. However, the next step is to reduce the mathematical model to a computable form; anatomically and physiologically realistic models account of the spatial gradients in concentrations within blood-tissue exchange units, while compartmental models simplify the equations by using the average concentrations. The former are known as distributed models and the latter as lumped compartmental or mixing chamber models. Since both are derived from the same ideas, the parameters are usually the same; their differences are in their ability to represent the hypothesis correctly, quantitatively, and sometimes in their computability. In this essay we review the philosophical and practical aspects of such modelling analysis for translating image sequences into physiological terms.

Introduction

As procedures used in nuclear medicine become increasingly elaborate and expensive in terms of time, space and personnel, it behooves us to ask how we can improve the yield of information from each test. Mathematical analysis of image sequences is a powerful tool, for it is a method of image enhancement that is designed to yield insight based on an understanding of the physiological processes underlying the raw observations. While the approach is most simply applicable to selected regions of interest in images from positron emission tomography (PET) and single-photon emission computed tomography (SPET), and X-ray computed tomography (CT), it can also be applied to magnetic resonance imaging. The physician’s objective in examining images from these various modalities is to ascertain the state of the tissue in anatomic or pathophysiologic terms. The virtue of analysing image sequences in terms of models is that it allows a translation from a set of single images related only be the observer’s eye and mind into an image (or a few images) representing the function or feature that one desires to identify. In this case “system identification” means that the display is expressed in terms of useful specifics, e.g. blood volume per millilitre tissue, flow per unit volume of tissue, or metabolic transformation rate in moles per gram tissue (Fleming and Goddard 1974; Peters et al. 1987; Andersen et al. 1988; Gambhir et al. 1989). Modeling is to construct an analogue that behaves like the real system (Berman 1963; Brownell 1968; Keinänen and Kuikka 1980; Bassingthwaighte and Goresky 1984). In the analysis of experimental data, the goal is to depict the dynamic behaviour of an organ or tissue under study. A model can be considered as a hypothesis to be tested against data; when data are of high quality, with good spatial and temporal resolution, then the hypothesis can be tested, evaluated and improved, an example of scientific evaluation. When data are low resolution, as in PET studies, one can use the models to estimate parameters, but not usually to test the model.

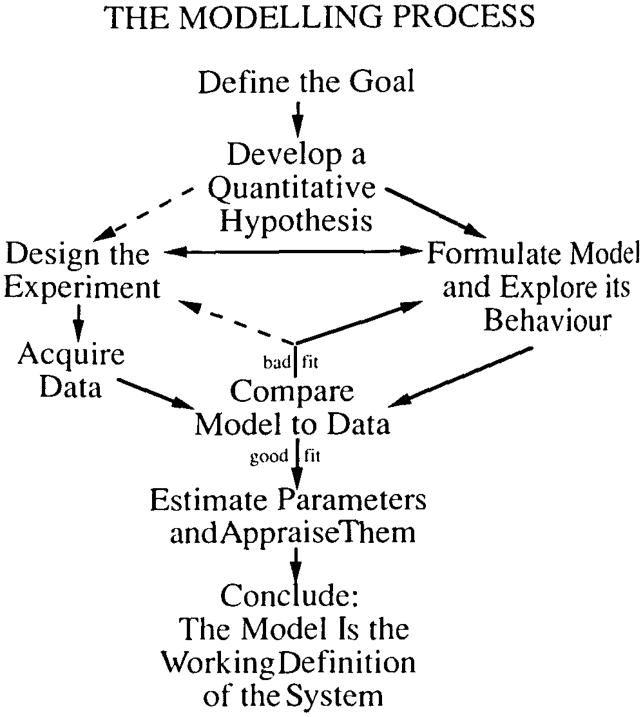
The objective is to derive dynamic information on flow and/or metabolic reactions and to interpret these data in physiological sense. An initial step is the formulation of the mathematical model (Fig. 1). The most critical step in model evaluation is the comparison of the response of the model, as represented by its mathematical formalism, with experimental data. If satisfactory agreement is obtained, then the model cannot be rejected. When different models are equally acceptable by the same criteria, one cannot choose between them from the particular data but must use other criteria. More discriminatory tests of the models must be devised. When model solutions differ systematically from high-resolution data, then the model (the hypothesis) is rejected; the next model is then devised, tested, and the process of evaluation repeated.

Fig. 1.

Diagrammatic presentation of the various features of model building. The objective is to determine the properties of the system under the study

A good fit of model to data is a failure to reject the hypothesis but a success is providing estimates of parameters such a flow, permeability or metabolic rate. The estimates are only as good as the model and are obtained from the best fit.

There is no such thing as true uniqueness in modeling: there is neither a “unique” model (because one can almost always find an alternative or a more detailed one) nor a “unique” fit of the model to the data (because the presence of noise or inexactness of fit always allows some range of confidence in the values of the parameter estimates). What Berman (1963) meant by “unique” was that there was some preferred model or parameter set, hopefully definable by specific criteria.

The study of living organs is sufficiently difficult that one is usually forced into making some assumptions, basing these wherever possible on previous physiological or anatomical observations. Moreover, the data obtained even by PET and other external detection techniques are degraded by scatter and reconstruction errors, giving rise to spillover from one region to another (partial volume effects). There is also dispersion or intravascular smearing of the tracers which may need to be corrected to find the “true” blood concentration-time curve at the input and which is needed to analyse the tissue (the residue) tracer concentrations (Budinger and Huesman 1985). When the input to the organ is known, the impulse response to the organ can be determined from the time course of tracer content within the organ by numerical deconvolution (Zierler 1965). Unfortunately, most deconvolution routines have inherent computational difficulties with noisy data and are not easy to implement. The usual strategy is to use the known input as input to the model (numeric or analytic) representing the impulse response function and thereby to convert a deconvolution problem to an initial value problem (Huang et al. 1980; Carson et al. 1983; Foster et al. 1988).

Tracers

Tracers must be chosen for specific purposes such as the estimation of tissue blood flow or rates of biochemical reactions (Feinendegen et al. 1981). The choice of radionuclides depends on capabilities for synthesis of specific compounds, the length of imaging time required and on availability. The selected radionuclides must be placed on to the substrates in such manner that there will be no interference with biochemical reactions to be observed. The biochemical fate of the tracers has to be known completely, and the effects of reactions which cannot be included in the model should be minimal.

Regional heterogeneities in tissue properties and functions

Spatial variation in regional blood flow within organs has been found whenever examined, e.g. King et al. (1985) and modern methods of analysis are beginning to account for this. We need also to look for heterogeneity in permeability, distribution volumes and metabolic rates (Cargill et al. 1988; Bassingthwaighte et al. 1990; Gonzalez and Bassingthwaighte 1990; Nelson 1990). We use the relative dispersion (which is the standard deviation divided by the mean and which is the coefficient of variation used by statisticians to describe the spread of the distribution of an observed property or function). Bassingthwaighte and Goresky (1984) have previously shown that if the spatial relative dispersion of regional flows is 40%, the myocardial capillary permeability-surface area products (PSs) for sugars are underestimated by over 30%. Flow heterogeneity can be approximated by dividing the region of interest into small voxels (sized from few millilitres down to tens of microlitres), thus estimating relative dispersion (i.e. standard deviation divided by the mean) at each of several “tissue” sample sizes. This allows characterization of the flow and distribution volume heterogeneity over a wide range of voxel sizes and, by a fractal analysis, approximation of the heterogeneity to be observed at the level of the functional exchange unit (Cargill et al. 1988; Bassingthwaighte et al. 1989a, b).

The input function

In modelling analysis the determination of the input function is most critical (Budinger and Huesman 1985; Bellina et al. 1990). The input may be in numerical form and need not be explicitly described in terms of a mathematical function. Usually the tracer bolus is given intravenously and not directly into the organ studied. Tracer particles travel slowly at the vessel wall and faster in midstream, causing intravascular dispersion and smearing of the bolus. Spreading of the bolus in an artery results in a standard deviation around the mean transit time of 20% (Bassingthwaighte 1966). In the lung the dispersion is twice this (Knopp and Bassingthwaighte 1969). Even if the input curve is measured from the arterial or heated venous blood samples, the external smearing due to the tracer dispersion in the limb vessels, in the catheter, and in the sampling system must be accounted for in the model analysis, a difficult deconvolution task (Dhawan et al. 1987; Iida et al. 1988). Moreover, the input function has to be corrected for recirculating metabolites and, in some cases multiple chemical species must be modelled simultaneously (Shields et al. 1990).

Impulse response of the model system for the organ

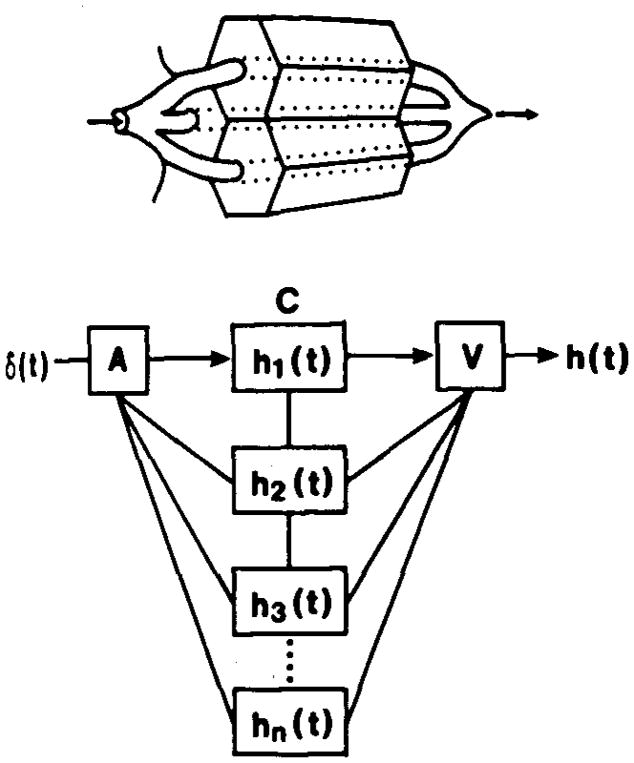
To permit applications of the model to experimental data, the impulse response function of the model system for the organ (frequency function of transit times), h(t), must be modelled so that the investigator could examine the whole system response to any form of input (Fig. 2). Assuming mathematical linearity and stationarity, the relationship between inflow and outflow is completely defined when h(t) is known by the convolution integral (Zierler 1965):

$$C_o(t)=C_i(t)\ast h(t)=\underset{0}{\overset{t}{\int }}{C}_i(s)h(t-s)ds$$ (1)

where the asterisk denotes the process of convolution and s is a dummy variable for integration.

Fig. 2.

The multicapillary model is composed of a set of parallel, independent capillary tissue units, each of which has an impulse response h₁(t) to the input δ(i) and relative plasma flow f₁. The residue content of a tracer in the tissue is the integral of the difference between the amount of a tracer entering and leaving, and in this illustrative case in which the input is a delta function: $R(t)=1-\underset{0}{\overset{t}{\int }}h(s)ds$. A = artery, C = capillary, and V = venula; and h(t) is the summarized impulse response at the venous end

There are more important properties of h(t) which have useful physiological information. If no tracer is lost, utilized or recirculated the areas of C_i and C_o are equal, and F times the area equals the dose injected. The first moments after injection give the mean transit times which are the average times of the tracer particles spent in a given part of the system:

$$t_h=t_o\sim t_i=V_{\text{dist}}/F$$ (2)

where t_o and t_t are the mean transit times for C_o and C_i and V_dist is the volume of distribution for the tracer in the system. These operational equations can be used independently of any model.

There are several simple models to study transcapillary passage and capillary tissue exchange of tracer. A general approach to describe intravascular transport of a tracer through the organ is based on the Stewart-Hamilton principle (Stewart 1897; Hamilton et al. 1931). A brief bolus of tracer of amount q_o is injected into the arterial inflow and the concentration time curve resuiting in the outflow is C(t). Given that it all emerges, then the impulse response of the organ to this tracer, h(t), is approximated by:

$$h(t)=F/q_{o}C(t).$$ (3)

The time integral of impulse response function is unity, and thus the time activity curve, can be used to calculate the flow F:

$$F=q_o/\underset{0}{\overset{\infty }{\int }}C(t)dt.$$ (4)

Time activity curves of tracers which remain intravascular (e.g. albumin) are widely used to calculate organ blood flow (Donato et al. 1962; Mullani and Gould 1983; Britton et al. 1985; Peters et al. 1987), but do not give direct information on exchange rates or metabolism.

Fick (1870) developed an equation which can be used to calculate the amount of a substance transported from the circulation to the tissue in steady state:

$$dQ/dt=-F[C_i-C_o],$$ (5)

where C_i and C_o are the tracer concentrations at the input and output ends of the studied organ.

The net flux of tracer across the capillary wall between blood and tissue is given by the steady-state fractional extraction E = (C_i − C_o)/C_i times flow times the input concentration: flux, moles/second = EFC_i. Since this is a net flux, the difference between two unidirectional fluxes, from blood to tissue and vice versa, and provides a measure of the rate of utilization or trapping of the tracer. It measures what does not come back, and so is useful for trapped or metabolized tracers, but this flux does not give a measure of permeability or of the clearance via metabolic reaction. These require measurements of unidirectional fluxes, which are necessarily equal to or greater than net fluxes.

Consequently, the technique introduced by Crone (1963), based on the use of tracer transients, has special utility. Two tracers are injected simultaneously; their characteristics are chosen so that one serves as a reference for the other: a solute of large size serves as a marker of the intravascular transport since it cannot escape, and a molecule of metabolic interest which can permeate the capillary wall can be assessed relative to it. This led to the expression for the instantaneous extraction,

$$E(t)=[{\text{C}}_{\text{ref}}(t)-{\text{C}}_{\text{d}}(t)]/{\text{C}}_{\text{ref}}(t)$$ (6)

where the extraction, E(t), can be used a measure of the unidirectional flux from blood to tissue at early moments before there is any return flux from the tissue to the blood. C_ref(t) is the outflow concentration for the intravascular reference and C_d(t) is that for the permeant solute. From this Crone estimated the capillary permeability-surface area product (PS)

$$\text{PS}=-Fln(1-E).$$ (7)

The validity of this approach is greatest when the organ has uniform flows and other characteristics (Bassingthwaighte 1974; Rahimian et al. 1981; Paulson and Hertz 1983), and more advanced techniques have evolved since to account for organ flow heterogeneity and for both capillary and cell membranes (Rose et al. 1977; Kuikka et al. 1986).

The residue function

In theory, outflow detection and residue detection techniques provide equivalent information (Zierler 1965), but the two techniques have different degrees of accuracy for different parts of the system studied. One can more accurately correct external smearing of tracer in outflow tubing than to find the “true” attenuation, spillover and partial volume corrections of the external gamma detection. There are several possibilities to correct these, both theoretical and true measurements (Budinger and Huesman 1985; Brown et al. 1988). Counting statistics, N, is a limiting factor in residue detection, and with reconstruction error is about 4N^−1/2. Outflow samples can be counted with long time intervals to give statistical error less than 1% for the sample with the lowest radioactivity (Kuikka et al. 1986). However, residue detection and especially PET and SPET have the advantage that data can be obtained for multiple regions of the tissue, which permits examining regional heterogeneity of flow and/or metabolism.

The formal residue function, R(t), is the integral of the Q(t)in Eq. (5), i.e. when diffusible/permeable tracers arc used, the substance is exchanged between the capillary and the adjacent tissue, and the residue content Q(t) in the tissue is the integral of the difference between the amount entering and leaving:

$$Q(t)=F\underset{0}{\overset{t}{\int }}[C_i(s)-C_o(s)]ds.$$ (8)

After a short bolus injection and at any time before tracer recirculation the residue function is directly calculated from the system impulse response, h(t):

$$R(t)=1-\underset{0}{\overset{t}{\int }}h(s)ds.$$ (9)

However, in practice any delay and dispersion between the organ and the input distorts this relationship. The implicit assumptions to use the residue function such as in Eq. (8) in the study of capillary tissue exchange are that all of the tracer is in the organ at time zero, a moment after the injection, none having escaped, and that the time required to achieve the peak is negligible compared to the time course of washout. Under special circumstances one can estimate the intracapillary extraction from the residue function alone. The idea is that the intravascular unextracted component undergoes relatively little dispersion and delay, while the fraction which permeated the capillary wall washes out smoothly in pure monoexponential form. By fitting the tail with a single exponential and back-extrapolating to the time of the initial peak, the expectation is that the fractional height at that moment is the extraction, E (Sejrsen 1970; Hercovitch et al. 1987; Cherry et al. 1990; Herrero et al. 1990). This is a good idea only in special circumstances if the system consists of a capillary and ISF alone, as in the models of Sangren and Sheppard (1953) and Bassingthwaighte (1974); if the capillary PS is so low that washout becomes almost monoexponential, then reasonable estimates of PS may be obtained. However, this technique has not been shown in organs with flow heterogeneity to give good estimates of PS even at low PS.

Translating model equations into computational models

From the idealized expression of the “quantitative hypothesis” defining the “goal” in Fig. 1, the next stage is to formulate computable model equations in order to explore its behaviour. For any set of equations there are various ways in which they can be computed: examples are to use analytic solutions versus numerical solutions. For each analytic solution, there are usually several different ways of obtaining the string of values that describes the function; for a single exponential the answer can be obtained by performing the exponentiation at each time step, but an alternative is to calculate the first time step only, then calculate the ratio of one step to the next for evenly spaced time intervals and then to multiply by this ratio repeatedly to obtain the whole curve. In a similar way, to account for the input function, one can obtain the model impulse response (by whatever means) and then convolute this solution with the input function to obtain an estimate to the output function; the alternative is to use the input function in the computation of the model solution at each time step and there-by completely avoid the extra computation of the convolution.

All of these models are simplifications of reality. In formulating whole-organ models, one considers the observed data signal to be a weighted sum of several capillary-tissue units in parallel, as in Fig. 2. Interactions between the units are usually ignored. By this approach one accounts for flow heterogeneity, as if an observed pixel were a composite of grey and white matter in the brain, for example. Even seemingly homogeneous organs have normally a broad dispersion in regional flows; in animal studies this can be measured independently using the microsphere technique and the results used to define the flow heterogeneity in the model, thereby avoiding biased and often large errors in parameter estimates. We have not yet learned how to account for independent heterogeneities in other features of the tissue.

A generic model of a capillary tissue unit is shown in Fig. 3, from which erythrocytes have been omitted for the sake of simplicity. The viewpoint suggests a route for solute permeation (PS_g) through the interendothelialiefts, the route for small hydrophilic solutes, but which is effectively closed to albumin and larger proteins. Permeation through both sides of the endothelial cell is another possibility; from the interstitium the conductance into the parenchymal cells is given by PS_pc. The volumes are not free parameters, but are anatomic volumes modified to account for asymmetrical transport across the membranes and by intracellular binding and so become virtual volumes of distribution. The Ds represent dispersion or diffusion coefficients; in the compartmental form these are all set at infinity so that there is uniformity of concentration along the length. The Gs represent gulosities or clearances by transformation or consumption, and have identical units to the flow F or the PSs.

Fig. 3.

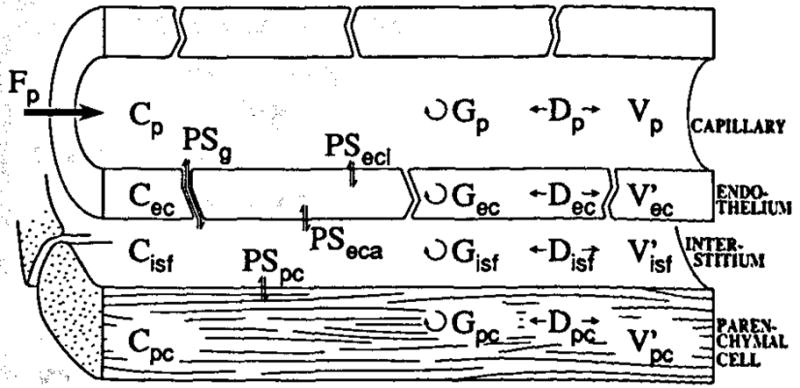
Schematic diagram of the three-barrier, four-region capillary tissue model. The model is composed of plasma at flow F_p and surrounding capillary endothelial wall, interstital fluid space, and parenchymal cell. The Vs are the volumes of distribution, PSs are the permeability surface-area products, Ds are the axial dispersions, and Gs are the intraregional reactions or consumptions. Concentrations of tracer in different spaces are given by C

For the convection-diffusion-reaction models used for image analysis, the standard approaches to obtaining solutions have been classed into two groups: distributed models and compartmental models. These are simply two different methods for getting numerical solutions. Having different methods of solution should not matter if the resultant forms of the model function are not different. For example, the sliding fluid element numerical method of Bassingthwaighte et al. (1989b) produces solutions within a small fraction of 1% different from the analytic solution of the analytic technique used by Rose et al. (1977), but is up to one million times faster for runs to fit data acquired over 3 min or longer, the trick was in using larger internal time steps and avoiding convolution integrations. Likewise, it would not matter if one computed exponents by repeated multiplies or by exponentiation, except for the time required. What does matter is whether or not the numerical representation does give the waveform defined in the “quantitative hypothesis”.

In the physiological literature, the use of compartmental models for flow and exchange problems has all but disappeared since the work of Sangren and Sheppard (1953), Renkin (1969), Zierler (1965, 1981), Crone (1963), Goresky et al. (1973) and Bassingthwaighte (1966). The reasons are two. Firstly, high resolution data cannot be fitted by compartmental models proving that they arc inadequate when you can test them against data. Secondly, they are based on the assumption of complete mixing along the length of blood vessels between the inflow and the outflow, an assumption that is proven incorrect by observations of the flow of radio contrast media through hearts or kidneys. The reasons for their persistence are basically that one cannot see from the time course of low-resolution residue functions obtained by SPET or PET or gamma imaging that the model solution is a poor fit and, secondly, that apparently useful results can be obtained with their computationally simple forms.

What is not commonly appreciated is that: compartmental models are merely mathematically poor representations of the same systems for which distributed models are used, and the numbers of independent parameters are exactly the same. (It is true that the users of distributed models to tend to use more complex models, for example accounting for both capillary and cell membranes rather than just the composite barrier, but this represents a more detailed hypothesis, and is a separate issue.)

Distributed and compartmental models compared

The basic difference between the distributed and compartmental models is that the former are designed to account for gradients in concentration along the length of the capillary and in the surrounding tissue. In the compartmental stirred tank model, the assumption of complete internal mixing has the corollary that there is a sharp discontinuity between the inflow concentration and the immediately adjacent capillary concentration, but there is no gradient within the tissue or at the outflow where the venous concentration is identical to that throughout the capillary. This sharp inflow discontinuity is intellectually offensive because it contrasts with what occurs in nature but, more importantly, is mathematically troubling because it distorts the waveform. This reduces the potential for considering the compartmental mathematics as adequate for the job of describing the anatomy and physiology. However, there is not a lot of documentation in the literature making this point; neither the Zierler article (1981) nor the Bassingthwaighte and Goresky (1984) review were published in places obvious to investigators in nuclear medicine, and there is no doubt that there is a need for specific examples of where such models succeed and fail.

One tool for making such comparisons is a model form which is a variant of the sliding fluid element algorithm of Bassingthwaighte (1974); it is the CTEX or compartmental capillary-tissue exchange version in which the capillary (and the surrounding tissue) is composed of a series of stirred tanks, accounting for the axial gradients in concentration and reducing the discontinuity at the inflow to a series of small discontinuities, one for each of the stirred tanks. Good numerical representation of the situation is obtainable by using 20 or 30 segments along the unit; comparison with the compartmental model can be made simply by reducing the number of tanks in the series to 1, without making any changes in the parameters. What is found is that the fits of the models to the data become poorer as the number of segments is reduced, and the values of the membrane conductances, the PSs, and the volumes and the consumption rates all change.

In real life some physiological parameters have gradients along the capillary length. Wiederhielm (1965) found that capillary permeability increased toward the venous end; accordingly, models have been devised to account for this (Bassingthwaighte 1974). Goresky et al. (1973) found in the liver that there were striking gradients along the hepatic sinusoid in trapped tracer galactose … virtually none reached the centrilobular vein. Most models do not account for these secondary effects since the influences on the residue functions and on the outflow responses are not great.

There is an extensive body of literature on these techniques which give exemplary applications. Compartmental approaches are covered by Berman et al. (1962), Sheppard (1962), Brown (1980), Carson et al. (1983), Godfrey (1983) and in most comprehensive detail by Jacquez (1985). The applications in nuclear medicine to describe biological processes have been covered by Berman (1963), Sokoloff et al. (1977), Huang et al. (1980), Gjedde and Christiansen (1984), Gambhir et al. (1987), Iida et al. (1988) and Herrero et al. (1990). Distributed modelling is covered in the specific references given in the preceding paragraphs, in extensive papers by Goresky and colleagues (1983), including those of Rose et al. (1977, 1980), Bassingthwaighte and colleagues, and the reviews by Bassingthwaighte and Goresky (1984) and by Keinänen and Kuikka (1980).

Limitations in modelling analysis

All of these models are incomplete, inexact, or just wrong in one way or another. The biology is never so precisely ordered that any model can be correct. Consequently, there is no basis for debates between users of different models where each claims that he has the “right way”. All models are compromises. The dicussion can then move to the higher plane, and centre on questions such as “Will this model formulation yield a correct, unbiased estimate of a metabolic transformation flux, within 5% error?”

In many studies, the purpose of estimating tracer uptake, or washout, is to estimate metabolic fluxes. Measurement of permeabilities of capillary and cell membranes is in such cases a secondary issue. When this is so, then it can be persuasively argued that the simplest and cheapest method of measuring metabolic flux is the method to choose. What one must then beware of is the temptation to think that the other parameters of the model solution are valid, even when the conditions for their validity are violated. An example is the use of fluorodeoxyglucose (FDG) for the estimation of the hexokinase-mediated phosphorylation of FDG. Because this reaction dominates the incorporation of the tracer fluorine-18 into a species pretty well retained in the tissue (at least in the brain the glucose-6-phosphatase is not highly active), the measurement of the flux is accurate within a few percent when using quite different models (compartmental or distributed types of various sub-forms). In the diagram of Fig. 3, this flux would be G_pc times C_pc. The different models give very different estimates of C_pc and G_pc, because the intracellular concentration C_pc is highly dependent on model form and thus on the values of the membrane PSs. The result is that none of the parameters of the model are reliably estimated, even though the flux is rather well estimated. The investigator however usually feels obliged to report the PSs and Gs since these are what the modelling provides and reporting the values gives a complete story about what the investigator has done. No one would say that this is an error, yet. The error comes next: the reader naturally tends to believe that the PSs and Gs are as valid as the fluxes, and the writer almost always fails to tell him that they are no good as physiological parameters. Thus we see the rate constants of the compartmental models, the ks which are mainly composites of PSs divided by Vs, reported and compared from one study to another. Here the case for multicapillary distributed models becomes stronger; the fact that these models can be fitted to high resolution data argues that the physical representation is more suitable, and raises one’s confidence in the reliability of these PSs. However, the generality remains that PSs and Vs are more model-dependent than simple fluxes which depend solely on mass balance.

As a generality one can say that the compartmental models are less erroneous when the obvious deviations from reality are smaller. When the arteriovenous difference for a solute is small, then the obnoxious discontinuity in concentrations between the inflow and capillary is small, and so one expects less error. Do not be mislead by this: it is not the steady state A-V difference for non-tracer mother substance that counts here, but it is the instantaneous extraction of the tracer relative to an intravascular reference solute that counts. The relevant concentration gradient that destroys the validity of the compartmental model is for tracer, not mother sub-stance. For glucose, the A-V difference across most organs is small, a few percent, because the net uptake is rather small. But the first pass tracer extraction in heart and brain is about 50%, a huge gradient, and so estimates of PSs and Ks by compartmental models tend to be much too high, sometimes by 2 to 4 times. Since the degree of overestimation depends on the actual conductances, the estimates are of limited utility and can be compared reliably for directional changes only when flows and metabolic fluxes are much the same.

The clearance concept for metabolic trapping of tracer

A general concept concerning steady-state tracer uptake by an organ or clearance from the blood is diagramed in Fig. 4 for one- and two-barrier models, a modification of Renkin’s diagram (1959). For both, the situation diagramed assumes total retention of all tracer that enters the tissue region farthest from the plasma space. For the two-barrier model there is bidirectional flux across the capillary barrier and unidirectional loss into the cell region. At low flow the clearance = flow, i.e. it is flow-limited, and all the tracer that is delivered is cleared from blood into the tissue. At the highest flows, extraction becomes a hyperbolic function of flow, flow × extraction = constant, and the clearance is governed by the barrier conductances. In the mid-range of flows, both F and PSs influence the uptake. The curvature in this intermediate regime depends on the model formulation. The physiology has an influence also, for recruitment will increase the PS. Therefore, different empirical equations are applied to define extraction for absolute quantification of flow (Mullani and Gould 1983; Herrero et al. 1990). The clearance applies to all model forms and is particularly useful when the return flux is small, as for brain FDG uptake or myocardial Rb uptake.

Fig. 4.

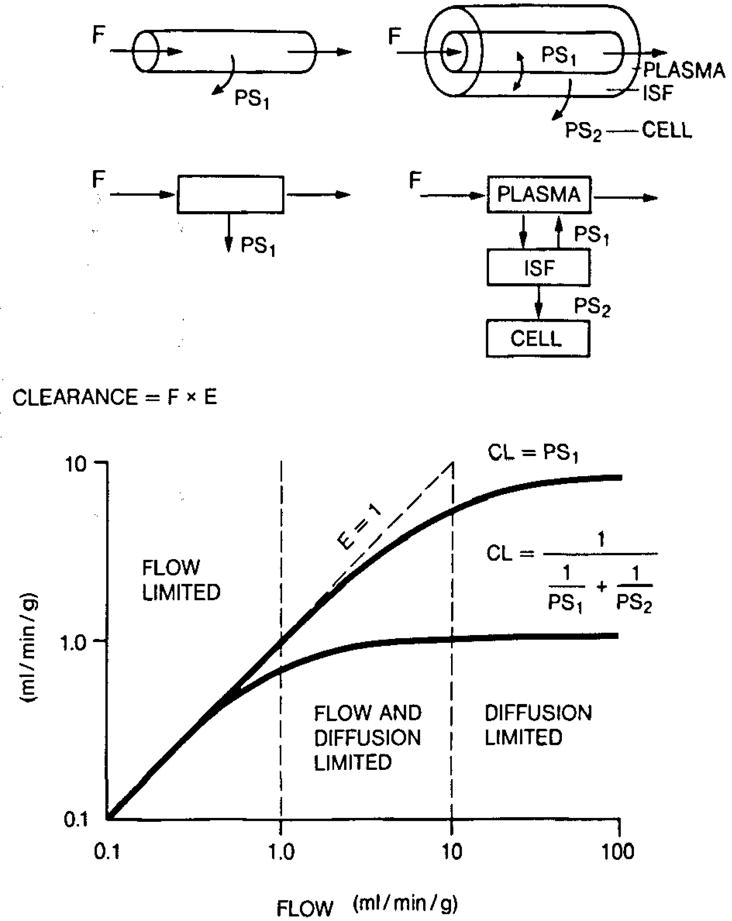
Clearance diagram for one- and two-barrier models with total absorption beyond the last barrier. Steady-state clearance CL = extraction × flow and can be given as CL= 1/(1/PS1 + 1/PS2). Note that for flow values greater than 1.0 ml/min per g there are smaller and smaller increases in clearance

For steady-state loss the compartmental models differ from the axially-distributed models. Traditionally in autoradiography and in PET and SPET modelling analysis investigators have considered tissues to be composed of a single cell type with a single barrier or no barrier between blood and tissue (Sokoloff et al. 1977; Gjedde and Christensen 1984; Herrera et al. 1990), but this oversimplification will not be necessary when models such as that in Fig. 3 become generally available in multicapillary, whole organ form. The drawback that the solutions of the partial-differential equations are complicated (Rose et al. 1980) has been overcome by the use of very fast numerical algorithms (Bassingthwaighte et al. 1989b).

A problem with PET and SPET data is that data are obtained from one tracer at a time. Since parameters are not so clearly identifiable with single tracer experiments, a series of runs with different tracers, characterizing separately the vascular and extracellular spaces is useful in enhancing the accuracy of parameter estimation with either compartmental or axially-distributed models.

An important concept helps us to deal with the inadequacy of single tracer data. It is to appreciate that other data on the same tissue must not be ignored when analysing the single tracer data. The data obtained from steady-state tracer experiments or from morphometry on the anatomic volumes of cells and interstitium and capillary volumes should be used as constraints on the modeling. While the values from another study may not be exactly applicable to the PET study, one can use one's judgement of the physiological situation to allow directed deviations from the anatomic data, and the constraints are very useful in increasing the accuracy of the estimates of the unknown parameters. Sometimes anatomic volumes are smaller than virtual volumes of distribution. For rubidium, which is concentrated in cells by the sodium pump, the volume of distribution in the cell, V_pc, will be approximately 30 times the anatomic volume. Thirty is the ratio of the intracellular to the extracellular potassium concentration and would apply if potassium and rubidium are handled identically by the pump. Obviously, such an assumption should be validated. When the sodium pump fails, for lack of ATP, then the volume of distribution must fall, but it cannot fall below the anatomic cell volume. Thus such ideas can be used in constraining the range of possible parameter values. The key principle is that when one cannot obtain all of the relevant data in the single experiment, it is vital to use what one knows of the anatomy and physiology from other studies.

Tools for computer simulation and fitting

Given the mathematical equations making up a model, it is essential that they are programmed and solved correctly. Solutions for sets of analytic equations (linear or non-linear) can be tested directly: by substituting a solution received back into the set of equations to see if they are satisfied. Solutions of differential or partial differential equations should be tested with smaller step sizes to see convergence or compared with other numeric methods. A valid model must have physiologically reasonable values for any parameters and have enough sensitivity, i.e. the model results must change when the parameter value is changed. On the other hand, a small change in a parameter value should not cause very large changes in the model behaviour. Moreover, a desirable quality in a model is that all or most of its parameters be identifiable in the time range where experimental data is available (Bellman and Åström 1970; Cobelli and DiStefano 1980; Godfrey 1983; Jacquez and Perry 1990). Particularly important is also the requirement that fundamental physical or chemical laws are not broken.

Table 1 shows a limited list of available non-commercial programs which have general utility. Some of these programs run relatively fast on modern microcomputers equipped with a sufficient amount of memory (> 2 Mb), with a hard disk and with 80386 + 80387 based processors or similar ones. Some, like SIMCON, are designed for workstations but can be run at PCs.

Table 1.

Some flexible, non-commercial software packages for modelling purposes

Program	Comments	Address for correspondence
SCOP & SCOPFIT	Needs TURBO C but works even in a PC-8086	National Biomedical Simulation Resource, Duke University Medical Center, Durham, NC 27710, USA
SAAM & CONS AMa	A massive software package; needs a 4 Mb memory. Runs under VAX, VMS or UNIX	Resource Facility for Kinetic Analysis, Center for Bioengineering, FL-20, University of Washington, Seattle, WA 98195, USA
BLD	Specially designed for PET under VAX, VMS or UNIX	Department of Nuclear Medicine NIH, Building 10, Room 1C-401, Bethesda, MD 20892, USA
SIMCON	Interface for interactive modelling under UNIX using FORTRAN or C	Simulation Resource Facility for Circulatory Transport and Exchange, University of Washington, WD-12, Seattle, WA 98195, USA

^aThe recent version is also available for PCs

For which purpose does one use modelling?

Model analysis is a complex procedure. It involves not only formal mathematics but also the investigator's intuition (Keinänen and Kuikka 1980). The modelling should be used to aid the intuition or to educate one to understand the dynamic behaviour of a system, which understanding we then call “intuition”. PET provides a unique tool to measure regional blood flow or metabolic events in vivo. However, the use of single tracer, or of a single image of the distribution of tracer at a given time, may not give good accuracy in measurements of metabolism. Dynamic studies with multiple tracers are needed for absolute estimation. A good strategy is to use a vascular tracer, an extravascular tracer and one for estimating intracellular metabolism. The one-site availability of tracers and the long duration of a study (hours) are strongly limiting factors. More work needs to be done on determining the least amount of data acquisition necessary for acceptable accuracy in estimating local tissue functions.

Mathematical modelling is used to interpret the data. Parametric imaging, the mapping of the regional estimates of particular parameters, is most useful in conveying a summary of the results to the investigator (Schad et al. 1990). The parametric image can be interpreted as a possible pathological finding against normal “landmarks”, as it “superimposes” the dynamic behaviour on the anatomy. Parametric imaging (Fig. 5) is generally used in nuclear ventriculography (phase and amplitude images), as well as in PET studies Gjedde-Patlak or k-value plots (Patlak et al. 1983). One likes to provide an image of the physiologic function (Sokoloff et al. 1977; Lammertsma et al. 1981; Gjedde and Christensen 1984; Farde et al. 1986). An important future approach will be the combining of the multiple indicator dilution method (Kuikka et al. 1986; Bassingthwaighte et al. 1989b) simultaneously with the PET tracer study. Since the presence of γ-emitting or β-emitting tracers does not interfere with the PET signal reconstruction, one can perform such rather definitive studies whenever a sequence of samples can be obtained by catheter from the venous effluent from an organ. Combining the multiple tracer technique with PET and analysing with axially distributed modelling is the ideal method, as it provides both high temporal and spatial resolution, as well as physiologically meaningful interpretation of data.

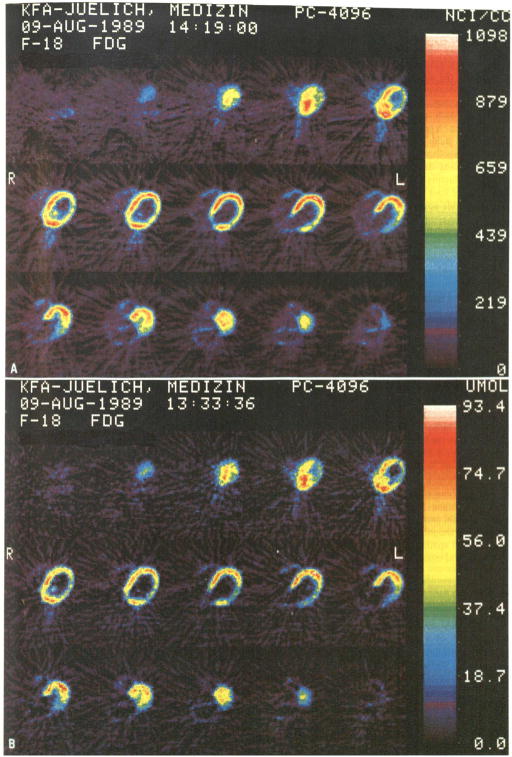
Fig. 5.

A, B .Dynamic PET investigation of the heart with FDG in a patient with myocardial infarction. Colour images of transaxial slices represent 18F concentration (A) and glucose consumption (B) in the myocardium. Note the “superimposed” consumption defect of the lateral wall in the consumption image, which is not as clearly visible in the original concentration images

Conclusions

Mathematical modelling and modern imaging technique offer a unique possibility for insight into the physiological and biological properties of the tissue. The choice of mathematical modelling depends on the rate of capillary tissue exchange, as much as on the investigator’s intuition. It remains fascinating, based on relatively simple concepts, which allow both quantitative estimation of flow and metabolism and introduce “superimposed” images of the dynamic behaviour of the tissue. These estimates, when carefully used with a knowledge of the underlying assumptions of the model, give more useful information and may help to make decisions about the clinical progress of patients.