Abstract
Infrared (IR) spectroscopic imaging seemingly matured as a technology in the mid-2000s, with commercially successful instrumentation and reports in numerous applications. Recent developments, however, have transformed our understanding of the recorded data, provided capability for new instrumentation, and greatly enhanced the ability to extract more useful information in less time. These developments are summarized here in three broad areas— data recording, interpretation of recorded data, and information extraction—and their critical review is employed to project emerging trends. Overall, the convergence of selected components from hardware, theory, algorithms, and applications is one trend. Instead of similar, general-purpose instrumentation, another trend is likely to be diverse and application-targeted designs of instrumentation driven by emerging component technologies. The recent renaissance in both fundamental science and instrumentation will likely spur investigations at the confluence of conventional spectroscopic analyses and optical physics for improved data interpretation. While chemometrics has dominated data processing, a trend will likely lie in the development of signal processing algorithms to optimally extract spectral and spatial information prior to conventional chemometric analyses. Finally, the sum of these recent advances is likely to provide unprecedented capability in measurement and scientific insight, which will present new opportunities for the applied spectroscopist.
Index Headings: Infrared spectroscopic imaging, Fourier transform infrared spectroscopy, FT-IR imaging, Infrared microspectroscopy, Mapping, Focal plane arrays, FPA, Discrete frequency IR imaging, Quantum cascade lasers, QCL, Synchrotron, Chemical imaging, Scalar wave theory, Electromagnetic theory, Compressive sensing, Reconstruction, Noise reduction
Introduction
The combination of infrared (IR) vibrational spectroscopy and optical microscopy has been the subject of many studies and the analytical approach has been employed in thousands of applications for many decades. The recent evolution of the field can be found in periodic reviews1–3 and compilations.4–7 While there are approaches in which optical microscopy can provide structural detail and point measurements of spectra provide chemical information,8 the two measurements are commonly performed today such that IR absorption provides the contrast mechanism for the entire field of view of the optical image.9 The underlying concept for obtaining spatially resolved spectroscopic data is to localize the interacting volume of a sample with propagating light such that data can be recorded and interpreted and information extracted from the targeted area. These three areas of spectrometry—data recording, interpretation, and information retrieval—form the core of the science of IR microspectroscopy. Applications to particular problems, using a combination of specific techniques in the three areas, are covered in other recent reviews.10–16 Here, we focus on the science of IR microspectrometry, especially on recent developments that can potentially transform imaging spectroscopy in the future.
A segmentation of IR microscopy systems for the purposes of study can be along the length scale of measurements. The spectral bandwidth of most mid-IR measurements (2–14 μm) provides a convenient reference length scale. Macroscopic or bulk measurements can be understood to be from configurations in which the spatial localization is approximately ten-fold larger than the longest wavelength of this bandpass (>100 μm), microscopic measurements from configurations in which the spatial localization is on the order of the wavelengths of interest (∼1 μm), and nanoscopic measurements from configurations in which the localization is ten-fold smaller than the shortest wavelength (<0.1 μm). The measurement of bulk samples is now a mature topic that is well-described in classic texts.17 Nanoscale measurements are less common than those in other spectral regions18 though they are strongly emerging in many configurations19–23 and are discussed in a recent compilation.24 We focus here on microscale measurements. Though an older field of study, the past few years have seen a renaissance driven by new concepts, theory, hardware, and algorithms. A review of the developments and their likely impact in the future are the subject of this manuscript. Microscale measurements can be conducted in two configurations that depend on the type of detector used.25 Point microscopy typically refers to the use of a single element detector. Spatial localization is not aided by the detector architecture in this case but rather achieved using selective illumination (using apertures) or local sensing (using probes). Apertures have been employed for decades and the technology26,27 has been essentially unaltered since the advent of Fourier transform infrared (FT-IR) microscopy. While scanning probes have received considerably more attention for nanoscale spectroscopic mapping, their use for microscale measurements28–31 is generally useful only to localize signal from specific regions or samples32 and not for large area mapping. IR imaging typically refers to the use of multichannel detectors to achieve spatial localization, which enables recording a reasonably sized image in short times. IR imaging is now the standard for microscopy due to the exceptionally large multichannel detection advantage (typically >.16 000) and robust detectors. New applications, hardware, and theory may well present situations in which point measurements are the better option for IR microscopy in the future. Hence, this review will focus primarily on imaging and discuss point microscopy only when new ideas are introduced that may lead to competitive technologies in the future.
Data Recording: Instrumentation
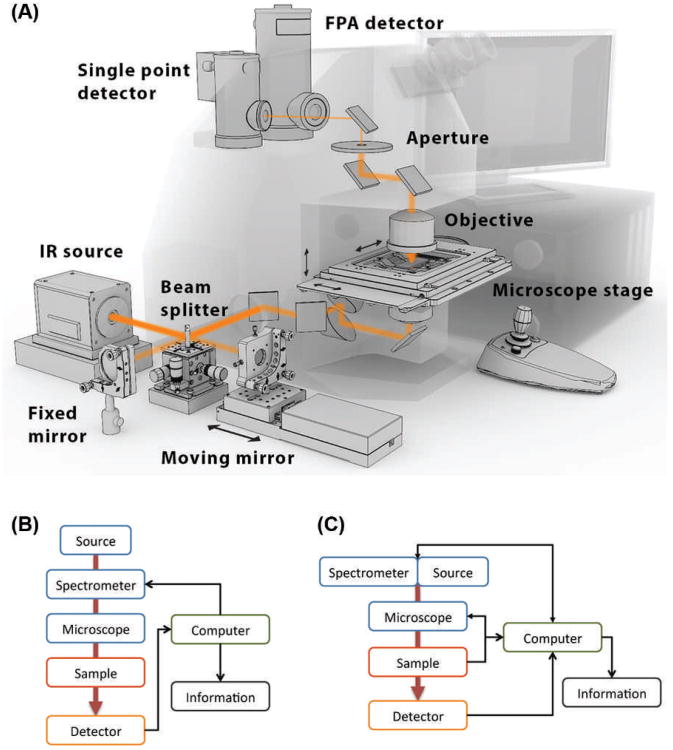
Fourier transform infrared spectroscopic imaging, which is most commonly referred to as FT-IR imaging, combines an interferometer, IR microscope, and array detector (Fig. 1).33 Data is recorded by spectral multiplexing in time using the interferometer and simultaneously by a large number of detectors (multichannel advantage). The genesis of this instrumentation can be traced to the availability of focal plane array (FPA) detectors with extended wavelength sensitivity,34 non-microscopy imaging attempts,35 and the use of filter-based imaging.36,37 From the initial, relatively crude, step-scan systems with attendant issues of sub-optimal data recording,38,39 instrumentation has now evolved into rapid-scan systems40,41 with improved detector electronics and fast signal processing. Step-scan imaging, similar to bulk step-scan spectroscopy, would still be useful for time-resolved FT-IR imaging42 but has only been reported in a few studies.43–45 Though imaging instrumentation is commercially available, no major conceptual innovations have occurred over the past 8 to 10 years in the available systems. To some extent, this is a sign of mature component technology. While some advances can be foreseen, such as detectors with improved speed and larger formats, the approach to imaging is largely the same as a decade ago. As argued later in this article, this stagnation is also a product of a lack of theoretical and fundamental understanding that can guide further development. The stagnation has also spurred a look elsewhere for competing technologies and alternate approaches that address specific shortcomings of present-day instrumentation.
Fig. 1.
(A) Typical layout of a Fourier transform infrared (FT-IR) spectrometer. Instrumentation is usually general purpose, with transmission and reflection sampling configurations in the same system (only the transmission path is shown here), dual detectors enabling both point mapping and imaging technology, as well as external interferometer and computer to acquire and process data [figure by Kevin Yeh]. (B) Conceptually, the optical path proceeds from a source to a spectrometer, microscope, sample, and to the detector. The computer serves to operate the spectrometer and process signals from the detector into information. (C) The ongoing evolution of technology will make computing and control central to imaging. The source/spectrometer combination will essentially function as a known and controlled light source. Information about the sample and microscope configuration will be fed to the computer and used to process signals from the detector via new theory and algorithms as described in this article. The quality of information extracted, as a consequence, will be considerably improved.
In a competing approach, which we term discrete frequency IR (DF-IR) imaging, data may be recorded at single frequencies of limited bandwidths without extensive spectral multiplexing in time. A frequency sweep, as for example with gratings, has long been out of favor for spectrometry due to the Fellgett and Jacquinot advantages offered by interferometry. Filters and gratings, nevertheless, have been used sporadically. While these attempts were useful for sampling a single frequency or a few bandwidth regions, they did not gain much favor for spectroscopy over appreciable spectral bandwidths. As opposed to bulk measurements, however, spatially resolved measurements are actually more favorable for these alternate forms of spectral recording. The throughput and multiplexing advantage can be recovered somewhat by relaxing slit width as lower spectral resolutions are typically required in imaging condensed matter while simultaneous recording with a multichannel focal plane array (FPA) detector alleviates the multiplexing advantage to some extent. While the use of gratings permits the recording of smaller bandwidths of data, instrumentation in other spectral regions46 has typically focused on specific applications requiring compact size, robust performance, and speed. These advantages are typically not the driving requirements for mid-IR microscopy systems, though they can potentially be used in this spectral region as well. The reduction in bandwidth can be continued to the level of recoding a single spectral resolution element at a time. Towards this end, there are two major emerging trends. In the first, lasers are becoming more available and practical for the mid-IR region. Quantum cascade laser (QCL) technology,47 in particular, is maturing and transitioning from academic to commercial success. The second trend is the increasing integration of powerful computers in spectroscopy. This trend will enable the extraction of significantly higher quality information, even from poorer quality recorded data. Spatial deconvolution, noise rejection, and other signal-processing approaches can potentially provide solutions that displace the need for sophisticated hardware. We examine these trends next and discuss progress in the context of recent advances.
Interferometers with Extended Frequency Sources
The globar has long been the source of choice for both IR spectrometry and imaging due to its broadband emission, sufficiency of light for most conventional applications, simplicity, robustness, and low cost. The output of a globar is matched well to the detector characteristics of modern single-element detectors and electronics such that photon flux is not a limitation for the vast majority of bulk measurements. For imaging, due to the need for focusing and uniform distribution of light over a large area, the flux per detector element is significantly smaller and requires longer observation times. At the same time, the miniaturized detector and electronics in an FPA are noisier. Hence, imaging data are inherently noisier than their corresponding single-point measurements.48 Interestingly, quantitative analyses of the expected signal-to-noise ratio (SNR) indicate that an increased SNR can be realized with miniaturized detectors—if the same flux can be maintained.49 Hence, a higher flux source is likely to prove beneficial for imaging.
Compared to thermal sources, a synchrotron provides high-brightness radiation that is particularly relevant for microscopy and imaging.50–54 A summary of the properties of synchrotrons and their applications for microscopy is available,55 and hence, we only focus on the features relevant for imaging. Details of recent developments and description of a major improvement in performance are available in a recent review.56 The emitted beam from a synchrotron is of high brightness, collimated, and of a small size. While this property was excellent for point microscopy in which light from a larger diameter would anyway be rejected, it was not very effective for wide-field imaging. There were reports of coupling a focal plane array to synchrotrons57,58 and the notion of improved data quality was proposed. A major recent advance was the combination of multiple beams to provide a bright, wide beam source that could be coupled into an interferometer.59 While SNR improvement was a major outcome, the work has changed IR imaging in a more fundamental manner. The resolution of any IR imaging system is limited by the diffraction limit and the numerical aperture (NA) of the objective. As demonstrated in the above study and shown theoretically (discussed further in this article in the Microscopy section),60 the sample size imaged per pixel was not optimized. Commercial instruments typically image ∼5 μm per pixel in order to ensure a sufficient SNR from the weak thermal source. Using a synchrotron source with the same setup alleviates the lack of throughput and enables smaller pixel sizes at the sample plane to be recorded. The resulting image quality clearly demonstrated the utility of the synchrotron source in providing diffraction-limited images for the first time. The quality of images was so dramatically different that these are dubbed “high-definition” (HD) images to distinguish them from the previous state-of-the-art. The study also highlighted the need to develop new sources and detectors and exposed the lack of rigorous considerations in the design of most instruments. A new set of synchrotron-based high-performing microscopes will probably result given the development of new beamlines that is currently underway and the convincing demonstration of HD imaging. The obvious drawback of this approach for applied spectroscopists is that synchrotron sources for IR imaging have limited availability due to their cost, size, and accessibility. Free electron lasers,61 another source using accelerated particles but using an undulator to achieve optical amplification, can generate an output with a much higher spectral brightness and coherence than a synchrotron. Used sporadically for microscopy of practical systems,62 their application for IR microscopy is even more limited than that of synchrotrons. These are perhaps better suited for fundamental spectroscopic studies,63 therapeutic use,64 or near-field nano-scopy65,66 approaches. In summary, no major advances in the technology of sources are anticipated but changes are likely forthcoming in the manner in which these sources are used, for example, for HD imaging.
Hybrid Spatial–Spectral Microscopy
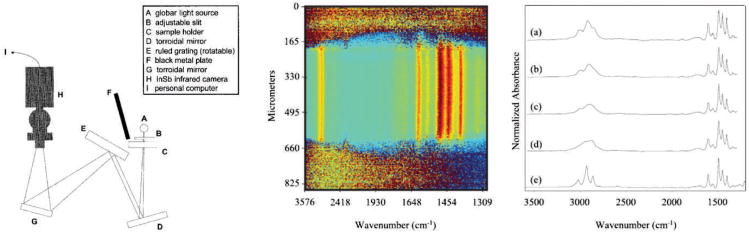
A new approach to spectrometry was described involving an FPA detector in which a conventional grating arrangement was used to disperse light and individual pixels in the array were employed to record a single resolution element region (Fig. 2, left).67 The spectrometer is termed planar array infrared (PA-IR) spectrograph. While the genesis of the PA-IR approach is both in the use of gratings and single-element detectors that preceded FT-IR spectroscopy as well as in the use of multichannel detection68 in ultrafast spectroscopy or nanoscale mapping,69 the approach has significant additional implications for microscopy and imaging. The approach is flexible as different bandwidths can be selected depending on the optical and array arrangements70 as well as very high fidelity in terms of speed71 and sensitivity.72 The spectrometer inherently involves multiplexing due to the multi-channel detection, and elimination of a narrow slit results in improved SNR. The flux is very efficiently utilized, enabling measurements even in aqueous solutions.73 Since there are no moving parts for recording a specific (though, limited) bandwidth, data acquisition can be rapid and is limited only by the integration times (∼10 μs) of the detector. The frame rate of the detector determines the temporal interval between spectral acquisitions (∼ 1 ms), making the rate of spectral acquisition quite comparable to the fastest FT-IR imaging systems. With the inevitable future availability of FPA detectors with faster electronics and larger sizes, ∼100 μs spectral acquisition is likely going to become possible and larger bandwidths may be accessible. The limited bandwidth problem of this approach can be overcome by using multiple pixel rows available in the FPA. Configurations have been proposed to illuminate the FPA with two or more separate and independent spectral bandwidths. Perhaps the greatest advantage of this technology lies in its ability to perform real-time background corrections by obtaining sample and background single beams from the same FPA image, virtually eliminating the effects of water vapor or source fluctuations. Despite these advantages, however, the use of this approach for imaging has not been actively pursued.
Fig. 2.
Hybrid spatial–spectral data recording is possible using a grating or a prism-based spectrograph coupled to a microscope. (Left) Experimental arrangement of components in the PA-IR spectrograph. (Middle) Spectra acquired (across a row) using a prism-based spectrograph. The detector image of Parylene can be used to extract spectra (right) that change with the optical parameters of the system. Spectra recorded at slit width settings of (a) 46, (b) 64, (c) 108, and (d) 153 lm with the sodium chloride single-pass prism spectrograph. (e) The CH stretching and fingerprint regions of the FT-IR spectrum were acquired at 22 and 14 cm−1 resolution, respectively. [Figure at left reproduced with permission from Ref. 67, copyright Society for Applied Spectroscopy. Figures in the center and to the right reproduced with permission from Ref. 75, copyright Society for Applied Spectroscopy.]
In principle, using an aperture and systematically translating the sample to collect spectra permits mapping of the sample in a manner comparable to point mapping. A similar concept has been implemented, though using prisms,74 for point-mapping measurements.75 The spatial area-defining aperture of the microscope at the sample plane also served as the entrance slit to the spectrograph and light is dispersed both along the column (spatial information) as well as across the row (spectral information) of the detector array (Fig. 2, middle). Prisms require a more complicated setup to provide the higher resolution typically afforded by grating-based systems but, for a particular array, the spectral coverage can be higher. Since FPA detectors are two dimensional, it also is possible to spectroscopically and spatially map the sample at the same time. A hybrid imaging approach has been proposed76,77 in which one dimension of the FPA is used for spectral recording while the other is used for spatial resolution. The line-scan approach to mapping, however, has not yet been extended to raster the sample. This could prove to be an exciting development for some applications. Recorded spectra compared very favorably with those from an FT-IR spectrometer (Fig. 2, right) and can be seen to depend strongly on the optical setup (slit width). Because the slit width would also be coupled to the spatial resolution, spectral and spatial resolution would be correlated in any mapping system using this architecture. Hence, considerable thought and optimization may be needed to design a flexible system that can provide both excellent spectral and spatial resolution. Given the ability to perform high fidelity spectroscopy, real-time corrections, and other advantages enumerated above, it should be possible to obtain data of very high quality using an appropriately designed instrument. Given the coupling between spectral and spatial domains as well as challenges in accessing vibrational modes over large bandwidths, hybrid mapping or point microscopy systems would likely only be useful for moderate performance applications where cost, robustness, and simplicity are significant considerations.
A practical benefit of a microscope based on PA-IR spectrometers would be in the rapid examination of small regions of exceptionally small signals, e.g., mapping of monolayers, an ability that is not easily available in FT-IR microscopes. The most exciting result, however, is probably the ability to provide exceptionally low levels of noise. The peak-to-peak noise level of the baseline in absorption spectra acquired in tens of minutes was reported to be of the level of 10−5. Combined with the spatial localization of microscopy, the SNR could potentially provide the capability to image domains, inclusions, or impurities at the sub-picogram level or lower in minutes. The sensitivity, speed, and robustness of such a microscope could potentially be useful for real-time quality control or forensics, for example, but no applications have been reported in those directions. While not explicitly stated or analyzed theoretically in the above works, there is a fundamental concept of significant value in using the PA-IR system for imaging. Interferometry has been so ingrained into the body of knowledge for decades that it has become synonymous with multiplexing. Multiplexing can also occur in the spatial domain. In the non-imaging version of the PA-IR setup, spectra from different spatial regions were simply averaged to provide an average “bulk” spectrum while a multichannel detection advantage was obtained using different pixels to record data. Thus, the spectral acquisition was multiplexed in both the spatial regions of the sample as well as the spatial extent of the detector. While Fellgett's advantage78 in temporal/spectral multiplexing is often cited as a major competitive advantage of interferometry, this spatial multiplexing confers an advantage of similar magnitude, though arising from different considerations. Hence, we argue that the long-accepted belief in the general utility of the Fellgett advantage for spectroscopy should be re-examined in the context of imaging, as discussed in the next section.
Discrete Frequency Infrared (DF-IR) Spectroscopic Imaging
The multiplex advantage has played a central role in the evolution of instrumentation in the mid-IR. Briefly, in an interferometer, all frequencies in the bandpass of the optical system are acquired all the time. Hence, as opposed to sequentially measuring each spectral resolution element individually, an N-fold higher signal is measured N times. Comparisons of interferometric methods with other methods often rely on the assumption that the entire spectrum of large bandwidth has to be measured, that the finite dynamic range of the detector does not play into the theoretical advantage, and that a high spectral resolution is required. A complete discussion of the relative merits of interferometric versus other approaches is in preparation;79 here, the most important considerations are summarized. The first pertinent aspect is the sheer size of the data. As opposed to N spectral data points in a single spectrum, there are Nx and Ny spatial resolution elements as well. Hence, the total data points that are to be measured is N × Nx × Ny in an imaging experiment. For the purposes of acquisition, which is limited by detector readout speed, and for recording and analyzing the fewest data needed, in the interest of conserving time and resources, it may not be necessary to record the entire spectrum. For many applications, such as imaging biological tissues,80 it may be beneficial to record only specific spectral bands of interest. A second pertinent issue is the one of limited performance of available array detectors, mainly their electronics and dynamic range. Interferometry encodes the intensity of the source such that that there is a massive signal recorded around zero optical retardation. The spectral SNR of the single beam is approximately equal to the SNR of the centerburst divided by √N. In a conventional spectrometer, the speed of the interferometer can be increased for large signals and signal averaging can be extensive, thereby reducing detector noise contributions in a given acquisition time. With FPA systems, the readout time of the detector is fixed, whereas the integration time for signal acquisition can be tailored to best fit the centerburst signal into the dynamic range of the ADC. Methods such as gain ranging,81 staggered step-scan,82 rapid scanning, interferometer modulation,83 and detector aperture matching84 have been proposed around this limitation but have not been able to address the limited dynamic range problem. Further, the full range is not utilized for fear of saturating the detector and some range is lost to thermal background. Since the globar bandwidth used in interferometry is large, N is typically 512–2048 points and the SNR for one scan at each pixel is no more than 250:1. Typically, studies report 100:185 and uncooled detectors86 would report SNR of 10:1. While small detectors provide impressive SNRs,5 spatial coverage suffers dramatically. Practitioners today have to tolerate the reduced multichannel advantage to gain high SNR, for example, for biomedical applications, or sacrifice SNR to gain imaging speed, for example, for kinetics experiments.87
An alternative approach to overcome these difficulties encountered with FT-IR imaging has been recently proposed.88 In this approach, a spectrally narrow-band beam is provided to the microscope and a spectral image at a specific frequency is recorded directly. Hence, high SNR can be achieved rapidly by averaging a small spectral range instead of spectrally scanning a large bandwidth. Since the recording of spectral elements is decoupled from recording the entire bandwidth (the FT-IR case), this approach is termed DF-IR spectroscopy (Fig. 3). The approach would ideally, first, greatly simplify instrumentation while providing performance at least comparable to an FT-IR spectrometer in terms of recording spectral elements of interest, resolution, and data recording speed. Second, it would make instrumentation more robust by replacing the sensitive interferometer with a simple moving part or solid-state lasers. The ability to selectively acquire data at a few or all wavelengths and to do so in random access is the obvious advantage of this approach. The same advantages are available using lasers. There are different approaches to lasers that are now becoming more prominent for the mid-IR spectral region. We divide spectroscopy candidates into two major groups based on the components and output of the laser system. The first group includes lasers in which mid-IR radiation is directly generated and available, including QCLs and lead-salt or CO2 lasers. The second group is based on frequency conversion, using well-established sources from other spectral regions, for example, using optical parametric generation in nonlinear crystals. While the DF-IR term was first introduced with respect to filters, the idea is essentially the same using lasers. Hence, we use the term to imply the general embodiment of imaging where selective and individually addressable wavelengths can be employed for imaging. In general, throughput in a laser system will be higher than filter-based systems, as will be cost and complexity.
Fig. 3.
(A) Essentials of the FT-IR and (B) DF-IR Setup. A broadband source (C) is encoded and decoded by FT-acquisition using (D) interferograms. (E) A small number of filters are used in DF mode to measure the informative spectral sections.
A second advantage of DF-IR approaches addresses the dynamic range problem directly. In DF-IR measurements, the dynamic range is simply filled by a narrowband signal and the single-beam SNR can be 1000:1 (cooled FPA) or 100:1 (uncooled FPA). The ability to use uncooled arrays is perhaps the most exciting aspect of DF-IR approaches. Uncooled FPAs are cheaper and have much larger formats than cooled arrays. Hence, coverage can be enhanced and more time can be spent averaging signal to improve SNR. Uncooled FPAs are also becoming increasingly available in larger formats, though only at near-video-rate readouts due to technological and market limitations, and are likely to be used for spectroscopy only in this format. Further, the ADC can be filled by integrating the signal for varying times for each spectral element. Hence, we can obtain uniform SNR (or by design, enhanced SNR at any frequency) simply by software control. This potential, though not implemented in any reports thus far, will also mean that the conventional notions of SNR will need to be reconsidered. In DF-IR spectroscopic imaging, SNR can be tailored for different elements of the spectrum such that SNR in absorbance, rather than baseline noise as obtained in interferometry, is constant across the spectrum. In summary, the DF-IR approach has the potential to be simpler, robust, and cheaper, as well as being superior to FT-IR imaging in some cases. We emphasize that these analyses do not imply that DF-IR is superior to FT-IR imaging in all cases. If the entire spectrum is required at high resolution, the detector is of large dynamic range and low noise, the source is exceptionally weak (emission spectra), or there are noise frequencies that can be filtered, then FT-IR imaging will be distinctly superior. DF-IR imaging will likely evolve for very specific uses, also providing additional opportunity to optimize performance and lower costs. In particular, its use is likely to be popular where a few spectral features provide all the information of interest,89 for example, in tissue typing.90
The possibility raised above points to a trend in which the source, spectrometer, and analysis need to be controlled and to be in sync with one another. This is not only required but can potentially provide improved performance. Efforts to maximize performance, however, also usually restrict the range of studies that one particular implementation can address. To become more generally applicable, optical arrangements for DF-IR systems would have to be flexible and configurable; implying again the use of software for optimization and control significantly more than presently implemented.
The critical technology for DF-IR imaging is obviously the “source”, which integrates a source of light at different wavelengths as well as a means to separate multiple frequencies into individual narrowband ones. The distinction from interferometric methods is that the source–spectrometer combination provides the opportunity to select a single narrowband illumination at one time, while the distinction from grating based methods is that the intensity at frequencies is unrelated to a single grating frequency that has been optimized. Three major classes of such sources are available and are worth following as the DF-IR approach becomes more prevalent. Technology for sources and software approaches are discussed in the next section.
Spectrometer Components for DF-IR Imaging: Filters
In IR imaging, a microscope is coupled to a spectrometer. Hence, for both DF-IR and FT-IR imaging, the microscope, sample mounting, and beam steering components are the same. The source of light and the spectrometer are the only differences. The effects of microscopy optics and sample are discussed in subsequent sections; here we examine the source– spectrometer component. The use of filters allows recording of spectral data directly using narrow linewidths. There are two major impediments to this ideal. The first is conceptual in that it is not simple to design narrowband filters of multiple bandpass (resolution) appropriate for spectroscopy. The second is practical in that conventional processes such as mechanical ruling used to manufacture gratings are far too slow and, consequently, too expensive to mass produce sets of filters. There are other minor concerns such as how an optical design would incorporate tens to hundreds of filters that may be needed. Recent renaissance in optical sciences provides technology that is capable of providing filters with characteristics sufficient for use in spectroscopy in the form of so-called guided-mode resonance filters (GMRF).91 Mass production of the filters is enabled by recent advances in nanofabrication technology, optical modeling, and use of unconventional materials for manufacture. For effective application in IR spectroscopy, the set of filters should provide high reflection efficiency over a narrow wavelength range for all spectral resolution elements. The resolution achieved must be the same as common FT-IR settings (4 to 16 cm−1). A set of filters should also be capable of spanning a large wavelength range (e.g., 3950 cm−1, the sampling cut-off for under-sampled FT-IR spectroscopy to 950 cm−1, the FPA cut-off). The materials and fabrication challenges to achieve these conditions are quite significant and, until recently, only wide (∼100 cm−1) band filters had been reported in the mid-IR. The efficient production of these filters and design of ones with tailored characteristics are likely to remain topics for research. Hence, we examine the concept behind these filters, their testing, and review the state of the art in the next few paragraphs.
Since their discovery more than a century ago92 and as described in recent analyses,93–96 anomalies in periodically modulated structures have attracted much attention for spectral selectivity. Resonant anomalies,97,98 termed guided-mode resonance (GMR), in waveguide-gratings result from structures with a sub-wavelength modulation in refractive index along one dimension. Designed structures can be used to function as filters that produce complete exchange of energy between forward- and backward-propagating diffracted waves. More importantly, for spectroscopy applications, it was shown that smooth line shapes and arbitrarily narrow linewidths could be obtained.99 GMR arises from the introduced periodicity that allows phase-matching of externally incident radiation into modes that can be re-radiated into free-space. They are often referred to as “leaky eigenmodes” of the structures as these modes possess finite lifetimes within such structures. GMRFs store energy at the resonance wavelength, which is manifested in optical near fields that interact with the device itself as well as with the external environment. For normal incidence illumination, the response of the GMRF is coupled to the second-order Bragg condition and therefore the spectral location of peak reflection can be given by:
| (1) |
where λ is the resonant wavelength, neff is the effective index, and Λ is the modulation period.100
The effective index is a weighted average of the refractive indices of the materials in which the standing wave generated at resonance is supported. Hence, structures to provide large numbers of resonant wavelengths needed for spectroscopy can be readily tailored by changing geometric parameters (modulation period). There were successful examples101 of making such structures for ultraviolet (UV), visible, and near-infrared (NIR) wavelengths and the first example for mid-IR wavelengths was also recently reported.91 Although modeling and simulation of these structures required additional details and accounting for dispersion in the materials used, actual fabrication and unproven manufacturing in the mid-IR were impediments that needed to be overcome. The primary challenge is that materials of the structure need to have little or no absorption at the resonant wavelength in order to maintain near 100% reflection efficiency. We have selected plasma-enhanced chemical vapor deposited (PE-CVD) silicon nitride (SiN) and fumed silica dielectrics specifically for their low mid-IR absorption and have produced highly efficient reflectance spectra. Since there are a large number of frequencies, a secondary challenge is to ensure both an efficient fabrication and use of these filters. A “filter wheel” has been developed using a single wafer to address both needs. One positive aspect of fabricating filters for mid-IR wavelengths is that the device period, which must be less than one-half the resonant wavelength, increases as wavelength increases according to Eq. 1. A device designed to measure the CH stretching mode, for example, is resonant at λ ∼ 3.45 μm and requires a period of Λ = 2.1 μm, which dictates that the size of etched features will be 1.1 μm. Features of this size are well within the dimensions of routine contact photolithography using conventional photoresists and chrome exposure masks. Hence, mass fabrication is possible and can be very cost effective. We have obtained filter parameters that can provide narrow linewidths at usual FT-IR resolutions. Filters with these characteristics were fabricated and demonstrate performance as per theory. These filters can be demonstrated in principle but have not been used for imaging spectroscopy due to fabrication and interfacing challenges at this time. This technology is in its earliest stages but the economic argument is compelling. Advances in modern fabrication and the wide availability of electronics manufacturing can be leveraged to provide fairly inexpensive spectrally resolved sources for microscopy. This aspect is likely to sustain interest in developing low-cost filters.
A typical GMRF and its use for mid-IR imaging is shown in Fig. 4. The filter (Fig. 4A) is conceptualized to comprise a low refractive index substrate (soda lime glass, n = 1.5) upon which a thin film of high refractive dielectric material (silicon nitride, n = 1.975) is deposited. A one-dimensional linear grating pattern upon the dielectric material is realized by photolithography and a reactive ion etch process is used to etch grooves partially into its surface (Fig. 4B). With theory-guided selection of the material refractive index parameters, dielectric layer thickness, and grating depth, the device structure performs the function of a highly efficient reflectance filter. At the resonant wavelength, the structure achieves high reflection efficiency for a narrow bandpass and other wavelengths are transmitted. They are eventually absorbed by the thick soda glass. A rigorous coupled wave analysis102 (RCWA) computer code was written for simulations of these structures and used to predict the reflection efficiency as a function of wavelength, that were subsequently validated in individual filters (Fig. 4C), though important differences between the predicted and observed performance could be seen. A number of filters could be co-housed on the same substrate (Fig. 4D), which is incorporated into an optical arrangement for both testing against an FT-IR spectrometer as well as for use in a microscopy system (Fig. 4E). A narrowband absorbance image obtained using the filters demonstrates that imaging is possible (Fig. 4F). Any frequency can, hence, be addressed rapidly and randomly by turning the wheel from software control.
Fig. 4.
Components and results from DF-IR imaging. (A) Schematic of a designed filter. (B) Characterization of the designed filter by microscopy and atomic force microscopy shows the ability to fabricate structures as per design and their uniformity. (C) The imperfect prediction and fabrication capabilities at this early stage, however, do present challenges in translating the narrowband predicted performance (for example, on the left) to actual filter performance (right). (D) Tens of filters can be placed on a single substrate and fabricated together on the same optical path using the concept of a filter wheel. (E) Schematic of setup for characterization of the filter, spectroscopy or for comparison with FT-IR imaging. (F) An absorbance image from an unoptimized system showing the antisymmetric CH stretching band absorbance of an SU-8 sample. The image size is approximately 500 μm × 500 μm. White levels indicate a higher beam attenuation and gray/black levels indicate little to no attenuation.
While the DF-IR approach enabled by GMRFs is an exciting avenue, many challenges remain. Filters have been designed and tested and important insights obtained into their design. However, the filter–optical setup is not optimized. Even in theory and simulations, smaller refinements need to be incorporated. For example, the refractive indices and dispersion due to small absorption within the fabrication materials are likely causes of the variance; hence, characterization and prediction of these properties is needed. The efficiency and FWHM of any filter depend both on the optical alignment as well as properties of the underlying materials. While the filters themselves can be fabricated and coupled to a globar source, great care must be taken in alignment. Alignment concerns can likely be resolved with the same dynamic approaches as used in an interferometer but beam collimation (restricted with an aperture similar to that in an FT-IR spectrometer) and its effect on spectra need to be studied. Spectra from the filter wheel show higher noise compared to a conventional single-element spectrometer, which is several thousand fold larger in area and lower resolution due to the broad spectral bandwidth. Hence, further optimization is needed for routine spectroscopy. As with all frequency selection methods via coherent processes, polarization is introduced into the beam. An alternative to GMRFs might be to use a conventional grating/slit monochromator, where serial adjustment of the monochromator slit position illuminates the sample one wavelength at a time. While such a method would suffice in principle, the GMRF approach has a number of advantages. By using the described approach, efficiency at all wavenumbers can be optimized, frequencies are individually selectable, ruling cost is much lower, and large wavelength regions can be covered in a single part (filter wheel). The fundamental limitation of a globar in terms of flux remains. For filters, the use of an aperture and polarizer further decreases total available intensity. Hence, the need for higher intensity sources is not addressed and actually becomes more acute in using filters. Tunable lasers are an obvious choice and two routes, discussed next, stand out in their potential for IR imaging.
Spectrometer Components for DF-IR Imaging: Lasers
Quantum Cascade Lasers
Quantum cascade lasers (QCLs)103,104 are a class of unipolar lasers based on inter-sub-band transitions in a semiconductor heterostructure. Most common embodiments involve using InGaAs/AlInAs/InP composites105 that are active at wavelengths longer than ∼3 μm. The most effective approach in this direction is emerging in the form of an external cavity (EC) QCL. A grating is coupled to a free-running semiconductor laser to select a specific band and tune the entire device into a single-band source. The setup consists of three components: the gain element (QCL chip), collimating mirrors, and grating.106 In principle, the setup is similar to the combination of a grating-based spectrometer and source. The major advantage, however, is that exceptionally narrowband light of unprecedented intensity can be obtained. QCLs function at room temperature,107 the source is compact, and, in principle, it can become fairly inexpensive after further development. Lasers have been widely used for spectroscopic analyses108 for a number of years and, similarly, various studies have used QCLs for IR spectroscopy109–113 as well as microscopy and imaging.114,115 The most widely reported studies in spectroscopy have been focused on using the narrow-band properties and high intensity of the QCL to profile specific species, aqueous environments116–118 or the integrated and compact instrumentation119,120 that may be developed for specific experimental configurations121 or applications.122–124 The technology has made rapid progress, specifically in spectral properties and power.125
A large effort in the QCL-related fields has been in the modeling, measurements, and optical properties of these devices. Imaging and microscopy instruments as well as applications have lagged significantly. Since their initial demonstration more than 15 years ago,47 the technology has matured and there are several commercial vendors offering QCL systems. Though realized around the same time, the maturation of IR imaging technology has been considerably faster, given the long history of IR microscopy. It is curious that combining the two technologies has received limited attention. The first factor in this lack of progress may be the limited spectral range, high cost, and restricted availability of stable, packaged QCL sources that are usable. The second is more fundamental. While QCL manufacturing technology is making rapid progress in developing broadband output devices appropriate for spectroscopy, turning them into viable sources for microscopy will likely require substantial further work on the part of spectroscopy and imaging scientists. Based on preliminary experiments thus far, a QCL cannot simply be integrated into existing microscopes in the manner that FPAs were integrated into single-point IR mapping microscopes. Though the single point-to-FPA detector transition required opening the apertures and changes in software, the beam size, spectroscopy, noise characteristics of the spectrometer, and optical performance of the microscope were not changed. These would all have to be reconsidered in using a QCL source. We illustrate one aspect from our work126 in Fig. 5. The coupling of the laser to a microscope required beam expansion, reduction of spatial coherence, and new optical elements for illumination. Without these measures, coherence makes data interpretation difficult; even with this design, illumination and recording are not trivial. The beam intensity and size, as well as its polarization, coherence, and narrowband emission all present significantly new challenges that are discussed and would require a careful analysis of the performance of an integrated system and a likely re-design of existing microscopy systems to be of significant value. An excellent recent example of integrating the unique advantages of this technology in designing instruments is available in the near-field microscopy arena,127 while new opportunities may lie in photoacoustic spectroscopy applications.128 The challenge for spectroscopists would be to integrate the new sources with a better understanding of their potential and of the implications of the limited-wavelength, coherence, and polarization for spectroscopic imaging. The challenge for QCL device manufacturers obviously lies in extending the wavelength coverage, providing compact and integrated sources with seamless transition between wavelengths, and high beam stability. Complementary sources to cover shorter wavelengths (<3.5 μm) will also be required to complete the mid-IR spectral coverage common for spectroscopy. This area is likely to remain very productive and important for imaging in the coming years.
Fig. 5.
USAF 1951 optical resolution target absorption images (cycle 3, elements 5 and 6) as acquired by three different instruments. As opposed to chrome-on-glass targets, these samples were designed to be a cross-linked photolithographic polymer (SU-8) on polished barium fluoride substrates. Top row: QCL + bolometer system without diffuser plate. Middle row: QCL + bolometer system with rotating diffuser plate. Bottom row: commercial FT-IR instrument. [Reproduced with permission from Ref. 126, copyright American Chemical Society.]
Other Laser Sources
While QCLs produce mid-IR light directly, the considerable advances in powerful sources in other spectral regions as well as photonic fibers can also be leveraged using frequency conversion.129,130 A complete discussion of these sources and their potential for imaging is beyond the scope of this article but compilation of the fundamentals of several potential technologies131 and recent advances are available.132 The development of appropriate materials such as periodically poled lithium niobate (LiNbO3) and the emergence of NIR sources have been most crucial to the development of tunable mid-IR sources by optical parametric generation (OPG). Advances in materials processing, microfabrication technology, and understanding of these systems has led to other candidates and materials for frequency conversion. Specific examples of successful technologies are using, for example, GaAs,133 which promises to considerably extend the capability of this approach. The most successful example of application is in coupling with a sub-micron scanning sensor134 and the commercial translation to nanoscale imaging,135,136 demonstrating that a system built from these sources may also be viable for microspectroscopy.
An excellent example of the potential of this approach is demonstrated in the coupling of an OPG-based system with a conventional IR microscope and FPA.137 The flux allowed the acquisition of images with sufficient SNR in ∼1 μs of acquisition, thereby considerably reducing the contributions from thermal background radiation and providing new opportunities for noise rejection. The primary limitations at present are the relatively coarse spectral resolutions attainable (∼10 cm−1) that cannot be arbitrarily changed, pulse-to-pulse stability, and complexity of the setup. Though pulses may be spectrally broader, spectroscopy can be performed by spacing the tuned peak wavenumber closer to provide a quasi-resolution that is comparable to those typically used for condensed-phase imaging. Further, in principle, computation can be used to recover the true spectrum at higher resolution using signal processing techniques. The sources will likely imply shot-noise-limited performance, though such an analysis has not been reported for imaging systems. Though the capability to image across the entire mid-IR bandwidth exists with OPG-based systems, a source with consistent spectral performance over the range is difficult to achieve in practical terms. Alternative materials with new crystals, for example, cadmium selenide (with an idler tuning range of 1160–850 cm−1), are becoming available. A comparison of IR imaging with a laser and thermal source has not been reported in terms of spectral or spatial performance, though spectra were found to be in reasonable agreement in qualitative terms.137 In addition to the optical and performance issues discussed for QCLs, cost is an additional factor in these systems. While the compact packaging and ability to use the same material for a variety of applications and wavelengths exists for QCLs, indirect production of mid-IR light inherently requires a larger capital cost and complexity of instrumentation for phase matching. In the opinion of the author, the rapid development of QCLs and their relative simplicity will eventually lead to their adoption over other laser technologies.
Compressed Sensing and Reconstruction
As seen in the discussion of the previous section, there is significant value in acquiring only a limited set of data. The obvious trade-off is that the spectral range and resolution of acquired data would also be limited. This tradeoff can be mitigated to some extent by the use of modern computational power and algorithms. Computational approaches to spectral reconstruction are an emerging area in which fewer data are acquired than would be dictated by classical sampling considerations and the deficiency in data quantity can be compensated by estimation algorithms. The estimation algorithms at one extreme can be completely blinded to spectroscopic details and use signal processing approaches that, essentially, operate to optimize entropy. Methods at the other extreme perform reconstructions of full spectral detail using a knowledgebase, either of expected spectra for the problem or a general understanding of spectral features, to predict missing details in the data. Applications in data reconstruction have also been reported for temporal measurements an interpolation sense, for example, to obtain time-resolved measurements with better accuracy.138 The reconstruction approach has also been proposed139 as an alternative to recovering SNR and circumventing some limitations of classical FT-IR approaches in some cases. An important conclusion was that reconstructions are relatively noise free. While not explicitly stated in the study, the important implication for imaging measurements (in which sensitivity is often limited by SNR) can be that the inaccuracy in reconstruction may be smaller than the noise for rapidly acquired data. Hence, it may actually be advantageous to acquire a smaller set of spectral points at high SNR and reconstruct the entire dataset rather than acquiring the entire data set at some low SNR. A demonstration of this possibility has not been reported.
Reconstruction approaches have been reported in spectroscopy but have not been extensively applied; their application to imaging data can provide significant benefit. In most cases, data are spectrally sparse, data acquisition times are long, and storage requirements are vast. At the same time, much is known about specific applications, for example, using the data to determine tissue types.140 In one study,141 a representation for IR absorption spectra was developed using a learned dictionary (Fig. 6, top row). A sparse representation of this dictionary is used as prior knowledge in regularizing the compressed sensing inverse problem. The reduced measurement during acquisition was modeled as a process of interferogram truncation, providing a benefit for data acquisition in terms of a reduced set of data as well as the centerburst to enhance the SNR at the cost of the sharper spectral components. The model was implemented using low-pass filtering and down-sampling in the spectral domain as dictated by the measurement process. Spectra could be obtained that closely resembled the spectra acquired without truncation (Fig. 6, middle row). In any reconstruction, there is no doubt that signal is lost and an estimate of the true signal is obtained. The critical measure of success then becomes whether the task at hand is accomplished. The developed approach was tested in its ability to predict cell types in a number of tissue samples and the results were compared to those obtained with full data acquisition. Hence, a number of tissues, which contained multiple cell types and were drawn from different patients reflecting the natural variance expected in the task, were used as a test bed. A down-sample factor of four was found to be adequate for accurate tissue classification and matched the performance of the data dacquire at full resolution. The method also provided an improvement in the SNR of the reconstructed signal, though the effect of this improvement on enhancing classification accuracy142 was not evaluated. The work was important in demonstrating that data storage and acquisition times in FT-IR imaging can be significantly reduced while preserving data quality by employing compressed sensing. Spatial correlation and spatial–spectral correlations may similarly be useful in specific cases. Approaches such as the one reported are likely to evolve with increasing sophistication.
Fig. 6.
Reconstruction of data from a small number of spectral measurements. (Top) The basis of the approach relies on reconstructing spectra from a representation of the data as a combination of sparsely measured data, parameters from a dictionary of known samples, and correlation coefficients. (Middle, left) Different parameters of the process result in reconstructed spectra (dashed lines) that may be lower resolution or closer to the recorded data (solid line). (Bottom, left) Gray colors indicate different cell types deduced from IR data measured at full resolution while the same information is sought from a reconstructed data set (bottom, right).
These studies represent a significant untapped area of inquiry in IR imaging, especially with the emergence of DF-IR approaches. Spectral reconstructions from a smaller measured set and strategies for sparse acquisition are likely to become more prominent. We strongly emphasize that there is a difference between recording spectroscopic imaging data and estimating it via reconstruction approaches, however. While the former can offer the greatest confidence, the latter offer speed. Care must be exercised in evaluating the relative merits of the approaches and claims must be tempered accordingly. It is not correct to assume, given the excellent quality and speed of reconstruction with modern computers and advanced algorithms, that one is superior to another. When the outcome of the imaging study relies on conclusions to be drawn from the data but the data itself are of limited interest, reconstruction approaches are especially relevant, for example, in rapid tissue or polymer identification when the range of possible solutions is limited. In general, reconstruction methods are ideally suited for repeated imaging of similar samples in which rigorous validation of the approach can be conducted to optimize both the parameters of reconstruction as well as determine the optimal results. This topic engenders another direction that is likely to evolve for imaging in the convergence of signal processing, theory, and spectral reconstruction with details of the experiment, as seen in some areas of spectroscopy.143 Computation, as used thus far, not only represents a necessity for imaging data analysis but can potentially tie together emerging instrumentation, theory, sensing, and analysis.
Microscopy Optics
While we have hitherto focused on describing spectral recording approaches, the other aspect of IR imaging lies in the optics of image formation. While several studies in IR microscopy and imaging have used predictions from optical microscopy, a complete model of the IR microscope was not available until recently.144 A model for light propagation in an imaging instrument is important to both the understanding of image quality as well as to the rational design of improved instruments that optimize quality. Theoretical models for instrumentation, based on ray (geometric) optics, have been proposed to describe IR microscopy for many years. Most efforts concentrated on the angular dependence of data related to focusing and corrections to measurements such as dichroicratios.145 Similarly, other methods of understanding spectral dependence on sampling geometry in conventional spectroscopy have often focused on molecular properties in thin films or at interfaces.146 It must be recalled that sample path lengths as well as microscopic features are often at the scale of the wavelength of light; hence, frameworks based on geometric (ray) optics that have been largely used in spectroscopy until now are inadequate in the investigation of effects associated with light–matter interaction. Full electromagnetic models capture all of the physics of image formation but are also significantly complex. They are most useful when a precise prediction of a combination of specific microscopy optics–sample is desired. For many other purposes, a simpler model suffices, especially to understand the effects of the optics of the microscope on the recorded data. The first attempt in this direction recently reported,144 in the author's opinion, the simplest approach to microscopy that incorporates all the phenomena of interest, forgoing full electromagnetic modeling in favor of the conceptually simpler and computationally easier model based on scalar wave theory. We capture the major aspects of this theory in the next section. While details of the theory are described in the original publication, the salient features and critical equations are captured here in a simplified notation for comparison with other studies and for the sake of completeness.
In the scalar wave theory model, the electric field at every plane in the microscope is explicitly calculated. For simplicity, consider a monochromatic component of the field with a wavenumber ῡ, and complex amplitude U. Since the spectral frequencies in any measurement are independent, the approach can simply be extended to the entire bandwidth of the instrument. The field, in any spatial plane for any wavenumber, is expressed as a superposition of plane waves described by functions of the form U(f) exp{i2π[f.r +fz(f) z]} where f = (fx, fy) and r = (rx, ry) are the two-dimensional frequency and spatial coordinate vectors, respectively, in Cartesian coordinates. The function fz is defined such that |f|2 +fz(f)2 = ῡ2, implying that the individual plane waves satisfy the Helmoltz equation.147 The microscopy system is assumed to be linear; hence, summation of individual plane waves can be employed to reconstruct the field and all linear transformations of the field. For each plane wave constituting the field, the amplitude determines its quantitative contribution and the phase determines its relative position. Both the amplitude and phase are necessary and sufficient for a complete description of the field. Subsequently, a plane wave decomposition can be achieved via the two-dimensional Fourier transform. Each plane wave constituting the field has a specific direction, or “angle” of propagation, and therefore the plane wave decomposition described above also describes the “angular spectrum” of the field. Complete description of light propagation, hence, consists of the related contributions of the three spatial coordinates, spectral wavenumber as well as individual amplitudes and phases describing the angular spectrum. The term “spatial frequency” is also used to describe f and this arises from the spatial Fourier transform interpretation of the fields.
In the most general sense, the goal of modeling an IR imaging instrument is to relate the field at the detector UD(f) to the sample S(f) via a function, or an operator A(f1, f2). The operator incorporates the details of the specific instrument. Formally, the relation between the detector field, the sample, and the instrument is described using the equation
| (2) |
The operator A(f1, f2) can be decomposed into constituent operators pertaining to various aspects of light propagation in air, through substrates and samples as well as optical components, as follows. The propagation of the field U1(f) in a plane to the field U2(f) in a plane at a distance d in free space is given by the equation
| (3) |
where the operator Kd(f1, f2) is defined as
| (4) |
The operator for the interferometer can be described in terms of a pair of propagation operators as
| (5) |
The Schwarzschild optic can be modeled as a Fresnel lens, which imparts a quadratic phase factor to the incident field, and is described by the operator
| (6) |
where Lf is the focal length of the Schwarzschild and QC(r) is a pupil function
| (7) |
The quadratic phase factor converts each plane wave incident on the Schwarzs-child optic into a spherical wave converging on its focal plane. The phase relation between incident plane waves and the imparted quadratic phase determines the final image position and size. Combining propagation operators and the lens functions allows us to construct an operator relating the scalar field in the image plane of the lens to the field in the object plane. If the object plane is at a distance d1 from the lens and the image plane is at a distance d2, then the relation between the object plane field U0(f) and the image plane field U1(f) is
| (8) |
where MC = d2/d1 is the magnification of the system. The above expression is for a Schwarzschild focusing light on to a sample (i.e., the “condenser”). The corresponding expression for the collector Schwarzschild (focusing lens) is
| (9) |
The imaging system consists of the condenser, C1, the focusing lens, C2, and the detector collection lens, CD. The interaction of the incident field, U1(f), with a thin sample, S(f), resulting in the field U2(f) can simply be described as a product in the spatial domain or, equivalently, a convolution in spatial frequency as
| (10) |
The field at the source is assumed to be Uz0(f). Light from the source passes through the interferometer, is focused on the sample, and is propagated via the microscope to the detector. Combining the operators described above allows us to construct an expression relating the sample, S(f), the instrument parameters, and the detector field, UzD(f), as follows:
| (11) |
This equation describes an IR imaging system, based on an interferometer in this case, under the scalar wave model. The same formalism may be extended to DF-IR systems as well to account for the effect of different spatial frequencies of features in the sample. While details on the validation and use of the model are available elsewhere,144 a crucial result is highlighted here.
The model was used to predict the behavior of two different optical arrangements as well as to obtain insights into the performance of imaging systems: a high numerical aperture (NA) system (74×, NA = 0.65) and a commercially available low NA system (15×, NA = 0.5) in terms of imaging a standard chrome-on-glass USAF target. Data from optical microscopy were used to simulate the object and simulations were compared with experiments (Fig. 7). The major conclusion was that the higher NA provided higher quality images, as expected, but that the sampling frequency at the detector was the limiting factor in the performance of current imaging systems. The correct pixel size for sampling the image without loss of detail was shown to be ∼40× smaller than previously believed. To date, there is one report of an HD imaging instrument with a globar source144 and one report of an application.148 An optimal pixel size, which balances the throughput, which determines spectral data quality, with small pixels, which determines spatial image quality, was determined at the highest usable wavenumber in most spectra to be ∼1.1 μm. This is approximately twofold larger than that reported for a synchrotron HD imaging system59 because of a careful optimization of throughput, maximum wavenumber, and the needs of the tissue system. As opposed to studies of HD spectroscopic imaging with a synchrotron in which there is sufficient flux to over-sample the spatial domain, the use of a globar for HD imaging requires maximizing throughput for the highest desired resolution. The two studies illustrate the success as well as the need to carefully understand the requirements, trade-offs, and performance using system modeling to make intelligent spectrometer design decisions.
Fig. 7.
(A) The original object consists of a set of bars of sizes with transmittance indicated to the left. Absorbance images from simulations (at 3950 cm−1) are shown for the focusing Schwarzschild with a (B) NA = 0.65, (F) NA = 0.50, and (G) NA = 0.50. The effective sample pixel size at the detector in (B) and (F) is 1.1 μm, whereas the pixel size in (G) is 5.5 μm. Measured absorbance images (also at 3950 cm−1) are shown with configurations (C) NA = 0.65, pixel size = 1.1 μm and (H) NA = 0.50, pixel size = 5.5 μm. (D), (E), (I), and (J) show magnified regions from corresponding images. [Reproduced with permission from Ref. 144, copyright Society for Applied Spectroscopy.]
Given the improvement in image quality, there is immense interest in the optical setup and use of this configuration. The decreased pixel size, however, results in a substantial loss in throughput and the SNR of the resulting data is poor. Synchrotrons and DF-IR sources may well be the answer as a hardware solution. A signal-processing approach to reducing noise (see section on noise reduction later in this article) can also be implemented. Ultimately, the choice between conventional and HD imaging will be determined by the necessity of HD imaging or of high spectral SNR. Spatial averaging could be a compromise in some cases and other methods that could potentially be useful have been previously discussed.149 Currently, almost all commercial instruments routinely provide approximately the same optical setup (0.5 NA, 15× objective). The demonstration of HD imaging has already spurred a number of different instrument configurations. While the diversity in image quality using different lenses is obvious, the spatial and spectral domains are intimately related in the recorded data and changing the lens changes the quality and content of the recorded data. A more complete theory is needed to understand this convolution of optics, sample structure, and recorded data. A framework for this approach is discussed in the next section.
Data Interpretation: Theory
Infrared microscopy and imaging have long been considered to be simple adjuncts to optical microscopy. The recorded data are usually considered to be a simple extension of the IR spectroscopy of bulk materials, with the additional trivial consideration that data are selectively obtained from specific points on the sample. Other than reflecting species concentration, the spatial structure of the sample was not thought to play a major role in the recorded data. The first major hint that there may be additional considerations arose almost at the same time FT-IR imaging with a focal plane array was first reported.150 It is only during the past three years, however, that the full import of structure–spectra relationships has been quantitatively explored by significant advances in theory and a number of experimental studies. It is now widely recognized that there are differences in the data recorded from a bulk measurement and a microscopic measurement, as there are between homogeneous and heterogeneous samples in a microscope. These differences arise from light focusing at the point of interaction with the sample as well as from the microstructure of samples on the scale of the wavelength. Recent work has provided a framework to understand these effects as a function of spatial and spectral properties of the sample.
In this section, we focus on discussing the forward problem, i.e., predicting the spectra recorded from a sample in a microscope. In particular, it is interesting to understand how spectra from heterogeneous materials in a microscope differ from those that would have been recorded from the bulk of the same material using conventional spectroscopy. These differences are often termed to be errors, distortions, or artifacts. We would emphasize here that these terms should not be used. There is ample understanding, from the theory summarized below and form confirmatory experimental evidence, to indicate that the spectral dependence on optical configuration and sample microstructure is deterministic and reliably reproducible. Hence, there are no errors or artifacts that arise from light–matter interactions and it would not be correct to term them as such. Rigorous electromagnetic models analyzing the interaction of light with heterogeneous samples have quantitatively predicted recorded spectra as a function of experimental parameters, clearly indicating that a deeper understanding of the recorded data is sorely needed. In fact, IR microscopy is an unusually rich area of investigation in the general realm of microscopy because the spectral diversity and unique light–matter interactions in the mid-IR spectral range give rise to interesting theoretical questions and instrument-design tradeoffs. We divide further discussion to summarize the framework for predicting the spectral response of homogeneous materials, which indicate the effects of focusing, as well as heterogeneous materials, which additionally describe the effect of scattering at interfaces and light transport within the sample structure. Details of the theory are described in the original publications. Here, we reproduce the critical equations, for parallelism with other studies and for the sake of completeness.
Theory for Homogeneous Samples
A rigorous electromagnetic model to describe light–sample interaction and its effect on recorded data has been reported.151 Just as for the scalar wave theory case, the sample is assumed to be a linear system consisting of multiple layers of varying (complex) refractive indices. This conceptual position allows a simplification of the general problem of light–sample interaction into understanding light transport between pairs of homogeneous layers. The approach is general in that it can isolate heterogeneity within layers, allowing for the extension of the same framework to heterogeneous samples. The electromagnetic field can be described as consisting of a linear combination of plane waves, each of which satisfy Maxwell's equations at the boundaries as the entire system is linear. Hence, the studies employ the same approach as the scalar wave framework in this case and analyze the response of the system to a single plane wave first. The total response of the system to illumination would then be the sum of each of these individual plane wave responses.
Let the electric, E, and magnetic, H, fields at a position, r, = (x, y, z)T be represented by their complex amplitudes and the permittivity and permeability of free space be denoted by ε0 and μ0, respectively. Let the real and imaginary parts of the refractive index of a single layer be denoted by n(ῡ) and k(ῡ), respectively. For homogeneous layers, the electric and magnetic fields can be written as
| (12) |
and
| (13) |
where s = (sx, sy, sz)T and |s| = ε(υ) = k[n(υ) + ik(υ)]2. The temporal dependence of the fields is not explicitly denoted above for notational simplicity. The field in the lth layer (between zl−1 and zl) is given by
| (14) |
where B is the angular spectrum in a transverse plane. Next, we set up boundary conditions at each layer interface. Gauss' law for electricity leads to
| (15) |
and
| (16) |
Faraday's law and Ampere's law require that the transverse components of the electric and magnetic fields be continuous. Hence,
| (17) |
| (18) |
and
| (19) |
| (20) |
Finally, note that there is no incoming light from the last boundary (L) and therefore,
| (21) |
The equations above summarize the complete set of boundary conditions for analyzing a multi-layer sample consisting of homogeneous layers. Assigning refractive indices and thickness to each layer allows for a complete solution for the system of equations. It is notable that the solution does not require any empirical parameters or adjustments. Hence, it can generally be used to predict the behavior of any specific system. A number of cases are considered in the complete report on this subject.151 One example is highlighted (Fig. 8) to illustrate the observed dependence of the spectral response on sample parameters and sampling configuration. Spectra are re-scaled by thickness, as would be appropriate for Beer's law, and compared to the ideal (obtained from tabulated values of the imaginary part of the refractive index). Deviations from the ideal demonstrate that the optical effects of anomalous dispersion152 can result in recorded spectra with significantly shifted band peaks and severely distorted relative intensities. The use of an aperture changes the optical configuration and similar effects were observed and quantified.153 The quantitative accuracy of these measurements as well as chemical specificity (e.g., drawing conclusions regarding hydrogen bonding or packing from peak shifts) is compromised even when using sophisticated spectral correction154 that does not explicitly take into account the optical phenomena in image formation. While extracting absorbance from spectra measured by a specific configuration is discussed in the next section, this forward modeling can be used to compare two different experimental configurations. If spectral dependence on thickness were to be calculated, in the example discussed here, highly accurate measurements could be made by switching from reflectance-based sampling (Au substrate) to measuring transmittance of the sample on a BaF2 substrate. Distortions in transflectance measurements of samples that can be considered to be layered have been experimentally noted elsewhere155, 156 and could be understood in terms of interference between the propagating and reflecting waves. The importance of the analysis based on first principles is that quantitative predictions and evaluations can now be made, which can provide an understanding of how recorded data are related to structure for the first time.
Fig. 8.
Comparison of the rescaled absorbance spectra from the same toluene film acquired in two different configurations, in transmission mode on a BaF2 substrate and in transmission-reflection (transflection) mode on a gold substrate. Simply changing the thickness of the film changes the recorded data. [Reproduced with permission from Ref. 151, copyright American Chemical Society.]
Theory for Heterogeneous Samples
While the previous formulation provided insight into layered samples, one approach to understanding thin films of heterogeneous materials could be to model spectra from each pixel independently. In heterogeneous films, however, light scatters, thus affecting neighboring pixels as well and a more complete description of the interaction of light with sample morphology is needed.157 For any IR imaging experiment with present day microscopes, the region of transverse heterogeneity in the film can always be assumed to be of finite area. Hence, the structure of the object can be reasonably approximated by its two-dimensional Fourier series. The properties of the heterogeneous layer can be characterized by a transversely varying complex refractive index or equivalently by its permittivity, ε, which follows its spatial structure. Truncating the Fourier series of ε and ε−1 to a finite number of coefficients gives
| (22) |
and
| (23) |
Due to the periodic nature of the sample, an incident plane wave exp[i(δx + σy)] is shifted only by integer spatial frequencies, resulting in plane waves with spatial frequency components given by
| (24) |
and
| (25) |
The electric and magnetic fields can be represented using plane wave decompositions as
| (26) |
and
| (27) |
Note that the electric and magnetic fields are not necessarily orthogonal in the presence of transverse heterogeneity, but can be related using Faraday's law and Ampere's law, resulting in
| (28) |
and
| (29) |
Expanding the above equations provides a system of equations that completely describe light–matter interactions in an IR microscope
| (30) |
| (31) |
| (32) |
| (33) |
and
| (34) |
These expressions can be reorganized into a matrix differential equation of the form
| (35) |
The above matrix equation couples the electric and magnetic fields. It is possible to decouple these equations by computing the eigenvalues and eigen-vectors of Φ and find X, Y, I, and J in terms of the eigenvalues and eigenvectors. The boundary conditions for each component can be evaluated in the same manner as those for homogeneous layers given above. Therefore, we can solve the matrix equation and find the electric (E) and magnetic (H) field at every plane in the heterogeneous sample as well as any underlying substrate. Just as in previous formalisms, the fields and intensities at the detector can again be computed by propagating light via the intervening optics. The detector intensity is the recorded data, which can be calculated given the source and sample properties, and compared to observations or ideal predictions. This framework provides a powerful mechanism to understand the behavior of IR imaging systems as well as effects on the recorded data of specific structures.
A key finding of this work lies in understanding the spatial extent of scattering by a single sharp interface as well as its effect on the spectrum recorded by pixels relative to the position of the scattering interface (Fig. 9). First, spectral contributions from a scattering pixel can be observed in neighboring pixels where there is no sample. The scattering contribution can be significant and can be calculated for particular materials and vibrational modes for different distances. Second, recorded data demonstrate a positional dependence both in intensities of bands and in the position of peak absorbance. Since normalization is a common practice in spectroscopic analysis, the effect is compounded on absorbance ratios. A baseline offset is also observed for pixels in the vicinity of the interface. Third, peak positions are not substantially altered and may be more reliable for chemical identification. Again, the results indicate that caution must be exercised in interpreting small wave-number shifts in spectra from imaging data. Finally, we note that these predictions are made for transmission mode measurements and will be substantially affected by the interference of the propagating and reflected waves in a transflection geometry.
Fig. 9.
(A) Pixels in the vicinity of an idealized edge are examined for responses from a single material. (B) Spectra (colors correspond to the arrows indicating positions in (A)) demonstrate baseline offsets, relative changes in band intensities, and shifts in peak positions. (C) Detailed examination in the fingerprint region shows the effect of scattering on the apparent position and relative ratio of peak absorbance. [Reproduced with permission from Ref. 157, copyright American Chemical Society.]
Information Retrieval
Even in one of the first applications of IR imaging,150 it was apparent that both the imaginary and the real part of the refractive index influence recorded data. In an elegant accompanying experiment, the real part of the refractive index was changed (with small changes in the imaginary part) and baseline offsets were seen to largely disappear as indices were matched (Fig. 10). Even at that early stage of the technology, it was cautioned that spectral changes indicative of molecular interaction should be interpreted with caution at interfaces as they may arise from purely optical effects due to the refractive index mismatch. Thus, information extraction from spectroscopic imaging data sets is not a straightforward process of treating a spectrum from each pixel as an independent measurement comparable to a spectrum from a conventional spectrometer. The same scattering effects are present in bulk measurements using a non-imaging spectrometer and could be used to understand structure formation, for example, to monitor the relationship between reaction, phase separation, and ordering in complex systems.158, 159 While one aspect of these effects is obviously useful and can be developed for specific applications, extracting spectra that resemble those that would be measured using bulk spectros-copy of the materials in the microdomains is worthwhile to separate the effects of microstructure and chemical content and realize the ideal of purely chemical information at specific sample locations. As the forward modeling results in the previous section indicate, spectral response from microdomains within samples of wavelength-comparable dimensions complicate interpretation. Hence, we focus this first section on approaches to recover purely chemical information from recorded data and term this the absorption spectrum to distinguish it from the recorded spectrum.
Fig. 10.
Refractive index mismatches cause baseline offsets and apparent absorption in a polymer dispersed liquid crystal. Chemically specific absorbance (top, left) and apparent absorbance (baseline offset) arising from optical mismatch of refractive indices can be observed in recorded data. The application of a voltage along the light propagation direction aligns liquid crystals in the microdomains, thereby changing the refractive index and matching the real part of the index closely to the surrounding matrix. Matching the refractive indices eliminates the baseline offset in spectra and the apparent absorbance at the interface that arises from scattering. [Reproduced from Ref. 158, copyright American Chemical Society.]
The delineation between these two types of useful spectra is an important distinction and cannot be over-emphasized here. The recorded data contain effects arising from both the real part of the refractive index (scattering, for example) and the imaginary part (absorption). They also contain the effects of the “interaction” term due to the relationship of the two components of the refractive index and especially due to anomalous dispersion. While the recorded data can be used directly to extract information, classical spectroscopic analyses have focused on relating the absorbance to specific molecular content via chemometric methods. We do not focus on chemometric methods here as there are several excellent compilations describing the same for spectroscopy,160 in general, and for imaging,161,162 in particular. The extraction of absorption spectra from recorded data occurs prior to the application of chemometric methods. Unless information is extracted in terms of the underlying molecular content and the contributions of structure recognized, in general, the application of chemometric methods cannot provide the correct results.
Extracting Spatial and Spectral Information
Three major groups of efforts can be discerned in the area of extracting information from recorded data. In the first, an understanding of the underlying physics of the problem is targeted and the goal is to recover the spectral and spatial structure of the sample as accurately as permitted by the measurements via maps of the real and imaginary parts of the refractive index. We term these “analytic” approaches. In the second, a sufficient recovery of absorption spectra is targeted to achieve the desired molecular identification or understanding. Approaches in this stream may range from simple signal processing approaches to more complex representations of the sample and optics but the underlying light–matter interaction is not directly targeted for the specific sample. We term these “model-based” approaches as they necessarily idealize the sample to a simple geometric structure such as a sphere and/or idealize the optics to a simple plane wave. The third set of approaches is essentially what largely exists today in commercial instruments' software and consists of simple baseline and offset correction or fitting a more complex shape to the spectrum. We term these “ad hoc” approaches as they rely largely on a subjective decision made by the investigator and only have a loose rationale in the selection of a particular approach. The benefit of the first set is clearly in the accuracy of understanding and purity of information available but also requires significant effort in algorithms and computation. Analogous to the development of the forward prediction, it is essentially a solution of the inverse problem. The speed of information extraction is the obvious benefit of the last approach but there is limited insight into the properties of the sample and no assurance that the most accurate molecular information contained in the data is extracted. The model-based approaches lie in the middle of these extremes. While they can be very effective for some samples, based on careful selection of the model, they do not offer a general solution and require some computational effort to extract information.
Analytic Approaches
Both the successes of IR imaging and the need for further analytic approaches are perhaps best illustrated with a case study, as shown in Fig. 11. Here, IR imaging is applied for latent print analysis.163 Oils and skin can be visualized easily from absorption spectra using appropriate vibrational modes. The first goal here was simply to visualize the presence of prints and organic material, which is easily accomplished without the need for any extensive spectral analysis (Fig. 11A). The power of IR imaging is apparent in further analysis, however. The spatial specificity of the technique leads to enhanced spectral sensitivity when a material of interest can be localized, for example in particulate trace evidence within prints. Again spectral features may be used to identify a molecular species associated with the particulate matter. In this case, the explosive RDX is easily detected using vibrational modes that are clearly indicative of this material and not found in most other materials. Delving further, simply examining the absorbance at a common vibrational mode such as CH stretching allows facile detection of other trace evidence such as fibers. Fibers, by themselves, form a very important class of forensic interest and their molecular identification can prove powerful. The recorded spectrum from a fiber that has the same diameter as the wavelength of light, however, demonstrates the effects of light scattering and diffraction that make molecular identification difficult. Thus, as the complexity of the problem and the need for information increase, the methods require progressively more effort. The first years of IR imaging technology proved very successful in applications without significant efforts in understanding the data as simpler applications (such as visualizing the structure of materials164 or measuring diffusion165) were targeted. Today, instrumentation is mature and the next level of complexity is being targeted for information extraction. Hence, approaches to extract absorption spectra from recorded data are going to become more commonly reported and used.
Fig. 11.
(A) RGB image of a fingerprint obtained using oil, protein, and particulate matter-specific absorbance modes, respectively. (B) Expanded view of the box in A. (C) Spectra of the components showing the bands indicative of the specific components. (D) A single fiber can be seen in the print with a particle next to it. The trace evidence can also be idealized to be cylindrical or spherical in shape. Modeling predicts the shape dependence of spectra, dramatically altering the recorded data for the same material. [Reproduced with permission from Refs. 163 (A–D, copyright Springer), 167 (cylinder spectra, copyright American Chemical Society), and 168 (sphere spectra, copyright Society for Applied Spectroscopy).]
The need for such methods is illustrated in the spectra from the particulate matter in Fig. 11, and the effect of shape is clearly evident in the predictions of recorded data in the spectra of fibers and spheres. Spectra from the same material are significantly affected, which can lead to erroneous conclusions. Fiber analysis by IR microscopy166 is widely reported and can be used easily for major classes of materials. Finer distinctions in molecular content and changes, however, are not easily measurable or quantitative and require special sample preparation. Clearly, if absorbance spectra cannot be extracted, recorded data would not provide accurate information, for example on polarization to understand molecular structure or surface modifications—both of which are important considerations in fibers. While forward modeling (Fig. 11D) indicates that recorded spectra are difficult to use directly, the same can be extended to predict dynamic spectral changes, effects on molecular orientation, or surface modifications, though no studies have been reported. More useful would be the extraction of absorption spectra from recorded data. An algorithm that enables this recovery from cylindrical objects that have physical dimensions of the order of the wavelength of light has been formulated.167 Spectra clearly corresponding to the bulk spectra of materials could be recovered and the effect of optical phenomena could be removed. A similar effort for spheres168 is reported and demonstrates a similar success in recovering molecular information.
As the studies for spheres and cylinders indicate, the use of analytic approaches for spectral extraction can be greatly simplified by knowledge of the sample. If the sample thickness is known a priori, for example, iterative techniques can be used to estimate the absorbance from IR imaging data for thin films. In the absence of thickness information, co-estimating both geometry and spectra is difficult and convergence to the correct result is not always guaranteed. Hence, an intelligent strategy is required to extract knowledge optimally, and no simple approach exists that is valid in all cases. In the case of uniform films, for example, reflection fringes can be used to estimate the real part of the refractive index and thickness, which can be subsequently used to inform the recovery of the imaginary part of the refractive index at other spectral positions. Despite the successes noted above for specific cases and the suggested approximations from the homogeneous case, simultaneously recovering both the geometry and spectra of samples using IR imaging is an open problem and the subject of current research. One example of the potential of the success of this approach can be seen in Fig. 12, which demonstrates the extraction of absorption spectra from cylindrical objects. We do not discuss other approaches under development here but it is clear that the near future will see the emergence of practical algorithms and their integration with instrumentation. It must be noted that the recovery of spectral information is dependent on the quality and extent of input information. High SNR, extended wavelength, and larger spatial areas than the sample would need to be measured to assure more accurate data recovery. It is expected that future instrumentation will be designed with the goal of recovering such information rather than simply acquiring data of the highest SNR and will be based partly on the insights offered by analytical approaches to recover molecular spectra. The computational burden on IR imaging will undoubtedly increase with the use of these algorithms, and effective strategies (both hardware and software) will be needed to extract molecular spectra.
Fig. 12.
The state of the art in available algorithms can successfully estimate the correct absorbance and refractive index from samples of known shapes. Reconstructions and true values of the complex refractive index are shown for fibers of radius 5 μm (A–C) and 10 μm (D–F). [Reproduced with permission from Ref. 167, copyright American Chemical Society.]
Model-Based Approaches
While the theory and corresponding approaches described above are effective in recovering absorption data, approximations have also been proposed to model real samples as consisting of absorbing and scattering objects. With a definite object and simplified optical interactions, facile fitting to scattering features observed in spectra can be conducted very rapidly, largely because the specifics of the particular sample do not have to be modeled. Considerable recent interest has focused on Mie-type scattering and absorption.169 The forward problem in this approach is rather straightforward in that the scattering of specific objects is well described in books.170 The inverse implementation for imaging is interesting. Details of the procedure are available in the studies described here; hence, we will summarize only the most interesting features of this approach. One of the popular means to correct for the effects of scattering on spectra has been essentially to model the effects for given properties of the sample and build a lookup table. Matching observed with known spectra can then be employed to correct for the observed changes compared to what may be expected in the absence of such chang-es.171,172 Using spheres, spectral distortion could be demonstrated, compared to the bulk spectrum of the same polymer film.173 The topic is relatively recent in the field of microscopy, though it has been recognized for spectroscopic measurements in other applications of IR spectroscopy.174 Variations on the use of a scattering model have been proposed. For example, resonant Mie scattering (RMieS) was claimed to be corrected using an improved iterative algorithm. The application of full Mie theory considerably enhances the computational load, which was alleviated by using graphical processing unit (GPU)-based processing.175 Another caveat in iterative methods is noise accumulation, which was avoided by using a curve-fitting step. To date, no modifications have been reported in the illumination and collection optics associated with the extraction. This extension is likely possible and the models could become more sophisticated. The increasing sophistication, however, will deprive methods of their computational simplicity and abilities in straightforward application. At the extreme, they will involve the same effort as analytical approaches. Hence, it is difficult to foresee that significant conceptual effort in increasing the sophistication of the models will result in more accurate analyses. Rather, in the opinion of the author, a diversity of models will likely be available and significant efforts will be spent in choosing one and validating it for use in a specific application.
The use of models to understand spectra and extract absorbance data is often stated as a correction. The author of this manuscript is not in favor of using the term “correct.” The spectra are already correct in that they correctly reflect the underlying chemical and physical (which are both related) structures. A better term would be to “extract” absorption spectra since the absorption measure is obtained from the recorded spectrum in which absorption and scattering are co-mingled. Hence, in this manuscript, we employ the term extraction and urge readers to do the same.
Significant caution should be exercised in employing model-based approaches to extract absorption spectra. To extract spectra accurately, the underlying structure of the sample must fit the model and approximations precisely to be valid under all conditions. For example, the extended multiplicative scatter correction approach was carefully developed and validated for a specific set of samples with a clear validation endpoint (indistinguishable performance in the calibration and test set).176 The algorithm, obviously, should not be applied to all types of spectra that may include other optical phenomena nor should accuracy in extracting chemical information be claimed in the absence of a strict and valid endpoint. Simply obtaining spectra that seem to be accurate does not guarantee that the intensities, band shapes, and positions are indeed correct. If rigorous tests for applicability are not conducted, the extracted spectrum may change (other than simple Beer's law re-scaling) with thickness of the sample, or change in the optical setup or with spectral resolution. Since model-based approaches are essentially an empirical test, not only should the ideal sample be tested but all possible combinations of thickness, optical effects, range of sample properties, and their variations with optical setups must be tested against a gold standard. While model-based approaches are convenient and useful, this stringent and onerous requirement for robustness is a likely barrier to their effective use. More sophisticated models of beam propagation and acquisition are needed and model-based approaches being replaced by analytical approaches will likely be a future trend.
Ad Hoc Approaches
The simplest approach to extracting absorbance from measured spectra, and the first good approximation in many cases, remains to choose points across a band and remove the baseline offset. The underlying assumption in this approach is that the effects of refractive index mismatch did not significantly change the recorded data's peak absorbance, position, or shape beyond the noise level. This type of approach, in conjunction with eliminating spectral features that likely did not benefit from this approach, provided excellent results in tissue classification, for example.177 The success in that study does not imply success for all cases, whereas there is no guarantee that more complicated methods to remove the effects of scattering would perform significantly better. Analytical absorption extraction methods will be better, in general, while model-based methods may perform better or worse or may be more effective in certain spectral regions than in others. Success depends on the optical setup and the characteristics of the sample. Hence, it remains unclear whether ad hoc approaches are any better or worse than model-based approaches. In any case, the two approaches cannot perform any better than what appropriate analytical modeling may provide. Hence, the value of ad hoc approaches will likely persist for exceptionally rapid but qualitative understanding of the data in the absence of a framework to correctly estimate optical properties of the sample along with its structure or as starting points for algorithms solving the inverse problem.
Improving Imaging Data by Computational Approaches
While the approaches above are focused on extracting molecular data, other approaches can be used in conjunction to estimate and improve the spectral and spatial content of information. The class of techniques discussed below, hence, lies between extracting information and chemometrics. Among the approaches to improve data, noise reduction strategies are of most importance. While noise determines the quantification limits and ultimate sensitivity of measurements, reduction of noise has taken on added importance with the advent of HD imaging and computational algorithms to extract absorbance. The second area would be in the domain of enhancing the clarity of an image or enhancing the features in a manner similar to optical microscopy.178 A note of caution must be repeated in the use of computational approaches to suppress noise or any other enhancements. Over-processing data may lead to such severe distortions that the underlying information may change. Even small implementations to improve visualization must be understood and interpreted correctly by the practicing spectroscopist. In IR imaging, the spectral and spatial domain are clearly linked. Hence, changes or improvements in one affect the other. Two areas that are likely to be the focus of activities in this theme are discussed next.
Noise Reduction
Spectral noise is a significantly greater concern in imaging compared to bulk spectroscopy. While appropriate data collection by optimizing the optical and experimental parameters is the ideal route to obtaining the highest SNR, limited time and resources may not always make that possible. Numerical methods for noise rejection have been proposed and can be useful for rapid acquisition of data. The transformation may involve simple smoothing since signals are generally of lower frequencies while noise is both high and low frequency, determining correlations using point-wise179 or multivariate means, or statistical recon-struction180 or wavelet transforms.181 Smoothing results in loss of spectral detail but can enhance spectral sensitivity and provide lower noise images, is rapid, and can be easily implemented. To take advantage of the statistical properties of many pixels in an imaging experiment, however, transform methods may be able to preserve both spectral and spatial quality. In transform or reconstruction methods, successful noise rejection first involves recognizing a property of noise that is distinct from that of the signal. Second, the noisy data need to be transformed such that the characteristic spectral features are collected in some components of the transformed space and noise is isolated in others. Third, a cut-off needs to be selected such that the information-rich components can be identified. Finally, an inverse transform of the components identified as bearing information needs to be conducted to recover high SNR data. The type and quantity of available data often dictates the optimal method.
The use of the multivariate covariance method is especially interesting when large numbers of spectra are available, which is usually the case for spectroscopic imaging data, for example, principal components analysis.183 One example of the potential of this approach can be seen using a method based on a modified principal components analysis, termed the minimum noise fraction (MNF),183 which has been used for several different systems and demonstrates broad efficacy.184–187 While the need for an observer to select eigenimages for transformation was often an impediment, this process can be effectively automated and excellent reliability can be obtained in recovering analytical ability of measurements.188 The quality improvement can be observed in Fig. 13. Upon de-noising, significant recovery of spectral and spatial details can be observed. Though very successful, it must be noted that any such method results in loss of information (signal). The goal should be to limit the loss to be no larger than the uncertainty introduced by measurement noise in the original data set. Though analysis and image quality are greatly improved, it must be realized that the noise-reduced signal in these cases contains a statistically estimated SNR and users must be cautious in drawing conclusions such as detection limits or estimating the variance in the data.189 While this approach to noise reduction was not particularly required for imaging with larger pixels, the HD imaging approach has resulted in a large reduction in the signal and the SNR. For HD imaging, signal processing represents a useful tool that can be routinely used.
Fig. 13.
(A) Acquired high SNR data and simulated noisy spectra (peak-to-peak noise = 0.001, 0.01, 0.1, and 0.4 a.u.), showing the degradation in data quality. Spectra are offset for clarity. (B) Spectra after noise reduction demonstrate the dramatic gains possible by chemometric methods. (C) Noise reduction was implemented to classify breast tissue and application of noise rejection allowed the same quality of classification (accuracy) to be recovered at higher noise levels. (D) In another example, image fidelity (here the nitrile stretching vibrational mode at 2227 cm−1) is much enhanced as a result of spectral noise rejection. [Figures A and C reproduced with permission from Ref. 188, copyright Royal Society of Chemistry. Figure D reproduced with permission from Ref. 184, copyright Society for Applied Spectroscopy.]
Deconvolution
Several studies have employed signal processing techniques to improve image quality.190 The techniques essentially rely on minimizing (or maximizing) a cost function and can be implemented without user input or knowledge of the actual instrumentation or sample. While these properties make such methods robust and widely applicable, they also lead to a general smoothing of features and sharpening of the related visualization parameters of image details and contrast. While these techniques are useful for visualization, the images are estimates of the true microstructure. The less information about the optical setup such methods contain, however, the greater is the chance they may deviate from the true sample structure. Given the recent advances in theory and modeling as well as the availability of computing power, the best approach may be to use the actual performance of the microscope to inform the reconstruction. An example of merging optical theory with signal processing approaches is also available.191 With the emergence of HD imaging and development of nanoscale imaging, the gap between imaging modalities is closing. Hence, given the ability to acquire data directly and the uncertainty associated with structures after reconstructions, simple techniques to estimate smaller than wavelength features are of diminishing value.
Concluding Remarks
This is an exciting time in the IR imaging and microscopy field. New theory and instruments have opened new capabilities. One of the most critical aspects of IR imaging technology is the FPA. Mercury-cadmium-telluride (MCT) FPAs are commonly employed due to their wide spectral sensitivity and good detection characteristics. While the first generation's problems of stability and device reliability have largely been addressed by chemical vapor deposition technology and the MCT alloy chemistry is well-established, the overall detector performance can be significantly improved. The electronics for these FPAs, in particular, are noisy and slow compared to state-of-the art readouts widely available in other spectral regions. Ten-fold-lower noise in ten-fold-faster readout electronics can potentially provide video rate IR spectroscopic imaging. The small format of available arrays (128 × 128) can also be improved. There are recent reports with faster detectors and larger formats192 that will considerably enhance the quality of available data. Even better performance may be expected from emerging technologies. While speed and size will increase, the impetus for the same has received a boost from recent developments. Given the limited flux from globar sources and smaller beam sizes from the brighter sources, significantly larger formats were not thought to be very important. With the advent of HD imaging, however, there is significant value in pursuing smaller pixel sizes and larger formats.
The availability of multiple new components that are driven by sound fundamental advances further portends an acceleration of activity. New concepts such as extraction of absorbance by separating chemical and structural effects as well as new computational concepts such as compressed sensing will not only change the practice of spectroscopy but will bring computing and instrumentation closer. While we have not discussed applications here, the development of new capabilities is likely to transform applications as well. The last major technological innovations in IR imaging are almost ten years old. The next cycle of advances is likely to come from the application of new theory. As a better understanding and availability of the new components improves, new optical configurations will likely be seen. Hardware developments are likely to enable new application areas and, in turn, spur the development of faster algorithms and signal-processing strategies to store data, perform spectral corrections, and extract information.
The various facets of IR imaging technology and applications actually form an integrated cycle as shown in Fig. 14. For each of the major categories in the inner circle, there are many choices available to the spectroscopist today in designing a particular study. The cycle of development of theory consisting of various approaches, individual components integrated into higher performing instrumentation, and algorithms and software for signal processing and data management must be tuned together with the application in mind for an optimal solution. While such an approach has not been commercially demonstrated, several research groups are working to include specific aspects of each into their particular solutions. Individual developments in each of these aspects and the synergistic integration of one or more of these components are likely to prove the most beneficial. Any of the factors can be central to this integration but, in the author's opinion, we will likely see evolution around applications. In principle, the recent advances make it possible to analytically predict the performance and utility of IR imaging for any application for a given system design. Hence, simulations from problem to solution can be developed for the design of instruments and analytical strategies by a careful combination of hardware, algorithms based on the physics of the setup, and robust reconstruction to provide the highest quality information. In the opinion of the author, the summary achievement of recent advances has been to enable the spectrometrist or engineer to quantitatively measure, model, and manufacture IR imaging systems guided by rigorous application of fundamental scientific principles. The resulting benefits, in turn, are likely to significantly enhance the applied spectroscopist's ability to extract meaningful information and solve important problems.
Fig 14.
Overview of IR imaging and developing areas of activity.
Acknowledgments
The author would like to acknowledge the contributions of colleagues and students who were involved in various studies on which this review is based, including Ira W. Levin, Stephen M. Hewitt, P. Scott Carney, Brian Cunningham, Brynmor Davis, Matthew Schulmerich, Michael J. Walsh, Anil K. Kodali, Rohith K. Reddy, Thomas van Dijk, Kevin Yeh, Matthew Kole, and Matthew Gelber. Support for this work from the National Institutes of Health (R01CA138882 and 1R01EB009745) and the National Science Foundation (CHE 0957849) is gratefully acknowledged. This article is dedicated to Prof. Peter Griffiths, from whose works the author has greatly benefited, on the completion of his term as the editor-in-chief of Applied Spectroscopy.
References
- 1.Colarusso P, Kidder LH, Levin IW, Fraser JC, Arens JF, Lewis EN. Infrared Spectroscopic Imaging: From Planetary to Cellular Systems. Appl Spectrosc. 1998;52:106A–120A. [Google Scholar]
- 2.Levin IW, Bhargava R. Fourier Transform Infrared Vibrational Spectroscopic Imaging: Integration of Microscopy and Molecular Recognition. Annu Rev Phys Chem. 2005;56:429–474. doi: 10.1146/annurev.physchem.56.092503.141205. [DOI] [PubMed] [Google Scholar]
- 3.Walsh MJ, Reddy RK, Bhargava R. Label-free Biomedical Imaging with Mid-Infrared Microspectroscopy. IEEE J Sel Top Quant. 2012;18(4):1502–1513. [Google Scholar]
- 4.Chan KLA, Kazarian SG. New opportunities in micro- and macro-attenuated total reflection infrared spectroscopic imaging: Spatial resolution and sampling versatility. Appl Spectrosc. 2003;57(4):381–389. doi: 10.1366/00037020360625907. [DOI] [PubMed] [Google Scholar]
- 5.Bhargava R, Levin IW, editors. Spectrochemical Analysis Using Infrared Multichannel Detectors. Oxford, UK: Wiley-Blackwell; 2005. [Google Scholar]
- 6.Salzer R, Siesler HW. Infrared and Raman Spectroscopic Imaging. New York, NY: Wiley-VCH; 2009. [Google Scholar]
- 7.Sasic S, Ozaki Y. Raman, Infrared and Near-Infrared Chemical Imaging. New York, NY: John Wiley; 2010. [Google Scholar]
- 8.Suci PA, Siedlecki KJ, Palmer RJ, White DC, Geesey GG. Combined Light Microscopy and Attenuated Total Reflection Fourier Transform Infrared Spectroscopy for Integration of Biofilm Structure, Distribution, and Chemistry at Solid-Liquid Interfaces. Appl Environ Microbiol. 1997;63(11):4600–4603. doi: 10.1128/aem.63.11.4600-4603.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Srinivasan G, Bhargava R. Fourier transform-infrared spectroscopic imaging: The emerging evolution from a microscopy tool to a cancer imaging modality. Spectroscopy. 2007;22(7):30. [Google Scholar]
- 10.Diem M, Romeo M, Boydston-White S, Miljkoviæ M, Matthäus C. A decade of vibrational micro-spectroscopy of human cells and tissue (1994–2004) Analyst. 2004;129(10):880–885. doi: 10.1039/b408952a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bhargava R, Wang SQ, Koenig JL. FTIR microspectroscopy of polymeric systems. Adv Polym Sci. 2003;163:137–191. [Google Scholar]
- 12.Diem M, Griffiths PR, Chalmers JM, editors. Vibrational Spectroscopy for Medical Diagnosis. Chichester, UK: Wiley; 2008. [Google Scholar]
- 13.Prati S, Joseph E, Sciutto G, Mazzeo R. New advances in the application of FTIR microscopy and spectroscopy for the characterization of artistic materials. Acc Chem Res. 2010;43(6):792–801. doi: 10.1021/ar900274f. [DOI] [PubMed] [Google Scholar]
- 14.Carter EA, Tam KK, Armstrong RS, Lay PA. Vibrational spectroscopic mapping and imaging of tissues and cells. Biophys Rev. 2009;1:95–103. doi: 10.1007/s12551-009-0012-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Petibois C, Desbat B. Clinical application of FTIR imaging: New reasons for hope. Trends Biotechnol. 2010;28(10):495–500. doi: 10.1016/j.tibtech.2010.07.003. [DOI] [PubMed] [Google Scholar]
- 16.Bellisola G, Sorio M. Infrared spectroscopy and microscopy in cancer research and diagnosis. Am J Cancer Res. 2012;2:1–21. [PMC free article] [PubMed] [Google Scholar]
- 17.Griffiths PR, DeHaseth JA. Fourier transform infrared spectrometry. 2nd Hoboken, NJ: John Wiley and Sons; 2007. [Google Scholar]
- 18.Lucas M, Riedo E. Combining scanning probe microscopy with optical spectroscopy for applications in biology and materials science. Rev Sci Instrum. 2012;83:061101. doi: 10.1063/1.4720102. [DOI] [PubMed] [Google Scholar]
- 19.Huth F, Govyadinov A, Amarie S, Nuansing W, Keilmann F, Hillenbrand R. Nano-FTIR absorption spectroscopy of molecular fingerprints at 20 nm spatial resolution. Nano Lett. 2012 doi: 10.1021/nl301159v. Paper in press. [DOI] [PubMed] [Google Scholar]
- 20.Paulite M, Li ITS, Gunari N, Tanur AE, Walker GC. Imaging Secondary Structure of Individual Amyloid Fibrils of a β2-Microglobulin Fragment Using Near-Field Infrared Spectroscopy. J Am Chem Soc. 2011;133(19):7376–7383. doi: 10.1021/ja109316p. [DOI] [PubMed] [Google Scholar]
- 21.Jones AC, Raschke MB. Thermal infrared near-field optical spectroscopy. Nano Lett. 2012;12(3):1475–1481. doi: 10.1021/nl204201g. [DOI] [PubMed] [Google Scholar]
- 22.Huth F, Schnell M, Wittborn J, Ocelic N, Hillenbrand R. Infrared-spectroscopic nanoimaging with a thermal source. Nature Mater. 2011;10:352–356. doi: 10.1038/nmat3006. [DOI] [PubMed] [Google Scholar]
- 23.Ishibe K, Nakada S, Mera Y, Maeda K. Nanoprobe Fourier-transform photoabsorption spectroscopy using a supercontinuum light source. Microsc Microanal. 2012;18(3):591–595. doi: 10.1017/S1431927612000219. [DOI] [PubMed] [Google Scholar]
- 24.Keilmann F, Hillenbrand R. Nano-Optics and Near-Field Optical Microscopy. Boston/London: Artech House; 2008. [Google Scholar]
- 25.Bhargava R, Wall BG, Koenig JL. Comparison of the FT-IR mapping and imaging techniques applied to polymeric systems. Appl Spectrosc. 2000;54:470–479. [Google Scholar]
- 26.Kwiatkoski JM, Reffner JA. FT-IR Microspectrometry Advances. Nature. 1987;328:837–838. [Google Scholar]
- 27.Wetzel DA, LeVine SM. Microspectroscopy - Imaging molecular chemistry with infrared microscopy. Science. 1999;285:1224–1225. doi: 10.1126/science.285.5431.1224. [DOI] [PubMed] [Google Scholar]
- 28.Reading M, et al. Thermally assisted nanosampling and analysis using micro-IR spectroscopy and other analytical methods. Vib Spectrosc. 2002;29(1–2):257–260. [Google Scholar]
- 29.Hammiche A, Pollock HM, Reading M, Claybourn M, Turner PH, Jewkes K. Photothermal FT-IR spectroscopy: A step towards FT-IR microscopy at a resolution better than the diffraction limit. Appl Spectrosc. 1999;53(7):810–815. [Google Scholar]
- 30.Kwon B, Wang C, Park K, Bhargava R, King WP. Thermomechanical Sensitivity of Microcantilevers in the Mid-infrared Spectral Region. Nano Micro. Thermophys Eng. 2011;15:16–28. [Google Scholar]
- 31.Kwon B, Rosenberger M, Bhargava R, Cahill DG, King WP. Dynamic Thermo-mechanical Response of Bimaterial Micro-cantilevers to Periodic Heating by Infrared Radiation. Rev Sci Instrum. 2012;83:015003. doi: 10.1063/1.3680107. [DOI] [PubMed] [Google Scholar]
- 32.Park K, Lee J, Bhargava R, King WP. Femtogram-Level Sampling for Spectroscopic Analysis Using Functional Self-Cleaning Scanning Probe Tips. Anal Chem. 2008;80:3221–3228. doi: 10.1021/ac702423c. [DOI] [PubMed] [Google Scholar]
- 33.Lewis EN, et al. Fourier transform spectroscopic imaging using an infrared focalplane array detector. Anal Chem. 1995;67(19):3377–81. doi: 10.1021/ac00115a003. [DOI] [PubMed] [Google Scholar]
- 34.Kidder L, Levin I, Lewis E, Kleiman V, Heilweil E. Mercury cadmium telluride focalplane array detection for mid-infrared Fourier-transform spectroscopic imaging. Opt Lett. 1997;22:742–744. doi: 10.1364/ol.22.000742. [DOI] [PubMed] [Google Scholar]
- 35.Bennett CL, Carter MR, Fields DJ. Hyperspectral imaging in the infrared using LIFTIRS. Proc SPIE. 1995;2552(1):274–283. [Google Scholar]
- 36.Treado PJ, Levin IW, Lewis EN. Near-Infrared Acousto-optic Filtered Spectroscopic Microscopy: A Solid-State Approach to Chemical Imaging. Appl Spectrosc. 1992;46:553–559. [Google Scholar]
- 37.Lewis EN, Levin IW. Real-Time, Mid-Infrared Spectroscopic Imaging Microscopy Using Indium Antimonide Focal-Plane Array Detection. Appl Spectrosc. 1995;49:672–678. [Google Scholar]
- 38.Snively CM, Koenig JL. Characterizing the Performance of a Fast FT-IR Imaging Spectrometer. Appl Spectrosc. 1999;53(2):170–177. [Google Scholar]
- 39.Bhargava R, Fernandez DC, Schaeberle MD, Levin IW. Towards Faster FTIR Imaging. Appl Spectrosc. 2001;55:1079–1084. [Google Scholar]
- 40.Snively CM, Katzenberger S, Oskarsdottir O, Lauterbach J. Fourier-transform infrared imaging using a rapid-scan spectrometer. Opt Lett. 1999;24(24):1841–1843. doi: 10.1364/ol.24.001841. [DOI] [PubMed] [Google Scholar]
- 41.Huffman SW, Bhargava R, Levin IW. A Generalized Implementation of Rapid-Scan Fourier Transform Infrared Spectroscopic Imaging. Appl Spectrosc. 2002;56:965–969. [Google Scholar]
- 42.Bhargava R, Levin IW. Time Resolved Fourier Transform Infrared Spectroscopic Imaging. Appl Spectrosc. 2003;57:357–366. doi: 10.1366/00037020360625880. [DOI] [PubMed] [Google Scholar]
- 43.Bhargava R, Levin IW. Non-invasive Imaging of Molecular Dynamics in Heterogeneous Materials. Macromolecules. 2003;36:92–96. [Google Scholar]
- 44.Bhargava R, Levin IW. Enhanced Timeresolved Fourier Transform Infrared Spectroscopic Imaging for Reversible Dynamics. J Phys Chem A. 2004;108:3896–3901. [Google Scholar]
- 45.Bhargava R, Levin IW. Probing the Structure and Dynamics of Macromolecular Composites by Infrared Spectroscopy and Imaging. Vib Spectrosc. 2004;34:13–24. [Google Scholar]
- 46.Kim MS, Delwiche SR, Chao K, Garrido-Varo A, Pérez-Marín D, Lefcourt AM, Chan DE. Visible to SWIR hyper-spectral imaging for produce safety and quality evaluation. Sens Instrum Food Qual Safety. 2011;5(5):155–164. [Google Scholar]
- 47.Faist J, Capasso F, Sivco DL, et al. Quantum cascade laser. Science. 1994;264:553–556. doi: 10.1126/science.264.5158.553. [DOI] [PubMed] [Google Scholar]
- 48.Koenig JL, Wang SQ, Bhargava R. FTIR Images: A picture is worth a thousand spectra. Anal Chem. 2001;73:351A–391A. doi: 10.1021/ac012471p. [DOI] [PubMed] [Google Scholar]
- 49.Bhargava R, Levin IW. FTIR imaging: Theory and Practice. Anal Chem. 2001;73:5157–5167. doi: 10.1021/ac010380m. [DOI] [PubMed] [Google Scholar]
- 50.Reffner JA, Martoglio PA, Williams GP. Fourier transform infrared microscopical analysis with synchrotron radiation: The microscope optics and system performance. Rev Sci Instrum. 1995;66(2):1298–1302. [Google Scholar]
- 51.Dumas P, Carr GL, Williams GP. Enhancing the lateral resolution in infrared microspectrometry by using synchrotron radiation: Applications and perspectives. Analusis. 2000;28(1):68–74. [Google Scholar]
- 52.Jamin N, Dumas P, Moncuit J, Fridman WH, Teillaud JL, Carr GL, Williams GP. Highly resolved chemical imaging of living cells by using synchrotron infrared microspectrometry. Proc Natl Acad Sci USA. 1998;95(9):4837–4840. doi: 10.1073/pnas.95.9.4837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Miller LM, Smith RJ. Synchrotrons versus globars, point-detectors versus focal plane arrays: Selecting the best source and detector for specific infrared microspectroscopy and imaging applications. Vib Spectrosc. 2005;38(1-2):237–240. [Google Scholar]
- 54.Petibois C, Piccinini M, CestelliGuidi M, Déléris G, Marcelli A. Infrared synchrotron sources—a boon for biology. Nat Photonics. 2009;3:177. [Google Scholar]
- 55.Martin MC, Schade U, Lerch P, Dumas P. Recent applications and current trends in analytical chemistry using synchrotron-based Fourier-transform infrared microspectroscopy. TrAC - Trends Anal Chem. 2010;29(6):453–463. [Google Scholar]
- 56.Hirschmugl CJ, Gough KM. Fourier Transform Infrared Spectrochemical Imaging: Review of Design and Applications with a Focal Plane Array and Multiple Beam Synchrotron Radiation Source. Appl Spectrosc. 2012;66(5):475–491. doi: 10.1366/12-06629. [DOI] [PubMed] [Google Scholar]
- 57.Carr GL, Chubar O, Dumas P, Bhargava R, Levin IW, editors. Spectrochemical Analysis Using Infrared Multichannel Detectors. Oxford, UK: Wiley-Blackwell; 2005. pp. 56–84. [Google Scholar]
- 58.Moss D, Gasharova B, Mathis YL. Practical tests of a focal plane array detector microscope at the ANKA-IR beamline. Inf Phys Tech. 2006;49(1-2):53–56. [Google Scholar]
- 59.Nasse MJ, Walsh MJ, Mattson EC, et al. High-resolution Fourier-transform infrared chemical imaging with multiple synchrotron beams. Nat Meth. 2011;8(5):413–416. doi: 10.1038/nmeth.1585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Yeh K, Reddy RK, Bhargava R. Fourier transform infrared spectroscopic imaging. In: Anastasio M, La Riviere P, editors. Emerging Imaging Technologies for Medicine. Boca Raton, FL: Taylor Francis/CRC Press; 2012. [Google Scholar]
- 61.Kim KJ, Sessler A. Free-electron lasers: present status and future prospects. Science. 1990;250:88. doi: 10.1126/science.250.4977.88. [DOI] [PubMed] [Google Scholar]
- 62.Hong MK, Jeung AG, Dokholyan NV, Smith TI, Schwettman HA, Huie P, Erramilli S. Imaging single living cells with a scanning near-field infrared microscope based on a free electron laser. Nucl Instrum Meth Phys Res B. 1998;144(1-4):246–255. [Google Scholar]
- 63.Edwards GS, Allen SJ, Haglund RF. Applications of free-electron lasers in the biological and material sciences. Photochem Photobiol. 2005;81(4):711–735. doi: 10.1562/2004-11-08-IR-363. [DOI] [PubMed] [Google Scholar]
- 64.Nakajima Y, Iwatsuki K, Ishii K, Suzuki S, Fujinaka T, Yoshimine T, Awazu K. Medical application of an infrared free-electron laser: selective removal of cholesterol ester in carotid artery atheromatous plaques. J Neurosurg. 2006;104(3):426–428. doi: 10.3171/jns.2006.104.3.426. [DOI] [PubMed] [Google Scholar]
- 65.Vobornik D, Margaritondo G, Sanghera JS, et al. Spectroscopic infrared scanning near-field optical microscopy (IR-SNOM) J Alloys Comp. 2005;401:80–85. [Google Scholar]
- 66.Policar C, Waern JB, Plamont MA, Clède S, Mayet C, Prazeres R, Ortega JM, Vessières A, Dazzi A. Subcellular IR Imaging of a Metal–Carbonyl Moiety Using Photothermally Induced Resonance. Angew Chem Int Ed. 2011;50:860–864. doi: 10.1002/anie.201003161. [DOI] [PubMed] [Google Scholar]
- 67.Elmore DL, Tsao MW, Frisk S, et al. Design and performance of a planar array infrared spectrograph that operates in the 3400 to 2000 cm−1 region. Appl Spectrosc. 2002;56(2):145–149. [Google Scholar]
- 68.Arrivo SM, Kleiman VD, Dougherty TP, Heilweil EJ. Broadband femtosecond transient infrared spectroscopy using a 256×256 element indium antimonide focal-plane detector. Opt Lett. 1997;22(19):1488–1490. doi: 10.1364/ol.22.001488. [DOI] [PubMed] [Google Scholar]
- 69.Michaels CA, Stranick SJ, Richter LJ, Cavanagh RR. Scanning near-field infrared microscopy and spectroscopy with a broadband laser source. J Appl Phys. 2000;88(8):4832–4839. [Google Scholar]
- 70.Pellerin C, Snively CM, Chase DB, et al. Performance and application of a new planar array infrared spectrograph operating in the mid-infrared (2000-975 cm(-1)) fingerprint region. Appl Spectrosc. 2004;58(6):639–646. doi: 10.1366/000370204873060. [DOI] [PubMed] [Google Scholar]
- 71.Snively CM, Pellerin C, Rabolt JF, et al. Acquisition of mid-infrared spectra from nonrepeatable events with sub-100-mu s temporal resolution using planar array infrared spectroscopy. Anal Chem. 2004;76(7):1811–1816. doi: 10.1021/ac0499118. [DOI] [PubMed] [Google Scholar]
- 72.Shin KY, Snively CM, Rabolt JF, et al. Development of a planar array infrared reflection spectrograph for reflection-absorption spectroscopy of thin films at metal and water surfaces. Appl Spectrosc. 2007;61(9):916–920. doi: 10.1366/000370207781745865. [DOI] [PubMed] [Google Scholar]
- 73.Snively CM, Kim YS, Chase DB, et al. Rapid detection of low concentrations of aqueous species in the presence of spectral overlap using planar array infrared spectroscopy. Appl Spectrosc. 2008;62(3):337–339. doi: 10.1366/000370208783759777. [DOI] [PubMed] [Google Scholar]
- 74.Keltner Z, Kayima K, Lanzarotta A, Lavalle L, Canepa M, Dowrey AE, Story GM, Marcott C, Sommer AJ. Prism Based Infrared Spectrographs using Modern-Day Detectors. Appl Spectrosc. 2007;61(9):909–915. doi: 10.1366/000370207781745982. [DOI] [PubMed] [Google Scholar]
- 75.Lanzarotta A, Marcott CA, Story GM, Dowrey AE, Sommer AJ. Infrared microspectroscopy using prism-based spectrographs and focal plane array detection. Appl Spectrosc. 2012;66(3):304–311. doi: 10.1366/11-06412. [DOI] [PubMed] [Google Scholar]
- 76.Elmore DL, Chase DB, Liu YJ, et al. Infrared spectroscopy and spectroscopic imaging of n-propyl trichlorosilane monolayer films self-assembled on glass substrates. Vib Spectrosc. 2004;34(1):37–45. [Google Scholar]
- 77.Elmore DL, Leverette CL, Chase DB, et al. Planar array infrared spectroscopic imaging of monolayer films in the 3200-2800 cm−1 region. Langmuir. 2003;19(8):3519–3524. [Google Scholar]
- 78.Hirschfeld T. Appl Spectrosc. 1976;30(1):68–69. [Google Scholar]
- 79.Bhargava R. Fellgett advantage in Fourier transform infrared imaging. Paper in preparation [Google Scholar]
- 80.Walsh MJ, Bhargava R. Infrared spectroscopic imaging: an integrative approach to pathology. In: Popescu G, editor. Nanobiophotonics. New York, NY: McGraw-Hill; 2010. [Google Scholar]
- 81.Bhargava R, Fernandez DC, Schae-berle MD, Levin IW. Gain Ranging for FTIR Imaging. Appl Spectrosc. 2001;54:1580–1589. [Google Scholar]
- 82.Bhargava R, Fernandez DC, Schaeberle MD, Levin IW. Towards Faster FTIR Imaging. Appl Spectrosc. 2001;55:1079–1084. [Google Scholar]
- 83.Bhargava R, Levin IW. Enhanced Timeresolved Fourier Transform Infrared Spectroscopic Imaging for Reversible Dynamics. J Phys Chem A. 2004;108:3896–3901. [Google Scholar]
- 84.Bhargava R, Fernandez DC, Schaeberle MD, Levin IW. Effect of Focal Plane Array Cold Shield Aperture Size on Fourier Transform Infrared Imaging Microspectrometer Performance. Appl Spectrosc. 2000;54:1743–1750. [Google Scholar]
- 85.Bhargava R, Levin IW. Effective time averaging of multiplexed measurements: a critical analysis. Anal Chem. 2002;74(6):1429–1435. doi: 10.1021/ac011153n. [DOI] [PubMed] [Google Scholar]
- 86.Haka AS, Levin IW, Lewis EN. Uncooled barium strontium titanium focal plane array detection for mid-infrared Fourier transform spectroscopic imaging. Appl Spectrosc. 2000;54(5):753–755. [Google Scholar]
- 87.Ribar T, Bhargava R, Koenig JL. Examining Polymer Dissolution by FTIR Imaging: 1. Good Solvents. Macromolecules. 2000;33:8842–8849. [Google Scholar]
- 88.Liu J, Schulmerich MV, Bhargava R, Cunningham BT. Optimally designed narrowband mid-infrared guided-mode resonance reflectance filters for mid-infrared optical spectroscopy. Opt Exp. 2011;19:24182–24197. doi: 10.1364/OE.19.024182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Bhargava R, et al. High throughput assessment of cells and tissues Bayesian classification of spectral metrics from infrared vibrational spectroscopic imaging data. Biochim Biophys Acta. 2006;1758(7):830–845. doi: 10.1016/j.bbamem.2006.05.007. [DOI] [PubMed] [Google Scholar]
- 90.Bhargava R. Practical FTIR chemical imaging for cancer pathology. Anal Bioanal Chem. 2008;389:1155–1169. doi: 10.1007/s00216-007-1511-9. [DOI] [PubMed] [Google Scholar]
- 91.Kodali AK, Schulmerich MV, Ip J, Yen G, Cunningham BT, Bhargava R. Narrowband Mid-infrared reflectance filters using guided mode resonance. Anal Chem. 2010;82:5697–5706. doi: 10.1021/ac1007128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Wood RW. On a remarkable case of uneven distribution of light in a diffraction grating spectrum. Philos Mag. 1902;4:392–402. [Google Scholar]
- 93.Rayleigh L. On the dynamical theory of gratings. Proc R Soc London Ser A. 1907;79:399–416. [Google Scholar]
- 94.Hessel A, Oliner AA. A new theory of Wood's anomalies on optical gratings. Appl Opt. 1965;4:1275–1297. [Google Scholar]
- 95.Popov E, Mashev L, Maystre D. Theoretical study of the anomalies of coated dielectric gratings. Opt Acta. 1986;33:607–619. [Google Scholar]
- 96.Bertoni HL, Cheo LHS, Tamir T. Frequency selective reflection and transmission by a periodic dielectric layer. IEEE Trans Antennas Propag. 1989;37:78–83. [Google Scholar]
- 97.Wang SS, Magnusson R, Bagby JS. Guided-mode resonances in planar dielectric-layer diffraction gratings. J Opt Soc Am A. 1990;7:1470–1474. [Google Scholar]
- 98.Wang SS, Magnusson R. New principle for optical filters. Appl Phys Lett. 1992;61:1022–1024. [Google Scholar]
- 99.Wang SS, Magnusson R. Theory and applications of guided-mode resonance filters. Appl Opt. 1993;32:2606–2613. doi: 10.1364/AO.32.002606. [DOI] [PubMed] [Google Scholar]
- 100.Peng S, Morris GM. Experimental demonstration of resonant anomalies in diffraction from two-dimensional gratings. Opt Lett. 1996;21(8):549–551. doi: 10.1364/ol.21.000549. [DOI] [PubMed] [Google Scholar]
- 101.Dobbs D, Cunningham BT. Optically tunable photonic crystal reflectance filters. Appl Opt. 2006;45(28):7286–7293. doi: 10.1364/ao.45.007286. [DOI] [PubMed] [Google Scholar]
- 102.Moharam MG, et al. Formulation for Stable and Efficient Implementation of the Rigorous Coupled-Wave Analysis of Binary Gratings. JOSA. 1995;12(5):1068–1076. [Google Scholar]
- 103.Faist J, Aellen T, Gresch T, Beck M, Giovannini M. Progress in quantum cascade lasers. The Netherlands: Springer; 2007. Mid-infrared Coherent Sources and Applications; pp. 171–192. [Google Scholar]
- 104.Cockburn J. Mid-infrared quantum cascade lasers. Vol. 118 Berlin: Springer; 2006. Mid-infrared Semiconductor Optoelectronics; pp. 323–355. Springer Series in Optical Sciences. [Google Scholar]
- 105.Faist J, Sirtori C. Long-Wave length Infrared Semiconductor Lasers InP- and GaAs-based quantum cascade lasers. New York: Wiley Interscience; 2004. pp. 217–278. [Google Scholar]
- 106.Maulini R, Beck M, Faist J, Gini E. 2004 Broadband tuning of external cavity bound-to-continuum quantum-cascade lasers. Appl Phys Lett. 2004;84:1659–1661. [Google Scholar]
- 107.Beck M, Hofstetter D, Aellen T, Faist J, Oesterle U, Ilegems M, Gini E, Melchior H. Continuous wave operation of a mid-infrared semiconductor laser at room temperature. Science. 2002;295:301–305. doi: 10.1126/science.1066408. [DOI] [PubMed] [Google Scholar]
- 108.Werle P, Slemr F, Maurer K, et al. Near-and mid-infrared laser-optical sensors for gas analysis. Opt Lasers Eng. 2002;37(2-3):101–114. [Google Scholar]
- 109.Kosterev AA, Tittel FK. Chemical sensors based on quantum cascade lasers. IEEE J Quant Elec. 2002;38(6):582–591. [Google Scholar]
- 110.Namjou K, Cai S, Whittaker EA, et al. Sensitive absorption spectroscopy with a room-temperature distributed-feedback quantum-cascade laser. Opt Lett. 1998;23(3):219–221. doi: 10.1364/ol.23.000219. [DOI] [PubMed] [Google Scholar]
- 111.Paldus BA, et al. Photoacoustic spectroscopy using quantum-cascade lasers. Opt Lett. 1999;24(3):178–180. doi: 10.1364/ol.24.000178. [DOI] [PubMed] [Google Scholar]
- 112.Hvozdara L, et al. Quantum cascade lasers for mid-infrared spectroscopy. Vib Spec-trosc. 2002;30(1):53–58. [Google Scholar]
- 113.Curl RF. Quantum cascade lasers in chemical physics. Chem Phys Lett. 2010;487(1-3):1–18. [Google Scholar]
- 114.Guo B, Wang Y, Peng C, et al. Multi-wavelength mid-infrared micro-spectral imaging using semiconductor lasers. Appl Spectrosc. 2003;57(7):811–822. doi: 10.1366/000370203322102906. [DOI] [PubMed] [Google Scholar]
- 115.Phillips MC, Ho N. Infrared hyperspectral imaging using a broadly tunable external cavity quantum cascade laser and micro-bolometer focal plane array. Opt Exp. 2008;16(3):1836–1845. doi: 10.1364/oe.16.001836. [DOI] [PubMed] [Google Scholar]
- 116.Kolhed M, Haberkorn M, Pustogov V, et al. Assessment of quantum cascade lasers as mid infrared light sources for measurement of aqueous samples. Vib Spectrosc. 2001;29(1-2):283–289. [Google Scholar]
- 117.Mizaikoff B. Infrared optical sensors for water quality monitoring. Water Sci Tech. 2003;47(2):35–42. [PubMed] [Google Scholar]
- 118.Schaden S, Haberkorn M, Frank J, et al. Direct determination of carbon dioxide in aqueous solution using mid-infrared quantum cascade lasers. Appl Spectrosc. 2004;58(6):667–670. doi: 10.1366/000370204872971. [DOI] [PubMed] [Google Scholar]
- 119.Charlton C, Katzir A, Mizaikoff B. Infrared evanescent field sensing with quantum cascade lasers and planar silver halide waveguides. Anal Chem. 2005;77(14):4398–4403. doi: 10.1021/ac048189a. [DOI] [PubMed] [Google Scholar]
- 120.Seong-Soo K, Christina Y, Mizaikoff B. Miniaturized mid-infrared sensor technologies. Anal Bioanal Chem. 2008;390(1):231–237. doi: 10.1007/s00216-007-1673-5. [DOI] [PubMed] [Google Scholar]
- 121.Lendl B, Frank J, Schindler R. Mid-infrared quantum cascade lasers for flow injection analysis. Anal Chem. 2000;72(7):1645–1648. doi: 10.1021/ac990833b. [DOI] [PubMed] [Google Scholar]
- 122.Edelmann A, Ruzicka C, Frank J, et al. Towards functional group-specific detection in high-performance liquid chromatography using mid-infrared quantum cascade lasers. J Chromatogr A. 2001;934(1-2):123–128. doi: 10.1016/s0021-9673(01)01288-2. [DOI] [PubMed] [Google Scholar]
- 123.Vrancic C, Fomichova A, Gretz N. Continuous glucose monitoring by means of mid-infrared transmission laser spectroscopy in vitro. Analyst. 2011;136(6):1192–1198. doi: 10.1039/c0an00537a. [DOI] [PubMed] [Google Scholar]
- 124.Kottmann J, Rey JM, Luginbuhl J. Glucose sensing in human epidermis using mid-infrared photoacoustic detection. Biomed Opt Exp. 2012;3(4):667–680. doi: 10.1364/BOE.3.000667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Yao Y, Hoffman AJ, Gmachl CF. Mid-infrared quantum cascade lasers. Nat Photonics. 2012;6(7):432–439. [Google Scholar]
- 126.Kole M, Schulmerich MV, Gelber M, Bhargava R. IR microscopy with a quantum cascade laser. Anal Chem. 2012 doi: 10.1021/ac302513f. Paper submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Lu F, Belkin MA. Infrared absorption nano-spectroscopy using sample photoexpansion induced by tunable quantum cascade lasers. Opt Exp. 1994;19(21):2–19947. doi: 10.1364/OE.19.019942. [DOI] [PubMed] [Google Scholar]
- 128.Farahi RH, Passian A, Tetard L, et al. Pump-probe photothermal spectroscopy using quantum cascade lasers. J Phys D– Appl Phys. 2012;45(12):125101. [Google Scholar]
- 129.Jackson SD. Towards high-power mid-infrared emission from a fibre laser. Nat Photonics. 2012;7(6):423–431. [Google Scholar]
- 130.Schliesser A, Picqué N, Hänsch TW. Mid-infrared frequency combs. Nat Photonics. 2012;7(6):440–449. [Google Scholar]
- 131.Sorokina IT, Vodopyanov KL, editors. Solid-State Mid-Infrared Laser Sources. Vol. 89 Berlin/Heidelberg: Springer Verlag; 2003. Topics in Applied Physics. [Google Scholar]
- 132.Vodopyanov KL, editor. Nonlinear Frequency Generation and Conversion: Materials, Devices, and Applications X: 24-27 January 2011. Vol. 7917 San Francisco, CA: Proc SPIE; 2011. [Google Scholar]
- 133.Vodopyanov KL, Levi O, Kuo PS, et al. Optical parametric oscillation in quasiphase-matched GaAs. Opt Lett. 2004;29(16):1912–1914. doi: 10.1364/ol.29.001912. [DOI] [PubMed] [Google Scholar]
- 134.Hill GA, Rice JH, Meech SR, et al. Submicrometer infrared surface imaging using a scanning-probe microscope and an optical parametric oscillator laser. Opt Lett. 2009;34:431–433. doi: 10.1364/ol.34.000431. [DOI] [PubMed] [Google Scholar]
- 135.Marcott C, Lo M, Kjoller K, Prater C, Noda I. Spatial differentiation of sub-micrometer domains in a poly(hydroxyalkanoate) copolymer using instrumentation that combines atomic force microscopy (AFM) and infrared (IR) spectroscopy. Appl Spectrosc. 2011;65:1145–1150. doi: 10.1366/11-06341. [DOI] [PubMed] [Google Scholar]
- 136.Eerdenbrugh BV, Lo M, Kjoller K. Nanoscale mid-infrared imaging of phase separation in a drug–polymer blend. J Pharm Sci. 2012;101(6):2066–2073. doi: 10.1002/jps.23099. [DOI] [PubMed] [Google Scholar]
- 137.Amrania H, McCrow AP, Matthews MR, et al. Ultrafast chemical imaging of live cells. Chem Sci. 2011;2:107–111. [Google Scholar]
- 138.Lorenz-Fonfria VA, Kandori H. Bayesian maximum entropy (two-dimensional) lifetime distribution reconstruction from time-resolved spectroscopic data. Appl Spec-trosc. 2007;61(4):428–443. doi: 10.1366/000370207780466172. [DOI] [PubMed] [Google Scholar]
- 139.Bialkowski SE. Overcoming the multiplex disadvantage by using maximum-likelihood inversion. Appl Spectrosc. 1998;52(4):591–598. [Google Scholar]
- 140.Fernandez DC, Bhargava R, Hewitt SM, Levin IW. Infrared Spectroscopic Imaging for Histopathologic Recognition. Nat Bio-technol. 2005;23:469–474. doi: 10.1038/nbt1080. [DOI] [PubMed] [Google Scholar]
- 141.Brady SP, Do MN, Bhargava R. Proc IEEE International Conference on Image Processing. Cairo, Egypt: 2009. Reconstructing FT-IR spectroscopic imaging data with a sparse prior. [Google Scholar]
- 142.Bhargava R. Practical FTIR chemical imaging for cancer pathology. Anal Bioa-nal Chem. 2007;389:1155–1169. doi: 10.1007/s00216-007-1511-9. [DOI] [PubMed] [Google Scholar]
- 143.Garland M. Combining operando spectros-copy with experimental design, signal processing and advanced chemometrics State-of-the-art and a glimpse of the future. Cat Today. 2010;155(3-4):266–270. [Google Scholar]
- 144.Reddy RK, Walsh MJ, Schulmerich MV, Carney PS, Bhargava R. High-definition infrared spectroscopic imaging. Appl Spec-trosc. 2012 doi: 10.1366/11-06568. Paper submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Zbinden R. Infrared spectroscopy of high polymers. New York, NY: Academic Press; 1964. [Google Scholar]
- 146.Trenary M. Reflection absorption infrared spectroscopy and the structure of molecular adsorbates on metal surfaces. Annu Rev Phys Chem. 2000;51:381–403. doi: 10.1146/annurev.physchem.51.1.381. [DOI] [PubMed] [Google Scholar]
- 147.Goodman JW. Introduction to Fourier Optics. Greenwood Village, CO: Roberts and Company Publishers; 2005. [Google Scholar]
- 148.Walsh MJ, Mayerich D, Kajdacsy-Balla A, Bhargava R. High-resolution mid-infrared imaging for disease diagnosis.Progress in Biomedical Optics and Imaging. Proc SPIE. 2012;8219:82190R. [Google Scholar]
- 149.Bhargava R, Wang SQ, Koenig JL. Processing FTIR Imaging Data for Morphology Visualization. Appl Spectrosc. 2000;54:1690–1706. [Google Scholar]
- 150.Bhargava R, Wang SQ, Koenig JL. FT-IR imaging of the interface in multicomponent systems using optical effects induced by differences in refractive index. Appl Spec-trosc. 1998;52:323–328. [Google Scholar]
- 151.Davis BJ, Carney PS, Bhargava R. Theory of mid-infrared absorption micro-spectroscopy. I. Homogeneous samples. Anal Chem. 2010;82:3474–3486. doi: 10.1021/ac902067p. [DOI] [PubMed] [Google Scholar]
- 152.Allara DL. Infrared spectra of polymer mixtures - problems caused by dispersion effects in difference spectra. Appl Spec-trosc. 1979;33(4):358–361. [Google Scholar]
- 153.Tisinger LG, Sommer AJ. Extinction coefficient determination of polymeric materials and their use in the optical characterization of infrared microscopes: A preliminary investigation into quantitative infrared microspectroscopy. Appl Spec-trosc. 2002;56(11):1397–1402. [Google Scholar]
- 154.Bertie JE, Lan Z. An accurate modified Kramers-Kronig transformation from reflectance to phase shift on attenuated total reflection. J Chem Phys. 1996;105(19):8502–8514. [Google Scholar]
- 155.Filik J, Frogley MD, Pijanka JK, Wehbe K, Cinque G. Optical standing-wave artifacts in reflection-absorption FTIR micro-spectroscopy of biological materials. J Phys: Conf Ser. 2012;359(1) doi: 10.1039/c2an15995c. [DOI] [PubMed] [Google Scholar]
- 156.Filik J, Frogley MD, Pijanka JK, Wehbe K, Cinque G. Electric field standing wave artefacts in FTIR micro-spectroscopy of biological materials. Analyst. 2012;137(4):853–861. doi: 10.1039/c2an15995c. [DOI] [PubMed] [Google Scholar]
- 157.Davis BJ, Carney PS, Bhargava R. Theory of mid-infrared absorption micro-spectroscopy. II. Heterogeneous samples. Anal Chem. 2010;82:3487–3499. doi: 10.1021/ac902068e. [DOI] [PubMed] [Google Scholar]
- 158.Bhargava R, Wang SQ, Koenig JL. Studying polymer-dispersed liquid-crystal formation by FTIR spectroscopy. 1. Monitoring curing reactions. Macromolecules. 1999;32:8982–8988. [Google Scholar]
- 159.Bhargava R, Wang SQ, Koenig JL. Studying polymer-dispersed liquid-crystal formation by FTIR spectroscopy. 1. Monitoring curing reactions. Macromolecules. 1999;32:8989–8995. [Google Scholar]
- 160.Kramer R. Chemometric Techniques for Quantitative Analysis. New York, NY: Marcel Dekker; 1998. [Google Scholar]
- 161.Martin FL, Kelly JG, Llabjani V, Martin-Hirsch PL, Patel II, Trevisan J, Fullwood NJ, Walsh MJ. Distinguishing cell types or populations based on the computational analysis of their infrared spectra. Nat Prot. 2010;5(11):1748–1760. doi: 10.1038/nprot.2010.133. [DOI] [PubMed] [Google Scholar]
- 162.Trevisan J, Angelov PP, Carmichael PL, Scott AD, Martin FL. Extracting biological information with computational analysis of Fourier-transform infrared (FTIR) biospectroscopy datasets: Current practices to future perspectives. Analyst. 2012;137(14):3202–3215. doi: 10.1039/c2an16300d. [DOI] [PubMed] [Google Scholar]
- 163.Bhargava R, Perlman RS, Fernandez DC, Levin IW, Bartick EG. Non-invasive detection of superimposed latent fingerprints and inter-ridge trace evidence by infrared spectroscopic imaging. Anal Bioanal Chem. 2009;394:2069–2075. doi: 10.1007/s00216-009-2817-6. [DOI] [PubMed] [Google Scholar]
- 164.Bhargava R, Wang SQ, Koenig JL. FTIR imaging studies of a new two-step process to produce polymer dispersed liquid crystals. Macromolecules. 1999;32:2748–2760. [Google Scholar]
- 165.Ribar T, Bhargava R, Koenig JL. Examining Polymer Dissolution by FTIR Imaging: 2. Good-Poor Solvent Mixtures. Macromolecules. 2001;34:8340–8346. [Google Scholar]
- 166.Lang PL, Katon JE, O’Keefe JF, Schiering DW. The identification of fibers by infrared and Raman microspectroscopy. Microchem J. 1986;34(3):319–331. [Google Scholar]
- 167.Davis BJ, Carney PS, Bhargava R. Infrared Microspectroscopy of Intact Fibers. Anal Chem. 2011;83:525–532. doi: 10.1021/ac102239b. [DOI] [PubMed] [Google Scholar]
- 168.van Dijk T, Carney PS, Bhargava R. Analysis of a sphere in an IR microscope. Appl Spectrosc. 2012 Paper in preparation. [Google Scholar]
- 169.Mohlenhoff B, Romeo M, Diem M, Wood BR. Mie-type scattering and non-Beer-Lambert absorption behavior of human cells in infrared microspectroscopy. Biophys J. 2005;88(5):3635–3640. doi: 10.1529/biophysj.104.057950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 170.Bohren CF, Huffman DR. Absorption and Scattering of Light by Small Particles. New York, NY: Wiley; 1983. [Google Scholar]
- 171.Kohler A, Kirschner C, Oust A, Martens H. Extended multiplicative signal correction as a tool for separation and characterization of physical and chemical information in Fourier transform infrared microscopy images of cryo-sections of beef loin. Appl Spectrosc. 2005;59(6):707–716. doi: 10.1366/0003702054280649. [DOI] [PubMed] [Google Scholar]
- 172.Köhler A, Sulé-Suso J, Sockalingum GD, Tobin M, Bahrami F, Yang Y, Pijanka J, Dumas P, Cotte M, Van Pittius DG, Parkes G, Martens H. Estimating and correcting Mie scattering in synchrotron-based microscopic Fourier transform infrared spectra by extended multiplicative signal correction. Appl Spectrosc. 2008;62(3):259–266. doi: 10.1366/000370208783759669. [DOI] [PubMed] [Google Scholar]
- 173.Bassan P, Byrne HJ, Bonnier F, Lee J, Dumas P, Gardner P. Resonant Mie scattering in infrared spectroscopy of biological materials - Understanding the ‘dispersion artefact”’. Analyst. 2009;134(8):1586–1593. doi: 10.1039/b904808a. [DOI] [PubMed] [Google Scholar]
- 174.Dunder T, Miller RE. Infrared spectroscopy and Mie scattering of acetylene aerosols formed in a low temperature diffusion cell. J Chem Phys. 1990;93(5):3693–3703. [Google Scholar]
- 175.Bassan P, Kohler A, Martens H, Lee J, Jackson E, Lockyer N, Dumas P, Brown M, Clarke N, Gardner P. RMieS-EMSC correction for infrared spectra of biological cells: Extension using full Mie theory and GPU computing. J Biophotonics. 2010;3(8-9):609–620. doi: 10.1002/jbio.201000036. [DOI] [PubMed] [Google Scholar]
- 176.Martens H, Nielsen JP, Engelsen SB. Light scattering and light absorbance separated by extended multiplicative signal correction. Application to near-infrared transmission analysis of powder mixtures. Anal Chem. 2003;75(3):394–404. doi: 10.1021/ac020194w. [DOI] [PubMed] [Google Scholar]
- 177.Fernandez DC, Bhargava R, Hewitt SM, Levin IW. Infrared spectroscopic imaging for histopathologic recognition. Nat Bio-technol. 2005;23(4):469–474. doi: 10.1038/nbt1080. [DOI] [PubMed] [Google Scholar]
- 178.Abramoff MD, Magalha0es PJ, Sunan-da Ram SJ. Image processing with ImageJ. Biophot Int. 2004;11(7):36–42. [Google Scholar]
- 179.Schulze HG, Greek LS, Barbosa CJ, Blades MW, Turner RFB. Signal detection of data sets with a signal-to-noise ratio of 1 or less with the use of a moving product filter. Appl Spectrosc. 1998;52(4):621–625. [Google Scholar]
- 180.Craggs C, Galloway KP, Gardiner DJ. Maximum Entropy Methods Applied to Simulated and Observed Raman Spectra. Appl Spectrosc. 1996;50(1):43–47. [Google Scholar]
- 181.Lang M, Guo H, Odegard JE, Burrus CS, Wells RO., Jr Noise. reduction using an undecimated discrete wavelet transform. IEEE Signal Proc Lett. 1996;3(1):10–12. [Google Scholar]
- 182.Šašić S, Clark DA, Mitchell JC, Snowden MJ. A Comparison of Raman Chemical Images Produced by Univariate and Multivariate Data Processing—A Simulation with an Example from Pharmaceutical Practice. Analyst. 2004;129(11):1001–1007. [Google Scholar]
- 183.Green A, Berman M, Switzer P, Craig M. A Transformation for Ordering Multispectral Data in Terms of Image Quality with Implications for Noise Removal. IEEE Trans Geosci Remote Sens. 1988;26:65–74. [Google Scholar]
- 184.Bhargava R, Wang S, Koenig JL. Route to Higher Fidelity FT-IR Imaging. Appl Spectrosc. 2000;54:486–495. [Google Scholar]
- 185.Wabomba MJ, Sulub Y, Small GW. Remote Detection of Volatile Organic Compounds by Passive Multispectral Infrared Imaging Measurements. Appl Spec-trosc. 2007;61:349–358. doi: 10.1366/000370207780466253. [DOI] [PubMed] [Google Scholar]
- 186.Wabomba MJ, Sulub Y, Small GW. Remote detection of volatile organic compounds by passive multispectral infrared imaging measurements. Appl Spectrosc. 2007;61(4):349–358. doi: 10.1366/000370207780466253. [DOI] [PubMed] [Google Scholar]
- 187.Bhargava R, Wang S, Koenig JL. Processing FT-IR Imaging Data for Morphology Visualization. Appl Spectrosc. 2000;54:1690–1706. [Google Scholar]
- 188.Reddy RK, Bhargava R. Automated noise reduction for accurate classification of tissue from low signal-to-noise ratio imaging data. Analyst. 2010;135:2818–2825. doi: 10.1039/c0an00350f. [DOI] [PubMed] [Google Scholar]
- 189.Kwak JT, Reddy RK, Sinha S, Bhargava R. An analysis of the sources of variance in Fourier transform infrared spectroscopic imaging of tissues. Anal Chem. 2012;84:1063–1069. doi: 10.1021/ac2026496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 190.Lasch P, Naumann D. Spatial resolution in infrared microspectroscopic imaging of tissues. Biochim Biophys Acta–Biomem-branes. 2006;1758(7):814–829. doi: 10.1016/j.bbamem.2006.06.008. [DOI] [PubMed] [Google Scholar]
- 191.Nguyen TH, Reddy RK, Walsh MJ, Schulmerich MV, Popescu G, Do MN, Bhargava R. De-noising and de-blurring of Fourier transform infrared spectroscopic Imaging data using a combined physics-based modeling and signal processing approach. Anal Chem. 2012 Paper submitted. [Google Scholar]
- 192.Amrania H, McCrow A, Phillips C. A Benchtop Ultrafast Infrared Spectroscopic Imaging System for Biomedical applications. Rev Sci Instrum. 2009;80:123702. doi: 10.1063/1.3262499. [DOI] [PubMed] [Google Scholar]