Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2013 Aug 29;3:2541. doi: 10.1038/srep02541

Non-uniformity of cell density and networks in the monkey brain

Masanori Shimono 1,a
PMCID: PMC3756338  PMID: 23985926

Abstract

The brain is a very complex structure. Over the past several decades, many studies have aimed to understand how various non-uniform variables relate to each other. The current study compared the whole-brain network organization and global spatial distribution of cell densities in the monkey brain. Wide comparisons between 27 graph theoretical measures and cell densities revealed that only participation coefficients (PCs) significantly correlated with cell densities. Interestingly, PCs did not show a significant correlation with spatial coordinates. Furthermore, the significance of the correlation between cell densities and spatial coordinates disappeared only with the removal of the visual module, while the significance of the correlation between cell densities and PCs disappeared with the removal of any one module. Taken together, these results suggested the presence of a combinatorial effect of modular architectures in the network organization related to the non-uniformity of cell densities additional to the spatially monotonic change.

How do various non-uniform quantities of the brain relate to each other? This has been a key question for many neuroinformatic studies. To answer this question, an evaluation of the whole-brain data is often essential. For example, over the past several decades, the uniformity of cell densities in the cortex has been wrongly assumed by generalizing the results observed in limited brain regions1. Later experimentation revealed non-uniformity of the densities of neurons and nonneurons in whole regions of the monkey cortex2,4. Similarly, integrated databases of brain connectivities were also developed to understand the global organization of brain connectivities5,6,7,8,9,10,11,12,13.

Several previous studies have compared network organization and cell densities in the brain. For example, French et al. (2011) demonstrated a relationship between network organizations of the whole-brain and cell densities in rodent brains14,15. In the monkey brain, it was shown that cell densities of the periarcuate and lateral intraparietal areas can predict laminar-specificity of connections between the two connected regions16. However, a comparison between the global organization of networks and cell densities in the whole monkey brain has not yet been performed. Thus, the current study aimed to investigate whether networks and cell densities relate to each other, and if so, how the relation can be characterized.

To pursue these questions, this study sought to integrate two independently developed databases of cell densities and network organization in the monkey brain onto a common three-dimensional space2,3,11. In addition, widely observed relationships between the cell densities of 69 cortical regions and 27 network variables were derived from the network organization.

Results

General concept

The aim of this study was to understand how the non-uniformity of cell densities relates to the non-randomness of brain connections (Figure 1). The cell densities and connections used in this study were obtained from 69 brain regions shown in Table S-15. Although further information on the quantities of the cell densities and connections are described in the Methods section, here, I will provide the minimum information needed to understand the contents and interpretations of results of this study. The connectivity presented in this report was obtained using the CoCoMac database, and the cell density was obtained from a previous report (Collins et al. (2010)). The cell densities were defined as the total number of neurons or nonneurons per weight of parcelled brain slices, and the neuron-per-nonneuron ratio was defined as the ratio between the two densities of neurons and nonneurons. I combined two maps via direct observation of the brain parcellation maps described in Collins et al. (2010) and Fellman and vanEssen (1991), which were originally used to create the parcellation map in the CoCoMac database. The comparisons of the indices in these two databases are also shown in Table S-1.

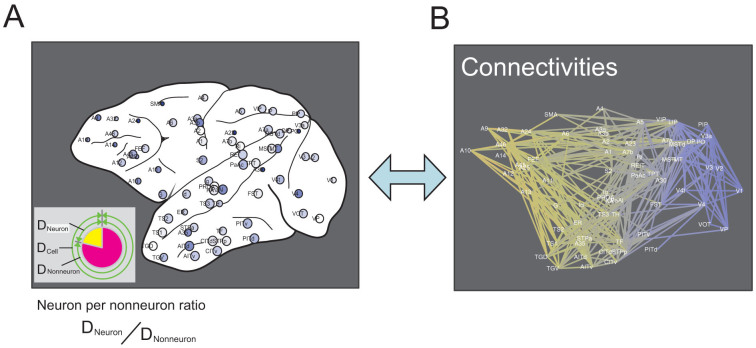
Figure 1. Concept of this study.

Figure 1

Open in a new tab

The main aim of this study was to compare cell densities (Figure A) and network organization, which consists of connecting brain regions (Figure B). As shown in Figure A, the cells were categorized into neurons and nonneurons. From these values, the neuron-per-nonneuron ratio was defined according to the equation shown below (A). The network organization was quantified using 27 network variables. Changes in color gradations correspond to the anterior–posterior coordinates.

Three-dimensional coordinates and gradient of cell densities

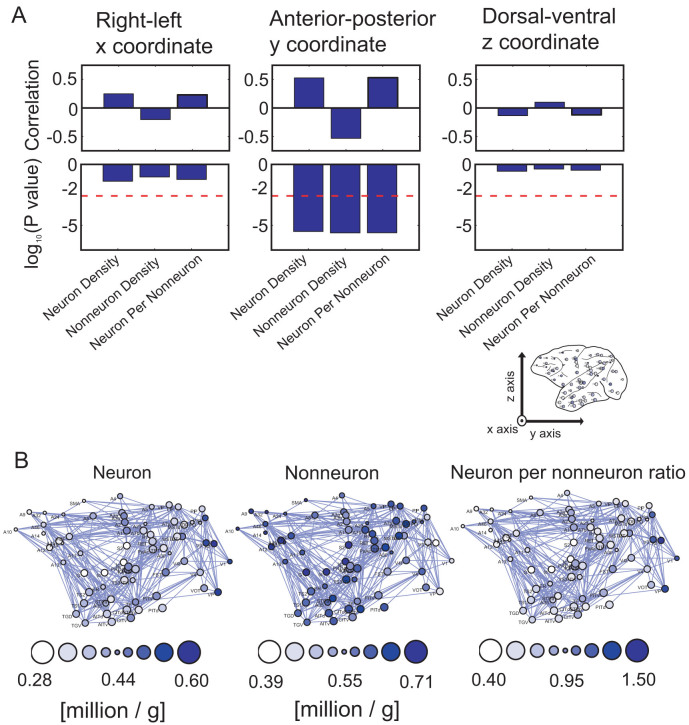
Cahalane et al. (2012) demonstrated that cell densities change monotonically on two-dimensional maps after segmentation of the cortical surface. Their coordinates were based on those described in Collins et al. (2010)17. To observe this directionality in a three-dimensional space, this report re-evaluated the spatial monotonic change in cell densities after reconstructing three-dimensional coordinates of the cortical regions. These results are shown in Figure 2. First, I evaluated the correlation between the three-dimensional coordinates and the distribution of three types of cell densities (Figure 2-A). These results revealed that only the anterior–posterior axis showed a significant correlation with cell densities. The spatial mapping of the cell densities is shown in Figure 2-B. These color maps show a clear gradient of cell densities on the anterior–posterior axis with several exceptions, such as the somatomotor and primary auditory regions. On the basis of these results, this report focused on the anterior–posterior axis in the following data analyses.

Figure 2. Coordinate dependencies of the cell densities.

Figure 2

Open in a new tab

The upper figures in Figure A show the correlations between the three spatial coordinates and cell densities. The lower figures indicate the p values of the t-test that correspond to these three correlations. The directions of the x, y and z axes are shown in the inserted figure of the brain at the bottom right of Figure A. The thick dotted line represents the threshold of significance (p < 0.05/9, t-test, Bonferroni correction). The figures in (B) represent the spatial distributions of these three cell densities on the y-z coordinates. From left to right, the three densities are the neuron density, glia cell density, and neuron-per-nonneuron density. Darker colored circles indicate higher densities or ratios, as shown in the bottom bubble. The sizes of the circles show the depth of the coordinates.

Comparison between network properties and cell densities

Next, I evaluated the correlations between three variables of cell densities and 27 network measures (Figure 3). Pairs of correlations and P-values for the statistical tests for neuron density, nonneuron density and the neuron-per-nonneuron ratio are shown in Figure 3A–C. Moreover, weak but significant negative correlations that were present only for the participant coefficients (thick, red dotted lines in Figure 3, p < 0.05/27, according to Bonferroni correction) are shown in Figure 3A–C. However, all of the network variables did not significantly correlate with the anterior–posterior coordinates, as shown in Figure 3D. The significance of the correlation between the participation coefficient and neuron-per-nonneuron ratio was robust even after exchanging approximately 16% of the adjacent brain regions (11/69 brain regions; Figure S-2). In addition, although the path lengths between all pairs of brain regions showed a significant correlation with the sum of the cell densities for the same pairs of brain regions (CC: 0.14, p = 6.3*10−4), the path lengths also significantly correlated with the anterior-posterior coordinate (CC: −0.05, p = 4.7*10−4).

Figure 3. Correlations and p values between the cell densities and network measures.

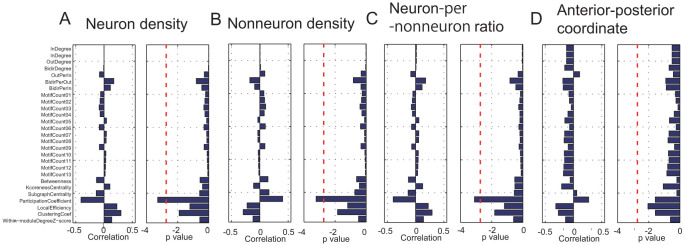
Figure 3

Open in a new tab

In Figure A, the bars in the left panel show correlations between the neuron densities and 27 network measures. Bars in the right panel show the p values of t-tests for individual correlations. The thick dotted line represents the threshold of significance (p = 0.05/27, t-test, Bonferroni correction). The column consisting of two panels in Figure B shows the results of the same evaluations of nonneuron densities. The column of panels in Figure C shows the results of the same evaluations of the neuron-per-nonneuron ratio. The column of panels in Figure D shows the results of the same evaluation of correlations between the anterior-posterior coordinates and 27 network measures and their corresponding p values.

Participation coefficient is a measure that evaluates how often a node connects to nodes in other modules (communities) from the module (community) in which the main node participates. Thus, intuitively, this measure is low at central locations in networks and is high at provincial locations in the networks.

Direct observation of participation coefficients

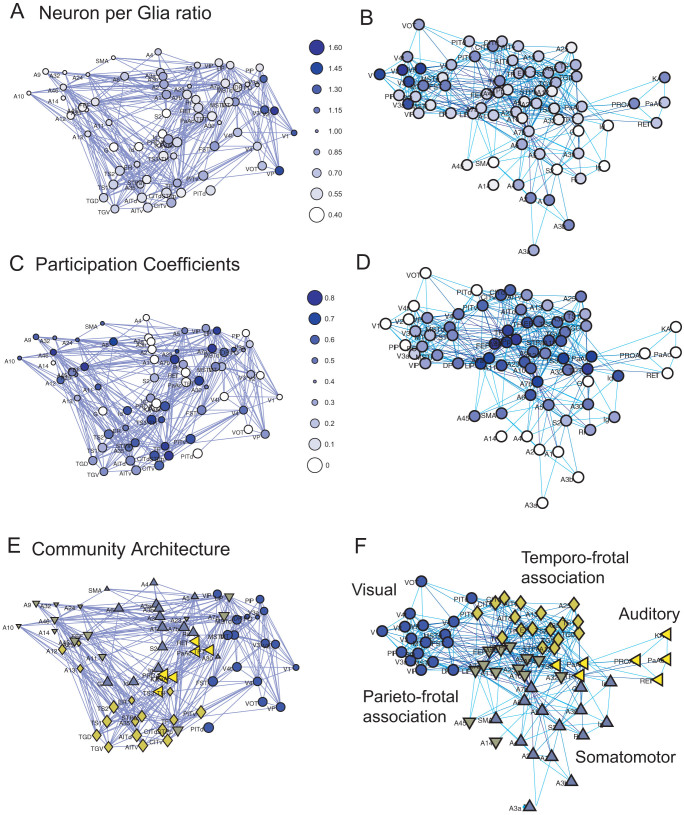
One intriguing question may be, “Why does only the participation coefficient show a significant correlation with the cell densities?” To answer this question, I sought to directly observe spatial distributions of the cell density and the participation coefficient (Figure 4). The following analyses focused on the properties of the neuron-per-nonneuron ratio because neuron density and 1/(nonneuron density), showed similar trends as the neuron-per-nonneuron ratio. Here, the observed brain networks in physical space are shown in Figures 4-A, C, and E, and the observed networks mapped using the Fruchterman–Reingold algorithm are shown in Figures 4-B, D, and F. Participation coefficients were defined on the basis of their modular architecture, which was automatically extracted by optimization of the community structure using the Louvain algorithm. During the optimization process, the significance of the correlation also gradually developed (Figure S-3).

Figure 4. Comparisons between the participation coefficients and cell densities.

Figure 4

Open in a new tab

The spatial maps of the neuron-per-nonneuron ratio, participation coefficient, and module (or community) architecture are shown in Figures A, C, and E, respectively. Figure A is the same as the right figure of Figure 2-B. Figures B, D, and F are their reorganized network architectures using the Fruchterman–Reingold algorithm. The values, which correspond to the colors, are shown as bubbles at the right side of Figure A and C. The denser blue dots in Figures A–D indicate the relatively higher values of each main variable. Five different markers in Figures E and F indicate the five modules (or communities), which were defined using the Louvain algorithm. In Figures A, C, and E, the marker sizes were changed according to the depth of the brain regions.

Unexpectedly, the modular architecture after the optimization process naturally segmented the visual, auditory and somatomotor systems (Figure 4-E and F). These indices are shown in the right column in Table S-1.

Among these communities, relatively lower participant coefficients were observed not only in the visual region but also in the somatomotor and auditory systems (Figure 4-C and D). These lower participation coefficients in individual systems were caused by less divergent inter-modular connections with the participating community.

As shown in Figure 2, a prominently higher neuron-per-nonneuron ratio was observed around the visual system, as observed in the upper-left community in the Fruchterman–Reingold network (Figure 4-B). However, a slightly higher neuron-per-nonneuron ratio was also present in different regions, such as the somatomotor and primary auditory regions. These findings were difficult to explain using only the anterior–posterior coordinates.

Effect of the removal of brain communities

What type of effect does each community have on the previously observed correlation significance? To quantify these relative contributions, I evaluated the correlations and p values between cell neuron-per-nonneuron ratio and participation coefficient after removing each community (Figure 5). Three correlations were obtained from three pairs of variables selected from the cell density, spatial coordinate, and network variable. The cell density, spatial coordinate, and network variable are represented by the neuron-per-nonneuron ratio, anterior–posterior coordinate, and participation ratio, respectively (Figure 5-A).

Figure 5. Selective removal of each brain community.

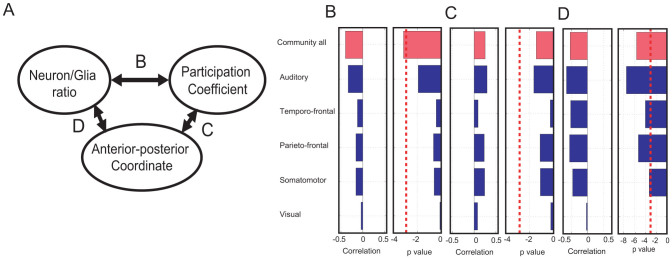
Figure 5

Open in a new tab

Figure A shows the scheme of the three comparisons depicted in Figures B–D. Figures B–D correspond to the comparisons among the three variables: the neuron-per-nonneuron ratios, anterior–posterior coordinate and participation coefficient, respectively. In each pair of panels in Figures B–D, the left panels indicate the correlations and the right panels represent the p values of the t-tests. The blue bars are the correlations and p values after the removal of the individual brain communities, and the original correlations and p values are shown as red bars at the top of each figure. The dotted lines in the right figures indicate the threshold of significance, which is the same p value in Figure 3.

Interestingly, although the significant correlation between the anterior–posterior coordinates and neuron-per-nonneuron ratio vanished only with the removal of the visual system (Figure 5-D), the significant correlation between the participation coefficients and neuron-per-nonneuron ratios always vanished with the removal of a brain community (Figure 5-B). These results indicated that the cell density selection information, which was included in the participation coefficients, was caused by non-uniformity of the participation coefficients in many widespread communities. Furthermore, the correlation between the participation coefficient and anterior–posterior coordinate was always non-significant (Figure 5-C). This result will be further discussed in the Discussion.

Cooperative use of coordinates and the network variable to estimate cell density

Next, I sought to use both the participation coefficient and spatial coordinates to estimate the non-uniform spatial distribution of the cell densities using Principle Component Regression (PCR) as shown in Figure 6-A. When fitting between two variables, this regression corresponded to the linear regression. The estimation of the accuracy of the neuron-per-nonneuron ratio was improved by including the participation coefficient rather than the estimation using only spatial coordinates (Figure 6-B). Although this was not a very surprising result, this result also indicated that the participation coefficient included information related to cell densities that was not included in the spatial coordinates. The partial least square regression (PLSR) also showed the same estimation result as the findings obtained using PCR (Figure 6-C). Importantly, this estimation was not performed to elucidate the causal directionalities from the network and spatial coordinates to cell density, but rather, for more practical reasons. For example, if any loss occurred in the cell density data, then it may be possible to recover this loss using other data.

Figure 6. Principle component regression using both spatial coordinates and participation coefficient.

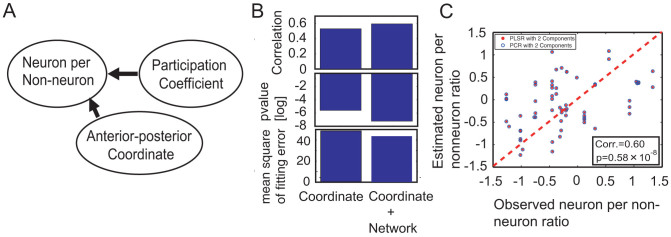
Figure 6

Open in a new tab

Figure A shows how accurately the neuron-per-nonneuron ratio can be estimated using the participation coefficient and spatial coordinate. Three panels in Figure B show the correlations between the estimated neuron-per-nonneuron ratios and observed neuron-per-nonneuron ratios, their p values (two sided t-test) and fitting error for PCR, respectively. The left bars indicate the results estimated from only the spatial coordinates, and the right bars indicate the results estimated from both the spatial coordinates and participation coefficients. As expected, the estimation was improved by including the participation coefficients. A direct comparison between the observed neuron-per-nonneuron ratio and the estimated neuron-per-nonneuron ratio from both the participation coefficient and anterior-posterior coordinate is shown in Figure C. The red dots and blue circles were estimated using PCR and PLSR, respectively. The red dotted line is the diagonal line.

Contribution of the connections between adjacent brain regions

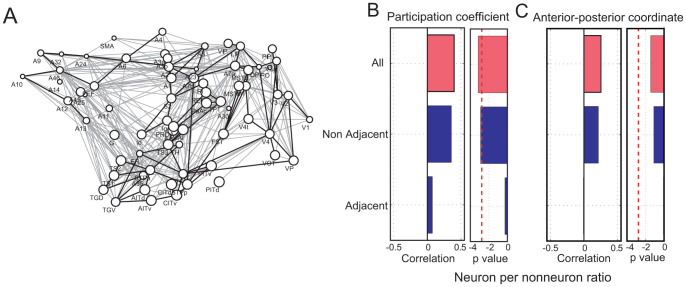
In addition, because adjacent pairs of brain regions have a higher connectivity probability compared to non-adjacent pairs, I examined the extent to which adjacent pairs of brain regions affected the significant correlation. Adjacency was defined using a spatial map of brain regions previously described in Felleman and Van Essen (1991). The connections between the adjacent pairs are shown as thick lines in Figure 7-A. Indirect observations of the correlations for adjacent pairs or non-adjacent pairs has been supported with results demonstrating that the significant correlation was mainly caused by pairs of non-adjacent brain regions (Figure 7-B and C).

Figure 7. Comparison between adjacent and non-adjacent connections.

Figure 7

Open in a new tab

In Figure A, the thick lines indicate the connections between adjacent pairs of brain regions, and the remaining thin lines indicate the non-adjacent pairs. In Figure B, the columns with two panels show the correlations and p values between the neuron-per-nonneuron ratios and participant coefficients. The three bars in the left panel are, from top to bottom, the participation coefficient given for all networks, networks only between non-adjacent brain regions, and networks only between adjacent brain regions. Three bars in the right panel show p values corresponding to correlations in the left panel. The correlations and p values between the anterior–posterior coordinates and participation coefficients are shown in Figure C. The meanings of the three bars are the same as in Figure B.

Discussion

This study reveals that the non-uniformity of the cell density in the brain relates not only with spatial coordinates but also with the participation coefficient, which represents the non-random organization of all brain networks. Interestingly, the spatial coordinate did not directly show a significant correlation with the participation coefficient, indicating that the participation coefficient has information relating to the non-uniformity of cell density that was not revealed in the monodirectional decrease in the anterior-posterior coordinate. This study was designed to understand and examine this intriguing phenomenon.

The removal of the brain communities helped with the understanding of this phenomenon. This study showed that although the significant correlations between the spatial coordinates and cell densities were caused by more prominent cell densities in the visual system compared to other regions, the significant correlations between the participation coefficients and cell densities were caused by the combinatorial effects of many brain regions. Phenomenologically, it has been shown that primary sensory and somatomotor regions exhibit a deviant higher neuronal density compared to a spatial monotonic change in the neuron-per-glia ratio from the occipital to the frontal side of the cortex17. Findings of my study could suggest that the modular architecture of the network organization of the brain relates to deviations derived from a spatially monotonic change. Generally, modular architectures characterize the segmentation and integration of the network organization, and the network organization may reflect information processes of the system18,19. For example, communities of visual, auditory and sensorimotor networks are located in provincial regions in the Fruchterman–Reingold map, while communities of the parieto-frontal and temporo-frontal association networks are located in the central regions in the Fruchterman–Reingold map (Figure 4-F). These locations may represent segregated but specific information processes in the former systems and integrating processes in the latter systems. For the past two decades, the balance between segmentation and integration has been regarded as an important property to understand the complexity of the brain20.

It is also possible to use the differences between the spatial coordinates and participation coefficients to improve the estimation performance of the cell densities (Figure 6-C). As natural extensions in this direction, several potential methods may exist to improve prediction performance. First, it may be possible to use a nonlinear model instead of a linear model. However, although a nonlinear model can realize better performance because of an increase in the number of free parameters, determining the best model is not easy. To address this question, future studies are required to gather additional data from a sufficient number of monkeys to assure statistical significance. Second, a finer separation of the brain regions may improve the estimation performance. Third, other factors beyond the spatial coordinates and participation coefficients should also be considered. Although the correlations between the participation coefficients and cell densities were significant, the correlation values were not very high (approximately 0.6). In the next section, I will specifically discuss the third possibility.

Improvement of the estimation performance can be achieved with a deeper understanding of the physiological factors related to the non-uniform distribution of neurons and nonneurons. Thus, it will be necessary to consider a more systematic understanding, which will include unknown factors. In the database used in this study, the cell density was determined using the brain tissue average, which included all layers in each brain region. However, cell density also demonstrates some clear differences among the cortical layers, particularly in layer 4, which exhibits a higher neuronal density compared to other layers in the cat visual cortex19 and rat barrel somatosensory cortex21. As previously mentioned, the non-uniformity of cell density among the cortical layers relates to the laminar-specificity of connections in studies of a limited brain region16. Furthermore, a recent study showed that the difference in cytoarchitectural types, which is defined by the relative thickness, density and granularization of layer 422, is the best factor to predict the laminar-specificity of projections compared to hierarchical levels and distances between brain regions25. Thus, these studies suggest local non-uniformity of cell densities between columnar layers, which are related to the selection of layers (local structures) in brain regions connected by global networks.

This study reported a general trend in the relationship between the non-uniformity of cell density, which is summed by all layers and global connections. If we could generate a database that includes both the cell density in a resolution of layers and the difference of the layers at every brain region, then we would be able to combine these findings, and may systematically improve the estimation performance of cell densities from network organization.

To understand in more detail the information processes of neuronal circuits, it will be necessary to understand how the target of global connections relates to the intricate microcircuits in the columnar architecture, which originates from global connections in every brain region. Several studies have reported that neurons in the frontal region demonstrate different local topological patterns depending on the difference in their connecting targets26,27,28,29. However, studies on whole brain regions have not yet been performed, and to resolve these challenges, various effective technologies must be developed to record the detailed architecture of the micro-neuronal circuits in the columnar architecture30,37,38.

Although we can posit many future studies, there are limitations that are present due to differences in the parcellation schemes used in the two databases. For example, we cannot answer questions relating to the detailed differences between adjacent regions. Furtheremore, comparison between different monkeys may potentially important to be solved. If possible, databases of different quantities should share a unified parcellation scheme, such as a parcellation scheme on the basis of cytoarchitectural type22,25, from the same individual monkeys.

Recently, Modha and Sigh (2010) generated a hierarchically organized network database of the monkey brain, which included subcortical regions13. The present study demonstrated a low participation coefficient and high neuron density as properties of the visual, auditory and somatosensory areas in cortical networks. Importantly, these regions have rich connections from subcortical regions. Some subcortical regions also play important roles in mediating interactions between two distanced cortical regions. Networks relating to this property have potential effects on changes in the participation coefficients, for example, secondary thalamic nuclei support information integration and regulation of connecting cortical regions31,32. Thus, how subcortical networks function as a whole system for cognitive tasks will also be an important topic to explore in the future33.

As a final remark, an understanding of the participation coefficient and modular architecture of cortical networks in relation to the non-uniformity of cell densities will help future neuroinformatic studies to uncover how non-uniformities of the brain play functional roles in information processes.

Methods

Introduction of databases

Due to the intensive efforts of previous studies, it is possible to use the data summaries of the cell densities in every cortical region (neuronal densities, cell densities, and neuron-per-nonneuron ratios)3 as well as databases of connectivity among brain regions covering the entire brain5,6,7,8,9,13. Specifically, the connectivity database known as Collations of Connectivity data on the Macaque brain (CoCoMac) has widely contributed to theoretical studies aimed to create a new research field by applying Graph theory to data10,11,12,34,35,36.

Evaluation of the connectivity properties of each brain region

The network was obtained from the CoCoMac database2,12. The parcellation scheme was based on Felleman and Van Essen (1991). Among the 27 network variables used in this study, I specifically introduce the participation coefficient in detail here because only this variable showed a significant correlation with cell densities. The definition of the participation coefficient is written as follows:

graphic file with name srep02541-m1.jpg

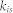Here, Inline graphic is the number of nodes in a community, s, connecting with node i, and 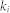Inline graphic is the total number of nodes connecting with node i. The ratio was summed using the number of communities 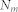Inline graphic. Thus, when links connecting with node i spread to many communities in a diverse manner, the participation coefficient 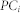Inline graphic is closer to 1, and if the connections are more concentrated in one community, then the participation coefficient 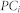Inline graphic is closer to 0. The community structure was determined by maximizing the modularity function Q (Girvan and Newman, 2002; Newman, 2004). The Q value is given by:

graphic file with name srep02541-m2.jpg

Here, ki and kj represent the degrees of nodes i and j, and 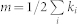Inline graphic represents the total number of nodes in the network. If nodes i and j belonged to the same community, c, then the delta function 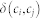Inline graphicis 1; otherwise, it is 0. Importantly, different groupings will affect the value of Q via this delta function. Here, 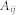Inline graphic provided the actual weight of the connection between nodes i and j. The term 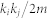Inline graphic provided the expected weight of the connection between node i and node j, if the network was randomized. It is known that optimization has an NP-hard problem23. Thus, to reach the most optimal solution, I repeated the optimization using the Louvain method40 1000 times and selected the community architecture that provided the highest Q value. Using the Louvain optimization method, the calculation was terminated when the Q value increased by less than 10−10 in one step, and the final community structure, including the number of communities, was stocked. The most stable community architecture among the final 1000 answers was regarded as the optimal community in this study. The community architecture used in this study was observed more than 100 times in 1000 repeating calculations.

Furthermore, this report observed 26 other network variables: in degree, out degree, bidirectional degree (degree of bidirectional connections), out degree per in degree, bidirectional degree per out degree, bidirectional degree per in degree, betweenness, k-core centrality, subgraph centrality, local efficiency, clustering coefficient, edge betweenness, within module degree z-score, and motif count (Figure 3). The in degree is the number of incoming connections. The out degree is the number of outgoing connections. The bidirectional degree is the number of bidirectional connections of each node. Betweenness centrality quantifies how often a node connects to other nodes using the shortest path41. The K-core centrality is defined based on the decomposition to subgraphs called K-cores. The K-core is a maximal group of nodes in which all nodes are connected to some number (K) of other nodes of the subgraph, and the value K is used to quantify the centrality42. The path length between two brain regions represents the number of necessary nodes to reach from one region to another region. The subgraph centrality is the weighted sum of the closed path lengths in a graph starting and ending at the same node. The weight is heavier for smaller subgraphs compared to larger ones43. The local efficiency is defined as the average of the nodal local efficiency computed as the global efficiency of the subgraph, which consists of its nearest neighbors28. The clustering coefficient is the fraction of connected pairs among the neighbors of a node44,45. The within module degree z score is a measure of how well node i connects with other nodes within its module46. The motif count is the number of connections included in the cluster of three nodes selected from all possible choices in all nodes. The motif counts are categorized into 13 patterns according to the indices defined by Milo et al. (2002)47. All of the data analyses were achieved using MATLAB software, and these measures were calculated using the Brain Connectivity Toolbox48.

Evaluation of local brain regions based on cell densities

Non-uniformity of neuron density is important in the characterization of changes in the brain depending on evolution4 and sex differences49. Furthermore, the importance of nonneurons on brain function has become increasingly recognized50,51. Similarly, in studies of neurodegeneration, the density of nonneurons is regarded as an important measure to characterize schizophrenia52, depression53,55, and bipolar disorder54. Moreover, neuron density is important as a basic measure related to aging56 and autism57. The neuron-per-nonneuron ratio is also regarded as an important characteristic in understanding the evolution of the brain58.

Recently, Collins et al. (2010) measured the number of neurons, number of cells, and weight of slices after segmenting the cortical surface in the monkey brain. From these basic variables, they determined the following three variables related to cell densities: The first variable is the density of neurons per weight, which is defined by the total number of neurons/weight of slice; the second variable is the density of nonneurons per weight, which is defined by the total number of nonneurons/weight of slice; and the third variable is the ratio of the number of neurons to the number of nonneurons in each slice. This report refers to these three variables as the neuron density, nonneuron density, and neuron-per-nonneuron ratio, respectively (Figure 1-A and C).

How were these two databases combined?

To compare the data of the brain connections and cell densities, it is necessary to combine the two independently developed databases2,12,3. The brain regions in the CoCoMac database included the A4, dorsal preluneate (DP) region, and auditory parakoniocortical rostal (PaAr) regions; however, these three regions were not clearly defined in Collins et al. (2010) to evaluate cell densities. Conversely, the corresponding brain regions for PAL in Collins et al. (2010) were not clearly found in the CoCoMac database. Thus, PAL was not included to evaluate the network architecture. I extracted three-dimensional brain coordinates, as shown in Figures 1-A and B, from a standardized brain atlas59.

Regression using both network and coordinates

In addition, I evaluated how accurately the non-uniformity of cell densities could be estimated using the coordinates and representative network variable – the participation coefficient – as explanatory variables for Principle Components Regression (PCR). PCR is a multiple regression method consisting of three steps: First, principle component analysis was applied to the explanatory variables. Second, an ordinary least square (OLS) regression was applied to the selected components using principle component analysis. Third, the model parameters were provided for each selected component. The merit of this method is that collinear problems can be naturally avoided. To evaluate the robustness of results, I also used the partial least squares regression (PLSR)24; however, there was no difference between the results obtained using PCR and PLSR for the data used in this study.

Network visualization

I used the Fruchterman–Reingold algorithm for the network visualization39. This algorithm is one of the Forth-based (FB) algorithms. FB algorithms regard nodes as electrically charged particles and edges as springs that connect them. The algorithms represent an optimized distribution of the nodes by solving for the equilibrium conditions where electrical repulsion between the nodes is balanced by the spring force attracting the nodes.

Supplementary Material

Supplementary Information

Supplemental material

srep02541-s1.pdf (662.2KB, pdf)

Acknowledgments

M.S. is grateful to Prof. Yasuo Kawaguchi for providing important suggestions for this study; Dr. Takumi Kobayashi, Prof. John M. Beggs, and Prof. Olaf Sporns for their discussions related to this study; and Prof. Daichi Nozaki for his support in helping to accomplish this study. This study was supported by a Grant-in-Aid for JSPS Fellows for General Research and Research Abroad.

References

  1. Rockel A. J., Hiorns R. W. & Powell T. P. The basic uniformity in structure of the neocortex. Brain 103, 221–244 (1980). [DOI] [PubMed] [Google Scholar]
  2. Kötter R. Online retrieval, processing, and visualization of primate connectivity data from the CoCoMac database. Neuroinformatics 2(2), 127–144 (2004). [DOI] [PubMed] [Google Scholar]
  3. Collins C. E., Airey D. C., Young N. A., Leitch D. B. & Kaas J. H. Neuron densities vary across and within cortical areas in primates. Proc Natl Acad Sci USA 107(36), 15927–15932 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Herculano-Houzel S., Collins C. E., Wong P., Kaas J. H. & Lent R. The basic nonuniformity of the cerebral cortex. Proc Natl Acad Sci USA 105, 12593–12598 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Felleman D. J. & Van Essen D. C. Distributed hierarchical processing in the primate cerebral cortex. Cerebral Cortex 1(1), 1–47 (1991). [DOI] [PubMed] [Google Scholar]
  6. Young M. P. Objective analysis of the topological organization of the primate cortical visual system. Nature 358(6382), 152–155 (1992). [DOI] [PubMed] [Google Scholar]
  7. Hilgetag C. C., Mark A. O. & Young M. P. ENHANCED PERSPECTIVE: Indeterminate Organization of the Visual System. Science 271(5250), 776 (1996). [DOI] [PubMed] [Google Scholar]
  8. Scannell J. W., Blakemore C. & Young M. P. Analysis of connectivity in the cat cerebral cortex. J. Neurosci. 15, 14631483 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Scannell J. W., Burns G. A. P. C., Hilgetag C. C., O'Neil M. A. & Young M. P. The connectional organization of the cortico-thalamic system of the cat. Cerebral Cortex 9(3), 277–299 (1999). [DOI] [PubMed] [Google Scholar]
  10. Stephan K. E., Zilles K. & Kötter R. Coordinate–independent mapping of structural and functional data by objective relational transformation (ORT). Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences 355(1393), 37–54 (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Stephan K. E. et al. Advanced database methodology for the Collation of Connectivity data on the Macaque brain (CoCoMac). Philosophical Transactions of the Royal Society of London. Series B: Biological Sciences 356(1412), 1159–1186 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Kötter R. & Wanke E. Mapping brains without coordinates. Philosophical Transactions of the Royal Society B: Biological Sciences 360(1456), 751–766 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Modha D. S. & Singh R. Network architecture of the long-distance pathways in the macaque brain. Proceedings of the National Academy of Sciences 107(30), 13485–13490 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. French L., Tan P. P. C. & Pavlidis P. Large-scale analysis of gene expression and connectivity in the rodent brain: insights through data integration. Frontiers in Neuroinformatics 5, 12 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. French L. & Pavlidis P. Relationships between gene expression and brain wiring in the adult rodent brain. PLoS computational biology 7(1), e1001049 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Barbas H. et al. Relationship of prefrontal connections to inhibitory systems in superior temporal areas in the rhesus monkey. Cerebral Cortex 15(9), 1356–1370 (2005). [DOI] [PubMed] [Google Scholar]
  17. Cahalane D. J., Charvet C. J. & Finlay B. L. Systematic, balancing gradients in neuron density and number across the primate isocortex. Frontiers in Neuroanatomy 6, 28 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Zamora-López G., Zhou C. & Kurths J. Exploring brain function from anatomical connectivity. Frontiers in neuroscience 5, 83 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Sporns O. Network attributes for segregation and integration in the human brain. Current opinion in neurobiology 23, 162–171 (2013). [DOI] [PubMed] [Google Scholar]
  20. Tononi G., Edelman G. M. & Sporns O. Complexity and the integration of information in the brain. Trends Cogn Sci 2, 44–52 (1998). [DOI] [PubMed] [Google Scholar]
  21. Meyer H. S. et al. Number and laminar distribution of neurons in a thalamocortical projection column of rat vibrissal cortex. Cerebral Cortex 20(10), 2277–2286 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Barbas H. Pattern in the laminar origin of corticocortical connections. Journal of Comparative Neurology 252(3), 415–422 (1986). [DOI] [PubMed] [Google Scholar]
  23. Fortunato S. Community detection in graphs. Physics Reports 486(3), 75–174 (2010). [Google Scholar]
  24. Vinzi V., Chin W. W., Henseler J. & Wang H. Handbook of Partial Least Squares. Wasserman S. & Faust K. Social Network Analysis University Press, Cambridge, 1994 (2010).
  25. Hilgetag C. C. & Grant S. Cytoarchitectural differences are a key determinant of laminar projection origins in the visual cortex. Neuroimage 51(3), 1006–1017 (2010). [DOI] [PubMed] [Google Scholar]
  26. Pucak M. L., Levitt J. B., Lund J. S. & Lewis D. A. Patterns of intrinsic and associational circuitry in monkey prefrontal cortex. Journal of Comparative Neurology 376(4), 614–630 (1996). [DOI] [PubMed] [Google Scholar]
  27. Otsuka T. & Kawaguchi Y. Cell diversity and connection specificity between callosal projection neurons in the frontal cortex. The Journal of Neuroscience 31(10), 3862–3870 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Morishima M. & Kawaguchi Y. Recurrent connection patterns of corticostriatal pyramidal cells in frontal cortex. The Journal of neuroscience 26(16), 4394–4405 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Brown S. P. & Hestrin S. Intracortical circuits of pyramidal neurons reflect their long-range axonal targets. Nature 457(7233), 1133–1136 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Kleinfeld D. et al. Large-scale automated histology in the pursuit of connectomes. The Journal of Neuroscience 31(45), 16125–16138 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Saalmann Y. B., Pinsk M. A., Wang L., Li X. & Kastner S. The pulvinar regulates information transmission between cortical areas based on attention demands. Science 337(6095), 753–756 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Shimono M., Mano H. & Niki K. The Brain Structural Hub of Interhemispheric Information Integration for Visual Motion Perception. Cerebral Cortex 22(2), 337–344 (2012). [DOI] [PubMed] [Google Scholar]
  33. Shimono M. & Niki K. Global Mapping of the Whole Brain Network Underlining Binocular Rivalry. Brain Connectivity 3(2), 212–221 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Sporns O. & Kötter R. Motifs in brain networks. PLoS biology 2(11), e369 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Kaiser M. & Hilgetag C. C. Modelling the development of cortical systems networks. Neurocomputing 58, 297–302 (2004). [Google Scholar]
  36. Sporns O., Honey C. J. & Kötter R. Identification and classification of hubs in brain networks. PLoS One 2(10), e1049 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Shimono M. & Beggs J. M. Mesoscopic neuronal activity and neuronal network architecture. Neuroscience Research 77, e304 (2011). [Google Scholar]
  38. Shimono M. & Beggs J. M. Spontaneous spike-trains reflect the detailed topological property of the structural neuronal network. JNNS 2011. (2011). [Google Scholar]
  39. Fruchterman T. M. & Reingold E. M. Graph drawing by force-directed placement. Software:. Practice and experience 21(11), 1129–1164 (1991). [Google Scholar]
  40. Blondel V. D., Guillaume J. L., Lambiotte R. & Lefebvre E. Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment 2008(10), P10008 (2008). [Google Scholar]
  41. Freeman L. A set of measures of centrality based on betweenness. Sociometry 40, 35–41 (1977). [Google Scholar]
  42. Alvarez-Hamelin J. I., Dall'Asta L., Barrat A. & Vespignani A. k-core decomposition: A tool for the visualization of large scale networks. arXiv preprint cs/0504107 (2005). [Google Scholar]
  43. Estrada E. & Rodríguez-Velázquez J. A. Subgraph centrality in complex networks. Phys. Rev. E 71 (5), 056103 (2005). [DOI] [PubMed] [Google Scholar]
  44. Holland P. W. & Leinhardt S. Transitivity in structural models of small groups. Comparative Group Studies 2, 107–124 (1971). [Google Scholar]
  45. Watts D. J. & Strogatz S. H. Collective dynamics of ‘small-world' networks. Nature 393(6684), 440–442 (1998). [DOI] [PubMed] [Google Scholar]
  46. Guimera R. & Amaral L. A. N. Functional cartography of complex metabolic networks. Nature 433, 895–900. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Milo R. et al. Network motifs: simple building blocks of complex networks. Science Signalling 298(5594), 824 (2002). [DOI] [PubMed] [Google Scholar]
  48. Rubinov M. & Sporns O. Complex network measures of brain connectivity: uses and interpretations. Neuroimage 52(3), 1059–1069 (2010). [DOI] [PubMed] [Google Scholar]
  49. Pakkenberg B. & Gundersen H. J. Neocortical neuron number in humans: Effect of sex and age. J. Comp. Neurol 384, 312–320 (1997). [PubMed] [Google Scholar]
  50. Allen N. J. & Barres B. A. Neuroscience: glia—more than just brain glue. Nature 457(7230), 675–677 (2009). [DOI] [PubMed] [Google Scholar]
  51. Barres B. A. The mystery and magic of glia: a perspective on their roles in health and disease. Neuron 60(3), 430–440 (2008). [DOI] [PubMed] [Google Scholar]
  52. Stark A. K., Uylings H. B. M., Sanz-Arigita E. & Pakkenberg B. Gliall cell loss in the anterior cingulate cortex, a subregion of the prefrontal cortex, in subjects with Schizophrenia. Am J Psychiatry 161, 882–888 (2004). [DOI] [PubMed] [Google Scholar]
  53. Rajkowska G. et al. Morphometric evidence for neuronal and glial prefrontal cell pathology in major depression. Biological psychiatry 45(9), 1085–1098 (1999). [DOI] [PubMed] [Google Scholar]
  54. Rajkowska G., Halaris A. & Selemon L. D. Reductions in neuronal and glial density characterize the dorsolateral prefrontal cortex in bipolar disorder. Biological psychiatry 49(9), 741–752 (2001). [DOI] [PubMed] [Google Scholar]
  55. Cotter D., Mackay D., Landau S., Kerwin R. & Everall I. (2001). Reduced glial cell density and neuronal size in the anterior cingulate cortex in major depressive disorder. Archives of General Psychiatry 58(6), 545. [DOI] [PubMed] [Google Scholar]
  56. Terry R. D., DeTeresa R. & Hansen L. A. Neocortical cell counts in normal human adult aging. Annals of neurology 21(6), 530–539 (1987). [DOI] [PubMed] [Google Scholar]
  57. Kemper T. L. & Bauman M. Neuropathology of infantile autism. Journal of neuropathology and experimental neurology 57(7), 645–652 (1998). [DOI] [PubMed] [Google Scholar]
  58. Herculano-Houzel S., Collins C. E., Wong P. & Kaas J. H. Cellular scaling rules for primate brains. Proceedings of the National Academy of Sciences 104(9), 3562–3567 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Martin R. F., Bowden D. M., Wu J., Dubach M. F. & Robertson J. E. Primate brain maps: Structure of the macaque brain. Elsevier Science, Amsterdam. (2000).

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplemental material

srep02541-s1.pdf (662.2KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES