Reflected wavefront manipulation based on ultrathin planar acoustic metasurfaces

Abstract

The introduction of metasurfaces has renewed the Snell's law and opened up new degrees of freedom to tailor the optical wavefront at will. Here, we theoretically demonstrate that the generalized Snell's law can be achieved for reflected acoustic waves based on ultrathin planar acoustic metasurfaces. The metasurfaces are constructed with eight units of a solid structure to provide discrete phase shifts covering the full 2π span with steps of π/4 by coiling up the space. By careful selection of the phase profiles in the transverse direction of the metasurfaces, some fascinating wavefront engineering phenomena are demonstrated, such as anomalous reflections, conversion of propagating waves into surface waves, planar aberration-free lens and nondiffracting Bessel beam generated by planar acoustic axicon. Our results could open up a new avenue for acoustic wavefront engineering and manipulations.

The angles of reflected and refracted waves are certainly determined when light impinges on a planar interface between two media with different refractive index due to the conservation of momentum along the tangential directions of the boundary, as is well known from the famous Snell's Law. Recently, the Snell's law was revisited in the context of metasurfaces with phase discontinuities constructed by metallic antennas capable of providing discrete phase shifts covering 2π span¹. The generalized Snell' law was introduced by applying Fermat's principle to interpret the anomalous reflection and refraction phenomena. Inspired by this pioneering work, fascinating optical wavefront engineering capabilities, such as light bending², anomalous reflection³, converting propagating waves to surface waves⁴, flat lens and axicons⁵, etc., have been demonstrated both theoretically and experimentally through metasurfaces with phase discontinuities⁶.

As another classical waves, acoustic waves also follow Snell' law. It is therefore apparent that the generalized Snell's law and metasurfaces, if could be successfully realized in acoustics, would have deep implications for acoustic devices, acoustic applications and the field of acoustics in general. A straightforward analogy between the optical and acoustic metasurfaces, however, is infeasible due to the inherent distinction between the electromagnetic and acoustic waves. In optics, the concept of metasurface is generally implemented by utilizing the plasmonic resonance mechanism through metallic antennas, which is able to tailor the wave phase from 0 to 2π but has no direct counterpart in acoustics so far. On the other hand, the use of plasmonic resonance inevitably leads to a direct result that the optical metasurface can hardly have a deep-subwavelength size and operate only with cross-polarized fields⁷. It is therefore necessary to explore intrinsically new physical mechanism in an attempt to achieve the acoustic metasurfaces with ultrathin structures, which will be particularly significant for the practical applications of the resulting devices. Considering the fact that the naturally available materials in acoustics can only provide limited phase shifts, the concept of generalized Snell's law cannot be analogously translated from electromagnetic waves to acoustic waves. The emergence of acoustic metamaterials⁸,⁹,¹⁰,¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶,¹⁷,¹⁸,¹⁹, which could provide unavailable parameters in nature, has significantly broadened the horizon for acoustic waves. Novel phenomena, such as extraordinary acoustic transmission²⁰,²¹,²²,²³,²⁴, sub-diffraction imaging²⁵,²⁶,²⁷, cloaking²⁸,²⁹, one-way transportation³⁰,³¹,³²,³³, super absorption³⁴, etc., have been demonstrated both theoretically and experimentally. Hence, the advance in acoustic metamaterials may provide possibility and should be good candidates to realize the acoustic metasurfaces.

In the following, we show that generalized Snell's law for acoustic reflected waves can be realized through ultrathin planar acoustic metasurfaces by coiling up space with two stiff corrugated beams. By appropriately selecting the geometrical parameters, eight units can support discrete phase shifts ranging from 0~2π with steps of π/4. Anomalous reflections, conversion of propagating waves to surface waves, flat acoustic aberration-free lens and nondiffracting Bessel beam generated by flat acoustic axicon are also demonstrated by imposing suitable phase profiles in the transverse direction of the metasurfaces. Our results should open up new degrees of freedom in acoustic wavefront engineering, such as the field of caustic engineering.

Results

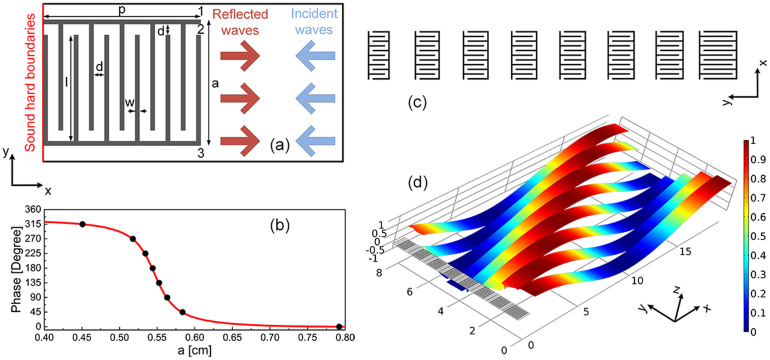
The acoustic metasurface, as shown in Fig. 1(a), is constructed by immersing identical thin rigid beams (width w and length l) in air in a way that forms fluid channels (width d). It has been proven that the coiling structure (width p and length a) could behave as an effective medium with extremely high refractive index¹⁸,³⁵, such that the reflected waves can be delayed heavily after the incident waves impinge on the structure and propagate within the zigzag path. It is therefore reasonable to infer that the phase of the reflected waves could be controlled at will by appropriately selecting the geometrical parameters of the structure, and will be demonstrated later. In order to ensure a planar structure, the length a of the metasurfaces associated to the length l of the rigid corrugations are tailored to yield the desired phase shifts, while the values of w, d and p are fixed in the calculations. The phase of the reflected waves as a function of a with free space wavelength λ = 19.6 cm is plotted in Fig. 1(b). It should be noted that, since acoustic waves, as scalar waves, can propagate within the channels freely, the reflected waves at the right-edge of the metasurface (containing three channels labeled with “1”, “2” and “3” in Fig. 1(a)) can be considered as the accumulated field of three sources, resulting in the inhomogeneous pressure distribution at the right edge of the metasurface. Therefore, the phase information at the right edge of the metasurface is retrieved by integration along extra line λ/8 (not shown in Fig. 1(a)) away from the edge. From Fig. 1(b), it is sufficient to frame eight units that could realize discrete phase shifts covering the full 2π span with steps of π/4. The exact values of a for achieving these discrete phase shifts are also illustrated with black dots in Fig. 1(b). Schematic diagrams of these eight units with different values of a are shown in Fig. 1(c). Planar acoustic metasurfaces are obviously constructed because the lengths of the units in x direction are entirely identical. To further verify the discrete phase shifts, the reflected waves by these eight units are shown in Fig. 1(d). The strips refer to the pressure filed patterns p(x,y) at the same time instant. The peak of the pressure field can shift up to a wavelength, which provide solid support that the phase shifts cover the whole 2π range. It therefore could be concluded that desirable discrete phase shifts can be realized by the eight units. The metasurfaces constructed by the eight units are ultrathin with the thickness approximately equal to λ/19.6, revealing that the metasurface is good candidate to realize acoustic devices easy for integration. It is worth pointing out that fascinating features of the coiling metamaterials such as negative refractions and zero refractive index are first presented theoretically and later verified experimentally¹⁸,³⁶,³⁷. Recently we have proved that by coiling up space it is possible to change the propagating phase of acoustic wave and thereby focus the waves, but the phase delay in that work is too limited to cover 2π range³⁵. In what follows we will further demonstrate the potential of coil-up acoustic metamaterials to design a more general metasurface that has an ultrathin structure and is capable of controlling reflected acoustic waves arbitrarily.

Figure 1. An acoustic metasurface for generalized Snell's law.

(a) The schematic diagram of an acoustic metasurface made of two stiff corrugated beams with a channel coiling up the space. The coiling structure has a width p = 1 cm and length a (a = 0.8 cm in this example). The width of the channel is d = 0.067p. The width of the beams is w = 0.03p, and the corrugation length is l = a − 2w − d. Sound hard boundary conditions are imposed to the left boundaries (red line) to mimic the fact that the metasurface is actually coated on a stiff plate. The light blue and dark red arrows refer to the propagation direction of incident and reflected waves, respectively. The label “1”, “2” and “3” refer to the three outlets of each element. (b) The phase of the reflected waves, as a function of the length a of the metasurface, with incident wavelength λ = 19.6p. The black dots refer to specific a values for eight units to fulfill the desired discrete phase shifts. (c) Schematic diagram of the eight units with the specific a values shown in (b) with black dots. The gap between each unit is 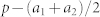, with a₁ and a₂ denoting the length of the two adjacent coiling structures. (d) The pressure strips of the reflected waves by the eight units. The high maps of pressure field are utilized to clearly show the different phase shifts by each unit.

The realization of 2π range phase shifts for the reflected acoustic waves allows us to revisit the Snell's law by selecting appropriately phase profile. Figure 2(a) illustrates the schematic diagram for the derivation of the generalized Snell's law. Considering the acoustic waves with normal incidence along the −x direction, due to the existing of discrete phase shifts along the y direction, the angle of the reflected wave θ_r (measured from the x direction) can be deduced by applying Fermat's principle¹:

where ϕ(y), dy represent the phase shift and the distance between two cross points along the y direction respectively, and k = 2π/λ is the wave vector in air. Equation (1) implies that the reflected angle can be engineered freely by designing the suitable phase profile along the y direction.

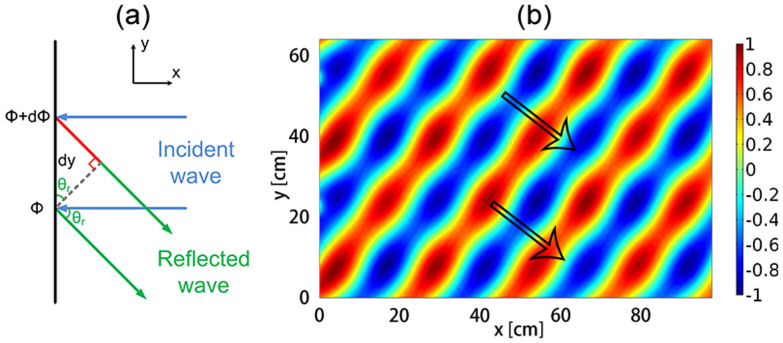
Figure 2. The generalized Snell's law of reflection and anomalous reflections.

(a) Schematics for the derivation of the angle of reflection. ϕ and ϕ + dϕ are the phases at the two cross points separated by dy along the y direction. θ_r represents the anomalous reflection angle induced by the discrete phase shifts. (b) Pressure field pattern for the gradient phase profile of 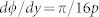. The black arrows refer to the theoretical value of the reflected angle.

Suppose that the gradient of the phase profile ϕ(y) on the metasurface is constant along the y direction. From Eq. (1), it can be concluded that the reflected waves should remain a plane wave and be independent of the location y. To demonstrate this feature, one type of phase profile is introduced. The phase profile is chosen as 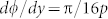, indicating that there are four identical units for each discrete phase shift of π/4. The pressure field pattern p(x, y) is illustrated in Fig. 2(b). Different from normal surfaces, by which the reflected waves can only propagate along the opposite direction of the normal incidence, anomalous reflection can be clearly observed after imposing the discrete phase profile. The theoretical angles of reflection for this case should be θ_r = 37.77°, which can be deduced from Eq. (1). Excellent agreement can be observed by comparing the theoretical value (shown as black arrows) and simulated pattern. Note that imperfect plane waves are obtained due to the mismatched pressure amplitude of the reflected acoustic waves along the metasurface as mentioned above.

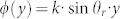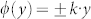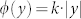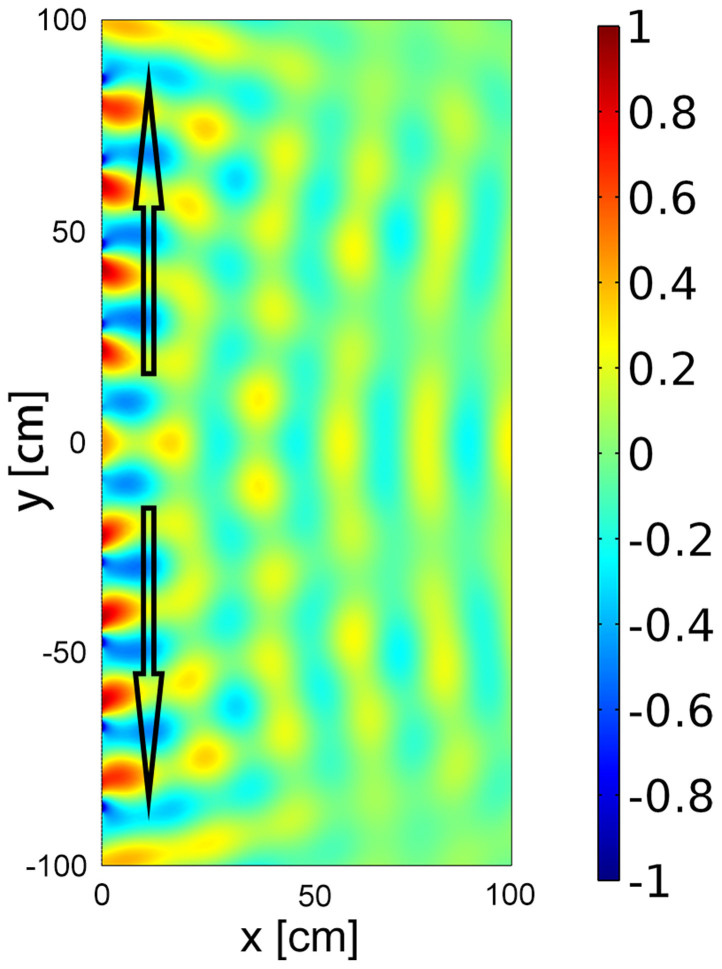
Moreover, we can design the specific distributions of to realize different wavefront manipulations. One interesting phenomenon is the conversion of a propagating wave into a surface wave. It can be verified from Eq. (1) that the reflected waves with θ_r = 90° could be obtained with the phase profile . Different from the Ref. 4, where is utilized to realize the directional surface waves, the phase profile 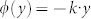is employed to generate two surface beams propagating along the y and −y directions, respectively. For the sake of clarity, it is necessary to build a rule to convert a continuous phase profile to a discrete phase profile. Throughout the paper, the rule is built as follows: for example, the units providing π/4 phase shift is utilized to displace the continuous phase range π/4 ± π/8 at the specified position in the y direction. The pressure field pattern p(x, y) of the reflected waves by the metasurfaces constructed from the rule is illustrated in Fig. 3. It is found that the surface waves are propagating near the metasurfaces along the ± y directions (black arrows) after the incident wave impinge on the metasurfaces. High efficiency conversion of propagating waves to surface waves is realized even though there is some diffraction upon the metasurfaces. Physically, the discrete phase shifts along the y direction provide extra momenta to compensate the momentum mismatch between the propagating wave and the surface wave on the metasurfaces, resulting in the high efficiency conversion.

Figure 3. Metasurfaces for converting propagating waves to surface waves.

Pressure field pattern for the conversion of propagating waves to surface waves on the metasurface with phase profile 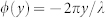. Surface waves can propagate near the metasurface with high-efficiency conversion. The black arrows indicate the wave vectors of the surface waves.

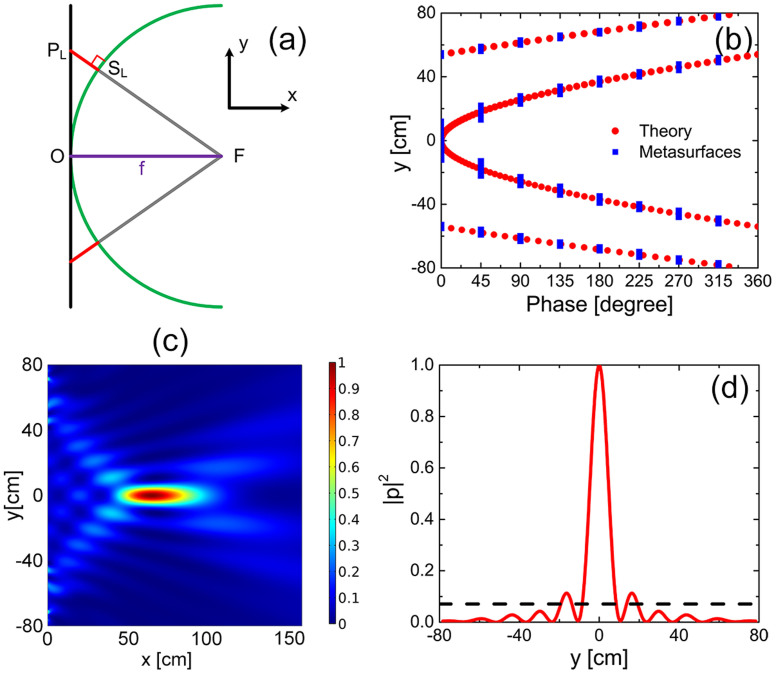
Next, we show that a flat lens and a flat axicon can be achieved successfully through acoustic metasurfaces. To design an acoustic flat lens, the hyperboloidal phase profile is employed on the metasurfaces, as shown in Fig. 4(a). For a given focal length f, the phase shift ϕ(y) imposed at every point 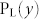must satisfy the following equation

By applying the aforementioned rule, the desirable continuous phase profile (red dots) and the discrete phase profile (blue squares) provided by the metasurfaces are plotted in Fig. 4(b). The physical structure of the lens is readily constructed according to the phase profile. Spatial intensity distribution 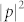of the acoustic lens with f = 3λ is shown in Fig. 4(c). To quantify the performance of the acoustic lens, the transverse cross-section intensity distribution at x = 63 cm is shown in Fig. 4(d). The intensity of pressure at the focal point is nearly 14.13 times larger than the one of the incident waves (shown as black dash line), which provides clear confirmation that excellent focusing effect can be realized by the proposed metasurfaces. Note that the hyperboloidal phase profile imposed along the y direction could produce a spherical wavefront even for nonparaxial conditions, which leads to excellent focusing effect without aberrations⁵.

Figure 4. Planar acoustic lens constructed by an acoustic metasurfaces.

(a) Schematic diagram of the design of lens. A hyperboloidal phase profile along y direction is utilized to focus acoustic plane wave to a single point at a distance f from the metasurfaces. The green spherical line with radius f is the desired equiphase surface of the reflected wave so that the phase shift at 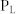should be proportional to the length of the red line 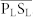. The theoretical continuous phase shifts (red dots) and the discrete phase shifts provided by the metasurfaces (blue squares) along the y direction are shown in (b). The half-height of the lens is chosen to be 80 cm. (c) Spatial distribution of the intensity field 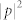for the designed lens with f = 3λ. (d) Transverse cross-section of intensity profile at x = 63 cm for the designed lens. The black dash line refers to the intensity of the incident waves.

To design a flat acoustic axicon with a base angle β, the conical phase profile should be employed so that the phase shift ϕ(y) at every point 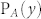along the 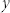direction satisfy the following equation

By applying the aforementioned rule, the theoretical continuous phase shift (red dots) and the discrete phase shifts (blue dots) provided by the acoustic metasurfaces are shown in Fig. 5(b). Spatial intensity distribution 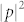of the acoustic axicon and the transverse cross-section of the intensity profile at x = 240 cm from the metasurface are shown in Figs. 5(c) and 5(d), respectively. Due to the good performance of the proposed acoustic metasurfaces, it is not surprising to observe a non-diffracting Bessel beam propagating along the x direction with a relatively long distance.

Figure 5. Acoustic axicon for the non-diffracting Bessel beam.

(a) Schematic diagram of the design of acoustic axicon. The green cone-like line with base angle 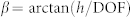is the desired equiphase surface for the acoustic axicon so that the phase shift at 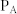should be proportional to the length of the red line . Here, the half-height of the axicon h is selected to be 100 cm. (b) The theoretical continuous phase shift (red dots) and the discrete phase shift provided by the metasurface (blue squares) along the y direction. (c) Spatial distribution of the intensity field 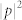for the designed axicon with 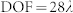. (d) Transverse cross-section of the intensity profile at x = 240 cm from the metasurfaces within the DOF.

Discussion

In summary, we have demonstrated that acoustic metasurfaces can be constructed by eight units of corrugated plates, which can tailor the reflected waves with discrete phase shifts covering the full 2π span. The generalized Snell's law can be extended to acoustic counterpart, which is otherwise difficult to realize with natural materials. By employing linear phase profiles, anomalous reflections and the conversion of propagating waves into surface waves can be realized. Furthermore, a planar acoustic lens and an acoustic axicon can be constructed by utilizing the hyperbolic and conical phase profiles. Our results should open the door for wavefront manipulation and engineering of acoustic waves.

Methods

Throughout the paper, Finite Element Method (FEM) based on commercial software COMSOL Multiphysics™ 4.3a is employed for the simulations. The materials applied in the simulations are air and stiff beams (sound hard boundaries). Plane wave radiation boundary condition is imposed on the incident boundaries and the periodic boundary condition are employed in the y direction to calculate the phase profile of the reflected wave for different length a (Fig. 1(c–d)) and the pressure field patterns (Fig. 2(b)). Each strips of pressure pattern shown in Fig. 1(d) is calculated independently. For Figs. 3,4,5, perfectly matched layers (PMLs) and background pressure field is utilized to eliminate the reflected waves by the outer boundaries because of the plane wave radiation boundaries are not sufficient to absorb the waves with oblique incidence.

Author Contributions

Y.L., Z.M.G. and X.Y.Z. conducted the theoretical simulations (FEM). B.L. and J.C.C. conceived and supervised the study. Y.L. wrote the article and B.L. and J.C.C. participate in the revision. All authors contributed to the discussions.