Children start elementary school with variable mathematics skills. Some children understand the fundamentals of numbers and mathematics, while others struggle with basic counting, number recognition, understanding of symbols, quantity discrimination, and concepts of addition and subtraction. Often, this set of early numerical competencies is referred to as number sense or early numeracy competencies. Students need to establish and understand these competencies before moving on to more complex mathematical tasks. This article describes important early numerical competencies and provides a description of how these competencies can be taught to students who struggle with mathematics.
EARLY NUMERICAL COMPETENCIES AND STUDENTS WITH MATHEMATICS DIFFICULTY
Before solving algebra, geometry, fractions, and computation problems, students must have a solid understanding of numbers (Malofeeva, Day, Saco, Young, & Ciancio, 2004). Sometimes this is called number sense (e.g., Jordan, 2007; Kaminski, 2002; Wagner & Davis, 2010) or early numeracy (e.g., Aunio, Hautamaki, Sajaniemi, & Van Luit, 2009; Bryant et al., 2011; VanDerHeyden et al., 2011). Regardless of the term used, the construct refers to the early numerical competencies that are foundational to building competence in mathematics. In this article, we refer to this collection of skills as early numerical competencies.
What Are Early Numerical Competencies?
Although there is no one definition of early numerical competencies, several researchers have identified early numerical competencies that are important for young students (Berch, 2005; Bryant et al., 2011; Gersten & Chard, 1999; Griffin & Case, 1997; Kaufmann. Handl, & Thony, 2003; Lago & DiPerna, 2010). See Figure 1 for a diagram of early numerical competencies. Some topics (i.e., place value or basic number combinations) require prerequisite knowledge of other topics (i.e., number recognition or comparing numbers). We present these early numerical competencies as a collection because students’ development of early numerical competencies is not always linear, and students differ in the timeline by which they acquire these skills.
FIGURE 1.

Early Numerical Competencies
Importance of Early Numerical Competencies
Children start school (i.e., kindergarten) with a wide array of early numerical competencies. Some children already appreciate quantities, know their number names, and are able to solve simple addition and subtraction problems; others struggle to identify numbers and count from 1 to 10 (Lembke & Foegen, 2009). Exposure to early numerical activities at home, in preschool, or in daycare plays an important role in the establishment of early numerical competencies for kindergarten students (Baroody & Benson, 2001 ; Jung, 2011 : Skwarchuk, 2009). The more exposure to early numerical competencies students receive through games, stories, or play before formal schooling begins, the more they understand the building blocks of mathematics (Ramani & Siegler, 2008).
One indication that these early numerical competencies are important is that they predict later mathematics achievement. For example, Locuniak and Jordan (2008) tested 198 students in the spring of kindergarten on early numerical measures and again in the winter of second grade on a calculation fluency measure. Students scoring below the 25th percentile at beginning of kindergarten were designated at risk of poor mathematics development. The early numerical measures included items about counting, knowledge of numbers, non-verbal calculation, number combinations, and story problems. The calculation fluency measure consisted of 25 addition and 25 subtraction number combinations. Early numerical competency measured in kindergarten was a significant predictor of calculation fluency at second grade. Over 50% of the at-risk students (identified in kindergarten) still performed below the 25th percentile in second grade, and 25% of at-risk students performed between the 25th and 50th percentiles. Locuniak and Jordan’s findings indicate that many students with weaker early numerical skills in kindergarten will continue to demonstrate lower mathematics performance after kindergarten. Jordan, Kaplan, Locuniak, and Ramineni (2007) found a similar pattern with 277 students from kindergarten to first grade. Number sense performance in the fall of kindergarten accounted for 66% of the variance on tests of mathematics calculation and problem solving administered at the end of first grade. Other studies (Duncan et al., 2007; Jordan, Glutting, Ramineni, & Watkins, 2010) also indicate that early numerical skills predict mathematics achievement in later grades.
Difficulties with Early Numerical Competencies
Many young students struggle with early numerical competencies (Lembke & Foegen, 2009; Lloyd, Irwin, & Hertzman, 2009). In the United States, differences emerge at the onset of schooling: Some children come to school with an established set of early numerical competencies: others demonstrate much lower performance on early numerical tasks (Jordan et al., 2007). For example, Jordan, Kaplan, Ramineni, and Locuniak (2009) administered early numerical measures of counting, number recognition, comparison, number combinations, and story problems in kindergarten. Lower income students in their sample demonstrated significantly lower early numerical scores than middle-income peers. While low income may not be the only factor contributing to differences in early numerical competencies, Jordan et al. (2009) demonstrated that kindergarten students display varying levels of early numerical skills. The same trend holds true for students in other countries (Ee, Wong, & Aunio, 2006; Lloyd et al., 2009). For example, Finnish students between 5 and 7 years old with special needs (i.e., attention deficit disorder, language difficulties, or developmental difficulties) demonstrated significantly lower early numerical performance than students without special needs (Aunio et al., 2009).
Because students who perform lower on early numerical tasks often demonstrate lower mathematics competence in later elementary and middle school (Duncan et al., 2007), early identification and early intervention are key (Dowker, 2005). While identification of struggling students may be difficult because of inadequate assessments (Mazzocco, 2005), with some students misidentified as struggling in mathematics (Locuniak & Jordan, 2008), research indicates that early intervention can help students with their early numerical skills (Berch, 2005; Bryant et al., 2011 ; Fuchs et al., 2005a).
Early Numerical Instruction
Based on experimental work with students who struggle with mathematics, Fuchs et al. (2008) provided several recommendations for important components of mathematics instruction. Instruction should be explicit with a focus on conceptual and procedural knowledge. Instruction should be designed in a meaningful way that minimizes challenges, and practice and review should be a part of any instructional program. Fuchs et al. also emphasized the use of motivational tools embedded within instruction to help students with on-task behavior and to monitor academic progress. Monitoring student progress is important so that teachers have objective indicators of when student response to the current instructional program is inadequate and unlikely to produce goal attainment. When a student’s data indicate inadequate response, the teacher adjusts the student’s instructional program.
Gersten et al. (2009) highlighted explicit instruction, use of strategies, student verbalizations, use of visual representations, progress monitoring, and using a variety of examples as important instructional practices for students who struggle with mathematics. Adding to these points, Gersten and Chard (1999) suggested working on mathematics fluency to integrate instruction on concepts and procedures with sufficient practice. These recommendations are especially important for students with mathematics difficulties, and the following examples demonstrate how these important instructional recommendations, when used to teach early numerical competencies, are beneficial to students with mathematics difficulties.
For example, Bryant et al. (2011) worked with first-grade students (N = 224) who performed below the 35th percentile on an early numerical competencies assessment. Some students (n = 151) were assigned to an early numerical program, whereas other students (n = 73) remained in their regular education classroom for mathematics instruction. Small-group tutoring for the early numerical program students lasted 22 weeks, four sessions per week, 25 minutes per session. Students participated in explicit instruction with guided and independent practice on the procedural and conceptual ideas of counting, number relationships, sets of 10, number combinations, and place value. At posttest, students who participated in the early numerical program performed significantly higher than students in the control group, with effect sizes (ES) of 0.18 on magnitude comparison, 0.47 on number sequences, 0.39 on place value, and 0.55 on addition and subtraction number combinations.
Fuchs et al. (2005a) also provided early numerical tutoring to first-grade students (N = 127) who were struggling with mathematics. Students were randomly assigned to receive early numerical tutoring (n = 64) or to participate in their regular mathematics instruction without tutoring (n = 63). Students received tutoring for 16 weeks, three times a week, 40 minutes a session. Tutoring focused on early numerical competencies such as number identification and writing, symbol use, counting, place value, and addition and subtraction combinations. After tutoring ended, students who received tutoring outperformed students without tutoring on tests of addition facts (ES = 0.40), subtraction facts (ES = 0.14), calculation (ES = 0.57), concepts and applications (ES = 0.67), and story problems (ES = 0.70).
In other countries, early numerical programs have also been shown to strengthen the mathematics performance of struggling students. Kaufmann et al. (2003) worked with six students with mathematics difficulties. These students participated in an early numerical program for 6 months, three times a week, 25 minutes a session. Students learned about counting, symbols, facts equal to 10, addition and subtraction facts, and place value through explicit instruction and working from the concrete (i.e., manipulatives) to the abstract (i.e., solving problems with numbers and symbols). The six students enjoyed strong growth over the course of the program compared to peers without mathematics difficulties. Kaufmann, Delazer, Pohl, Semenza, and Dowker (2005) expanded this work by comparing an early numerical program focused on procedural and conceptual learning versus a program focused on training of basic skills. Students who participated in the procedural and conceptual program demonstrated significant gains on measures of counting, cardinality, comparisons, and calculations over students who participated in the basic skills program. Van Luit and Schopman (2000) worked with kindergarten students (N = 124) who performed below the 25th percentile on an early numerical measure. Half the students were assigned to receive early numerical instruction; the other half participated in their regular classroom program. The early numerical instruction focused on counting skills, and teaching was explicit and interactive and followed a sequence of concrete to representational to abstract (Hudson & Miller, 2006). After twenty 30-minute sessions, students who participated in the early numerical program outperformed control students on early numerical measures of comparing numbers, counting, and understanding the meaning of numbers.
These results from early numerical investigations in the United States and abroad indicate that struggling mathematics students benefit from programs focused on early numerical competencies. All the instruction in these programs was explicit and focused on teaching students the meaning (i.e., concepts) behind early numerical competencies along with the procedures to solve mathematics problems.
EARLY NUMERICAL COMPETENCIES
For this article, we highlight four main categories of early numerical competencies: counting, comparing numbers, understanding symbols, and addition and subtraction concepts. In this section, we describe each of these categories and how students may struggle with skills in that category. We then present an example of an intervention to help students who are struggling with these early numerical competencies. Finally, we provide suggestions for practitioners.
Counting
There is more to counting than reciting, “1, 2, 3, 4, 5.…” Students can often count to 10, but they may not understand what the numbers represent (Bermejo, Morales, & deOsuna, 2004; Bruce & Threlfall, 2004). For example, students may not assign meaning to their counting or realize that the number words map onto counted items. Counting encompasses five principles: stable order, one-to-one correspondence, cardinality, abstraction, and order irrelevance (Gelman & Gallistel, 1978). Students can struggle with one or more of these principles (Bruce & Threlfall, 2004). These principles are often combined (i.e., students say number names and point to each counted object), and, because of this, these principles should be practiced together (Camos, Barrouillet, & Fayol, 2001).
Many students develop counting skills before entering kindergarten (Gelman & Gallistel, 1978). Some students, however, come to school with inadequate counting skills or a lack of understanding of the principles of counting. For example, many students can count to five without difficulty, but they may struggle with counting larger sets (i.e., sets larger than 5 or 6), make more errors, and not understand how to use counting to identify the number of items in a set (Carrasumada, Vendrell, Ribera, & Montserrat, 2006). Counting skills, however, can be taught and improve with instruction and practice (Camos et al., 2001; Xin & Holmdal, 2003). Often, a helpful way to understand whether students understand counting principles is to demonstrate counting and miscounting with a puppet (Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007; Muldoon, Lewis, & Francis, 2007). Recommendations for counting instruction can be determined by awareness (or lack of) of the puppet’s counting skills. For example, if a student says that it is incorrect for a puppet to count from the student’s right to left, then the student should receive instruction on the counting principle of order irrelevance.
For counting, students should know the number words in order (Slusser & Sarnecka, 2011), a concept called stable order. These words are usually recited in forward order (e.g., “one, two, three, four, five”), and the sequence of these counting words needs to be used consistently (Frye, Braisby, Lowe, Maroudas, & Nicholls, 1989). Stable order is often learned and practiced through songs, chants, or stories.
Also, when counting, students must count each item only once (Van De Walle, Karp, & Bay-Williams, 2010). This is called one-to-one correspondence. When practicing one-to-one correspondence, it is easier for students to keep track of items in a row or items that have been tagged and partitioned rather than items that are counted randomly (Potter & Levy, 1968). To count using one-to-one correspondence, students must know number names, appreciate stable order, and understand the relationship between counts and number names (Potter & Levy, 1968). One-to-one correspondence is often practiced by passing out items (like cookies) and ensuring that each student receives one cookie (Van De Walle et al., 2010).
By combining stable order and one-to-one correspondence, students start to count sets of objects to determine the number in the set (i.e., the cardinality principle). When counting a set of items, the final count (e.g., “4” after counting four dinosaurs) represents the set. Cardinality refers to understanding that the final or last count represents the total of items counted (Bermejo et al., 2004). Often this is practiced by asking students to count a set of objects and then asking them to answer the question, “How many?” (Muldoon, Lewis, & Freeman, 2003).
While the counting principle of abstraction is not a necessity for counting, it is helpful for students to understand that any objects can comprise a set (Frye et al., 1989). For example, the counting set does not have to contain only frogs. The counting set can contain frogs, toads, trucks, and pencils. Counting can be applied to any set of items no matter how abstract those items may be. Similar to abstraction, order irrelevance is not as important as other counting principles (Kamawar et al., 2010). The principle of order irrelevance dictates that the order in which items are counted does not matter as long as each item is counted only once (i.e., one-to-one correspondence). Many students count from left to right and top to bottom because that is how they read in English, so it may be confusing to these students that counting does not have to occur in a linear fashion.
Students should move from counting items one by one to subitizing (Bruce & Threlfall, 2004; Hannula, Rasanen, & Lehtinen, 2007). Subitizing is the ability to instantly recognize how many items are in a group. See Figure 2 for subitizing examples. Students should be able to look at each of the examples and instantly recognize that there are four boxes, three circles, one hexagon, and six squares. Often, students who struggle with mathematics struggle with subitizing (Schleifer & Landerl, 2011 ), but practice can help to improve their skills (Clements, 1999; Fischer, Köngeter, & Hartnegg, 2008). Subitizing is often viewed as a central component of early numerical competency, and we mention it here because students may subitize (instead of count) to compare amounts and work with addition and subtraction.
FIGURE 2.

Subitizing Examples
Appreciating Quantity
Subitizing is related to children’s appreciation of quantity, a related early numerical competency. This is sometimes referred to as quantity discrimination, magnitude, or comparing numbers. On the most basic level, students look at two numbers (e.g., 4 and 9) and answer the question, “Which is more?” (9) or “Which is less?” (4). Students can use manipulatives or pictures to aid in discriminating between the two quantities. Students have an easier time discriminating between quantities that are much farther apart (e.g., 9 and 2) than those that are closer in magnitude (e.g., 9 and 8; Murray & Mayer, 1988). When comparing larger, two-digit numbers, students have an easier time discriminating between numbers where the tens place is different than when the decade is the same but the ones place differs (Ganor-Stern, Pinhas, & Tzelgov, 2009).
Students with difficulty in mathematics often struggle with comparing numbers and perform lower on comparing tasks than peers without mathematics difficulties (De Smedt & Gilmore, 2011; Holloway & Ansari, 2009). It is interesting that students may perform better on number magnitude tasks that do not involve the number symbols (Rousselle & Noel, 2007). For example, when presented with a group of six candies and four candies, students are able to determine that six is more than lour When students have to compare two number symbols (e.g., “6” and “4”), this generally is more difficult (De Smedt & Gilmore, 2011).
Preschool students, when presented with two sets for comparison, often do not count and use the principal of cardinality for comparing the two sets. Typically, students instead rely on visual (i.e., nonsymbolic) inspection (Zhou, 2002). Relying on visual scanning can help students only for a while, generally when numbers are between 1 and 3. Therefore, providing instruction on counting to determine differences between sets can be helpful (Muldoon et al., 2003). Often students do not realize that counting can be used for comparison because teachers generally ask, “How many?” with every counting task instead of questions like, “How many fewer?” or “Which has more?”
Mathematical Symbols
With the early numerical skill of counting, eventually students will associate counts (e.g., one, two, three) with the number symbols (e.g., 1, 2, 3). Students can often repeat the numbers words in stable order, use one-to-one correspondence, and understand cardinality without using number symbols. Students can also compare amounts without using number symbols (i.e., when provided with visual representations of two sets). Once students begin kindergarten, however, most activities involving counting and comparing numbers require students to have knowledge of number symbols and the meaning of these symbols to complete mathematical tasks. Mathematical symbols are important because most of mathematics is represented using symbols.
Ten number symbols (i.e., 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9) can be used alone or combined to represent any number (e.g., 14,597). Besides the ten number symbols, early elementary students learn two operation symbols: the plus sign (+) for addition and the minus sign (−) for subtraction. Students also use the equal sign (=) in number sentences. Students might also use the inequality symbols for greater than (>) and less than (<) when comparing amounts. Students usually learn the number symbols before any other symbols (Zhou, Wang, Wang, & Wang, 2006).
Students need to learn how to write and interpret the symbols because they do not automatically assign meaning to symbols. Meaning of the symbols develops over time and with practice. For example, students learn that “three” or * * * or three manipulative bears can be represented by the written symbol 3 and vice versa. Students must learn to put items together when they see a plus (+) symbol and to take an item away or find the difference when they see the minus (−) symbol. Many students understand the operations indicated by the plus and minus signs, but fewer students correctly interpret the equal sign and the inequality symbols (e.g., Hattikudur & Alibali, 2010; Matthews & Rittle-Johnson, 2009; McNeil. 2008). The equal sign should be understood as a relational symbol, indicating that a balanced relationship exists between numbers on the two sides of the equal sign (=) symbol (Jacobs, Franke, Carpenter, Levi, & Battey, 2007). The inequality symbols (< and >) should also be understood as relational, with one side of the symbol representing a larger or smaller quantity.
Unfortunately, students come to misunderstand symbols as teachers provide instruction or practice that does not promote full understanding of the symbol (Capraro, Ding, Matteson, Capraro, & Li, 2007; McNeil, 2008). For example, students often practice hundreds of equations like 2 + 3 = _, which require little understanding of the equal sign in a relational manner (Powell, in press). By contrast, students, even those who struggle with mathematics, learn to interpret the equal sign relationally with appropriate instruction and practice (Powell & Fuchs, 2010). Without adequate instruction and practice, however, students continue to misuse or misinterpret symbols well into middle and high school (Knuth, Alibali, Hattikudur, McNeil, & Stephens, 2008; Rowntree, 2009; Verikios & Farmaki, 2010).
Addition and Subtraction Concepts
Learning the concepts of addition and subtraction does not necessarily follow mastery of counting, comparing numbers, and mathematical symbols. Children can often solve simple addition and subtraction problems presented without symbols (i.e., presented orally and/or solved with manipulatives or counting; Cobb, 1987; Sherman & Bisanz, 2009). Adequate counting, comparing, and symbol knowledge skills, however, are necessary to carry out most addition and subtraction problems presented to students in early elementary school.
When starting to learn about the addition and subtraction number combinations (i.e., basic facts), students often work on simple problems with manipulatives. With practice, students rely less on manipulatives and more on their fingers for counting (Groen & Resniek, 1977). Because counting is often involved in solving addition and subtraction number combinations, counting skills are important (Baroody, Bajwa, & Eiland, 2009). Most of the time, young students use counting by ones as their default counting mechanism. Counting by twos or other increments or utilizing subitizing skills is not prevalent until second grade or later (Camos, 2003). Students then move from counting to solving number combinations using reasoning strategies or from memory. Mastery and fluency, of course, is the end goal of number combinations. Typically, students should know all 100 addition and 100 subtraction number combinations by the end of first grade (Baroody et al., 2009).
When beginning addition and subtraction, students often solve addition problems more successfully than subtraction problems (Shinskey, Chan, Coleman, Moxom, & Yamamoto, 2009). This is related to the fact that students learn counting forward well before they succeed in counting backward. The addition skills of students, even students who are struggling with mathematics, are generally stronger than their subtraction skills. This is apparent in that many students solve subtraction problems more efficiently when they use addition skills (Torbeyns, De Smedt, Stassens, Ghesquière, & Verschaffel, 2009). For example, when presented with the problem 14 – 9 = _, many students find it easier to think, “What can I add to 9 to make 14?” and a counting forwards strategy can be employed.
While students may understand the principle of subtraction, they often lag in their ability to understand that subtraction is the inverse of addition (Baroody, Lai, Li, & Baroody, 2009). Because students do not automatically understand the inverse relationship between addition and subtraction, this concept should be made more explicit through instruction and practice (Baroody, 1999). Students who understand the relationship between addition and subtraction (i.e., addition is the inverse of subtraction and vice versa) demonstrate better conceptual knowledge and better subtraction performance than students who do not understand this relationship (Gilmore & Papadatou-Pastou, 2009).
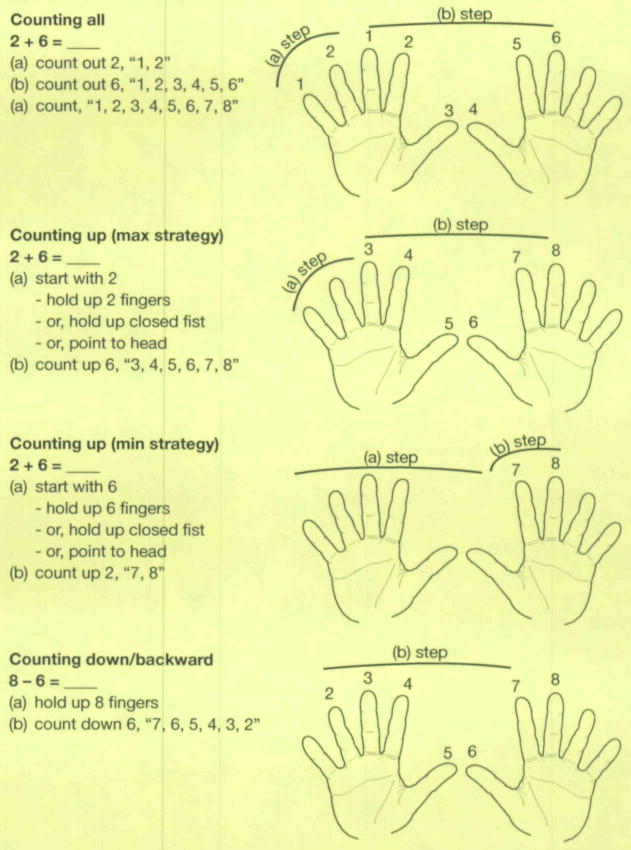
Counting strategies (i.e., counting to find the answer to an addition or subtraction number combination) are an aid to help students solve combinations. Not all students, however, use a counting strategy (Saxton & Cakir, 2006). Some students simply guess. For many students, especially those who struggle with early numerical competencies, counting strategies to solve number combinations are helpful and can be learned with relative ease. There are several counting strategies that students might employ when solving addition and subtraction number combinations. See Figure 3 for diagrams. With counting all, students count out the first addend, count out the second addend, and then count both addends together starting at 1. This is usually the first counting strategy for addition that students employ (Fuson & Secada, 1986). The counting all strategy is not terribly efficient and, given the numbers of counts required, it often results in incorrect answers. Students generally abandon use of counting all in favor of the more advanced “counting up” or “counting on” strategy (Fuson & Secada, 1986). Counting up can be carried out in two ways: Start with the larger addend and count up the smaller addend (i.e., the “min” strategy because the student counts the minimum amount) or vice versa (i.e., the “max” strategy because the student counts the maximum amount). Before students learn the commutative property of addition (i.e., the order of addition does not make a difference to the sum), they often start with the first addend in the number sentence (e.g.. 4 of 4 + 9 = _) without realizing the greater efficiency of starting with the larger addend and counting up the smaller addend (Groen & Parkman, 1972). For example, if presented with 5 + 9 = _, students start at 9 and count 5 more: “10, 11, 12, 13, 14.” Students often develop this counting strategy through experience and practice (Weiland, 2007), but it may be necessary, especially for students who struggle with mathematics, to provide explicit instruction on this more efficient counting strategy (Powell, Fuchs, Fuchs, Cirino, & Fletcher, 2009).
FIGURE 3.
Counting Strategies
With each of these strategies, students may hold up fingers, fold in fingers, or tap fingers. Students may work with their palms facing toward or away from them. Also, students may count from left-to-right or right-to-left. They may start counting with their index finger or thumb or another finger.
To solve subtraction number combinations, students often count down. That is, they start with the minuend and count down the amount of the subtrahend. For 9 – 4 = _, students start with 9 and count back 4: “8, 7, 6, 5.” Counting down or counting backwards is difficult for students, especially students with mathematics difficulties, because fluency with counting backwards is limited compared to fluency counting forward (Passolunghi & Cornoldi, 2008). Students also tend to make many more mistakes counting backwards than counting forwards. A more efficient strategy for solving subtraction problems is counting up. Students start with the subtrahend and count up to the minuend. For 9 – 4 = _, students start with 4 and count, “5. 6. 7, 8, 9.” They count 5 fingers or make 5 counts, so 9 – 4 = 5. This strategy makes use of students’ quick forward-counting skills and has shown to be a beneficial strategy for students with mathematics difficulties (Fuchs et al., 2009; Fuchs, Powell, et al., 2010). Using counting up for subtraction also underscores the fact that subtraction represents the difference between two amounts (i.e., the minuend and subtrahend).
With addition and subtraction, practice on using counting strategies and working towards fluency improves the performance of struggling students (Fuchs, Powell, et al., 2010). Students need to understand the concepts behind number combinations (Baroody, Lai, et al., 2009), but they also need to be presented with routine, even daily, practice to build fluency and help students make frequent, correct associations between problem stems and their answers (Fuchs, Powell, et al., 2010). This leads to students building representations in long-term memory and helps students rely on the most efficient strategy for solving addition and subtraction problems: automatic retrieval of answers (Fuchs et al., 2011). For this reason, students need practice on all the number combinations, especially the number combinations that involve double digits (e.g., 9 + 7 = 16; 14 – 8 = 6) because they generally receive much more exposure to the easier number combinations (Hamann & Ashcraft, 1986).
EXAMPLE OF AN EARLY NUMERICAL INTERVENTION FOR STRUGGLING STUDENTS
We discussed four early numerical competencies: counting, comparing numbers, understanding symbols, and concepts of addition and subtraction. While this is not an exhaustive list of early numerical competencies, these four are critical components of an effective early numerical program for struggling students. The four components are related to one another and build upon each another as students learn more and more mathematics in the early elementary grades. While students may struggle with one or more of these early numerical competencies, instruction and practice can improve the early numerical skill of students.
In this next section, we describe an early numerical program for first-grade students who struggle with mathematics. We describe this program to illustrate how teachers and parents of struggling students may incorporate four early numerical competencies discussed in this article into a successful instructional program for struggling students. This is not the only early numerical intervention available, so teachers should research options before choosing a program for their students. Galaxy Math, also referred to as Number Rockets, (Fuchs et al., 2011) was designed to help prevent long-term difficulty in mathematics by remediating early numerical skill deficits and promoting number knowledge and skill with number combinations and other key components of the first-grade mathematics curriculum. The program is called Galaxy Math because a space theme is used throughout the lessons to help motivate students. Tutors encourage students to “Blast off into the math galaxy!” and the students use mathematics manipulatives shaped as rockets. See Figure 4 for an example of the galaxy-themed motivation chart.
FIGURE 4.
Galaxy Math Motivation Chart
Experimental Investigation of Galaxy Math
At the beginning of first grade, students with parental consent were screened to identify those at risk for inadequate mathematics development, although most students did not have a school-diagnosed learning disability. These students were randomly assigned to continue in their normal school program (i.e., the control group) or to one of two versions of Galaxy Math. In both versions of Galaxy Math, the main focus (25 minutes of each 30-minute tutoring session) is the types of early numerical competencies discussed in this article. One version of Galaxy Math (the standard version) added 5 minutes of practice at the end of each session; the other version added 5 minutes of games. In both tutoring conditions. Galaxy Math students received 48 individual sessions, three times a week.
See Table 1 for a list of Galaxy Math units and concepts. In Unit 1, students use manipulatives such as a number line, counting beans, and “Mr. Greater Gator” to learn magnitudes, practice counting, compare numbers, and learn symbols. See Figures 5 and 6 for example activities working on counting and learning about the terminology of equal. These activities are conducted during the first few lessons of Galaxy Math. See Figure 7 for a sample number line. The numbers on the number line increase in size as the numbers increase in value to help students understand the magnitude of the numbers. See Figure 8 for Mr. Greater Gator. This alligator has a mouth open wide with the inequality symbols (i.e., greater than or less than signs) superimposed over the open mouth. Students learn that the alligator is very hungry, and he wants to eat the larger number when presented with two amounts. The open mouth always faces the larger number. Also in Unit 1, the students learn the counting strategies of counting in (for addition) and counting up (for subtraction). With counting in, students hold up the smaller addend on their fingers and then count by folding in one finger at a time until no fingers remain (i.e., closed fist). For example, with 3 + 6 the student would hold up 3 fingers and then counts: “7” (folds 1 finger in), “8” (folds another finger in), “9” (folds last finger in). The answer is the last number the student says (in this case, 9). Counting in is one version of the counting up strategy. Counting in was found useful for first-grade students because it helped them keep track of the counting amount. With counting up for subtraction, students start with a closed fist. They start with the subtrahend and use their fingers to count up to the minuend. For example, with 9 – 3 students count, “4, 5, 6, 7, 8, 9” (each time holding up another finger). Once students reaches the minuend, they count the number of fingers (in this case, 6) and 6 is recorded as the answer. In Unit 1, students also solve story problems with manipulatives, pictures, or actions. For example, when presented with the problem, “John has 4 apples in his grocery cart. He puts 1 more apple in the cart. How many apples are in John’s cart now?” students could draw apples or use manipulative blocks to solve the problem.
TABLE 1.
Galaxy Math Lessons
| Unit | Lessons | Topics |
|---|---|---|
| 1 | 1–3 | Number line (0–9) |
| Counting aloud | ||
| Reading and writing numbers | ||
| Counting objects | ||
| Using hands to show numbers less than 10 | ||
| 4 | Using hands to show numbers less than 10 | |
| Discussion of 0 and numbers 11–19 | ||
| Counting forwards | ||
| Counting backwards | ||
| 5 | Identifying largest and smallest numbers with number line | |
| 6, 7 | Comparing numbers with language and symbols | |
| 8 | Concept of addition | |
| Meaning of + and = | ||
| 9 | Addition of 1 with number line | |
| Using manipulatives, pictures, and actions to solve story problems | ||
| 10 | Addition of 0 and 1 with number line | |
| Using manipulatives, pictures, and actions to solve story problems | ||
| 11 | Counting in | |
| 12 | Addition of 0, 1, and 2 with counting in | |
| 13 | Concept of subtraction | |
| Meaning of - Review of counting in for addition | ||
| 14 | Addition and subtraction of 1 with number line | |
| Using manipulatives, pictures, and actions to solve story problems | ||
| 15 | Addition of 0 and 1 with number line | |
| Using manipulatives, pictures, and actions to solve story problems | ||
| 16 | Counting up | |
| 17 | Addition and subtraction of 0, 1, and 2 with counting in/up | |
| 18 | Review of counting in/up | |
| 2 | 19–20 | Doubles |
| 3 | 21–24 | 5 Set |
| 25–28 | 6 Set | |
| 29–32 | 7 Set | |
| 33–36 | 8 Set | |
| 37–40 | 9 Set | |
| 41–44 | 10 Set | |
| 45–48 | 11 Set | |
| 49–52 | 12 Set | |
| 4 | 53 | Number line to 100 |
| Numbers 20–29 | ||
| 54–56 | Number line to 100 | |
| Double-digit addition | ||
| 57 | Counting by tens | |
| Using hands to represents tens and ones | ||
| 58 | Introduction to place value | |
| 59 | Introduction to rods and cubes | |
| Regrouping 10 cubes into 1 rod | ||
| 60 | Regrouping | |
| 61 | Representing one- and two-digit numbers with rods and cubes | |
| Meaning of 0 in place value | ||
| 62 | Representing one- and two-digit numbers with rods and cubes | |
| 63 | Identifying larger and smaller numbers using place value and number line | |
| 64–66 | Practicing place value | |
| 5 | 67–74 | Review |
FIGURE 5.

Counting Activity
FIGURE 6.

Equal Activity
FIGURE 7.

Number Line
FIGURE 8.

Mr. Greater Gator
In Unit 2, students use beans and the number line to learn about doubles 0 through 6 (i.e., 0 + 0, 1 + 1, 2 + 2, 3 + 3, 4 + 4, 5 + 5, 6 + 6, 0 – 0, 2 – 1, 4 – 2, 6 – 3, 8 – 4, 10 – 5, 12 – 6). Doubles are practiced early in the program because students usually have little difficulty memorizing doubles, and students can use doubles to solve other number combinations (Van De Walle et al., 2010).
In Unit 3, students begin learning number combinations in sets. Each set includes all number combinations with the sum and minuend as the target set number. For example, the 5 set consists of alt number combinations with a sum of 5 or 5 as the minuend (i.e., 0 + 5, 1 + 4, 2 + 3, 3 + 2, 4 + 1, 5 + 0, 5 – 0, 5 – 1, 5 – 2, 5 – 3, 5 – 4, 5 – 5). Tutors start with the 5 set and continue through the 12 set. While working on each set, the tutor conducts five activities with the student. First, the tutor and student use unifix cubes to see how cubes can be combined in different ways to make the addition and subtraction number combinations of the set. See Figure 9 for examples from the 5 set. With the manipulatives, students can also see how 1 + 4, 4 + 1, 5 – 1, and 5 – 4 are related as a “family,” and the second activity of each lesson focuses on the families that constitute the relevant set. Third, students either answer number combination set problems on a worksheet or show all combinations in the number set with manipulative rockets. Next, the tutor and student work together to solve a story problem involving a number combination from the set. The student solves the problem and explains why the story problem is specific to the number set. The fifth activity each day is an oral review of previous number sets.
FIGURE 9.
Manipulative Examples of 5 Set
For each set, students work for one to four lessons. After the first lesson in a set, each subsequent lesson begins with a flash card mastery test by which students can advance to the next set by answering cards correctly. Students have to answer within 3 seconds, with no more than one error. Students who achieve mastery prior to the full complement of four lessons within each set complete the 12 set. Other students complete the 10 set and then continue to Unit 4. This rule ensures appropriate content coverage.
In Unit 4, the focus is on place value: counting by tens to 100, showing and writing ones and tens, regrouping, and double-digit addition. Students also review the number sets during this unit. Unit 5 is designed for students who demonstrate mastery while working on the number sets. In this unit, students review the number sets and place value concepts.
In the last 5 minutes of each tutoring session, Fuchs et al. (2011) isolated the effects of providing practice. To do this, half the students in the study did systematic practice in the last 5 minutes; the other half played games. In the practice and games conditions, the content was the same: material related to that day’s lesson. Random assignment determined whether students participated in games or practice during the conclusion of each day’s lesson.
In the games condition, students play games with manipulative rockets to practice concepts. For example, with one game, students spin to learn how many rockets are called to the space station, and they place that number of rockets on a game board. Then they spin again to see how many rockets are called away, back to earth, and they remove the corresponding number of rockets from the board. They then generate the number sentence representing this series of events. Throughout games, tutors encourage students to know the answer or to use fingers, beans, or number lines to calculate the answer. Tutors explain that “knowing the answer right off the bat” is the preferred strategy, if the student is sure of the answer.
In the practice condition, students practice content from the lessons with the “Meet or Beat Your Score Activity,” which relies on flash cards. For example, once addition/subtraction sets are introduced, students practice number combinations. Tutors encourage children to retrieve the combination from memory or, if they arc unsure of the answer, use the counting strategy they learned in Galaxy Math to solve the combination. When the student answers correctly, the flash card is placed in a pile on the desk. When a student answers incorrectly, the tutor requires the students to use a counting strategy (i.e., counting in or counting up) to find the correct answer. The corrected card is then placed in the pile on the desk. At the end of 90 seconds, the student graphs the number of flash cards answered correctly. See Figure 10 for a sample flash card graph. Students then have two chances to meet or beat their first flash card score.
FIGURE 10.

Practice Flash Card Graph
In both conditions, tutors promote on-task behavior and motivation to work hard (Fuchs et al., 2008) using a systematic reward program. Tutors teach students that on-task behavior means paying attention and trying hard to answer questions correctly. Students learn that on-task behavior is important for “blasting off into the math galaxy.” Students earn stickers for on-task behavior and hard, correct work. They place their stickers on the Galaxy Math chart (see Figure 4). Students earn a prize (i.e., small toy, sticker, or pencil) when they reach the sun on the galaxy chart.
In the study (Fuchs et al., 2011), results showed that students who participated in the Galaxy Math tutoring improved on number knowledge, simple arithmetic, more complex calculations, and word problems significantly better than control students. Students in the practice condition improved more than games students on simple arithmetic and more complex calculations, with no harm to their number knowledge or performance on word problems. This, along with other early numerical intervention studies (e.g., Bryant et al., 2011; Fuchs et al., 2005b), demonstrates positive outcomes for at-risk students when early numerical intervention occurs early and with intensity. The Fuchs et al. (2011) study also shows the specific importance of incorporating frequent, well-designed practice that supports correct responding.
SUGGESTIONS FOR PRACTITIONERS
As students enter kindergarten and often progress to first grade with varying degrees of early numerical competency, practitioners should provide early assessment and early intervention to help students who struggle with the fundamentals of mathematics. For assessment, progress-monitoring measures (e.g., Lembke & Foegen, 2009; Seethaler & Fuchs, 2011) and screening measures that target specific mathematics skills (e.g., Geary et al., 2007; Jordan et al., 2009) can be used to determine which students warrant early numerical intervention.
After identifying students who struggle with early numerical competencies in kindergarten or first grade, practitioners need to evaluate early numerical programs and choose a program that best fits the needs of their students.
Based on experimental work with young students (e.g., Bryant et al., 2011; Fuchs et al., 2011), early numerical competencies programs should include the following; (a) explicit instruction focused on conceptual knowledge and procedural skill, (b) a sequence of instruction that is meaningful and relevant, (c) review of topics previously taught, (d) practice of current topics, and (e) fluency work on addition and subtraction number combinations. The focus of instruction (i.e., counting skills, addition concepts) should be determined based on student needs. One program may not be the best for all students, so practitioners must monitor student progress while students participate in instruction to determine response. If students are not demonstrating appropriate learning, their instructional program should be modified to formatively develop a program tailored to the student’s needs.
Because early numerical skill at kindergarten is predictive of mathematical achievement in later grades (Duncan et al., 2007; Jordan et al., 2010), providing timely intervention to students who lack skill in the early numerical competencies is vital. Researchers need to continue to refine early numerical assessments and interventions that will help schools in timely identification and effective intervention to ensure student competence with the basic building blocks of mathematics.
Acknowledgments
This research was supported by Award Number R01HD059179 from the Eunice Kennedy Shriver National Institute of Child Health & Human Development to Vanderbilt University. The content is solely the responsibility of the authors and does not necessarily represent the official views of the Eunice Kennedy Shriver National Institute of Child Health & Human Development.
Contributor Information
Dr. Sarah R. Powell, Department of Curriculum, Instruction, and Special Education at the University of Virginia.
Dr. Lynn S. Fuchs, Department of Special Education at Vanderbilt University.
References
- Aunio P, Hautamaki J, Sajaniemi N, Van Luit JEH. Early numeracy in low-performing young children. British Educational Research Journal. 2009;35(1):25–46. 10.1080/01411920802041822. [Google Scholar]
- Baroody AJ. Children’s relational knowledge of addition and subtraction. Cognition & Instruction. 1999;17(2):137–175. [Google Scholar]
- Baroody AJ, Bajwa NP, Eiland M. Why can’t Johnny remember the basic facts? Developmental Disabilities Research Reviews. 2009;15(1):69–79. doi: 10.1002/ddrr.45. 10.1002/ddrr.45. [DOI] [PubMed] [Google Scholar]
- Baroody AJ, Benson A. Early number instruction. Teaching Children Mathematics. 2001;8(3):154–158. [Google Scholar]
- Baroody AJ, Lai M, Li X, Baroody AE. Preschoolers’ understanding of subtraction-related principles. Mathematical Thinking and Learning: An International Journal. 2009;11(1–2):41–60. [Google Scholar]
- Berch DB. Making sense of number sense: Implications for children with mathematical disabilities. Journal of Learning Disabilities. 2005;38(4):333–339. doi: 10.1177/00222194050380040901. [DOI] [PubMed] [Google Scholar]
- Bermejo V, Morales S, deOsuna JG. Supporting children’s development of cardinality understanding. Learning and Instruction. 2004;14(4):381–398. [Google Scholar]
- Bruce RA, Threlfall J. One, two, three and counting. Educational Studies in Mathematics. 2004;55(1–3):3–26. [Google Scholar]
- Bryant DP, Bryant BR, Roberts C, Vaughn S, Pfanncnstiel KH, Porterfield J, Gersten R. Early numeracy intervention program for first-grade students with mathematics difficulties. Exceptional Children. 2011;78(1):7–23. [Google Scholar]
- Camos V. Counting strategies from 5 years to adulthood: Adaptation to structural features. European Journal of Psychology of Education–EJPE. 2003;18(3):251–265. [Google Scholar]
- Camos V, Barrouillet P, Fayol M. Does the coordination of verbal and motor information explain the development of counting in children? Journal of Experimental Child Psychology. 2001;78(3):240–62. doi: 10.1006/jecp.2000.2570. [DOI] [PubMed] [Google Scholar]
- Capraro MM, Ding M, Matteson S, Capraro RM, Li X. Representational implications for understanding equivalence. School Science & Mathematics. 2007;107(3):86–88. [Google Scholar]
- Carrasumada S, Vendrell R, Ribera G, Montserrat M. Cognitive processes related to counting in students with special educational needs. European Journal of Special Needs Education. 2006;21(2):135–150. [Google Scholar]
- Clements DH. Subitizing. Teaching Children Mathematics. 1999;5(1):400–405. [Google Scholar]
- Cobb P. An investigation of young children’s academic arithmetic contexts. Educational Studies in Mathematics. 1987;18(2):109–24. [Google Scholar]
- De Smedt B, Gilmore CK. Defective number module or impaired access? numerical magnitude processing in first graders with mathematical difficulties. Journal of Experimental Child Psychology. 2011;108(2):278–292. doi: 10.1016/j.jecp.2010.09.003. [DOI] [PubMed] [Google Scholar]
- Dowker A. Early identification and intervention for students with mathematics difficulties. Journal of Learning Disabilities. 2005;38(4):324–332. doi: 10.1177/00222194050380040801. [DOI] [PubMed] [Google Scholar]
- Duncan GJ, Dowsett CJ, Claessens A, Magnuson K, Huston AC, Klebanov P, American PA. School readiness and later achievement. Developmental Psychology. 2007;43(6):1428–1446. doi: 10.1037/0012-1649.43.6.1428. [DOI] [PubMed] [Google Scholar]
- Ee J, Wong KY, Aunio P. Numeracy of young children in Singapore, Beijing and Helsinki. Early Childhood Education Journal. 2006;33(5):325–332. [Google Scholar]
- Fischer B, Köngeter A, Hartnegg K. Effects of daily practice on subitizing, visual counting, and basic arithmetic skills. Optometry & Vision Development. 2008;39(1):30–34. [Google Scholar]
- Frye D, Braisby N, Lowe J, Maroudas C, Nicholls J. Young children’s understanding of counting and cardinality. Child Development. 1989;60(5):1158. 10.1111/1467-8624.ep9676220. [PubMed] [Google Scholar]
- Fuchs LS, Compton DL, Fuchs D, Paulsen K, Bryant JD, Hamlett CL. The prevention, identification, and cognitive determinants of math difficulty. Journal of Educational Psychology. 2005a;97(3):493–513. 10.1037/0022-0663.97.3.493. [Google Scholar]
- Fuchs LS, Compton DL, Fuchs D, Paulsen K, Bryant J, Hamlett CL. Responsiveness to intervention: Preventing and identifying mathematics disability. Teaching Exceptional Children. 2005b;37(4):60–63. [Google Scholar]
- Fuchs LS, Fuchs D, Powell SR, Seethaler PM, Cirino PT, Fletcher JM. Intensive intervention for students with mathematics disabilities: Seven principles of effective practice. Learning Disability Quarterly. 2008;31(2):79–92. [PMC free article] [PubMed] [Google Scholar]
- Fuchs LS, Geary DC, Fuchs D, Schatschneider C, Hamlett CL, DeSelms-Wolfe J, Changas P. Understanding and promoting at-risk learners’ mathematics development in first grade: A randomized control trial. 2011 Manuscript submitted for publication. [Google Scholar]
- Fuchs LS, Powell SR, Seethaler PM, Cirino PT, Fletcher JM, Fuchs D, Hamlett CL. The effects of strategic counting instruction, with and without deliberate practice, on number combination skill among students with mathematics difficulties. Learning and Individual Differences. 2010;20(2):89–100. doi: 10.1016/j.lindif.2009.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuchs LS, Powell SR, Seethaler PM, Cirino PT, Fletcher JM, Fuchs D, Zumeta RO. Remediating number combination and word problem deficits among students with mathematics difficulties: A randomized control trial. Journal of Educational Psychology. 2009;101(3):561–576. doi: 10.1037/a0014701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuson KC, Secada WG. Teaching children to add by counting-on with one-handed finger patterns. Cognition & Instruction. 1986;3(3):229–260. [Google Scholar]
- Ganor-Stern D, Pinhas M, Tzelgov J. Comparing two-digit numbers: The importance of being presented together. Quarterly Journal of Experimental Psychology. 2009;62(3):444–452. doi: 10.1080/17470210802391631. 10.1080/17470210802391631. [DOI] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Byrd-Craven J, Nugent L, Numtee C. Cognitive mechanisms underlying achievement deficits in children with mathematical learning disability. Child Development. 2007;74(4):1343–1359. doi: 10.1111/j.1467-8624.2007.01069.x. 10.1111/j.1467-8624.2007.01069.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelman R, Gallistel CR. The child’s understanding of number. Cambridge, MA: Harvard University Press; 1978. [Google Scholar]
- Gersten R, Chard D. Number sense: Rethinking arithmetic instruction for students with mathematical disabilities. Journal of Special Education. 1999;33(1):18–28. [Google Scholar]
- Gersten R, Chard DJ, Jayanthi M, Baker SK, Morphy P, Flojo J. Mathematics instruction for students with learning disabilities: A meta-analysis of instructional components. Review of Educational Research. 2009;79(3):1202–1242. [Google Scholar]
- Gilmore CK, Papadatou-Pastou M. Patterns of individual differences in conceptual understanding and arithmetical skill: A meta-analysis. Mathematical Thinking & Learning. 2009;11(1):25–40. 10.1080/10986060802583923. [Google Scholar]
- Griffin S, Case R. Re-thinking the primary school math curriculum: An approach based on cognitive science. Issues in Education. 1997;3(1):1–49. [Google Scholar]
- Groen GJ, Parkman JM. A Chronometric analysis of simple addition. Psychological Review. 1972;79(4):329–343. [Google Scholar]
- Groen G, Resnick LB. Can preschool children invent addition algorithms? Journal of Educational Psychology. 1977;69(6):645–652. [Google Scholar]
- Hamann MS, Ashcraft MH. Textbook presentations of the basic addition facts. Cognition & Instruction. 1986;3(3):173–192. [Google Scholar]
- Hannula MM, Rasanen P, Lehtinen E. Development of counting skills: Role of spontaneous focusing on numerosity and subitizing-based enumeration. Mathematical Thinking & Learning: An International Journal. 2007;9(1):51–57. [Google Scholar]
- Hattikudur S, Alibali MW. Learning about the equal sign: Does comparing with inequality symbols help? Journal of Experimental Child Psychology. 2010;107(1):15–30. doi: 10.1016/j.jecp.2010.03.004. [DOI] [PubMed] [Google Scholar]
- Holloway ID, Ansari D. Mapping numerical magnitudes onto symbols: The numerical distance effect and individual differences in children’s mathematics achievement. Journal of Experimental Child Psychology. 2009;103(1):17–29. doi: 10.1016/j.jecp.2008.04.001. [DOI] [PubMed] [Google Scholar]
- Hudson P, Miller SP. Designing atid implementing mathematics instruction for students with diverse learning needs. Boston: Pearson; 2006. [Google Scholar]
- Jacobs VR, Franke ML, Carpenter TP, Levi L, Battey D. Professional development focused on children’s algebraic reasoning in elementary school. Journal for Research in Mathematics Education. 2007;38(3):258–288. [Google Scholar]
- Jordan NC. The need for number sense. Educational leadership. 2007;65(2):63–66. [Google Scholar]
- Jordan NC, Glutting J, Ramineni C, Watkins MW. Validating a number sense screening tool for use in kindergarten and first grade: Prediction of mathematics proficiency in third grade. School Psychology Review. 2010;39(2):181–195. [Google Scholar]
- Jordan NC, Kaplan D, Locuniak MN, Ramineni C. Predicting first-grade math achievement from developmental number sense trajectories. Learning Disabilities Research & Practice. 2007;22(1):36–46. 10.1111/j.1540-5826.2007.00229.x. [Google Scholar]
- Jordan NC, Kaplan D, Ramineni C, Locuniak MN. Early math matters: Kindergarten number competence and later mathematics outcomes. Developmental Psychology. 2009;45(3):850–867. doi: 10.1037/a0014939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung M. Number relationships in preschool. Teaching Children Mathematics. 2011;17(9):550–557. [Google Scholar]
- Kamawar D, LeFevre J, Bisanz J, Fast L, Skwarchuk S, Smith-Chant B, Penner-Wilger M. Knowledge of counting principles: How relevant is order irrelevance? Journal of Experimental Child Psychology. 2010;105(1):138–145. doi: 10.1016/j.jecp.2009.08.004. 10.1016/j.jecp. 2009.08.004. [DOI] [PubMed] [Google Scholar]
- Kaminski E. Promoting mathematical understanding: Number sense in action. Mathematics Education Research Journal. 2002;14(2):133–49. [Google Scholar]
- Kaufmann L, Delazer M, Pohl R, Semenza C, Dowker A. Effects of a specific numeracy educational program in kindergarten children: A pilot study. Educational Research & Evaluation. 2005;11(5):405–431. 10.1080/13803610500110497. [Google Scholar]
- Kaufmann L, Handl P, Thony B. Evaluation of a numeracy intervention program focusing on basic numerical knowledge and conceptual knowledge: A pilot study. Journal of Learning Disabilities. 2003;36(6):564–573. doi: 10.1177/00222194030360060701. [DOI] [PubMed] [Google Scholar]
- Knuth EJ, Alibali MW, Hattikudur S, McNeil NM, Stephens AC. The importance of equal sign understanding in the middle grades. Mathematics Teaching in the Middle School. 2008;13(9):514–519. [Google Scholar]
- Lago RM, DiPerna JC. Number sense in kindergarten: A factor-analytic study of the construct. School Psychology Review. 2010;39(2):164–180. [Google Scholar]
- Lembke E, Foegen A. Identifying early numeracy indicators for kindergarten and first-grade students. Learning Disabilities Research & Practice. 2009;24(1):12–20. [Google Scholar]
- Lloyd JEV, Irwin LG, Hertzman C. Kindergarten school readiness and fourth-grade literacy and numeracy outcomes of children with special needs: A population-based study. Educational Psychology. 2009;29(5):583–602. [Google Scholar]
- Locuniak MN, Jordan NC. Using kindergarten number sense to predict calculation fluency in second grade. Journal of Learning Disabilities. 2008;41(5):451–459. doi: 10.1177/0022219408321126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malofeeva E, Day J, Saco X, Young L, Ciancio D. Construction and evaluation of a number sense test with head start children. Journal of Educational Psychology. 2004;96(4):648–659. [Google Scholar]
- Matthews P, Rittle-Johnson B. In pursuit of knowledge: Comparing self-explanations, concepts, and procedures as pedagogical tools. Journal of Experimental Child Psychology. 2009;104(1):1–21. doi: 10.1016/j.jecp.2008.08.004. [DOI] [PubMed] [Google Scholar]
- Mazzoceo MMM. Challenges in identifying target skills for math disability screening and intervention. Journal of Learning Disabilities. 2005;38(4):318–323. doi: 10.1177/00222194050380040701. [DOI] [PubMed] [Google Scholar]
- McNeil NM. Limitations to teaching children 2 + 2 = 4: Typical arithmetic problems can hinder learning of mathematical equivalence. Child Development. 2008;79(5):1524–1537. doi: 10.1111/j.1467-8624.2008.01203.x. 10.1111/j.1467-8624.2008.01203.x. [DOI] [PubMed] [Google Scholar]
- Muldoon KP, Lewis C, Francis B. Using cardinality to compare quantities: The role of social-cognitive conflict in early numeracy. Developmental Science. 2007;10(5):694–711. doi: 10.1111/j.1467-7687.2007.00618.x. 10.1111/j.1467-7687.2007.00618.x. [DOI] [PubMed] [Google Scholar]
- Muldoon K, Lewis C, Freeman NH. Putting counting to work: Preschoolers’ understanding of cardinal extension. International Journal of Educational Research. 2003;39(7):695–718. [Google Scholar]
- Murray PL, Mayer RE. Preschool children’s judgments of number magnitude. Journal of Educational Psychology. 1988;80(2):206–209. [Google Scholar]
- Passolunghi MC, Cornoldi C. Working memory failures in children with arithmetical difficulties. Child Neuropsychology. 2008;14(5):387–400. doi: 10.1080/09297040701566662. l0.1080/09297040701566662. [DOI] [PubMed] [Google Scholar]
- Potter MC, Levy EI. Spatial enumeration without counting. Child Development. 1968;39(1):265–272. [PubMed] [Google Scholar]
- Powell SR. Equations and the equal sign in elementary mathematics textbooks. Elementary School Journal. doi: 10.1086/665009. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powell SR, Fuchs LS. Contribution of equal-sign instruction beyond word-problem tutoring for third-grade students with mathematics difficulty. Journal of Educational Psychology. 2010;102(2):381–394. doi: 10.1037/a0018447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powell SR, Fuchs LS, Fuchs D, Cirino PT, Fletcher JM. Effects of fact retrieval tutoring on third-grade students with math difficulties with and without reading difficulties. Learning Disabilities Research & Practice. 2009;24(1):1–11. doi: 10.1111/j.1540-5826.2008.01272.x. 10.1111/j.1540-5826.2008.01272.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramani GB, Siegler RS. Promoting broad and stable improvements in low-income children’s numerical knowledge through playing number board games. Child Development. 2008;79(2):375–394. doi: 10.1111/j.1467-8624.2007.01131.x. [DOI] [PubMed] [Google Scholar]
- Rousselle L, Noel M. Basic numerical skills in children with mathematics learning disabilities: A comparison of symbolic vs non-symbolic number magnitude processing. Cognition. 2007;102(3):361–395. doi: 10.1016/j.cognition.2006.01.005. [DOI] [PubMed] [Google Scholar]
- Rowntree RV. Students’ understandings and misconceptions of algebraic inequalities. School Science and Mathematics. 2009;109(6):311–312. [Google Scholar]
- Saxton M, Cakir K. Counting-on, trading and partitioning: Effects of training and prior knowledge on performance on base-10 tasks. Child Development. 2006;77(3):767–785. doi: 10.1111/j.1467-8624.2006.00902.x. 10.1111/j.1467–8624.2006.00902.x. [DOI] [PubMed] [Google Scholar]
- Schleifer P, Landerl K. Subitizing and counting in typical and atypical development. Developmental Science. 2011;14(2):280–291. doi: 10.1111/j.1467-7687.2010.00976.x. 10.1111/J.1467-7687.2010.0O976.X. [DOI] [PubMed] [Google Scholar]
- Seethaler PM, Fuchs LS. Using curriculum-based measurement to monitor kindergartners’ mathematics development. Assessment for Effective Instruction. 2011;36(4):219–229. 10.1177/1534508411413566. [Google Scholar]
- Sherman J, Bisanz J. Equivalence in symbolic and non-symbolic contexts: Benefits of solving problems with manipulatives. Journal of Educational Psychology. 2009;101(1):88–100. [Google Scholar]
- Shinskey JL, Chan CH, Coleman R, Moxom L, Yamamoto E. Preschoolers’ nonsymbolic arithmetic with large sets: Is addition more accurate than subtraction? Journal of Experimental Child Psychology. 2009;103(4):409–420. doi: 10.1016/j.jecp.2009.01.012. [DOI] [PubMed] [Google Scholar]
- Skwarchuk S. How do parents support preschoolers’ numeracy learning experiences at home? Early Childhood Education Journal. 2009;37(3):189–197. [Google Scholar]
- Slusser EB, Sarnecka BW. Find the picture of eight turtles: A link between children’s counting and their knowledge of number word semantics. Journal of Experimental Child Psychology. 2011;110(1):38–51. doi: 10.1016/j.jecp.2011.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torbeyns J, De Smedt B, Stassens N, Ghesquière P, Verschaffel L. Solving subtraction problems by means of indirect addition. Mathematical Thinking & Learning. 2009;11(1):79–91. 10.1080/10986060802583998. [Google Scholar]
- Van De Walle JA, Karp KS, Bay-Williams JM. Elementary and middle school mathematics: Teaching developmentally. 7. Boston: Allyn & Bacon; 2010. [Google Scholar]
- Van Luit JEH, Schopman EAM. Improving early numeracy of young children with special educational needs. Remedial & Special Education. 2000;21(1):21–40. [Google Scholar]
- VanDerHeyden AM, Broussard C, Snyder P, George J, Lafleur SM, Williams C. Measurement of kindergartners’ understanding of early mathematical concepts. School Psychology Review. 2011;40(2):296–306. [Google Scholar]
- Verikios P, Farmaki V. From equation to inequality using a function-based approach. International Journal of Mathematical Education in Science and Technology. 2010;41(4):515–530. [Google Scholar]
- Wagner D, Davis B. Feeling number: Grounding number sense in a sense of quantity. Educational Studies in Mathematics. 2010;74(1):39–51. 10.1007/s10649-009-9226–9. [Google Scholar]
- Weiland L. Experiences to help children learn to count on. Teaching Children Mathematics. 2007;14(3):188–192. [Google Scholar]
- Xin JF, Holmdal P. Snacks and skills: Teaching children functional counting skills. Teaching Exceptional Children. 2003;35(5):46–51. [Google Scholar]
- Zhou X. Preschool children’s use of counting to compare two sets in cardinal situations. Early Child Development and Care. 2002;172(2):99–111. [Google Scholar]
- Zhou X, Wang Y, Wang L, Wang B. Kindergarten children’s representation and understanding of written number symbols. Early Child Development & Care. 2006;176(1):33–45. 10.1080/0300443042000302645. [Google Scholar]