Assessing the Accuracy of Inhomogeneous Fluid Solvation Theory in Predicting Hydration Free Energies of Simple Solutes

Abstract

Accurate prediction of hydration free energies is a key objective of any free energy method that is applied to modeling and understanding interactions in the aqueous phase. Inhomogeneous fluid solvation theory (IFST) is a statistical mechanical method for calculating solvation free energies by quantifying the effect of a solute acting as a perturbation to bulk water. IFST has found wide application in understanding hydration phenomena in biological systems, but quantitative applications have not been comprehensively assessed. In this study, we report the hydration free energies of six simple solutes calculated using IFST and independently using free energy perturbation (FEP). This facilitates a validation of IFST that is independent of the accuracy of the force field. The results demonstrate that IFST shows good agreement with FEP, with an R² coefficient of determination of 0.99 and a mean unsigned difference of 0.7 kcal/mol. However, sampling is a major issue that plagues IFST calculations and the results suggest that a histogram method may require prohibitively long simulations to achieve convergence of the entropies, for bin sizes which effectively capture the underlying probability distributions. Results also highlight the sensitivity of IFST to the reference interaction energy of a water molecule in bulk, with a difference of 0.01 kcal/mol changing the predicted hydration free energies by approximately 2.4 kcal/mol for the systems studied here. One of the major advantages of IFST over perturbation methods such as FEP is that the systems are spatially decomposed to consider the contribution of specific regions to the total solvation free energies. Visualizing these contributions can yield detailed insights into solvation thermodynamics. An insight from this work is the identification and explanation of regions with unfavorable free energy density relative to bulk water. These regions contribute unfavorably to the hydration free energy. Further work is necessary before IFST can be extended to yield accurate predictions of binding free energies, but the work presented here demonstrates its potential.

Introduction

Inhomogeneous fluid solvation theory¹ (IFST) is a statistical mechanical framework for calculating the effect of a solute on the free energy of the surrounding solvent relative to its bulk state.² The solute can be a protein,³ peptide,⁴ or small molecule⁵ and the solvent is commonly water.⁶ IFST has found particular use in the pharmaceutical industry with the advent of Schrödinger’s WaterMap software.⁷ It has also been developed in the solvation theory of ordered water (STOW) package,⁸ and recent work using grid inhomogeneous solvation theory (GIST) has explored the results of performing IFST calculations on a Cartesian grid.⁹ One of the useful features of IFST is that the free energy changes are calculated for small subvolumes surrounding the solute and this allows the contribution of different regions of space to be calculated and visualized. This has been used to understand the determinants of binding affinity¹⁰ and design new inhibitors in the hit-to-lead and lead optimization stages of drug development.¹¹ Work in this lab has focused on the importance of modeling solvation at protein surfaces¹² and the data requirements for convergence of the thermodynamic quantities computed by IFST.¹³ One important issue that has not been addressed in detail is the quantitative accuracy of IFST. Initial work suggested a reasonable comparison with the experimental solvation free energy of methane⁵ and recent work notes solvation free energies as a key benchmark for the method.⁹ While a direct comparison with experiment is interesting, the results rely on the force field and particularly the water model that is used.¹⁴ Thus, a more useful comparison is with an equivalent computational technique. This decouples testing of the method from testing of the parameters. In this work, we compute solvation free energies for six simple molecules using IFST and compare the results with solvation free energies calculated using free energy perturbation (FEP).¹⁵

Simulation Details

Hydration free energies for six simple molecule were calculated using two statistical mechanical computational methods, FEP and IFST. FEP calculates the hydration free energies directly, whereas IFST calculates the hydration enthalpies and entropies and these are combined to yield the predicted hydration free energy. All molecular dynamics (MD) simulations in this work were performed with the TIP4P-2005 water model.¹⁶

Systems Setup

The six solutes studied were acetamide, benzene, isobutane, methane, methanol, and N-methylacetamide. The parameters for acetamide, benzene, isobutane, methanol, and N-methylacetamide were taken from the CHARMM36 force field.¹⁷ The parameters for methane were not present in the CHARMM36 force field and were thus adapted from ethane. The methane carbon atom was assigned an atom type of CG331 and a partial charge of −0.36. The methane hydrogen atoms were assigned an atom type of HGA3 and a partial charge of +0.09. The bond lengths, bond angles, and dihedral angles were set to their force field equilibrium values for all molecules.

Water Setup

To generate a reasonable initial water density, a water shell of radius 50.0 Å was generated around each biomolecule with the SOLVATE program version 1.0 from the Max Planck Institute.¹⁸ The resulting water globules were then cut to rhombic dodecahedral unit cells with side lengths of 25.0 Å. To standardize the geometries of the water molecules, every hydrogen atom was deleted and all the necessary hydrogen atoms and lone pairs were built using the appropriate geometry for TIP4P-2005 water. The boxes contained 384, 371, 376, 394, 376, and 374 water molecules for the molecules acetamide, benzene, isobutane, methane, methanol, and N-methylacetamide, respectively. No ions were included in the systems.

IFST Equilibration

Equilibration was performed for 1.0 ns in an NPT ensemble at 300 K and 1 atm using Langevin temperature control and Nosé–Hoover¹⁹ Langevin piston pressure control.²⁰ All systems were brought to equilibrium before continuing, by verifying that the energy fluctuations were stable. MD simulations were performed using an MD time step of 2.0 fs. Electrostatic interactions were modeled with a uniform dielectric and a dielectric constant of 1.0 throughout the equilibration and production runs. van der Waals interactions were truncated at 11.0 Å with switching from 9.0 Å. Electrostatics were modeled using the particle mesh Ewald method,²¹ and the systems were treated using rhombic dodecahedral periodic boundary conditions. All solute atoms were fixed for the entirety of the equilibration and production simulations.

IFST Simulation

100.0 ns of production simulation in an NPT ensemble were performed at 300 K and 1 atm for each system. System snapshots were saved every 10.0 fs, yielding 10 000 000 snapshots in total for each system. MD simulations for IFST were performed using NAMD²² version 2.8 compiled for use with CUDA-accelerated GPUs.

IFST Implementation

An important decision in implementing IFST is the choice of subvolumes over which to perform the calculations. In protein binding sites, water molecules commonly cluster in distinct locations and the concept of a hydration site is useful to calculate contributions to the free energy from spherical regions. In the context of small molecule solvation, the water molecules do not cluster in distinct locations and the concept of a hydration site is not useful. Two approaches have been used to account for this in previous work. In the Lazaridis work on the solvation of methane,⁵ the region surrounding the solute was split into subshells at different distances from the origin. For more complex molecules, spherical polar coordinates could usefully be used to further split these subshells. In the recent work on GIST, the region surrounding the solute was split into cubic voxels on a Cartesian grid.⁹ This has the advantage that each subvolume has the same volume. There are a number of other possibilities for partitioning a volume into subvolumes and these different methods of honeycombing space are likely to affect the performance of IFST. In this work, we have used a Cartesian grid to honeycomb the volume and we use the term voxel to specify one cubic unit in this space. We consider all voxels within 12.0 Å of the origin in the calculation, where the centroid of each solute lies at the origin. In this study, we have not taken advantage of the symmetry of the solute molecules, which would provide more data, as we are interested in applying IFST to systems that do not have such symmetry in the future.

IFST Calculations

IFST calculates the difference in interaction energy (ΔE_IFST) and correlation entropy (ΔS_IFST) between each subvolume (v) and the equivalent number of bulk water molecules (n). These can be termed the local quantities. The contribution of each subvolume to ΔE_IFST was calculated from the mean solute–water interaction energy (E_sw), the mean water–water interaction energy (E_ww), and the mean interaction energy of a bulk water molecule (E_bulk) as follows:

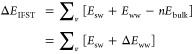1

For the TIP4P-2005 water model, E_bulk is calculated from a 100 ns NPT simulation of bulk water at 300 K and 1 atm as −11.5813 kcal/mol. In this work, E_bulk and E_ww are defined as half the interaction energy of one water molecule with all other water molecules. Previous work have defined E_bulk and E_ww as the total interaction energy of one water molecule with all other water molecules and included factors of one-half in eq 1.^13,23 The two approaches are identical. The difference in correlation entropy is calculated from solute–water entropy (S_sw), the water–water entropy (S_ww), and the entropy of a bulk water molecule (S_bulk) as follows:

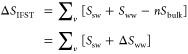2

All entropies calculated in this work exclude vibrational entropy changes. For each subvolume, S_sw is calculated from the translational and orientational contributions using the translational and orientational correlation functions, g_sw(r) and g_sw(ω|r).

3

4

k is Boltzmann’s constant, ρ° is the number density of bulk water, and Ω is the integral over the angles. For the TIP4P-2005 water model, ρ° is calculated from a 100 ns NPT simulation of bulk water at 300 K and 1 atm as 0.0331 707 molecules/ų. The solute–water orientational correlation functions were calculated using Euler angles by computing α, cos β, and γ in a fixed reference frame. The limits of integration for the water molecule are between 0 and 2π for α, between −1 and 1 for cos β, and between 0 and π for γ, due to water’s C_2v symmetry. The orientational correlation functions were assumed to be independent of the position within the hydration sites. The default grid resolution was 0.5 Å and the default angular bin size was 45°. This leads to 8, 4, and 4 angular bins for α, cos β and γ and thus 128 angular bins in total. The ΔS_ww term can also be calculated from translational and orientational contributions. A rigorous treatment would use the inhomogeneous water–water pair-correlation functions g_ww(r,r′) and g_ww(ω,ω′|r,r′) from the system and the homogeneous water–water pair-correlation functions g_ww(R) and g_ww(ω^rel|R) from bulk water. R and ω^rel are the distance and relative orientation between two water molecules in bulk water.

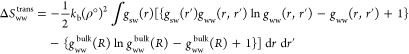5

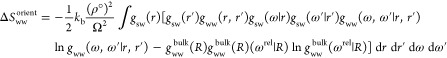6

However, converging calculations of the inhomogeneous water–water pair-correlation functions requires a very large amount of data and thus the Kirkwood superposition approximation (KSA) is used.²⁴ The KSA provides an approximation of a third-order correlation function in terms of lower order correlation functions. In this context, the KSA is applied to the homogeneous triplet solute–water–water correlation function. The inhomogeneous water–water correlation function is then assumed to be independent of the solute–water correlation functions and thus equal to the water–water correlation function in bulk solvent. The KSA is used for both g_ww(r,r′) and g_ww(ω,ω′|r,r′):

7

8

These correlation functions can be converged in bulk water due the increased data available from it being a homogeneous and isotropic system. Previous work on the solvation of methane suggests that these KSAs lead to reasonable results due to the cancellation of errors between more and less structured regions.⁵ In this work, S_ww was only calculated for pairs of voxels within 3.6 Å. This is likely a good assumption for the translational contributions, which in bulk water are derived almost exclusively from the excluded volume and the first solvation shell.²⁵ The orientational contributions to S_ww (and S_bulk) are expected to be underestimated, as only approximately 75% of the orientational entropy in bulk water is derived from the first solvation shell.^25,26 Calculations for g_ww(R) and g_ww(ω^rel|R) were performed on pairs of voxels on the Cartesian grid from the 100 ns NPT simulation of bulk water at 300 K and 1 atm. The difference in free energy (ΔG_IFST) for each voxel is then calculated from ΔE and ΔS.

9

FEP Protocol

The equilibrated systems generated for the IFST simulations were used as the start points for the FEP systems. These systems consist of the solute in water and correspond to the λ = 0.0 states. FEP calculations were performed in both forward and backward directions to yield corresponding predictions for annihilation (λ = 0.0 to λ = 1.0) and creation (λ = 1.0 to λ = 0.0) of the solutes. Each annihilation and creation was split into 24 steps to yield 48 λ windows per system. The lambda schedules are reported in Table 1. Two measures were adopted to avoid the numerical instabilities termed “end-point catastrophes” that occur when λ approaches 0.0 or 1.0. First, a soft-core potential was employed with a van der Waals radius-shifting coefficient of 5.0.^27,28 Second, van der Waals interactions were scaled down to zero between λ = 0.0 and λ = 1.0 whereas electrostatic interactions were scaled down to zero between λ = 0.0 and λ = 0.4.²⁹ MD simulations for FEP were performed using NAMD version 2.8.²²

Table 1. Lambda Schedules for FEP Annihilation and Creation^a.

	annihilation		creation
window	λinitial	λfinal	λinitial	λfinal
1	0.000	0.015	1.000	0.975
2	0.015	0.030	0.975	0.925
3	0.030	0.045	0.925	0.850
4	0.045	0.060	0.850	0.600
5	0.060	0.075	0.600	0.450
6	0.075	0.090	0.450	0.350
7	0.090	0.105	0.350	0.300
8	0.105	0.120	0.300	0.275
9	0.120	0.135	0.275	0.250
10	0.135	0.150	0.250	0.230
11	0.150	0.170	0.230	0.210
12	0.170	0.190	0.210	0.190
13	0.190	0.210	0.190	0.170
14	0.210	0.230	0.170	0.150
15	0.230	0.250	0.150	0.135
16	0.250	0.275	0.135	0.120
17	0.275	0.300	0.120	0.105
18	0.300	0.350	0.105	0.090
19	0.350	0.450	0.090	0.075
20	0.450	0.600	0.075	0.060
21	0.600	0.850	0.060	0.045
22	0.850	0.925	0.045	0.030
23	0.925	0.975	0.030	0.015
24	0.975	1.000	0.015	0.000

^aThe 24 FEP windows used in the annihilation and creation simulations of the six solutes. The initial and final values of λ are given for each window.

FEP Equilibration

Starting with the equilibrated systems generated for the IFST simulations, further equilibration was performed for 800 ps in an NPT ensemble for each lambda window.

FEP Simulation

7.0 ns of production simulation in an NPT ensemble were performed at 300 K and 1 atm for each lambda window.

FEP Calculations

For FEP, the free energy of a change (ΔG_FEP) is calculated as the sum of free energy changes for a series of N small steps between intermediate states a and b.¹⁵

10

The free energy change for each small step (ΔG_a→b) is calculated using the partition functions (Q) for the two states which are calculated using the Hamiltonians (H) for the two states.

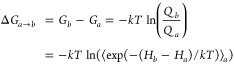11

We employed the Bennett acceptance ratio (BAR) method,³⁰ a technique that combines forward and backward FEP simulations to provide efficient estimates of free energy changes.²⁹ BAR was implemented using the ParseFEP Plugin from VMD. The ParseFEP Plugin is described in “A Toolkit for the Analysis of Free-Energy Perturbation Calculations” and the free energy and the statistical error are computed using eqs 11 and 14 from that paper.³¹ The estimated statistical error in the FEP free energy predictions using BAR was less than 0.1 kcal/mol in all cases.

Additional Considerations

IFST calculations equate the change in enthalpy (ΔH) with the change in potential energy (ΔE). For calculations in an NPT ensemble, there is an additional contribution to the free energy of PΔV, where P is the pressure and ΔV is the change in volume. However, for solvation of small molecules in water under ambient conditions, PΔVis significantly smaller than ΔE and can be safely neglected.³² In addition, the FEP and IFST calculations in this study both use a nonpolarizable force field. The parameters for the solutes are for prepolarized molecules and thus the free energy change associated with polarization of the solutes is ignored.¹⁴ The calculated values are thus expected to differ from the experimental values. As noted previously, such calculations also ignore the difference in polarization of the water molecules between bulk water and the solution.¹⁴ An additional consideration when comparing IFST calculations to experiment are terms that arise from the thermal motion of the solute and the change in ideal solvent entropy upon solute insertion. The additional terms are commonly termed the liberation contributions (ΔE_lib and ΔS_lib) and the volume entropy contribution (S_ve).³³ Collectively, they are termed the nonlocal contributions and are distinct from the correlation terms in eqs 1 and 2.¹ The local contributions ΔE_IFST, ΔS_IFST, and ΔG_IFST represent Ben-Naim’s standard energy, entropy, and free energy of solvation.³⁴ The liberation enthalpy ΔE_lib is calculated from the solvent’s thermal expansion coefficient α and isothermal compressibility κ:

12

For solvation in water under standard ambient conditions, ΔE_lib is approximately +0.05 kcal/mol. IFST is formulated in such a way that portions of ΔS_lib and S_ve cancel with some of the correlation terms.¹ The entropy from the nonlocal contributions ΔS_nonlocal is calculated from the remaining terms:

13

For solvation in water under standard ambient conditions ΔS_nonlocal makes a contribution of +0.55 kcal/mol to the free energy. In this work, we compare the predictions of FEP and IFST with Ben-Naim’s experimentally determined standard energy, entropy, and free energy of solvation. These do not include the nonlocal contributions, which are thus excluded from our calculations.

Experimental Data

The standard energies, entropies, and free energies of solvation of solvation for benzene, isobutane, methane, and methanol are taken from the same source.³⁵ The standard free energies of solvation for acetamide and N-methylacetamide are derived from Wolfenden³⁶ and taken from the same source.³⁷ The enthalpies of solvation for acetamide and N-methylacetamide are taken from the same source³⁸ and then modified to yield the standard enthalpies of solvation.³⁹ The entropies of solvation were determined from the standard energies and free energies.

Results and Discussion

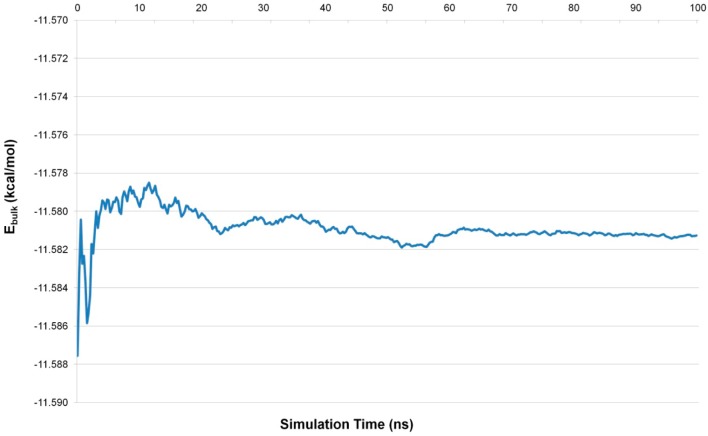
The simulation of bulk water is a key part of this work, as ΔE_IFST depends critically upon the calculated value of E_bulk. This is because the volume of solvent we are considering (voxels within 12.0 Å of the origin) contains approximately 240 water molecules. Thus, a difference of 0.01 kcal/mol in E_bulk leads to a difference of 2.4 kcal/mol in ΔE_IFST and ΔE_FEP. This is significant in the context of predicting solvation free energies. A simple calculation suggests that E_bulk must be correctly converged to within 0.0002 kcal/mol for ΔE_IFST and ΔE_FEP to be correctly calculated to within 0.1 kcal/mol. This extreme dependence means that it is thus vital that the calculation of E_bulk is converged. Figure 1 shows the convergence of E_bulk for the 100.0 ns NPT simulation. After approximately 75 ns, the running average remains within 0.0002 kcal/mol of the final calculated value, yielding a final E_bulk of −11.5813 kcal/mol for the TIP4P-2005 water model.

Figure 1.

Convergence of E_bulk for a 100 ns simulation of bulk TIP4P-2005 water: the running average of E_bulk for a 100 ns NPT simulation of bulk TIP4P-2005 water at 300 K and 1 atm. The running average is calculated for 400 blocks of 250 ps. Each block is the average potential energy per water molecule taken from 2500 samples with one every 100 fs.

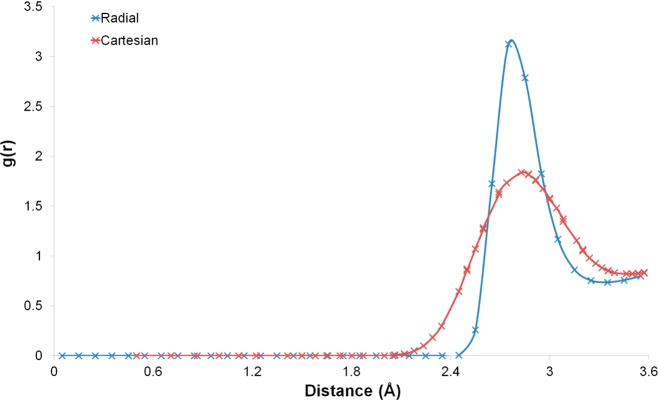
The simulation of bulk water also allows calculation of the excess entropy (S_bulk). Numerous works have reported the excess translational entropy of bulk water based on IFST calculations using spherical polar coordinates.^{25,26,40−43} Due to bulk water being isotropic, the excess translational entropy can be calculated from the radial distribution function (RDF). Using the RDF with a radial bin size of 0.1 Å, the excess translational entropy in the first solvation shell (between 0.0 and 3.6 Å) is calculated to be −3.29 cal/mol/K for the TIP4P-2005 water model. This makes a contribution of +0.98 kcal/mol to the excess free energy. It is interesting to compare this with the translational entropy based on IFST calculations using a Cartesian coordinate system. Using the default grid resolution of 0.5 Å, the excess translational entropy for voxels within the first solvation shell (between 0.0 and 3.6 Å) is calculated to be −2.10 cal/mol/K. This makes a contribution of +0.63 kcal/mol to the excess free energy. The true RDF and an “effective RDF” using the Cartesian coordinate system can be seen in Figure 2.

Figure 2.

Translational correlation function for TIP4P-2005 between 0.0 and 3.6 Å. The RDF between 0.0 and 3.6 Å from the bulk water simulation of TIP4P-2005 (blue line) and an “effective RDF” computed for voxels at the given distance from the origin (red line). The effective RDF is calculated by first computing the distance between the origin and the center of each voxel. Voxels at the same distance from the origin are then grouped together. The value of g(r) at each distance is calculated from the average number of water molecules in the group of voxels at that distance and their summed volume.

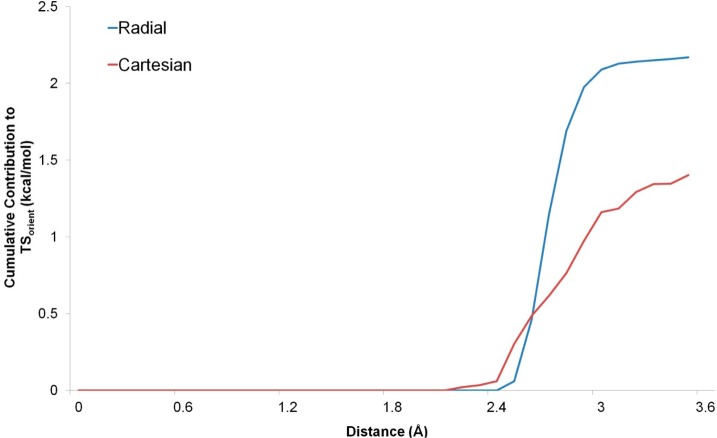
The curve is much flatter for the Cartesian coordinate system, with a significantly reduced contribution from the excluded volume. This suggests that a Cartesian grid of 0.5 Å may be too coarse to fully capture the translation probability density function. However, similar results are observed for the solute water RDFs (data not shown) and the errors in the translational entropy for the bulk system and the solute–water systems largely cancel. A similar approach can also be taken for the orientational entropy. Using spherical polar coordinates with a radial bin size of 0.1 Å and an angular bin size of 10°, the excess orientational entropy in the first solvation shell (between 0.0 and 3.6 Å) is calculated to be −7.28 cal/mol/K for the TIP4P-2005 water model. This makes a contribution of +2.17 kcal/mol to the excess free energy. For the Cartesian coordinate system using a grid resolution of 0.5 Å and an angular bin size of 10°, the excess orientational entropy in the first solvation shell (between 0.0 and 3.6 Å) is calculated to be −4.70 cal/mol/K. This makes a contribution of +1.40 kcal/mol to the excess free energy. Figure 3 shows the cumulative orientational contributions to S_bulk between 0.0 and 3.6 Å for the radial and Cartesian coordinate calculations. These findings show that S_bulk is underestimated using a grid resolution of 0.5 and this suggests that S_ww is likely to be misestimated.

Figure 3.

Cumulative orientational contribution to TS_bulk for bulk TIP4P-2005 water: the cumulative contribution to TS_bulk between 0.0 and 3.6 Å from the bulk water simulation of TIP4P-2005 using the radial coordinate system (blue line) and the Cartesian coordinate system (red line).

After calculating the necessary values for the bulk water simulation, we tested the method by using the bulk simulation as a basis for IFST calculations. The IFST quantities were calculated for all voxels within 12.0 Å of the origin. In all the following work, we report the entropic contributions to the free energy (−TΔS_IFST) in kcal/mol rather than the entropies (ΔS_IFST) in cal/mol/K, as this allows a direct comparison with the enthalpic contributions to the free energy. The second column of Table 2 shows the contributions from the different IFST quantities for the bulk water simulation, which should all be zero when there is no perturbation from a solute. It is clear that the orientational contributions to –TS_sw are overestimated by this method and this is due to the inherent bias in the histogram method. The overestimate is very small for each voxel (approximately 0.000 015 kcal/mol) but there are approximately 60 000 voxels and this leads to a significant overestimate in total. For this reason, we expect that the orientational contributions to S_sw will be overestimated for the solute systems. The other contributions to the free energy are close enough to zero to be acceptable.

Table 2. Results of IFST Calculations on Bulk Water and the Six Solutes^a.

thermodynamic quantity (kcal/mol)	bulk water	acetamide	benzene	isobutane	methane	methanol	N-methylacetamide
–TSsw trans	0.1	3.7	4.7	4.6	2.3	3.1	4.5
–TSsw orient	0.8	2.9	2.7	2.4	1.6	2.5	3.2
–TΔSww trans	0.1	–0.4	–0.5	–0.4	–0.4	–0.4	–0.6
–TΔSww orient	0.1	1.2	1.9	1.8	0.9	1.3	1.6
–TΔS trans	0.1	3.3	4.1	4.1	2.0	2.7	3.9
–TΔS orient	0.8	4.1	4.6	4.2	2.6	3.8	4.8
–TΔSIFST	1.0	7.4	8.8	8.3	4.5	6.5	8.6
Esw	0.0	–29.4	–15.8	–9.8	–3.6	–19.7	–29.1
ΔEww	0.2	14.8	8.3	4.8	1.2	9.7	14.2
ΔEIFST	0.2	–14.7	–7.4	–5.1	–2.5	–10.0	–14.9
ΔGIFST	1.2	–7.2	1.3	3.2	2.1	–3.4	–6.2

^aThe calculated IFST quantities for bulk water and the six solutes from the 100 ns simulations. The total translational and orientational contributions are the sums of the solute–water and water–water terms.

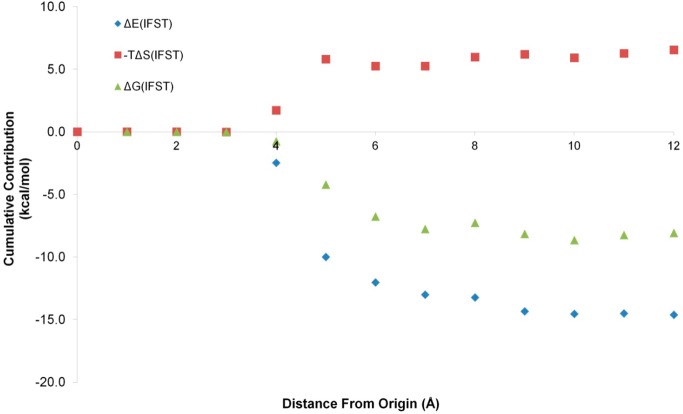
We then moved on to consider the solute–water systems. A key question that we have previously attempted to address is the size of the solvation shell around a solute that is affected by its presence.^13,23 However, previous studies were incomplete because they considered the per voxel values of ΔE_IFST, ΔS_IFST, and ΔG_IFST with increasing distance from the origin rather than the total ΔE_IFST, ΔS_IFST, and ΔG_IFST. These total values are affected by the volume increasing with the cube of the distance from the origin and are more revealing. We have calculated these values for the six solutes to more thoroughly address this issue. The results can be seen in Figure 4 for acetamide.

Figure 4.

Cumulative contributions to ΔE_IFST, ΔS_IFST, and ΔG_IFST for acetamide at increasing distances from the origin: the cumulative contributions to ΔE_IFST (blue diamonds), TΔS_IFST (red squares), and ΔG_IFST (green triangles) for acetamide between 0.0 and 12.0 Å from the origin.

The total ΔS_IFST approaches its final value at around 5.0 Å from the origin whereas the total ΔE_IFST and thus the total ΔG_IFST approach their final value at around 9.0 Å from the origin. The slight peaks in ΔS_IFST at 5.0 and 9.0 Å are due to the first and second solvation shells, as the plot is of the distance from the origin and acetamide has an approximate “radius” of 3.0 Å. When the size of the solutes is considered, the results indicate that the solvent is perturbed to a distance of approximately 7.0 Å from the surface of a solute. This corresponds to the first two solvation shells, with the first solvation shell contributing around 80% to ΔG_IFST. As discussed previously, these distances may be much larger for charged systems and they may also be different for larger solutes. Indeed, studies on a 16-residue peptide suggest that significant perturbations may extend to the third solvation shell at around 10 Å from the surface.⁴⁴

We also wished to study the convergence of the IFST quantities. As previously, we distinguish between the convergence with increased simulation time for a given sampling frequency and the convergence with increased sampling frequency for a given simulation time.^13,23 The convergence with increased simulation time can be seen for acetamide in Table 3 for a sampling frequency of 10 fs. The result for ΔE_IFST after 20.0 ns differs from the result after 100 ns by only 0.1 kcal/mol but the result for TΔS_IFST differs by more than 0.1 kcal/mol, even after 50.0 ns. It is the difference in the orientational component of S_sw that is notably different as the simulation time is decreased. This is not unexpected, as there are 128 times as many histogram bins for the orientational component of S_sw as for the translational component. These calculations suggest that converged predictions for IFST require at least 100 ns of simulation with a grid resolution of 0.5 Å and an angular bin size of 45° but that simulations of 20 ns may be sufficient to predict ΔE_IFST. The convergence with increased sampling frequency for acetamide can be seen in Table 4 for a simulation time of 100 ns. The result for ΔE_IFST using a sampling frequency of 1000 fs is the same as the result using a sampling frequency of 10 fs to one decimal place, and the result for TΔS_IFST using a sampling frequency of 20 fs is the same as the result using a sampling frequency of 10 fs to one decimal place. Again, it is the orientational component of TS_sw that is notably different as the sampling frequency is decreased. These calculations suggest that converged predictions for IFST using a histogram method require at least 5 000 000 samples from a 100 ns simulation with a grid resolution of 0.5 Å and an angular bin size of 45°. Other methods, such as the k-nearest neighbors (k-NN) algorithm,⁴⁵ may require shorter simulations and less sampling.^9,42

Table 3. Convergence of IFST Predictions with Increasing Simulation Time^a.

time (ns)	10	20	50	100
–TSsw trans (kcal/mol)	4.0	3.9	3.7	3.7
–TSsw orient (kcal/mol)	9.2	5.7	3.6	2.9
–TΔSww trans (kcal/mol)	–0.3	–0.3	–0.4	–0.4
–TΔSww orient (kcal/mol)	1.7	1.5	1.3	1.2
–TΔSIFST (kcal/mol)	14.5	10.8	8.2	7.4
Esw (kcal/mol)	–29.4	–29.4	–29.4	–29.4
ΔEww (kcal/mol)	15.4	14.9	14.9	14.8
ΔEIFST (kcal/mol)	–14.0	–14.5	–14.5	–14.6
ΔGIFST (kcal/mol)	0.6	–3.8	–6.3	–7.2

^aThe calculated enthalpic and entropic contributions to the free energy of acetamide calculated using all snapshots within 10, 20, 50, and 100 ns. Snapshots are taken every 10 fs.

Table 4. Convergence of IFST Predictions with Increased Sampling^a.

sampling freq (fs)	1000	500	200	100	50	20	10
–TSsw trans (kcal/mol)	3.8	3.8	3.7	3.7	3.7	3.7	3.7
–TSsw orient (kcal/mol)	13.8	7.8	4.6	3.6	3.1	2.9	2.9
–TΔSww trans (kcal/mol)	–0.4	–0.4	–0.4	–0.4	–0.4	–0.4	–0.4
–TΔSww orient (kcal/mol)	1.2	1.2	1.2	1.2	1.2	1.2	1.2
–TΔSIFST (kcal/mol)	18.5	12.4	9.1	8.1	7.7	7.5	7.4
Esw (kcal/mol)	–29.4	–29.4	–29.4	–29.4	–29.4	–29.4	–29.4
ΔEww (kcal/mol)	14.9	14.9	14.8	14.8	14.8	14.8	14.8
ΔEIFST (kcal/mol)	–14.6	–14.6	–14.6	–14.6	–14.6	–14.6	–14.6
ΔGIFST (kcal/mol)	3.9	–2.2	–5.5	–6.5	–6.9	–7.1	–7.2

^aThe calculated enthalpic and entropic contributions to the free energy of acetamide calculated using 100 ns of data with sampling frequencies of 1000, 500, 200, 100, 50, 20, and 10 fs.

We also wished to consider the effect of the grid resolution and angular bin size on the orientational and translational components of S_sw. The results in Tables 3 and 4 indicate that the translational component of S_sw is well converged for a grid resolution of 0.5 Å. We also studied the results for grid resolutions of 0.25 and 0.75 Å to assess whether the translational component of S_sw is fully quantified with the default grid resolution of 0.5 Å. The results for acetamide are reported in Table 5 and indicate that the answer is no. A grid resolution of 0.25 Å yields a converged value of 4.3 kcal/mol for the translational component of −TS_sw in comparison with a value of 3.7 kcal/mol for a grid resolution of 0.5 Å. Smaller grid resolutions, which may yield a higher prediction, were not tested. Testing the orientational component of −TS_sw in this fashion is more complicated because it requires a grid resolution in addition to an angular bin size. In this work, we have only explored the variation in entropy with respect to the angular bin size at the default grid resolution of 0.5 Å. We studied the results for angular bin sizes of 36° and 60° to assess whether the translational component of −TS_sw is fully quantified with the default angular bin size of 45°. The results for acetamide are reported in Table 6. An angular bin size of 36° yields a value of 3.6 kcal/mol for the orientational component of −TS_sw in comparison with a value of 2.9 kcal/mol for an angular bin size of 45°. However, it is not clear that the results for an angular bin size of 36° are fully converged from 10 000 000 samples over 100 ns and thus the question cannot be answered. Indeed, the results from the simulation of bulk water presented in the first column of Table 2 suggest that the orientational component of −TS_sw is not fully converged from 10 000 000 samples over 100 ns for an angular bin size of 45°. Due to computational restrictions, we have not tested effect of the grid resolution and angular bin size on the orientational and translational components of ΔS_ww. However, the results from the simulation of bulk water suggest that the effects on S_sw and ΔS_ww may counterbalance one another.

Table 5. Effect of the Grid Resolution on the Translational Component of −TS_sw^a.

		samples
thermodynamic quantity (kcal/mol)	grid resolution (Å)	1000000	2000000	5000000	10000000
–TSsw trans	0.25	4.4	4.3	4.3	4.3
–TSsw trans	0.5	3.7	3.7	3.7	3.7
–TSsw trans	0.75	3.1	3.1	3.1	3.1

^aThe translational component of −TS_sw for acetamide, calculated from 1 000 000, 2 000 000, 5 000 000, and 10 000 000 samples with grid resolutions of 0.25, 0.5, and 0.75 Å..

Table 6. Effect of the Angular Bin Size on the Orientational Component of −TS_sw^a.

			samples
thermodynamic quantity (kcal/mol)	bins	angular bin size (deg)	1000000	2000000	5000000	10000000
–TSsw orient	6	60	2.3	2.1	2.0	2.0
–TSsw orient	8	45	3.6	3.1	2.9	2.9
–TSsw orient	10	36	5.1	4.2	3.7	3.6

^aThe orientational component of −TS_sw for acetamide, calculated from 1 000 000, 2 000 000, 5 000 000, and 10 000 000 samples with angular bin sizes of 30°, 45°, and 60°.

The IFST predictions can be seen in Table 2. Calculations suggest that the translational and orientational contributions to the solvation entropy are of a similar magnitude in all cases, though the orientational contributions are always slightly larger. In addition, the solute–water terms are predicted to be 5–8-fold larger than the water–water terms. This is partly because the contribution of the translational water–water term is negative due to the solute excluded volume, but the orientational water–water term is also small. However, there are two issues to be considered. The first is that the water–water terms depend on the validity of the KSAs, which have not been thoroughly explored. The second is that our calculations suggest that the water–water terms are misestimated using a Cartesian grid with a resolution of 0.5 Å. It is interesting to note that the solute–water interactions (E_sw) are highly favorable in all cases, at the expense of an unfavorable change in water–water interactions (ΔE_ww). This leads to a favorable change in overall energy (ΔE_IFST) that is approximately half the magnitude of E_sw for the majority of solutes.

Assessing the data generated using IFST, it is clear that there are a number of issues with the method. The selection of grid resolution and angular bin size affects all the calculated entropies and in addition the use of the KSAs has not been comprehensively validated. However, these issues affect all solutes and thus we might expect a systematic misestimation of the entropies in comparison with FEP. We proceed, with this in mind. The results from experiment along with the predictions from FEP and IFST can be seen in Table 7. The correlation plots between experiment, IFST, and FEP can be seen in Figure 5.

Table 7. Results of the FEP and IFST Calculations Compared to Experiment^a.

solute	thermodynamic quantity	expt (kcal/mol)	FEP prediction (kcal/mol)	IFST prediction (kcal/mol)
acetamide	ΔG	–9.7	–8.3 ± 0.0	–7.2
	ΔH	–16.3		–14.7
	–TΔS	6.6		7.4
benzene	ΔG	–0.8	0.3 ± 0.1	1.3
	ΔH	–7.1		–7.4
	–TΔS	6.3		8.8
isobutane	ΔG	2.3	3.1 ± 0.1	3.2
	ΔH	–4.8		–5.1
	–TΔS	7.1		8.3
methane	ΔG	2.0	2.5 ± 0.0	2.1
	ΔH	–2.7		–2.5
	–TΔS	4.8		4.5
methanol	ΔG	–5.1	–4.6 ± 0.0	–3.5
	ΔH	–10.3		–10.0
	–TΔS	5.2		6.5
N-methylacetamide	ΔG	–10.1	–6.8 ± 0.0	–6.3
	ΔH	–17.1		–14.9
	–TΔS	7.0		8.6

^aThe experimental hydration enthalpy, entropy, and free energy for the six solutes, along with the predictions of FEP and IFST. The statistical errors are reported for the FEP calculations.

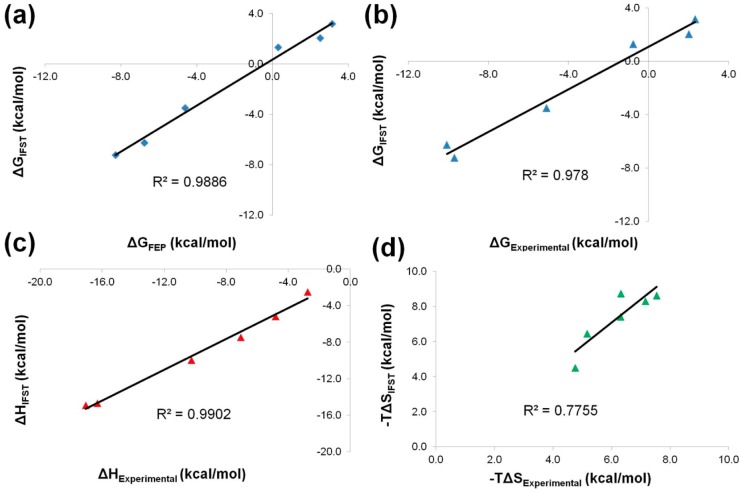
Figure 5.

Correlation plots between ΔG, ΔH, and TΔS for experiment and the predictions of FEP and IFST. Plots of the correlation between (a) ΔG_IFST and ΔG_FEP with blue diamonds, (b) ΔG_IFST and ΔG_Experimental with blue triangles, (c) ΔH_IFST and ΔH_Experimental with red triangles, and (d) TΔS_IFST and TΔS_Experimental with green triangles.

Of primary interest is the agreement between FEP and IFST. The mean unsigned difference in the solvation free energies is 0.7 kcal/mol, with the IFST predictions tending to be less favorable than the FEP predictions. FEP and IFST both yield reasonable predictions of the experimental quantities with mean unsigned errors for the solvation free energies of 1.3 and 1.8 kcal/mol, respectively. N-Methylacetamide is particularly poorly predicted by both methods. Agreement of IFST with the experimental enthalpic and entropic contributions is reasonable, with mean unsigned errors of 0.9 and 1.2 kcal/mol, respectively. However, the results suggest that the entropic component −TΔS tends to be overestimated by IFST, with a mean signed error of +1.2 kcal/mol. These results may explain why the IFST predictions of the hydration free energies tend to be less favorable than the FEP predictions. They are also commensurate with the overestimation of TΔS by 1.0 kcal/mol for the simulation of bulk water.

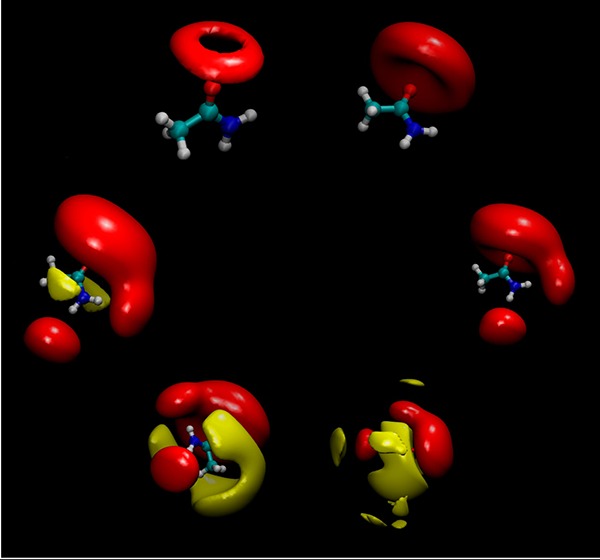
One of the main advantages of IFST calculations is the ability to break the solvation free energies into contributions from different regions and visualize these contributions. This promotes understanding of the system being studied and an insight into the thermodynamics of solvation. Figure 6 shows the contributions from different regions to the hydration free energy of acetamide at different contour levels, visualized using VMD.⁴⁶

Figure 6.

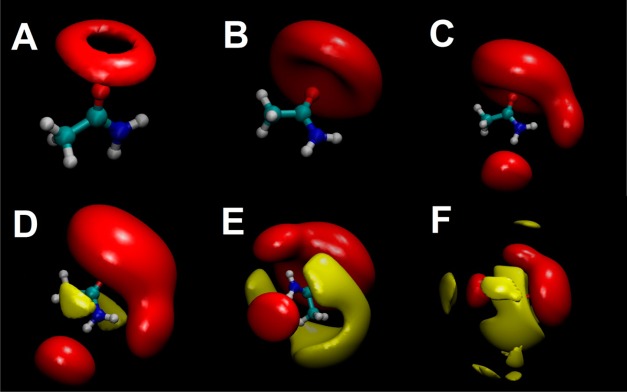
Visualizations of the relative free energy density relative to bulk water for regions surrounding acetamide. Six views of acetamide, with the relative free energy density contoured at different levels. Favorable relative free energy density is contoured in red and unfavorable relative free energy density is contoured in yellow. The contouring for the favorable relative free energy increases from (A) to (B) to (C). The contouring for the unfavorable relative free energy decreases from (D) to (E) to (F).

The region with the highest relative free energy density is a ring surrounding the carbonyl oxygen (Figure 6A). The carbonyl group is actually predicted to contribute approximately −6.0 kcal/mol to the hydration free energy of acetamide (Figure 6B). At lower contour levels, the contributions from the amide hydrogens are visible, with each contributing approximately −1.5 kcal/mol to the hydration free energy (Figure 6C). It is worth noting that the favorable regions surrounding the amide hydrogens would be well described by spherical hydration sites but the favorable regions surrounding the carbonyl oxygen would not. Contouring from positive values, the regions contributing most unfavorably to the hydration free energy are above and below the plain of the amide bond (Figure 6D). This effect has been noted in previous studies using WaterMap⁴⁷ and agrees with observations from the Cambridge Crystallographic Data Centre on the hydrophobic character above and below the plane of amide bonds (personal communication with Oliver Korb). It may also explain why defectively packed backbone hydrogen bonds, which have been termed dehydrons, lead to hotspots at protein surfaces.⁴⁸ At lower contour levels, the contributions from the methyl group are visible, again contributing unfavorably to the solvation free energy (Figure 6E). At very low contour levels, one can observe the small and unfavorable contributions from water molecules in the second solvation shell (Figure 6F).

The presence of regions with high number density that contribute unfavorably to a favorable hydration free energy may seem counterintuitive. The reason why a vacuum is not present within such regions can be understood using a simple example. Consider water molecules in a voxel with weak solute–water interactions (E_sw = −1.0 kcal/mol) and water–water interactions that are more favorable than in bulk (ΔE_ww = −2.0 kcal/mol) that is strongly ordered (−TS_sw = +3.0 kcal/mol and −TΔS_ww = +0.5 kcal/mol). For this voxel, ΔG_IFST = +0.5 kcal/mol and the region contributes unfavorably to the solvation free energy. One could view these water molecules as “icelike” given their unfavorable entropy and favorable enthalpy compared with bulk water. However, if such a region is vacated (without allowing solvent rearrangement) then all surrounding voxels also lose their pair interactions and correlations with water molecules inside the voxel. The total change in free energy (going to this unphysical state) can thus be unfavorable. If subsequent solvent rearrangement around the vacuum region cannot overcome this loss, then the voxel will be occupied despite contributing unfavorably to the solvation free energy. Clearly, there are cases where water can rearrange around a vacuum, but water molecules at the vacuum interface are likely to show reduced water–water interactions. It is worth noting that the unfavorable contributions are smaller in magnitude than the favorable contributions. Considering all voxels in the case of acetamide, the most favorable relative free energy density is −0.28 kcal/mol/ų whereas the least favorable relative free energy density is +0.04 kcal/mol/ų. Because the exact free energy densities calculated will depend on the grid resolution and angular bin size used, it will be important to test this principle in future work. If these results accurately reflect the thermodynamics, an interesting consequence is the potential for hydration sites in protein binding sites that contribute unfavorably to the hydration free energy. Such sites would be major hotspots of binding.

There is one additional issue which must be mentioned. ΔE_IFST, −TΔS_IFST, and ΔG_IFST are calculated as the sum of contributions from each voxel inside a given volume V. The contributions from each voxel include pairwise contributions due to correlations with every other voxel. In the IFST framework, the pairwise contributions are split equally between the two voxels of the pair. Importantly, there are pairs where one of the voxels is not inside the volume V and thus there are regions outside the volume V which contribute to ΔE_IFST, −TΔS_IFST, and ΔG_IFST. This must be considered when implementing IFST by counting pair contributions consistently. However, the contribution of voxels outside the volume V is expected to be very small if the volume V is significantly larger than the perturbing solute. In this case, a voxel outside V will only have significant correlations with voxels inside V that are close to the periodic boundary. These will have bulklike properties, leading to E_sw ≈ 0, ΔE_ww ≈ 0, S_sw ≈ 0, ΔS_ww ≈ 0, and ΔG_IFST ≈ 0.

Conclusions

IFST is a useful method to model solvation and has found particular application in understanding hydration phenomena in biological systems.^3,7,10,12 However, there has been little analysis to assess the quantitative predictions of IFST.³ This study addresses this issue by comparing hydration free energies from IFST with hydration free energies from FEP. The findings of this study are that IFST calculations show a good agreement with FEP calculations, with a mean unsigned difference of 0.7 kcal/mol in the predicted hydration free energies. Comparison of IFST predictions with the experimental hydration enthalpies and entropies suggests that there is a systematic overestimation of the entropies, which leads to a systematic underestimation of the free energies. For the CHARMM36 force field and the TIP4P-2005 water model, the agreement with the experimental hydration free energies is reasonable for FEP and IFST, with mean unsigned errors of 1.3 and 1.8 kcal/mol, respectively. Both IFST and FEP rely on the force field and are thus subject to the same problems in this respect. For IFST, the fine dependence of ΔE_IFST on E_bulk means that it is thus vital that the calculation of E_bulk is converged correctly. E_bulk will depend on the force field, water model, simulation package, and simulation parameters employed. Due to cancellation, this fine dependence will be of less importance in calculations of hydration free energy differences or binding energies, but only if the number of water molecules considered is similar. In addition, the systematic overestimations of −TΔS_IFST are expected to be similar if the grid resolution and bin sizes are the same. Thus, predictions for different molecules and different regions are directly comparable for a given IFST implementation, but not necessarily between different IFST implementations.

In addition to these results, there are a number of important points raised by the study. IFST has a number of limitations that should be addressed before widespread quantitative application. Current implementations are only rigorously valid for a fixed solute and this limits the utility. Flexible solutes can be considered in the IFST framework by performing an analysis on a number of solute conformations,⁹ but this will require yet more data. One of the major approximations in IFST is the use of the KSAs for the water–water entropy calculations. Previous work on the solvation of methane suggests that these KSAs lead to reasonable results due to the cancellation of errors between more and less structured regions. However, this may not be the case for polar solutes and further testing of the KSAs should be a focus of future work. Sampling is also a problem for IFST. Previous work has explored the data requirements for convergence of the solvation energy and entropy.^13,23 However, the comparison with FEP in this work allows a more thorough analysis. The results suggest that converged energies can be effectively sampled from 10 000 snapshots over a 20 ns simulation whereas the orientational component of the solute–water entropy term requires at least 5 000 000 snapshots over a 100 ns simulation to reach a converged prediction even with a modest angular bin size of 45°. However, the histogram method introduces a systematic overestimating bias to the entropies and this will scale with the volume of the system. Other work has shown that it is also difficult to estimate entropies using perturbation methods such as FEP and thermodynamic integration (TI).⁴⁹ In the context of IFST, assessment of the entropies may be more feasible using the k-NN algorithm,^9,42 particularly for the increased sampling requirements of considering a highly flexible solute. It is difficult to fairly assess the computation times required, because the FEP calculations are integrated into NAMD whereas the IFST calculations are not. This requires postprocessing of large-trajectory files at considerable computational cost. Comparing just the simulation times, each solute was simulated for a total of 336 ns for FEP and 100 ns for IFST. While FEP is inherently more parallelizable than IFST in its current format, it should be possible to apply IFST to multiple independent MD simulations, which would parallelize it effectively.

While suffering a number of drawbacks noted above, IFST does have a number of advantages over perturbation methods such as FEP and TI. Because IFST calculations are performed on a single simulation, there is no need for a lambda window schedule and no need to monitor overlap between lambda windows. In addition, there are no end points and thus there are no end-point catastrophes and no need for soft-core potentials. Importantly, there is no pathway and thus small and large perturbations can be considered with the same degree of sampling. However, perhaps the most useful feature of IFST is the spatial decomposition of the solvation free energies. This yields results that are more insightful than the total solvation free energies. Such visualization has also proved useful in 3D-RISM.⁵⁰ Indeed, it would be interesting to compare IFST results with the results of 3D-RISM⁵¹ and cell theory,^52,53 which can provide spatially decomposed predictions of solvation free energies using different methods.

This work represents a preliminary study on the quantitative application of IFST using a very small set of solutes. Future work should explore a number of avenues. A wide range of solutes would provide a sterner test for the methods. The inclusion of charged solutes may necessitate the use of a polarizable force field. Prior to this, it would be very useful to test the validity of the KSAs for a number of solutes, using the true inhomogeneous water–water correlation functions or via comparison with lower order entropy approximations. This should be done in concert with a thorough determination of the time scales and sampling requirements that are necessary for effective convergence of the thermodynamic predictions at the desired level of accuracy. In addition, care must be taken to employ methods that effectively capture the underlying probability distributions. The combination of ΔG_IFST with an assessment of protein–ligand interactions will facilitate the calculation of binding free energies. This will augment binding affinity predictions based on a single unbound state simulation,⁵⁴ albeit at increased computational cost. To achieve this, it will be necessary to incorporate solute flexibility into IFST.⁹

In conclusion, the agreement between hydration free energy predictions for IFST and FEP is very encouraging. It is clear that the entropic contributions are overestimated by IFST and further work is needed. However, the insight gained by visualizing the relative free energy densities provides a major advantage of IFST that make this a worthwhile objective.

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.