Abstract
We assessed the agreement between sampling windows of different size and orientation on packing density estimates in images of the parafoveal cone mosaic acquired using a flood-illumination adaptive optics retinal camera. Horizontal and vertical oriented sampling windows of different size (320x160 µm, 160x80 µm and 80x40 µm) were selected in two retinal locations along the horizontal meridian in one eye of ten subjects. At each location, cone density tended to decline with decreasing sampling area. Although the differences in cone density estimates were not statistically significant, Bland-Altman plots showed that the agreement between cone density estimated within the different sampling window conditions was moderate. The percentage of the preferred packing arrangements of cones by Voronoi tiles was slightly affected by window size and orientation. The results illustrated the high importance of specifying the size and orientation of the sampling window used to derive cone metric estimates to facilitate comparison of different studies.
OCIS codes: (110.1080) Active or adaptive optics, (170.1610) Clinical applications, (110.3925) Metrics
1. Introduction
The increasing interest in adaptive optics (AO) retinal imaging for its promise to provide a sensitive tool for early detection of retinal diseases is asking for reliable methods to describe and categorize retinal data acquired in patients [1–3]. Efforts from many research groups are aiming to solve the major clinical needs of AO retinal imaging, which include the development of reliable descriptors of the photoreceptor mosaic integrity and disruption.
Metrics currently used to analyze AO images of the cone mosaic include the estimation of cone density and spacing and the preferred packing arrangement of cones. Although a number of methods have been used to derive these metrics [4–15], only for a few of them reliability measurements have been reported [15–18]. Previous studies [16,17,19–23] showed a decrease in repeatability and an increase in measurement error as the sampling window size decreased from 64x64 µm to 25x25 µm. In general, authors used 50x50 µm to 60x60 µm areas to calculate cone density. This approach was used in order to compare in vivo data with those shown by Curcio et al. [24–26] in cadaver eyes. Recently, abnormalities of the cone mosaic have been shown to occur even when estimates of cone density were within normal limits [19–22]. Description of the preferred packing arrangement of cones using Voronoi analysis has been shown to capture additional features of the photoreceptor mosaic that density estimates cannot do [18–21,27–29]. If the goal of AO imaging would detect retinal diseases before conventional clinical imaging, the use of only the cone density method cannot be considered a valid metric to define a threshold between normal and diseased retina. Wide sampling areas should be used in order to provide a more comprehensive view of the photoreceptor mosaic geometry.
In sight of understanding the clinical utility of AO retinal imaging, we are evaluating the current methods used to describe the health and integrity of the cone mosaic. In previous work [18], we described the preferred packing arrangement of parafoveal cones as a function of retinal eccentricity using 820x102 µm sampling windows, showing that the percentage of hexagonal Voronoi tiles diminishes as the retinal eccentricity increases. In an effort to optimize the use of multiple metrics to describe the cone mosaic geometry, we aim to evaluate the effect of sampling window size and orientation on density estimates of parafoveal cones and their preferred packing arrangement.
2. Materials and methods
All research procedures described in this work adhered to the tenets of Declaration of Helsinki. The protocol was approved by the local Ethical Committee and all subjects recruited gave written informed consent after a full explanation of the procedure. Inclusion criteria were an age >18 years old and no history of systemic or ocular diseases and no previous eye surgery. Subjects recruited for the study received a complete eye examination, including non-contact ocular biometry using the IOL Master (Carl Zeiss Meditec Inc, Jena, Germany) and retinal imaging using a Spectralis SD-OCT (Heidelberg Engineering GmbH, Heidelberg, Germany).
A flood-illumination AO retinal camera (rtx1, Imagine Eyes, France) was used to acquire images of the cone mosaic. The imaging sessions were conducted after dilating the pupil with one drop of 1% tropicamide. In this study, image sequences of 40 frames each, subtending 4 degrees of visual angle, were acquired at 1.20 degree nasal and 1.70 degree temporal from the foveal reference fixation point (x = 0 degree, y = 0 degree) in the right eye of each subject. During AO imaging, fixation was maintained by instructing the patient to fixate the internal target of the instrument moved by the investigator.
A proprietary program provided by the manufacturer has been used to correct for distortions within frames of the raw image sequence and to correlate and frame-average in order to produce a final image with enhanced signal-to-noise ratio prior to further analysis. Frames exhibiting large motion artefacts due to eye movement or blinking were manually removed before processing; more than 32 frames were used for each location in each eye.
2.1 Image analysis
Before analysis, each image was converted from degrees of visual angle to micrometers on the retina: for this purpose, we used the nonlinear formula of Drasdo and Fowler and the Gullstrand schematic model eye parameterized by the biometry measurements [11,15,18,30,31]. The spectacle corrected magnification factor (RMFcorr) was calculated in order to correct for the differences in optical magnification and thus retinal image size between eyes. The RMFcorr was estimated for each eye by consideration of the axial length and the trial lens added to the system to compensate for defocus [11,15,18]. The spectacle vertex distance was set at 14 mm for all eyes.
At both retinal fixation locations, three different retinal areas (320x160 µm, 160x80 µm and 80x40 µm) centered in each final image were cropped and used for subsequent analysis of cone density and preferred packing arrangements of cones at each location. Each sampling window was cropped with the major axis oriented along both the horizontal and vertical meridians of each image. Furthermore, a 55x55 µm sampling window within the central portion of each image was cropped for analysis of cone density at each location. This approach was used in order to compare data obtained in the various window conditions to those estimated via the common approach currently used to derive density estimates.
Image cone labelling process was performed using an algorithm implemented with the image processing toolbox in Matlab (The Mathworks Inc, Natick MA, USA), as previously described by Li and Roorda [6]. Filtering and morphological image processing were applied to isolate the higher intensity signals corresponding to cone photoreceptors in each retinal area [6,18]. Filtering parameters were manually selected based on the estimated minimum cone diameter in order to avoid potential mistakes by eliminating locations that were too close together to be cones. An empirically determined intensity threshold (0.18 – peak intensity of the image normalised to 1) was applied on the set of identified local maxima to further reduce false positive. A different value of the filtering parameter was used at the nasal (minimum diameter: 4.0 µm) and temporal (4.5 µm) eccentricity locations. Cones were selected independently in each sampling window condition. The performance of the cone identification algorithm was verified by an expert investigator (ML) and the results for each sampling window condition recorded. The x,y coordinates of the cones were then stored in a text array and used to calculate cone density and packing arrangement. For a given retinal eccentricity, cone density (cones/mm2) was composed by the data values among sampling windows of different size and orientation along the horizontal or vertical major axis.
Cone packing arrangement was analyzed using Voronoi diagrams [6,32]. The Voronoi tessellation was implemented by the voronoi Matlab function from the bidimensional coordinates of labelled cones [18]. Each Voronoi cell was coded by a different colour corresponding to the number of their neighbouring cones: gray = tetragonal (4n) arrangement, yellow = pentagonal (5n) arrangement, green = hexagonal (6n) arrangement; blue = heptagonal (7n) arrangement and white = octagonal (8n) arrangement. The Voronoi regions containing pixels that extended beyond the bounds of each section were excluded from further analysis, thus creating a buffer zone to minimize the boundary effect [33].
2.2 Statistics
Retinal data were expressed as mean ± standard deviation. Statistics were performed using the SPSS software (SPSS Inc., version 17.0). The normal data distribution has been verified using the P-P plot within the software. The analysis of variance and the Tukey pairwise test were used to test significance between cone density measurements and preferred packing arrangements of cones taken within windows of same size and different orientation and windows of same orientation and different size at the same fixation location.
The intraclass correlation coefficient (ICC; two-way random effects model) was calculated in order to estimate the association between cone density values calculated within the various sampling windows. Bland-Altman plots [34] were used to assess the limits of agreements (LoA) and their 95% confidence interval (CI) between the cone density values estimated between the various sampling window conditions at the same fixation location. Statistical significance was set at P<0.05 for all the tests performed.
3. Results
Ten adult subjects (4 males and 6 females) were recruited. The healthy subjects were 23 to 46 years old (31.60 ± 7.46 yrs), the manifest refraction ranged between emmetropia and −6.25 D (mean, −2.48 ± 2.59 D). The average axial length was 24.61 ± 1.62 mm (range, 21.66 to 27.04 mm). The average RMFcorr was 0.286 ± 0.017 mm/deg (range, 0.252 - 0.313 mm/deg).
The performance of the cone identification algorithm was slightly variable according to window size. As the sampling window size decreased, we observed a slight decrease in the performance of the cone identification algorithm. The performance of the cone identification algorithm is shown in Fig. 1 . The mean percentage of manually identified cones spanned from 0.1 ± 0.2% to 1.3 ± 0.7% and 2.8 ± 2.1% in the three horizontal oriented windows of different size (160x320 µm, 80x160 µm and 40x80 µm) respectively.
Fig. 1.
Performance of the cone identification algorithm. Shown are images from three cases acquired at the nasal location (upper row). Scale bar is 25 µm. Red crosses represent cones identified by the algorithm, blue and yellow squares indicate those added and removed by the user respectively (lower row). The average number of cones added manually across all images within the vertical oriented sampling windows of 160x80 µm size was 0.8 ± 0.6%. In general, misidentified cones were more frequently located near the edge of the sampling windows (boundary effect). Cones whose edges were, also in part, outside the image section were not labelled.
It was 0.2 ± 0.1%, 0.8 ± 0.6% and 3.6 ± 2.7% for the vertical oriented windows (320x160 µm, 160x80 µm and 80x40 µm) respectively. These differences were statistically significant (P<0.05). On the other hand, there were no differences of the algorithm performance for cone identification in relation to the fixation location.
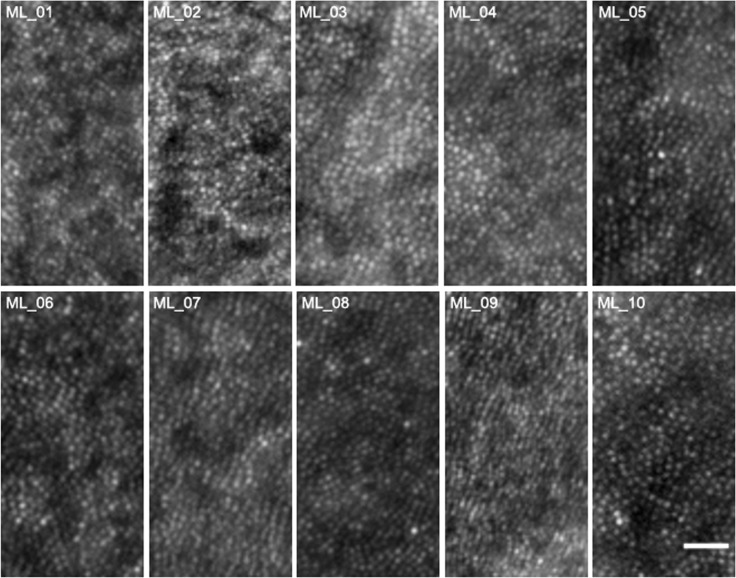
Figure 2 shows representative images, acquired at the temporal fixation location of the parafoveal cone mosaic, for all ten subjects. A summary of the cone density measurements is shown in Table 1 . The average cone density ranged between 51995 ± 4042 cones/mm2 and 48063 ± 3969 cones/mm2 across the various sampling window conditions at the nasal fixation location and between 48082 ± 2018 cones/mm2 and 43219 ± 3197 cones/mm2 at the temporal location.
Fig. 2.
Photoreceptor mosaic images for all 10 subject acquired at 1.70 degree temporal fixation location. Scale bar is 25 µm.
Table 1. Average ( ± SD, cones/mm2) Estimates of Cone Density Calculated across the Different Sampling Window Conditions at Both Fixation Locations.
| Fixation location | Horizontal sampling windows (size) | Vertical sampling windows (size) | ||||
|---|---|---|---|---|---|---|
| 160x320 µm | 80x160 µm | 40x80 µm | 320x160 µm | 160x80 µm | 80x40 µm | |
| 1.20 degree Nasal | 51955 ± 4042 | 51672 ± 4691 | 48063 ± 3969 | 50369 ± 2850 | 50781 ± 3515 | 48719 ± 5136 |
| 1.70 degree Temporal | 48082 ± 2018 | 46359 ± 2990 | 43219 ± 3197 | 46520 ± 4032 | 46234 ± 4913 | 44000 ± 5311 |
The highest and lowest cone density estimates were found within the 160x320 µm and 40x80 µm horizontal oriented sampling windows respectively. There were no statistically significant differences (P>0.05) between the cone density estimates taken within windows of same orientation and different size at the same fixation location. Furthermore, the differences between the cone density values obtained within the horizontal and vertical oriented windows of same size at the same fixation location were not statistically significant (P>0.05).
Cone density was further calculated within a 55 x 55 µm sampling area at each location. Average values were 47800 ± 3504 cones/mm2 and 43167 ± 3330 cones/mm2 at the nasal and temporal retinal location respectively. The average cone density differences between the 55 x 55 µm sampling area and those obtained in sampling areas of different size and orientation were no statistically significant (P>0.05) at any location.
Table 2 shows the correlation matrix of the average ICC values between cone density values estimated within the windows of different size at both fixation locations. The estimates of cone density taken within the vertical oriented windows of different size showed, on average, higher correlation (ICC≥0.83; P<0.001) than those taken within the horizontal oriented windows (ICC≥0.71; P<0.001) at the same fixation location.
Table 2. Correlation Matrix of Cone Density Values Estimated within Sampling Windows of Different Size and Orientation at Both Fixation Locations.
| Hor320/Nas | 1.00 | |||||||||||
| Hor320/Temp | 1.00 | |||||||||||
| Hor160/Nas | .83 | 1.00 | ||||||||||
| Hor160/Temp | .96 | 1.00 | ||||||||||
| Hor80/Nas | .71 | .95 | 1.00 | |||||||||
| Hor80/Temp | .79 | .82 | 1.00 | |||||||||
| Vert320/Nas | 0.48 | 0.60 | 0.44 | 1.00 | ||||||||
| Vert320/Temp | 0.27 | 0.29 | 0.29 | 1.00 | ||||||||
| Vert160/Nas | 0.35 | 0.41 | 0.23 | .83 | 1.00 | |||||||
| Vert160/Temp | 0.43 | 0.46 | 0.39 | .96 | 1.00 | |||||||
| Vert80/Nas | 0.41 | 0.58 | 0.44 | .85 | .84 | 1.00 | ||||||
| Vert80/Temp | 0.38 | 0.41 | 0.27 | .92 | .94 | 1.00 | ||||||
| Window/Location | Hor 320/Nas | Hor 320/Temp | Hor 160/Nas | Hor 160/Temp | Hor 80/Nas | Hor 80/Temp | Vert 320/Nas | Vert 320/Temp | Vert 160/Nas | Vert 160/Temp | Vert 80/Nas | Vert 80/Temp |
Italics = average ICC values between cone density values estimated within the Vertical oriented windows of different size taken at the same location.
Bold = average ICC values between cone density values estimated within the Horizontal oriented windows of different size taken at the same location.
Black = average ICC values between cone density values estimated within the Vertical and Horizontal oriented windows taken at the same location.
Low correlation (ICC≤0.50; P<0.001) was found between the cone density values obtained within the vertical and horizontal oriented windows of same size.
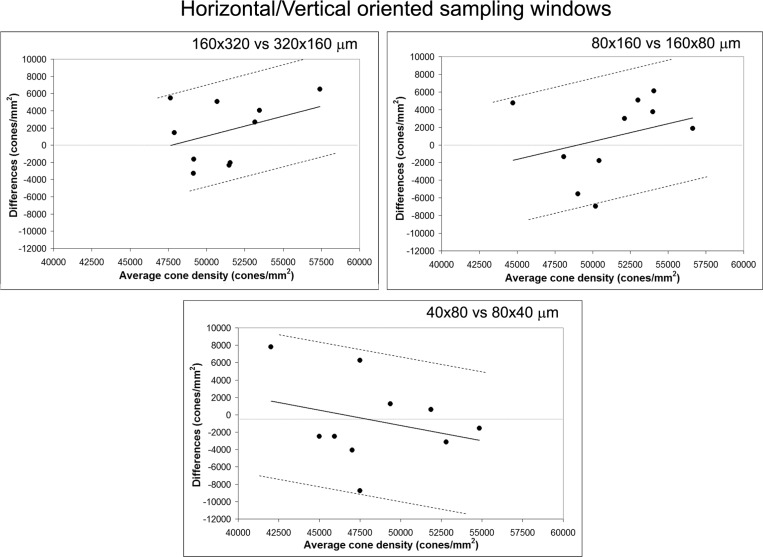
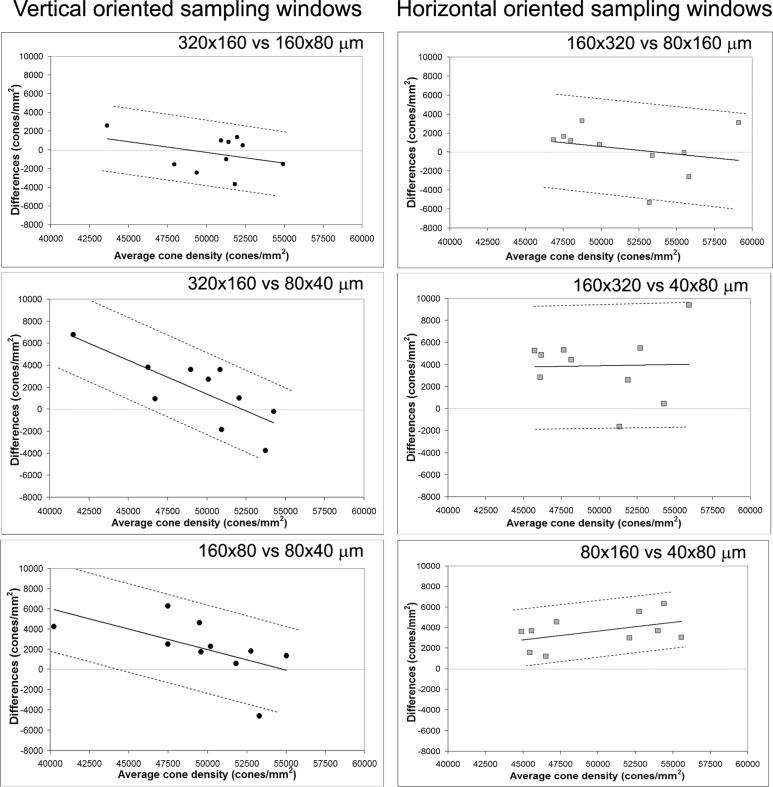
Since cone density values tended to decline with decreasing sampling size along both window orientations, we used a regression approach to determine the agreement between cone density estimated within the different sampling window conditions. According to previous work by Bland and Altman [35], we regressed the difference (D) between each pair of windows on their average (A), as D = b0 + b1A. Thereafter, the 95% CI was calculated as , where R represents the absolute values of the residuals. Figures 3 and 4 show the Bland-Altman plots between cone density taken within sampling windows of different orientation and size at the nasal fixation location respectively. The agreement between the sampling windows of same size and different orientation was moderate at both retinal fixation locations. Looking at the agreement between the sampling windows of same orientation and different size, the highest LoA was found between the cone density values estimated within the vertical oriented windows of 320x160 µm and 160x80 µm at both retinal fixation locations. Moderate agreement was found between the cone density values estimated within the other window conditions along both orientations at both retinal fixation locations.
Fig. 3.
Bland-Altman plots showing the agreement between cone density values calculated within horizontal and vertical oriented sampling windows of same size at the 1.20 degree nasal retinal location. Average and difference density values between sampling windows are plotted in the x- and y-axes respectively. The presentation of the 95% limits of agreement is for visual judgement of how well two methods of measurement agree. The smaller the range between these two limits the better the agreement is. The average difference and the distribution of points across the diagram, however, provide further information on the agreement between the two measurements. A wide 95% CI has been calculated between sampling windows of different orientation and same size.
Fig. 4.
Bland-Altman plots showing the agreement between cone density values calculated within vertical (left column) and horizontal (right column) oriented sampling windows of different sizes. Average and difference density values between sampling windows are plotted in the x- and y-axes respectively. Cone density values estimated within the vertical oriented windows of 320x160 µm and 160x80 µm showed low average difference and small 95% CI. The average differences calculated between windows of different sizes increased as the window size decreased. The 95% CI was wider between the horizontal oriented windows of different size than the vertical ones, except for the horizontal windows of 80x160 µm and 40x80 µm.
The percentage of hexagonal Voronoi tiles ranged between 49.8 ± 7.7% and 46.4 ± 3.6% at the nasal fixation location (Tukey; P>0.05) and between 49.9 ± 6.4% and 47.6 ± 2.4% at the temporal location (Tukey; P>0.05). The highest and lowest percentage of hexagonal arrangement was found within the horizontal 40x80 µm window and the vertical 320x160 µm window at both fixation locations respectively. The percentage of 5n arrangement was highest within the vertical 40x80 µm window at both fixation locations. The percentage of 8n arrangement was slightly higher within the vertical 320x160 µm window than in other sampling areas at both fixation locations. No preference in window size and orientation was observed for 4n and 7n arrangements. Overall, the differences between the preferred 6n arrangement across all the sampling window conditions were ≤3.5%. For 4n, 5n, 7n and 8n arrangements, they were ≤0.7%, ≤4.0%, ≤2.8% and ≤1.8% respectively. A summary of the preferred cone packing arrangement is provided in Tables 3 and 4 .
Table 3. Preferred Packing Arrangement of Cones (average ± SD, %) Calculated Using Voronoi Tiles at the Nasal Fixation Location.
| Preferred arrangement | Horizontal sampling windows (size) | Vertical sampling windows (size) | ||||
|---|---|---|---|---|---|---|
| 160x320 µm | 80x160 µm | 40x80 µm | 320x160 µm | 160x80 µm | 80x40 µm | |
| 4n | 2.5 ± 0.5 | 2.1 ± 1.3 | 2.1 ± 1.4 | 2.8 ± 0.8 | 2.6 ± 0.8 | 2.5 ± 1.1 |
| 5n | 25.9 ± 1.2 | 26.7 ± 2.5 | 27.2 ± 2.7 | 26.2 ± 1.4 | 26.9 ± 2.8 | 27.4 ± 3.6 |
| 6n | 48.2 ± 2.8 | 48.5 ± 5.5 | 49.8 ± 7.7 | 46.4 ± 3.6 | 46.8 ± 5.0 | 47.8 ± 5.2 |
| 7n | 20.1 ± 0.5 | 19.4 ± 1.7 | 19.0 ± 3.5 | 20.9 ± 0.9 | 20.5 ± 1.3 | 19.4 ± 3.5 |
| 8n | 3.5 ± 1.0 | 3.2 ± 1.9 | 1.8 ± 1.4 | 3.6 ± 0.9 | 3.2 ± 1.3 | 2.8 ± 1.4 |
Table 4. Preferred Packing Arrangement of Cones (average ± SD, %) Calculated Using Voronoi Tiles at the Temporal Fixation Location.
| Preferred arrangement | Horizontal sampling windows (size) | Vertical sampling windows (size) | ||||
|---|---|---|---|---|---|---|
| 160x320 µm | 80x160 µm | 40x80 µm | 320x160 µm | 160x80 µm | 80x40 µm | |
| 4n | 2.3 ± 0.4 | 2.3 ± 0.8 | 3.0 ± 1.8 | 2.3 ± 0.5 | 2.3 ± 0.9 | 1.9 ± 0.9 |
| 5n | 25.5 ± 1.2 | 26.4 ± 2.3 | 25.9 ± 3.6 | 26.2 ± 1.2 | 26.1 ± 3.1 | 29.5 ± 4.5 |
| 6n | 48.5 ± 2.3 | 47.9 ± 3.6 | 49.9 ± 6.4 | 47.6 ± 2.4 | 48.8 ± 6.0 | 48.6 ± 6.4 |
| 7n | 20.5 ± 0.6 | 20.7 ± 1.2 | 18.5 ± 2.8 | 20.3 ± 0.8 | 19.8 ± 2.4 | 17.9 ± 2.5 |
| 8n | 3.2 ± 0.6 | 2.7 ± 0.9 | 2.6 ± 1.7 | 3.5 ± 0.9 | 2.9 ± 1.3 | 2.1 ± 1.6 |
A part of the difference in percentage of the preferred packing arrangements of cones with decreasing sampling size was caused by the re-selection of cones in each sampling window. The number of neighbours between some Voronoi tiles of the same cone mosaic changed because of small differences in the position of cones between each image section. Moreover, the boundary effect increased with decreasing sampling area. Figures 5 and 6 show, in four representative cases, the Voronoi maps created within vertical and horizontal sampling windows of different size at the nasal and temporal fixation locations respectively.
Fig. 5.
Voronoi maps obtained from cone coordinates estimated within the three sampling vertical window conditions at the nasal fixation location in two subjects (ML_05 and ML_06). The percentage of 6n arrangements (green tiles) is 50.9% and 47.5% within the 160x320 µm windows respectively. It was 56.2% and 46.4% within the 80x160 µm windows and 50.6% and 51.3% within the 40x80 µm windows respectively. In subject ML_06 (i.e., the case showing the lower % of 6n arrangement), the percentage of 5n arrangement (yellow tiles) increased from 26.6% to 31.9% from the largest to the smallest sampling window. The corresponding images of the cone mosaic at the same retinal location are shown for subject ML_06. The boundary effect may influence the estimation of the preferred packing arrangement of cones near the edge of the image section. The algorithm’s performance and the subsequent manual check to identify cones are additional sources of error for accurate reconstruction of a Voronoi map.
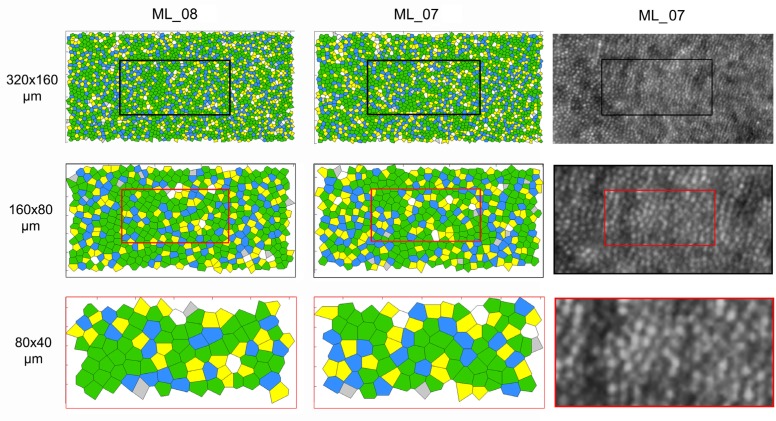
Fig. 6.
Voronoi maps obtained from cone coordinates estimated within the three sampling horizontal window conditions at the temporal fixation location in two subjects (ML_08 and ML_07). Across the horizontal oriented sampling window, the percentage of 6n arrangement tended to increase with decreasing area. In these cases, it ranged from 49.7% and 49.8% to 53.3% and 46.6% respectively. In subject ML_07, the percentage of each of the preferred cone packing arrangements showed differences ≤2.3% between the three sampling window conditions. The images of the cone mosaic at the same retinal location are shown for subject ML_07.
4. Discussion
Adaptive optics ophthalmic instruments are translating into clinical applications that are rapidly expanding. Reliable methods have recently been reported for full-automatic or semi-automatic location of cones in high-resolution AO retinal images. The results obtained are in general agreement with the information from histological studies of human retina [3–18,24–26]. The increasing quantity of data in normative population allows researchers to analyze the spatial properties of the healthy retinal sampling array. Work is under way in several research institutes to develop accurate methods to describe and quantify the photoreceptor mosaic integrity and make the AO imaging a valid tool for clinical ophthalmology.
Several methods used sampling windows of 60x60 µm or smaller to quantify the cone density [6,8,11,15,16]. However, the analysis of data obtained within sampling windows wider than 60x60 µm has been shown to provide a more comprehensive description of the cone mosaic geometry [6,18,20,22]. This can be achieved by representing graphically the arrangement of cones using Voronoi maps. Furthermore, statistical descriptors of mosaic non-order could be more efficient when analyzing wide retinal areas and help better classify the normal distribution of cone packing arrangement [6,10,18–22,36,37].
In this work, we aimed to evaluate the effect of the sampling window size and orientation on density and preferred packing arrangement of parafoveal cones. We estimated the two image metrics of the cone mosaic within sampling windows of three different sizes each of which showing two different orientations. The estimates of cone density tended to decrease with decreasing window size for both window orientation, as shown in Table 1. On average, the absolute differences were higher between the horizontal sampling windows of different size (3892 and 4863 cones/mm2 between the largest and smallest sampling window size at the nasal and temporal locations respectively) than between the vertical oriented sampling windows (1650 and 2520 cones/mm2 between the largest and smallest sampling window size at the nasal and temporal locations respectively). This is not surprising, since cone density was estimated along the horizontal meridian of the retina and the relative distances from the foveal reference fixation point of several cones in the 160x320 µm horizontal oriented window were greater than those in smaller horizontal windows and in all vertical windows. The differences of cone density estimates between the horizontal and vertical oriented sampling windows decreased as the window size decreased, as expected. It was worth noting to understand that cone density estimated within a 55 x 55 µm sampling area (used for reference purpose) showed the lowest, though not statistically significant, values at both retinal locations.
The correlation between estimates of cone density taken in different sampling window conditions was mainly associated with the orientation of the window. The cone density values calculated within the vertical oriented sampling windows showed higher absolute agreement than those taken within the horizontal oriented windows. A low absolute agreement (ICC≤0.50; P<0.001) was found between the vertical and horizontal oriented windows of same size. However, a high correlation between cone density data, as shown by ICC analysis, did not imply that the values could be used interchangeably (correlation measures the strength of a relation between two variables, not the agreement between them). For this reason, we calculated LoA from Bland-Altmann plots in order to evaluate whether or not cone density values calculated within the different sampling window conditions could be considered interchangeable. A regression approach for nonuniform differences was used to plot differences and mean of the various sampling windows. The highest LoA was found between cone density values estimated within the vertical oriented windows of 320x160 µm and 160x80 µm at both retinal locations. This was the only case for which cone density data taken within two different sampling windows could be used interchangeably without incurring in any type of error. The lowest LoA was found when comparing cone density values estimated between the horizontal oriented windows of 160x320 µm and 40x80 µm and between the horizontal and vertical sampling windows at both retinal fixation locations. Care should be therefore taken when comparing cone density calculated between sampling windows of different orientation, without considering the proportional error related to the retinal location and the window size and orientation used to estimate density.
As it regards the analysis of the preferred packing arrangement of cones, the greatest average difference of 6n arrangement, though not statistically significant, was 3.4% and was found between the 40x80 µm horizontal sampling window and the 320x160 µm vertical sampling window at the nasal fixation location. The average differences of 6n arrangement between the other sampling window conditions were ≤2%. The average % of non hexagonal arrangements was quite similar between sampling windows of different size (difference ≤2%), except for the 5n arrangement between the horizontal oriented 160x320 µm window and the vertical oriented 40x80 µm window at the temporal location (average difference of 4%). Overall, the graphical representation of the cone mosaic geometry appeared to be less sensitive to window size and orientation than cone density. This is in principle due to the fact that Voronoi tessellation is not dependent on the window size but only on the number of the labelled cones and their relative arrangements. Limits of Voronoi analysis are related to the accuracy of the cone identification algorithm and to the boundary effect, which increases as the sampling window area decreases. Manual checking of the cone identification algorithm performance is necessary to avoid error in Voronoi tessellation, especially in areas showing defects in the image of the cone mosaic (e.g., large retinal vessels, image artifacts, rods etc.) [18]. In this study, the cones were re-selected in each sampling window showing that small changes in their relative position may in part change the number of tiles between Voronois even in the same cone mosaic.
The performance of the cone identification algorithm was slightly variable according to window size, as previously shown [16]. As the sampling window size decreased, we observed a slight, although significant, decrease in the performance of the cone identification algorithm. The mean percentage of manually identified cones increased from an average 0.1-0.2% to 2.8-3.6% from the greatest to the smallest horizontal and vertical oriented sampling windows respectively. There is no clear understanding about this variable performance of the cone identification algorithm with respect to the sampling window size both in AO flood illumination and AOSLO instruments [15,16,18]. This presumably reflects the fact that as the sampling window decreases in size, the relative proportion of “point defects” in the image of the cone mosaic increases; furthermore, we observed an increased boundary effect as the window size decreased [18].
A few limitations to our study should be pointed out, with the goal of stimulating further work on this issue so as to accelerate the development of robust image analysis tools for in vivo images of the photoreceptor mosaic. First, our images were acquired between 1 and 2 degrees from the foveal fixation and the results from the present work cannot be directly extended to areas closer to the fovea where cone density is changing most rapidly. Differences in cone density estimates between sampling windows of different size could be greater than those reported here. A second issue relates to the fact that we only examined the cone mosaic. As the distance from the foveal center increases, the intrusion of rods greatly contributes to change the spatial arrangement of cones. Investigation of the preferred packing arrangement of rods in the retinal periphery could add valuable information about their normal distribution in the healthy retina [4]. A third issue is that analysis was performed only along the horizontal retinal meridian; the effect of sampling windows size and orientation could be influenced by local variance of the photoreceptor mosaic as a consequence of its different expansion between the horizontal and vertical meridians [10,18,24,38,39]. If the results of the present work were extended to the vertical meridian, it is very likely that the vertical oriented windows had a higher cone density than the horizontal ones. The differences, however, (considering sampling windows of same size of those used in the present study) should not be higher than 10%, as found here. On the contrary, the estimation of cone density within squared sampling windows can be influenced only by window size and not also by retinal meridian [23].
In conclusion, we showed the effect of sampling window size and orientation on cone density and packing arrangement estimates in images of the parafoveal cone mosaic. The data illustrated the high importance of specifying the size and orientation of the sampling window used to derive cone metric estimates to facilitate comparison of different studies. Average differences to a maximum of 10% in the parafoveal cone density occurred between sampling windows of 320x160 µm and either 80x40 µm or 55x55 µm. This finding can be of interest when comparing data from normative and pathological cases in clinical studies that used different sampling window conditions. Care should be taken when comparing data estimated within wide sampling areas with those from previous studies [5–13,15,16,18], in which 50x50µm, 55x55 µm or 60x60 µm windows were used, as shown in the present study. The graphical representation of preferred packing arrangements of cones by Voronoi tiles was slightly affected by window size and orientation.
References and links
- 1.Godara P., Dubis A. M., Roorda A., Duncan J. L., Carroll J., “Adaptive optics retinal imaging: emerging clinical applications,” Optom. Vis. Sci. 87(12), 930–941 (2010). 10.1097/OPX.0b013e3181ff9a8b [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Huang G., Qi X., Chui T. Y., Zhong Z., Burns S. A., “A clinical planning module for adaptive optics SLO imaging,” Optom. Vis. Sci. 89(5), 593–601 (2012). 10.1097/OPX.0b013e318253e081 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lombardo M., Serrao S., Devaney N., Parravano M., Lombardo G., “Adaptive optics technology for high-resolution retinal imaging,” Sensors (Basel) 13(1), 334–366 (2013). 10.3390/s130100334 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Dubra A., Sulai Y., Norris J. L., Cooper R. F., Dubis A. M., Williams D. R., Carroll J., “Noninvasive imaging of the human rod photoreceptor mosaic using a confocal adaptive optics scanning ophthalmoscope,” Biomed. Opt. Express 2(7), 1864–1876 (2011). 10.1364/BOE.2.001864 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lombardo M., Lombardo G., Ducoli P., Serrao S., “Adaptive optics photoreceptor imaging,” Ophthalmology 119(7), 1498–, e2. (2012). 10.1016/j.ophtha.2012.03.019 [DOI] [PubMed] [Google Scholar]
- 6.Li K. Y., Roorda A., “Automated identification of cone photoreceptors in adaptive optics retinal images,” J. Opt. Soc. Am. A 24(5), 1358–1363 (2007). 10.1364/JOSAA.24.001358 [DOI] [PubMed] [Google Scholar]
- 7.Xue B., Choi S. S., Doble N., Werner J. S., “Photoreceptor counting and montaging of en-face retinal images from an adaptive optics fundus camera,” J. Opt. Soc. Am. A 24(5), 1364–1372 (2007). 10.1364/JOSAA.24.001364 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Song H., Chui T. Y. P., Zhong Z., Elsner A. E., Burns S. A., “Variation of cone photoreceptor packing density with retinal eccentricity and age,” Invest. Ophthalmol. Vis. Sci. 52(10), 7376–7384 (2011). 10.1167/iovs.11-7199 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Li K. Y., Tiruveedhula P., Roorda A., “Intersubject variability of foveal cone photoreceptor density in relation to eye length,” Invest. Ophthalmol. Vis. Sci. 51(12), 6858–6867 (2010). 10.1167/iovs.10-5499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chui T. Y. P., Song H., Burns S. A., “Adaptive-optics imaging of human cone photoreceptor distribution,” J. Opt. Soc. Am. A 25(12), 3021–3029 (2008). 10.1364/JOSAA.25.003021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lombardo M., Serrao S., Ducoli P., Lombardo G., “Variations in image optical quality of the eye and the sampling limit of resolution of the cone mosaic with axial length in young adults,” J. Cataract Refract. Surg. 38(7), 1147–1155 (2012). 10.1016/j.jcrs.2012.02.033 [DOI] [PubMed] [Google Scholar]
- 12.Chui T. Y. P., Song H., Burns S. A., “Individual variations in human cone photoreceptor packing density: variations with refractive error,” Invest. Ophthalmol. Vis. Sci. 49(10), 4679–4687 (2008). 10.1167/iovs.08-2135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Merino D., Duncan J. L., Tiruveedhula P., Roorda A., “Observation of cone and rod photoreceptors in normal subjects and patients using a new generation adaptive optics scanning laser ophthalmoscope,” Biomed. Opt. Express 2(8), 2189–2201 (2011). 10.1364/BOE.2.002189 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dees E. W., Dubra A., Baraas R. C., “Variability in parafoveal cone mosaic in normal trichromatic individuals,” Biomed. Opt. Express 2(5), 1351–1358 (2011). 10.1364/BOE.2.001351 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lombardo M., Lombardo G., Lomoriello D. S., Ducoli P., Stirpe M., Serrao S., “Interocular symmetry of parafoveal photoreceptor cone density distribution,” Retina E-published (2013). 10.1097/IAE.0b013e3182807642 [DOI] [PubMed] [Google Scholar]
- 16.Garrioch R., Langlo C., Dubis A. M., Cooper R. F., Dubra A., Carroll J., “Repeatability of in vivo parafoveal cone density and spacing measurements,” Optom. Vis. Sci. 89(5), 632–643 (2012). 10.1097/OPX.0b013e3182540562 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Talcott K. E., Ratnam K., Sundquist S. M., Lucero A. S., Lujan B. J., Tao W., Porco T. C., Roorda A., Duncan J. L., “Longitudinal study of cone photoreceptors during retinal degeneration and in response to ciliary neurotrophic factor treatment,” Invest. Ophthalmol. Vis. Sci. 52(5), 2219–2226 (2011). 10.1167/iovs.10-6479 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lombardo M., Serrao S., Ducoli P., Lombardo G., “Eccentricity dependent changes of density, spacing and packing arrangement of parafoveal cones,” Ophthalmic Physiol. Opt. E-published (2013). 10.1111/opo.12053 [DOI] [PubMed] [Google Scholar]
- 19.Godara P., Siebe C., Rha J., Michaelides M., Carroll J., “Assessing the photoreceptor mosaic over drusen using adaptive optics and SD-OCT,” Ophthalmic Surg. Lasers Imaging 41(6Suppl), S104–S108 (2010). 10.3928/15428877-20101031-07 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Godara P., Wagner-Schuman M., Rha J., Connor T. B., Jr, Stepien K. E., Carroll J., “Imaging the photoreceptor mosaic with adaptive optics: beyond counting cones,” Adv. Exp. Med. Biol. 723, 451–458 (2012). 10.1007/978-1-4614-0631-0_57 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ooto S., Hangai M., Takayama K., Sakamoto A., Tsujikawa A., Oshima S., Inoue T., Yoshimura N., “High-resolution imaging of the photoreceptor layer in epiretinal membrane using adaptive optics scanning laser ophthalmoscopy,” Ophthalmology 118(5), 873–881 (2011). 10.1016/j.ophtha.2010.08.032 [DOI] [PubMed] [Google Scholar]
- 22.Boretsky A., Khan F., Burnett G., Hammer D. X., Ferguson R. D., van Kuijk F., Motamedi M., “In vivo imaging of photoreceptor disruption associated with age-related macular degeneration: a pilot study,” Lasers Surg. Med. 44(8), 603–610 (2012). 10.1002/lsm.22070 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hirsch J., Miller W. H., “Does cone positional disorder limit resolution?” J. Opt. Soc. Am. A 4(8), 1481–1492 (1987). 10.1364/JOSAA.4.001481 [DOI] [PubMed] [Google Scholar]
- 24.Curcio C. A., Sloan K. R., “Packing geometry of human cone photoreceptors: variation with eccentricity and evidence for local anisotropy,” Vis. Neurosci. 9(02), 169–180 (1992). 10.1017/S0952523800009639 [DOI] [PubMed] [Google Scholar]
- 25.Curcio C. A., Sloan K. R., Kalina R. E., Hendrickson A. E., “Human photoreceptor topography,” J. Comp. Neurol. 292(4), 497–523 (1990). 10.1002/cne.902920402 [DOI] [PubMed] [Google Scholar]
- 26.Curcio C. A., Sloan K. R., “Packing geometry of human cone photoreceptors: variation with eccentricity and evidence for local anisotropy,” Vis. Neurosci. 9(02), 169–180 (1992). 10.1017/S0952523800009639 [DOI] [PubMed] [Google Scholar]
- 27.Costa Lda. F., Bonci D. M., Saito C. A., Rocha F. A., Silveira L. C., Ventura D. F., “Voronoi analysis uncovers relationship between mosaics of normally placed and displaced amacrine cells in the thraira retina,” Neuroinformatics 5(1), 59–78 (2007). [DOI] [PubMed] [Google Scholar]
- 28.Shapiro M. B., Schein S. J., De Monasterio F. M., “Regularity and structure of the spatial pattern of blue cones of macaque retina,” J. Am. Stat. Assoc. 80(392), 803–812 (1985). 10.1080/01621459.1985.10478185 [DOI] [Google Scholar]
- 29.Kram Y. A., Mantey S., Corbo J. C., “Avian cone photoreceptors tile the retina as five independent, self-organizing mosaics,” PLoS ONE 5(2), e8992 (2010). 10.1371/journal.pone.0008992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Drasdo N., Fowler C. W., “Non-linear projection of the retinal image in a wide-angle schematic eye,” Br. J. Ophthalmol. 58(8), 709–714 (1974). 10.1136/bjo.58.8.709 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Coletta N. J., Watson T., “Effect of myopia on visual acuity measured with laser interference fringes,” Vision Res. 46(5), 636–651 (2006). 10.1016/j.visres.2005.05.025 [DOI] [PubMed] [Google Scholar]
- 32.Brostow W., Dussault J. P., Fox B. L., “Construction of Voronoi polyhedra,” J. Comput. Phys. 29(1), 81–92 (1978). 10.1016/0021-9991(78)90110-9 [DOI] [Google Scholar]
- 33.Rodieck R. W., “The density recovery profile: a method for the analysis of points in the plane applicable to retinal studies,” Vis. Neurosci. 6(02), 95–111 (1991). 10.1017/S095252380001049X [DOI] [PubMed] [Google Scholar]
- 34.Bland J. M., Altman D. G., “Statistical methods for assessing agreement between two methods of clinical measurement,” Lancet 327(8476), 307–310 (1986). 10.1016/S0140-6736(86)90837-8 [DOI] [PubMed] [Google Scholar]
- 35.Bland J. M., Altman D. G., “Measuring agreement in method comparison studies,” Stat. Methods Med. Res. 8(2), 135–160 (1999). 10.1191/096228099673819272 [DOI] [PubMed] [Google Scholar]
- 36.da Fontoura Costa L., Rocha F., Araújo de Lima S. M., “Characterizing polygonality in biological structures,” Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 73(1), 011913 (2006). 10.1103/PhysRevE.73.011913 [DOI] [PubMed] [Google Scholar]
- 37.Cook J. E., “Spatial properties of retinal mosaics: an empirical evaluation of some existing measures,” Vis. Neurosci. 13(01), 15–30 (1996). 10.1017/S0952523800007094 [DOI] [PubMed] [Google Scholar]
- 38.Wojtas D. H., Wu B., Ahnelt P. K., Bones P. J., Millane R. P., “Automated analysis of differential interference contrast microscopy images of the foveal cone mosaic,” J. Opt. Soc. Am. A 25(5), 1181–1189 (2008). 10.1364/JOSAA.25.001181 [DOI] [PubMed] [Google Scholar]
- 39.Pum D., Ahnelt P. K., Grasl M., “Iso-orientation areas in the foveal cone mosaic,” Vis. Neurosci. 5(06), 511–523 (1990). 10.1017/S0952523800000687 [DOI] [PubMed] [Google Scholar]