Abstract
Despite the general acceptance that functional specialization plays an important role in brain function, there is little consensus about its extent in the brain. We sought to advance the understanding of this question by employing a data-driven approach that capitalizes on the existence of large databases of neuroimaging data. We quantified the diversity of activation in brain regions as a way to characterize the degree of functional specialization. To do so, brain activations were classified in terms of task domains, such as vision, attention, and language, which determined a region’s functional fingerprint. We found that the degree of diversity varied considerably across the brain. We also quantified novel properties of regions and of networks that inform our understanding of several task-positive and task-negative networks described in the literature, including defining functional fingerprints for entire networks and measuring their functional assortativity, namely the degree to which they are composed of regions with similar functional fingerprints. Our results demonstrate that some brain networks exhibit strong assortativity, whereas other networks consist of relatively heterogeneous parts. In sum, rather than characterizing the contributions of individual brain regions using task-based functional attributions, we instead quantified their dispositional tendencies, and related those to each region’s affiliative properties in both task-positive and task-negative contexts.
Keywords: fMRI, functional specialization, structure-function, fingerprint, assortativity, diversity
Advancing our understanding of neuroscience centrally depends on characterizing how structure and function are related in the brain. The idea of functional specialization has led to major success stories in neuroscience, as exemplified by the elucidation of the organization of the visual system. Building on the findings of Hubel and Wiesel, work in the 1970s and 1980s described the visual system as comprising (at the time) 10–15 separate regions exhibiting a fair degree of specialization, including regions with selectivity for motion, color, and object processing (Zeki, 1993). The apparent success of the functional specialization framework is not confined to vision, but extends to other sensory modalities, as well as motor control and cognition, as examination of standard textbooks will attest. More recently, functional neuroimaging has also contributed to our understanding of functional specialization in the brain, and has led to some stark examples of purported selective processing tied to face processing and “place” processing, for example (Kanwisher, 2010).
Neuroscience also recognizes that brain regions are not islands but communicate with and influence each other. In particular, characterization of the connectivity of the prefrontal cortex with other parts of the brain helped solidify the idea that brain architecture might support “parallel distributed networks” (Goldman-Rakic, 1988). In the past decade, work in neuroimaging has also highlighted functional integration, and current techniques of network science are popular in characterizing regional interactions. Yet, given the observed degree of interaction, understanding functional specialization becomes considerably more complex. Acknowledging these issues in structure-function mappings, Passingham and colleagues (2002) proposed the idea of a functional fingerprint, namely a multidimensional representation of area function based on a small set of “dimensions”. In the case of the motor areas they investigated, they employed dimensions such as “motor coupling”, “movement/muscle”, and “proprioceptive/cutaneous”.
In the present study, we sought to advance the understanding of functional specialization by employing a data-driven approach that capitalizes on the existence of large databases that summarize human neuroimaging findings. This type of data has been used in a growing number of meta-analytic studies (Laird et al., 2011; Yarkoni et al., 2010). Like Passingham and colleagues (2002), we determined functional fingerprints as a way to characterize the roles of brain regions in a multidimensional manner. Related approaches have been described by Fox and collaborators in studying specific brain regions (Narayana et al., 2012; Robinson et al., 2012), as well as Poldrack and collaborators (2009) in performing whole-brain analysis. Here, functional activations were classified in terms of task domains as defined in the BrainMap database (Laird et al., 2005). The functional fingerprint for a given region thus represented both the set of domains that systematically engaged the region and the relative degree of engagement. From these fingerprints, we calculated a diversity index to further characterize the degree of functional diversity. A brain region with high diversity would be one engaged by tasks in many of these domains, whereas a low-diversity region would be engaged by a few domains. Furthermore, quantification of functional fingerprints allowed us to probe properties of brain networks, including the degree to which they are composed of regions with similar functional fingerprints. In general, the proposed approach permits a nuanced exploration of both local function and functional cooperation in networks, opening–we hope–new avenues for future work.
Materials and methods
Functional fingerprint and diversity analysis
To estimate functional fingerprints and diversity, we analyzed studies from the BrainMap database (Laird, et al., 2005). As there are no widely accepted ontologies of mental processes (Price & Friston, 2005; Yarkoni, et al., 2010), we employed the BrainMap taxonomy, which has undergone considerable refinement in the past decade (Fox et al., 2005; Fox & Lancaster, 2002; Laird, Lancaster, et al., 2009). Twenty task domains were considered, spanning perception, action, cognition, and emotion, an approach similar to that employed in recent studies (e.g., Laird et al., 2009; Smith et al., 2009). All studies considered involved healthy adults and used a within-subjects, whole-brain, univariate design. That is, brain activity during an experimental task was observed over the whole brain and compared voxelwise to activity observed in the same participant during a control task. Here, we use the term “observation” to refer to the pairing of a reported activation and a task domain. For example, for an experiment filed in the database under both “emotion” and “vision” domains (due to the task manipulation), each reported activation would count as two observations (one per domain) at its activation site.
A functional fingerprint was defined as a 20-dimensional vector, each dimension corresponding to a task domain. Each of the 20 values represented the proportion of local observations in the corresponding task domain (local number of observations divided by the number of observations over the entire database), normalized (i.e., all 20 values summed to 1). See Figure 1 for illustration of the process. The 20 domains employed were as follows (the term following the hyphen corresponds to the more general domain category): Execution-Action; Imagination-Action; Inhibition-Action; Motor Learning-Action; Observation-Action; Preparation-Action; Attention-Cognition; Working Memory-Cognition; Reasoning-Cognition; Memory-Cognition; Language Semantics-Cognition; Language Other-Cognition; Anger-Emotion; Disgust-Emotion; Fear-Emotion; Happiness-Emotion; Sadness-Emotion; Audition-Perception; Somesthesis-Perception; Vision-Perception.
Figure 1.
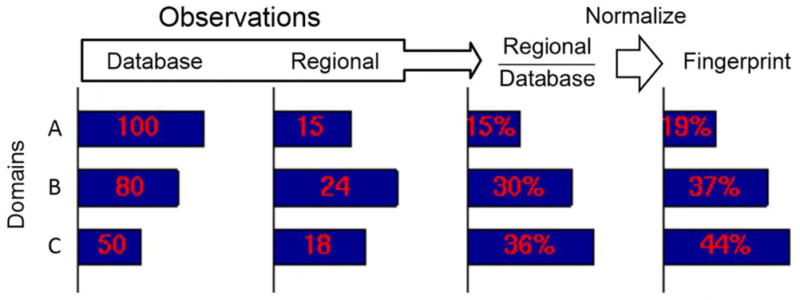
Determination of functional fingerprints. To illustrate the process, only three task domains are shown. The actual fingerprints used in the paper were 20-dimensional. The label “regional” refers to voxels in cortex (via the searchlight), subcortical regions, or networks. The final normalization step ensures that the fingerprint values all sum to 1.
For cortex, functional fingerprints were calculated in a voxelwise manner using a spherical searchlight. In other words, a spherical region was moved voxel by voxel along cortex, and the resulting fingerprint determined. Because of this, a fair amount of “smoothness” would be expected in the resulting maps, as indeed seen in Figure 3. Note, however, that despite the overlap between adjacent “searchlights”, the results also reveal many zones of considerable “contrast”. In other words, the method clearly demonstrates a landscape of “low”, “intermediate”, and “high” diversity brain regions. Voxel size was 3 mm isotropic. A probabilistic gray matter mask was applied to prevent consideration of activations that fell either outside of the brain or within white matter. Only activations with at least 25% probability of being in gray matter were retained (based on the Talairach atlas provided in the AFNI package; specifically, the TT_caez_gw_18 mask). Any activation observed within the searchlight was considered to contribute to the voxel’s functional fingerprint. The results shown here were obtained with a searchlight with a 10-mm radius. Various searchlight radii were investigated and yielded qualitatively similar results for radii ≥5 mm. For subcortical regions, all activations within the region (as defined via AFNI’s Talairach atlas) were considered. When considering the functional fingerprint of an entire network, the same procedures were applied after pooling the activations of the constituent regions.
Figure 3.
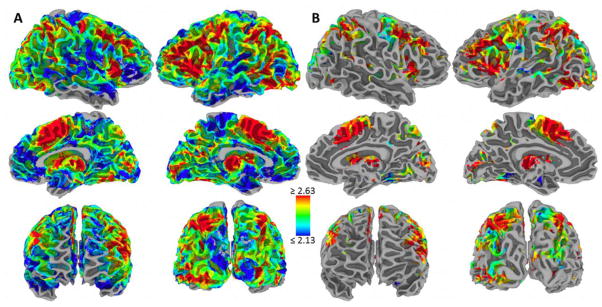
Functional diversity map. (A) Areas of higher diversity are shown in warm colors and areas of lower diversity are shown in cool colors (color bar represents Shannon entropy values). Locations without colors did not have enough studies for the estimation of diversity. (B) Same as in part A, but masked so as to show only the locations where diversity was estimated with greater confidence. This was the case when the variability in Shannon diversity was less than 10% (specifically, the highest density interval did not exceed .3).
For the network analyses (see Figures 5–7), we employed regions of interest (ROIs) from published papers describing several task- positive and task-negative networks (Tables 1 and S1). Initial ROI coordinates were transformed to Talairach space via the icbm2tal routine provided with the BrainMap database (Lancaster et al., 2007). Because having a sufficient number of activations is critical to producing reliable fingerprints, the initial seed coordinates of the ROIs for the networks in Table 1 were automatically shifted to nearby voxels (within 6 mm) that had the highest number of activations.
Figure 5.
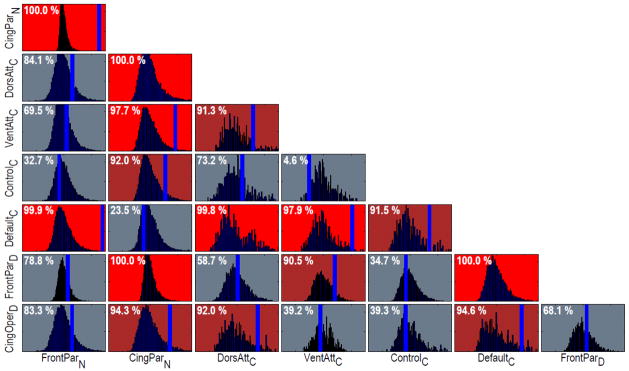
Network comparison. A multivariate comparison with permutation testing was used to compare pairs of networks. The distributions portray the null distribution of possible differences between each pair. The blue vertical bars indicate the observed difference, which is shown on top of each box in terms of its percentile relative to the null distribution (when not shown, the bar was located to the right of the displayed area). For illustration, comparisons with percentiles > 95% are shown in red and comparisons with percentiles > 90% are shown in magenta. For example: FrontoParietalN and CinguloParietalN were very different, DorsalAttentionC and VentralAttentionC were distinct but to a lesser extent, and CinguloParietalN and DefaultC were similar.
Figure 7.
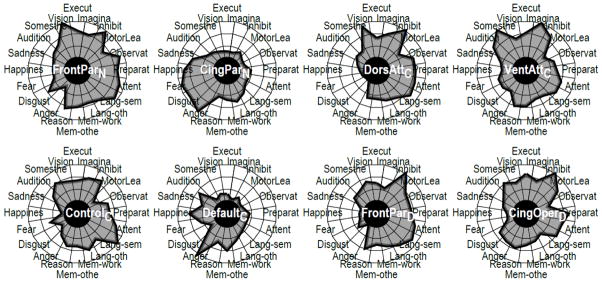
Network functional fingerprints.
Table 1.
Network definitions.
| Network | Abbreviation | Function/label |
|---|---|---|
| Fronto-parietal, seeded from the left intraparietal sulcus as in (Toro, et al., 2008) | FrontParN | Task-positive |
| Cingulo-parietal, seeded from the anterior cingulate cortex as in (Toro, et al., 2008) | CingParN | Task-negative |
| Dorsal Attention (Yeo, et al., 2011) | DorsAttC | Goal-directed attention |
| Ventral Attention (Yeo, et al., 2011) | VentAttC | Stimulus-driven attention |
| Control (Yeo, et al., 2011) | ControlC | Control |
| Default (Yeo, et al., 2011) | DefaultC | Default |
| Fronto-parietal (Dosenbach, et al., 2007) | FrontParD | Rapid adaptive control |
| Cingulo-opercular (Dosenbach, et al., 2007) | CingOperD | Stable set control |
The literature is replete with measures of diversity, particularly in biology and economics (e.g., Magurran, 2004). The Shannon diversity, H, of a fingerprint was defined as (Shannon, 1948)
where S = 20 was the number of task domains and pi corresponded to the ith domain proportion. As Shannon diversity is negatively biased (i.e., it tends to underestimate diversity), as proposed by Chao and Shen (2003), the correction term (S − 1)/(2n) was added to H, where n was the number of observations used in the determination of the fingerprint. This correction is suggested if n > S; thus, voxels with fewer than 21 observations were excluded from further analysis.
Functional fingerprint highest density interval
Functional fingerprints and respective diversity values were determined for all voxels/regions with more than 20 observations. Although this threshold allowed us to apply bias correction as described above, not all voxels/regions contained the same number of observations. Consequently, we determined the range of possible estimates of functional fingerprints and diversity via a bootstrapping procedure. For fingerprints, bootstrap resampling was performed on the set of observations defining the fingerprint. Specifically, the observed proportions for each task domain were used to estimate the population discrete probability distribution from which resampled fingerprints were obtained. A total of 10,000 resampled fingerprints were generated and bootstrapped diversity indices were generated directly from the bootstrapped functional profiles. For Figures 2 and 3B, the “highest density interval” was defined as the central 80% of the distribution (i.e., from the 10th to the 90th percentile). Note that we use the highest density interval as a way of summarizing the bootstrapped distribution (Krushke, 2010), and not in terms of making a yes/no decision, as in standard inferential statistics.
Figure 2.
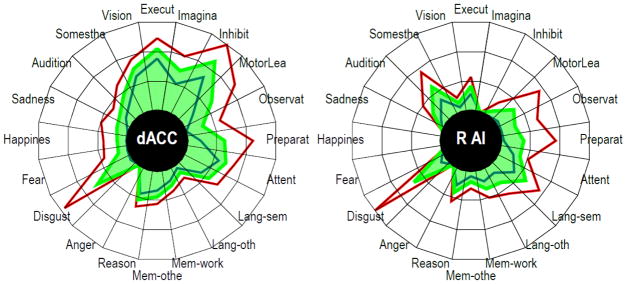
Diversity profiles. The polar plots illustrate the diversity profile of two brain regions, the dorsal anterior cingulate cortex (ACC) and the right anterior insula (AI). Each plot was scaled separately. Each vertex corresponds to one of the domains investigated. See Table S1 for coordinates from the original study by Dosenbach and collegues (2007) and Methods for full description of domains. The green line is the observed fingerprint. The red and blue lines indicate the upper and lower values of the estimates for each domain (see Methods). This range is provided to give an idea of variability, but should not be interpreted directly. Because of normalization (proportions sum to 1), a very high proportion in one domain will imply that other proportions need to be reduced; in other words, the values are not independent of each other.
Zero occurrence problem
Several research areas face the so-called “zero occurrence problem”, such that a sample may lack observations of a certain kind. In the present context, the problem is that domains with no reported observations for a given voxel/region would have an associated pi = 0, implying that bootstrapped fingerprints would never have observations in that domain. This is equivalent to placing absolute faith in the claim that the voxel/region is not involved in that domain because it was not observed in the sample. A common solution to this problem is the “smoothing” method proposed by Jelinek and Mercer (1980). The method adjusts the observed proportion pi for domain i by combining it with a “prior” proportion qi according to a weighted average:
For our “prior”, we used task proportions as observed in the initial database. In other words, the prior proportion was defined as if the entire brain were a region of interest. The observed proportions were adjusted by weights according to a sigmoidal function dependent on the number of observations n. We created a logistic equation ranging in value from .5 to 1, with inflection point at n = 40 observations (λ(40) = .75). The exponent was scaled so as to obtain λ values around .5 for ~20 observations and λ values near 1 for 80 observations:
In this way, for example, for n ≈ 20, p̂i was approximately the average of the proportion observed in the voxel/region and that observed in the entire database; when n = 40, p̂i, was ¾ based on the observed proportions and ¼ based on the database; and when n ≥ 80, p̂i was nearly 100% based on the observed proportion.
Comparing brain networks
To contrast brain networks to each other in terms of the functional fingerprints of the component regions, we employed a multivariate test based on “statistical energy” (Aslan & Zech, 2005). Briefly, statistical energy was used to evaluate whether two sets (i.e., networks) of fingerprints were drawn from the same parent distribution. As stated, the functional fingerprint for each constituent ROI within a network was represented as a 20-dimensional vector. The statistical energy metric compared distances of fingerprints within the same network relative to distances of fingerprints between different networks. Formally,
φXY = Statistical Energy between networks X and Y
PD(a,b) = physical distances between centers of ROIs “a” and “b”
where xi and yj corresponded to the functional fingerprint of the ith and jth member regions of networks X and Y, respectively. An overbar indicates the mean of a set (e.g., is the mean of set DXY). The function PD(a,b) was used to censor the comparison of regions that were too close to each other (here, r = 10 mm). This was particularly important to avoid comparing two ROIs from two networks that were effectively the “same” (e.g., a dorsolateral PFC ROI in network X that was very close to a dorsolateral PFC ROI in network Y). As suggested by Aslan and Zech (2005), the distance function R was a transform of the input Euclidean distance, here chosen as
where ε is simply a very small constant to avoid the d = 0 case (the precise value of ε has only a negligible effect on results).
The statistical energy provided a single point estimate of the multivariate distance between two networks. To characterize the magnitude of the distance, we employed a percentile permutation method. Specifically, we determined the distribution of possible distances by randomizing the labels of the regions. That is, the assignment of a given region to a specific network X or Y was randomized. By repeating this process 10,000 times, the “null” distributions shown in Figure 5 were generated. The final index of distance corresponded to the percentile of the actual observed distance within the permutation distribution (i.e., the null distribution).
Assortativity index
Assortativity is a concept that conveys the extent to which elements that group together are similar to one another (Crow and Felsenstein, 1968; Burley, 1983). A common measure of assortativity in network science is defined as the Pearson correlation coefficient of node degree (for a binary network, this amounts to the number of connections of a node) between pairs of linked nodes (Newman, 2002). An assortative graph is one in which, for instance, well-connected nodes link with well-connected nodes. Because we were interested in region function, we propose a different framework here. Specifically, a positively assortative network was one in which the distances within the network were smaller than distances between regions of that network and regions outside that network. In other words, functional fingerprints within an assortative network were relatively similar to each other and relatively dissimilar to fingerprints from other networks. We adapted the concept of statistical energy to create such an assortativity metric. Simply, the assortativity of a network X was defined as
where Dx and Dxy were defined as above. Network Y, in this case, was generated as the union of all networks in Table 1 with the exception of network X itself.
To characterize the magnitude of the assortativity index, we used the permutation method described in the previous section. Our assortativity measure was thus defined in a relative manner. To illustrate it here, we considered the 8 networks of Table 1. Thus, on average, 62 regions comprised the “comparison network” Y. More generally, the framework allows one to evaluate assortativity relative to different sets of regions: for example, a given network X relative to all other nodes in the brain; or a given task-negative network relative to a large group of task-positive networks; and so on. In cases in which the evaluations are based on specific hypotheses, the percentile index can be directly interpreted as a p value.
Task-based co-activation map
We wished to analyze the findings by Toro and colleagues (2008), who described a task-positive and a task-negative network based on an analysis of task-based co-activation of BrainMap studies. To avoid any circularity in the analysis process, we defined these networks here by seeding the same regions as Toro and colleagues, but by computing task-based co-activation from a separate collection of neuroimaging studies available as part of the Neurosynth database (Yarkoni et al., 2011). Neurosynth contained 144,680 activation peaks from 4,393 studies (as of the access date of January, 2012), after removing duplicates with BrainMap. A given voxel was considered active in any experiment where an activation peak was reported within 6 mm of its location. Co-activation was defined as the correlation between voxel pairs. Only significant correlations were considered (False Discovery Rate correction, q < .00005). Local co-activation peaks were identified via AFNI’s 3d Extrema command. Peaks were required to be at least 15 mm apart. Finally, we examined the neighborhoods of each peak, looking for peaks that were part of well-sized clusters. Local clusters were required to have a volume of at least 25 mm3.
Results
This section is organized as follows. First, we describe how functional fingerprints can be generated for voxels in cortex, as well as subcortical regions. Functional fingerprints are multidimensional representations that allow the description of cortical and subcortical areas in terms of their “functional diversity” –essentially, how broad is an area’s functional fingerprint? Second, we compute functional diversity across cortex and in subcortical regions, thus generating “diversity maps”. Third, we show how the idea of functional fingerprint can be used to refine the characterization and understanding of brain networks. To do so, we studied the extent to which regions within a network exhibit similar functional profiles. One possibility is that “like goes with like”, namely that regions comprising commonly identified networks share functional patterns. Alternatively, networks could be comprised by relatively heterogeneous regions that might functionally complement one another. Finally, we briefly illustrate how the multidimensional representation of a functional fingerprint can be extended straightforwardly to networks of brain regions.
Functional fingerprints and diversity
Initially, we sought to characterize the functional repertoire of sites across cortex and of subcortical regions. To do so, we computed functional fingerprints, which were defined as 20-dimensional vectors, each dimension corresponding to a task domain. Specifically, each dimension corresponded to the proportion of the total observed activations of the region that were due to tasks in the associated domain. These corresponded to “mental domains” (see Figure 2) adopted in the BrainMap database and chosen to represent a range of mental processes, including perception, action, emotion, and cognition (see Methods, and Figure 1). Fingerprints were calculated for every voxel in the brain by considering all voxels within a local neighborhood of the voxel (10-mm radius). Thus, all studies with peak coordinates within this “searchlight” contributed to the voxel’s functional fingerprint. The analysis was based on 2,603 neuroimaging experiments collectively reporting 21,553 locations of peak activation obtained from statistical contrasts (see Experimental Procedures). Figure 2 illustrates fingerprints from two sample regions.
Fingerprints exhibited a multitude of “shapes”, some encompassing more domains than others. To evaluate functional diversity of a fingerprint, we computed Shannon’s information index. The idea is that diversity (or entropy) can be measured in a way that is similar to the information contained in a code or message. Thus, the Shannon diversity, H, of a fingerprint captures “uncertainty” or“informational content” (see Methods). Diversity varied considerably across cortex (Figure 3), with “hot spots” apparent in dorsomedial prefrontal cortex (PFC), dorsolateral PFC, and anterior insula, among others; “cool spots” were observed in lateral temporal cortex, parts of posterior medial frontal/parietal cortex, and ventral medial PFC/orbitofrontal cortex, among others. Diversity of subcortical regions varied considerably, too (Figure 4). Other measures of diversity as well as other searchlight radii produced qualitatively similar results. In particular, maps based on the Simpson diversity index, which is also a popular measure, were very similar (thus not shown here).
Figure 4.
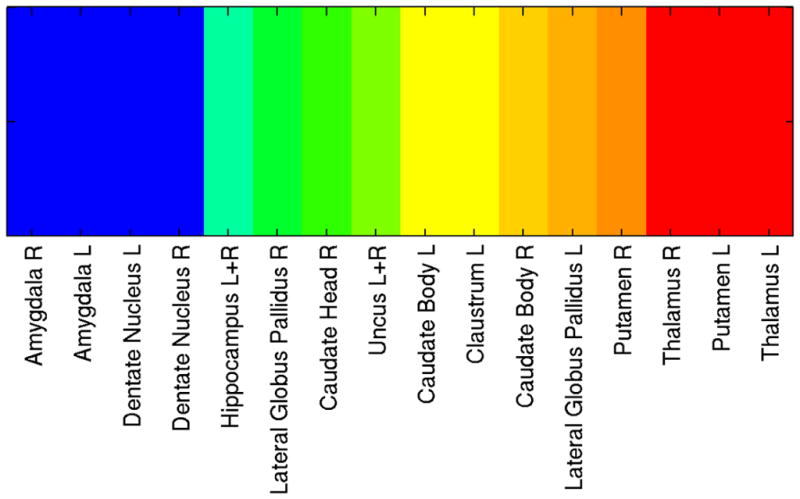
Subcortical diversity. Color scale and range as in Figure 3. For the dentate nucleus and hippocampus, the right and left hemispheres were pooled so as to yield enough observations for the determination of functional diversity. L, left; R, right.
Brain networks
In recent years, investigators have amassed considerable support for the functional significance of several brain networks, including general “task-positive” and “task-negative” networks, as well as more specific ones, such as “dorsal attention”, “ventral attention”, and “executive control” networks. Our next objective was to investigate the relationship between the functional repertoires of regions belonging to a given network. In other words, how homogeneous are the set of fingerprints of a specific network? Are fingerprints from network X more similar to each other than to those from network Y? Addressing this question is important because it may help advance our understanding of the structure of brain networks, and possibly reveal common principles of organization.
We investigated a sample of networks discussed in the literature (see Tables 1 and S1 for a complete list). Based on a meta-analysis of co-activation task data, Toro and colleagues (2008) identified a large task-positive network and a large task-negative network. We employed similar networks here but generated them based on co-activation results that employed a different database to avoid any potential circularity issues. We call these networks FrontoParietalN (seeded via the left intraparietal cortex) and CinguloParietalN (seeded via the rostral anterior cingulate cortex); the subscript “N” reminds the reader that they were obtained from Neurosynth data. Four networks, DorsalAttentionC, VentralAttentionC, ControlC, and DefaultC, were defined via resting-state data and labeled according to their purported function (Yeo et al., 2011). For these four networks, we considered only the six “core” regions listed by Yeo and colleagues, which summarize the key nodes of these networks (we use the subscript “C” to remind the reader of this convention). The two final networks were first proposed based on activations studies (Dosenbach et al., 2006) and correspond to a fronto-parietal “adjustcontrol” network (FrontoParietalD) and a cingulo-opercular “maintain task set” network(CinguloOpercularD). The coordinates employed here were defined via resting-state data (Dosenbach et al., 2007) (the subscript reminds the reader of the first author’s last name). It is important to emphasize that our goal was not to investigate a unique set of networks, but instead consider possibly related (or even closely related) networks defined by different research groups and approaches, including meta-analysis, resting-state, and task-based approaches. We believe this is important given current efforts to discover and characterize brain networks by employing diverse strategies. Naturally, future studies may target other networks.
In studying the set of fingerprints of the regions within a network, it is valuable to draw upon the concept of assortativity, a concept extensively utilized in network science (e.g., Christakis and Fowler, 2007). Assortativity refers to the tendency of “like to connect with like”. Are brain networks assortative? Networks defined via task-based co-activation history, by construction, would be expected to exhibit some assortativity–as co-activation means that the regions of the network were engaged by the same task. However, it is less clear that the same would be observed for networks defined via resting-state data. But, because resting-state connectivity may reflect, at least in part, the co-activation history of two regions, it is possible that resting-state networks display assortativity, too.
We investigated network assortativity in two ways. First, we asked if brain networks tend to be comprised of regions that are relatively cohesive in terms of functional fingerprints by “contrasting” networks (see Methods). Here, for illustration, we compared all networks in Table 1 to each other (Figure 5), although in some cases they may have constituted different “versions” of the same presumed network (such as CinguloParietalN and DefaultC, both versions of the “default” network; FrontoParietalN and FrontoParietalD, related versions of dorsal “task-positive” networks). Several network pairs were found to be fairly distinct (shown in red) or modestly distinct (shown in magenta). In Figure 5, each box shows the estimated null distribution and the observed difference between two networks (blue vertical line): the more extreme the observed difference relative to the null distribution, the greater the difference between two networks. To index the strength of this difference, the percentile of the observed difference was determined relative to the null distribution (which corresponded to the set of potential differences between networks that one would obtain “by chance”, namely without knowledge of the correct network affiliation of a given region). For instance, a clear difference was detected between FrontoParietalN vs. CinguloParietalN, task-positive and task-negative networks, respectively, defined via task co-activation data. Naturally, percentile values of the observed distance between two networks that are sufficiently large (say, > 95%) can be used to signal “significant” differences when this method is employed inferentially in the case of specific hypotheses (with correction for multiple comparisons when appropriate). In any event, the results demonstrate that common networks employed in the literature, in many instances, are distinct from one another under the task domain structure investigated here. The findings are also informative insofar as they illustrate that, based on the functional repertoire of their components’ nodes, some of the networks that have been distinguished from one another in the past are not strongly distinct. As an example, FrontoParietalD and CinguloOpercularD were not found to be strongly distinct (see Discussion).
The strategy of the previous paragraph was used to compare pairs of networks. But how does a specific network compare to a set of other networks? The method used previously can easily be generalized (see Methods). To illustrate the idea, we again considered the set of networks in Table 1 and compared each network to the set of all “other” networks (Figure 6). In this analysis, three of the networks exhibited robust positive assortativity (here taken as values above the 95th percentile): FrontoParietalN, DorsalAttentionC, and FrontoParietalD. Interestingly, one version of the task-negative network, CinguloParietalN, was somewhat dis-assortative (note the relatively “extreme” [low] percentile value). That is, its regions tended to be more dissimilar to each other that to those of other networks.
Figure 6.
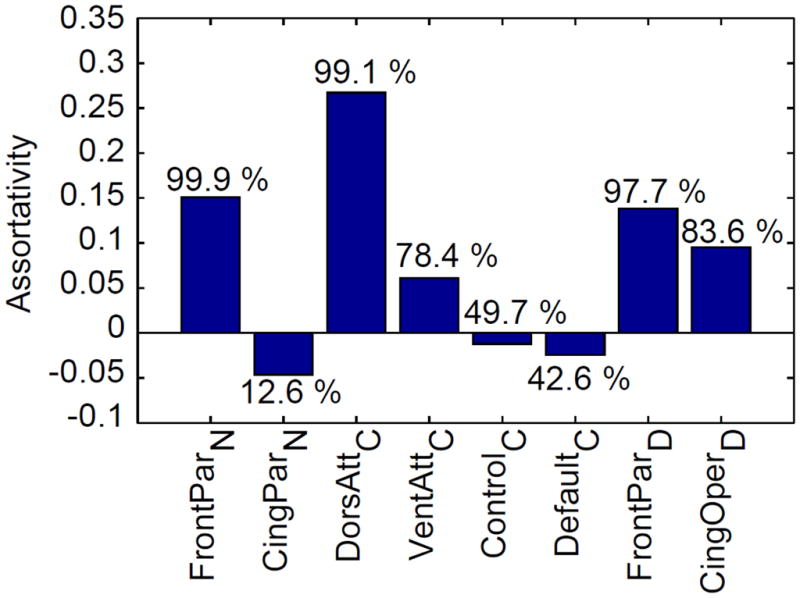
Network assortativity. Assortativity measures the extent to which functional fingerprints from regions of the same network are more similar to each other than to fingerprints from other networks. The percentile scores provide an indication of the degree of assortativity (or dis-assortativity in the case of CinguloParietalN)
Network functional fingerprints
The concept of functional fingerprint can be extended to networks, too. In this case, fingerprints can be computed by simultaneously considering all nodes within a network. Several definitions of network fingerprint are possible. Here, we illustrate the notion by using one that considered activations engaging any of the constituent regions of the network, a type of “union” operation (similar results were observed when a mean profile was computed). Figure 7 shows the functional fingerprints of the networks considered here. It is noteworthy, for instance, that the task-positive FrontoParietalN network and the task-negative CinguloParietalN network exhibited fairly complementary profiles, matching the intuition that these networks are at times “anti-correlated” (Fox et al., 2005).
Discussion
In the present study, we employed a data-driven approach to investigate the functional repertoire of brain regions based on a large set of functional MRI studies. The function of brain regions was characterized in a multidimensional manner via their functional fingerprint. To determine the diversity of fingerprints across the brain, Shannon’s information measure was computed in a voxelwise manner. The cohesiveness of functional fingerprints within networks discussed in the literature was assessed by studying network assortativity. Finally, we illustrated how the idea of functional fingerprints can be extended to brain networks themselves.
Great advances in neuroscience have been made by investigating the function of individual local circuits and computations. The continuation of these advances is guaranteed by the development of new genetic and molecular techniques, such as optogenetics. For instance, in a recent paper, Lin and colleagues isolated a functional circuit in the ventrolateral hypothalamus that was described as an “aggression locus” (Lin et al., 2011). A complementary approach investigates a large corpus of studies, all considered simultaneously. From the perspective adopted here, a brain region is characterized not by a specific function but via its functional fingerprint, a multidimensional vector spanning multiple task domains.
Our analysis revealed that functional diversity varied considerably across the brain. Regions with high diversity (top 10%) were found in parietal, frontal, and insular cortices, among others. Prominent regions of high diversity comprised the medial PFC, anterior insula, and parts of lateral parietal and lateral PFC (the latter two especially on the left hemisphere). The only high-diversity subcortical regions were the thalamus bilaterally and the left putamen. Regions with low diversity (bottom 10%) were also found across the brain, including lateral temporal cortex, right lateral inferior PFC, and ventral medial PFC/orbitofrontal cortex. Low-diversity subcortical regions comprised the dentate and amygdala (but see below for discussion of the latter).
To further study functional diversity in the brain, we investigated a sample of common networks discussed in the literature. Our objective was to characterize functional fingerprints both within and between networks. In network science, assortative networks are those in which highly connected nodes are themselves preferentially connected to high-degree nodes (Newman, 2002). Unfortunately, this type of description completely neglects node function. Here, we proposed an evaluation of assortativity that incorporates function by utilizing the information contained in functional fingerprints. These ideas were illustrated in a set of networks commonly identified in the human neuroimaging literature. Before discussing some of our findings, we discuss a more general point.
Brain networks have been investigated for many decades and different tools have been employed to characterize them. Networks offer distinctive interpretational challenges. For example, concluding a particularly lucid discussion of large-scale networks, Mesulam (1990, p. 610) commented: “Pathways that carry information from sensory receptors toward motor effectors have a self-explanatory purpose. But what about the luxuriant web that interlinks limbic, paralimbic, and association areas in almost every possible permutation?” As descriptions of networks have proliferated in the literature, we believe that additional tools are needed to understand and characterize them. Furthermore, the framework presented here may help in parsing some of the emerging results in the literature. For instance, what is the relationship between the “salience network” (Bressler and Menon, 2010) and the “ventral attention network” (Corbetta and Shulman, 2002)? How should we understand the relationship between the potentially multiple components of the “default mode network” (Andrews-Hanna et al., 2010)? And so on. The description of brain networks in terms of the functional repertoires of component regions lends itself to several potential analysis strategies. In particular, networks can be contrasted to each other in terms of their purported functions. The idea of contrasting networks can be extended via the assortativity measure introduced here–which summarizes the “functional distance” between pairs of regions within a network relative to the distance to other regions/networks of interest. In addition, automated tools such as those associated with the BrainMap database further expand the types of functional/behavioral analysis at the investigator’s disposal (Lancaster et al., 2012).
Our analyses revealed that three versions of fronto-parietal task-positive networks exhibited robust assortativity values (Figure 6). One of the fronto-parietal networks (FrontoParietalN), following the strategy used by Toro and colleagues (2008), was defined by “seeding” the left intraparietal sulcus and computing a task-based co-activation map. Although Toro and colleagues labeled the resulting co-activations as “fronto-parietal attention network”, the overall co-activation obtained by our analysis, like theirs, was extensive and included ventral occipital cortex, inferior parietal lobule, and cerebellum, in addition to more common fronto-parietal sites. Despite the broad set of regions, our analysis suggests that this network is assortative, that is, it is comprised of regions with similar functional tendencies.
For networks identified in the literature via task-based co-activation, functional similarity of component regions is perhaps relatively unsurprising. This is because, if regions frequently co-activate, they would be expected to be engaged by similar tasks, at least in part. It is thus instructive to consider the co-activation network obtained by seeding a site in the rostral anterior cingulate cortex (again, as done by Toro and colleagues (2008); CinguloParietalN). This seed co-activated with regions commonly interpreted as the “resting-state/default” network observed during the absence of overt tasks (regions included the posterior cingulate cortex and superior frontal cortex). Importantly, although this network was also defined via task-based co-activation data, it had a negative assortativity value. Indeed, the percentile score indicates that the network tended in fact to be dis-assortative, namely its regions exhibited functional profiles that tended to be more dissimilar to each other than to fingerprints of the other networks.
We further note that the dorsal attention “core” network (DorsalAttentionC) exhibited a high level of assortativity. Unlike the FrontoParietalN network, this network was based on resting-state data. Taken together with the findings of the preceding paragraphs, the results illustrate that assortativity is not a simple consequence of the method used to identify a network. For one, a network derived from task co-activation data can exhibit high or low assortativity; and networks can exhibit high assortativity when identified via task co-activation (FrontoParietalN) or resting-state data (DorsalAttentionC).
Of the four resting-state networks investigated by Yeo and colleagues (2011) that we studied here, as stated, only the dorsal attention was found to be robustly assortative. This finding is intriguing in light of the fact that the dorsal attention network is a “generalist” network that is engaged by a broad set of experimental tasks requiring effortful, attentive processing. In contrast, the ventral attention network is engaged by a more narrow set of conditions involving “reorienting”, as observed in exogenous attention tasks (Corbetta et al., 2008). Intriguingly, VentralAttentionC was found here to be mildly assortative. The Default network, another version of the “resting-state” network exhibited near- zero assortativity. This result, together with the negative assortativity of the CinguloParietalN network discussed above, is consistent with the notion that task-negative networks are relatively heterogeneous. Along these lines, recent work has suggested that task-negative networks can be subdivided in a number of ways (Andrews-Hanna et al., 2010). Finally, although Yeo and colleagues (2011) interpreted their Control resting state-based network as a “fronto-parietal control” network, the locations of the nodes make it difficult to interpret this network as a typical “control network” found in the literature. Because of this, it is difficult to comment on the observed assortativity value.
The determination of assortativity offers one way to characterize a network. As formalized here, assortativity captures the relationship between within-network fingerprint differences relative to between-network differences. The network comparison quantification displayed in Figure 5 provides a complementary illustration of assortativity by contrasting specific pairs of regions. Take, for instance, the comparison of the dorsal attention and ventral attention networks defined via resting-state data. The observed separation matches the existing knowledge that dorsal and ventral attention networks are largely functionally distinct (Corbetta & Shulman, 2002) (though note that the difference did not quite reach the 95% percentile). Contrast this situation to that of the fronto-parietal “adjust control” network (FrontalParietalD) and the cingulo-opercular “maintain task set” network (CinguloOpercularD) described by Dosenbach and colleagues (2008). Based on our results, these networks were only weakly distinct from each other (68th percentile when 50th would be expected if they completely “overlapped”). Finally, note that two versions of the “resting-state” network, were fairly similar, although these were defined via different methods, namely via resting-state data (DefaultC) and via co-activation data (CinguloParietalN).
It is noteworthy that our results do not align themselves cleanly with the suggestion of distinct fronto-parietal and cingulo-opercular networks by Dosenbach and colleagues (2008). Whereas we do not have a clear answer for this discrepancy, it is interesting to note that the two “core” nodes of the cingulo-operacular network as identified by Dosenbach and collegues were the dorsal ACC and the anterior insula. They note that these two regions “were set apart from other brain regions, in that they carried start-cue [the core feature of their fronto-parietal network] and sustained [the core feature of their cingulo-opercular network] activity across most of the tasks included in our analysis” (pp. 803–804). They also noted reliable error feedback activity in these regions. Thus, not only is there notable functional overlap between the two networks, but the core regions of the Cingulo-Opercular network have diverse functional repertoires (as shown in Figure 2). These might be some of the reasons that our analysis did not identify them as strongly different from one another.
Functional assortativity, the tendency of regions with similar functional fingerprints to be active in the same experimental conditions, appears to be a genuine feature of the functional organization of some brain networks, although the strength of the relationship clearly varies. Some of this variability will be driven by our ability to accurately measure the functional fingerprints of regions, but our results suggest that different levels of assortativity reflect different organizational strategies of brain networks. Some networks are generally comprised of functionally similar regions, while other networks make use of a relatively diverse collection of regions. Interactions between regions may play a role here, for instance, inhibition between functionally similar regions as they compete to influence behavioral responses.
We also showed how networks can be characterized in terms of a network functional fingerprint based on the domains of all of its constituent regions. More generally, network fingerprints allow one to quantify and visualize the mixture of individual elements that comprise the network. It is intriguing to consider the possibility that the profiles of those elements need not reflect the functional selectivity of the network as a whole. Thus, for instance, an attention network need not be built of purely attention-selective constituents. This much is suggested by our finding networks with low assortativity scores, but a more detailed investigation is left to future work. Specifically, it will be important to unravel how individual regions precisely contribute to a network’s functional repertoire. It will also be informative to characterize how alternative sets of task dimensions account for variance in responsivity and connectivity across the brain (Poldrack, et al., 2009).
We highlight that our approach allows us to characterize and quantify functional properties of regions and networks without attribution of a unique function. A growing number of studies are finding evidence for the activity of brain regions across multiple task domains (Anderson, 2010; Hanson & Schmidt, 2011; Poldrack, 2006). In many cases, this has led to the attribution of a generic function to the local circuit, such as “multi-modal integration” (Kurth et al., 2010). Our framework instead quantifies the dispositional tendencies of brain regions across multiple task categories, with the understanding that this fingerprint indexes the functional contributions of the region.
Our findings illustrate how data-driven approaches can contribute to unraveling functional organization in the brain. However, there are a number of considerations that need to be mentioned (see also Yarkoni et al., 2011). First, our methods do not take into account methodological study details, such as type of paradigm (blocked vs. event-related design) and type of statistical analysis (fixed vs. random effects). Second, the approach was demonstrated for one task domain structure only (namely, that adopted by BrainMap). Although empirically our findings appear fairly robust to changes in the task domains considered, an in-depth evaluation of the impact of specific mental ontologies (Poldrack et al., 2011; Poldrack, 2010) on the structure of functional organization in the brain awaits further investigation. Third, our methods cannot account for confirmation bias present in the literature. For example, researchers often associate amygdala activation with emotion and are thus more likely to publish results reflecting this association. This bias will increase the association between amygdala and emotion. Indeed, we attribute the rather low functional diversity of the amygdala to just such bias. Support for this possibility comes from considering several review papers that have highlighted the scope of amygdala mechanisms – ranging from attention, valuation, reward processing, to decision making (Pessoa, 2010). Whereas this is a limitation of the present approach, the problem is also present in other meta-analytic methods and, in fact, in individual studies as well.
In summary, our investigation allowed us to characterize the contributions of individual brain regions and networks of brain regions without using singular task- or role-bound functional attributions. We described a quantitative property of networks—functional assortativity—that can be useful in understanding the functional and compositional similarities and differences between networks.
Supplementary Material
Highlights.
Evaluated functional specialization via meta-analysis of human neuroimaging findings.
Established functional fingerprints to characterize the roles of brain regions.
Approach permits nuanced exploration of functional cooperation in networks.
Fingerprint diversity further characterizes the degree of functional diversity.
Established assortativity metric for the functional similarities between networks.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Anderson ML. Neural reuse: a fundamental organizational principle of the brain. Behavioral and Brain Sciences. 2010;33(4):245–266. doi: 10.1017/s0140525×10000853. discussion 266–313. [DOI] [PubMed] [Google Scholar]
- Andrews-Hanna JR, Reidler JS, Sepulcre J, Poulin R, Buckner RL. Functional-anatomic fractionation of the brain’s default network. Neuron. 2010;65(4):550–562. doi: 10.1016/j.neuron.2010.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aslan B, Zech G. New test for the multivariate two-sample problem based on the concept of minimum energy. Journal of Statistical Computation and Simulation. 2005;75(2):109–119. [Google Scholar]
- Bressler SL, Menon V. Large-scale brain networks in cognition: emerging methods and principles. Trends in cognitive sciences. 2010;14(6):277–290. doi: 10.1016/j.tics.2010.04.004. [DOI] [PubMed] [Google Scholar]
- Burley N. The meaning of assortative mating. Ethology and Sociobiology. 1983;4(4):191–203. [Google Scholar]
- Chao A, Shen TJ. Nonparametric estimation of Shannon’s index of diversity when there are unseen species in sample. Environmental and ecological statistics. 2003;10(4):429–443. [Google Scholar]
- Christakis NA, Fowler JH. The spread of obesity in a large social network over 32 years. New England journal of medicine. 2007;357(4):370–379. doi: 10.1056/NEJMsa066082. [DOI] [PubMed] [Google Scholar]
- Corbetta M, Patel G, Shulman GL. The reorienting system of the human brain: from environment to theory of mind. Neuron. 2008;58(3):306–324. doi: 10.1016/j.neuron.2008.04.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbetta M, Shulman GL. Control of goal-directed and stimulus-driven attention in the brain. Nature Reviews Neuroscience. 2002;3(3):201–215. doi: 10.1038/nrn755. [DOI] [PubMed] [Google Scholar]
- Crow James F, Felsenstein Joseph. The effect of assortative mating on the genetic composition of a population. Biodemography and Social Biology. 1968;15.2:85–97. [PubMed] [Google Scholar]
- Dosenbach NU, Fair DA, Cohen AL, Schlaggar BL, Petersen SE. A dual-networks architecture of top-down control. Trends in Cognitive Sciences. 2008;12(3):99–105. doi: 10.1016/j.tics.2008.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dosenbach NU, Fair DA, Miezin FM, Cohen AL, Wenger KK, Dosenbach RA, Petersen SE. Distinct brain networks for adaptive and stable task control in humans. Proceedings of the National Academy of Sciences USA. 2007;104(26):11073–11078. doi: 10.1073/pnas.0704320104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dosenbach NU, Visscher KM, Palmer ED, Miezin FM, Wenger KK, Kang HC, Petersen SE. A core system for the implementation of task sets. Neuron. 2006;50(5):799–812. doi: 10.1016/j.neuron.2006.04.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proceedings of the National Academy of Sciences of the United States of America. 2005;102(27):9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox PT, Laird AR, Fox SP, Fox PM, Uecker AM, Crank M, Lancaster JL. BrainMap taxonomy of experimental design: description and evaluation. [B] Human Brain Mapping. 2005;25(1):185–198. doi: 10.1002/hbm.20141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox PT, Lancaster JL. Opinion: Mapping context and content: the BrainMap model. Nature Reviews Neuroscience. 2002;3(4):319–321. doi: 10.1038/nrn789. [DOI] [PubMed] [Google Scholar]
- Goldman-Rakic PS. Topography of cognition: parallel distributed networks in primate association cortex. Annual Review of Neuroscience. 1988;11:137–156. doi: 10.1146/annurev.ne.11.030188.001033. [DOI] [PubMed] [Google Scholar]
- Hanson SJ, Schmidt A. High-resolution imaging of the fusiform face area (FFA) using multivariate non-linear classifiers shows diagnosticity for non-face categories. NeuroImage. 2011;54(2):1715–1734. doi: 10.1016/j.neuroimage.2010.08.028. [DOI] [PubMed] [Google Scholar]
- Jelinek F, Mercer R. Interpolated estimation of Markov source parameters from sparse data. In: Gelsema ES, Kanal LN, editors. Pattern Recognition in Practice. North Holland; Amsterdam: 1980. pp. 381–402. [Google Scholar]
- Kanwisher N. Functional specificity in the human brain: a window into the functional architecture of the mind. Proceedings of the National Academy of Sciences USA. 2010;107(25):11163–11170. doi: 10.1073/pnas.1005062107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krushke JK. Doing Bayesian Data Analysis: A Tutorial Introduction with R and BUGS. Oxford: Academic Press; 2010. [Google Scholar]
- Kurth F, Zilles K, Fox PT, Laird AR, Eickhoff SB. A link between the systems: functional differentiation and integration within the human insula revealed by meta-analysis. Brain Structure & Function. 2010;214(5–6):519–534. doi: 10.1007/s00429-010-0255-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird AR, Eickhoff SB, Fox PM, Uecker AM, Ray KL, Saenz JJ, Jr, Fox PT. The BrainMap strategy for standardization, sharing, and meta-analysis of neuroimaging data. BMC Research Notes. 2011;4:349. doi: 10.1186/1756-0500-4-349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird AR, Eickhoff SB, Li K, Robin DA, Glahn DC, Fox PT. Investigating the functional heterogeneity of the default mode network using coordinate-based meta-analytic modeling. Journal of Neuroscience. 2009;29(46):14496–14505. doi: 10.1523/jneurosci.4004-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird AR, Lancaster JL, Fox PT. BrainMap: the social evolution of a human brain mapping database. Neuroinformatics. 2005;3(1):65–78. doi: 10.1385/ni:3:1:065. [DOI] [PubMed] [Google Scholar]
- Laird AR, Lancaster JL, Fox PT. Lost in localization? The focus is meta-analysis. NeuroImage. 2009;48(1):18–20. doi: 10.1016/j.neuroimage.2009.06.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lancaster JL, Tordesillas-Gutierrez D, Martinez M, Salinas F, Evans A, Zilles K, Fox PT. Bias between MNI and Talairach coordinates analyzed using the ICBM-152 brain template. Human Brain Mapping. 2007;28(11):1194–1205. doi: 10.1002/hbm.20345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin D, Boyle MP, Dollar P, Lee H, Lein ES, Perona P, Anderson DJ. Functional identification of an aggression locus in the mouse hypothalamus. Nature. 2011;470(7333):221–226. doi: 10.1038/nature09736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magurran AE. Measuring Biological Diversity. Oxford: Blackwell; 2004. [DOI] [PubMed] [Google Scholar]
- Narayana S, Laird AR, Tandon N, Franklin C, Lancaster JL, Fox PT. Electrophysiological and functional connectivity of the human supplementary motor area. NeuroImage. 2012;62(1):250–265. doi: 10.1016/j.neuroimage.2012.04.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newman MEJ. Assortative Mixing in Networks. Physical Review Letters. 2002;89(20):208701. doi: 10.1103/PhysRevLett.89.208701. [DOI] [PubMed] [Google Scholar]
- Passingham RE, Stephan KE, Kotter R. The anatomical basis of functional localization in the cortex. Nature Reviews Neuroscience. 2002;3(8):606–616. doi: 10.1038/nrn893. [DOI] [PubMed] [Google Scholar]
- Pessoa L. Emotion and cognition and the amygdala: from “what is it?” to “what’s to be done?”. Neuropsychologia. 2010;48(12):3416. doi: 10.1016/j.neuropsychologia.2010.06.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poldrack RA. Can cognitive processes be inferred from neuroimaging data? Trends in Cognitive Sciences. 2006;10(2):59–63. doi: 10.1016/j.tics.2005.12.004. [DOI] [PubMed] [Google Scholar]
- Poldrack RA, Kittur A, Kalar D, Miller E, Seppa C, Gil Y, Bilder RM. The cognitive atlas: toward a knowledge foundation for cognitive neuroscience. Frontiers in Neuroinformatics. 2011;5:17. doi: 10.3389/fninf.2011.00017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poldrack RA. Mapping mental function to brain structure: how can cognitive neuroimaging succeed? Perspectives on Psychological Science. 2010;5(6):753–761. doi: 10.1177/1745691610388777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poldrack RA, Halchenko YO, Hanson SJ. Decoding the large-scale structure of brain function by classifying mental States across individuals. Psychological Science. 2009;20(11):1364–1372. doi: 10.1111/j.1467-9280.2009.02460.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price CJ, Friston KJ. Functional ontologies for cognition: The systematic definition of structure and function. Cognitive Neuropsychology. 2005;22(3/4):262–275. doi: 10.1080/02643290442000095. [DOI] [PubMed] [Google Scholar]
- Robinson JL, Laird AR, Glahn DC, Blangero J, Sanghera MK, Pessoa L, Fox PT. The functional connectivity of the human caudate: an application of meta-analytic connectivity modeling with behavioral filtering. NeuroImage. 2012;60(1):117–129. doi: 10.1016/j.neuroimage.2011.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shannon CE. A mathematical theory of communication. The Bell System Technical Journal. 1948;27:379–423. 623–656. [Google Scholar]
- Smith SM, Fox PT, Miller KL, Glahn DC, Fox PM, Mackay CE, Beckmann CF. Correspondence of the brain’s functional architecture during activation and rest. Proceedings of the National Academy of Sciences USA. 2009;106(31):13040–13045. doi: 10.1073/pnas.0905267106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toro R, Fox PT, Paus T. Functional coactivation map of the human brain. Cerebral Cortex. 2008;18(11):2553–2559. doi: 10.1093/cercor/bhn014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yarkoni T, Poldrack RA, Nichols TE, Van Essen DC, Wager TD. Large-scale automated synthesis of human functional neuroimaging data. Nature Methods. 2011;8(8):665–670. doi: 10.1038/nmeth.1635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yarkoni T, Poldrack RA, Van Essen DC, Wager TD. Cognitive neuroscience 2.0: building a cumulative science of human brain function. Trends in Cognitive Sciences. 2010;14(11):489–496. doi: 10.1016/j.tics.2010.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeo BT, Krienen FM, Sepulcre J, Sabuncu MR, Lashkari D, Hollinshead M, Buckner RL. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. Journal of Neurophysiology. 2011;106(3):1125–1165. doi: 10.1152/jn.00338.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeki S. A Vision of the Brain. Wiley-Blackwell; 1993. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


