Follow-the-leader cell migration requires biased cell-cell contact and local microenvironmental signals

Abstract

Directed cell migration often involves at least two types of cell motility that include multicellular streaming and chain migration. However, what is unclear is how cell contact dynamics and the distinct microenvironments through which cells travel influence the selection of one migratory mode or the other. The embryonic and highly invasive neural crest (NC) are an excellent model system to study this question since NC cells have been observed in vivo to display both of these types of cell motility. Here, we present data from tissue transplantation experiments in chick and in silico modeling that test our hypothesis that cell contact dynamics with each other and the microenvironment promote and sustain either multicellular stream or chain migration. We show that when premigratory cranial NC cells (at the pre-otic level) are transplanted into a more caudal region in the head (at the post-otic level), cells alter their characteristic stream behavior and migrate in chains. Similarly, post-otic NC cells migrate in streams after transplantation into the pre-otic hindbrain, suggesting that local microenvironmental signals dictate the mode of NC cell migration. Simulations of an agent based model (ABM) that integrates the NC cell behavioral data predict that chain migration critically depends on the interplay of biased cell-cell contact and local microenvironment signals. Together, this integrated modeling and experimental approach suggests new experiments and offers a powerful tool to examine mechanisms that underlie complex cell migration patterns.

1. Introduction

Long distance cell migration often involves directed cell movement and cell-cell contact that persists as cells travel to precise targets. When individual cells travel in a linear array and persist in cell contact, the behavior is termed follow-the-leader or chain migration. Chain migration has been observed in vivo and in tissue slice culture during embryo and adult morphogenesis and cancer (Lois, GarciaVerdugo et al. 1996; Kulesa and Fraser 1998; Young, Anderson et al. 2004; Kulesa, Kasemeier-Kulesa et al. 2006; Friedl and Alexander, 2011; Friedl et al., 2012). Another type of cell motility observed during long distance cell migration is multicellular streaming (Kulesa and Gammill et al., 2010; Bravo-Cordero et al., 2012; Friedl and Alexander, 2011). During multicellular streaming, cells move as a loosely connected subgroup but do not remain adhered to each other. Descriptions of the cellular features of long distance cell migration have advanced with better imaging techniques (Druckenbrod and Epstein 2007; Rupp and Kulesa 2007; Nishiyama, Uesaka et al. 2012; Zhang, Kim et al. 2012; Entenberg et al., 2013). However, the mechanisms that promote and sustain multicellular streaming or chain migration remain unclear.

The embryonic neural crest (NC) is an excellent model system to study mechanisms of cell migration since NC cells are accessible to in vivo observation and intervention in many vertebrate model systems. NC cells crawl through a variety of extracellular matrix (ECM) including regions rich in fibronectin and laminin (Newgreen and Thiery, 1980; Strachan and Condic, 2003; Brauer and Markwald, 1987). Evidence from chick and mouse time-lapse imaging has revealed that NC cell chain migration occurs in the cranial, trunk and intestinal subregions of the embryo (Kulesa and Fraser 1998; Young, Anderson et al. 2004; Kasemeier-Kulesa, Bradley et al. 2006; Druckenbrod and Epstein 2007; Rupp and Kulesa 2007; Nishiyama, Uesaka et al. 2012; Zhang, Kim et al. 2012). NC cells in nearly every vertebrate model system (chick, mouse, zebrafish, axolotl, turtle, snake) have also been observed to travel in multicellular streams (Reyes et al., 2010; Kulesa and Fraser, 1998; Schilling and Kimmel, 1994; Golding et al., 2000; Epperlein et al., 2007; Gilbert et al., 2007). Interestingly, Xenopus NC cells travel as a cohesive sheet, resembling a spreading epithelial tissue layer (DeSimone et al., 2005; Carmona-Fontaine et al., 2008). Together, this suggests that NC cells interpret various microenvironmental signals and adapt to move in a particular migratory mode. Although details of NC cell migration have provided a significant amount of data, a mechanistic explanation for this complex set of cell behaviors remains unclear.

The primary mechanisms of NC cell chain migration may involve a variety of spatiotemporal factors that include cell-ECM and cell-cell interactions. Consequently, it is difficult for experimental analyses alone to provide an integrative view of such a complex mechanism. The use of theoretical modeling techniques can help identify and isolate parameters critical for chain migration as well as generate predictions that can be used to direct future experiments. Much of the data available on chain migration are derived from descriptive non-quantitative measurements and observations. As a consequence, it is difficult to construct a continuous mathematical model of chain migration, and for that matter, multicellular streaming. Agent-based models (ABMs), where cells are treated as autonomous discrete decision-making agents, are an alternative computational tool for investigating complex phenomena that are out of reach of traditional experimental or mathematical methods (Alexrod, 1997).

In a previous work we developed two ABMs based on distinct mechanistic hypotheses of chain migration persistence (Wynn, Kulesa et al. 2012). The first, termed the ECM model, was based on the hypothesis that trailing cells follow a path of lesser resistance in the ECM formed by another cell. The second, termed the Contact model, was based on the hypothesis that cells use contact guidance from cell–neighbor interactions to follow other cells. Chain persistence, which we defined as the number of time steps agents moved as a chain during a simulation, was a sensitivity measure used to evaluate each mechanistic hypothesis under distinct parameter regimes. In that work, we started each ABM simulation with a fully formed chain consisting of eight cells (or agents) and systematically perturbed the chain by varying each parameter over a range of values. If the simulation operated in a parametrically sensitive region, we expected the chain pattern to break with small variations in parameter values. A primary conclusion from our previous work was that an interplay between cell-cell contact and the ECM is likely essential for chain migration persistence. However, the previous models were not designed to explicitly investigate the formation of chain migration and, therefore, were not concerned with emergent migratory behaviors.

In this study, we expand our ABM computational framework to examine the formation of chain migration in a large population of cells. We test the hypothesis that emergent chain formation relies on the interplay between cell-cell contact and the ECM. We use a hybrid form of our Contact and ECM models to explore parameter regimes that support chain formation. We focus on pre-and post-otic cranial NC cells that tend to migrate in streams or chains, respectively. We measure changes to NC cell migratory behaviors after transplantation from one microenvironment to another, and test model parameter conditions that predict the formation of NC cell chains or multicellular streams. By working at the interface of modeling and experiment, we show how model predictions offer mechanistic insights into the two types of cell motility.

2. Materials and Methods

Tissue Transplantation Experiments and Unbiased Designation of a Neural Crest Cell Migratory Stream or Chain

The neural tube lumen of donor chick embryos (8-10 somites) was co-injected with a plasmid construct in the form of a control EGFP empty vector named pMES (a kind gift from Cathy Krull, University of Michigan) at 2.5ug/ul and the lipophilic dye DiI (D-282, Molecular Probes). Embryos were allowed to recover for one hour at 38°C prior to the dorsal one-third of the neural tube (NT) being dissected at the rhombomere 4 (r4) and r7 axial levels. The labeled NC cells were transplanted into host embryos (8-10 somites) in which the dorsal one-third of r4 or r7 had been unilaterally ablated. All combinations of homotopic and heterotopic transplants between r4 and r7 were performed. Host embryos containing transplanted tissue were reincubated for 18 hours at 38°C. The embryos were then fixed in 4% paraformaldehyde and static 3D confocal z-stacks of the fluorescently labeled embryos were collected (LSM Pascal, Carl Zeiss Microimaging).

So as to not introduce bias into the analysis of chain or stream formation in the tissue transplantation experiments, we measured the mean fluorescence intensity within rectangular rows of a grid overlaid on images of each embryo. First, a fluorescence image of the area of interest was opened in MetaMorph (Molecular Devices, LLC; Sunnyvale, CA). A rectangular grid was created that covered the medio-to-lateral width and antero-to-posterior length of the NC cell migratory pathways. Each row of the grid was 10 um wide and included as many rows as needed to cover the anterior-to-posterior length of the transplant. The mean fluorescence intensity was then calculated for each rectangular row and exported to an Excel spreadsheet. The mean fluorescence intensity versus each rectangular row position was plotted in a bar graph. An example of such an analysis using a DiI-labeled embryo is shown in Fig. 2.

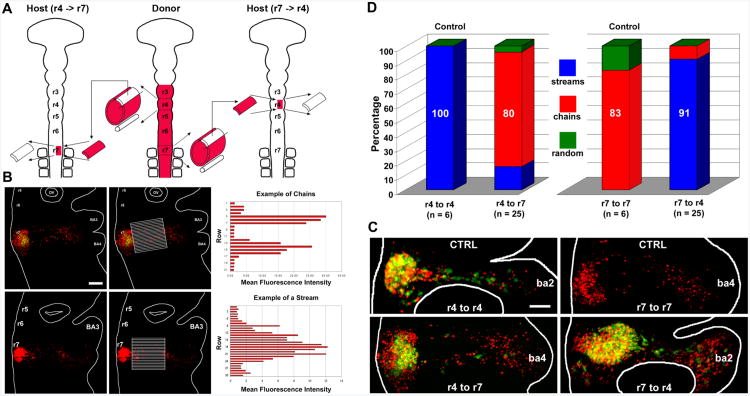
Figure 2. Tissue transplantation experiments highlight microenvironmental influence on neural crest cell migratory behaviors.

(A) A schematic diagram representing the pre-migratory NC cell transplant experiments. (B) An example of the measurements of the mean fluorescence intensity within rectangular rows of a grid overlaid on images of each embryo. (C) Typical stream-forming r4 NC cells migrate in chain-like arrays when transplanted into r7 axial levels, whereas r7 NC cells convert to stream migration when placed into r4 hosts. (D) Bar graph depicting results of transplantation of r4 pre-migratory NC into either r4 or r7 host sites, and r7 pre-migratory NC cell transplantation into the r7 or r4 host site. The scalebar in (B) is 100um and in (C) is 50um.

Agent-Based Model Formulation

In an ABM, a system is modeled as a collection of autonomous agents that execute behaviors according to a set of rules defined from empirical or experimental observations. Live cell imaging experiments have identified distinct cellular phenotypes associated with NC cell migration consisting of hairy leading cells and more polarized trailing cells (Teddy and Kulesa 2004). The objective of our computational ABM framework is to simplify experimentally observed cell behaviors into a model capable of providing insight into the underlying mechanisms driving follow-the-leader chain migration. As a consequence, our ABM uses two types of agents: Leaders and Followers. The rule algorithm used each time an agent was randomly selected for update is summarized in the Fig. 5. We did not explicitly define a timescale because the interval between successive time steps in an ABM has arbitrary physical units. However, we assume a time step is roughly on the order of hours because the models simulated coarse-grained movements in increments of 30 um. In addition, a number of experimental observations were used to formulate the rules controlling agent movement. These are discussed in detail in a previous model of chain migration using simulations and perturbation analysis of two ABMs (which considered the interactions between 8 cells): the Contact model and the ECM model (Wynn, Kulesa et al. 2012).

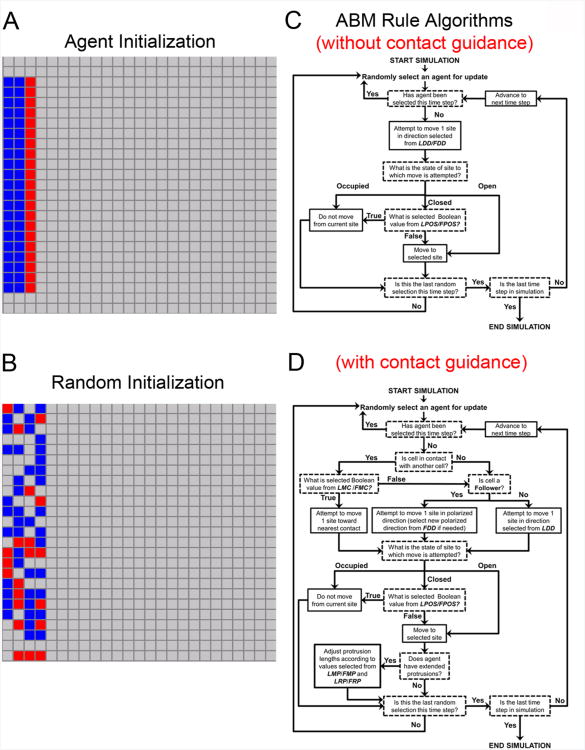
Figure 5. Agent initialization in simulations, standard ABM rule algorithm.

(A) All simulations started with 63 agents (21 Leaders and 42 Followers). Agent initialization at the start of simulations in Fig. 3. When contact-guidance was included in Fig. 4A,B, initialization was the same except red Leader agents started with extended protrusions. (B) All simulations were repeated with a random initialization. The random example given is a representative example of a random initialization. We ran parallel random initializations to confirm the results we observed were not associated to artifacts related to the ordered initialization. (C) This is the algorithm executed for the simulations run in Fig. 3. (D) This is the algorithm executed for the simulations run in Fig. 4.

Determination of the factors affecting the assembly of chain migration and formation of streams

We ran simulations under a variety of parameter regimes and evaluated whether agents in the simulations formed migratory streams (similar to the migration typically observed in the r4 NC cell migratory stream, Fig. 1C) or chains (similar to the migration typically observed lateral to r7, Fig. 1D). We used dynamic simulation results, which we compared to experimental observations from time-lapse confocal microscopy data of NC cell migration (Kulesa and Fraser 1998; Teddy and Kulesa 2004; Rupp and Kulesa 2007).

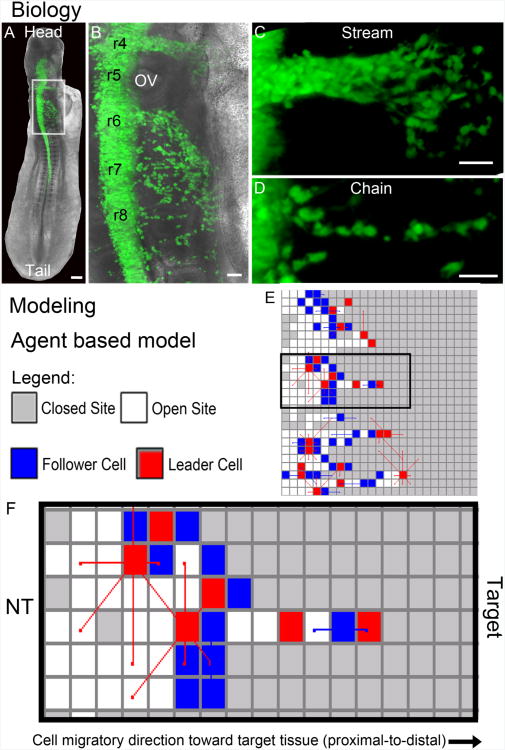
Figure 1. Neural crest cell migratory pattern in development and computational model schematic.

(A-D) Biology. (A) Typical fluorescently labeled chick embryo at approximately 20 somites with labeled neural crest cells (pMES-GFP; green) emigrating from the dorsal neural tube and migrating throughout the head and post-otic region. (B) A close-up view of the box in (A) showing the rhombomere (r) segments r4-r8 and variation in neural crest cell migratory behaviors in (C) streams and (D) chains. (E-F) Modeling. (E) The agent based model framework with an example simulation, including the (F) expanded view of the middle simulation with the neural tube (left) and target (right) and cell migratory direction pointing from left to right. The scalebars are (A) 100um, (B-D) 50um.

3. Results

The NC cell migratory pattern is diverse and occurs throughout the embryo (Fig. 1A,B) such that in some regions, NC cells migrate in multicellular streams (Fig. 1B,C) or in chains (Fig. 1B,D). We performed NC tissue transplantation experiments to examine the effect of the local microenvironment on cell migratory behaviors and, subsequently, ran computer simulations using an agent based modeling framework (Fig. 1E,F) to generate hypotheses related to the mechanisms likely driving experimental observations.

3.1 Dependence on the local microenvironment to form and sustain NC cell chain migration

To determine whether the collective NC cell chain migratory behavior is cell autonomous or due to environmental factors lateral to the neural tube, pre-migratory NC cells were transplanted between two distinct hindbrain axial levels (Fig. 2). Pre-migratory NC cells from the rhombomere (r) r4 and r7 axial levels were selected because of the differences in cell migratory behaviors observed at those levels. NC cells from r4 migrate as individuals within dense streams. In contrast, NC cells from r7 migrate collectively, forming linear chain-like arrays. DiI-labeled r4 NC cells that were isochronically transplanted into unlabeled host embryos, in which the dorsal one-third of r7 was unilaterally removed, adopted chain-like migration in 80% of the transplanted embryos (Fig. 2; n = 20/25). As a control, r4 NC cells were transplanted into host embryos in which the dorsal one-third of r4 was unilaterally ablated (Fig. 2). In all cases, the r4 NC cells formed dense migratory streams (100%, n = 4/4).

In a similar role reversal, DiI-labeled r7 NC cells, placed into host embryos in which the dorsal one-third of r4 was unilaterally ablated, mimicked stream migration in 91% of the transplanted embryos (Fig. 2; n = 20/22). The transplanted r7 NC cells coalesced into dense migratory streams. The r7 to r7 control transplants yielded 83% chain-like arrays (Fig. 2; n = 5/6). Overall in only two cases, the cell migration pattern could not be classified as either chain or stream and therefore was designated as random (Fig. 2). All embryos were evaluated at 18 hours post-transplantation to allow for the migration of transplanted NC cells to the branchial arches.

3.2 Agent based simulations of NC cell migration

We began all simulations with agents initialized (either ordered or randomized; Fig. 5) in 3 vertical columns on the proximal edge of the grid, to represent cells exiting the neural tube (Fig. 1E). The direction of migration was proximal to distal in all simulations and a representative example of a model simulation is presented in Fig. 1E,F. Parameter definitions are provided in Table 1. Parameter values used in each parameter regime simulated are summarized in Figs. 3,4. All simulations were repeated with a random initialization (Fig. 5) to ensure results were not artifacts of the initial agent configuration used (Fig. 5). We also used an alternate leader initialization (see Supplemental Fig. 1) where agents were initialized with only 10 leaders, organized in a central cluster at the start of simulations. We did not observe substantial differences in simulations under any of these initialization conditions.

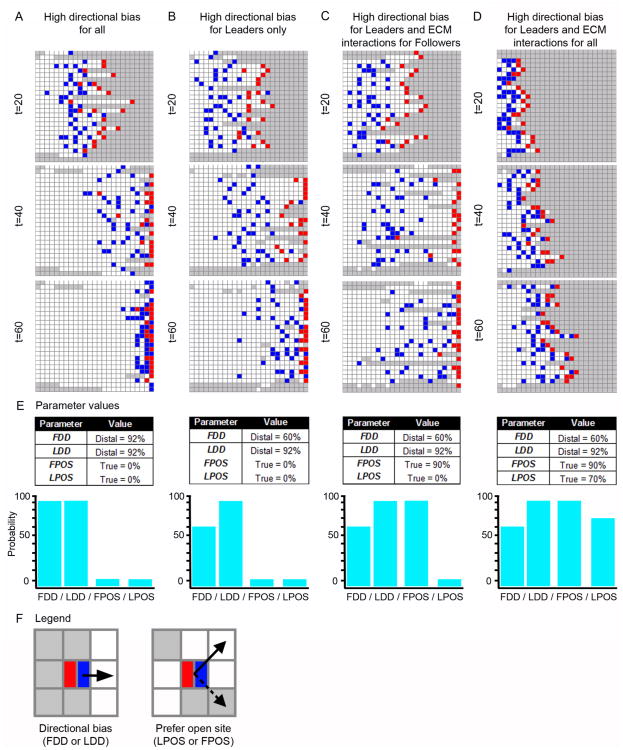
Figure 3. Simulation results for high directional bias and ECM interactions.

Simulated NC cell migratory behaviors under four distinct parameter regimes, shown at time (t) = 20, 40, and 60. (A) A representative simulation under a parameter regime with high directional bias for all agents (see (E) for parameter values). (B) A representative simulation under a parameter regime with high Leader directional bias and moderate Follower directional bias (see (E)). (C) A representative simulation under a parameter regime with high Leader directional bias, moderate Follower directional bias, and Followers with a strong preference to only move in OPEN sites on the grid (see (E) for parameter values). (D) A representative simulation under a parameter regime with high Leader directional bias, moderate Follower directional bias, Followers with a strong preference to only move to OPEN sites on the grid, and Leaders with a moderate preference to only to OPEN sites on the grid (see (E) for parameter values). (E) Parameter values and graphs of the parameter values for each of the scenarios from (A-D). (F) Legend, with an example of directional bias (FDD/LDD) and preference for an open site (LPOS/FPOS). Agents: Leader (red) and Follower (blue).

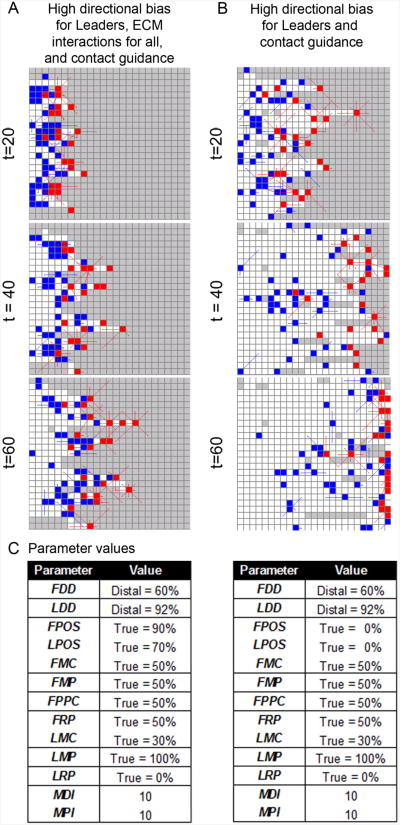
Figure 4. Simulation results with agents guided by cell-cell contact.

Simulated NC cells under two distinct parameter regimes that allow contact guidance are shown at time (t) = 20, 40, and 60. (A) A representative simulation using the same parameter regime as (Fig. 3D) except now with contact guidance (see (C) for parameter values. (B) A representative simulation using the same parameter values as (A) except now Leader and Follower agents no longer have a preference for moving to OPEN sites (i.e., LPOS and FPOS are 0%). (C) Parameter values for (A-B). Lines extending from agents are protrusions that can extend and retract according to probabilty distributions, random timers, and contact with other agents. Agents: Leader (red) and Follower (blue).

3.2.1 Simulations with high agent directional bias

First, we ran simulations where the only parameters influencing agent movement were the Follower Directionality Distribution (FDD) and Leader Directionality Distribution (LDD) probability distributions. These parameters control the directionality of Follower and Leader agents, respectively (Fig. 3E,F; Table 1). The objective of this parameter regime was to test whether a strong chemical signal contributes to the formation of a multicellular stream or of chain migration. The FDD and LDD parameters were set so that all agents had a 92% probability to select the target direction (distal). As expected, high directional bias in all agents induced the agents to move rapidly across the grid, with almost all agents at the distal edge within 60 time steps (Fig. 3A). The large number of white OPEN sites at t = 60 indicates that agents explored the entire grid as they traveled to the distal edge (Fig. 3A). CLOSED sites, in contrast, are colored grey on the grid to indicate that no agent has occupied that site. At t = 20, some agents appear to travel in close proximity to one another (Fig. 3A). However, in general, the collective population moves as a multicellular stream rather than in chains (Fig. 3A). These results suggest that high directional bias alone is not enough to drive chain migration in a population of cells. Next, we ran simulations where the Follower directionality (FDD-Distal) was decreased to 60% but the Leader directionality (LDD-Distal) remained very high at 92% (Fig 3B,E). Multicellular stream migratory behavior was observed under these conditions with Followers taking longer to reach the target than in the previous simulation scenario (compare Fig. 3B with Fig. 3A).

3.2.2 Simulations with high agent directional bias and ECM interactions

Because chain migration involves follow-the-leader behavior, we are interested in identifying the conditions that encourage Follower agents to track Leader agents. To examine this, we kept LDD-Distal = 92% and FDD-Distal = 60% but modulated the likelihood that Follower agents will move into CLOSED sites (Fig. 3E,F). The Follower Prefers Open Sites (FPOS) and Leader Prefers Open Sites (LPOS) probability distribution parameters control how likely Follower and Leader agents, respectively, are to prefer an OPEN site over a CLOSED site when moving. For example, a low FPOS value simulates the condition where a Follower is willing to explore unopened areas of the ECM (biologically this may be because the cell exerts the physical energy to do so or because it expresses enough ECM degrading enzymes to do so). In our ABM, the only condition that allows an agent to move to a CLOSED site on the grid (i.e., one that has not been visited by another agent) is when FALSE is returned from the FPOS or LPOS probability distributions, respectively, for Followers or Leaders. In the simulations run in Fig. 3A,B, agents were not inhibited in any way from moving into an OPEN or CLOSED site on the grid.

In Fig. 3C, however, FPOS was increased from 0% to 90%. In other words, Follower agents now had only a 10% probability to move into unexplored regions of the ECM. Under these conditions, a similar stream pattern is observed (Fig. 3C) when compared to the previous result (Fig. 3B). Next, LPOS was increased from 0% to 70% (Fig. 3D) so that Leader agents now had a 30% probability to move into unexplored regions of the ECM. We set LPOS to 70% and FPOS to 90% because we assumed the hairy Leader phenotype is more exploratory than the Follower phenotype and, therefore, more willing to expand into new regions of the ECM. In these simulations the migration of the agents appear to be far less stream-like (compare Fig. 3D with Fig. 3A,B,C). In addition, in a few cases, agents can be seen to move in close proximity to one another, suggestive of chain migration (Fig. 3D).

3.2.3 Simulations with agents guided by cell-cell contact

To examine the ability of cell-contact to promote chain formation, we ran simulations where, in addition to directional bias and ECM interactions, cell-cell contact influenced agent movement decisions (Fig. 4; the lines extending from agents are protrusions). We used the parameter regime of Fig. 3D, but added the ability for agents to protrude and retract protrusions as well as the ability to move toward (or away from) contact with another agent (Fig. 4C). That is, ten additional parameters were added to the model to control this behavior (Fig. 4C). For example, the probability that a Leader agent maintained contact with other agents when it moved was controlled by the Leader Move Toward Contact (LMC) probability distribution (Table 1). This type of cell contact maintenance is assumed to be a critical component of NC cell-cell contact because NC cells have been observed extending or retracting their filopodia in shortlived cell contacts which are frequently broken and re-established (Kulesa and Fraser 1998; Kasemeier-Kulesa, Kulesa et al. 2005; Teddy and Kulesa, 2004). In addition, filopodia have been observed to shorten or lengthen between linked cells as one cell moves away or towards the neighboring cell (Teddy and Kulesa 2004). Based on these observations, we believe the majority of agents in Fig. 4, t=60, for example, are in configurations representative of the chain migratory phenotype.

The selection of the parameter values used for the contact parameters (Fig. 4C) was informed by our previously published model of contact guidance (which considered only 8 cells in a single chain, rather than the entire population of cells) (Wynn, Kulesa et al. 2012). In simulations run under this parameter regime, agents can be seen to migrate in linear arrays (Fig. 4A) that are representative of stereotypic NC cell chains observed experimentally in the chick embryo (Kulesa and Fraser 1998; Kasemeier-Kulesa, Kulesa et al. 2005). In this migratory mode, a few hairy lead cells are followed by polarized trailing cells with filopodial contacts between cells (Rupp and Kulesa, 2007). To probe whether contact guidance alone can promote chain migration, we ran simulations using the parameter regime of Fig. 4A, but with FPOS and LPOS set to 0% (Fig. 4B). This new parameter regime effectively eliminated the interactions with the ECM from the model, which produced a migration pattern that is more stream-like than the simulations run under the parameter regime of Fig. 4A. From these simulations, we conclude that cell-cell contact alone is not sufficient to promote chain migration and instead, an interplay between interactions with the ECM, microenvironmental signals, and cell contact are likely to be mutually involved in the promotion of chain migration.

4. Discussion

We examined the mechanistic basis of two types of cell motility, chain migration and multicellular streaming. We used the embryonic neural crest (NC) as a model system and integrated biological data into an ABM computational framework that simulated cell migratory behaviors under various parameter conditions. The NC model had the advantage that cells travel in streams or chains depending on their axial level of origin and microenvironments they encounter in the embryo (Kulesa and Fraser, 1998). This allowed us to study changes in cell migratory mode when NC cells were removed and transplanted to different axial levels. Our in silico experiments tested whether cell-ECM and/or cell-cell interactions lead to one migratory mode versus the other and determined parameter conditions for which a NC cell's migratory mode was more likely to be in chains or streams. This integrated experimental and theoretical approach yielded several key insights and suggested three new experiments.

First, model simulations predict that a microenvironment which is difficult to move through (that is, does not promote cells to move into un-populated regions) produces chain migration (Fig. 3D). This suggests that chain migration is more likely to form when NC cells have difficulty in degrading the ECM. In this scenario, lead NC cells would not fan out at the migratory front to explore multiple directions; as observed in ovo (Kulesa and Fraser, 1998; Teddy and Kulesa, 2004), and follower NC cells would tend to track behind leaders to form a chain-like array. Interestingly, gene expression profiling of a typical cranial NC cell migratory stream in chick has shown that lead cells express significantly higher levels of matrix degrading enzymes including metalloproteases (MMPs) and the ADAMs family of molecules (McLennan et al., 2012). Whether post-otic NC cells that migrate in chains are less efficient at breaking down the ECM is unknown, but could be addressed by gene profiling. Thus, the model suggests a testable experiment that alterations in NC cell proteolytic activity should promote chain migration by loss of function.

Second, model simulations also predict that differences in microenvironmental properties promote either chain or stream migration. That is, the NC cell microenvironment of the head may be more permissive to NC cell exploration than the post-otic region, and supportive of stream migration. A testable experiment would be to alter the pre-otic microenvironment to make it less permissive by microinjection of either collagen or fibronectin and increase the density of the ECM. We would then expect pre-otic NC cells to switch to a chain migratory mode.

A direct example of how our model predicts the emergence of chain migration is evident in experiments where the embryonic NC cell microenvironment has been altered. During embryogenesis, NC cell free zones exist adjacent to the odd-numbered rhombomere (r) segments in the head (Farlie et al., 1999). Chick NC cells have been observed to enter these regions, but cells will quickly reverse direction to rejoin neighboring streams or collapse filopodia and stop (Kulesa and Fraser, 1998). When receptor tyrosine kinase ErbB4 signaling is disrupted, mouse cranial NC cells deviate from a stereotypical stream and enter into the NC cell free zones, displaying chain migration as they invade (Golding et al., 2000). Since wildtype and mutant NC cells both migrate in a pattern consistent with the host microenvironment (deviating only when transplanted into the mutant embryos) these data support the interpretation that in ErbB4-deficient mice the cranial NC cell free zones become less inhibitory but still not completely permissive to NC cell invasion (Golding et al., 2000). Thus, our model simulations that show a less permissive microenvironment supports chain migration appear to predict this outcome.

Third, our model predicts that variation in cell adhesion parameters leads to either chain or stream migration. That is, model simulations included parameters for cell contact persistence and cell movement in response to contact, either towards or away from the contact (Fig. 4). When cell-cell contact positively influenced cell movement towards each other and maintenance of contacts, the model predicted that cells form chains (Fig. 4A). Our previous perturbation of RhoA signaling (regulating the ability of a cell to efficiently retract its protrusions) in post-otic NC cells did show that NC cell chains would not form and persist and cells were more likely to move as a multicellular stream (Rupp and Kulesa, 2007). Model predictions also suggested that loss of function of cell-cell adhesion in the post-otic NC, that typically form chains, would cause cells to be less sticky and form a multicellular stream. Thus, it will be interesting to follow up on this prediction with functional testing of a few of the candidate cell adhesion genes known to be expressed in migrating NC cells.

5. Perspectives

Follow-the-leader chain migration and multicellular streams may appear simplistic cell migratory modes, yet such phenomena are often associated with surprisingly complex cell dynamics. By integrating theory and experiment, we examined the differences between chain migration and multicellular streaming, two distinct cell migratory modes. We identified model parameter regimes under which chain migration was more likely to form and suggest 3 experiments to further test our hypothesis. Our ABM modeling framework provides a foundation on which to further study the mechanistic details of chain versus stream migration, using the embryonic NC model, and probe which individual parameters are most important for promoting chain formation in a systematic way, using a to be developed quantitative sensitivity measure. We plan to pursue this quantitative analyses in future work. Also, it may be possible to perform a quantitative sensitivity analysis of our ABM with a partial rank correlation coefficient for each parameter as described by Marino and colleagues (Marino, Hogue et al., 2008). Lastly, our modeling framework is generalizable to other cell migratory systems that exhibit multicellular streaming or chain migration (Lois et al., 1996; Young et al., 2004; Landman et al., 2011; 2012; Wanner and Price, 2013), and provides a powerful means to directly integrate biological data and test hypothetical mechanisms of cell migration.

Supplementary Material

PB448694suppdata.pdf

Supplemental Figure 1. Alternate Leader initialization. Simulations where agents were initialized with only 10 Leaders, organized in a central cluster at the start. (A) A representative simulation under this initialization condition using the ECM based parameter regime of Fig. 3A is presented. Agents migrate in a stream migratory mode. (B) A representative simulation under this initialization condition using the hybrid Contact-ECM based parameter regime of Fig. 4A. Agents migrate in a chain migratory mode.

Appendix.

Each simulation was run on a 25 × 25 grid with non-cyclic boundaries and initialized with 63 agents (21 Leader agents in red and 42 Follower agents in blue), which were arranged as depicted in (Fig. 5). The dynamics of NC cell migration from the dorsal neural tube are still unclear. As a result, we elected to arrange agents at the start of simulations with Leader agents positioned in front of Follower agents. To test that our results were not artifacts of this initial condition, we repeated all simulations using a randomized initialization (Fig. 5) and compared the qualitative results of each. Up to 14 model parameters (defined in Table 1) controlled how agents moved on the grid. All simulations ran for 80 time steps and were used to evaluate emergent migratory behaviors with respect to chain and stream migration. The ABM framework was implemented in Java.

A1. Agent based model implementation

The ABM used in this work was an extension of a simulation framework previously developed (Wynn, Kulesa et al. 2012). While the ABM presented here differs from the two ABMs previously published in a number of ways, both works leverage a similar set of assumptions related to NC cell behavior, which were derived from in vivo observations of NC cells in chick embryos using live cell microscopy. These assumptions have been previously discussed in (Wynn, Kulesa et al. 2012) and summarized in table form in that work.

An important difference between the current ABM and our previous ABM models is that the objective of the current ABM is the identification of parameter regimes that contribute to the emergent formation of chain migration behavior in a population of cells. The previous ABMs developed were interested only in identifying parameters most important for persistence of a single follow-the leader chain where persistence was defined as “the number of time steps agents traveled as a chain during a simulation.” The previous models included 8 agents arranged as a single chain at the start of the simulation. The current works initializes 63 agents in an ordered or random configuration (Fig. 5).

A2. Limiting Simulation Artifacts

Simulation Grid

Agents were allowed to move within a Moore neighborhood (Deutsch and Dormann 2005), which permits movement in 8 directions. Grima and Schnell (Grima and Schnell 2006) compared discrete simulation dynamics on a lattice where 4 directions were permitted (a Von Neumann neighborhood), on a lattice where 8 directions were permitted (a Moore neighborhood), and off-lattice simulations where directional movement was not constrained. Their results revealed no significant difference in agent dynamics between a Moore neighborhood and off-lattice simulations when the agent density was low. The agent density of the current model is 10% of the total grid, thus we assume that directional constraints do not significantly contribute to artifacts in our ABM.

Random Update Order

A random selection with replacement yields results considered to produce fewer artifacts in discrete simulation dynamics compared to when agents are selected in a deterministic manner (Schönfisch and de Roos 1999). Agent updates in the ABM were performed each time step where 63 agents were randomly selected with replacement. In this scheme, not every agent was updated every time step. If an agent was selected more than once in a given time step, it would only be updated once that time step.

A3. Simulation Algorithm and Update Rules

Each time an agent was selected for update, a series of rules would execute (so long as that agent had not already been updated in the current time step). A summary of the ABM rule algorithms used are presented in Fig. 5.

A4. Parameters and Timers

There were two main types of parameters used the model: discrete numeric values and probability distributions. Probability distribution parameters were of two main types: directional or Boolean. Each time a probability distribution parameter was queried in a simulation, a value was returned according to probability distribution assigned to that parameter at the start of the simulation. For example, the Leader Move Toward Contact (LMC) parameter used in the algorithm summarized in Fig. 5 controlled the probability that a Leader agent will respond to protrusion based contact with another agent by moving in its direction. If LMC = 0%, then Leaders would never perform this behavior because FALSE would always be returned. If LMC = 50%, then Leaders would perform this behavior approximately half the time.

Timers (also referred to as clocks), which were unique to each agent in the simulation, were used to stochastically control the following behavior in the contact guidance algorithm summarized in Fig. 5: (1) when an agent would extend or retract its protrusions and (2) when a Follower agent would select a new polarized direction. Followers are a polarized phenotype in this version of the model and we assume they have a preference to move in the direction of polarization until they received a signal to alter directions. We do not, however, know the precise signals that would trigger a polarization change. In the model, we assumed that either contact with another agent or an internal signal (generated when the agents polarized direction timer reached zero) were capable of inducing this change in a Follower agent. All timers were randomly set at the start of a simulation (and reset when they reached zero) by randomly choosing a value between zero and a ceiling set by the Maximum Direction Interval (MDI) and the Maximum Protrusion Interval (MPI), respectively, for a Follower's polarized direction clock and for any agent's protrusion clock.

A5. Parameter regimes tested

Six distinct parameter regimes were examined

In Fig. 3A, the ABM is tested under parameter conditions where agents have a high directional bias to move toward the target. We assume this bias is related to a chemoattractant in the environment. FDD and LDD are the most important probability distributions in this parameter set. The other probability distributions are set so that the effect of the parameters do not influence agent movement decisions. Fig. 3E lists the parameter values used for these simulations conditions.

In Fig. 3B, the ABM is tested under parameter conditions where Leader agents have a high directional bias to move toward the target and Follower agents have a reduced directional bias. Fig. 3E lists the parameter values used for these simulations conditions.

In Fig. 3C, the ABM is tested under parameter conditions where Leader agents have a high directional bias to move toward the target and Follower agents have a reduced directional bias. In addition, Follower agents have a reduced ability to forge into CLOSED sites on the grid. Fig. 3E lists the parameter values used for these simulations conditions.

In Fig. 3D, the ABM is tested under parameter conditions identical to Fig. 3C, except now the Leader agents also have a reduced ability to forge into CLOSED sites (LPOS = 70%), though this ability is not as diminished as that of Follower agents (FPOS = 90%) (Fig. 3E).

In Fig. 4A, the ABM is tested under parameter conditions identical to Fig. 3D, except now all agents can extend and retract protrustions and make movement decisions related to protrusion driven contact with other agents. The rule algorithm used in this simulation is summarized in Fig. 5. The contact parameter values (FMC, LMC, FMP, LMP, FRP, LRP, and FPPC) were set so that both types of agents were influenced by contact with other agents. Leader agent parameters (LMC, LMP, and LRP) were set so that Leaders were more likely than Follower agents to make movement decisions based on contact. This is in agreement with results reported in our previously published Contact Model of cell chain migration persistence (Wynn, Kulesa et al. 2012).

Finally, in Fig. 4B, the ABM is tested under parameter conditions identical to Fig. 4B, except now Leader and Follower agents no longer have a preference for moving to OPEN sites (i.e., LPOS and FPOS = 0%) and are, thus, unconstrained in their ECM related movements. Parameter values for the simulations in Fig. 4 are summarized in Fig. 4C.